Reinterpretation of Multi-Stage Methods for Stiff Systems: A Comprehensive Review on Current Perspectives and Recommendations
Abstract
1. Introduction
2. Preliminary
2.1. Methods
2.2. Simplified Newton Iteration and Eigenvalue Decomposition Method
3. Numerical Comparison
3.1. Simple Linear ODE
3.2. Nonlinear Stiff ODE System: Multi-Mode Problem
3.3. Linear PDE—Heat Equation
3.4. Nonlinear PDE: Medical Akzo Nobel Problem
3.5. Kepler Problem
4. Conclusions and Further Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Atkinson, K.E. Divisions of numerical methods for ordinary differential equations. In An Introduction to Numerical Analysis, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1989; pp. 333–462. [Google Scholar]
- Gear, C.W. Numerical Initial Value Problems in Ordinary Differential Equations; Prentice Hall: Upper Saddle River, NJ, USA, 1971. [Google Scholar]
- Hairer, E.; Nørsett, S.P.; Wanner, G. Solving Ordinary Differential Equations I: Nonstiff Problems; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1996. [Google Scholar]
- Kirchgraber, U. Multi-step Method Are Essentially One-step Methods. Numer. Math. 1986, 48, 85–90. [Google Scholar] [CrossRef]
- Alolyan, I.; Simos, T.E. New multiple stages multistep method with best possible phase properties for second order initial/boundary value problems. J. Math. Chem. 2019, 57, 834–857. [Google Scholar] [CrossRef]
- Berg, D.B.; Simos, T.E. Three stages symmetric six-step method with eliminated phase-lag and its derivatives for the solution of the Schrödinger equation. J. Chem. Phys. 2017, 55, 1213–1235. [Google Scholar] [CrossRef]
- Butcher, J.C. Numerical Analysis of Ordinary Differential Equations: Runge–Kutta and General Linear Methods; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1987. [Google Scholar]
- Enright, W.; Hull, T.; Lindberg, B. Comparing numerical methods for stiff systems of O.D.E.’s. BIT Numer. Math. 1975, 15, 10–48. [Google Scholar] [CrossRef]
- Fathoni, M.F.; Wuryandari, A.I. Comparison between Euler, Heun, Runge–Kutta and Adams-Bashforth Moulton integration methods in the particle dynamic simulation. In Proceedings of the 2015 4th International Conference on Interactive Digital Media (ICIDM), Bandung, Indonesia, 1–5 December 2015; pp. 1–7. [Google Scholar]
- Liniger, W.; Willoughby, R.A. Efficient Integration Methods for Stiff Systems of Ordinary Differential Equations. SIAM J. Numer. Anal. 1970, 7, 47–66. [Google Scholar] [CrossRef]
- Song, X. Parallel Multi-stage and Multi-step Method in ODEs. J. Comput. Math. 2000, 18, 157–164. [Google Scholar]
- Barrio1, M.; Burrage, K.; Burrage, P. Stochastic linear multistep methods for the simulation of chemical kinetics. J. Chem. Phys. 2015, 142, 064101. [Google Scholar] [CrossRef]
- Bu, S. New construction of higher-order local continuous platforms for Error Correction Methods. J. Appl. Anal. Comput. 2016, 6, 443–462. [Google Scholar]
- Cohen, E.B. Analysis of a Class of Multi-stage, Multi-step Runge Kutta Methods. Comput. Math. Appl. 1994, 27, 103–116. [Google Scholar] [CrossRef][Green Version]
- Guo, L.; Zeng, F.; Turner, I.; Burrage, K.; Karniadakis, G.E. Efficient multistep methods for tempered fractional calculus: Algorithms and Simulations. SIAM J. Sci. Comput. 2019, 41, A2510–A2535. [Google Scholar] [CrossRef]
- Han, T.M.; Han, Y. Solving Implicit Equations Arising from Adams-Moulton Methods. BIT Numer. Math. 2002, 42, 336–350. [Google Scholar] [CrossRef]
- Ghawadri, N.; Senu, N.; Fawzi, F.A.; Ismail, F.; Ibrahim, Z.B. Explicit Integrator of Runge–Kutta Type for Direct Solution of u(4) = f(x, u, ú, ü). Symmetry 2019, 10, 246. [Google Scholar] [CrossRef]
- Kim, S.D.; Kwon, J.; Piao, X.; Kim, P. A Chebyshev Collocation Method for Stiff Initial Value Problems and Its Stability. Kyungpook Math. J. 2011, 51, 435–456. [Google Scholar] [CrossRef]
- Kim, P.; Piao, X.; Jung, W.; Bu, S. A new approach to estimating a numerical solution in the error embedded correction framework. Adv. Differ. Equ. 2018, 68, 1–21. [Google Scholar] [CrossRef]
- Kim, P.; Kim, J.; Jung, W.; Bu, S. An Error Embedded Method Based on Generalized Chebyshev Polynomials. J. Comput. Phys. 2016, 306, 55–72. [Google Scholar] [CrossRef]
- Piao, X.; Bu, S.; Kim, D.; Kim, P. An embedded formula of the Chebyshev collocation method for stiff problems. J. Comput. Phys. 2017, 351, 376–391. [Google Scholar] [CrossRef]
- Xia, K.; Cong, Y.; Sun, G. Symplectic Runge–Kutta methods of high order based on W-transformation. J. Appl. Anal. Comput. 2001, 3, 1185–1199. [Google Scholar]
- Marin, M. Effect of microtemperatures for micropolar thermoelastic bodies. Struct. Eng. Mech. 2017, 61, 381–387. [Google Scholar] [CrossRef]
- Marin, M.; Abd-Alla, A.; Raducanu, D.; Abo-Dahab, S. Structural Continuous Dependence in Micropolar Porous Bodies. Comput. Mater. Contin. 2015, 45, 107–125. [Google Scholar]
- Bak, S. High-order characteristic-tracking strategy for simulation of a nonlinear advection-diffusion equations. Numer. Methods Partial Differ. Equ. 2019, 35, 1756–1776. [Google Scholar] [CrossRef]
- Dahlquist, G. Numerical integration of ordinary differential equations. Math. Scand. 1956, 4, 33–50. [Google Scholar] [CrossRef]
- Pazner, W.; Persson, P. Stage-parallel fully implicit Runge–Kutta solvers for discontinuous Galerkin fluid simulationse. J. Comput. Phys. 2017, 335, 700–717. [Google Scholar] [CrossRef]
- Piao, X.; Kim, P.; Kim, D. One-step L (α)-stable temporal integration for the backward semi-Lagrangian method and its application in guiding center problems. J. Comput. Phys. 2018, 366, 327–340. [Google Scholar] [CrossRef]
- Prothero, A.; Robinson, A. On the Stability and Accuracy of One-step Methods for Solving Stiff Systems of Ordinary Differential Equations. Math. Comput. 1974, 28, 145–162. [Google Scholar] [CrossRef]
- Bickart, T.A. An Efficient Solution Process for Implicit Runge–Kutta Methods. SIAM J. Numer. Anal. 1977, 14, 1022–1027. [Google Scholar] [CrossRef]
- Butcher, J.C. On the Implementation of Implicit Runge–Kutta Methods. BIT Numer. Math. 1976, 16, 237–240. [Google Scholar] [CrossRef]
- Curtiss, C.F.; Hirschfelder, J.O. Integration of Stiff Equations. Proc. Natl. Acad. Sci. USA 1952, 38, 235–243. [Google Scholar] [CrossRef]
- Jeon, Y.; Bu, S.; Bak, S. A comparison of multi-Step and multi-stage methods. Int. J. Circuits Signal Process. 2017, 11, 250–253. [Google Scholar]
- Coper, G.J.; Butcher, J.C. An iteration method for implicit Runge–Kutta methods. IMA J. Numer. Anal. 1983, 3, 127–140. [Google Scholar] [CrossRef]
- Cooper, G.J.; Vignesvaran, R. Some methods for the implementation of implicit Runge–Kutta methods. J. Comput. Appl. Math. 1993, 45, 213–225. [Google Scholar] [CrossRef]
- Frank, R.; Ueberhuber, C.W. Iterated defect correction for the efficient solution of stiff systems of ordinary differential equations. BIT Numer. Math. 1977, 17, 146–159. [Google Scholar] [CrossRef]
- Gonzalez-Pinto, S.; Rojas-Bello, R. Speeding up Newton-type iterations for stiff problems. J. Comput. Appl. Math. 2005, 181, 266–279. [Google Scholar] [CrossRef][Green Version]
- Hairer, E.; Wanner, G. Solving Ordinary Differential Equations II: Stiff and Differential Algebraic Problems; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1996. [Google Scholar]
- Huang, J.; Jia, J.; Minion, M.L. Accelerating the convergence of spectral deferred correction methods. J. Comput. Phys. 2006, 214, 633–656. [Google Scholar] [CrossRef]
- Süli, E.; Mayers, D.F. An Introduction to Numerical Analysis; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Dahlquist, G. A special stability problem for linear multistep methods. BIT Numer. Math. 1963, 3, 27–43. [Google Scholar] [CrossRef]
- Shampine, L.F.; Reichelt, M.W. The MATLAB ODE Suite. SIAM J. Sci. Comput. 1997, 18, 1–22. [Google Scholar] [CrossRef]
- Mazzia, F.; Magherini, C. Test Set for Initial Value Problem Solvers; Department of Mathematics, University of Bari: Bari, Italy, 2008. [Google Scholar]
- Brugnano, L.; Iavernaro, F.; Trigiante, D. Energy- and Quadratic Invariants–Preserving Integrators Based upon Gauss Collocation Formulae. SIAM J. Numer. Anal. 2012, 50, 2897–2916. [Google Scholar] [CrossRef]
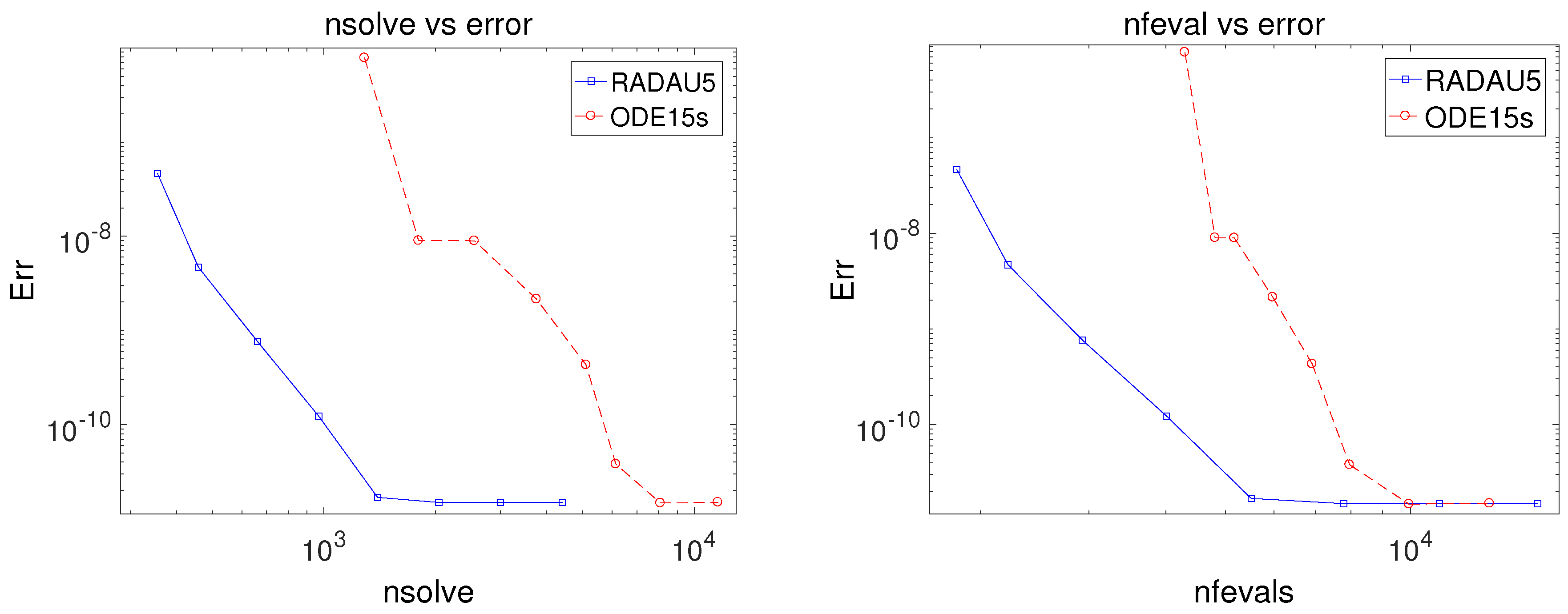
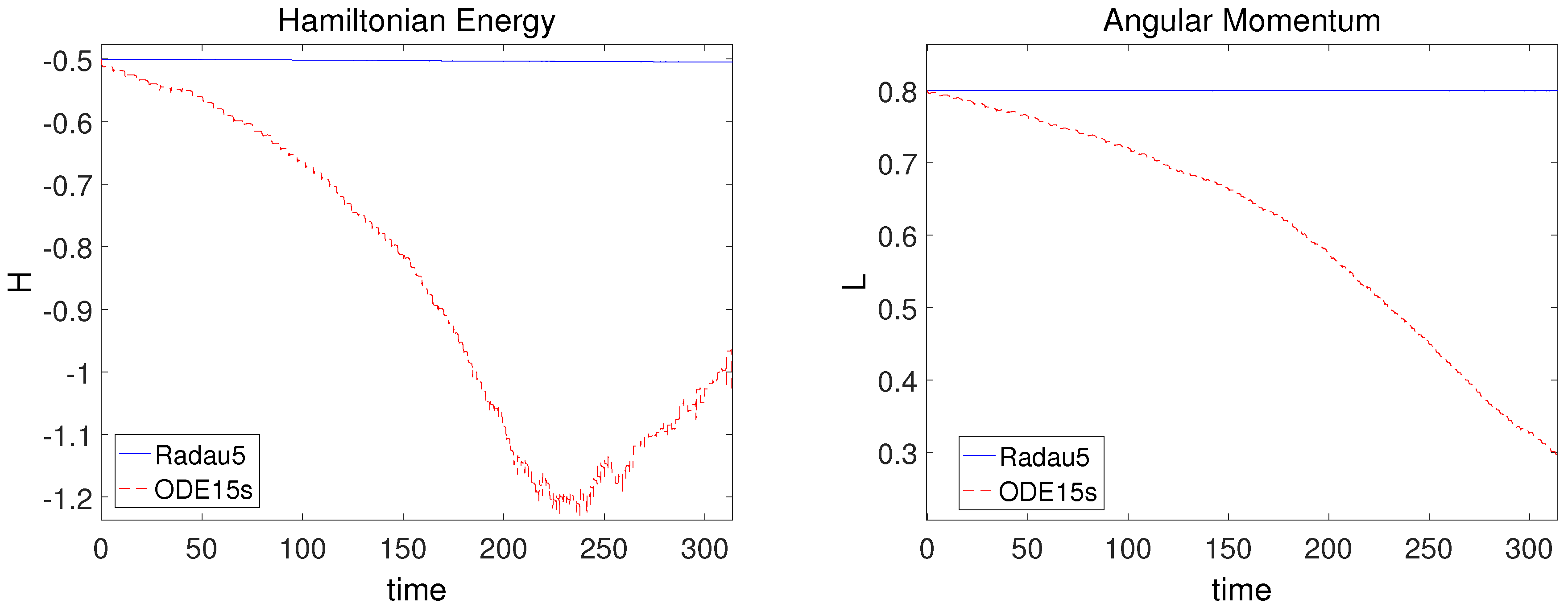
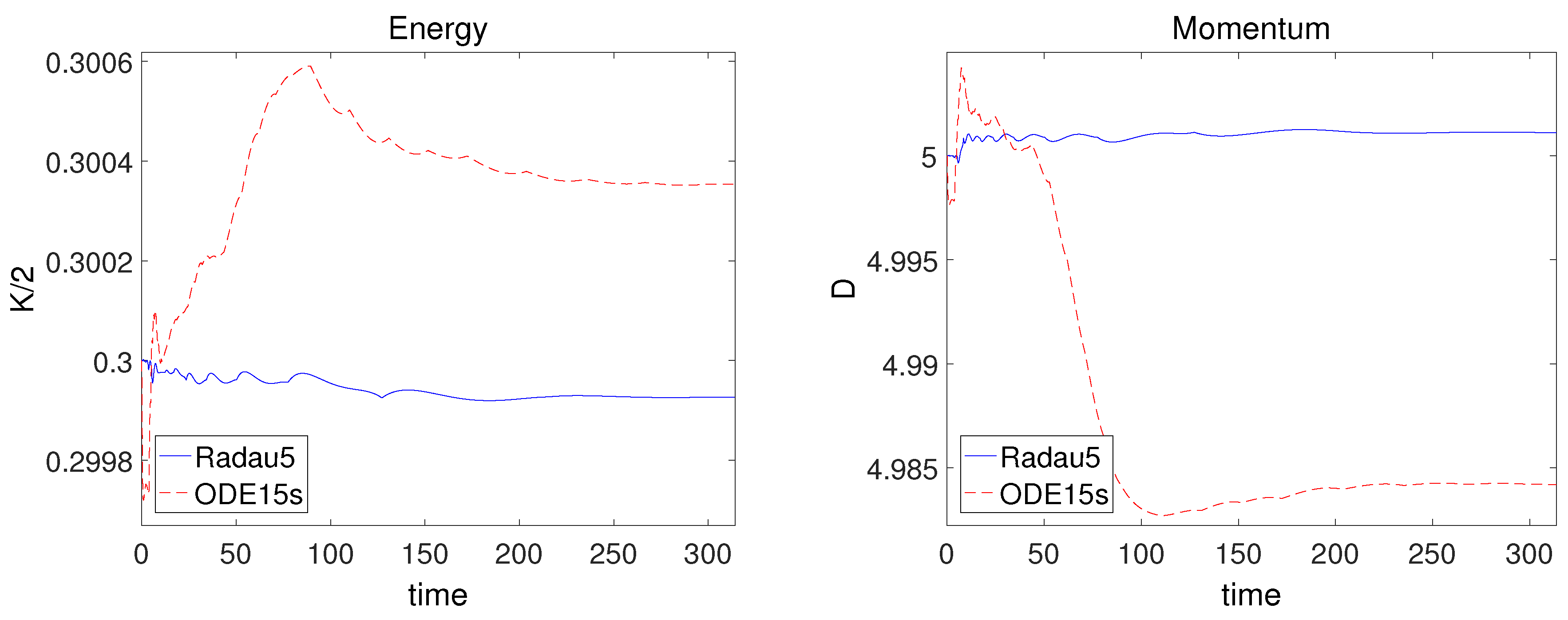
| Reference Solution | Reference Solution | ||
|---|---|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeon, Y.; Bak, S.; Bu, S. Reinterpretation of Multi-Stage Methods for Stiff Systems: A Comprehensive Review on Current Perspectives and Recommendations. Mathematics 2019, 7, 1158. https://doi.org/10.3390/math7121158
Jeon Y, Bak S, Bu S. Reinterpretation of Multi-Stage Methods for Stiff Systems: A Comprehensive Review on Current Perspectives and Recommendations. Mathematics. 2019; 7(12):1158. https://doi.org/10.3390/math7121158
Chicago/Turabian StyleJeon, Yonghyeon, Soyoon Bak, and Sunyoung Bu. 2019. "Reinterpretation of Multi-Stage Methods for Stiff Systems: A Comprehensive Review on Current Perspectives and Recommendations" Mathematics 7, no. 12: 1158. https://doi.org/10.3390/math7121158
APA StyleJeon, Y., Bak, S., & Bu, S. (2019). Reinterpretation of Multi-Stage Methods for Stiff Systems: A Comprehensive Review on Current Perspectives and Recommendations. Mathematics, 7(12), 1158. https://doi.org/10.3390/math7121158




