Analysis and Nonstandard Numerical Design of a Discrete Three-Dimensional Hepatitis B Epidemic Model
Abstract
:1. Introduction
2. Qualitative Analysis
2.1. Stability
2.2. Bifurcation Value
3. Numerical Models
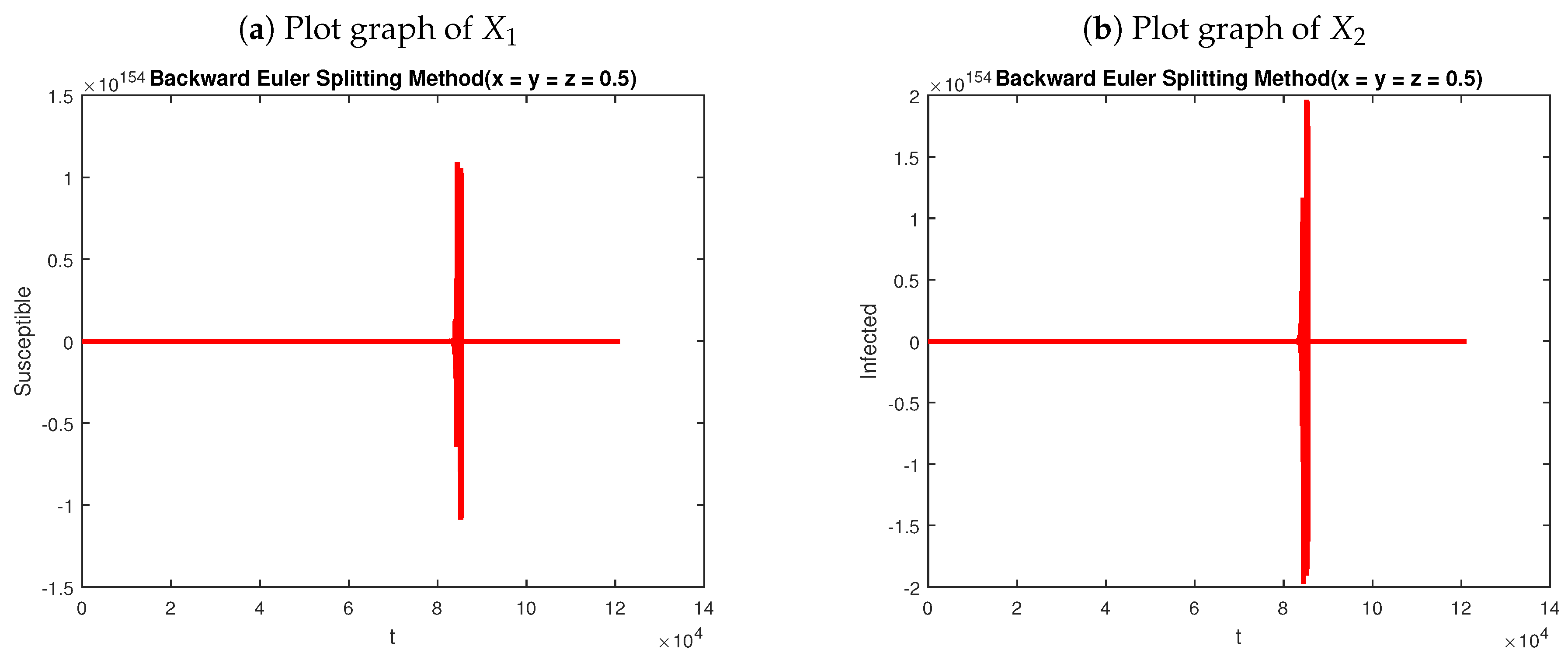
3.1. Backward Euler Scheme
3.2. Nonstandard Scheme
4. Numerical Properties
- 1.
- If the vectors and are positive then and are likewise positive.
- 2.
- If and are positive then so are and .
- 3.
- If and are positive then and are also positive.
5. Computer Simulations
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yuen, M.F.; Chen, D.S.; Dusheiko, G.M.; Janssen, H.L.; Lau, D.T.; Locarnini, S.A.; Peters, M.G.; Lai, C.L. Hepatitis B virus infection. Nat. Rev. Dis. Prim. 2018, 4, 18035. [Google Scholar] [CrossRef]
- Tedder, R.; Zuckerman, M.; Brink, N.; Goldstone, A.; Fielding, A.; Blair, S.; Patterson, K.; Hawkins, A.; Gormon, A.; Heptonstall, J.; et al. Hepatitis B transmission from contaminated cryopreservation tank. Lancet 1995, 346, 137–140. [Google Scholar] [CrossRef]
- Jonas, M.M. Hepatitis B and pregnancy: An underestimated issue. Liver Int. 2009, 29, 133–139. [Google Scholar] [CrossRef]
- Terrault, N.A.; Lok, A.S.; McMahon, B.J.; Chang, K.M.; Hwang, J.P.; Jonas, M.M.; Brown, R.S.; Bzowej, N.H.; Wong, J.B. Update on prevention, diagnosis, and treatment of chronic hepatitis B: AASLD 2018 hepatitis B guidance. Hepatology 2018, 67, 1560–1599. [Google Scholar] [CrossRef] [PubMed]
- Sarin, S.; Kumar, M.; Lau, G.; Abbas, Z.; Chan, H.; Chen, C.; Chen, D.; Chen, H.; Chen, P.; Chien, R.; et al. Asian-Pacific clinical practice guidelines on the management of hepatitis B: A 2015 update. Hepatol. Int. 2016, 10, 1–98. [Google Scholar] [CrossRef] [PubMed]
- CDC. Progress in hepatitis B prevention through universal infant vaccination–China, 1997–2006. MMWR Morb. Mortal. Wkly. Rep. 2007, 56, 441–445. [Google Scholar]
- Lavanchy, D.; Kane, M. Global epidemiology of hepatitis B virus infection. In Hepatitis B Virus in Human Diseases; Springer: Berlin, Germany, 2016; pp. 187–203. [Google Scholar]
- Mantzoukis, K.; Rodríguez-Perálvarez, M.; Buzzetti, E.; Thorburn, D.; Davidson, B.R.; Tsochatzis, E.; Gurusamy, K.S. Pharmacological interventions for acute hepatitis B infection. Cochrane Database Syst. Rev. 2017, 3, CD011645. [Google Scholar] [CrossRef]
- Milner, B.P.; Wang, J. Acute Hepatitis B Viral Infection in a Patient with Common Variable Immunodeficiency: A Case Report: 2448. Am. J. Gastroenterol. 2018, 113, S1362. [Google Scholar] [CrossRef]
- Chang, M.H. Hepatitis B virus infection. In Seminars in Fetal and Neonatal Medicine; Elsevier: New York, NY, USA, 2007; Volume 12, pp. 160–167. [Google Scholar]
- Terrault, N.A.; Bzowej, N.H.; Chang, K.M.; Hwang, J.P.; Jonas, M.M.; Murad, M.H. A ASLD guidelines for treatment of chronic hepatitis B. Hepatology 2016, 63, 261–283. [Google Scholar] [CrossRef]
- El-Serag, H.B. Epidemiology of viral hepatitis and hepatocellular carcinoma. Gastroenterology 2012, 142, 1264–1273. [Google Scholar] [CrossRef]
- Safi, M.A. Global Stability Analysis of Two-Stage Quarantine-Isolation Model with Holling Type II Incidence Function. Mathematics 2019, 7, 350. [Google Scholar] [CrossRef]
- Nistal, R.; De la Sen, M.; Alonso-Quesada, S.; Ibeas, A. On a new discrete SEIADR model with mixed controls: Study of its properties. Mathematics 2019, 7, 18. [Google Scholar] [CrossRef]
- Abouelkheir, I.; Kihal, F.E.; Rachik, M.; Elmouki, I. Optimal Impulse Vaccination Approach for an SIR Control Model with Short-Term Immunity. Mathematics 2019, 7, 420. [Google Scholar] [CrossRef]
- Liu, X.L.; Pan, S. Spreading speed in a nonmonotone equation with dispersal and delay. Mathematics 2019, 7, 291. [Google Scholar] [CrossRef]
- Mann, J.; Roberts, M. Modelling the epidemiology of hepatitis B in New Zealand. J. Theor. Biol. 2011, 269, 266–272. [Google Scholar] [CrossRef] [PubMed]
- Tilahun, G.T.; Makinde, O.D.; Malonza, D. Co-dynamics of pneumonia and typhoid fever diseases with cost effective optimal control analysis. Appl. Math. Comput. 2018, 316, 438–459. [Google Scholar] [CrossRef]
- Martin, N.K.; Vickerman, P.; Hickman, M. Mathematical modelling of hepatitis C treatment for injecting drug users. J. Theor. Biol. 2011, 274, 58–66. [Google Scholar] [CrossRef]
- Lemos-Paião, A.P.; Silva, C.J.; Torres, D.F. An epidemic model for cholera with optimal control treatment. J. Comput. Appl. Math. 2017, 318, 168–180. [Google Scholar] [CrossRef]
- White, M.T.; Verity, R.; Churcher, T.S.; Ghani, A.C. Vaccine approaches to malaria control and elimination: Insights from mathematical models. Vaccine 2015, 33, 7544–7550. [Google Scholar] [CrossRef]
- Agusto, F.; Bewick, S.; Fagan, W. Mathematical model for Zika virus dynamics with sexual transmission route. Ecol. Complex. 2017, 29, 61–81. [Google Scholar] [CrossRef]
- Cheng, Q.; Jing, Q.; Spear, R.C.; Marshall, J.M.; Yang, Z.; Gong, P. Climate and the timing of imported cases as determinants of the dengue outbreak in Guangzhou, 2014: Evidence from a mathematical model. PLoS Neglect. Trop. Dis. 2016, 10, e0004417. [Google Scholar] [CrossRef] [PubMed]
- Parham, P.E.; Waldock, J.; Christophides, G.K.; Hemming, D.; Agusto, F.; Evans, K.J.; Fefferman, N.; Gaff, H.; Gumel, A.; LaDeau, S.; et al. Climate, environmental and socio-economic change: Weighing up the balance in vector-borne disease transmission. Philos. Trans. R. Soc. B Biol. Sci. 2015, 370, 20130551. [Google Scholar] [CrossRef] [PubMed]
- Medlock, J.; Kot, M. Spreading disease: Integro-differential equations old and new. Math. Biosci. 2003, 184, 201–222. [Google Scholar] [CrossRef]
- Khan, T.; Zaman, G. Classification of different Hepatitis B infected individuals with saturated incidence rate. SpringerPlus 2016, 5, 1082. [Google Scholar] [CrossRef] [PubMed]
- Parsamanesh, M.; Erfanian, M. Global dynamics of an epidemic model with standard incidence rate and vaccination strategy. Chaos Solitons Fractals 2018, 117, 192–199. [Google Scholar] [CrossRef]
- Ahmed, N.; Shahid, N.; Iqbal, Z.; Jawaz, M.; Rafiq, M.; Tahira, S.; Ahmad, M. Numerical Modeling of SEIQV Epidemic Model with Saturated Incidence Rate. J. Appl. Environ. Biol. Sci. 2018, 8, 67–82. [Google Scholar]
- Khan, T.; Ullah, Z.; Ali, N.; Zaman, G. Modeling and control of the hepatitis B virus spreading using an epidemic model. Chaos Solitons Fractals 2019, 124, 1–9. [Google Scholar] [CrossRef]
- Ervin, V.J.; Macías-Díaz, J.E.; Ruiz-Ramírez, J. A positive and bounded finite element approximation of the generalized Burgers–Huxley equation. J. Math. Anal. Appl. 2015, 424, 1143–1160. [Google Scholar] [CrossRef]
- Macías-Díaz, J.E.; Villa-Morales, J. A deterministic model for the distribution of the stopping time in a stochastic equation and its numerical solution. J. Comput. Appl. Math. 2017, 318, 93–106. [Google Scholar] [CrossRef]
- Macías-Díaz, J.E.; Landry, R.; Puri, A. A finite-difference scheme in the computational modelling of a coupled substrate-biomass system. Int. J. Comput. Math. 2014, 91, 2199–2214. [Google Scholar] [CrossRef]
- Ahmed, N.; Tahira, S.; Rafiq, M.; Rehman, M.; Ali, M.; Ahmad, M. Positivity preserving operator splitting nonstandard finite difference methods for SEIR reaction diffusion model. Open Math. 2019, 17, 313–330. [Google Scholar] [CrossRef]
- Ahmed, N.; Rafiq, M.; Rehman, M.; Iqbal, M.; Ali, M. Numerical modeling of three dimensional Brusselator reaction diffusion system. AIP Adv. 2019, 9, 015205. [Google Scholar] [CrossRef]
- Macías-Díaz, J.E.; Puri, A. An explicit positivity-preserving finite-difference scheme for the classical Fisher–Kolmogorov–Petrovsky–Piscounov equation. Appl. Math. Comput. 2012, 218, 5829–5837. [Google Scholar] [CrossRef]
- Macías-Díaz, J.E. Sufficient conditions for the preservation of the boundedness in a numerical method for a physical model with transport memory and nonlinear damping. Comput. Phys. Commun. 2011, 182, 2471–2478. [Google Scholar] [CrossRef]
- Macías-Díaz, J.E.; Puri, A. A boundedness-preserving finite-difference scheme for a damped nonlinear wave equation. Appl. Numer. Math. 2010, 60, 934–948. [Google Scholar] [CrossRef]
- Tomasiello, S. A note on three numerical procedures to solve Volterra integrodifferential equations in structural analysis. Comput. Math. Appl. 2011, 62, 3183–3193. [Google Scholar] [CrossRef] [Green Version]
- Tomasiello, S. Some remarks on a new DQ-based method for solving a class of Volterra integro-differential equations. Appl. Math. Comput. 2012, 219, 399–407. [Google Scholar] [CrossRef]
- Mickens, R.E. Nonstandard Finite Difference Models of Differential Equations; World Scientific: Singerpore, 1994. [Google Scholar]
- Fujimoto, T.; Ranade, R.R. Two characterizations of inverse-positive matrices: The Hawkins-Simon condition and the Le Chatelier-Braun principle. Electron. J. Linear Algebra 2004, 11, 6. [Google Scholar] [CrossRef] [Green Version]
- Harwood, R.C.; Manoranjan, V.S.; Edwards, D.B. Lead-acid battery model under discharge with a fast splitting method. IEEE Trans. Energy Convers. 2011, 26, 1109–1117. [Google Scholar] [CrossRef]
- Tian, G.X.; Huang, T.Z. Inequalities for the minimum eigenvalue of M-matrices. ELA Electron. J. Linear Algebra 2010, 20. [Google Scholar] [CrossRef]
- Macías-Díaz, J.E. An explicit dissipation-preserving method for Riesz space-fractional nonlinear wave equations in multiple dimensions. Commun. Nonlinear Sci. Numer. Simul. 2018, 59, 67–87. [Google Scholar] [CrossRef]
- Macías-Díaz, J.E. Numerical simulation of the nonlinear dynamics of harmonically driven Riesz-fractional extensions of the Fermi–Pasta–Ulam chains. Commun. Nonlinear Sci. Numer. Simul. 2018, 55, 248–264. [Google Scholar] [CrossRef]
- Macías-Díaz, J.E. Numerical study of the transmission of energy in discrete arrays of sine-Gordon equations in two space dimensions. Phys. Rev. E 2008, 77, 016602. [Google Scholar] [CrossRef]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Macías-Díaz, J.E.; Ahmed, N.; Rafiq, M. Analysis and Nonstandard Numerical Design of a Discrete Three-Dimensional Hepatitis B Epidemic Model. Mathematics 2019, 7, 1157. https://doi.org/10.3390/math7121157
Macías-Díaz JE, Ahmed N, Rafiq M. Analysis and Nonstandard Numerical Design of a Discrete Three-Dimensional Hepatitis B Epidemic Model. Mathematics. 2019; 7(12):1157. https://doi.org/10.3390/math7121157
Chicago/Turabian StyleMacías-Díaz, Jorge E., Nauman Ahmed, and Muhammad Rafiq. 2019. "Analysis and Nonstandard Numerical Design of a Discrete Three-Dimensional Hepatitis B Epidemic Model" Mathematics 7, no. 12: 1157. https://doi.org/10.3390/math7121157
APA StyleMacías-Díaz, J. E., Ahmed, N., & Rafiq, M. (2019). Analysis and Nonstandard Numerical Design of a Discrete Three-Dimensional Hepatitis B Epidemic Model. Mathematics, 7(12), 1157. https://doi.org/10.3390/math7121157







