1. Introduction and Motivation
Divisor functions, Euler
-function, and Möbius
-function are widely studied in the field of elementary number theory. The absolute Möbius divisor function is defined by
Here,
n is a positive integer and
is the Möbius function. It is well known ([
1], p. 23) that
where
denotes the Euler
-function (totient function). If
n is a square-free integer, then
. The first twenty values of
and
are given in
Table 1.
Let , and , where .
Next, to study the iteration properties of ( resp., ), we say the order (resp., class) of n, m-gonal (resp., -gonal) absolute Möbius ( resp., totient) shape numbers, and shape polygons derived from the sum of absolute Möbius divisor (resp., Euler totient) function are as follows.
Definition 1. (Order Notion) To study when the positive integer is terminated at one, we consider a notation as follows. The order of a positive integer denoted , which is the least positive integer m when and . The positive integers of order 2 are usually called involutions. Naturally, we define . The first 20 values of and are given by Table 2. See [2]. Remark 1. Define , and for all . Shapiro [2] defines the class number of n by that integer C such that . Some values of are equal to them of . Shapiro [2] defined . Here, we define and . A similar notation of is in [3]. Definition 2. (Absolute Möbius m-gonal shape number and totient -gonal shape number) If Ord (resp., , we consider the set (resp., and add . We then put (resp., . Then we find a m-gon (resp., -gon) derived from (resp., ). Here, we call n an absolute Möbius m-gonal shape number (resp., totient -gonal shape number derived from U and (resp., φ and ) except .
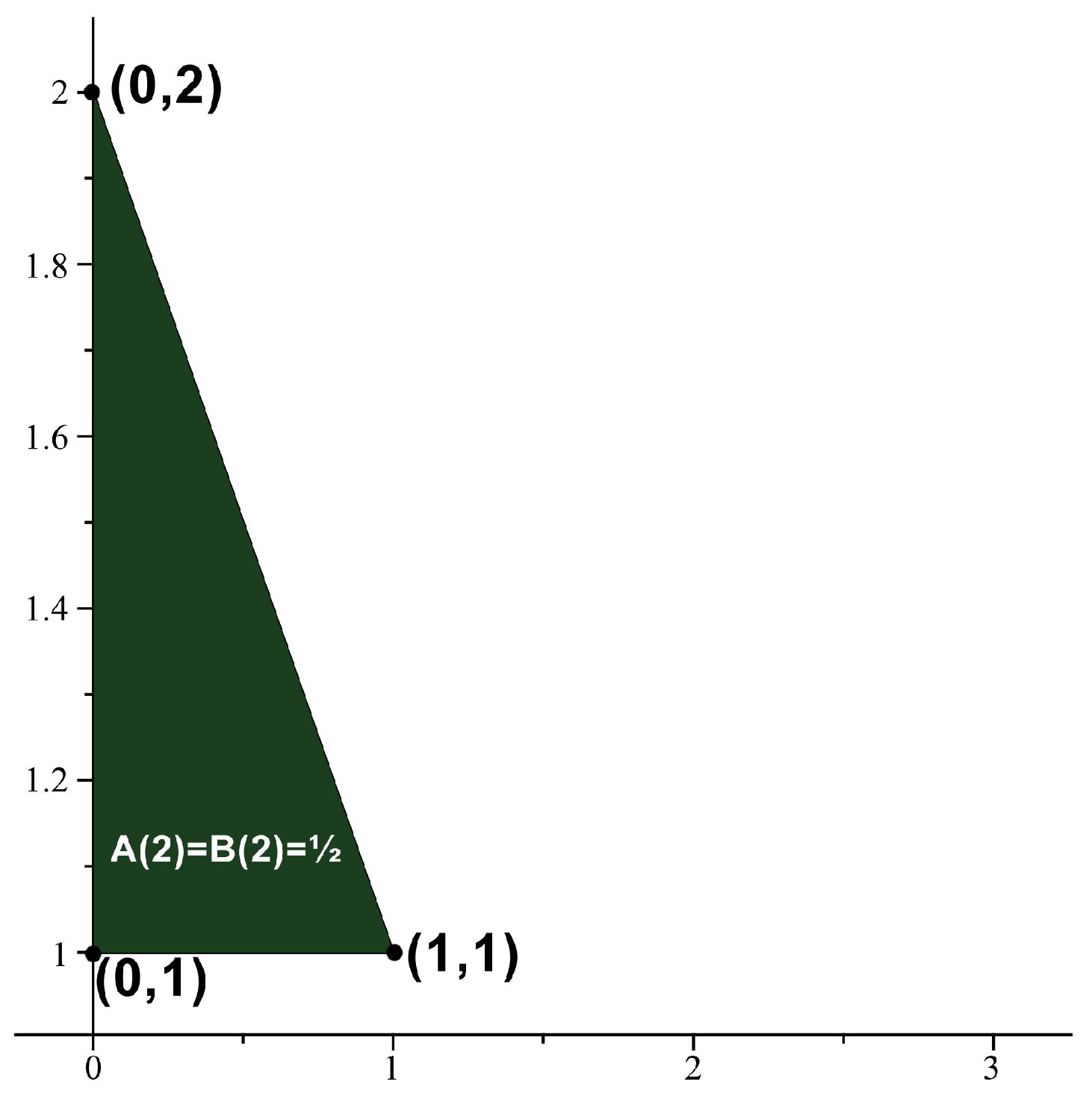
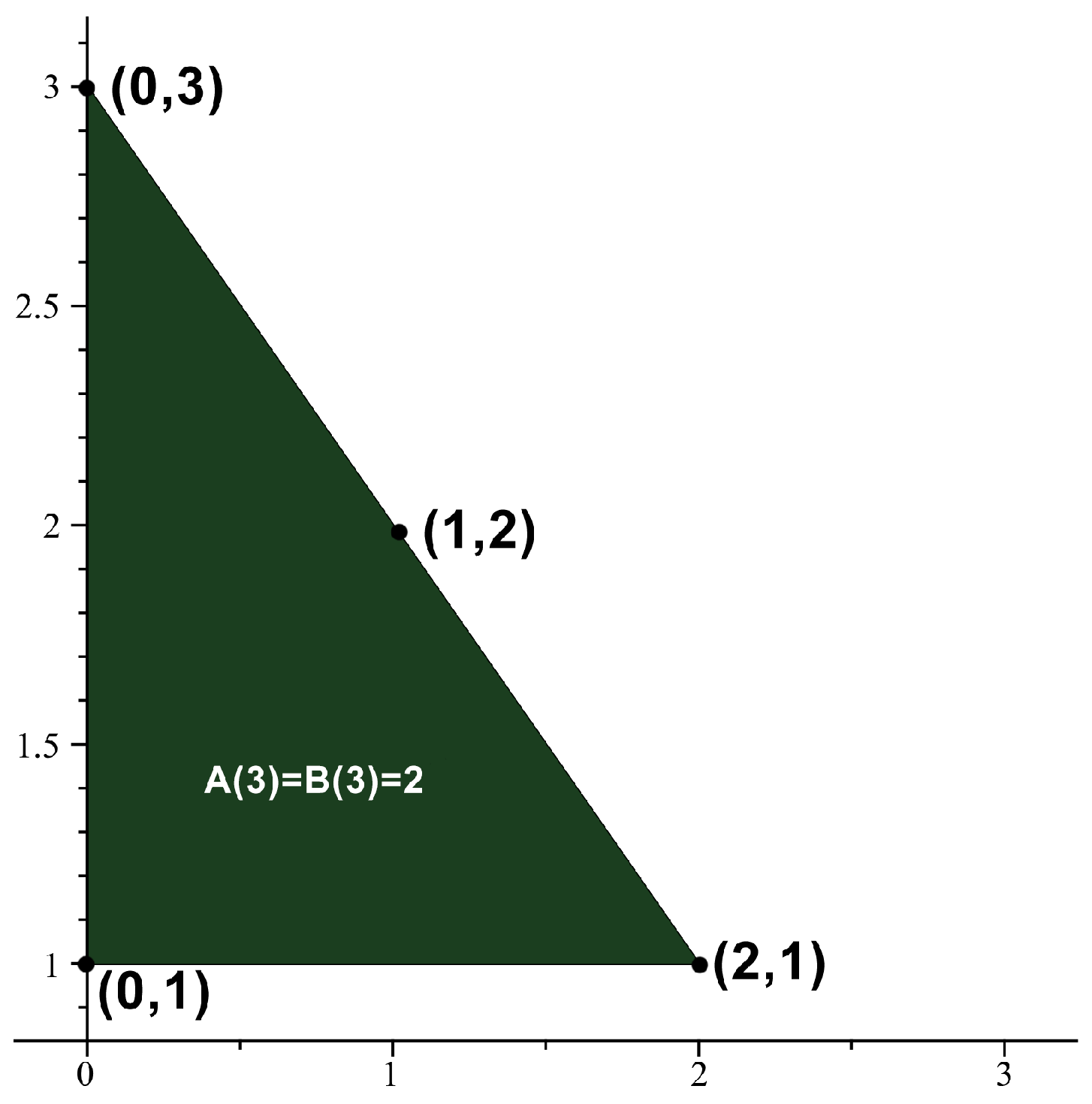
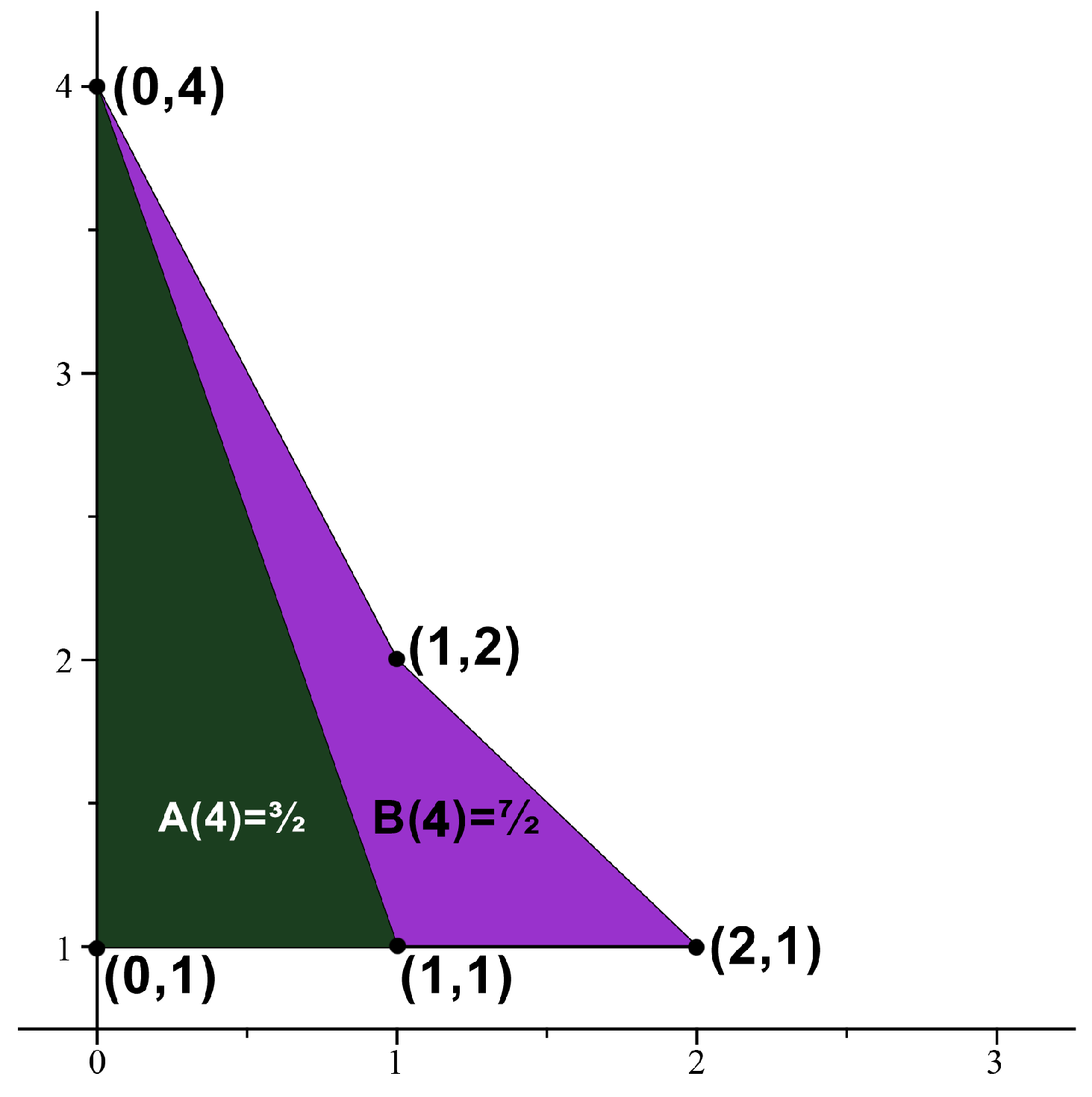
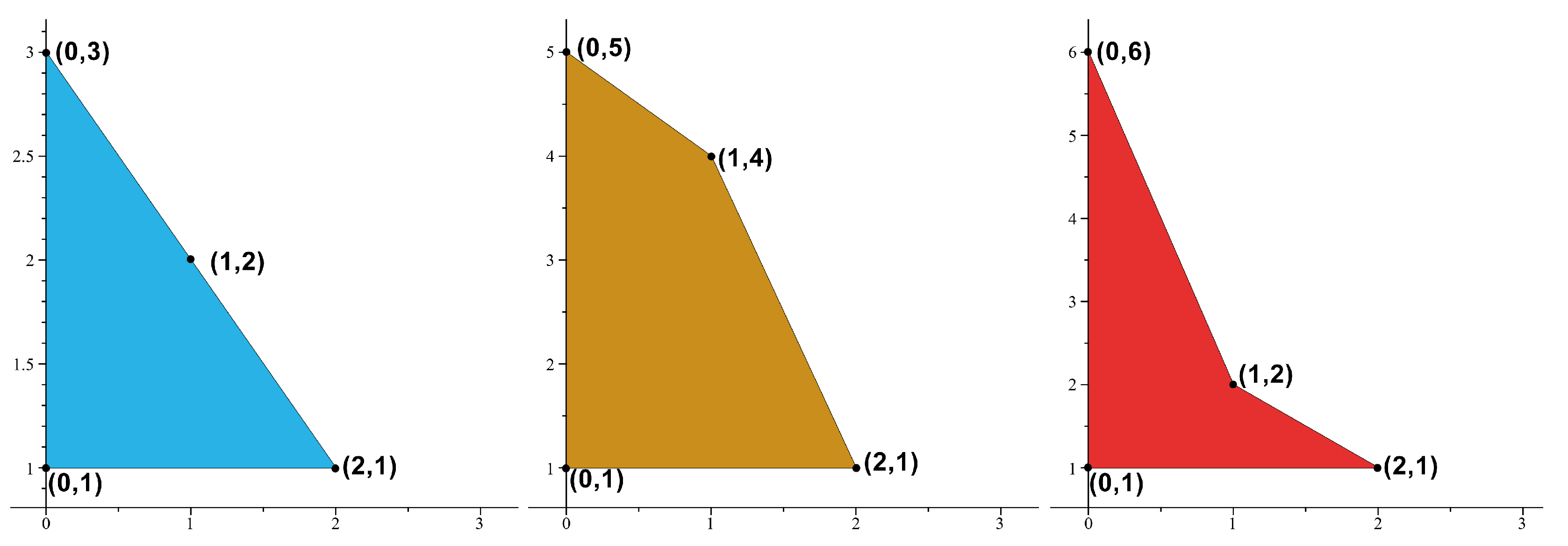
Definition 3. (Convexity and Area) We use same notations, convex, non-convex, and area in [3]. We say that n is an absolute Möbius m-gonal convex (resp., non-convex) shape number with respect to the absolute Möbius divisor function U if is convex (resp., non-convex). Let denote the area of the absolute Möbius m-gon derived from the absolute Möbius m-gonal shape number. Similarly, we define the totient -gonal convex (resp., non-convex) shape number and denote the area of the totient -gon. Example 1. If then we obtain the set of points . Thus, 2 is an absolute Möbius 3-gonal convex number with . See Figure 1. See Figure 2, Figure 3 and Figure 4 for absolute Möbius n-gonal shape numbers and totient n-gonal shape numbers with . The first 19 values of and are given by Table 3. Kim and Bayad [
3] considered the iteration of the odd divisor function
S, polygon shape, convex, order, etc.
In this article, we considered the iteration of the absolute Möbius divisor function and Euler totient function and polygon types.
Now we state the main result of this article. To do this, let us examine the following theorem. For the proof of this theorem, the definitions and lemmas in the other chapters of this study have been utilized.
Theorem 1. (Main Theorem) Let be Fermat primes with ,
,
,
.
If or 2 then a positive integer is Remark 2. Shapiro [2] computed positive integer m when That is, Let Then - (1)
If then m are totient 3-gonal (triangular) numbers.
- (2)
If then m are totient 4-gonal non-convex numbers.
2. Some Properties of and
It is well known [
1,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14] that Euler
-function have several interesting formula. For example, if
with two positive integers
x and
y, then
. On the other hand, if
x is a multiple of
y, then
[
2]. In this section, we will consider the arithmetic functions
and
.
Lemma 1. Let be a factorization of n, where be distinct prime integers and be positive integers. Then, Proof. If
is an arbitrary integer, then we easily check
This is completed the proof of Lemma 1. □
Corollary 1. If p is a prime integer and α is a positive integer, then and . In particular, .
Proof. It is trivial by Lemma 1. □
Corollary 2. Let be a positive integer and let . Then, Proof. It is trivial by Lemma 1. □
Remark 3. We compare with as follow on Table 4. Lemma 2. The function U is multiplicative function. That is, with . Furthermore, if m is a multiple of n, then .
Proof. Let
and
be positive integers. Then
and
are distinct primes. If
and also
,
,
, and
by Lemma 1, we note that
Let m be a multiple of n. If then . Thus, by Lemma 1, . This is completed the proof of Lemma 2. □
Remark 4. Two functions and have similar results as follows on Table 5. Here, means that m is a multiple of n. Theorem 2. For all , there exists satisfying .
Proof. Let , where be distinct prime integers with .
We note that by Lemma 1.
If and , then by Corollary 1.
If is an odd positive prime integer, then by Corollary 1.
We note that
is an even integer. Then there exist distinct prime integers
satisfying
where
,
and
. It is well known that
.
By Lemma 2, we get
By using the same method in (
2) for
, we get
with
. It is easily checked that
.
Using this technique, we can find
l satisfying
with
.
By
Appendix A (Values of
), we easily find a positive integer
v that
for
. Thus, we get
. Therefore, we can find
satisfying
. □
Corollary 3. For all , there exists satisfying .
Proof. It is trivial by Theorem 2. □
Remark 5. Kim and Bayad [3] considered iterated functions of odd divisor functions and order of n. For order of divisor functions, we do not know or not. But, functions (resp., ), we know by Corollary 3 (resp., [15]). Theorem 3. Let be a positive integer. Then if and only if for some .
Proof. Let . It is easy to see that .
Let
be a factorization of
n, and all
are distinct prime integers. If
, then by using Lemma 1 we can note that,
According to all are distinct prime integers, then it is easy to see that there is only exist and that is . Hereby for some .
This is completed the proof of Theorem 3. □
Remark 6. If then is an absolute Möbius 3-gonal (triangular) shape number with by Theorem 3.
Theorem 4. Let n, m and be positive integers with greater than 1 and let and . Then, if and only if . Furthermore,and Proof. First, we consider
. We find the set
. Thus, we have
Similarly, we get (
5). These complete the proof of Theorem 4. □
3. Classification of the Absolute Möbius Divisor Function with
In this section, we study integers
n when
. If
, then
n has three cases which are 3-gonal (triangular) shape number, 4-gonal convex shape number, and 4-gonal non-convex shape numbers in
Figure 5.
Theorem 5. Let be Fermat primes and be positive integers. If , then .
Proof. Let
be Fermat primes. By Corollary 1 and Lemma 2 we have
Thus, we can see that
and
. Therefore, we get Theorem 5. □
The First 32 values of
and
for
are given by
Table A2 (see
Appendix B).
Remark 7. Iterations of the odd divisor function , the absolute Möbius divisor function , and Euler totient function have small different properties. Table 6. gives an example of differences of , and with . Lemma 3. Let be Fermat primes. Then 3 is an absolute Möbius 3-gonal (triangular) shape number and are absolute Möbius 4-gonal convex numbers.
Proof. The set
makes a triangle. Let
be a Fermat primes except 3. We get
. So, we get
Because of , the set gives a convex shape. This completes the proof Lemma 3. □
Lemma 4. Let be Fermat primes. Then and are absolute Möbius 4-gonal non-convex shape numbers with positive integers.
Proof. Let
be a Fermat primes. Consider
So, . Thus, are absolute Möbius 4-gonal non-convex shape numbers. Similarly, we get .
Thus, these complete the proof Lemma 4. □
Lemma 5. Let be Fermat primes. Then are absolute Möbius 4-gonal non-convex shape numbers.
Furthermore, if are positive integers then are absolute Möbius 4-gonal non-convex shape numbers.
Proof. The proof is similar to Lemma 4. □
Lemma 6. Let r be a positive integer. Then Proof. Let . Thus . This is completed the proof of Lemma 6. □
Corollary 4. Let . Then is an absolute Möbius 3-gonal (triangular) shape number.
Proof. It is trivial by Lemma 6. □
Remark 8. Fermat first conjectured that all the numbers in the form of are primes [16]. Up-to-date there are only five known Fermat primes. That is, , , , , and . Though we find a new Fermat prime , 6th Fermat primes, we cannot find a new absolute Möbius 3-gonal (triangular) number by Lemma 7. Let be Fermat primes with and . If then are absolute Möbius 4-gonal convex shape numbers.
Proof. Let
be a Fermat prime, where
k is a positive integer. We note that
and
. In a similar way in (
7), we obtain
By Theorem 5,
. By (
8),
is an absolute Möbius 4-gonal convex shape number.
This completes the proof of Lemma 7. □
Lemma 8. Let be Fermat primes with .
Then are absolute Möbius 4-gonal non-convex shape numbers except .
Proof. Similar to Lemmas 5 and 7. □
Proof of Theorem 1 (Main Theorem). It is completed by Remark 6, Theorem 5, Lemmas 3 and 4, Corollary 4, Remark 8, Lemmas 7 and 8. □
Remark 9. If n are absolute Möbius 3-gonal (triangular) or 4-gonal convex shape numbers then n is the regular n-gon by Gauss Theorem.
Example 2. The set is . Thus, a positive integer 3 is an absolute Möbius 3-gonal convex shape number.
Similarly, 15, 255, 65535, 4294967295 are absolute Möbius 3-gonal convex numbers derived from
,
,
,
.
Remark 10. Let denote the minimal number of m-gonal number. By using Maple 13 Program, Table 7 shows us minimal numbers about from 3-gonal (triangular) to 14-gonal shape number. Conjecture 1. For any positive integer , is a prime integer.