On Common Fixed Point Results for New Contractions with Applications to Graph and Integral Equations

Abstract

The investigation of symmetric/asymmetric structures and their applications in mathematics (in particular in operator theory and functional analysis) is useful and fruitful. A metric space has the property of symmetry. By looking in the same direction and using the $\alpha$-admissibility with regard to $\eta$ and $\theta$-functions, we demonstrate some existence and uniqueness fixed point theorems. The obtained results extend and generalize the main result of Isik et al. (2019). At the end, some illustrated applications are presented.

1. Introduction and Preliminaries

The known work in fixed point theory is the Banach contraction principle which ensured the existence of a fixed point for a contractive self-mapping over a complete metric space. Numerous researchers have built up the existence of fixed points in many directions, see [1,2,3,4,5,6,7,8,9,10,11,12,13].

In 2014, Jleli and Samet [14] presented a new type of contractive mappings, named as $\theta$-contractions.

Definition 1

([14]). Let T be self-mapping on a complete metric space $(\mathsf{{\rm Y}},\rho )$. Such a T is named as a θ-contraction if there is $k\in$ (0,1) such that

$$\nu ,\varpi \in \mathsf{{\rm Y}},\rho (T\nu ,T\varpi )>0\Rightarrow \theta \left(\rho (T\nu ,T\varpi )\right)\le {\left[\theta \left(\rho (\nu ,\varpi )\right)\right]}^k,$$

(1)

where Θ is the family of functions $\theta :(0,\infty )\to (1,\infty )$ verifying the following:

(θ1)

θ is nondecreasing;

(θ2)

for every sequence $\left\{{\nu }_n\right\}\subset (0,\infty ),$ we have ${\displaystyle \underset{n\to \infty }{lim}\theta \left({\nu }_n\right)=1}$ iff ${lim}_{n\to \infty }{\nu }_n=0;$

(θ3)

there are $\beta \in (0,1)$ and $\sigma \in (0,\infty ]$ such that ${\displaystyle \underset{\nu \to 0^{+}}{lim}{\displaystyle \frac{\theta \left(\nu \right)-1}{{\nu }^{\beta }}}=\sigma .}$

Theorem 1

([14]). Let $(\mathsf{{\rm Y}},\rho )$ be a complete metric space and $T:\mathsf{{\rm Y}}\to \mathsf{{\rm Y}}$ be a θ-contraction. Then T admits a unique fixed point ${\nu }^{☆}.$ Moreover, for each $\nu \in \mathsf{{\rm Y}},$ the sequence $\left\{T^n\nu \right\}$ converges to ${\nu }^{☆}.$

Later, Ahmad et al. [15] introduced the following.

Definition 2

([15]). Let Γ be the set of functions $\xi :(0,\infty )\to (1,\infty )$ verifying:

(ξ₁)

ξ is nondecreasing,

(ξ₂)

for a sequence $\left\{{\nu }_n\right\}\subseteq (0,\infty )$, we have ${\displaystyle \underset{n\to \infty }{lim}\xi \left({\nu }_n\right)=1}$ if and only if ${\displaystyle \underset{n\to \infty }{lim}{\nu }_n=0}$,

(ξ₃)

ξ is continuous on $(0,\infty )$.

Lemma 1

([15]). Let $(\mathsf{{\rm Y}},\rho )$ be a complete metric space and $\xi \in \mathsf{\Gamma }$. Then $(\mathsf{{\rm Y}},\xi \circ \rho )$ is also a complete metric space.

Example 1.

The following functions ${\xi }_1\left(\nu \right)=e^{\nu }$, ${\xi }_2\left(\nu \right)=e^{\sqrt{\nu }}$, ${\xi }_3\left(\nu \right)=e^{\sqrt{\nu e^{\nu }}}$, ${\xi }_4\left(\nu \right)=cosh\nu$, ${\xi }_5\left(\nu \right)=1+ln(1+\nu )$ and ${\xi }_6\left(\nu \right)=e^{\nu e^{\nu }}$, are elements in Γ.

The concept of $\alpha$-admissibility is given as follows:

Definition 3

([16]). Given $f:\mathsf{{\rm Y}}\to \mathsf{{\rm Y}}$ and $\alpha :\mathsf{{\rm Y}}\times \mathsf{{\rm Y}}\to [0,\infty )$. Such an f is designated α-admissible if $\forall \nu ,\varpi \in \mathsf{{\rm Y}}$ with $\alpha (\nu ,\varpi )\ge 1$ implies $\alpha (f\nu ,f\varpi )\ge 1$.

The notion of $\alpha$-admissibility in regards to a function $\eta$ is given as follows:

Definition 4

([17]). Given $f:\mathsf{{\rm Y}}\to \mathsf{{\rm Y}}$ and $\alpha ,\eta :\mathsf{{\rm Y}}\times \mathsf{{\rm Y}}\to [0,\infty )$. Such an f is α-admissible with respect to η if $\nu ,\varpi \in \mathsf{{\rm Y}}$ with $\alpha (\nu ,\varpi )\ge \eta (\nu ,\varpi )$ implies $\alpha (f\nu ,f\varpi )\ge \eta (f\nu ,f\varpi )$.

Many fixed point results using the above notion appeared, see [18,19,20,21,22]. The perception of triangular $\alpha$-admissibility is stated in the following:

Definition 5

([4]). Given $S,T:\mathsf{{\rm Y}}\to \mathsf{{\rm Y}}$ and $\alpha ,\eta :\mathsf{{\rm Y}}\times \mathsf{{\rm Y}}\to [0,\infty )$ so that

1 

if $\alpha (\nu ,\varpi )\ge \eta (\nu ,\varpi )$, then $\alpha (S\nu ,T\varpi )\ge \eta (S\nu ,T\varpi )$ and $\alpha (TS\nu ,ST\varpi )\ge \eta (TS\nu ,ST\varpi )$;

2 

if $\alpha (\nu ,z)\ge \eta (\nu ,z)$ and $\alpha (z,\varpi )\ge \eta (z,\varpi )$, then $\alpha (\nu ,\varpi )\ge \eta (\nu ,\varpi )$.

Then we designate that the pair $(S,T)$ is triangular α-admissible, appertaining to the function η.

Example 2

([4]). Let $\mathsf{{\rm Y}}=[0,\infty )$. Define $S,T:\mathsf{{\rm Y}}\to \mathsf{{\rm Y}}$ by $S\nu =\nu$ and $T\nu ={\nu }^2$. Consider $\alpha ,\eta :\mathsf{{\rm Y}}\times \mathsf{{\rm Y}}\to [0,\infty )$ as $\alpha (\nu ,\varpi )=e^{\nu +\varpi }$ and $\eta (\nu ,\varpi )=e^{\varpi -\nu }$. Clearly, the pair $(S,T)$ is triangular α-admissible regarding η.

Samet et al. [16] initiated the concept of $\alpha$-$\psi$-contractions and they demonstrated the existence and uniqueness of common fixed points. Denote by $\mathsf{\Psi }$ the family of nondecreasing functions $\psi :[0,\infty )\to [0,\infty )$ such that ${\displaystyle \sum _{n=1}^{\infty }{\psi }^n\left(\nu \right)<\infty }$ for all $\nu >0.$ If $\psi \in \mathsf{\Psi },$ then $\psi \left(\nu \right)<\nu$ for all $\nu >0.$

Definition 6

([23]). Let $\mathsf{{\rm Y}}=[0,\infty )$. Any $\psi \in \mathsf{\Psi }$ is said to be an altering distance function if

1. 

ψ is nondecreasing and continuous;

2. 

$\psi \left(\nu \right)=0⟺\nu =0$.

The results presented in [16] can be abstracted as follows.

Theorem 2

([16]). Let $(\mathsf{{\rm Y}},\rho )$ be a complete metric space and $T:\mathsf{{\rm Y}}\to \mathsf{{\rm Y}}$ be an $\alpha ,\psi$-admissible contraction. Assume that the subsequent conditions are satisfied:

(i) 

there is ${\nu }_0\in \mathsf{{\rm Y}}$ such that $\alpha \left(x_0,T{\nu }_0\right)\ge 1$;

(ii) 

either T is continuous, or

(ii)′ 

for each sequence $\left\{{\nu }_n\right\}$ in Υ such that ${\nu }_n\to \nu \in \mathsf{{\rm Y}}$ and $\alpha \left({\nu }_n,{\nu }_{n+1}\right)\ge 1,$ then $\alpha \left({\nu }_n,\nu \right)\ge 1$ for all $n\in \mathbb{N}.$

Then T admits a fixed point. Furthermore, if in addition we assume that for every $(u,v)\in \mathsf{{\rm Y}}\times \mathsf{{\rm Y}}$, there exists $z\in \mathsf{{\rm Y}}$ so that $\alpha (u,z)\ge 1$ and $\alpha (v,z)\ge 1,$ then we have a unique fixed point.

In this paper, we originate a new type of contraction by using the concepts of $\alpha$-admissibility in regards to a function $\eta$, and $\xi$-functions. We establish the existence and uniqueness of some common fixed points results. Our obtained results improve and generalize Theorems 1 and 2 and many others in the literature (by taking particular choices of $\xi$, $\psi$, $\alpha$ and $\eta$).

2. Main Results

To begin, we state some principal notations.

Definition 7.

Let $S,T$ be self-mappings on a complete metric space $(\mathsf{{\rm Y}},\rho )$ and $\alpha ,\eta :\mathsf{{\rm Y}}\times \mathsf{{\rm Y}}\to [0,\infty )$ be given functions. Define $\mathcal{A}\subseteq \mathsf{{\rm Y}}\times \mathsf{{\rm Y}}$ as

$$\mathcal{A}(S,T,\alpha ,\eta )=\left\{(\nu ,\varpi ):\rho (T\nu ,T\varpi )>0\mathit{and}\alpha (\nu ,\varpi )\ge \eta (\nu ,\varpi )\right\}.$$

Then the pair $(S,T)$ is named an $(\alpha ,\eta ,\xi ,\psi )$-contraction, if there are $k\in (0,1),$$\psi \in \mathsf{\Psi }$ and $\xi \in \mathsf{\Gamma }$ or Θ such that

$$\xi \left(\rho (S\nu ,T\varpi )\right)\le {\left[\xi \left(\psi \left(K(\nu ,\varpi )\right)\right)\right]}^k,\mathit{for}\mathit{all}(\nu ,\varpi )\in \mathcal{A}(S,T,\alpha ,\eta ),$$

(2)

where

$$K(\nu ,\varpi )=max\left\{\rho \right(\nu ,\varpi ),\rho (\nu ,S\nu ),\rho (\varpi ,T\varpi \left)\right\}.$$

Remark 1.

Let $(\mathsf{{\rm Y}},\rho )$ be a metric space. Let $S,T:\mathsf{{\rm Y}}\to \mathsf{{\rm Y}}$ be self-mappings. If the pair $(S,T)$ is an $(\alpha ,\eta ,\xi ,\psi )$-contraction, then by (2), we deduce

$$ln\left[\xi \right(\rho (S\nu ,T\varpi )\left)\right]\le kln\left(\xi \right(\psi \left(\rho \right(\nu ,\varpi \left)\right)\left)\right)<ln\left(\xi \right(\psi \left(\rho \right(\nu ,\varpi \left)\right)\left)\right),$$

which infers from $\left(\xi 1\right)$ that

$$\rho (S\nu ,T\varpi )<\psi \left(\rho \right(\nu ,\varpi \left)\right),\mathit{for}\mathit{all}(\nu ,\varpi )\in \mathcal{A}(S,T,\alpha ,\eta ).$$

It implies the following:

$$\nu ,\varpi \in \mathsf{{\rm Y}},\alpha (\nu ,\varpi )\ge \eta (\nu ,\varpi )⟹\rho (S\nu ,T\varpi )\le \psi \left(\rho \right(\nu ,\varpi \left)\right).$$

Theorem 3.

Let $(\mathsf{{\rm Y}},\rho )$ be a complete metric space. Let $S,T:\mathsf{{\rm Y}}\to \mathsf{{\rm Y}}$ be self-mappings. Suppose that the following assumptions hold:

(i) 

the pair $(S,T)$ is α-admissible regarding to the function η;

(ii) 

$(S,T)$ is an $(\alpha ,\eta ,\xi ,\psi )$-contraction;

(iii) 

there exists ${\nu }_0\in \mathsf{{\rm Y}}$ so that $\alpha \left({\nu }_0,S{\nu }_0\right)\ge \eta \left({\nu }_0,S{\nu }_0\right)$ and $\alpha \left({\nu }_0,T{\nu }_0\right)\ge \eta \left({\nu }_0,T{\nu }_0\right)$;

(iv) 

S and T are continuous.

Then S and T have a common fixed point.

Proof. 

In view of the condition $\left(ii\right),$ there is ${\nu }_0\in \mathsf{{\rm Y}}$ so that $\alpha \left({\nu }_0,S{\nu }_0\right)\ge \eta \eta \left({\nu }_0,S{\nu }_0\right).$ Define the sequence $\left\{{\nu }_n\right\}$ in $\mathsf{{\rm Y}}$ by ${\nu }_n=S{\nu }_{n-1}=S^n{\nu }_0$ and ${\nu }_{n+1}=T{\nu }_n=T^n{\nu }_0$ for all $n\ge 1.$ If there is $n_0\in \mathbb{N}$ such that ${\nu }_{n_0}={\nu }_{n_0+1},$ then ${\nu }_{n_0}=S{\nu }_{n_0}=T{\nu }_{n_0}.$ Thus, S and T have a common fixed point. It completes the proof. Thus, suppose that ${\nu }_n\ne {\nu }_{n+1},$ for all $n,$ that is,

$$\begin{array}{c}\hfill \rho (S{\nu }_{n-1},T{\nu }_n)>0,\mathrm{for}\mathrm{all}n\in \mathbb{N}.\end{array}$$

(3)

Since $\alpha \left({\nu }_0,{\nu }_1\right)=\alpha \left(S{\nu }_1,T{\nu }_0\right)\ge \eta \left({\nu }_0,{\nu }_1\right)=\eta \left(S{\nu }_1,T{\nu }_0\right)$ and the pair $(S,T)$ is $\alpha$-admissible, one writes

$$\alpha ({\nu }_1,{\nu }_2)=\alpha (S{\nu }_0,T{\nu }_1)\ge \eta (S{\nu }_0,T{\nu }_1)=\eta ({\nu }_1,{\nu }_2).$$

Once more, by utilizing the $\alpha$-admissible concept to the function $\eta$, we have

$$\alpha ({\nu }_2,{\nu }_3)=\alpha (T{\nu }_1,S{\nu }_2)\ge \eta (T{\nu }_1,S{\nu }_2)=\eta ({\nu }_2,{\nu }_3).$$

Repeating this strategy n-times, we deduce

$$\begin{array}{c}\hfill \alpha ({\nu }_n,{\nu }_{n+1})\ge \eta ({\nu }_n,{\nu }_{n+1}),\mathrm{for}\mathrm{all}n\in \mathbb{N}\cup \left\{0\right\}.\end{array}$$

(4)

Combining (3) and (4), we deduce that

$$\begin{array}{c}\hfill ({\nu }_n,{\nu }_{n+1})\in \mathcal{A}(S,T,\alpha ,\eta ),\mathrm{for}\mathrm{all}n\ge 0\cup \left\{0\right\}.\end{array}$$

(5)

Taking (2) and (5) into consideration, we find that

$$\begin{array}{c}\hfill \xi \left(\rho ({\nu }_n,{\nu }_{n+1})\right)=\xi \left(\rho (S{\nu }_{n-1},T{\nu }_n)\right)\le {\left[\xi \left(\psi \left(K({\nu }_{n-1},{\nu }_n)\right)\right)\right]}^k,\mathrm{for}\mathrm{all}n\in \mathbb{N},\end{array}$$

where

$$\begin{array}{ccc}K({\nu }_{n-1},{\nu }_n)\hfill & =& max\{\rho ({\nu }_{n-1},{\nu }_n),\rho ({\nu }_{n-1},S{\nu }_{n-1}),\rho ({\nu }_n,T{\nu }_n)\}\hfill \\ & =& max\{\rho ({\nu }_{n-1},{\nu }_n),\rho ({\nu }_{n-1},{\nu }_n),\rho ({\nu }_n,{\nu }_n)\}\hfill \\ & =& \rho ({\nu }_{n-1},{\nu }_n).\hfill \end{array}$$

(6)

Since $\xi$ is nondecreasing, one writes that

$$\xi \left(\rho ({\nu }_n,{\nu }_{n+1})\right)<{\left[\xi \left(\rho ({\nu }_{n-1},{\nu }_n)\right)\right]}^k,\mathrm{for}\mathrm{all}n\in \mathbb{N}.$$

Letting ${\nu }_n=\rho ({\nu }_n,{\nu }_{n+1})$ for all $n\in \mathbb{N}$ and from the over inequality, we infer

$$\xi \left({\nu }_n\right)<{\left[\xi \left(t_{n-1}\right)\right]}^k<{\left[\xi \left(t_{n-1}\right)\right]}^{k^2}<\cdots <{\left[\xi \left(t_0\right)\right]}^{k^n}.$$

Thus, for all $n\in \mathbb{N},$ we deduce

$$1<\xi \left({\nu }_n\right)<{\left[\xi \left(t_0\right)\right]}^{k^n}.$$

(7)

Carrying out the limit of term (7) as n tends to $\infty ,$

$$\underset{n\to +\infty }{lim}\xi \left({\nu }_n\right)=1,$$

which implies by $\left({\xi }_2\right)$ that

$$\underset{n\to +\infty }{lim}{\nu }_n=0.$$

(8)

To demonstrate that $\left\{{\nu }_n\right\}$ is a Cauchy sequence, we take two cases.

Case I: Let us consider condition $\left(\xi 3\right)$ as it is defined in Definition 1. Then there are $r\in (0,1)$ and $\lambda \in (0,\infty ]$ such that

$$\underset{n\to \infty }{lim}\frac{\xi \left({\nu }_n\right)-1}{{\left({\nu }_n\right)}^r}=\lambda .$$

(9)

Choose $\delta \in (0,\lambda ).$ By the conception of limit, there involves $n_1\in \mathbb{N}$ so that

$${\left[{\nu }_n\right]}^r\le {\delta }^{-1}[\xi \left({\nu }_n\right)-1],\mathrm{for}\mathrm{all}n>n_1.$$

Using (7) and the over inequality, we deduce

$$n{\left[{\nu }_n\right]}^r\le {\delta }^{-1}n({\left[\xi \left(t_0\right)\right]}^{k^n}-1),\mathrm{for}\mathrm{all}n>n_1.$$

This infers that

$$\begin{array}{c}\hfill \underset{n\to +\infty }{lim}n{\left[{\nu }_n\right]}^r=\underset{n\to +\infty }{lim}n{\left[\rho ({\nu }_n,{\nu }_{n+1})\right]}^r=0.\end{array}$$

Hence there is $n_2\in \mathbb{N}$ so that

$$\begin{array}{c}\hfill \rho ({\nu }_n,{\nu }_{n+1})\le \frac{1}{n^{1/r}},\mathrm{for}\mathrm{all}n>n_2.\end{array}$$

(10)

Given $m>n>n_2.$ At that point, utilizing the triangular inequality concept and (10), we deduce

$$\begin{array}{c}\hfill \rho ({\nu }_n,{\nu }_m)\le \sum _{k=n}^{m-1}\rho ({\nu }_k,{\nu }_{k+1})\le \sum _{k=n}^{m-1}\frac{1}{k^{1/r}}\le \sum _{k=n}^{\infty }\frac{1}{k^{1/r}}\end{array}$$

and hence $\left\{{\nu }_n\right\}$ is a Cauchy sequence in $\mathsf{{\rm Y}}.$

Case II: Let us consider condition $\left(\xi 3\right)$ as it is defined in Definition 2. We proceed in the beginning of proof as

$$\underset{n\to \infty }{lim}{\nu }_n=\underset{n\to +\infty }{lim}\rho ({\nu }_n,{\nu }_{n+1})=0,$$

and

$$\begin{array}{ccc}K({\nu }_{n-1},{\nu }_n)\hfill & =& max\{\rho ({\nu }_{n-1},{\nu }_n),\rho ({\nu }_{n-1},S{\nu }_{n-1}),\rho ({\nu }_n,T{\nu }_n)\}\hfill \\ & =& max\{\rho ({\nu }_{n-1},{\nu }_n),\rho ({\nu }_{n-1},{\nu }_n),\rho ({\nu }_n,{\nu }_n)\}\hfill \\ & =& \rho ({\nu }_{n-1},{\nu }_n).\hfill \end{array}$$

(11)

Also, since $\xi$ is non-decreasing, we deduce

$$\begin{array}{ccc}\hfill \xi \left(\rho ({\nu }_n,{\nu }_{n+1})\right)=\xi \left(\rho (S{\nu }_{n-1},T{\nu }_n)\right)& \le & {\left[\xi \left(\rho ({\nu }_{n-1},{\nu }_n)\right)\right]}^k\hfill \\ & \le & {\left[\xi \left(\rho ({\nu }_{n-2},{\nu }_{n-1})\right)\right]}^{k^2}\hfill \\ & \le & {\left[\xi \left(\rho ({\nu }_{n-3},{\nu }_{n-2})\right)\right]}^{k^3}\hfill \\ & ⋮& \hfill \\ & \le & \xi {\left(\rho ({\nu }_0,{\nu }_1)\right)}^{k^n},\hfill \end{array}$$

(12)

for all $n\in \mathbb{N}$.

Since $\xi$ is continuous on $(0,\infty )$ and by taking the limit as $n\to \infty$ in (12), we have again

$$\underset{n\to \infty }{lim}\xi \left(\rho ({\nu }_n,{\nu }_{n+1})\right)=1⟺\underset{n\to \infty }{lim}\rho ({\nu }_n,{\nu }_{n+1})=0,$$

Now, we claim that the sequence $\left\{{\nu }_n\right\}$ is Cauchy. Suppose the contrary. Then there exist $ϵ>0$ and two subsequences $\left\{{\nu }_{o\left(k\right)}\right\}$ and $\left\{{\nu }_{w\left(k\right)}\right\}$ of $\left\{{\nu }_n\right\}$ with $o_k>w_k>k$ such that

$$\rho ({\nu }_{w\left(k\right)},{\nu }_{o\left(k\right)})\ge ϵ,\rho ({\nu }_{w\left(k\right)-1},{\nu }_{o\left(k\right)})<ϵ,$$

for all $n\in \mathbb{N}$. By utilizing the triangular property,

$$\begin{array}{ccc}\hfill ϵ& \le & \rho ({\nu }_{w\left(k\right)},{\nu }_{o\left(k\right)})\le \rho ({\nu }_{w\left(k\right)},{\nu }_{o\left(k\right)-1})+\rho ({\nu }_{o\left(k\right)-1},{\nu }_{o\left(k\right)})\hfill \end{array}$$

(13)

$$\begin{array}{cc}<& ϵ+\rho ({\nu }_{o\left(k\right)-1},{\nu }_{o\left(k\right)}).\hfill \end{array}$$

(14)

By taking $k\to \infty$ in (12), we have

$$\underset{k\to \infty }{lim}\rho ({\nu }_{w\left(k\right)},{\nu }_{o\left(k\right)})=ϵ.$$

(15)

Since

$$\mid \rho ({\nu }_{w\left(k\right)},{\nu }_{o\left(k\right)-1})-\rho ({\nu }_{w\left(k\right)},{\nu }_{o\left(k\right)})\mid \le \rho ({\nu }_{o\left(k\right)},{\nu }_{o\left(k\right)-1})$$

we have ${lim}_{k\to \infty }\rho (S{\nu }_{w\left(k\right)-1},T{\nu }_{o\left(k\right)-2})={lim}_{k\to \infty }\rho ({\nu }_{w\left(k\right)},{\nu }_{o\left(k\right)-1})=ϵ.$ Essentially, we get that

$$\underset{k\to \infty }{lim}\rho ({\nu }_{w\left(k\right)},{\nu }_{o\left(k\right)-1})=\underset{k\to \infty }{lim}\rho ({\nu }_{w\left(k\right)-1},{\nu }_{o\left(k\right)-1})=\underset{k\to \infty }{lim}\rho (S{\nu }_{w\left(k\right)-2},T{\nu }_{o\left(k\right)-2})=ϵ.$$

Then, by the above assumptions, we have

$$\underset{n\to +\infty }{lim}\xi \left(\rho (S{\nu }_{w\left(k\right)},T{\nu }_{o\left(k\right)})\right)\le \xi {\left(\psi \left(\rho ({\nu }_{w\left(k\right)},{\nu }_{o\left(k\right)})\right)\right)}^k.$$

(16)

By taking $k\to \infty$ in (16), we have

$$\xi \left(ϵ\right)\le \xi {\left(\psi \left(ϵ\right)\right)}^k,$$

which is a contradiction since $k\in (0,1)$ and $\psi \left(t\right)<t$ for all $t>0$. Therefore, $\left\{{\nu }_n\right\}$ is a Cauchy sequence.

By the completeness of $(\mathsf{{\rm Y}},\rho )$, there is $u\in \mathsf{{\rm Y}}$ so that ${\nu }_n\to u$ as $n\to \infty .$ If $S,T$ are continuous, then ${\nu }_n=S{\nu }_{n-1}\to Su$ and ${\nu }_{n+1}=T{\nu }_n\to Tu.$ The uniqueness of the limit implies that $u=Su=Tu.$

Assume that there exists another common fixed point z of $S,T$ distinct from u, that is, $u\ne z$. At that point, it follows from the above assumptions that

$$\xi \left(\rho (u,z)\right)=\xi \left(\rho (Su,Tz)\right)\le \xi {\left(\psi \left(\rho (u,z)\right)\right)}^k,$$

which is a contradiction with respect to $k\in (0,1)$ and $\psi \left(t\right)<t$ for all $t>0$. Thus u is the unique common fixed point of S and T. □

The continuity of mappings in Theorem 3 can be replaced by a reasonable condition.

Theorem 4.

Let $(\mathsf{{\rm Y}},\rho )$ be a complete metric space and $S,T:\mathsf{{\rm Y}}\to \mathsf{{\rm Y}}$ be self-mappings. Assume that the following assumptions hold:

(i) 

the pair $(S,T)$ is α-admissible regarding to the function η;

(ii) 

the pair $(S,T)$ is an $(\alpha ,\eta ,\xi ,\psi )$-contraction;

(iii) 

there exists ${\nu }_0\in \mathsf{{\rm Y}}$ so that $\alpha \left({\nu }_0,S{\nu }_0\right)\ge \eta \left({\nu }_0,S{\nu }_0\right)$;

(iv) 

for every ${\left\{{\nu }_n\right\}}_{n\in \mathbb{N}}\subset \mathsf{{\rm Y}}$ such that ${\nu }_n\to \nu \in \mathsf{{\rm Y}}$ and $\alpha \left({\nu }_n,{\nu }_{n+1}\right)\ge \eta \left({\nu }_n,{\nu }_{n+1}\right)$ for all $n\in \mathbb{N},$ then $\alpha \left({\nu }_n,\nu \right)\ge \eta \left({\nu }_n,\nu \right)$ for all $n\in \mathbb{N}.$

Then S and T have a common fixed point.

Proof. 

Let us consider condition $\left(\xi 3\right)$ as it is defined in Definition 1 and by using the full proof of Theorem 3, define $\left\{{\nu }_n\right\}$ as ${\nu }_n=S{\nu }_{n-1}=S^n{\nu }_0$ and ${\nu }_{n+1}=T{\nu }_n=T^n{\nu }_0$ for all $n\in \mathbb{N}$. Assume that the sequence $\left\{{\nu }_n\right\}$ such that $\alpha ({\nu }_n,{\nu }_{n+1})\ge \eta ({\nu }_n,{\nu }_{n+1})$ for all $n\in \mathbb{N}$, is converging to $u\in \mathsf{{\rm Y}}$.

In the case that $\left(iv\right)$ holds, we have $\alpha ({\nu }_n,u)\ge \eta ({\nu }_n,u)$ for all $n\ge 0.$ If there is $k\in \mathbb{N}$ so that $\rho ({\nu }_{k+1},Tu)=0$ and $\rho (Su,{\nu }_{k+1})=0$, then clearly, $Su=Tu=u.$ So the proof is completed. Hence, there is $n_3\in \mathbb{N}$ so that $\rho (S{\nu }_n,Tu)>0$ for all $n>n_3.$ Thus, $({\nu }_n,u)\in \mathcal{A}(S,T,\alpha ,\eta )$ for all $n>n_3.$ Using Remark 1, we get

$$\begin{array}{c}\hfill \rho ({\nu }_{n+1},Tu)=\rho (S{\nu }_n,Tu)\le \psi \left(\rho ({\nu }_n,u)\right),\end{array}$$

and so

$$\begin{array}{c}\hfill 0<\rho ({\nu }_{n+1},Tu)<\rho ({\nu }_n,u)\mathrm{and}0<\rho (Su,{\nu }_{n+1})<\rho (u,{\nu }_n)\mathrm{for}\mathrm{all}n>n_3.\end{array}$$

By carrying the limit as n goes to ∞, we obtain $\rho (u,Tu)=0\Rightarrow u=Tu$ and $\rho (Su,u)=0\Rightarrow Su=u$. Hence, $Su=Tu=u.$

To demonstrate the uniqueness of the common fixed point, suppose that $\mathfrak{p},\mathfrak{q}$ are two common fixed points of S and T such that $\rho (\mathfrak{p},\mathfrak{q})>0.$ Then $\rho (S\mathfrak{p},T\mathfrak{q})>0$ and by the hypothesis $\alpha (\mathfrak{p},\mathfrak{q})\ge \eta (\mathfrak{p},\mathfrak{q})$, $(\mathfrak{p},\mathfrak{q})\in \mathcal{A}(S,T,\alpha ,\eta ).$ Regarding Remark 1, we get

$$\begin{array}{c}\hfill \rho (\mathfrak{p},\mathfrak{q})=\rho (S\mathfrak{p},T\mathfrak{q})\le \psi \left(\rho \right(\mathfrak{p},\mathfrak{q}\left)\right)<\rho (\mathfrak{p},\mathfrak{q}),\end{array}$$

which infers that $\mathfrak{p}=\mathfrak{q}.$ □

Example 3.

Let $\mathsf{{\rm Y}}=[0,\infty )$ be endowed with the complete metric ρ defined by

$$\rho \left(\nu ,\varpi \right)=|\nu -\varpi |,$$

for all $\nu ,\varpi \in \mathsf{{\rm Y}}.$ Define $S,T:\mathsf{{\rm Y}}\to \mathsf{{\rm Y}}$ and $\alpha ,\eta :\mathsf{{\rm Y}}\times \mathsf{{\rm Y}}\to [0,\infty )$ by

$$S\nu =\left\{\begin{array}{cc}{\displaystyle \frac{1}{3}}{e}^{-4}\nu ,\hfill & if \nu \in \left[0,4\right],\hfill \\ 2\nu ,\hfill & if \nu >4,\hfill \end{array}\right.\mathit{and}T\nu =\left\{\begin{array}{cc}{\displaystyle \frac{1}{2}}{e}^{-4}\nu ,\hfill & if \nu \in \left[0,4\right],\hfill \\ 3\nu ,\hfill & if \nu >4.\hfill \end{array}\right.$$

$$\alpha \left(\nu ,\varpi \right)=\left\{\begin{array}{cc}{e}^{\nu +\varpi },\hfill & if \nu ,\varpi \in \left[0,4\right],\hfill \\ 0,\hfill & if \nu >4 or \varpi >4,\hfill \end{array}\right.\mathit{and}\eta \left(\nu ,\varpi \right)=\left\{\begin{array}{cc}{e}^{\nu },\hfill & if \nu ,\varpi \in \left[0,4\right],\hfill \\ 0,\hfill & if \nu >4 or \varpi >4.\hfill \end{array}\right.$$

We have

$$\begin{array}{cc}\hfill \mathcal{A}(S,T,\alpha ,\eta )& =\left\{(\nu ,\varpi )\in \mathsf{{\rm Y}}\times \mathsf{{\rm Y}}:\rho (S\nu ,T\varpi )>0\mathit{and}\alpha (\nu ,\varpi )\ge \eta (\nu ,\varpi )\right\}\hfill \\ \hfill & =\left\{(\nu ,\varpi )\in \mathsf{{\rm Y}}\times \mathsf{{\rm Y}}:\nu \ne \varpi \mathit{and}\nu ,\varpi \in \left[0,4\right]\right\}.\hfill \end{array}$$

Firstly, $(S,T)$ is an $(\alpha ,\eta ,\xi ,\psi )$-contraction with $k=e^{-2},$ $\psi \left(t\right)=\frac{t}{3}$ and $\xi \left(t\right)=e^{\sqrt{t{e}^t}}.$ Let $\nu ,\varpi \in \mathcal{A}(T,\alpha ),$ then $\nu ,\varpi \in \left[0,4\right]$ with $\nu \ne \varpi ,$

$$\begin{array}{cc}\hfill \xi \left(d\left(T\nu ,T\varpi \right)\right)& =\xi \left(e^{-4}\frac{\left|\nu -\varpi \right|}{3}\right)\hfill \\ \hfill & =e^{\sqrt{e^{-4}\frac{\left|\nu -\varpi \right|}{3}{e}^{e^{-4}\frac{\left|\nu -\varpi \right|}{3}}}}\hfill \\ \hfill & \le e^{e^{-2}\sqrt{\frac{\left|\nu -\varpi \right|}{3}{e}^{\frac{\left|\nu -\varpi \right|}{3}}}}\hfill \\ \hfill & =e^{e^{-2}\sqrt{\psi \left(K(\nu ,\varpi )\right)e^{\psi \left(\rho \right(\nu ,\varpi \left)\right)}}}\hfill \\ \hfill & ={\left[\xi \left(\psi \left(K(\nu ,\varpi )\right)\right)\right]}^k.\hfill \end{array}$$

This means that $(S,T)$ is an $(\alpha ,\eta ,\xi ,\psi )$-contraction.

Now, let $\nu ,\varpi \in \mathsf{{\rm Y}}$ be such that $\alpha \left(\nu ,\varpi \right)\ge \eta \left(\nu ,\varpi \right).$ Here, $\nu ,\varpi \in \left[0,4\right]$. Then $S\nu ,T\varpi \in \left[0,4\right]$ and so $\alpha \left(S\nu ,T\varpi \right)\ge \eta \left(S\nu ,T\varpi \right).$ Hence, the pair $(S,T)$ is α-admissible regarding η. Moreover, there exists ${\nu }_0=4$ so that $\alpha \left({\nu }_0,T{\nu }_0\right)$$\ge \eta \left({\nu }_0,T{\nu }_0\right)$ and $\alpha \left(S{\nu }_0,{\nu }_0\right)$$\ge \eta \left(S{\nu }_0,{\nu }_0\right).$

Let $\left\{{\nu }_n\right\}$ be a sequence in Υ so that ${\nu }_n\to \nu$ and $\alpha \left({\nu }_n,{\nu }_{n+1}\right)\ge \eta \left({\nu }_n,{\nu }_{n+1}\right)$ for all $n.$ Then, ${\nu }_n\in \left[0,4\right]$ and so $\nu \in \left[0,4\right]$ as ${\nu }_n\to \nu .$ Thus, $\alpha \left({\nu }_n,\nu \right)\ge \eta \left({\nu }_n,\nu \right)$.

Finally, all conditions of Theorems 3 and 4 are fulfilled, and so S and T have a unique common fixed point, which is $0.$

Furthermore, for $\nu =\varpi =0,$ we have

$$\begin{array}{c}\hfill \xi \left(d\left(S\nu ,T\varpi \right)\right)=\xi \left(\rho \left(S0,T0\right)\right)=\xi \left(0\right)\le {\left[\xi \left(0\right)\right]}^k={\left[\xi \left(\rho (\nu ,\varpi )\right)\right]}^k.\end{array}$$

For $\nu =\varpi =4$, we have

$$\begin{array}{c}\hfill \xi \left(d\left(S\nu ,T\varpi \right)\right)=\xi \left(\rho \left(S4,T4\right)\right)=\xi \left(0\right)\le {\left[\xi \left(0\right)\right]}^k={\left[\xi \left(\rho (\nu ,\varpi )\right)\right]}^k.\end{array}$$

Also, for $\nu =0$ and $\varpi =4,$ we have

$$\begin{array}{c}\hfill \xi \left(d\left(S\nu ,T\varpi \right)\right)=\xi \left(d\left(S0,T4\right)\right)=\xi \left(\frac{1}{3}{e}^{-4}4\right)\le {\left[\xi \left(4\right)\right]}^k={\left[\xi \left(\rho (\nu ,\varpi )\right)\right]}^k,\end{array}$$

for all $\xi \in \mathsf{\Gamma } and k\in (0,1).$ Therefore, Theorem 3 can applied to this example.

Corollary 1.

Let $(\mathsf{{\rm Y}},\rho )$ be a complete metric space and $S,T:\mathsf{{\rm Y}}\to \mathsf{{\rm Y}}$ be self-mappings. Then the pair $(S,T)$ has a unique common fixed point if the following assumptions hold:

(i) 

the pair $(S,T)$ is α-admissible;

(ii) 

there exists ${\nu }_0\in \mathsf{{\rm Y}}$ in which $\alpha \left({\nu }_0,S{\nu }_0\right)\ge 1$ and $\alpha \left({\nu }_0,T{\nu }_0\right)\ge 1$;

(iii) 

S and T are continuous;

(iv) 

there are $k\in (0,1),$$\psi \in \mathsf{\Psi }$ and $\xi \in \mathsf{\Gamma }$ or Θ so that

$$\nu ,\varpi \in \mathsf{{\rm Y}},\rho (S\nu ,T\varpi )>0⟹\xi \left(\alpha (\nu ,\varpi )\rho (S\nu ,T\varpi )\right)\le {\left[\xi \left(\psi \left(K(\nu ,\varpi )\right)\right)\right]}^k,$$

(17)

where

$$K(\nu ,\varpi )=max\left\{\rho \right(\nu ,\varpi ),\rho (\nu ,S\nu ),\rho (\varpi ,T\varpi \left)\right\}.$$

Proof. 

It follows from Theorem 3 by considering $\eta :\mathsf{{\rm Y}}\times \mathsf{{\rm Y}}\to \mathbb{R}$ via $\eta (\nu ,\varpi )=1.$ □

Corollary 2.

Let $(\mathsf{{\rm Y}},\rho )$ be a complete metric space and $S,T:\mathsf{{\rm Y}}\to \mathsf{{\rm Y}}$ be given mappings. Then the pair $(S,T)$ has a unique common fixed point if the following assumptions hold:

(i) 

the pair $(S,T)$ is α-admissible;

(ii) 

there exists ${\nu }_0\in \mathsf{{\rm Y}}$ so that $\alpha \left({\nu }_0,S{\nu }_0\right)\ge 1$ and $\alpha \left({\nu }_0,T{\nu }_0\right)\ge 1$;

(iii) 

for every ${\left\{{\nu }_n\right\}}_{n\in \mathbb{N}}\subset \mathsf{{\rm Y}}$ such that ${\nu }_n\to \nu \in \mathsf{{\rm Y}}$ and $\alpha \left({\nu }_n,{\nu }_{n+1}\right)\ge 1$ for all $n\in \mathbb{N},$ then $\alpha \left({\nu }_n,\nu \right)\ge 1$ for all $n\in \mathbb{N};$

(iv) 

there are $k\in (0,1),$$\psi \in \mathsf{\Psi }$ and $\xi \in \mathsf{\Gamma }$ or Θ so that

$$\nu ,\varpi \in \mathsf{{\rm Y}},\rho (S\nu ,T\varpi )>0⟹\xi \left(\alpha (\nu ,\varpi )\rho (S\nu ,T\varpi )\right)\le {\left[\xi \left(\psi \left(K(\nu ,\varpi )\right)\right)\right]}^k,$$

(18)

where

$$K(\nu ,\varpi )=max\left\{\rho \right(\nu ,\varpi ),\rho (\nu ,S\nu ),\rho (\varpi ,T\varpi \left)\right\}.$$

Proof. 

The rest of proof follows from Theorem 4 by considering $\eta :\mathsf{{\rm Y}}\times \mathsf{{\rm Y}}\to \mathbb{R}$ via $\eta (\nu ,\varpi )=1$. □

Corollary 3.

Let $S:\mathsf{{\rm Y}}\to \mathsf{{\rm Y}}$ be defined on a complete metric space $(\mathsf{{\rm Y}},\rho )$. Assume there are $k\in (0,1),$$\psi \in \mathsf{\Psi }$ and $\xi \in \mathsf{\Gamma }$ or Θ such that

$$\nu ,\varpi \in \mathsf{{\rm Y}},\rho (S\nu ,S\varpi )>0⟹\xi \left(\rho (S\nu ,S\varpi )\right)\le {\left[\xi \left(\psi \left(K(\nu ,\varpi )\right)\right)\right]}^k.$$

$$K(\nu ,\varpi )=max\left\{\rho \right(\nu ,\varpi ),\rho (\nu ,S\nu ),\rho (\varpi ,S\varpi \left)\right\}.$$

Then S has a unique fixed point if:

(i) 

S is α-admissible;

(ii) 

there exists ${\nu }_0\in \mathsf{{\rm Y}}$ so that $\alpha \left({\nu }_0,S{\nu }_0\right)\ge 1;$

(iii) 

S is continuous.

Proof. 

It follows from Corollary 1 by regarding $S=T$ and $\alpha (\nu ,\varpi )=1$. □

Corollary 4.

Let $S:\mathsf{{\rm Y}}\to \mathsf{{\rm Y}}$ be defined on a complete metric space $(\mathsf{{\rm Y}},\rho )$. Assume there are $k\in (0,1),$$\psi \in \mathsf{\Psi }$ and $\xi \in \mathsf{\Gamma }$ or Θ such that

$$\nu ,\varpi \in \mathsf{{\rm Y}},\rho (S\nu ,S\varpi )>0⟹\xi \left(\rho (S\nu ,S\varpi )\right)\le {\left[\xi \left(\psi \left(K(\nu ,\varpi )\right)\right)\right]}^k,$$

where

$$K(\nu ,\varpi )=max\left\{\rho \right(\nu ,\varpi ),\rho (\nu ,S\nu ),\rho (\varpi ,S\varpi \left)\right\}.$$

Then S has a unique fixed point if the following assumptions hold:

(i) 

S is α-admissible;

(ii) 

there exists ${\nu }_0\in \mathsf{{\rm Y}}$ so that $\alpha \left({\nu }_0,S{\nu }_0\right)\ge 1;$

(iii) 

for every ${\left\{{\nu }_n\right\}}_{n\in \mathbb{N}}\subset \mathsf{{\rm Y}}$ such that ${\nu }_n\to \nu \in \mathsf{{\rm Y}}$ and $\alpha \left({\nu }_n,{\nu }_{n+1}\right)\ge 1$ for all $n\in \mathbb{N},$ then $\alpha \left({\nu }_n,\nu \right)\ge 1$ for all $n\in \mathbb{N}.$

Proof. 

It follows from Corollary 2 by regarding $S=T$ and $\alpha (\nu ,\varpi )=1$. □

Corollary 5.

Let $S:\mathsf{{\rm Y}}\to \mathsf{{\rm Y}}$ be defined on a complete metric space $(\mathsf{{\rm Y}},\rho )$. Assume there exist $k\in (0,1)$ and $\xi \in \mathsf{\Gamma }$ or Θ such that

$$\nu ,\varpi \in \mathsf{{\rm Y}},\rho (S\nu ,S\varpi )>0⟹\xi \left(\rho (S\nu ,S\varpi )\right)\le {\left[\xi \left(\rho (\nu ,\varpi )\right)\right]}^k.$$

Then S has a unique fixed point if the following assumptions hold:

(i) 

S is α-admissible;

(ii) 

there is ${\nu }_0\in \mathsf{{\rm Y}}$ so that $\alpha \left({\nu }_0,S{\nu }_0\right)\ge 1;$

(iii) 

S is continuous.

Proof. 

It follows from Corollary 3 and the fact that $\rho (\nu ,\varpi )\le K(\nu ,\varpi ).$ □

Corollary 6.

Let $S:\mathsf{{\rm Y}}\to \mathsf{{\rm Y}}$ be a mapping on a complete metric space $(\mathsf{{\rm Y}},\rho )$. Assume there exist $k\in (0,1)$ and $\xi \in \mathsf{\Gamma }$ or Θ so that

$$\nu ,\varpi \in \mathsf{{\rm Y}},\rho (S\nu ,S\varpi )>0⟹\xi \left(\rho (S\nu ,S\varpi )\right)\le {\left[\xi \left(\rho (\nu ,\varpi )\right)\right]}^k.$$

Then S has a unique fixed point if the following assumptions hold:

(i) 

S is α-admissible;

(ii) 

there exists ${\nu }_0\in \mathsf{{\rm Y}}$ in order that $\alpha \left({\nu }_0,S{\nu }_0\right)\ge 1;$

(iii) 

for every ${\left\{{\nu }_n\right\}}_{n\in \mathbb{N}}\subset \mathsf{{\rm Y}}$ such that ${\nu }_n\to \nu \in \mathsf{{\rm Y}}$ and $\alpha \left({\nu }_n,{\nu }_{n+1}\right)\ge 1$ for all $n\in \mathbb{N},$ then $\alpha \left({\nu }_n,\nu \right)\ge 1$ for all $n\in \mathbb{N}.$

Proof. 

It comes from Corollary 4 and the fact that $\rho (\nu ,\varpi )\le K(\nu ,\varpi ).$ □

3. Applications

We start with giving some fixed point results on a metric space endowed with a graph. We also ensure the existence of a solution for a functional equation originating in dynamic programming.

3.1. Graphic Contractions

In view of the paper of Jachymski [24], we consider the following assumptions:

(a) 

$\left(\mathsf{{\rm Y}},\rho \right)$ is a metric space;

(b) 

$\Delta :=\left\{\left(\nu ,\nu \right):x\in \mathsf{{\rm Y}}\right\}$ is the diagonal of the Cartesian product $\mathsf{{\rm Y}}\times \mathsf{{\rm Y}}$;

(c) 

$\mathcal{G}$ is a graph of the set of its vertices $V\left(\mathcal{G}\right)$ and the set of its edges contains all loops $E\left(\mathcal{G}\right)$ such that each edge of graph $\mathcal{G}$ represents the distance between two vertices or a loop of the same vertex.

(For more details, see [25,26,27,28]).

Now, we give some notions and definitions related to a metric space endowed with a graph.

Definition 8

([24]). A map $T:\mathsf{{\rm Y}}\to \mathsf{{\rm Y}}$ is a $\mathcal{G}$-contractive map, if T preserves edges of $\mathcal{G},$ that is,

$$\forall \nu ,\varpi \in \mathsf{{\rm Y}},\left(\nu ,\varpi \right)\in E\left(\mathcal{G}\right)\Rightarrow \left(T\nu ,T\varpi \right)\in E\left(\mathcal{G}\right),$$

(19)

and T relates with weights of edges of $\mathcal{G}$ as the subsequent way:

$$\exists k\in (0,1),\forall \nu ,\varpi \in \mathsf{{\rm Y}},\left(\nu ,\varpi \right)\in E\left(\mathcal{G}\right)\Rightarrow d\left(T\nu ,T\varpi \right)\le k\rho (\nu ,\varpi ).$$

(20)

Definition 9

([24]). A map $T:\mathsf{{\rm Y}}\to \mathsf{{\rm Y}}$ is $\mathcal{G}$-continuous if given $\nu \in \mathsf{{\rm Y}}$ and a sequence $\left\{{\nu }_n\right\}$ with ${\nu }_n\to \nu$ as $n\to +\infty$ and $({\nu }_n,{\nu }_{n+1})\in E\left(\mathcal{G}\right)$ for all $n\in \mathbb{N}$, we have $T{\nu }_n\to T\nu$ as $n\to +\infty .$

The $\mathcal{G}$-continuity implies the continuity. Whereas generally, the contrary of this explanation is not true.

Definition 10.

Let $\left(\mathsf{{\rm Y}},\rho \right)$ be a metric space provided with a graph $\mathcal{G}$ and $S,T:\mathsf{{\rm Y}}\to \mathsf{{\rm Y}}$ be self-mappings. Let $E\left(\mathcal{G}\right)\subseteq \mathcal{G}\subseteq \mathsf{{\rm Y}}\times \mathsf{{\rm Y}}$ be defined by

$$\mathcal{G}(S,T)=\left\{(\nu ,\varpi ):\rho (S\nu ,T\varpi )>0\mathit{and}\left(\nu ,\varpi \right)\in E\left(\mathcal{G}\right)\right\}.$$

Then the pair $(S,T)$ is an (α-ξ-ψ)-$\mathcal{G}$-contraction if there are $k\in (0,1),$$\psi \in \mathsf{\Psi }$ and $\xi \in \mathsf{\Gamma }$ or Θ so that

$$\xi \left(\rho (S\nu ,T\varpi )\right)\le {\left[\xi \left(\psi \left(K(\nu ,\varpi )\right)\right)\right]}^k,\mathit{for}\mathit{all}(\nu ,\varpi )\in \mathcal{G}(S,T,G),$$

(21)

where

$$K(\nu ,\varpi )=max\left\{\rho \right(\nu ,\varpi ),\rho (\nu ,S\nu ),\rho (\varpi ,T\varpi \left)\right\}.$$

Theorem 5.

Let $\left(\mathsf{{\rm Y}},\rho \right)$ be a complete metric space endowed with a graph $\mathcal{G}$ and $S,T:\mathsf{{\rm Y}}\to \mathsf{{\rm Y}}$ be self-mappings. Suppose that the pair $(S,T)$ is an (α-ξ-ψ)-$\mathcal{G}$-contraction. Then S and T have a common fixed point if the following conditions are fulfilled:

(i) 

S and T preserve the edges of $\mathcal{G}$;

(ii) 

there exists ${\nu }_0\in \mathsf{{\rm Y}}$ so that $\left({\nu }_0,S{\nu }_0\right),\left({\nu }_0,T{\nu }_0\right)\in E\left(\mathcal{G}\right)$;

(iii) 

S and T are $\mathcal{G}$-continuous.

Moreover, if $(\nu ,\varpi )\in E\left(G\right)$ for all $\nu ,\varpi \in Fix\left(T\right),$ then the common fixed point is unique.

Proof. 

Define $\alpha :\mathsf{{\rm Y}}\times \mathsf{{\rm Y}}\to [0,\infty )$ by

$$\alpha \left(\nu ,\varpi \right)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if} \left(\nu ,\varpi \right)\in E\left(\mathcal{G}\right),\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Let $(\nu ,\varpi )\in \mathcal{A}(S,T,\alpha ).$ Then $\rho (S\nu ,T\varpi )>0$ and $\alpha \left(\nu ,\varpi \right)\ge 1.$ By definition of $\alpha ,$$\rho (S\nu ,T\varpi )>0$ and $(\nu ,\varpi )\in E\left(\mathcal{G}\right),$ that is, $(\nu ,\varpi )\in \mathcal{G}(S,T).$ Since $(S,T)$ is an ($\alpha$-$\xi$-$\psi$)-$\mathcal{G}$-contraction, we get

$$\xi \left(\rho (S\nu ,T\varpi )\right)\le {\left[\xi \left(\psi \left(K(\nu ,\varpi )\right)\right)\right]}^k,$$

then for

$$\begin{array}{c}\hfill ({\nu }_n,{\nu }_{n+1})\in \mathcal{A}(S,T,\mathcal{G},\alpha ),\mathrm{for}\mathrm{all}n\in \mathbb{N}\cup \left\{0\right\},\end{array}$$

we get

$$\begin{array}{c}\hfill \xi \left(\rho ({\nu }_n,{\nu }_{n+1})\right)=\xi \left(\rho (S{\nu }_{n-1},T{\nu }_n)\right)\le {\left[\xi \left(\psi \left(K({\nu }_{n-1},{\nu }_n)\right)\right)\right]}^k,\mathrm{for}\mathrm{all}n\in \mathbb{N},\end{array}$$

where

$$\begin{array}{ccc}\hfill K({\nu }_{n-1},{\nu }_n)& =& max\{\rho ({\nu }_{n-1},{\nu }_n),\rho ({\nu }_{n-1},S{\nu }_{n-1}),\rho ({\nu }_n,T{\nu }_n)\}\hfill \\ & =& max\{\rho ({\nu }_{n-1},{\nu }_n),\rho ({\nu }_{n-1},{\nu }_n),\rho ({\nu }_n,{\nu }_n)\}\hfill \\ & =& \rho ({\nu }_{n-1},{\nu }_n).\hfill \end{array}$$

(22)

Therefore,

$$\xi \left(\rho (S\nu ,T\varpi )\right)\le {\left[\xi \left(\psi \left(\rho (\nu ,\varpi )\right)\right)\right]}^k,\mathrm{for}\mathrm{all}(\nu ,\varpi )\in \mathcal{A}(S,T,\mathcal{G},\alpha ).$$

Now, we demonstrate that $(S,T)$ is $\alpha$-admissible. Let $\alpha \left(\nu ,\varpi \right)\ge 1$ for all $\nu ,\varpi \in \mathsf{{\rm Y}}.$ Then $\left(\nu ,\varpi \right)\in E\left(\mathcal{G}\right).$ By the virtue of $\left(i\right),$ we get $(S\nu ,T\varpi )\in E\left(\mathcal{G}\right),$ and hence $\alpha (S\nu ,T\varpi )\ge 1.$ This proves that the pair $(S,T)$ is $\alpha$-admissible. Also, it is easy to see that the condition $\left(iii\right)$ implies the condition $\left(iii\right)$ of Theorem 3. Thus, since all conditions of Theorem 3 hold, S and T have a common fixed point. Also, we show that S and T have a unique common fixed point. On the contrary, suppose that $\nu ,\varpi \in Fix\left(T\right).$ Then, by the hypothesis $\left(\nu ,\varpi \right)\in E\left(\mathcal{G}\right)$ and so $\alpha \left(\nu ,\varpi \right)\ge 1.$ By Theorem 3, S and T have a unique common fixed point. □

Example 4.

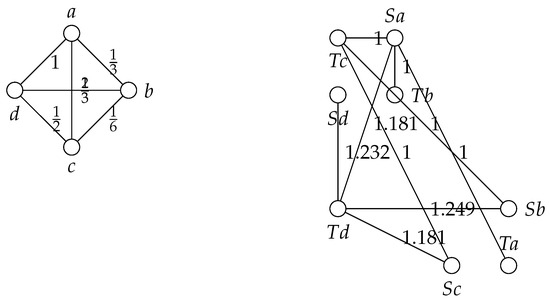
Following Example 2.8 in [28], let $\mathsf{{\rm Y}}=[0,1]$ be endowed with the usual metric. Let $\mathcal{G}$ be a graph with $V\left(\mathcal{G}\right)=\mathsf{{\rm Y}}$ and $E\left(\mathcal{G}\right)=\Delta \cup \left\{\left(\frac{1}{n},\frac{1}{n+1}\right):n\in \mathbb{N}\right\}\cup \left\{\left(\frac{1}{8},\frac{1}{4}\right)\right\}\cup \left\{\left(\frac{1}{n},0\right):n\in \mathbb{N}\right\}.$ Define $T:\mathsf{{\rm Y}}\to \mathsf{{\rm Y}}$ by

$$S\nu =\left\{\begin{array}{cc}{\displaystyle \frac{1}{2}},\hfill & if 0\le \nu <1,\hfill \\ {\displaystyle \frac{1}{3}},\hfill & if \nu =1.\hfill \end{array}\right.\mathit{and}T\nu =\left\{\begin{array}{cc}{\displaystyle \frac{1}{2}},\hfill & if 0\le \nu <1,\hfill \\ {\displaystyle \frac{1}{8}},\hfill & if \nu =1.\hfill \end{array}\right.$$

Now, we demonstrate that $S,T$ are (α,ξ,ψ)-$\mathcal{G}$-contractive maps with $k=\frac{1}{3},$ $\psi \left(t\right)=t$ and $\xi \left(t\right)=e^t.$ Note that $(\nu ,\varpi )\in \mathcal{G}(S,T)$ if and only if $\nu =1$ and $\varpi \in \{0,\frac{1}{3},\frac{1}{2}\}.$ Then, we need to check the subsequent cases:

Case 1.If $\nu =1$ and $\varpi =0,$ we have

$$\begin{array}{cc}\hfill & \left.\begin{array}{c}\xi \left(\rho \left(S1,T0\right)\right)=\xi \left(\left|{\displaystyle \frac{1}{3}}-{\displaystyle \frac{1}{2}}\right|\right)=\xi \left({\displaystyle \frac{1}{6}}\right)=e^{{\displaystyle \frac{1}{6}}}=1.181\hfill \\ {\left[\xi \left(\psi \left(\rho \left(1,0\right)\right)\right)\right]}^k={\left[\xi \left(1\right)\right]}^{\frac{1}{3}}={\left(e^1\right)}^{\frac{1}{3}}=1.396\hfill \end{array}\right\}\hfill \\ \hfill & ⟹\xi \left(\rho \left(S1,T0\right)\right)\le {\left[\xi \left(\psi \left(\rho \left(1,0\right)\right)\right)\right]}^k.\hfill \end{array}$$

Case 2.If $\nu =1$ and $\varpi =\frac{1}{3},$ we have

$$\begin{array}{cc}\hfill & \left.\begin{array}{c}\xi \left(\rho \left(S1,T\frac{1}{3}\right)\right)=\xi \left(\left|{\displaystyle \frac{1}{3}}-{\displaystyle \frac{1}{2}}\right|\right)=\xi \left({\displaystyle \frac{1}{6}}\right)=e^{{\displaystyle \frac{1}{6}}}=1.181\hfill \\ {\left[\xi \left(\psi \left(\rho \left(1,\frac{1}{3}\right)\right)\right)\right]}^k={\left[\xi \left({\displaystyle \frac{2}{3}}\right)\right]}^{\frac{1}{3}}={\left(e^{{\displaystyle \frac{2}{3}}}\right)}^{\frac{1}{3}}=1.249\hfill \end{array}\right\}\hfill \\ \hfill & ⟹\xi \left(\rho \left(S1,T\frac{1}{3}\right)\right)\le {\left[\xi \left(\psi \left(\rho \left(1,\frac{1}{3}\right)\right)\right)\right]}^k.\hfill \end{array}$$

Case 3.If $\nu =1$ and $\varpi =\frac{1}{2},$ we have

$$\begin{array}{cc}\hfill & \left.\begin{array}{c}\xi \left(\rho \left(S1,T\frac{1}{2}\right)\right)=\xi \left(\left|{\displaystyle \frac{1}{3}}-{\displaystyle \frac{1}{2}}\right|\right)=\xi \left({\displaystyle \frac{1}{6}}\right)=e^{{\displaystyle \frac{1}{6}}}=1.181\hfill \\ {\left[\xi \left(\psi \left(\rho \left(1,\frac{1}{2}\right)\right)\right)\right]}^k={\left[\xi \left({\displaystyle \frac{1}{2}}\right)\right]}^{\frac{1}{3}}={\left(e^{{\displaystyle \frac{1}{2}}}\right)}^{\frac{1}{3}}=1.181\hfill \end{array}\right\}\hfill \\ \hfill & ⟹\xi \left(\rho \left(S1,T\frac{1}{2}\right)\right)\le {\left[\xi \left(\psi \left(\rho \left(1,\frac{1}{2}\right)\right)\right)\right]}^k.\hfill \end{array}$$

Now, as we suppose $a=0,b=\frac{1}{3},c=\frac{1}{2},d=1$, we can represent these results by the two following matrices (see Table 1 and Table 2) and graphs (see Figure 1):

Table 1. A metric indicated by distances between vertices.

	a	b	c	d
a	0	$\frac{1}{3}$	$\frac{1}{3}$	1
b		0	$\frac{1}{6}$	$\frac{2}{3}$
c			0	$\frac{1}{2}$
d				0

Table 2. A metric indicated by distances between images of vertices under $\xi$-contractions.

	$\mathit{Ta}$	$\mathit{Tb}$	$\mathit{Tc}$	$\mathit{Td}$
$Sa$	1	1	1	$1.181$
$Sb$		1	1	$1.249$
$Sc$			1	$1.181$
$Sd$				$1.232$

Figure 1. A graph indicated by distances and $\xi$-contractions of distances between the vertices.

Thus, the pair $(S,T)$ is an (α-ξ-ψ)-$\mathcal{G}$-contraction in all possible cases. Also, all conditions of Theorem 5 are satisfied.

3.2. Existence Theorem for a Solution of a Functional Equation

In this subsection, as an application, we utilize the fixed point results proved in Section 3 to demonstrate the existence and uniqueness solutions for some nonlinear integral equations by regarding Corollary 3.

Let $\mathsf{{\rm Y}}=C\left(\right[a,b],\mathbb{R})$ denote to the set of all continuous functions specified on the interval $[a,b]$. We endow on $\mathsf{{\rm Y}}$ the metric $\rho :\mathsf{{\rm Y}}\times \mathsf{{\rm Y}}\to [0,\infty )$ defined by

$$\rho (\nu ,\varpi )=\underset{t\in [a,b]}{sup}\mid \nu \left(t\right)-\varpi \left(t\right)\mid ,$$

for all $\nu ,\varpi \in \mathsf{{\rm Y}}.$ Here, $(\mathsf{{\rm Y}},\rho )$ is a complete metric space. Let ⪯ be a partial order on $\mathsf{{\rm Y}}$ given as

$$\nu ⪯\varpi ⟺\nu \left(r\right)\le \varpi \left(r\right),r\in [a,b].$$

We consider the following integral equation:

$$\nu \left(t\right)=h\left(t\right)+{\int }_0^{t}P(t,r)f(r,\nu \left(r\right))dr,$$

(23)

where $h:[a,b]\to \mathbb{R}$, $P:[a,b]\times [a,b]\to [0,\infty )$ and $f:[a,b]\times \mathbb{R}\to \mathbb{R}$ are continuous functions.

Also, we define the operator $S:\mathsf{{\rm Y}}\to \mathsf{{\rm Y}}$ by

$$S\nu \left(t\right)=h\left(t\right)+{\int }_a^{b}P(t,r)f(r,\nu \left(r\right))dr.$$

(24)

Note that a solution of the integral Equation (23) is identical to that where the operator S has a fixed point.

Consider the following assumptions:

(A1) 

there exists $t_0\in [a,b]$ such that $\nu \left(t_0\right)\le S\nu \left(t_0\right);$

(A2) 

for all $\nu ,\varpi \in \mathsf{{\rm Y}}$ with $\nu ⪯\varpi$, there exists $\alpha \in (0,1)$ such that

$$\left|f\left(r,\nu \left(r\right)\right)-f\left(r,\varpi \left(r\right)\right)\right|\le \alpha \left|\nu \left(r\right)-\varpi \left(r\right)\right|,r\in [a,b];$$

(A3) 

${\displaystyle \underset{r\in [a,b]}{sup}\mid P(t,r)\mid \le 1}$ for all $t\in [a,b];$

(A4) 

S is nondecreasing and continuous on $[a,b].$

Theorem 6.

Assume the assumptions $\left(A1\right)$–$\left(A4\right)$ are fulfilled. Then the nonlinear integral Equation (23) has a unique solution.

Proof. 

Let $\nu ,\varpi \in \mathsf{{\rm Y}}$ be such that $\nu ⪯\varpi$. For all $t\in [a,b]$, we have

$$\begin{array}{cc}\hfill \left|S\nu \left(t\right)-S\varpi \left(t\right)\right|& =\left|{\int }_a^{b}P(t,r)(f(r,\nu \left(r\right))-f(r,\varpi \left(r\right)))dr\right|\hfill \\ \hfill & \le {\int }_a^{b}P(t,r)\left|\left(f\right(r,\nu \left(r\right))-f(r,\varpi \left(r\right)\left)\right)\right|dr\hfill \\ \hfill & \le {\int }_a^b\alpha |\nu \left(r\right)-\varpi \left(r\right)|dr\hfill \\ \hfill & \le \alpha K(\nu ,\varpi ),\hfill \end{array}$$

where

$$K(\nu ,\varpi )=max\left\{\rho \right(\nu ,\varpi ),\rho (\nu ,S\nu ),\rho (\varpi ,S\varpi \left)\right\}.$$

This implicates that

$$\rho (S\nu ,S\varpi )\le \alpha K(\nu ,\varpi ).$$

By defining $\xi \left(t\right)=e^{\sqrt{t}}$ ($t>0$) and $\psi \left(t\right)={\alpha }^{\frac{1}{2}}t$, we get

$$e^{\sqrt{\rho (S\nu ,S\varpi )}}\le e^{{\alpha }^{\frac{1}{4}}\sqrt{{\alpha }^{\frac{1}{2}}K(\nu ,\varpi )}}={\left[e^{\sqrt{\psi \left(K\right(\nu ,\varpi \left)\right)}}\right]}^k,$$

where $k={\alpha }^{\frac{1}{4}}$. Therefore, by Corollary 3 (by endowing on the function $\alpha$, the partial order on $\mathsf{{\rm Y}}$), S has a unique fixed point. Hence, the nonlinear integral Equation (23) has a unique solution. □