Iterating the Sum of Möbius Divisor Function and Euler Totient Function

Abstract

In this paper, according to some numerical computational evidence, we investigate and prove certain identities and properties on the absolute Möbius divisor functions and Euler totient function when they are iterated. Subsequently, the relationship between the absolute Möbius divisor function with Fermat primes has been researched and some results have been obtained.

1. Introduction and Motivation

Divisor functions, Euler $\phi$-function, and Möbius $\mu$-function are widely studied in the field of elementary number theory. The absolute Möbius divisor function is defined by

$$U\left(n\right):=|\sum _{d|n}d\mu \left(d\right)|.$$

Here, n is a positive integer and $\mu$ is the Möbius function. It is well known ([1], p. 23) that

$$\phi \left(n\right)=\sum _{d|n}\mu \left(d\right)\frac{n}{d},$$

where $\phi$ denotes the Euler $\phi$-function (totient function). If n is a square-free integer, then $U\left(n\right)=\phi \left(n\right)$. The first twenty values of $U\left(n\right)$ and $\phi \left(n\right)$ are given in Table 1.

Table 1. Values of $U\left(n\right)$ and $\phi \left(n\right)$$(1\le n\le 20)$.

n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
$U\left(n\right)$	1	1	2	1	4	2	6	1	2	4	10	2	12	6	8	1	16	2	18	4
$\phi \left(n\right)$	1	1	2	2	4	2	6	4	6	4	10	4	12	6	8	8	16	6	18	8

Let $U_0\left(n\right):=n$, $U\left(n\right):=U_1\left(n\right)$ and $U_m\left(n\right):=U_{m-1}\left(U\left(n\right)\right)$, where $m\ge 1$.

Next, to study the iteration properties of $U_m\left(n\right)$ ( resp., ${\phi }_{m^{\prime }}\left(n\right)$), we say the order (resp., class) of n, m-gonal (resp., $m^{\prime }$-gonal) absolute Möbius ( resp., totient) shape numbers, and shape polygons derived from the sum of absolute Möbius divisor (resp., Euler totient) function are as follows.

Definition 1.

(Order Notion) To study when the positive integer $U_m\left(n\right)$ is terminated at one, we consider a notation as follows. The order of a positive integer $n>1$ denoted $Or{d}_2\left(n\right)=m$, which is the least positive integer m when $U_m\left(n\right)=1$ and $U_{m-1}\left(n\right)\ne 1$. The positive integers of order 2 are usually called involutions. Naturally, we define $Or{d}_2\left(1\right)=0$. The first 20 values of $Or{d}_2\left(n\right)$ and $C\left(n\right)+1$ are given by Table 2. See [2].

Table 2. Values of $Or{d}_2\left(n\right)$ and $C\left(n\right)+1$$(1\le n\le 20)$.

n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
$Or{d}_2\left(n\right)$	0	1	2	1	2	2	3	1	2	2	3	2	3	3	2	1	2	2	3	2
$C\left(n\right)+1$	0	1	2	2	3	2	3	3	3	3	4	3	4	3	4	4	5	3	4	4

Remark 1.

Define ${\phi }_0\left(n\right)=n$, ${\phi }_1\left(n\right)=\phi \left(n\right)$ and ${\phi }_k\left(n\right)=\phi \left({\phi }_{k-1}\left(n\right)\right)$ for all $k\ge 2$. Shapiro [2] defines the class number $C\left(n\right)$ of n by that integer C such that ${\phi }_C\left(n\right)=2$. Some values of $Or{d}_2\left(n\right)$ are equal to them of $C\left(n\right)+1$. Shapiro [2] defined $C\left(1\right)+1=C\left(2\right)+1=1$. Here, we define $C\left(1\right)+1=0$ and $C\left(2\right)+1=1$. A similar notation of $Ord\left(n\right)$ is in [3].

Definition 2.

(Absolute Möbius m-gonal shape number and totient $m^{\prime }$-gonal shape number) If Ord${}_2\left(n\right)=m-2$ (resp., $C\left(n\right)+1=m^{\prime }$, we consider the set $\left\{(i,U_i\left(n\right))\right|i=0,\dots ,m-2\}$ (resp., $\left\{(i,{\phi }_i\left(n\right))\right|i=0,\dots ,m^{\prime }-2\}$ and add $\left(0,1\right)$. We then put $V_n=\left\{(i,U_i\left(n\right)\left)|i=0,\dots ,m-2\right.\right\}\cup \left\{\left(0,1\right)\right\}$ (resp., $R_n=\left\{(i,{\phi }_i\left(n\right)\left)|i=0,\dots ,m^{\prime }-2\right.\right\}\cup \left\{\left(0,1\right)\right\})$. Then we find a m-gon (resp., $m^{\prime }$-gon) derived from $V_n$ (resp., $R_n$). Here, we call n an absolute Möbius m-gonal shape number (resp., totient $m^{\prime }$-gonal shape number derived from U and $V_n$ (resp., φ and $R_n$) except $n=1$.

Definition 3.

(Convexity and Area) We use same notations, convex, non-convex, and area in [3]. We say that n is an absolute Möbius m-gonal convex (resp., non-convex) shape number with respect to the absolute Möbius divisor function U if $\left\{(i,U_i\left(n\right))\left|i=0,\dots ,m-2\right.\right\}$$\cup \left\{(0,1\right)\}$ is convex (resp., non-convex). Let $A\left(n\right)$ denote the area of the absolute Möbius m-gon derived from the absolute Möbius m-gonal shape number. Similarly, we define the totient $m^{\prime }$-gonal convex (resp., non-convex) shape number and $B\left(n\right)$ denote the area of the totient $m^{\prime }$-gon.

Example 1.

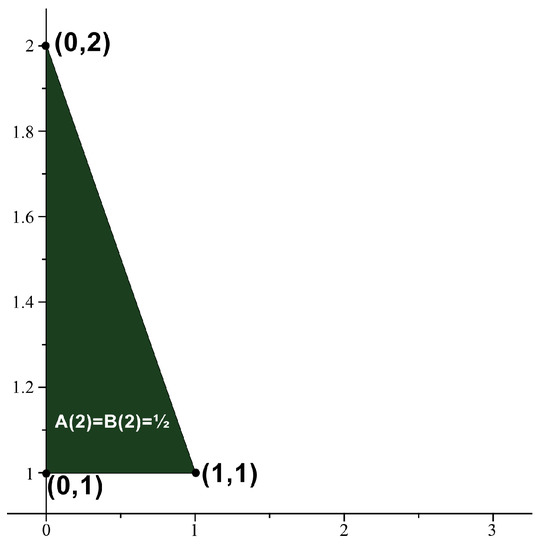
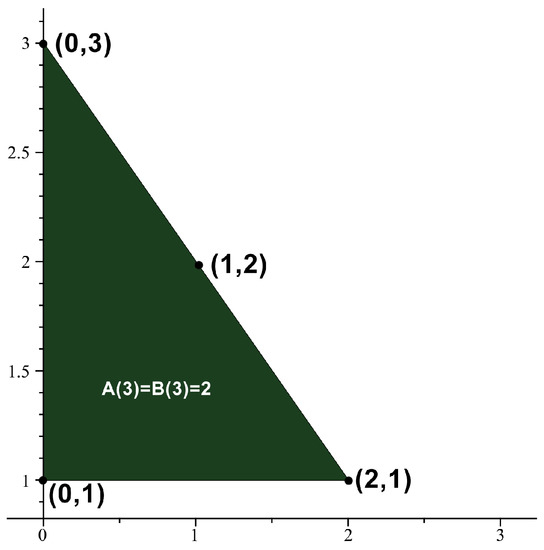
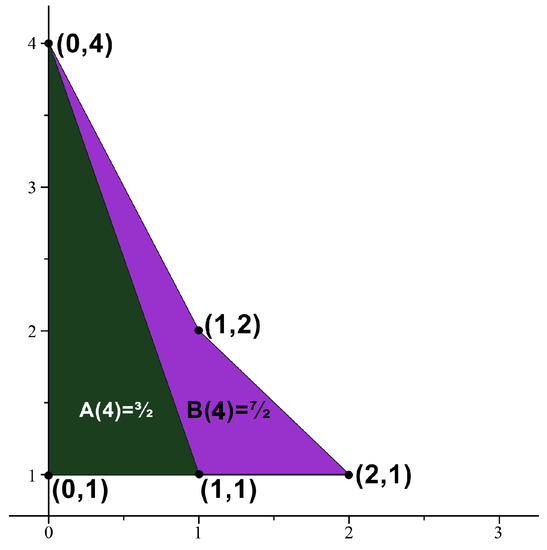
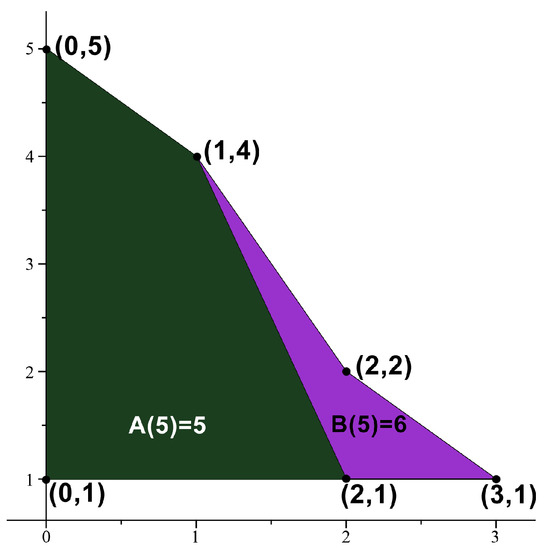
If $n=2$ then we obtain the set of points $V_2=R_2=\left\{\left(0,2\right),\left(1,1\right),\left(0,1\right)\right\}$. Thus, 2 is an absolute Möbius 3-gonal convex number with $A\left(2\right)=\frac{1}{2}$. See Figure 1. See Figure 2, Figure 3 and Figure 4 for absolute Möbius n-gonal shape numbers and totient n-gonal shape numbers with $n=2,3,4,5$. The first 19 values of $A\left(n\right)$ and $B\left(n\right)$ are given by Table 3.

Figure 1. $U\left(2\right)=\phi \left(2\right)$.

Figure 2. $U\left(3\right)=\phi \left(3\right)$.

Figure 3. $U\left(4\right)$ and $\phi \left(4\right)$.

Figure 4. $U\left(5\right)$ and $\phi \left(5\right)$.

Table 3. Values of $A\left(n\right)$ and $B\left(n\right)$ $(2\le n\le 20)$.

n	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
$A\left(n\right)$	$\frac{1}{2}$	2	$\frac{3}{2}$	5	$\frac{7}{2}$	9	$\frac{7}{2}$	5	$\frac{15}{2}$	17	$\frac{13}{2}$	18	$\frac{25}{2}$	14	$\frac{15}{2}$	23	$\frac{19}{2}$	27	$\frac{25}{2}$
$B\left(n\right)$	$\frac{1}{2}$	2	$\frac{5}{2}$	6	$\frac{7}{2}$	9	$\frac{15}{2}$	10	$\frac{17}{2}$	18	$\frac{19}{2}$	21	$\frac{25}{2}$	18	$\frac{37}{2}$	34	$\frac{29}{2}$	32	$\frac{41}{2}$

Kim and Bayad [3] considered the iteration of the odd divisor function S, polygon shape, convex, order, etc.

In this article, we considered the iteration of the absolute Möbius divisor function and Euler totient function and polygon types.

Now we state the main result of this article. To do this, let us examine the following theorem. For the proof of this theorem, the definitions and lemmas in the other chapters of this study have been utilized.

Theorem 1.

(Main Theorem) Let $p_1,\dots ,p_u$ be Fermat primes with $p_1<p_2\dots <p_u$,

$F_0:=\left\{p_1,\dots ,p_u\right\}$,

$F_1:=\left\{\prod _{i=1}^t{p}_i\mid p_i\in F_0,1\le t\le 5\right\}$,

$F_2:=\left\{\prod _{j=1}^r{p}_{i_j}\mid p_{i_j}\in F_0,p_1\le p_{i_1}<p_{i_2}\dots <p_{i_r}\le p_u,r\le u\right\}-\left(F_0\cup F_1\right)$.

If $Or{d}_2\left(m\right)=1$ or 2 then a positive integer $m>1$ is

$$\left\{\begin{array}{cc}\mathit{an}\mathit{absolute}Mö\mathit{bius}3\text{-}\mathit{gonal}\left(\mathit{triangular}\right)\mathit{shape}\mathit{number},& \mathit{if}m=2^k\mathit{or}m\in F_1\\ \mathit{an}\mathit{absolute}Mö\mathit{bius}4\text{-}\mathit{gonal}\mathit{convex}\mathit{shape}\mathit{number},& \mathit{if}m\in {\mathit{F}}_0-\left\{3\right\}\mathit{or}\mathit{m}\in {\mathit{F}}_2\\ \mathit{an}\mathit{absolute}Mö\mathit{bius}4\text{-}\mathit{gonal}\mathit{non}\text{-}\mathit{convex}\mathit{shape}\mathit{number},& \mathit{otherwise}.\end{array}\right.$$

Remark 2.

Shapiro [2] computed positive integer m when $C\left(m\right)+1=2.$ That is, $m=3,4,6.$ Let $C\left(m\right)+1=1or2.$ Then

(1) 

If $m=2,3$ then m are totient 3-gonal (triangular) numbers.

(2) 

If $m=4,5$ then m are totient 4-gonal non-convex numbers.

2. Some Properties of $U\left(n\right)$ and $\phi \left(n\right)$

It is well known [1,4,5,6,7,8,9,10,11,12,13,14] that Euler $\phi$-function have several interesting formula. For example, if $(x,y)=1$ with two positive integers x and y, then $\phi \left(xy\right)=\phi \left(x\right)\phi \left(y\right)$. On the other hand, if x is a multiple of y, then $\phi \left(xy\right)=y\phi \left(x\right)$ [2]. In this section, we will consider the arithmetic functions $U\left(n\right)$ and $\phi \left(n\right)$.

Lemma 1.

Let $n=p_1^{e_1}{p}_2^{e_2}\cdots p_r^{e_r}$ be a factorization of n, where $p_r$ be distinct prime integers and $e_r$ be positive integers. Then,

$$U\left(n\right)=\prod _{i=1}^r(p_i-1).$$

Proof. 

If $n=p_1^{e_1}{p}_2^{e_2}\cdots p_r^{e_r}$ is an arbitrary integer, then we easily check

$$\begin{array}{cc}\hfill U\left(n\right)& =\left|\sum _{d|n}\mu \left(d\right)d\right|\hfill \\ \hfill & =\left|1-p_1-p_2-\dots -p_r+p_1{p}_2+\dots +{\left(-1\right)}^n{p}_1{p}_2\dots p_r\right|\hfill \\ \hfill & =\left(p_1-1\right)\left(p_2-1\right)\dots \left(p_r-1\right).\hfill \end{array}$$

This is completed the proof of Lemma 1. □

Corollary 1.

If p is a prime integer and α is a positive integer, then $U\left(p\right)=p-1$ and $U\left(p^{\alpha }\right)=U\left(p\right)$. In particular, $U\left(2^{\alpha }\right)=1$.

Proof. 

It is trivial by Lemma 1. □

Corollary 2.

Let $n>1$ be a positive integer and let $Or{d}_2\left(n\right)=m$. Then,

$$U_0\left(n\right)>U_1\left(n\right)>U_2\left(n\right)>\cdots >U_m\left(n\right).$$

(1)

Proof. 

It is trivial by Lemma 1. □

Remark 3.

We compare $U\left(n\right)$ with $\phi \left(n\right)$ as follow on Table 4.

Table 4. $U\left(n\right)$ and $\phi \left(n\right)$.

	$\mathit{U}\left(\mathit{n}\right)$	$\mathit{\phi }\left(\mathit{n}\right)$
$n=p_1^{e_1}\cdots p_r^{e_r}$	$(p_1-1)\cdots (p_r-1)$	$(p_1^{e_1}-p_1^{e_1-1})\cdots (p_r^{e_r}-p_r^{e_r-1})$
$n=2^k$	1	$2^{k-1}$
sequences	$U_0\left(n\right)>U_1\left(n\right)>U_2\left(n\right)>\cdots$	${\phi }_0\left(n\right)>{\phi }_1\left(n\right)>{\phi }_2\left(n\right)>\cdots$

Lemma 2.

The function U is multiplicative function. That is, $U\left(mn\right)=U\left(m\right)U\left(n\right)$ with $(m,n)=1$. Furthermore, if m is a multiple of n, then $U\left(mn\right)=U\left(m\right)$.

Proof. 

Let $m=p_1^{e_1}{p}_2^{e_2}\dots p_i^{e_i}$ and $n=q_1^{f_1}{q}_2^{f_2}\dots q_s^{f_s}$ be positive integers. Then $p_1^{e_1},p_2^{e_2},\dots ,p_i^{e_i}$ and $q_1^{f_1},q_2^{f_2},\dots ,q_s^{f_s}$ are distinct primes. If $(m,n)=1$ and also $p|m$, $pn$, $q|n$, and $qm$ by Lemma 1, we note that

$$\begin{array}{cc}\hfill U\left(mn\right)& =\prod _{t_k\left|mn\right.}\left(t_k-1\right)\hfill \\ & =\prod _{p_i\left|m\right.}\left(p_i-1\right)\prod _{q_s\left|n\right.}\left(q_s-1\right)\hfill \\ & =U\left(m\right)U\left(n\right).\hfill \end{array}$$

Let m be a multiple of n. If $p_i|n$ then $p_i|m$. Thus, by Lemma 1, $U\left(mn\right)=U\left(m\right)$. This is completed the proof of Lemma 2. □

Remark 4.

Two functions $U\left(n\right)$ and $\phi \left(n\right)$ have similar results as follows on Table 5. Here, $n|m$ means that m is a multiple of n.

Table 5. $U\left(n\right)$ and $\phi \left(n\right)$.

	$(\mathit{m},\mathit{n})=1$	$\mathit{n}|\mathit{m}$
$U\left(mn\right)$	$U\left(m\right)U\left(n\right)$	$U\left(m\right)$
$\phi \left(mn\right)$	$\phi \left(m\right)\phi \left(n\right)$	$n\phi \left(m\right)$

Theorem 2.

For all $n\in \mathbb{N}-\left\{1\right\}$, there exists $m\in \mathbb{N}$ satisfying $U_m\left(n\right)=1$.

Proof. 

Let $n=p_1^{e_1}{p}_2^{e_2}\dots p_r^{e_r}$, where $p_1,\dots ,p_r$ be distinct prime integers with $p_1<p_2<\dots <p_r$.

We note that $U\left(n\right)=\prod _{i=1}^r\left(p_i-1\right)$ by Lemma 1.

If $r=1$ and $p_1=2$, then $U\left(n\right)=1$ by Corollary 1.

If $p_i$ is an odd positive prime integer, then $U\left(p_i^{e_i}\right)=p_i-1$ by Corollary 1.

We note that $p_i-1$ is an even integer. Then there exist distinct prime integers $q_{i_1},\dots ,q_{i_s}$ satisfying

$$p_i-1=2^{l_i}{q}_{i_1}^{f_{i_1}}\cdots q_{i_s}^{f_{i_s}},$$

where $f_{i_s}\ge 1$, $l_i\ge 1$ and $q_{i_1}<\cdots <q_{i_s}$. It is well known that $q_{i_s}\le \frac{p_i-1}{2}\le \frac{p_r-1}{2}$.

By Lemma 2, we get

$$U_2\left(p_i^{e_i}\right)=U(p_i-1)=U\left(q_{i_1}\right)\cdots U\left(q_{i_s}\right).$$

(2)

By using the same method in (2) for $1\le i_j\le s$, we get

$$\begin{array}{cc}\hfill U_2\left(n\right)& =U\left(\prod _{i=1}^r\left(p_i-1\right)\right)\hfill \\ \hfill & =U\left(2^{l_1+l_2+\dots +l_r}\prod _{i=1}^r{q}_{i_1}^{e_{i{}_1}}\dots q_{i_u}^{e_{i{}_u}}\right)\hfill \\ \hfill & =U\left(\prod _{i=1}^r{q}_{i_1}^{e_{i{}_1}}\dots q_{i_u}^{e_{i{}_u}}\right)\hfill \\ \hfill & =\prod _{i=1}^r(q_{i_1}-1)\cdots (q_{i_u}-1)\hfill \\ \hfill & =q_{j_1}^{\left(2\right)}\cdots q_{j_k}^{\left(2\right)}\hfill \end{array}$$

with $q_{j_1}^{\left(2\right)}<q_{j_2}^{\left(2\right)}<\dots <q_{j_k}^{\left(2\right)}$. It is easily checked that $q_{j_k}^{\left(2\right)}\le \max \{\frac{q_{1_u}-1}{2},\dots ,\frac{q_{r_u}-1}{2}\}$.

Using this technique, we can find l satisfying

$$U_{l-1}\left(n\right)=\left(q_{j_1}^{\left(l-1\right)}-1\right)\cdots \left(q_{j_u}^{\left(l-1\right)}-1\right)=2^h\prod _{u=1}^{s^{\prime }}{q}_{j_u}^{\left(l\right)}$$

with $q_{j_u}^{\left(l\right)}<100$.

By Appendix A (Values of $U\left(n\right)$$(1\le n\le 100)$), we easily find a positive integer v that $U_v\left(n^{\prime }\right)=1$ for $1\le n^{\prime }\le 100$. Thus, we get $U_v\left(U_{l-1}\left(n\right)\right)=1$. Therefore, we can find $m=v+l-1\in \mathbb{N}$ satisfying $U_m\left(n\right)=1$. □

Corollary 3.

For all $n\in \mathbb{N}-\left\{1\right\}$, there exists $m\in \mathbb{N}$ satisfying $Ord\left(n\right)=m$.

Proof. 

It is trivial by Theorem 2. □

Remark 5.

Kim and Bayad [3] considered iterated functions of odd divisor functions $S_m\left(n\right)$ and order of n. For order of divisor functions, we do not know $Ord\left(n\right)=\infty$ or not. But, functions $U_m\left(n\right)$ (resp., ${\phi }_l\left(n\right)$), we know $Ord\left(n\right)<\infty$ by Corollary 3 (resp., [15]).

Theorem 3.

Let $n>1$ be a positive integer. Then $Or{d}_2\left(n\right)=1$ if and only if $n=2^k$ for some $k\in \mathbb{N}$.

Proof. 

$\left(\Leftarrow \right)$ Let $n=2^k$. It is easy to see that $U\left(n\right)=U_1\left(n\right)=1$.

$\left(\Rightarrow \right)$ Let $n=p_1^{e_1}{p}_2^{e_2}\dots p_r^{e_r}$ be a factorization of n, and all $p_r$ are distinct prime integers. If $Or{d}_2\left(n\right)=1$, then by using Lemma 1 we can note that,

$$1=\left(p_1-1\right)\left(p_2-1\right)\dots \left(p_r-1\right).$$

(3)

According to all $p_r$ are distinct prime integers, then it is easy to see that there is only exist $p_1$ and that is $p_1=2$. Hereby $n=2^k$ for some $k\in \mathbb{N}$.

This is completed the proof of Theorem 3. □

Remark 6.

If $k>0$ then $2^k$ is an absolute Möbius 3-gonal (triangular) shape number with $A\left(2^k\right)=\frac{1}{2}\left(2^k-1\right)$ by Theorem 3.

Theorem 4.

Let n, m and $m^{\prime }$ be positive integers with greater than 1 and let $Or{d}_2\left(n\right)=m$ and $C\left(n\right)+1=m^{\prime }$. Then, $A\left(n\right),B\left(n\right)\in \mathbb{Z}$ if and only if $n\equiv 1(mod2)$. Furthermore,

$$A\left(n\right)=\sum _{k=1}^{m-1}{U}_k\left(n\right)+\frac{1}{2}(1+n)-m$$

(4)

and

$$B\left(n\right)=\sum _{k=1}^{m^{\prime }-1}{\phi }_k\left(n\right)+\frac{1}{2}(1+n)-m^{\prime }.$$

(5)

Proof. 

First, we consider $A\left(n\right)$. We find the set $\left\{\left(0,U_0\left(n\right)\right),\left(1,U_1\left(n\right)\right),\dots ,\left(m,U_m\left(n\right)\right)\right\}$. Thus, we have

$$\begin{array}{cc}\hfill A\left(n\right)& =\frac{1}{2}\left(U_0\left(n\right)+U_1\left(n\right)\right)+\frac{1}{2}\left(U_1\left(n\right)+U_2\left(n\right)\right)+\dots +\frac{1}{2}\left(U_{m-1}\left(n\right)+U_m\left(n\right)\right)-m\hfill \\ & =U_1\left(n\right)+\dots +U_{m-1}\left(n\right)+\frac{1}{2}\left(1+n\right)-m.\hfill \\ & \equiv \frac{1}{2}\left(1+n\right)(mod1).\hfill \end{array}$$

Similarly, we get (5). These complete the proof of Theorem 4. □

3. Classification of the Absolute Möbius Divisor Function $\mathit{U}\mathbf{\left(}\mathit{n}\mathbf{\right)}$ with $\mathit{O}\mathit{r}{\mathit{d}}_{\mathbf{2}}\mathbf{\left(}\mathit{n}\mathbf{\right)}\mathbf{=}\mathbf{2}$

In this section, we study integers n when $Or{d}_2\left(n\right)=2$. If $Or{d}_2\left(n\right)=2$, then n has three cases which are 3-gonal (triangular) shape number, 4-gonal convex shape number, and 4-gonal non-convex shape numbers in Figure 5.

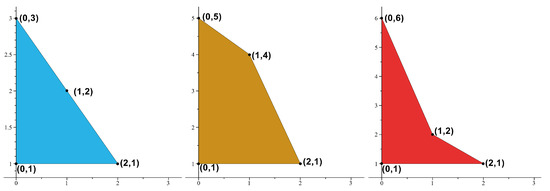
Figure 5. 3-gonal (triangular), 4-gonal convex, 4-gonal non-convex shapes.

Theorem 5.

Let $p_1,\dots ,p_r$ be Fermat primes and $e_1,\dots ,e_r$ be positive integers. If $n=2^k{p}_1^{e_1}{p}_2^{e_2}\dots p_r^{e_r}$, then $Or{d}_2\left(n\right)=2$.

Proof. 

Let

$$p_i=2^{2^{m_i}}+1\left(1\le i\le r\right)$$

(6)

be Fermat primes. By Corollary 1 and Lemma 2 we have

$$\begin{array}{cc}\hfill U\left(n\right)& =U\left(2^k{p}_1^{e_1}{p}_2^{e_2}\dots p_r^{e_r}\right)\hfill \\ & =U\left(2^k\right)U\left(p_1^{e_1}\right)U\left(p_2^{e_2}\right)\dots U\left(p_r^{e_r}\right)\hfill \\ & =\left(p_1-1\right)\left(p_2-1\right)\dots \left(p_r-1\right)\hfill \\ & =2^{2^{m_1}}{2}^{2^{m_2}}{\dots 2}^{2^{m_r}}\hfill \\ & =2^t.\hfill \end{array}$$

Thus, we can see that $U\left(n\right)=U_1\left(n\right)=2^t$ and $U_2\left(n\right)=U\left(U_1\left(n\right)\right)=U\left(2^t\right)=1$. Therefore, we get Theorem 5. □

The First 32 values of $U\left(n\right)$ and $\phi \left(n\right)$ for $n=2^k{p}_1^{e_1}{p}_2^{e_2}\dots p_r^{e_r}$ are given by Table A2 (see Appendix B).

Remark 7.

Iterations of the odd divisor function $S\left(n\right)$, the absolute Möbius divisor function $U\left(n\right)$, and Euler totient function $\phi \left(n\right)$ have small different properties. Table 6. gives an example of differences of ${\phi }_k\left(n\right),U_k\left(n\right)$, and $S_k\left(n\right)$ with $k=1,2$.

Table 6. ${\phi }_k\left(n\right),U_k\left(n\right)$, and $S_k\left(n\right)$ with $k=1,2$.

Function f	$\mathit{U}\left(\mathit{n}\right)$	$\mathit{\phi }\left(\mathit{n}\right)$	$\mathit{S}\left(\mathit{n}\right)$
$f_1\left(n\right)=1$	$n=2^k$	$n=2^k$	$n=2^k$
	$(k\ge 0)$	$(k=0,1)$	$(k\ge 0)$
$f_2\left(n\right)=1$	$n=2^k{p}_1^{e_1}\dots p_r^{e_r}$	$n=2^{k_1}{3}^{k_2}$	$n=2^k{q}_1\dots q_s$
	$(k\ge 0)$	$(k_1=0,1)$	$(k\ge 0$)
	$p_i:$ Fermat primes	$(k_2=0,1)$	$q_i:$ Mersenne primes
	(Theorem 5)	([2], p. 21)	([3], p. 3)

Lemma 3.

Let $n=p_i$ be Fermat primes. Then 3 is an absolute Möbius 3-gonal (triangular) shape number and $p_i(\ne 3)$ are absolute Möbius 4-gonal convex numbers.

Proof. 

The set $\left\{\left(0,3\right),\left(1,2\right),\left(2,1\right),\left(1,0\right)\right\}$ makes a triangle. Let $p_i=2^{2^{m_i}}+1$ be a Fermat primes except 3. We get $U\left(p_i\right)=2^{2^{m_i}}$. So, we get

$$\mathbf{A}=\left\{\left({0,2}^{2^{m_i}}+1\right),\left({1,2}^{2^{m_i}}\right),\left(2,1\right),\left(0,1\right)\right\}.$$

Because of $\left(2^{2^{m_i}}+1-2^{2^{m_i}}\right)<\left(2^{2^{m_i}}-1\right)$, the set $\mathbf{A}$ gives a convex shape. This completes the proof Lemma 3. □

Lemma 4.

Let $p_i$ be Fermat primes. Then $2^{m_1}{p}_i$ and $p_i^{m_2}$ are absolute Möbius 4-gonal non-convex shape numbers with $m_1,m_2(\ge 2)$ positive integers.

Proof. 

Let $p_i=2^{2^{m_i}}+1$ be a Fermat primes. Consider

$$2^{m_1}{p}_i-(p_i-1)=2^{m_1}·2^{2^{m_i}}-2^{2^{m_i}}and\left(p_i-1\right)-1=2^{2^{m_i}}-1.$$

So, $2^{m_1}{p}_i-(p_i-1)>\left(p_i-1\right)-1$. Thus, $2^{m_1}{p}_i$ are absolute Möbius 4-gonal non-convex shape numbers. Similarly, we get ${p_i}^{m_1}-(p_i-1)>\left(p_i-1\right)-1$.

Thus, these complete the proof Lemma 4. □

Lemma 5.

Let $p_1,\dots ,p_r$ be Fermat primes. Then $2p_1\dots p_r$ are absolute Möbius 4-gonal non-convex shape numbers.

Furthermore, if $m,e_1,\dots e_r$ are positive integers then $2^m{p}_1^{e_1}\dots p_r^{e_r}$ are absolute Möbius 4-gonal non-convex shape numbers.

Proof. 

The proof is similar to Lemma 4. □

Lemma 6.

Let r be a positive integer. Then

$$\prod _{i=0}^r\left(2^{2^i}+1\right)-2\prod _{i=0}^r{2}^{2^i}+1=0.$$

Proof. 

We note that

$$\prod _{i=0}^r\left(x^{2^i}+1\right)=\frac{x^{2^{r+1}}-1}{x-1}and\prod _{i=0}^r{x}^{2^i}=x^{2^{r+1}-1}.$$

Let $f\left(x\right):={\prod }_{i=0}^r\left(2^{2^i}+1\right)-2{\prod }_{i=0}^r{2}^{2^i}+1$. Thus $f\left(2\right)=0$. This is completed the proof of Lemma 6. □

Corollary 4.

Let $f_i\in F_1$. Then $f_i$ is an absolute Möbius 3-gonal (triangular) shape number.

Proof. 

It is trivial by Lemma 6. □

Remark 8.

Fermat first conjectured that all the numbers in the form of $f_n=2^{2^n}+1$ are primes [16]. Up-to-date there are only five known Fermat primes. That is, $f_0=3$, $f_1=5$, $f_2=17$, $f_3=257$, and $f_4=65537$.

Though we find a new Fermat prime $p_6$, 6th Fermat primes, we cannot find a new absolute Möbius 3-gonal (triangular) number by

$$\prod _{i=0}^4\left(2^{2^i}+1\right)\times \left(2^{2^{r^{\prime }}}+1\right)-2\left(\prod _{i=0}^4{2}^{2^i}\right)2^{2^{r^{\prime }}}+1>0.$$

(7)

Lemma 7.

Let $p_1,p_2,\dots ,p_r,p_t$ be Fermat primes with $p_1<p_2<\dots <p_r<p_t$ and $t>5$. If $n={\displaystyle \prod _{i=1}^r}{p}_i\in F_1$ then $n\times p_t$ are absolute Möbius 4-gonal convex shape numbers.

Proof. 

Let $p_t=2^{2^k}+1$ be a Fermat prime, where k is a positive integer. We note that $r\le 5$ and $p_t=2^{2^k}+1>2^{2^6}+1$. In a similar way in (7), we obtain

$$\begin{array}{cc}& p_1\dots p_r{p}_t-2\left(p_1-1\right)\dots \left(p_r-1\right)\left(p_t-1\right)+1=\\ & \left\{{\displaystyle \coprod _{i=0}^{r-1}}\left(2^{2^i}+1\right)\right\}\left(2^{2^k}-1\right)-2^{1+2^0+2^1+\dots +2^{r-1}+2^k}+1>0.\end{array}$$

(8)

By Theorem 5, $Or{d}_2(n\times p_t)=2$. By (8), $n\times p_t$ is an absolute Möbius 4-gonal convex shape number.

This completes the proof of Lemma 7. □

Lemma 8.

Let $p_1,p_2,\dots ,p_r,p_t$ be Fermat primes with $p_1<p_2<\dots <p_r<p_t$.

Then $m=p_1^{f_1}\cdots p_u^{f_u}$ are absolute Möbius 4-gonal non-convex shape numbers except $m\in F_0\cup F_1\cup F_2$.

Proof. 

Similar to Lemmas 5 and 7. □

Proof of Theorem 1 (Main Theorem).

It is completed by Remark 6, Theorem 5, Lemmas 3 and 4, Corollary 4, Remark 8, Lemmas 7 and 8. □

Remark 9.

If n are absolute Möbius 3-gonal (triangular) or 4-gonal convex shape numbers then n is the regular n-gon by Gauss Theorem.

Example 2.

The set $V_3$ is $\left\{\left(0,3\right),\left(1,2\right),\left(2,1\right),\left(0,1\right)\right\}$. Thus, a positive integer 3 is an absolute Möbius 3-gonal convex shape number.

Similarly, 15, 255, 65535, 4294967295 are absolute Möbius 3-gonal convex numbers derived from

$V_{15}=\left\{\left(0,15\right),\left(1,8\right),\left(2,1\right),\left(0,1\right)\right\}$,

$V_{255}=\left\{\left(0,255\right),\left(1,128\right),\left(2,1\right),\left(0,1\right)\right\}$,

$V_{65535}=\left\{\left(0,65535\right),\left(1,32768\right),\left(2,1\right),\left(0,1\right)\right\}$,

$V_{4294967295}=\{(0,4294967295),(1,2147483648),(2,1),(0,1)\}$.

Remark 10.

Let $Min\left(m\right)$ denote the minimal number of m-gonal number. By using Maple 13 Program, Table 7 shows us minimal numbers $Min\left(m\right)$ about from 3-gonal (triangular) to 14-gonal shape number.

Table 7. Values of Min(m).

m	Min(m)	Prime or Not	m	Min(m)	Prime or Not
3	2	prime	9	719	prime
4	5	prime	10	1439	prime
5	7	prime	11	2879	prime
6	23	prime	12	34,549	prime
7	47	prime	13	138,197	prime
8	283	prime	14	1,266,767	prime

Conjecture 1.

For any positive integer $m\left(\ge 3\right)$, $Min\left(m\right)$ is a prime integer.