Existence, Uniqueness and Exponential Stability of Periodic Solution for Discrete-Time Delayed BAM Neural Networks Based on Coincidence Degree Theory and Graph Theoretic Method
Abstract
1. Introduction
- According to the survey, there are few works on the exponential stability of periodic solution for discrete time delayed BAMNNs(DDBAMNNs).
- In this manuscript, together with the discrete and continuously distributed delay, the existence and periodic solution of discrete time BAMNNs is firstly proposed in the base of the graph theoretic approach, which generalizes and improves on the existing literature.
- To avoid the complication of finding the Lyapunov function, we construct a suitable Lyapunov function for a vertex system by using the results from graph theory.
2. Preliminaries and Model Description
Assumption
- (A1)
- For any and a continuous and bounded function and there exist constants such that
- (A2)
- The Kernel function , is bounded.
- (A3)
- and
- 1.
- , for all and .
- 2.
- , for all .
- 3.
- where denotes the Brouwer degree.
3. The Existence of Periodic Solution for DBAMNNs
- (P1)
- There exists a Lyapunov function such that
- (P2)
- There exist the constants and the matrix , the arbitrary function , for any such thatwhere .
- (P3)
- Along with each dicycle of a weighted strongly connected directed graph such that
- (P4)
- Suppose thatwhere is a non-singular matrix. Then (2) has at least one T-Periodic solution.
4. Uniqueness and Exponential Stability of Periodic Solution
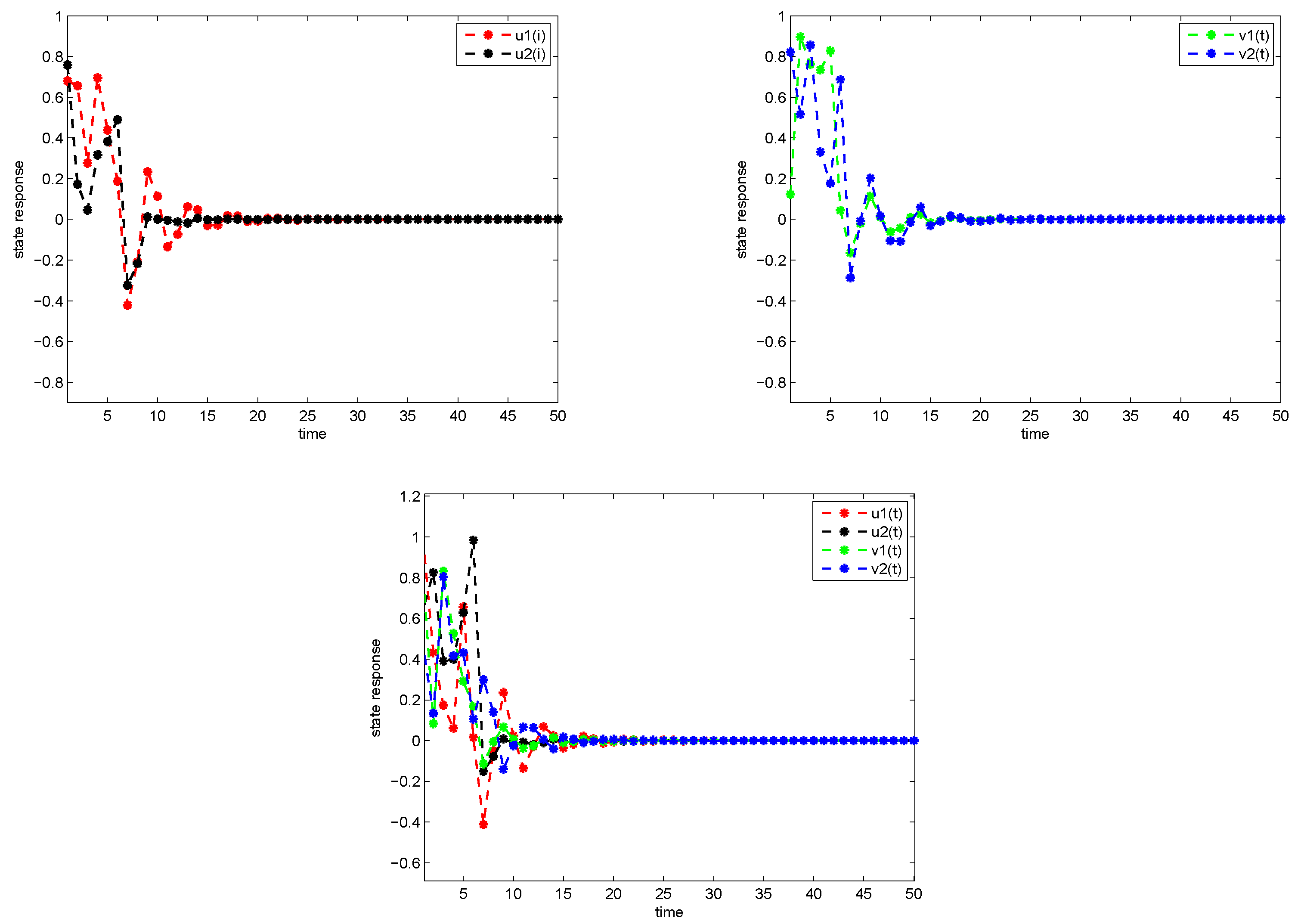
5. Illustrative Example
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, T.; Huang, L.; Yu, P.; Huang, W. Bifurcation of limit cycles at infinity in piecewise polynomial systems. Nonlinear Anal. Real World Appl. 2018, 41, 82–106. [Google Scholar] [CrossRef]
- Huang, C.; Cao, J.; Wen, F.; Yang, X. Stability Analysis of SIR Model with Distributed Delay on Complex Networks. PLoS ONE 2016, 11, e0158813. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Yi, T.; Zou, X. On spatial-temporal dynamics of Fisher-KPP equation with a shifting environment. Proc. Am. Math. Soc. 2019. [Google Scholar] [CrossRef]
- Hu, H.; Yuan, X.; Huang, L.; Huang, C. Global dynamics of an SIRS model with demographics and transfer from infectious to susceptible on heterogeneous networks. Math. Biosci. Eng. 2019, 16, 5729–5749. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Zou, X. Existence of an extinction wave in the fisher equation with a shifting habitat. Proc. Am. Math. Soc. 2017, 145, 4763–4771. [Google Scholar] [CrossRef]
- Huang, C.; Long, X.; Huang, L.; Fu, S. Stability of almost periodic Nicholson’s blowflies model involving patch structure and mortality terms. Can. Math. Bull. 2019. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, X.; Zhu, H.; Huang, C.; Tian, Z. The Heterogeneous Effects of FDI and Foreign Trade on CO2 Emissions: Evidence from China. Math. Probl. Eng. 2019, 2019, 9612492. [Google Scholar] [CrossRef]
- Kumari, S.; Chugh, R.; Cao, J.; Huang, C. Multi Fractals of Generalized Multivalued Iterated Function Systems in b-Metric Spaces with Applications. Mathematics 2019, 7, 967. [Google Scholar] [CrossRef]
- Tan, Y.; Huang, C.; Sun, B.; Wang, T. Dynamics of a class of delayed reaction-diffusion systems with Neumann boundary condition. J. Math. Anal. Appl. 2018, 458, 1115–1130. [Google Scholar] [CrossRef]
- Tan, Y.; Zhang, M. Global exponential stability of periodic solutions in a nonsmooth model of hematopoiesis with time-varying delays. Math. Methods Appl. Sci. 2017, 40, 5986–5995. [Google Scholar] [CrossRef]
- Wang, J.; Huang, C.; Huang, L. Discontinuity-induced limit cycles in a general planar piecewise linear system of saddleCfocus type. Nonlinear Anal. Hybrid Syst. 2019, 33, 162–178. [Google Scholar] [CrossRef]
- Yang, X.; Wen, S.; Liu, Z.; Li, C.; Huang, C. Dynamic Properties of Foreign Exchange Complex Network. Mathematics 2019, 7, 832. [Google Scholar] [CrossRef]
- Kosko, B. Adaptive bidirectional associative memories. Appl. Opt. 1987, 26, 4947–4960. [Google Scholar] [CrossRef] [PubMed]
- Rajchakit, G.; Pratap, A.; Raja, R.; Cao, J.; Alzabut, J.; Huang, C. Hybrid Control Scheme for Projective Lag Synchronization of RiemannCLiouville Sense Fractional Order Memristive BAM Neural Networks with Mixed Delays. Mathematics 2019, 7, 759. [Google Scholar] [CrossRef]
- Zuo, Y.; Wang, Y.; Liu, X. Adaptive robust control strategy for rhombus-type lunar exploration wheeled mobile robot using wavelet transform and probabilistic neural network. Comput. Appl. Math. 2018, 37, 314–337. [Google Scholar] [CrossRef]
- Kosko, B. Bidirectional associative memories. IEEE Trans. Syst. Man Cybern. 1988, 18, 49–60. [Google Scholar] [CrossRef]
- Zhu, Q.; Huang, C.; Yang, X. Exponential stability for stochastic jumping BAM neural networks with time-varying and distributed delays. Nonlinear Anal. Hybrid Syst. 2011, 5, 52–77. [Google Scholar] [CrossRef]
- Yang, C.; Huang, L.; Li, F. Exponential synchronization control of discontinuous nonautonomous networks and autonomous coupled networks. Complexity 2018, 2018, 6164786. [Google Scholar] [CrossRef]
- Duan, L.; Huang, L.; Guo, Z.; Fang, X. Periodic attractor for reactiondiffusion high-order hopfield neural networks with time-varying delays. Comput. Math. Appl. 2017, 73, 233–245. [Google Scholar] [CrossRef]
- Aouiti, C.; Gharbia, I.B.; Cao, J.; Alsaedi, A. Dynamics of impulsive neutral-type BAM neural networks. J. Frankl. Inst. 2019, 356, 2294–2324. [Google Scholar]
- Su, H.; Zhao, Y.; Li, W.; Ding, X. A graph-theoretic approach to exponential stability of stochastic BAM neural networks with time-varying delays. Neural Comput. Appl. 2016, 27, 2055–2063. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, D. Existence and global exponential stability of a periodic solution for a discrete-time interval general BAM neural networks. J. Frank. Inst. 2010, 347, 763–780. [Google Scholar] [CrossRef]
- Cai, Z.; Huang, J.; Huang, L. Generalized Lyapunov-Razumikhin method for retarded differential inclusions: Applications to discontinuous neural networks. Discret. Contin. Dyn. Syst. Ser. B 2017, 22, 3591–3614. [Google Scholar] [CrossRef]
- Duan, L.; Fang, X.; Huang, C. Global exponential convergence in a delayed almost periodic nicholsons blowflies model with discontinuous harvesting. Math. Methods Appl. Sci. 2017, 41, 1954–1965. [Google Scholar] [CrossRef]
- Huang, C.; Liu, B.; Tian, X.; Yang, L.; Zhang, X. Global convergence on asymptotically almost periodic SICNNs with nonlinear decay functions. Neural Process. Lett. 2019, 49, 625–641. [Google Scholar] [CrossRef]
- Agliari, E.; Migliozzi, D.; Tantari, D. Non-convex Multi-species Hopfield Models. J. Stat. Phys. 2018, 172, 1247–1269. [Google Scholar] [CrossRef]
- Kurchan, J.; Peliti, L.; Saber, M. Bidirectional associative memories. J. Phys. 1994, 11, 1627–1639. [Google Scholar]
- Liu, X.; Tang, M.; Martin, R.; Liu, X. Discrete-time BAM neural networks with variable delays. Phys. Lett. A 2007, 357, 322–330. [Google Scholar] [CrossRef]
- Maharajan, C.; Raja, R.; Cao, J.; Rajchakit, G.; Tu, Z.; Alsaedif, A. LMI-based results on exponential stability of BAM-type neural networks with leakage and both time-varying delays: A non-fragile state estimation approach. Appl. Math. Comput. 2018, 326, 33–55. [Google Scholar] [CrossRef]
- Maharajana, C.; Raja, R.; Cao, J.; Rajchakit, G. Novel global robust exponential stability criterion for uncertain inertial-type BAM neural networks with discrete and distributed time-varying delays via Lagrange sense. J. Frank. Inst. 2018, 355, 4727–4754. [Google Scholar]
- Sowmiya, C.; Raja, R.; Cao, J.; Li, X. Rajchakit, G. Discrete-time stochastic impulsive BAM neural networks with leakage and mixed time delays: An exponential stability problem. J. Frank. Inst. 2018, 355, 4404–4435. [Google Scholar] [CrossRef]
- Huang, C.; Liu, B. New studies on dynamic analysis of inertial neural networks involving non-reduced order method. Neurocomputing 2019, 325, 283–287. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, H. Periodicity of non-autonomous inertial neural networks involving proportional delays and non-reduced order method. Int. J. Biometh. 2019, 12, 1950016. [Google Scholar] [CrossRef]
- Huang, C.; Su, R.; Cao, J.; Xiao, S. Asymptotically stable high-order neutral cellular neural networks with proportional delays and D operators. Math. Comput. Simul. 2019. [Google Scholar] [CrossRef]
- Mohamad, S.; Gopalsamy, K. Exponential stability of continuous-time and discrete-time cellular neural networks with delays. Appl. Math. Comput. 2003, 135, 17–38. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, H.; Cao, J.; Hu, H. Stability and Hopf bifurcation of a delayed prey-predator model with disease in the predator. Int. J. Bifurc. Chaos 2019, 29, 1950091. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, H.; Huang, L. Almost periodicity analysis for a delayed Nicholson’s blowflies model with nonlinear density-dependent mortality term. Commun. Pure Appl. Anal. 2019, 18, 3337–3349. [Google Scholar] [CrossRef]
- Yue, D.; Li, H. Synchronization stability of continuous/discrete complex dynamical networks with interval time-varying delays. Neurocomputing 2010, 73, 809–891. [Google Scholar] [CrossRef]
- Liang, J.; Cao, J. Global asymptotic stability of bi-directional associative memory networks with distributed delays. Appl. Math. Comput. 2004, 152, 415–424. [Google Scholar] [CrossRef]
- Huang, C.; Qiao, Y.; Huang, L.; Agarwal, R. Dynamical behaviors of a food-chain model with stage structure and time delays. Adv. Differ. Equ. 2018, 2018, 186. [Google Scholar] [CrossRef]
- Huang, C.; Yang, Z.; Yi, T.; Zou, X. On the basins of attraction for a class of delay differential equations with non-monotone bistable nonlinearities. J. Differ. Equ. 2014, 256, 2101–2114. [Google Scholar] [CrossRef]
- Long, X.; Gong, S. New results on stability of Nicholson’s blowflies equation with multiple pairs of time-varying delays. Appl. Math. Lett. 2019. [Google Scholar] [CrossRef]
- Song, C.; Fei, S.; Cao, J.; Huang, C. Robust Synchronization of Fractional-Order Uncertain Chaotic Systems Based on Output Feedback Sliding Mode Control. Mathematics 2019, 7, 599. [Google Scholar] [CrossRef]
- Yang, X.; Zhu, Q.; Huang, C. Generalized lag-synchronization of chaotic mix-delayed systems with uncertain parameters and unknown perturbations. Nonlinear Anal. Real World Appl. 2011, 12, 93–105. [Google Scholar] [CrossRef]
- Raja, R.; Sakthivel, R.; Anthoni, S.M. Stability analysis for discrete-time stochastic neural networks with mixed time delays and impulsive effects. Can. J. Phys. 2010, 88, 885–898. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Z.; Liu, X. Robust stability of discrete-time stochastic neural networks with time-varying delays. Neurocomputing 2008, 71, 823–833. [Google Scholar] [CrossRef]
- Gao, S.; Li, S.; Wu, B. Periodic solution of discrete time periodic time-vayrying coupled systems on networks. Chaos Solitons Fract. 2017, 103, 246–253. [Google Scholar] [CrossRef]
- Huang, C.; Wen, S.; Huang, L. Dynamics of anti-periodic solutions on shunting inhibitory cellular neural networks with multi-proportional delays. Neurocomputing 2019, 357, 47–52. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, H.; Hu, C. Existence and stability of periodic solution of discrete-time Cohen-Grossberg neural networks with delays and impulses. Neurocomputing 2014, 142, 542–550. [Google Scholar] [CrossRef]
- Zhang, X.; Li, W.; Wang, K. The existence, uniqueness and global exponential stability of periodic solution for a coupled system on networks with time delays. Neurocomputing 2015, 173, 971–978. [Google Scholar] [CrossRef]
- Huang, C. Convergence on non-autonomous inertial neural networks with unbounded distributed delays. J. Exp. Theor. Artif. Intell. 2019. [Google Scholar] [CrossRef]
- Huang, C.; Cao, J.; Wang, P. Attractor and Boundedness of Switched Stochastic Cohen-Grossberg Neural Networks. Discret. Dyn. Nat. Soc. 2016, 2016, 4958217. [Google Scholar] [CrossRef]
- Li, M.Y.; Shuai, Z. Global-stability problem for coupled systems of differential equations on networks. J. Differ. Equ. 2010, 248, 1–20. [Google Scholar] [CrossRef]
- Zhang, C.; Li, W.; Wang, K. Boundedness for network of stochastic coupled van der Pol oscillators with time-varying delayed coupling. Appl. Math. Model. 2013, 37, 5394–5402. [Google Scholar] [CrossRef]
- Zhang, C.; Li, W.; Su, H.; Wang, K. Asymptotic boundedness for stochastic coupled systems on networks with Markovian switching. Neurocomputing 2014, 136, 180–189. [Google Scholar] [CrossRef]
- Zhang, C.; Li, W.; Wang, K. A graph-theoretic approach to stability of neutral stochastic coupled oscillators network with time-varying delayed coupling. Math. Meth. Appl. Sci. 2014, 79, 1179–1190. [Google Scholar] [CrossRef]
- Gui, Z.; Ge, W. Existence and uniqueness of periodic solutions of nonautonomous cellular neural networks with impulses. Phys. Lett. A 2006, 354, 84–94. [Google Scholar] [CrossRef]
- Xiang, H.; Yan, K.; Wang, B. Existence and global exponential stability of periodic solution for delayed high-order Hopfield-type neural networks. Phys. Lett. A 2006, 352, 341–349. [Google Scholar] [CrossRef]
- West, D.B. Introduction to Graph Theory; Prentice Hall: Upper Saller River, NJ, USA, 1996; pp. 1–57. [Google Scholar]
- Gaines, R.; Mawhin, J. Coincidence Degree and Nonlinear Diffential Equations; Springer: Berlin, Germany, 1977. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iswarya, M.; Raja, R.; Rajchakit, G.; Cao, J.; Alzabut, J.; Huang, C. Existence, Uniqueness and Exponential Stability of Periodic Solution for Discrete-Time Delayed BAM Neural Networks Based on Coincidence Degree Theory and Graph Theoretic Method. Mathematics 2019, 7, 1055. https://doi.org/10.3390/math7111055
Iswarya M, Raja R, Rajchakit G, Cao J, Alzabut J, Huang C. Existence, Uniqueness and Exponential Stability of Periodic Solution for Discrete-Time Delayed BAM Neural Networks Based on Coincidence Degree Theory and Graph Theoretic Method. Mathematics. 2019; 7(11):1055. https://doi.org/10.3390/math7111055
Chicago/Turabian StyleIswarya, Manickam, Ramachandran Raja, Grienggrai Rajchakit, Jinde Cao, Jehad Alzabut, and Chuangxia Huang. 2019. "Existence, Uniqueness and Exponential Stability of Periodic Solution for Discrete-Time Delayed BAM Neural Networks Based on Coincidence Degree Theory and Graph Theoretic Method" Mathematics 7, no. 11: 1055. https://doi.org/10.3390/math7111055
APA StyleIswarya, M., Raja, R., Rajchakit, G., Cao, J., Alzabut, J., & Huang, C. (2019). Existence, Uniqueness and Exponential Stability of Periodic Solution for Discrete-Time Delayed BAM Neural Networks Based on Coincidence Degree Theory and Graph Theoretic Method. Mathematics, 7(11), 1055. https://doi.org/10.3390/math7111055






