The Impact of Sinusoidal Surface Temperature on the Natural Convective Flow of a Ferrofluid along a Vertical Plate
Abstract
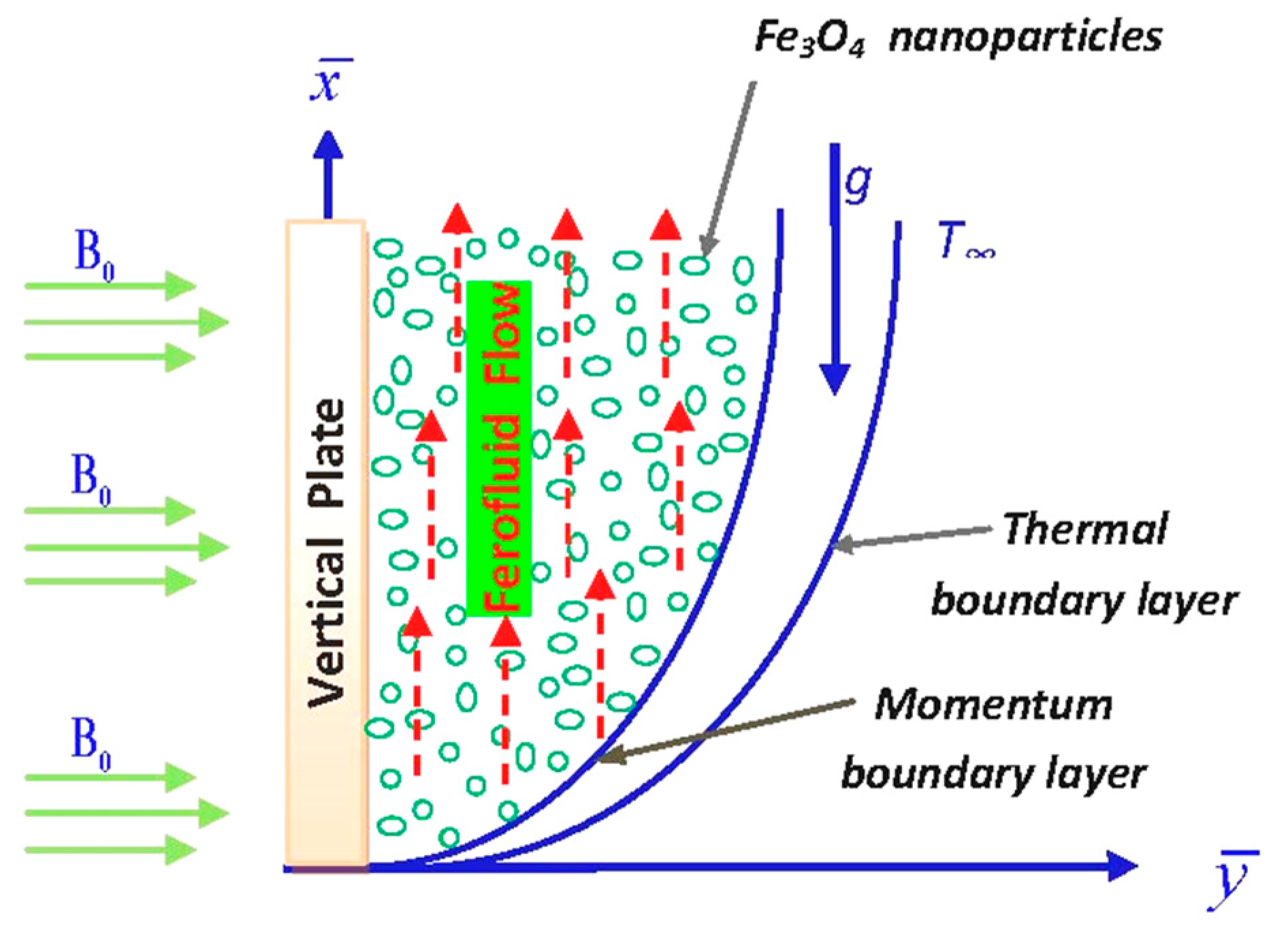
1. Introduction
2. Governing Equations
3. Hybrid Linearization–Differential Quadrature Method (HLDQM)
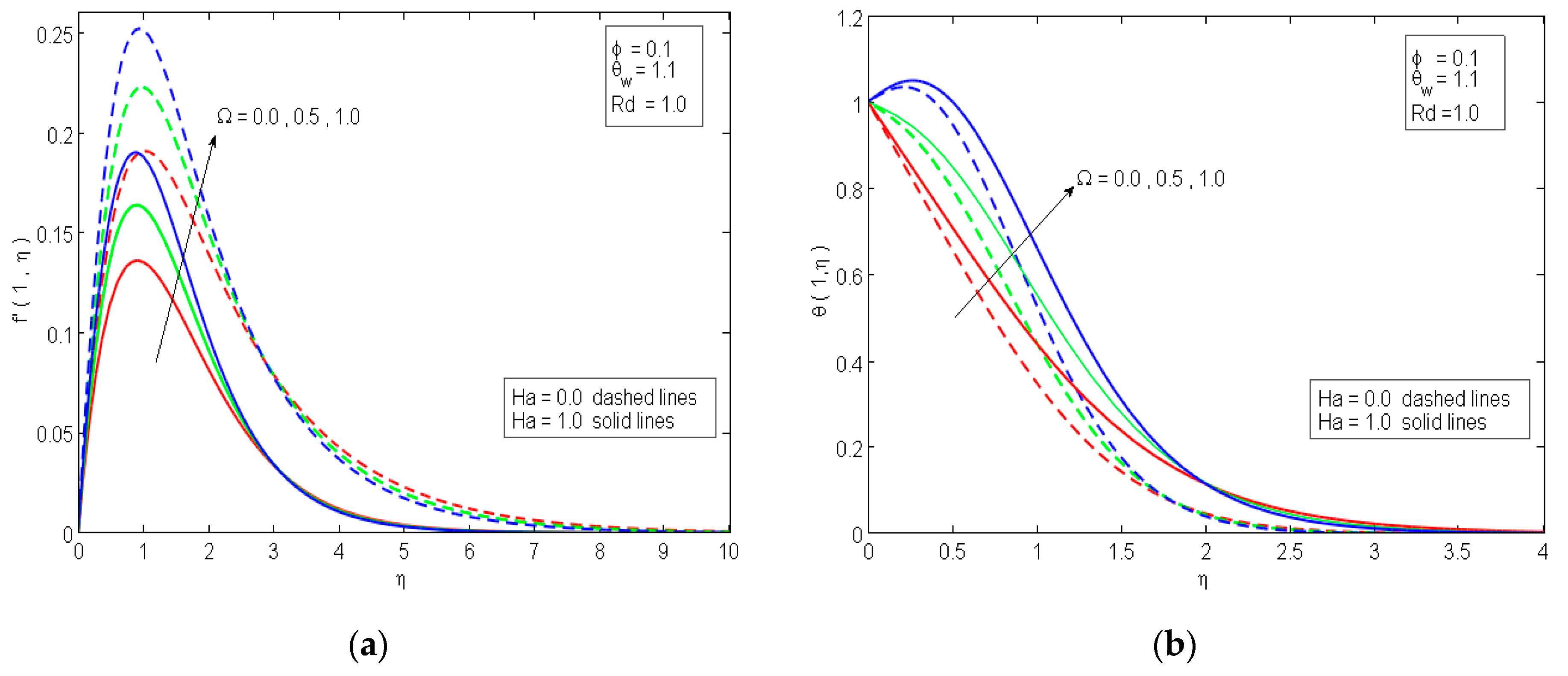
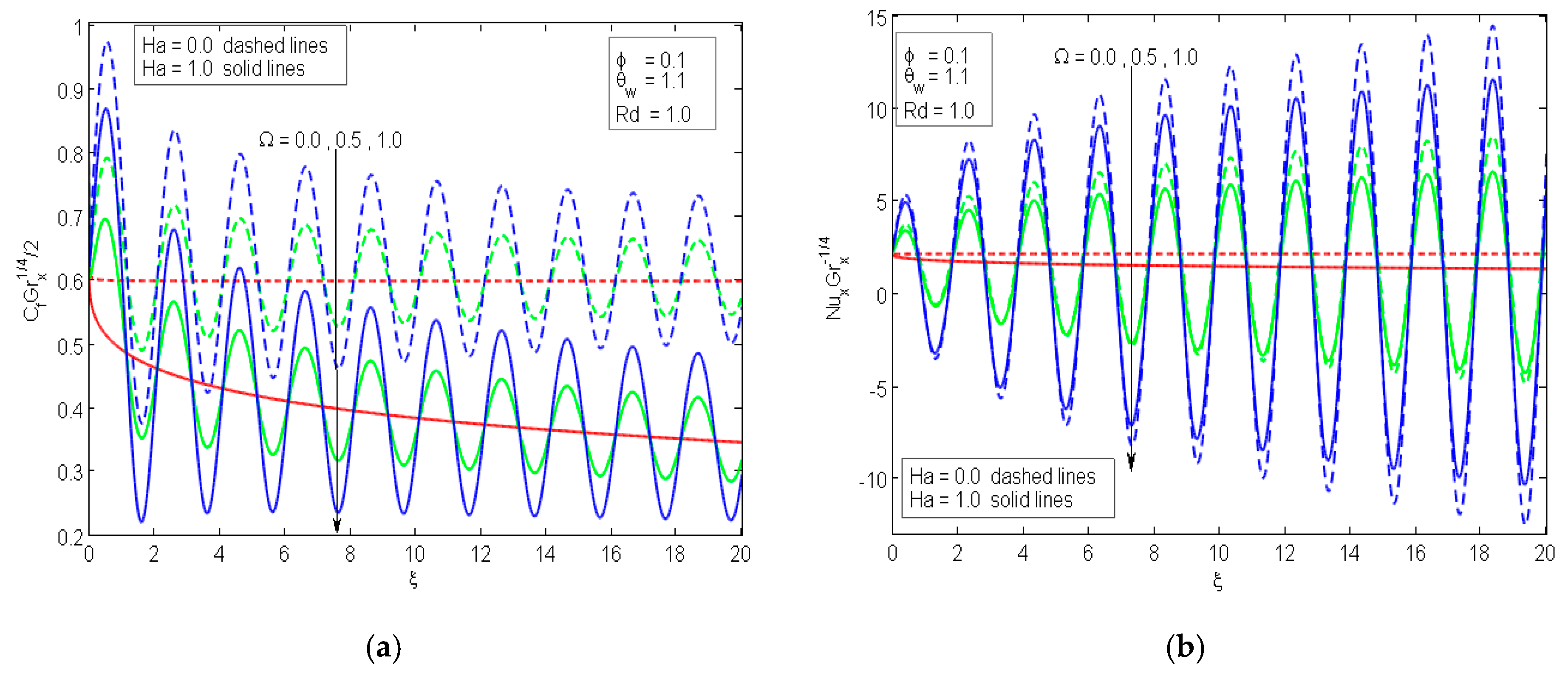
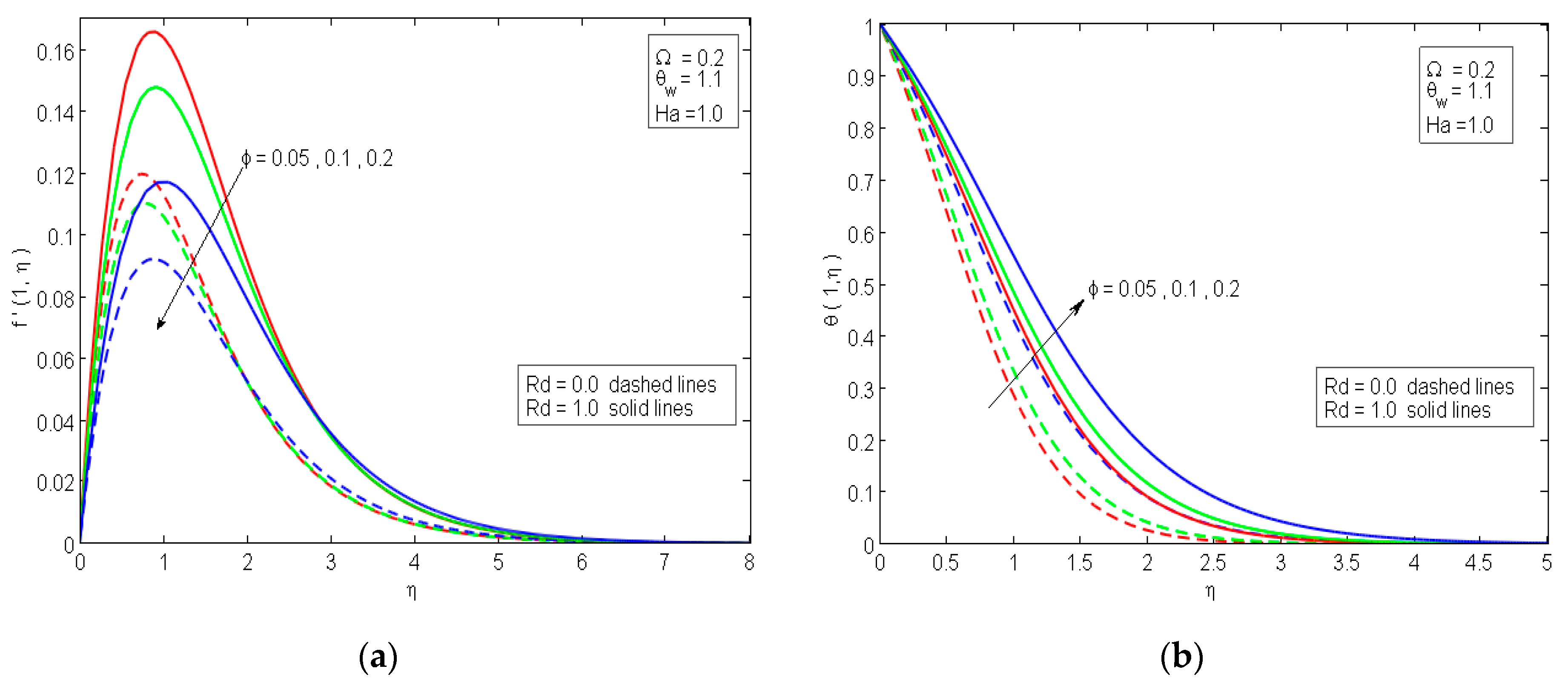
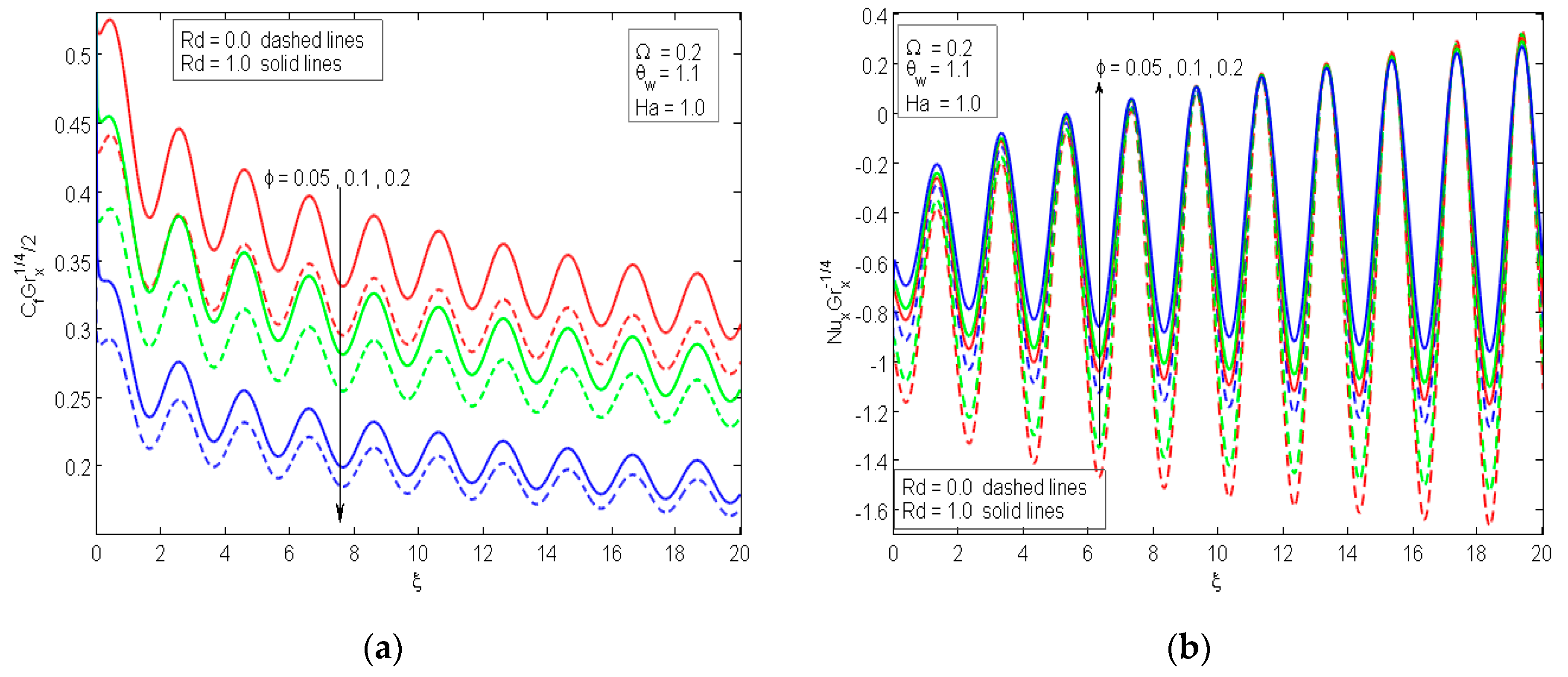
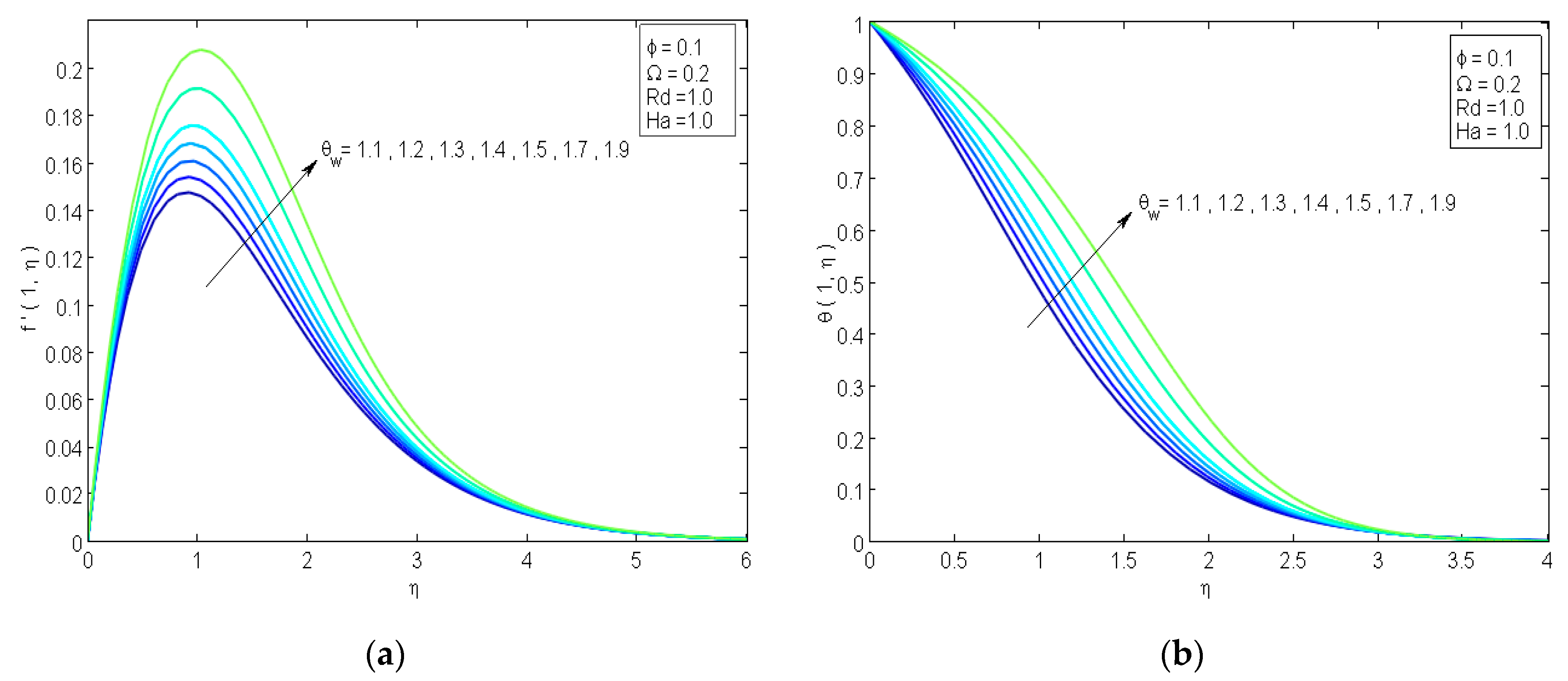
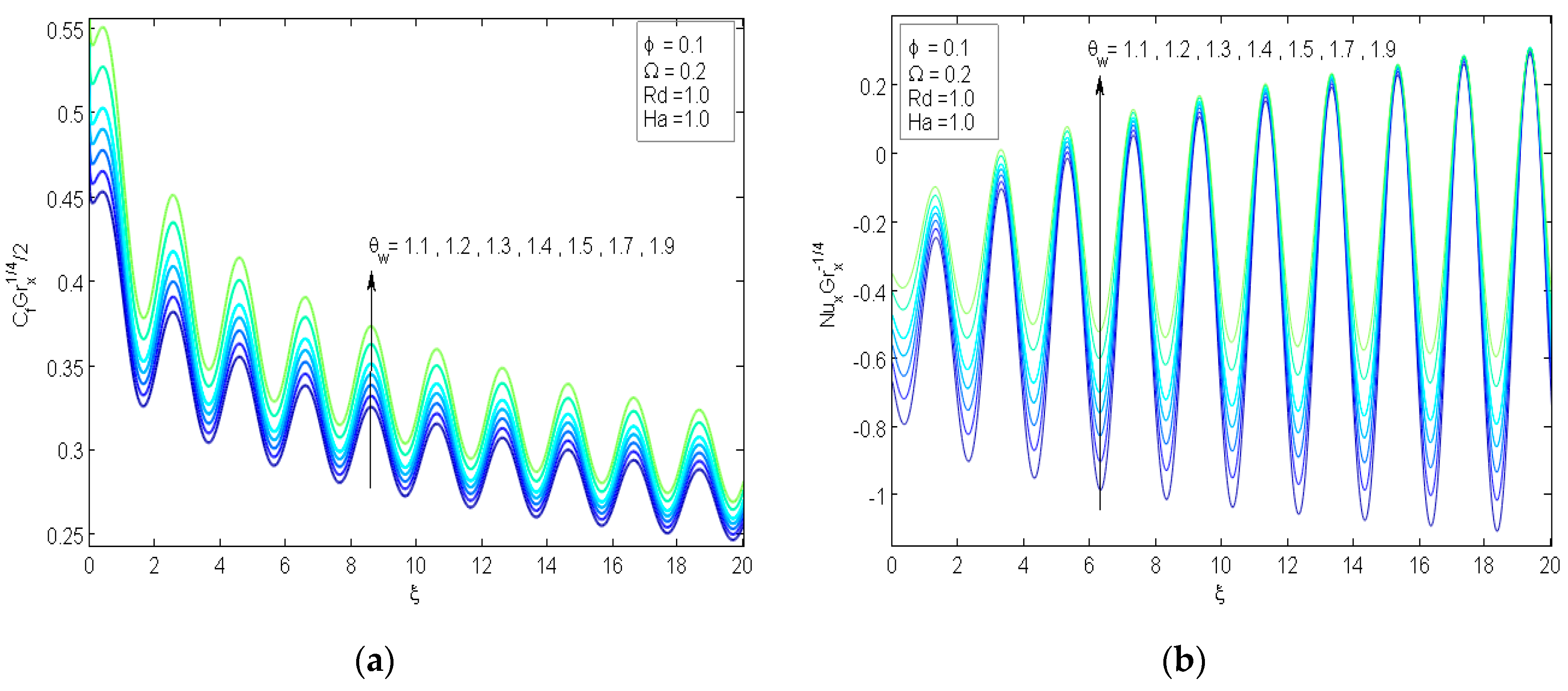
4. Analysis of the Results
5. Conclusions
- Applying the magnetic field to the ferroliquid generates a dragging force that decelerates the ferrofluid velocity and boosts the temperature curves;
- Higher estimations of thermal radiation have the potential to boost the velocity and temperature curves;
- The drag coefficient diminishes sufficiently, while an augmentation in the rate of heat transfer occurs as nanoparticles volume fraction builds;
- A boost in the temperature ratio parameter signifies a considerable enhancement in both the drag coefficient and local Nusselt number.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab.: Lemont, IL, USA, 1995. [Google Scholar]
- Choi, S.U.; Singer, D.A.; Wang, H.P. Developments and applications of non-Newtonian flows. Asme Fed 1995, 66, 99–105. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Kuznetsov, A.V.; Nield, D.A. Natural convective boundary-layer flow of a nanofluid past a vertical plate: A revised model. Int. J. Therm. Sci. 2014, 77, 126–129. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Pop, I. Boundary-layer flow of nanofluids over a moving surface in a flowing fluid. Int. J. Therm. Sci. 2010, 49, 1663–1668. [Google Scholar] [CrossRef]
- Rashad, A.M.; El-Hakiem, M.A.; Abdou, M.M. Natural convection boundary layer of a non-Newtonian fluid about a permeable vertical cone embedded in a porous medium saturated with a nanofluid. Comput. Math. Appl. 2011, 62, 3140–3151. [Google Scholar] [CrossRef]
- Rashad, A.M.; Abbasbandy, S.; Chamkha, A.J. Non-Darcy natural convection from a vertical cylinder embedded in a thermally stratified and nanofluid-saturated porous media. J. Heat Transf. 2014, 136, 022503. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Abbasbandy, S.; Rashad, A.M.; Vajravelu, K. Radiation effects on mixed convection over a wedge embedded in a porous medium filled with a nanofluid. Transp. Porous Media 2012, 91, 261–279. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Modather, M.; EL-Kabeir, S.M.M.; Rashad, A.M. Radiative effects on boundary-layer flow of a nanofluid on a continuously moving or fixed permeable surface. Recent Pat. Mech. Eng. 2012, 5, 176–183. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Rashad, A.M. Natural convection from a vertical permeable cone in a nanofluid saturated porous media for uniform heat and nanoparticles volume fraction fluxes. Int. J. Numer. Methods Heat Fluid Flow 2012, 22, 1073–1085. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Abbasbandy, S.; Rashad, A.M.; Vajravelu, K. Radiation effects on mixed convection about a cone embedded in a porous medium filled with a nanofluid. Meccanica 2013, 48, 275–285. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Rashad, A.M.; Aly, A.M. Transient natural convection flow of a nanofluid over a vertical cylinder. Meccanica 2013, 48, 71–81. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Rashad, A.M.; EL-Zahar, E.R.; EL-Mky, H.A. Analytical and Numerical Investigation of Fe3 O4–Water Nanofluid Flow over a Moveable Plane in a Parallel Stream with High Suction. Energies 2019, 12, 198. [Google Scholar] [CrossRef]
- Mahajan, A.; Sharma, M.K. Convection in magnetic nanofluids in porous media. J. Porous Media 2014, 17, 439–455. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Rashidi, M.M. Ferrofluid heat transfer treatment in the presence of variable magnetic field. Eur. Phys. J. Plus 2015, 130, 115. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Rashidi, M.M.; Ganji, D.D. Numerical investigation of magnetic nanofluid forced convective heat transfer in existence of variable magnetic field using two-phase model. J. Mol. Liq. 2015, 212, 117–126. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Rashidi, M.M.; Hayat, T.; Ganji, D.D. Free convection of magnetic nanofluid considering MFD viscosity effect. J. Mol. Liq. 2016, 218, 393–399. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Rashad, A.M. MHD forced convection flow of a nanofluid adjacent to a non-isothermal wedge. Comput. Therm. Sci. 2014, 6, 27–39. [Google Scholar] [CrossRef]
- Kumar, K.G.; Ramesh, G.K.; Gireesha, B.J.; Rashad, A.M. On stretched magnetic flow of Carreau nanofluid with slip effects and nonlinear thermal radiation. Nonlinear Eng. 2019, 8, 340–349. [Google Scholar] [CrossRef]
- Hayat, T.; Imtiaz, M.; Alsaedi, A.; Kutbi, M.A. MHD three-dimensional flow of nanofluid with velocity slip and nonlinear thermal radiation. J. Magn. Magn. Mater. 2015, 396, 31–37. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Alsaedi, A.; Alhuthali, M.S. Magnetohydrodynamic three-dimensional flow of viscoelastic nanofluid in the presence of nonlinear thermal radiation. J. Magn. Magn. Mater. 2015, 385, 222–229. [Google Scholar] [CrossRef]
- Rashad, A.M. Impact of thermal radiation on MHD slip flow of a ferrofluid over a non-isothermal wedge. J. Magn. Magn. Mater. 2017, 422, 25–31. [Google Scholar] [CrossRef]
- Waqas, M.; Khan, M.I.; Hayat, T.; Alsaedi, A. Numerical simulation for magneto Carreau nanofluid model with thermal radiation: A revised model. Comput. Methods. Appl. Mech. Eng. 2017, 324, 640–653. [Google Scholar] [CrossRef]
- El-Kabeir, S.M.; El-Zahar, E.R.; Modather, M.; Gorla, R.S.; Rashad, A.M. Unsteady MHD slip flow of a ferrofluid over an impulsively stretched vertical surface. AIP Adv. 2019, 9, 045112. [Google Scholar] [CrossRef]
- Rees, D.A. The effect of steady streamwise surface temperature variations on vertical free convection. Int. J. Heat Mass Transf. 1999, 42, 2455–2464. [Google Scholar] [CrossRef]
- Molla, M.M.; Saha, S.C.; Hossain, M.A. Radiation effect on free convection laminar flow along a vertical flat plate with streamwise sinusoidal surface temperature. Math. Comput. Model. 2011, 53, 1310–1319. [Google Scholar] [CrossRef]
- Bert, C.W.; Malik, M. Differential quadrature method in computational mechanics: A review. Appl. Mech. Rev. 1996, 49, 1–28. [Google Scholar] [CrossRef]
- Shu, C. Differential Quadrature and Its Application in Engineering; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Zong, Z.; Zhang, Y. Advanced Differential Quadrature Methods; Chapman and Hall/CRC: London, UK, 2009. [Google Scholar]
- Nassar, M.; Matbuly, M.S.; Ragb, O. Vibration analysis of structural elements using differential quadrature method. J. Adv. Res. 2013, 4, 93–102. [Google Scholar] [CrossRef]
- Jiwari, R.; Gupta, R.K.; Kumar, V. Polynomial differential quadrature method for numerical solutions of the generalized Fitzhugh—Nagumo equation with time-dependent coefficients. Ain Shams Eng. J. 2014, 5, 1343–1350. [Google Scholar] [CrossRef]
- Korkmaz, A.; Dag, I. Polynomial based differential quadrature method for numerical solution of nonlinear Burgers’ equation. J. Frankl. Inst. 2011, 348, 2863–2875. [Google Scholar] [CrossRef]
- Mohammed, O.H.; Saeed, M.A. Numerical solution of thin plates problem via differential quadrature method using G-spline. J. King Saud Univ. Sci. 2019, 31, 209–214. [Google Scholar] [CrossRef]
- Mohamed, N.; Eltaher, M.A.; Mohamed, S.A.; Seddek, L.F. Energy equivalent model in analysis of postbuckling of imperfect carbon nanotubes resting on nonlinear elastic foundation. Struct. Eng. Mech. 2019, 70, 737–750. [Google Scholar]
- Eltaher, M.A.; Mohamed, N.; Mohamed, S.A.; Seddek, L.F. Periodic and nonperiodic modes of postbuckling and nonlinear vibration of beams attached to nonlinear foundations. Appl. Math. Model. 2019, 75, 414–445. [Google Scholar] [CrossRef]
- Eltaher, M.A.; Mohamed, N.; Mohamed, S.; Seddek, L.F. Postbuckling of curved carbon nanotubes using energy equivalent model. J. Nano Res. 2019, 57, 136–157. [Google Scholar] [CrossRef]
- Mohamed, N.; Eltaher, M.A.; Mohamed, S.A.; Seddek, L.F. Numerical analysis of nonlinear free and forced vibrations of buckled curved beams resting on nonlinear elastic foundations. Int. J. Non-Linear Mech. 2018, 101, 157–173. [Google Scholar] [CrossRef]
- Ragb, O.; Seddek, L.F.; Matbuly, M.S. Iterative differential quadrature solutions for Bratu problem. Comput. Math. Appl. 2017, 74, 249–257. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
EL-Zahar, E.R.; Rashad, A.M.; Seddek, L.F. The Impact of Sinusoidal Surface Temperature on the Natural Convective Flow of a Ferrofluid along a Vertical Plate. Mathematics 2019, 7, 1014. https://doi.org/10.3390/math7111014
EL-Zahar ER, Rashad AM, Seddek LF. The Impact of Sinusoidal Surface Temperature on the Natural Convective Flow of a Ferrofluid along a Vertical Plate. Mathematics. 2019; 7(11):1014. https://doi.org/10.3390/math7111014
Chicago/Turabian StyleEL-Zahar, Essam R., Ahmed M. Rashad, and Laila F. Seddek. 2019. "The Impact of Sinusoidal Surface Temperature on the Natural Convective Flow of a Ferrofluid along a Vertical Plate" Mathematics 7, no. 11: 1014. https://doi.org/10.3390/math7111014
APA StyleEL-Zahar, E. R., Rashad, A. M., & Seddek, L. F. (2019). The Impact of Sinusoidal Surface Temperature on the Natural Convective Flow of a Ferrofluid along a Vertical Plate. Mathematics, 7(11), 1014. https://doi.org/10.3390/math7111014






