Continuum Modeling of Discrete Plant Communities: Why Does It Work and Why Is It Advantageous?
Abstract
1. Introduction
2. Distinctive Aspects of Plant Populations
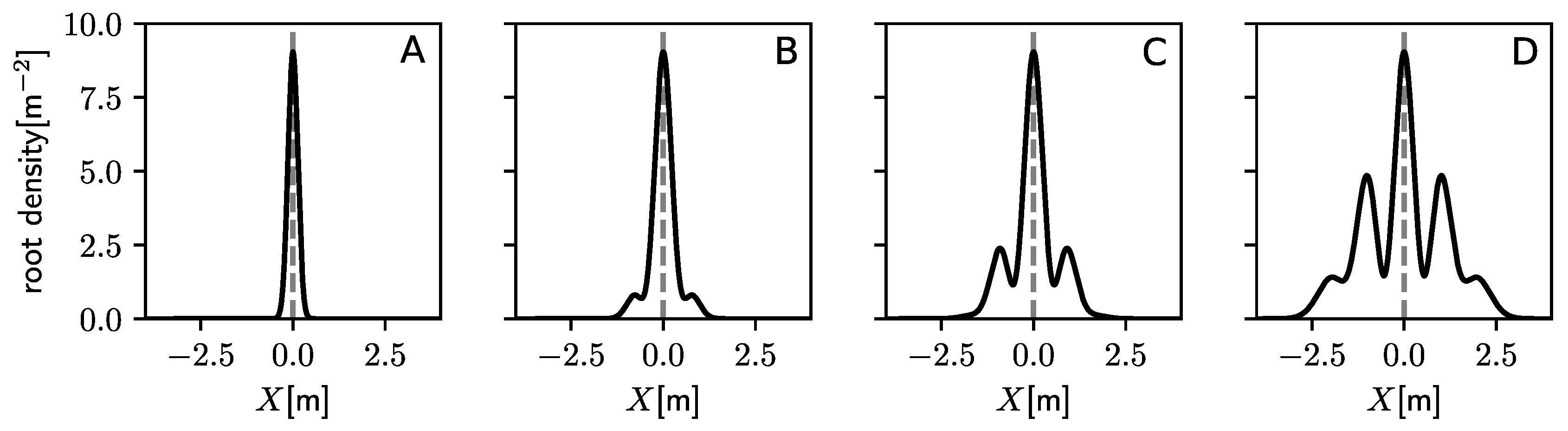
2.1. Phenotypic Plasticity and Plant Adaptation to Variable Environments
2.2. Seed Persistence in the Soil
3. Modeling Dryland Vegetation
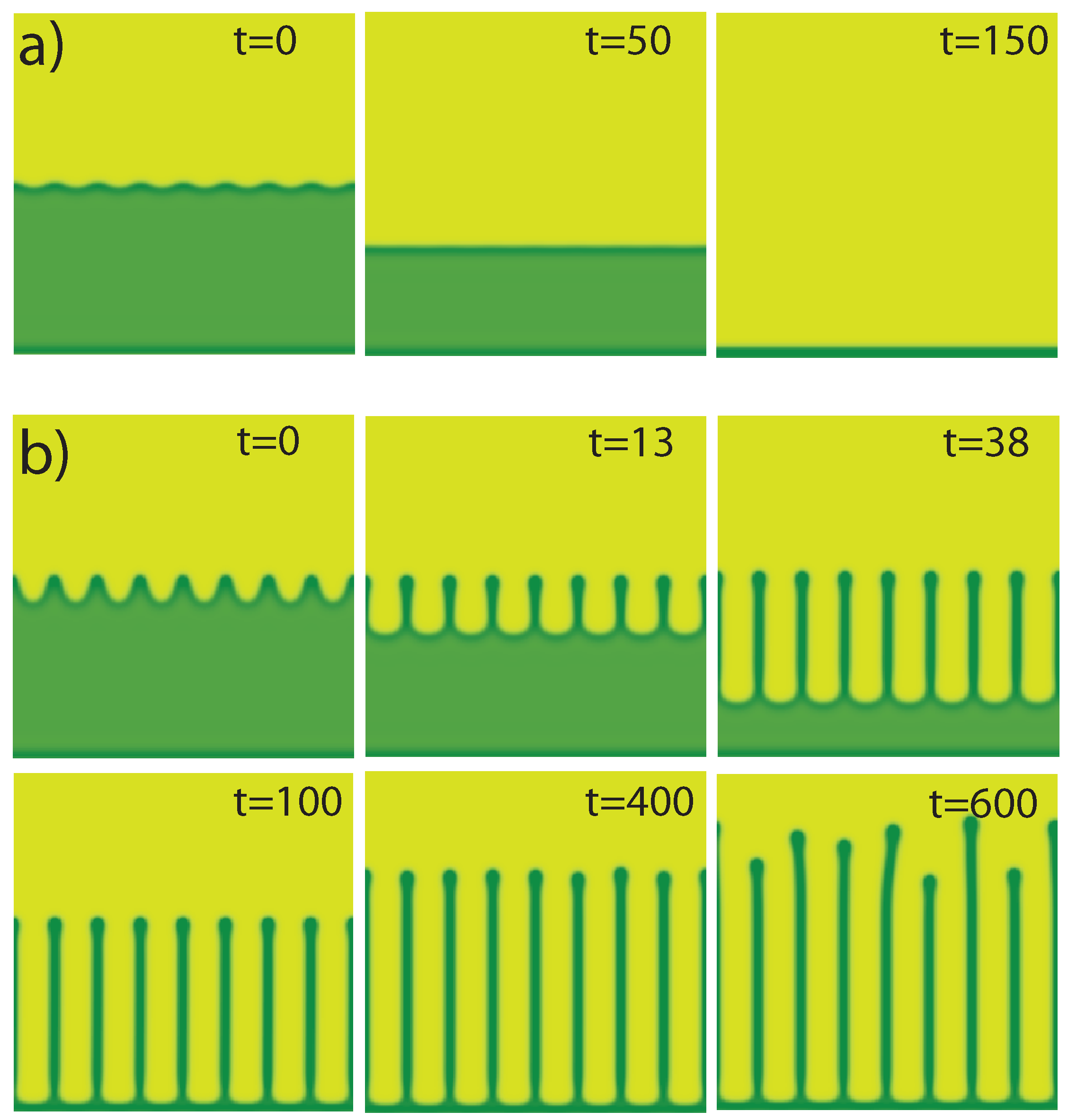
3.1. Pattern-Forming Feedbacks
3.1.1. Infiltration Feedback
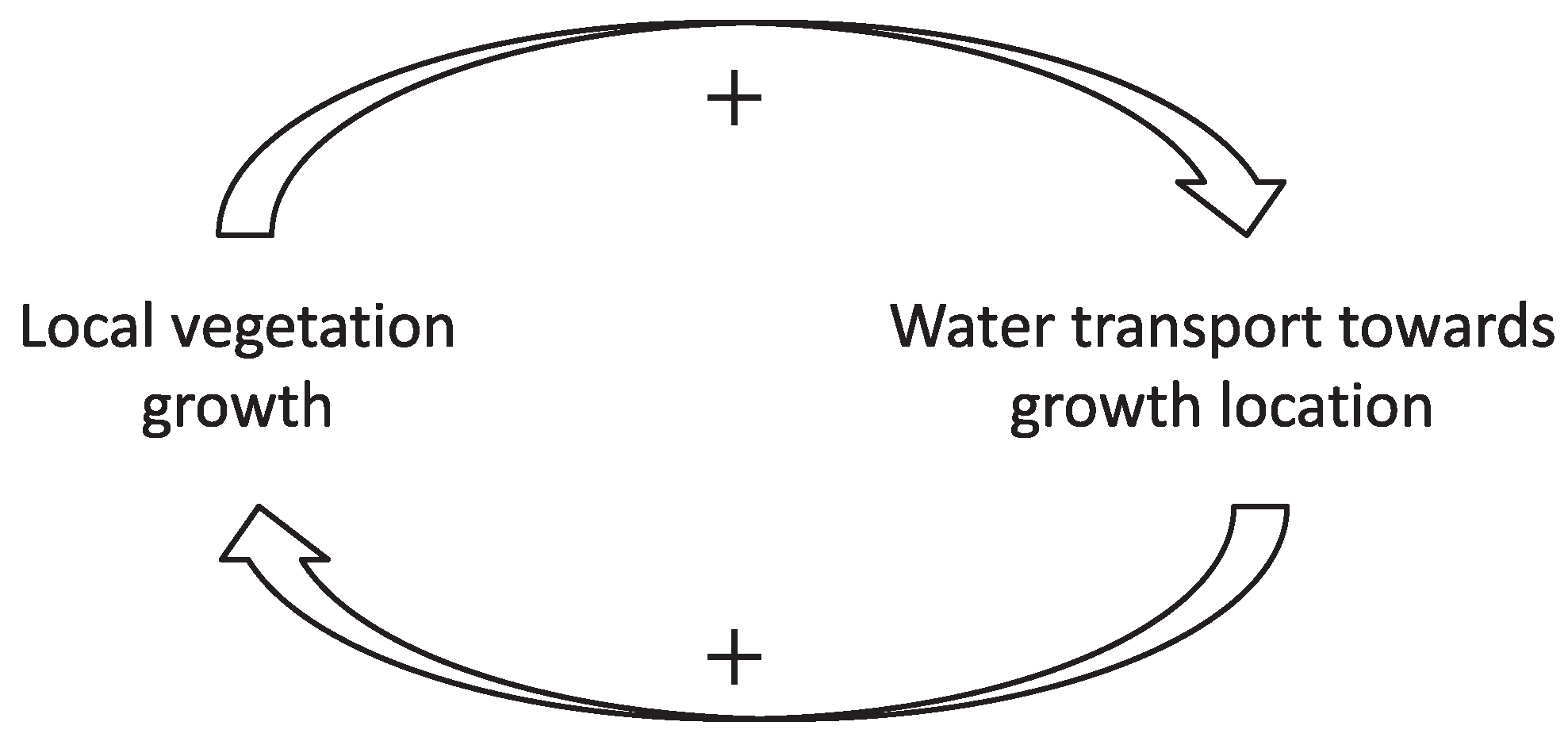
3.1.2. Root-Augmentation Feedback
3.1.3. Soil–Water Diffusion Feedback
3.2. Mathematical Models
4. Advantages of Continuum PDE Models
4.1. Instability Thresholds
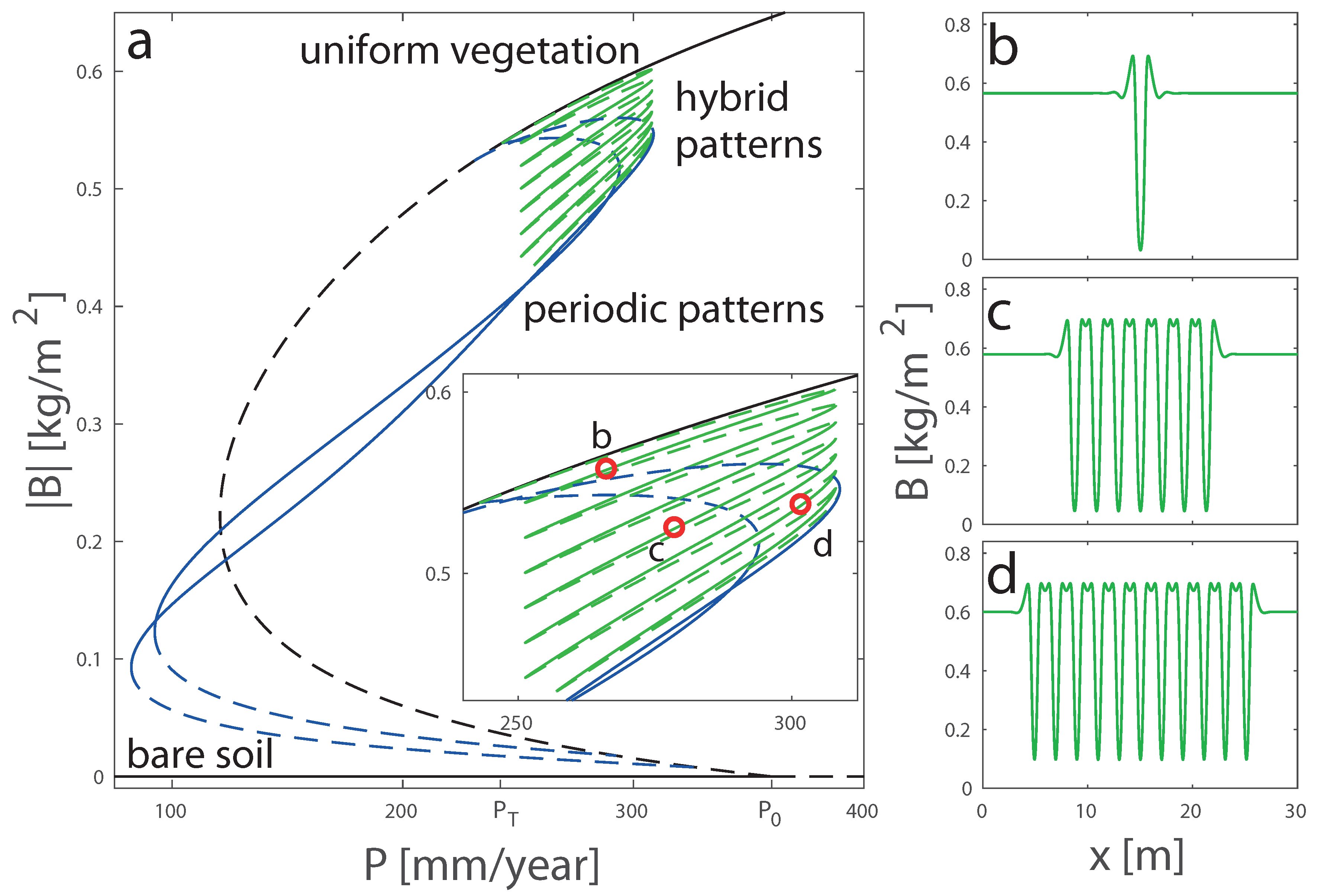
4.2. Bifurcation Diagrams
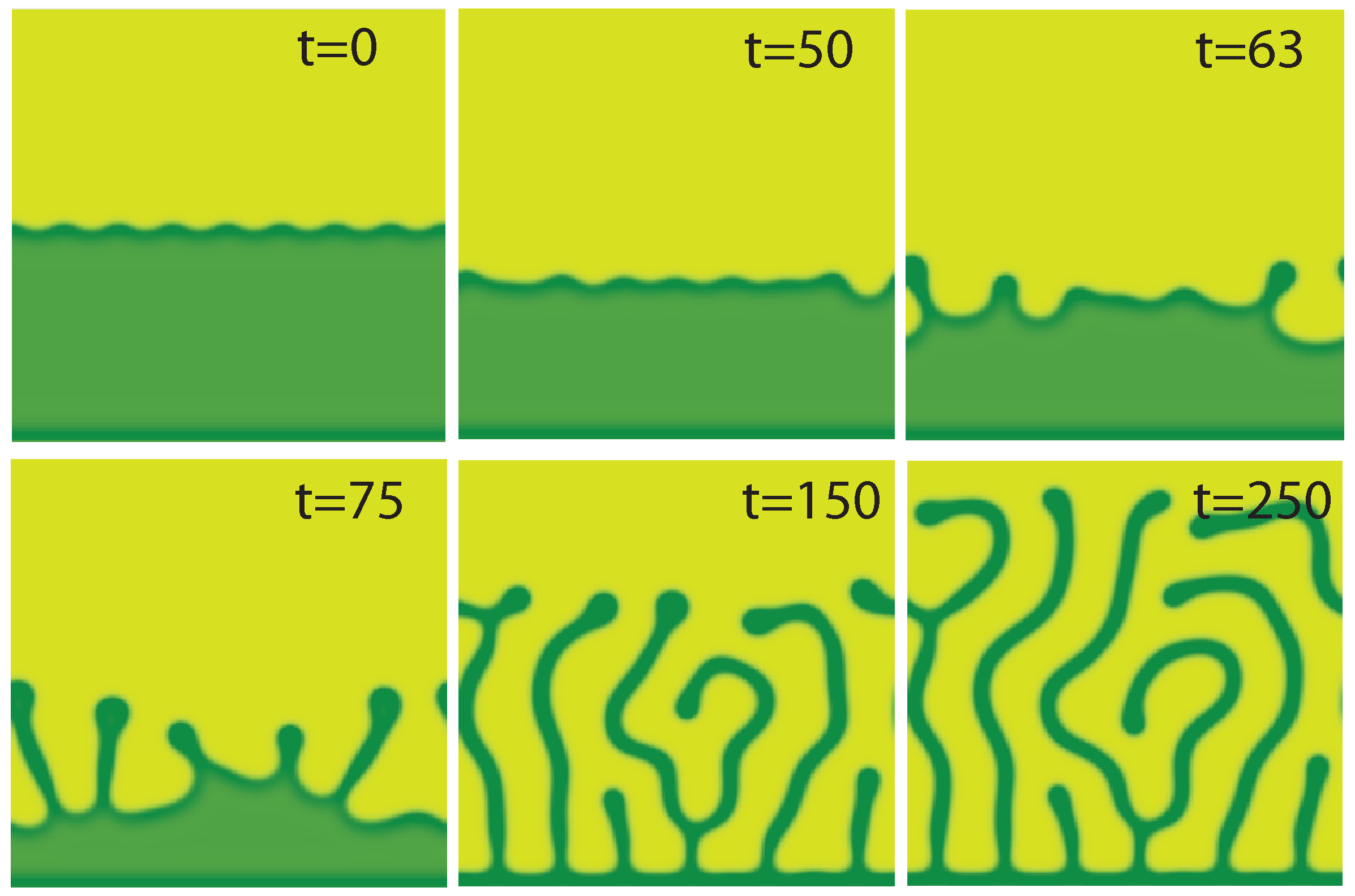
4.3. Front Dynamics
5. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A. Model for Laterally Extended Roots

Appendix B. Model for Laterally Confined Roots
References
- Hansen, J.; Sato, M.; Ruedy, R. Perception of climate change. Proc. Natl. Acad. Sci. USA 2012, 109, E2415–E2423. [Google Scholar] [CrossRef] [PubMed]
- Hoerling, M.; Eischeid, J.; Perlwitz, J.; Quan, X.; Zhang, T.; Pegion, P. On the Increased Frequency of Mediterranean Drought. J. Clim. 2012, 25, 2146–2161. [Google Scholar] [CrossRef]
- Cook, B.I.; Ault, T.R.; Smerdon, J.E. Unprecedented 21st century drought risk in the American Southwest and Central Plains. Sci. Adv. 2015, 1, e1400082. [Google Scholar] [CrossRef] [PubMed]
- DeAngelis, D.; Grimm, V. Individual-based models in ecology after four decades. F1000Prime 2014, 6, 39. [Google Scholar] [CrossRef] [PubMed]
- Grimm, V.; Railsback, S.F. Individual-Based Modeling and Ecology; Princeton University Press: Princeton, NJ, USA, 2005. [Google Scholar]
- DeAngelis, D.L.; Yurek, S. Spatially Explicit Modeling in Ecology: A Review. Ecosystems 2016. [Google Scholar] [CrossRef]
- Holmes, E.E.; Lewis, M.A.; Banks, J.E.; Veit, R.R. Partial Differential Equations in Ecology: Spatial Interactions and Population Dynamics. Ecology 1994, 75, 17–29. [Google Scholar] [CrossRef]
- Petrovskii, S.V.; Li, B.L. Exactly Solvable Models of Biological Invasion; Chapman and Hall/CRC Mathematical and Computational Biology; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Petrovskii, S.V.; Morozov, A.Y.; Venturino, E. Allee effect makes possible patchy invasion in a predator–prey system. Ecol. Lett. 2002, 5, 345–352. [Google Scholar] [CrossRef]
- Cantrell, R.S.; Cosner, C. Spatial Ecology via Reaction-Diffusion Equations; Wiley Series in Mathematical & Computational Biology; Wiley: San Francisco, CA, USA, 2003. [Google Scholar]
- Meron, E. Nonlinear Physics of Ecosystems; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2015. [Google Scholar]
- Ovaskainen, O.; Meerson, B. Stochastic models of population extinction. Trends Ecol. Evol. 2010, 25, 643–652. [Google Scholar] [CrossRef]
- Bonachela, J.A.; Muñoz, M.A.; Levin, S.A. Patchiness and demographic noise in three ecological examples. J. Stat. Phys. 2012, 148, 723–739. [Google Scholar] [CrossRef]
- Pigliucci, M. Evolution of phenotypic plasticity: Where are we going now? Trends Ecol. Evol. 2005, 20, 481–486. [Google Scholar] [CrossRef]
- Aichinger, E.; Kornet, N.; Friedrich, T.; Laux, T. Plant stem cell niches. Annu. Rev. Plant Biol. 2012, 63, 615–636. [Google Scholar] [CrossRef] [PubMed]
- Mokany, K.; Raison, J.; Prokushkin, A. Critical analysis of root-shoot rations in terrestrial biomes. Glob. Chang. Biol. 2006, 12, 84–96. [Google Scholar] [CrossRef]
- Khadka, J.; Yadav, N.; Granot, G.; Grafi, G. Summer dormancy is associated with loss of the permissive epigenetic marker dimethyl H3K4 and extensive reduction in proteins involved in basic cell functions. Plants 2018, 7, 59. [Google Scholar] [CrossRef] [PubMed]
- Grafi, G. A “mille-feuilles” of stress tolerance in the desert plant Zygophyllum dumosum Boiss. Isr. J. Plant Sci. 2019, 66, 52–59. [Google Scholar] [CrossRef]
- Evenari, M.; Shanan, L.; Tadmor, N. The Negev: The Challenge of a Desert; Harvard University Press: Cambridge, MA, USA, 1982. [Google Scholar]
- Terwilliger, V.; Zeroni, M. Gas exchange of a desert shrub (Zygophyllum dumosum Boiss.) under different soil moisture regimes during summer drought. J. Plant Ecol. 1994, 115, 133–144. [Google Scholar]
- Schenk, J.H.; Espino, S.; Goedhart, C.M.; Nordenstahl, M.; Cabrera, H.I.; Jones, C.S. Hydraulic integration and shrub growth form linked across continental aridity gradients. Proc. Natl. Acad. Sci. USA 2008, 105, 11248–11253. [Google Scholar] [CrossRef] [PubMed]
- Ginzburg, C. Some anatomic features of splitting of desert shrubs. Annu. Rev. Plant Biol. 1963, 13, 92–97. [Google Scholar]
- Orshan, G.; Zand, G. Seasonal body reduction of certain desert halfshrubs. Bull. Res. Counc. Isr. 1962, 11D, 35–42. [Google Scholar]
- Cunningham, G.; Strain, B. An ecological significance of seasonal leaf variability in a desert shrub. Ecology 1969, 50, 400–408. [Google Scholar] [CrossRef]
- Dalling, J.; Davis, A.; Schutte, B.; Elizabeth, A.A. Seed survival in soil: Interacting effects of predation, dormancy and the soil microbial community. J. Ecol. 2011, 99, 89–95. [Google Scholar] [CrossRef]
- Kivilaan, A.; Bandurski, R. The one hundred-year period for Dr. Beal’s seed viability experiment. Am. J. Bot. 1981, 68, 1290–1292. [Google Scholar] [CrossRef]
- Shen-Miller, J.; Mudgett, M.; Schopf, J.; Clarke, S.; Berger, R. Exceptional seed longevity and robust growth: Ancient sacred lotus from China. Am. J. Bot. 1995, 82, 1367–1380. [Google Scholar] [CrossRef]
- Long, R.; Gorecki, M.; Renton, M.; Scott, J.; Colville, L.; Goggin, D.; Commander, L.; Westcott, D.; Cherry, H.; Finch-Savage, W. The ecophysiology of seed persistence: A mechanistic view of the journey to germination or demise. Biol. Rev. Camb. Philos. Soc. 2015, 90, 31–59. [Google Scholar] [CrossRef] [PubMed]
- Cohen, D. A general model of optimal reproduction in a randomly varying environment. Am. J. Bot. 1966, 56, 219–228. [Google Scholar] [CrossRef]
- Venable, D.; Brown, J. The selective interactions of dispersal, dormancy, and seed size as adaptations for reducing risk in variable environments. Am. Nat. 1988, 131, 360–384. [Google Scholar] [CrossRef]
- Ooi, M. Seed bank persistence and climate change. Seed Sci. Res. 2012, 22, S53–S60. [Google Scholar] [CrossRef]
- Walck, J.; Hidayati, S.; Dixon, K.; Thompson, K.; Poschlod, P. Climate change and plant regeneration from seed. Glob. Chang. Biol. 2011, 17, 2145–2161. [Google Scholar] [CrossRef]
- Raviv, B.; Godwin, J.; Granot, G.; Grafi, G. The dead can nurture: Novel insights into the function of dead organs enclosing embryos. Int. J. Mol. Sci. 2018, 19, 2455. [Google Scholar] [CrossRef]
- Lefever, R.; Lejeune, O. On the origin of tiger bush. Bull. Math. Biol. 1997, 59, 263–294. [Google Scholar] [CrossRef]
- Klausmeier, C. Regular and irregular patterns in semiarid vegetation. Science 1999, 284, 1826–1828. [Google Scholar] [CrossRef]
- Von Hardenberg, J.; Meron, E.; Shachak, M.; Zarmi, Y. Diversity of Vegitation Patterns and Desertification. Phys. Rev. Lett. 2001, 87, 198101. [Google Scholar] [CrossRef] [PubMed]
- Shnerb, N.; Sarah, P.; Lavee, H.; Solomon, S. Reactive glass and vegetation patterns. Phys. Rev. Lett. 2003, 90, 0381011. [Google Scholar] [CrossRef] [PubMed]
- HilleRisLambers, R.; Rietkerk, M.; Van den Bosch, F.; Prins, H.; de Kroon, H. Vegetation pattern formation in semi-arid grazing systems. Ecology 2001, 82, 50–61. [Google Scholar] [CrossRef]
- Gilad, E.; Von Hardenberg, J.; Provenzale, A.; Shachak, M.; Meron, E. Ecosystem Engineers: From Pattern Formation to Habitat Creation. Phys. Rev. Lett. 2004, 93, 098105. [Google Scholar] [CrossRef] [PubMed]
- Gilad, E.; Von Hardenberg, J.; Provenzale, A.; Shachak, M.; Meron, E. A Mathematical Model for Plants as Ecosystem Engineers. J. Theor. Biol. 2007, 244, 680. [Google Scholar] [CrossRef]
- Gilad, E.; Shachak, M.; Meron, E. Dynamics and Spatial Organization of Plant Communities in Water Limited Systems. Theor. Popul. Biol. 2007, 72, 214–230. [Google Scholar] [CrossRef] [PubMed]
- Kinast, S.; Zelnik, Y.R.; Bel, G.; Meron, E. Interplay between Turing Mechanisms can Increase Pattern Diversity. Phys. Rev. Lett. 2014, 112, 078701. [Google Scholar] [CrossRef]
- Meron, E. From Patterns to Function in Living Systems: Dryland Ecosystems as a Case Study. Annu. Rev. Condens. Matter Phys. 2018, 9, 79–103. [Google Scholar] [CrossRef]
- Meron, E. Pattern formation—A missing link in the study of ecosystem response to environmental changes. Math. Biosci. 2016, 271, 1–18. [Google Scholar] [CrossRef]
- Meinhardt, H. Pattern formation in biology: A comparison of models and experiments. Rep. Prog. Phys. 1992, 55, 797. [Google Scholar] [CrossRef]
- Rietkerk, M.; van de Koppel, J. Regular pattern formation in real ecosystems. Trends Ecol. Evol. 2008, 23, 169–175. [Google Scholar] [CrossRef] [PubMed]
- Verrecchia, E.; Yair, A.; Kidron, G.J.; Verrecchia, K. Physical properties of the psammophile cryptogamic crust and their consequences to the water regime of sandy softs, north-western Negev Desert, Israel. J. Arid Environ. 1995, 29, 427–437. [Google Scholar] [CrossRef]
- Eldridge, D.J.; Zaady, E.; Shachak, M. Infiltration through three contrasting biological soil crusts in patterned landscapes in the Negev, Israel. J. Stat. Phys. 2012, 148, 723–739. [Google Scholar] [CrossRef]
- Walker, B.; Ludwig, D.; Holling, C.; Peterman, R. Stability of semi-arid savana grazing systems. J. Ecol. 1981, 69, 473–498. [Google Scholar] [CrossRef]
- Atkinson, J.A.; Rasmussen, A.; Traini, R.; Voß, U.; Sturrock, C.; Mooney, S.; Wells, D.M.; Bennett, M.J. Branching Out in Roots: Uncovering Form, Function, and Regulation. Plant Physiol. 2014, 166, 538–550. [Google Scholar] [CrossRef] [PubMed]
- Zelnik, Y.R.; Meron, E.; Bel, G. Gradual Regime Shifts in Fairy Circles. Proc. Natl. Acad. Sci. USA 2015, 112, 12327–12331. [Google Scholar] [CrossRef]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; Westview Press: Pittsburgh, PA, USA, 2001. [Google Scholar]
- Newell, A.C.; Passot, T.; Lega, J. Order parameter equations for patterns. Ann. Rev. Fluid Mech. 1993, 25, 399–453. [Google Scholar] [CrossRef]
- Elphick, C.; Tirapegui, E.; Brachet, M.E.; Coullet, P.; Iooss, G. A simple global characterization for normal forms of singular vector fields. Phys. D 1987, 29, 95–127. [Google Scholar] [CrossRef]
- Cross, M.; Greenside, H. Pattern Formation and Dynamics in Nonequilibrium Systems; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Getzin, S.; Yizhaq, H.; Bell, B.; Erickson, T.E.; Postle, A.C.; Katra, I.; Tzuk, O.; Zelnik, Y.R.; Wiegand, K.; Wiegand, T.; et al. Discovery of fairy circles in Australia supports self-organization theory. Proc. Natl. Acad. Sci. USA 2016, 113, 3551–3556. [Google Scholar] [CrossRef]
- Lejeune, O.; Tlidi, M.; Lefever, R. Vegetation spots and stripes: Dissipative structures in arid landscapes. Int. J. Quantum Chem. 2004, 98, 261–271. [Google Scholar] [CrossRef]
- Gowda, K.; Riecke, H.; Silber, M. Transitions between patterned states in vegetation models for semiarid ecosystems. Phys. Rev. E 2014, 89, 022701. [Google Scholar] [CrossRef] [PubMed]
- Doedel, E.; Paffenroth, R.C.; Champneys, A.R.; Fairgrieve, T.F.; Kuznetsov, Y.A.; Oldeman, B.E.; Sandstede, B.; Wang, X. AUTO2000; Technical report; Concordia University: Montréal, QC, Canada, 2002. [Google Scholar]
- Uecker, H.; Wetzel, D.; Rademacher, J.D. pde2path-A Matlab package for continuation and bifurcation in 2D elliptic systems. Numer. Math. Theory Methods Appl. 2014, 7, 58–106. [Google Scholar] [CrossRef]
- Kozyreff, G.; Chapman, S.J. Asymptotics of Large Bound States of Localized Structures. Phys. Rev. Lett. 2006, 97, 044502. [Google Scholar] [CrossRef] [PubMed]
- Burke, J.; Knobloch, E. Snakes and ladders: Localized states in the Swift-Hohenberg equation. Phys. Lett. A 2007, 360, 681–688. [Google Scholar] [CrossRef]
- Dawes, J. Localized Pattern Formation with a Large-Scale Mode: Slanted Snaking. SIAM J. Appl. Dyn. Syst. 2008, 7, 186–206. [Google Scholar] [CrossRef][Green Version]
- Lloyd, D.J.B.; Sandstede, B.; Avitabile, D.; Champneys, A.R. Localized Hexagon Patterns of the Planar Swift-Hohenberg Equation. SIAM J. Appl. Dyn. Syst. 2008, 7, 1049–1100. [Google Scholar] [CrossRef]
- Avitabile, D.; Lloyd, D.; Burke, J.; Knobloch, E.; Sandstede, B. To Snake or Not to Snake in the Planar Swift–Hohenberg Equation. SIAM J. Appl. Dyn. Syst. 2010, 9, 704–733. [Google Scholar] [CrossRef]
- Knobloch, E. Spatial Localization in Dissipative Systems. Annu. Rev. Condens. Matter Phys. 2015, 6, 325–359. [Google Scholar] [CrossRef]
- Pomeau, Y. Front motion, metastability and subcritical bifurcations in hydrodynamics. Physica D 1986, 23, 3. [Google Scholar] [CrossRef]
- Bel, G.; Hagberg, A.; Meron, E. Gradual regime shifts in spatially extended ecosystems. Theor. Ecol. 2012, 5, 591–604. [Google Scholar] [CrossRef]
- Clerc, M.G.; Fernandez-Oto, C.; García-Ñustes, M.A.; Louvergneaux, E. Origin of the Pinning of Drifting Monostable Patterns. Phys. Rev. Lett. 2012, 109, 104101. [Google Scholar] [CrossRef] [PubMed]
- Juergens, N. The biological underpinnings of Namib Desert fairy circles. Science 2013, 339, 1618–1621. [Google Scholar] [CrossRef] [PubMed]
- Fernandez-Oto, C.; Tlidi, M.; Escaff, D.; Clerc, M.G. Strong interaction between plants induces circular barren patches: Fairy circles. Philos. Trans. A Math. Phys. Eng. Sci. 2014, 372, 20140009. [Google Scholar] [CrossRef] [PubMed]
- Tarnita, C.; Bonachela, J.A.; Sheffer, E.; Guyton, J.A.; Coverdale, T.C.; Long, R.A.; Pringle, R.M. A theoretical foundation for multi-scale regular vegetation patterns. Nature 2017, 541, 398–401. [Google Scholar] [CrossRef] [PubMed]
- Getzin, S.; Wiegand, K.; Wiegand, T.; Yizhaq, H.; von Hardenberg, J.; Meron, E. Adopting a spatially explicit perspective to study the mysterious fairy circles of Namibia. Ecography 2015, 38, 1–11. [Google Scholar] [CrossRef]
- Tschinkel, W. The Life Cycle and Life Span of Namibian Fairy Circles. PLoS ONE 2012, 7, e38056. [Google Scholar] [CrossRef]
- Zelnik, Y.R.; Meron, E.; Bel, G. Localized states qualitatively change the response of ecosystems to varying conditions and local disturbances. Ecol. Complex. 2016, 25, 26–34. [Google Scholar] [CrossRef]
- Dawes, J.; Williams, J. Localised pattern formation in a model for dryland vegetation. J. Math. Biol. 2016, 73, 63–90. [Google Scholar] [CrossRef]
- Zelnik, Y.R.; Gandhi, P.; Knobloch, E.; Meron, E. Implications of tristability in pattern-forming ecosystems. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 033609. [Google Scholar] [CrossRef]
- Mau, Y.; Haim, L.; Meron, E. Reversing desertification as a spatial resonance problem. Phys. Rev. E 2015, 91, 012903. [Google Scholar] [CrossRef]
- Xu, C.; Van Nes, E.H.; Holmgren, M.; Kéfi, S.; Scheffer, M. Local Facilitation May Cause Tipping Points on a Landscape Level Preceded by Early-Warning Indicators. Am. Nat. 2015, 186, E81–E90. [Google Scholar] [CrossRef] [PubMed]
- Van Strien, M.J.; Huber, S.H.; Anderies, J.M.; Grêt-Regamey, A. Resilience in social-ecological systems: Identifying stable and unstable equilibria with agent-based models. Ecol. Soc. 2019, 24, 8. [Google Scholar] [CrossRef]
- Scheffer, M.; Carpenter, S.; Foley, J.; Folke, C.; Walkerk, B. Catastrophic shifts in ecosystems. Nature 2001, 413, 591–596. [Google Scholar] [CrossRef] [PubMed]
- Ashwin, P.; Wieczorek, S.; Vitolo, R.; Cox, P. Tipping points in open systems: Bifurcation, noise-induced and rate-dependent examples in the climate system. Philos. Trans. Math. Phys. Eng. Sci. 2012, 370, 1166–1184. [Google Scholar] [CrossRef] [PubMed]
- Feudel, U.; Pisarchik, A.N.; Showalter, K. Multistability and tipping: From mathematics and physics to climate and brain—Minireview and preface to the focus issue. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 033501. [Google Scholar] [CrossRef] [PubMed]
- Zelnik, Y.R.; Meron, E. Regime shifts by front dynamics. Ecol. Indic. 2018, 94, 544–552. [Google Scholar] [CrossRef]
- Fernandez-Oto, C.; Tzuk, O.; Meron, E. Front Instabilities Can Reverse Desertification. Phys. Rev. Lett. 2019, 122, 048101. [Google Scholar] [CrossRef]
- Hagberg, A.; Meron, E. Complex Patterns in reaction Diffusion Systems: A Tale of Two Front Instabilities. Chaos 1994, 4, 477–484. [Google Scholar] [CrossRef][Green Version]
- Goldstein, R.E.; Muraki, D.J.; Petrich, D.M. Interface proliferation and the growth of labyrinths in a reaction-diffusion system. Phys. Rev. E 1996, 53, 3933–3957. [Google Scholar] [CrossRef]
- Hagberg, A.; Yochelis, A.; Yizhaq, H.; Elphick, C.; Pismen, L.; Meron, E. Linear and nonlinear front instabilities in bistable systems. Phys. D Nonlinear Phenom. 2006, 217, 186–192. [Google Scholar] [CrossRef]
- Ursino, N. The influence of soil properties on the formation of unstable vegetation patterns on hillsides of semiarid catchments. Adv. Water Resour. 2005, 28, 956–963. [Google Scholar] [CrossRef]
- Sherratt, J.A. An Analysis of Vegetation Stripe Formation in Semi-Arid Landscapes. J. Math. Biol. 2005, 51, 183–197. [Google Scholar] [CrossRef] [PubMed]
- Deblauwe, V.; Couteron, P.; Bogaert, J.; Barbier, N. Determinants and dynamics of banded vegetation pattern migration in arid climates. Ecol. Monogr. 2012, 82, 3–21. [Google Scholar] [CrossRef]
- Sherratt, J.A. Pattern Solutions of the Klausmeier Model for Banded Vegetation in Semiarid Environments V: The Transition from Patterns to Desert. SIAM J. Appl. Math. 2013, 73, 1347–1367. [Google Scholar] [CrossRef]
- Sherratt, J.A. Using wavelength and slope to infer the historical origin of semiarid vegetation bands. Proc. Natl. Acad. Sci. USA 2015, 112, 4202–4207. [Google Scholar] [CrossRef]
- Sherratt, J.A.; Lord, G.J. Nonlinear dynamics and pattern bifurcations in a model for vegetation stripes in semi-arid environments. Theor. Popul. Biol. 2007, 71, 1–11. [Google Scholar] [CrossRef]
- Zelnik, Y.R.; Kinast, S.; Yizhaq, H.; Bel, G.; Meron, E. Regime shifts in models of dryland vegetation. Philos. Trans. R. Soc. A 2013, 371, 20120358. [Google Scholar] [CrossRef]
- Siteur, K.; Siero, E.; Eppinga, M.B.; Rademacher, J.D.M.; Doelman, A.; Rietkerk, M. Beyond Turing: The response of patterned ecosystems to environmental change. Ecol. Complex. 2014, 20, 81–96. [Google Scholar] [CrossRef]
- Yizhaq, H.; Gilad, E.; Meron, E. Banded Vegetation: Biological Productivity and Resilience. Physica A 2005, 356, 139. [Google Scholar] [CrossRef]
- Bastiaansen, R.; Jaïbi, O.; Deblauwe, V.; Eppinga, M.B.; Siteur, K.; Siero, E.; Mermoz, S.; Bouvet, A.; Doelman, A.; Rietkerk, M. Multistability of model and real dryland ecosystems through spatial self-organization. Proc. Natl. Acad. Sci. USA 2018, 115, 11256–11261. [Google Scholar] [CrossRef]
- Rietkerk, M.; Dekker, S.C.; de Ruiter, P.C.; van de Koppel, J. Self-Organized Patchiness and Catastrophic Shifts in Ecosystems. Science 2004, 305, 1926–1929. [Google Scholar] [CrossRef] [PubMed]
- Valentine, C.; d’Herbes, J.; Poesen, J. Soil and water components of banded vegetation patterns. Catena 1999, 37, 1–24. [Google Scholar] [CrossRef]
- Deblauwe, V.; Barbier, N.; Couteron, P.; Lejeune, O.; Bogaert, J. The global biogeography of semi-arid periodic vegetation patterns. Glob. Ecol. Biogeogr. 2008, 17, 715–723. [Google Scholar] [CrossRef]
- Borgogno, F.; D’Odorico, P.; Laio, F.; Ridolfi, L. Mathematical models of vegetation pattern formation in ecohydrology. Rev. Geophys. 2009, 47, RG1005. [Google Scholar] [CrossRef]
- Kyriazopoulos, P.; Jonathan, N.; Meron, E. Species coexistence by front pinning. Ecol. Complex. 2014, 20, 271–281. [Google Scholar] [CrossRef]
- Malkinson, D.; Tielbörger, K. What does the stress-gradient hypothesis predict? Resolving the discrepancies. Oikos 2010, 119, 1546–1552. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meron, E.; Bennett, J.J.R.; Fernandez-Oto, C.; Tzuk, O.; Zelnik, Y.R.; Grafi, G. Continuum Modeling of Discrete Plant Communities: Why Does It Work and Why Is It Advantageous? Mathematics 2019, 7, 987. https://doi.org/10.3390/math7100987
Meron E, Bennett JJR, Fernandez-Oto C, Tzuk O, Zelnik YR, Grafi G. Continuum Modeling of Discrete Plant Communities: Why Does It Work and Why Is It Advantageous? Mathematics. 2019; 7(10):987. https://doi.org/10.3390/math7100987
Chicago/Turabian StyleMeron, Ehud, Jamie J. R. Bennett, Cristian Fernandez-Oto, Omer Tzuk, Yuval R. Zelnik, and Gideon Grafi. 2019. "Continuum Modeling of Discrete Plant Communities: Why Does It Work and Why Is It Advantageous?" Mathematics 7, no. 10: 987. https://doi.org/10.3390/math7100987
APA StyleMeron, E., Bennett, J. J. R., Fernandez-Oto, C., Tzuk, O., Zelnik, Y. R., & Grafi, G. (2019). Continuum Modeling of Discrete Plant Communities: Why Does It Work and Why Is It Advantageous? Mathematics, 7(10), 987. https://doi.org/10.3390/math7100987





