A Note on a Generalized Gerber–Shiu Discounted Penalty Function for a Compound Poisson Risk Model
Abstract
1. Introduction
2. Recursion Calculation of
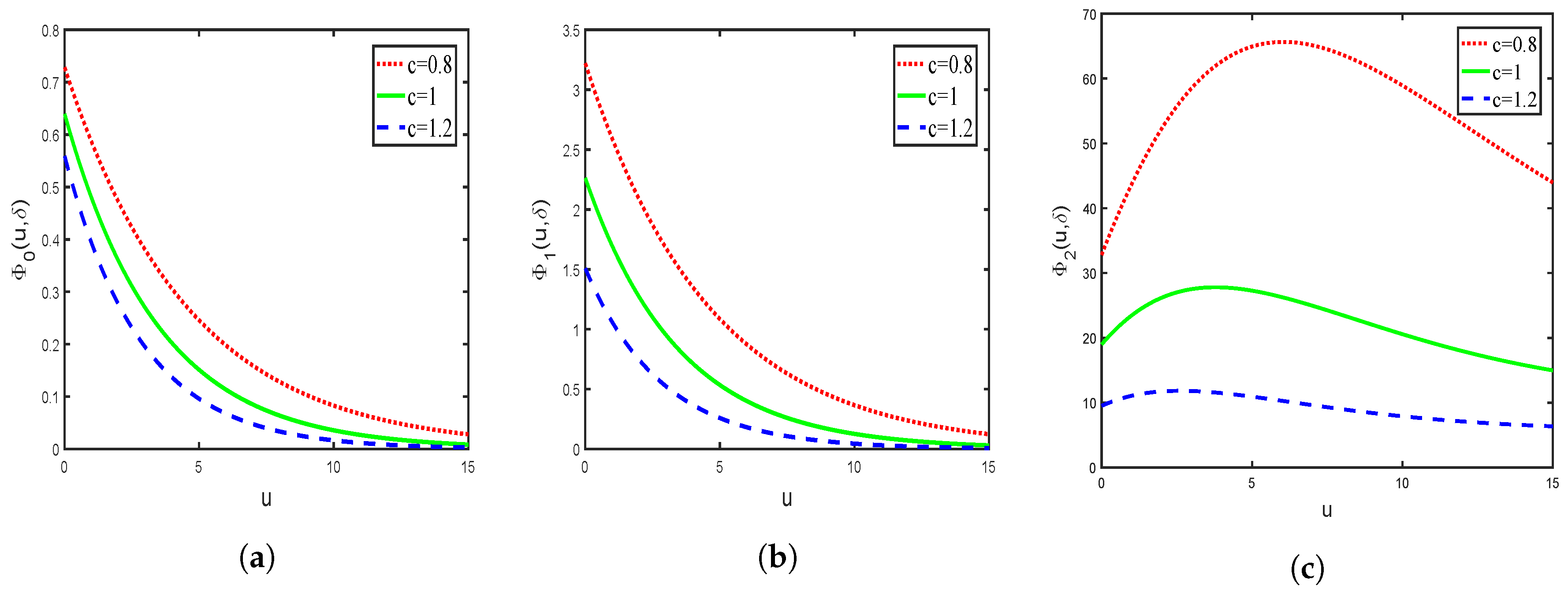
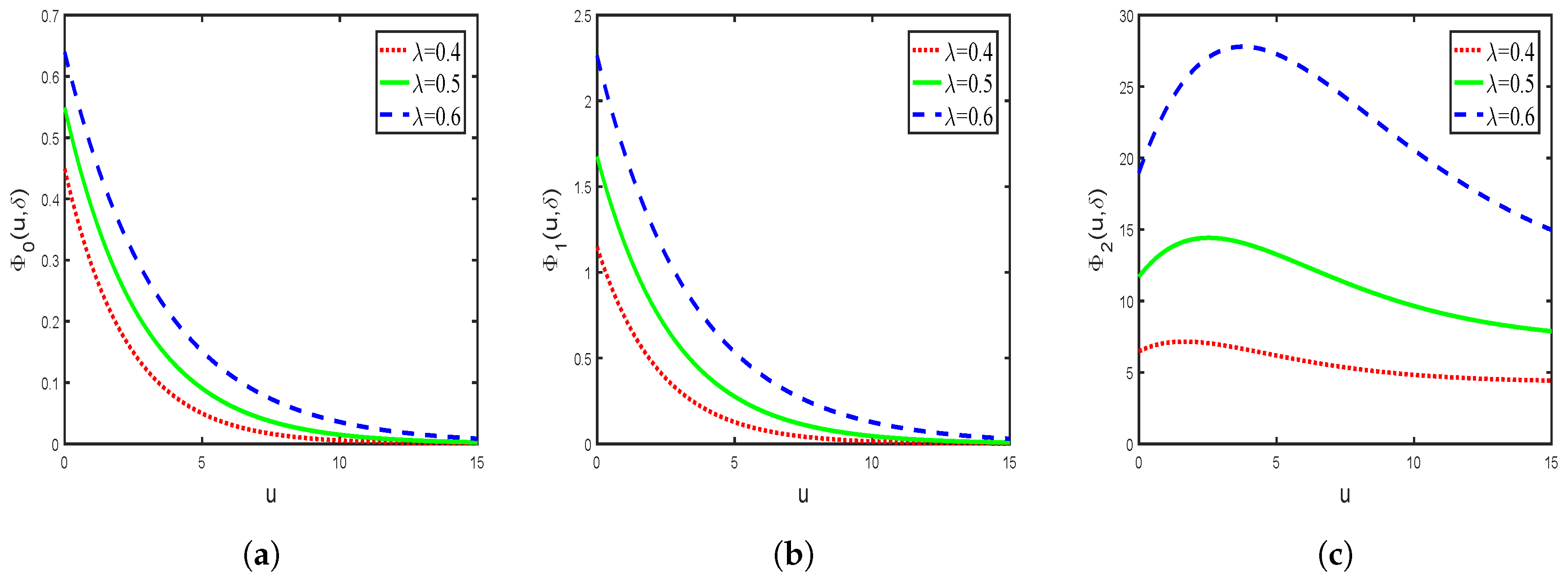
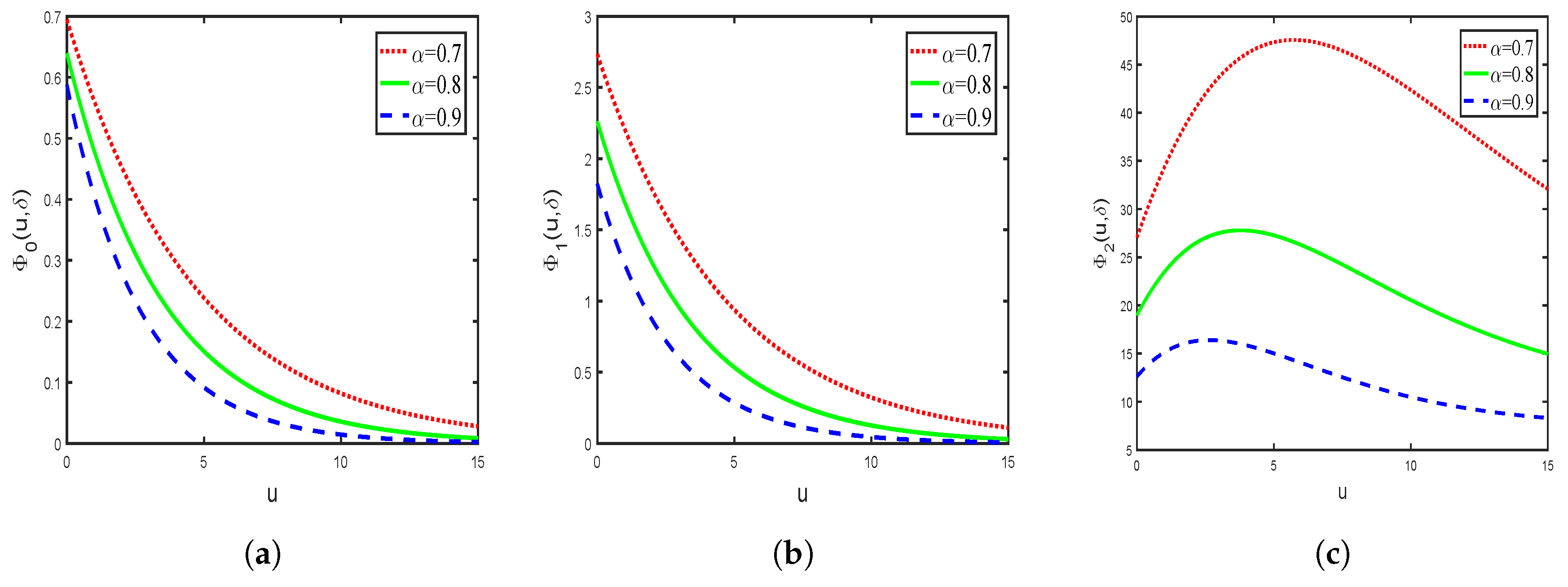
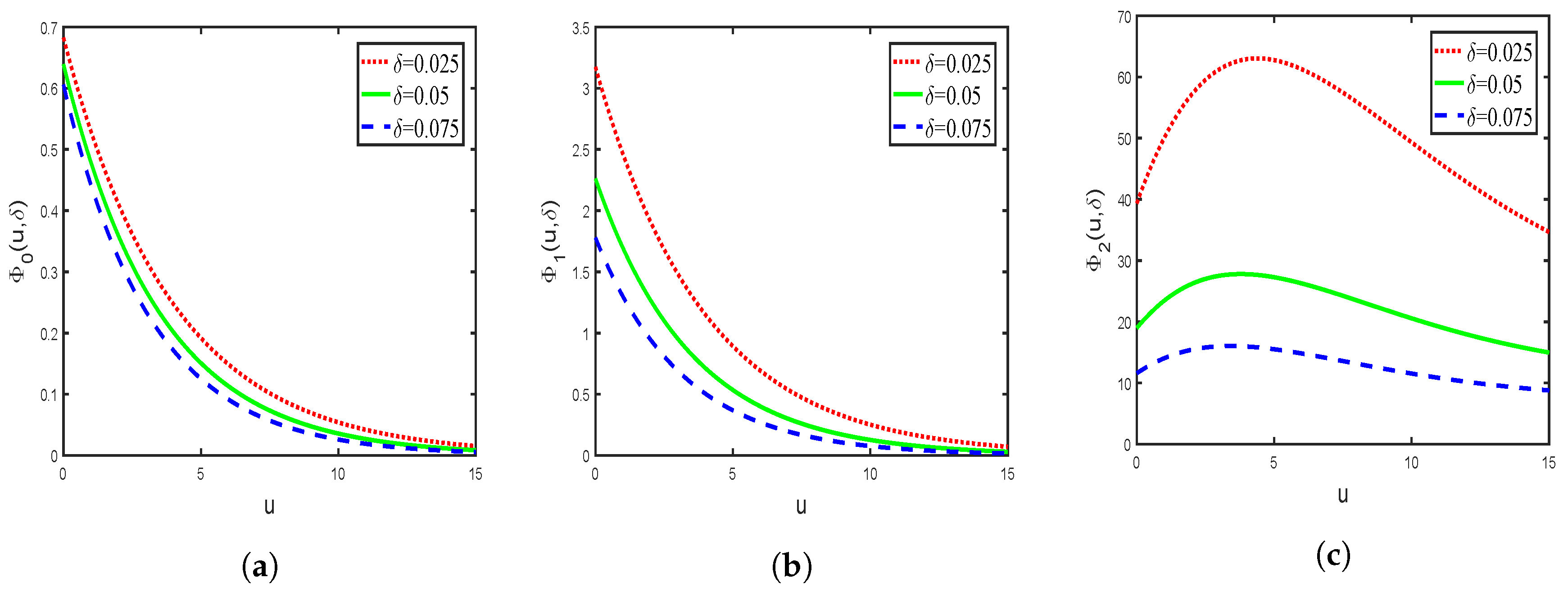
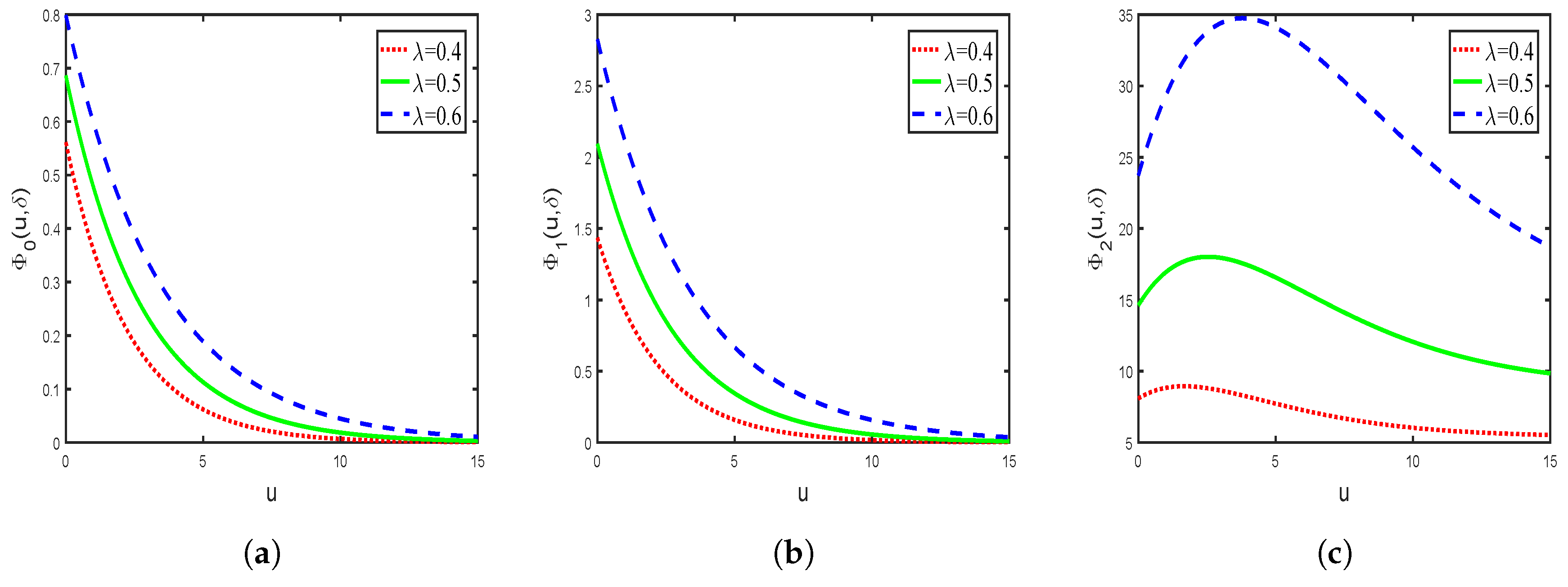
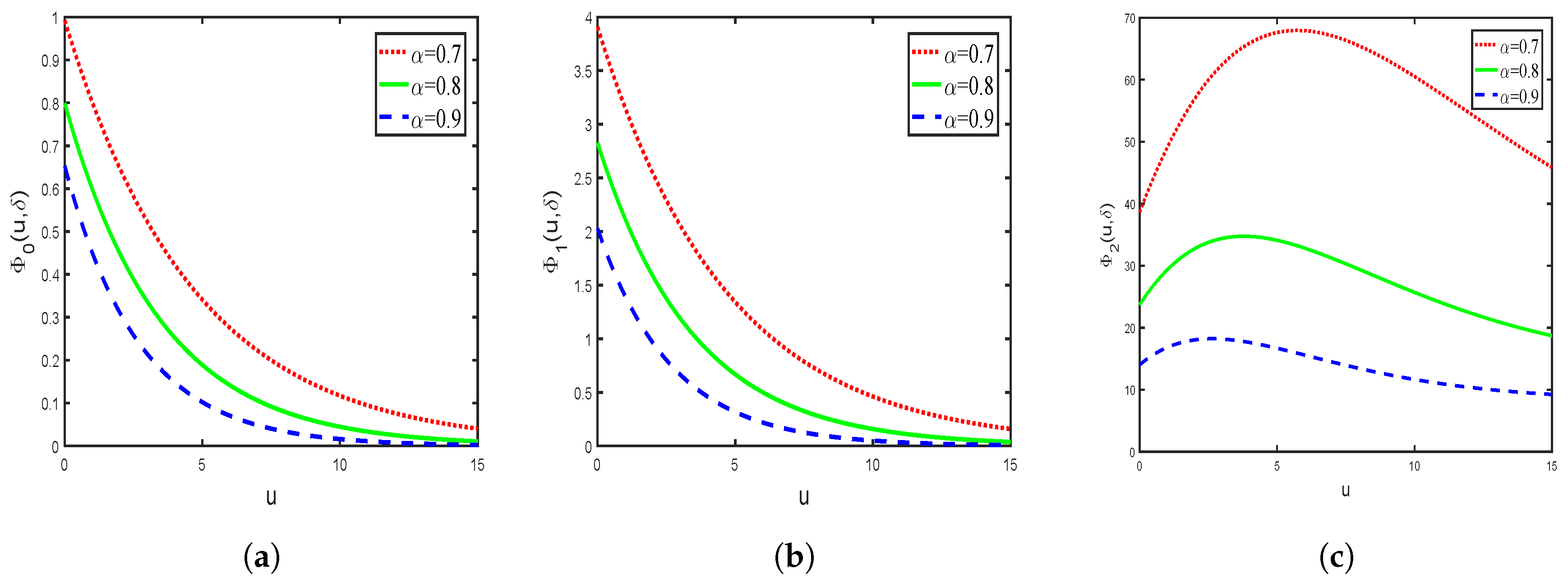
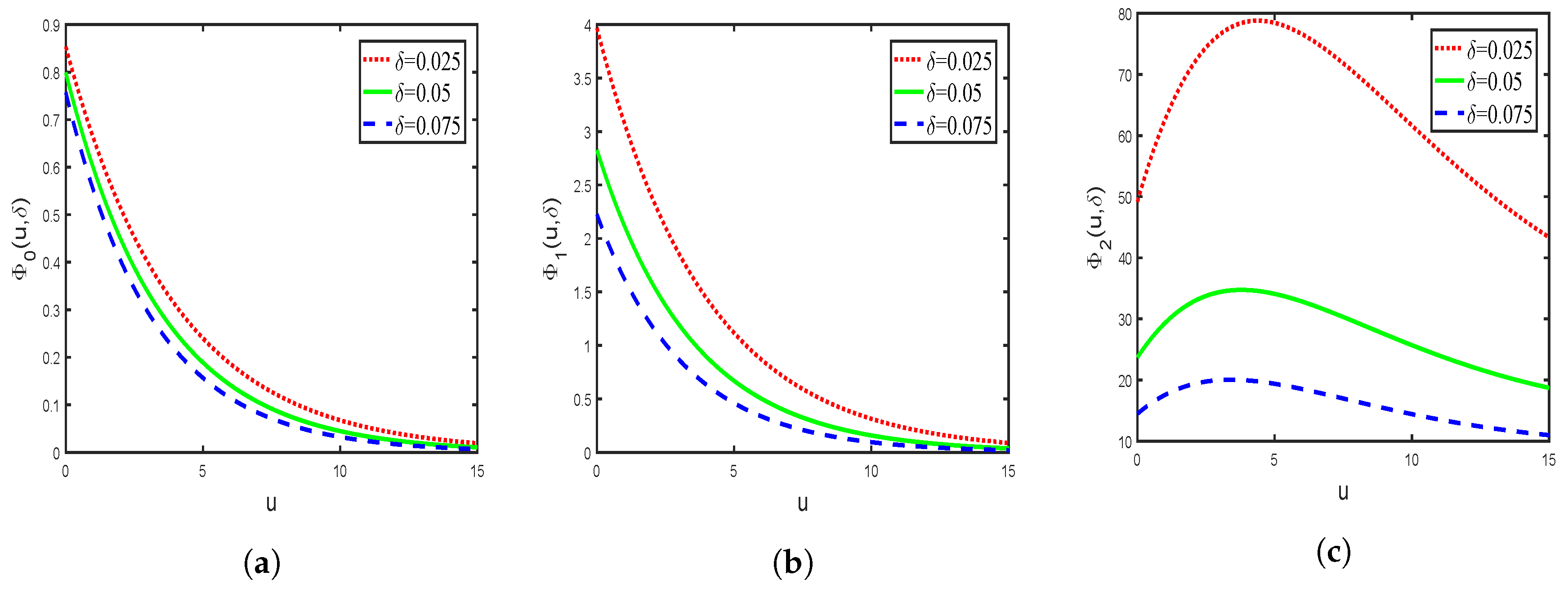
3. Explicit Expressions for Exponential Claim Distribution and Numerical Examples
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lin, X.S.; Willmot, G.E.; Drekic, S. The classical risk model with a constant dividend barrier: Analysis of the Gerber–Shiu discounted penalty function. Insur. Math. Econ. 2003, 33, 391–408. [Google Scholar]
- Zhang, H.Y.; Zhou, M.; Guo, J.Y. The Gerber–Shiu discounted penalty function for classical risk model with a two-step premium rate. Stat. Probab. Lett. 2006, 76, 1211–1218. [Google Scholar] [CrossRef]
- Yu, W.G. Some results on absolute ruin in the perturbed insurance risk model with investment and debit interests. Econ. Model. 2013, 31, 625–634. [Google Scholar] [CrossRef]
- Yu, W.G. On the expected discounted penalty function for a Markov regime switching risk model with stochastic premium income. Discret. Dyn. Nat. Soc. 2013, 2013, 1–9. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Yu, W.G.; Huang, Y.J.; Yu, X.L.; Fan, H.L. Estimating the expected discounted penalty function in a compound Poisson insurance risk model with mixed premium income. Mathematics 2019, 7, 305. [Google Scholar] [CrossRef]
- Avram, F.; Palmowski, Z.; Pistorius, M.R. On Gerber–Shiu functions and optimal dividend distribution for a Lévy risk process in the presence of a penalty function. Ann. Appl. Probab. 2015, 25, 1868–1935. [Google Scholar] [CrossRef]
- Zhang, Z.M. Estimating the Gerber–Shiu function by Fourier-Sinc series expansion. Scand. Actuar. J. 2017, 2017, 898–919. [Google Scholar] [CrossRef]
- Chi, Y.C. Analysis of expected discounted penalty function for a general jump diffusion risk model and applications in finance. Insur. Math. Econ. 2010, 46, 385–396. [Google Scholar] [CrossRef]
- Peng, J.Y.; Wang, D.C. Uniform asymptotics for ruin probabilities in a dependent renewal risk model with stochastic return on investments. Stochastics 2018, 90, 432–471. [Google Scholar] [CrossRef]
- Li, S.M.; Lu, Y.; Sendova, K.P. The expected discounted penalty function: From infinite time to finite time. Scand. Actuar. J. 2019, 2019, 336–354. [Google Scholar] [CrossRef]
- Huang, Y.J.; Yu, W.G.; Pan, Y.; Cui, C.R. Estimating the Gerber–Shiu expected discounted penalty function for Lévy risk model. Discrete Dyn. Nat. Soc. 2019, 2019, 1–15. [Google Scholar] [CrossRef]
- Preischl, M.; Thonhauser, S. Optimal reinsurance for Gerber–Shiu functions in the Cramér-Lundberg model. Insur. Math. Econ. 2019, 87, 82–91. [Google Scholar] [CrossRef]
- Zeng, Y.; Li, D.P.; Chen, Z.; Yang, Z. Ambiguity aversion and optimal derivative–based pension investment with stochastic income and volatility. J. Econ. Dyn. Control 2018, 88, 70–103. [Google Scholar] [CrossRef]
- Zeng, Y.; Li, D.P.; Gu, A.L. Robust equilibrium reinsurance–investment strategy for a mean–variance insurer in a model with jumps. Insur. Math. Econ. 2016, 66, 138–152. [Google Scholar] [CrossRef]
- Yu, W.G.; Huang, Y.J.; Cui, C.R. The absolute ruin insurance risk model with a threshold dividend strategy. Symmetry 2018, 10, 377. [Google Scholar] [CrossRef]
- Dickson, D.C.M.; Qazvini, M. Gerber–Shiu analysis of a risk model with capital injections. Eur. Actuar. J. 2016, 6, 409–440. [Google Scholar] [CrossRef]
- Zhang, Z.M.; Su, W. A new efficient method for estimating the Gerber–Shiu function in the classical risk model. Scand. Actuar. J. 2018, 2018, 426–449. [Google Scholar] [CrossRef]
- Zhang, Z.M.; Su, W. Estimating the Gerber–Shiu function in a Lévy risk model by Laguerre series expansion. J. Comput. Appl. Math. 2019, 346, 133–149. [Google Scholar] [CrossRef]
- Li, J.C.; Dickson, D.C.M.; Li, S.M. Some ruin problems for the MAP risk model. Insur. Math. Econ. 2015, 65, 1–8. [Google Scholar] [CrossRef]
- Zhao, Y.X.; Yin, C.C. The expected discounted penalty function under a renewal risk model with stochastic income. Appl. Math. Comput. 2012, 218, 6144–6154. [Google Scholar] [CrossRef]
- Cai, J.; Feng, R.; Willmot, G.E. On the total discounted operating costs up to default and its applications. Adv. Appl. Probab. 2009, 41, 495–522. [Google Scholar] [CrossRef]
- Cheung, E.C.K. A generalized penalty function in Sparre–Andersen risk models with surplus-dependent premium. Insur. Math. Econ. 2011, 48, 384–397. [Google Scholar] [CrossRef][Green Version]
- Cheung, E.C.K. Moments of discounted aggregate claim costs until ruin in a Sparre–Andersen risk model with general interclaim times. Insur. Math. Econ. 2013, 53, 343–354. [Google Scholar] [CrossRef]
- Cheung, E.C.K.; Woo, J.K. On the discounted aggregate claim costs until ruin in dependent Sparre–Andersen risk processes. Scand. Actuar. J. 2016, 2016, 63–91. [Google Scholar] [CrossRef]
- Cheung, E.C.K.; Feng, R. A unified analysis of claim costs up to ruin in a Markovian arrival risk process. Insur. Math. Econ. 2013, 53, 98–109. [Google Scholar] [CrossRef]
- Wang, H.C.; Li, N.X. On the Gerber–Shiu function with random discount rate. Commun. Stat. Theory Methods 2017, 46, 210–220. [Google Scholar] [CrossRef]
- Wang, W.Y.; Zhang, Z.M. Computing the Gerber–Shiu function by frame duality projection. Scand. Actuar. J. 2019, 2019, 291–307. [Google Scholar] [CrossRef]
- Egidio dos Reis, A.D. On the moments of ruin and recovery times. Insur. Math. Econ. 2000, 27, 331–343. [Google Scholar] [CrossRef]
- Lin, X.S.; Willmot, G.E. The moments of the time of ruin, the surplus before ruin, and the deficit at ruin. Insur. Math. Econ. 2000, 27, 19–44. [Google Scholar] [CrossRef]
- Drekic, S.; Willmot, G.E. On the moments of the time of ruin with applications to phase-type claims. N. Am. Actuar. J. 2005, 9, 17–30. [Google Scholar] [CrossRef]
- Pitts, S.M.; Politis, K. Approximations for the moments of ruin time in the compound Poisson model. Insur. Math. Econ. 2008, 42, 668–679. [Google Scholar] [CrossRef]
- Yu, K.; Ren, J.; Stanford, D.A. The moments of the time of ruin in Markovian risk models. N. Am. Actuar. J. 2010, 14, 464–471. [Google Scholar] [CrossRef]
- Lee, W.Y.; Willmot, G.E. On the moments of the time to ruin in dependent Sparre–Andersen models with emphasis on Coxian interclaim times. Insur. Math. Econ. 2014, 59, 1–10. [Google Scholar] [CrossRef]
- Lee, W.Y.; Willmot, G.E. The moments of the time to ruin in dependent Sparre–Andersen models with Coxian claim sizes. Scand. Actuar. J. 2016, 2016, 550–564. [Google Scholar] [CrossRef]
- Schmidli, H. Extended Gerber–Shiu functions in a risk model with interest. Insur. Math. Econ. 2015, 61, 271–275. [Google Scholar] [CrossRef]
- Deng, Y.C.; Liu, J.; Huang, Y.; Li, M.; Zhou, J.M. On a discrete interaction risk model with delayed claims and stochastic incomes under random discount rates. Commun. Stat. Theory Methods 2018, 47, 5867–5883. [Google Scholar] [CrossRef]
- Li, S.M.; Lu, Y. On the generalized Gerber–Shiu function for surplus processes with interest. Insur. Math. Econ. 2013, 52, 127–134. [Google Scholar] [CrossRef]
- Dickson, D.C.M.; Hipp, C. On the time to ruin for Erlang (2) risk processes. Insur. Math. Econ. 2001, 29, 333–344. [Google Scholar] [CrossRef]
- Li, S.M.; Garrido, J. On ruin for the Erlang(n) risk process. Insur. Math. Econ. 2004, 34, 391–408. [Google Scholar] [CrossRef]
- Gerber, H.U.; Shiu, E.S.W. On the time value of ruin. N. Am. Actuar. J. 1998, 2, 48–72. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruan, J.; Yu, W.; Song, K.; Sun, Y.; Huang, Y.; Yu, X. A Note on a Generalized Gerber–Shiu Discounted Penalty Function for a Compound Poisson Risk Model. Mathematics 2019, 7, 891. https://doi.org/10.3390/math7100891
Ruan J, Yu W, Song K, Sun Y, Huang Y, Yu X. A Note on a Generalized Gerber–Shiu Discounted Penalty Function for a Compound Poisson Risk Model. Mathematics. 2019; 7(10):891. https://doi.org/10.3390/math7100891
Chicago/Turabian StyleRuan, Jiechang, Wenguang Yu, Ke Song, Yihan Sun, Yujuan Huang, and Xinliang Yu. 2019. "A Note on a Generalized Gerber–Shiu Discounted Penalty Function for a Compound Poisson Risk Model" Mathematics 7, no. 10: 891. https://doi.org/10.3390/math7100891
APA StyleRuan, J., Yu, W., Song, K., Sun, Y., Huang, Y., & Yu, X. (2019). A Note on a Generalized Gerber–Shiu Discounted Penalty Function for a Compound Poisson Risk Model. Mathematics, 7(10), 891. https://doi.org/10.3390/math7100891




