Abstract
In this paper, we introduce and study a new three-parameter lifetime distribution constructed from the so-called type I half-logistic-G family and the inverted Kumaraswamy distribution, naturally called the type I half-logistic inverted Kumaraswamy distribution. The main feature of this new distribution is to add a new tuning parameter to the inverted Kumaraswamy (according to the type I half-logistic structure), with the aim to increase the flexibility of the related inverted Kumaraswamy model and thus offering more precise diagnostics in data analyses. The new distribution is discussed in detail, exhibiting various mathematical and statistical properties, with related graphics and numerical results. An exhaustive simulation was conducted to investigate the estimation of the model parameters via several well-established methods, including the method of maximum likelihood estimation, methods of least squares and weighted least squares estimation, and method of Cramer-von Mises minimum distance estimation, showing their numerical efficiency. Finally, by considering the method of maximum likelihood estimation, we apply the new model to fit two practical data sets. In this regards, it is proved to be better than recent models, also derived to the inverted Kumaraswamy distribution.
Keywords:
half-logistic distribution; inverted Kumaraswamy distribution; estimation methods; data analysis MSC:
60E05; 62E15; 62F10
1. Introduction
Over the last years, numerous families of distributions have been introduced, providing new opportunities in terms of statistical modeling and data analysis. One of the most promising of them is the so-called type I half-logistic-G (TIHL-G) family introduced by [1]. The TIHL-G family is characterized by the cumulative distribution function (cdf) given by
where is a baseline cdf of a continuous distribution depending on a parameter vector and . The definition of is derived to the T-X technique of [2] applied with the half-logistic distribution as main generator, that is, , where , , is the probability density function (pdf) of the half-logistic distribution. Among the qualities of the TIHL-G family, we would like to mention the tractability of the corresponding functions and the fact that the additional parameters can significantly increase the flexibility of the mode and the tails of the former distribution characterized by . That explains why several special members have been recently studied in detail. We refer the reader to [3] for the type I half-logistic Burr XII distribution (also called extended Bur XII distribution), [4] for the type I half-logistic generalized Weibull distribution, [5] for the type I half-logistic Lomax distribution, and [6] for the type I half-logistic exponential distribution. Also, with the use of an additional parameter, the type I half-logistic-G family was recently generalized by [7].
In parallel, several new flexible continuous distributions was studied. In particular, [8] recently introduced a new two-parameter lifetime distribution, called the inverted Kumaraswamy (IK) distribution. It is characterized by the cdf given by
where . The basics of the IK distribution is as follows: It is the distribution of the random variable , where U is a random variable following the standard Kumaraswamy distribution introduced by [9], i.e., with the cdf given by , . Among the features of this distribution, it covers many well-established distributions as the Lomax (Pareto type II) distribution when , the beta type II (inverted beta) distribution when , the log-logistic (Fisk) distribution when , the inverted Weibull distribution when and the generalized exponential distribution when . Also, the IK distribution demonstrates a great flexibility in terms of curvature of the distribution functions, specially on the mode and the tails of the distribution.
In this paper, we define a new three-parameter lifetime distribution by mixing the TIHL-G family and the IK distribution. Thus, it can be viewed as a new special member of the TIHL-G family benefiting from the qualities of the IK distribution, naturally called the type I half-logistic inverted Kumaraswamy (TIHLIK) distribution. This study is devoted to both its theoretical and practical features, with an emphasis on the applied side. Indeed, a substantial part is devoted to the estimation of the model parameters via various methods, with all the details. Nice performance of the estimates are observed, with discussions. Then, we show that the related TIHLIK model shows better fits for some data sets when compared to recent rivals, also defined with the IK model as baseline. The required computations are carried out in the R-language introduced by R Development Core Team [10]. Beyond the data analysis, the TIHLIK distribution (and its symmetric version around 0) can find applications in many other applied domains. For instance, it can be used to construct new prior distributions in a Bayesian setting and new mixtures of distributions in a discriminant analysis framework. Modern developments in these directions can be found in [11,12].
The rest of the paper is divided into six sections. Section 2 presents the TIHLIK distribution. Some mixture representations of the main functions in terms of Lomax distribution functions are given in Section 3. In Section 4, we attempt to derive the main mathematical and statistical properties of the TIHLIK distribution. Section 5 is devoted to the estimation of the model parameters, with a simulation study. Applications are given in Section 6. Section 7 provides concluding remarks.
2. The TIHLIK Distribution
By mixing the TIHL-G family and the IK distribution, the cdf of the TIHLIK distribution is given by
Upon differentiation, the corresponding pdf is given by
Also, the hazard rate function (hrf) of the TIHLIK distribution is given by
and the corresponding cumulative hazard rate function (chrf) is given by
In order to illustrate the flexibility of the TIHLIK distribution, Figure 1 and Figure 2 present plots of the above pdfs and hrfs. We would like to mention that the values for the parameters , a, and b have been taken arbitrarily until we get a wide variety of shapes for the involved functions.
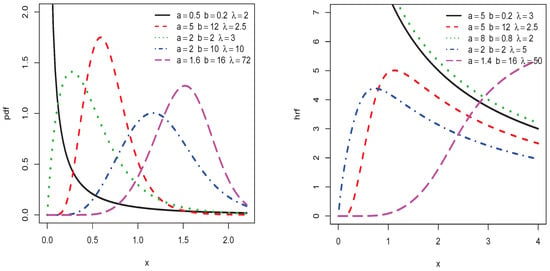
Figure 1.
Plots of some probability density functions (pdfs) and hazard rate functions (hrfs) of the type I half-logistic inverted Kumaraswamy (TIHLIK) distribution.
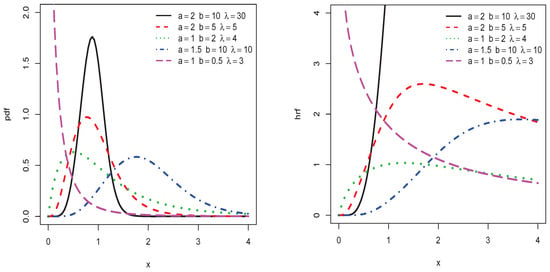
Figure 2.
Plots of some pdfs and hrfs of the TIHLIK distribution.
We observe that the pdf is left, right skewed, symmetrical, and reverse J shaped while the hrf is increasing, decreasing, and upside-down bathtub shaped.
3. Mixture Representations
In this section, we will express the pdf and cdf of the TIHLIK distribution in terms of pdfs and cdfs of the well-established Lomax distribution (also called the Pareto Type II distribution).
Proposition 1.
We have the following mixture representation for :
where (with ) and denotes the survival function of the Lomax distribution with parameters and 1, i.e., .
Proof.
Since , the power series formula gives
Since and , it follows from the binomial formula applied two times in a row that
By putting the above equalities together, we obtain
This ends the proof of Proposition 1. □
Corollary 1.
Upon differentiation of , we obtain the following mixture representation for :
where and denotes the pdf of the Lomax distribution with parameters and 1, i.e., .
In Corollary 1, we would like to mention that the sum of m begins with 1 since , which remains an important detail for the coming technical developments involving the distributional properties of the Lomax distribution.
The following result considers a mixture representation for the exponentiated .
Proposition 2.
Let ζ be a positive integer. Then, we have the following mixture representation:
where and denotes the survival function of the Lomax distribution with parameters and 1.
Proof.
Owing to the (standard) binomial formula, we get
Since , and , the general binomial formula applied three times in a row gives
We obtain the desired result by combining the above equalities together, ending the proof of Proposition 2. □
4. Mathematical and Statistical Properties
This section deals with the mathematical and statistical properties of the TIHLIK distribution. Hereafter, we consider a random variable X following the TIHLIK distribution, i.e., with the cdf given by Equation (1) and the pdf given by Equation (2).
4.1. Shapes and Asymptotes
When , we have
From these equivalences, when , we get , when , we obtain and when , we have . The same holds for , under the same conditions. When , we have
So, and in all circumstances.
The shapes of also depend on the critical point(s) of the function, given by the solution(s) of the following equation: , i.e.,
In a same way, the shapes of also depend on the critical point(s) of the function, given by the solution(s) of the following equation: , i.e., , i.e.,
4.2. Quantile Function
The quantile function (qf) of X is given by
The median of X is given by . The other quartiles can be defined in a similar manner.
Simulated values from the TIHLIK distribution can be performed by using the following result. For any random variable U following the uniform distribution , follows the TIHLIK distribution.
Upon differentiation of , the corresponding quantile density function is given by
4.3. Ordinary Moments
We begin the study of the ordinary moments of X by an existence result.
Proposition 3.
Let r be a positive integer. Then, the r-th ordinary moment of X, i.e., , exists if, and only, if .
Proof.
The proof is centered around the equivalence results presented in Section 4.1. When , we have and, for any , by the Riemann integral criteria, exists since . When , we have and, for any , by the Riemann integral criteria, exists if, and only if, . This ends the proof of Proposition 3. □
Then, when , the r-th ordinary moment of X is defined by
This integral can be evaluated by any mathematical software.
If , an alternative expression, with possible gain in precision in terms of errors, is given by using Corollary 1, i.e.,
where , . After some algebra, one can remark that . For practical purpose, one can consider finite limit for the sums, say a large integer as 40.
As consequence, if , the mean and the variance of X can be expressed as, respectively, and , i.e.,
Table 1 presents the numerical values of some moments (and variance) of X for some values of the parameters (respecting the condition ).

Table 1.
Some moments and variance of X for the following parameters values respecting the order ; (i): , (ii): , (iii): (iv): (v): , and (vi): .
4.4. Skewness and Kurtosis
Assuming that , the first four moments of X can be used to determine the measures of skewness and kurtosis of X defined by, respectively,
To relax the assumption , one can consider measures of skewness and kurtosis based on the qf, as the Bowley skewness and Moors kurtosis defined by, respectively,
and
They was introduced by [13,14], respectively.
The plots of and are shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8, for different parameter ranges. We see smooth non-monotonic variation of these measures, attesting a significant effect of a, b, and on them.
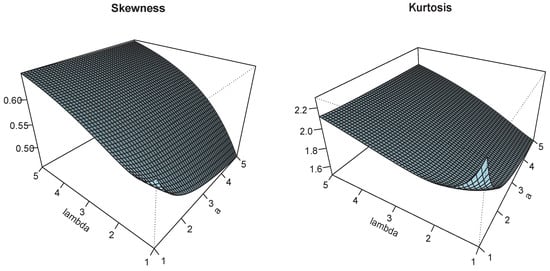
Figure 3.
Plots of and for and .
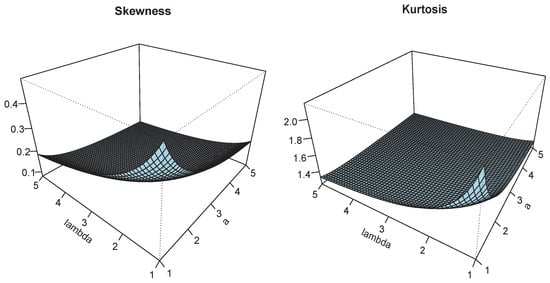
Figure 4.
Plots of and for and .
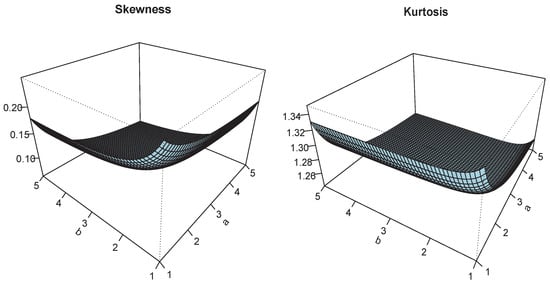
Figure 5.
Plots of and for and .
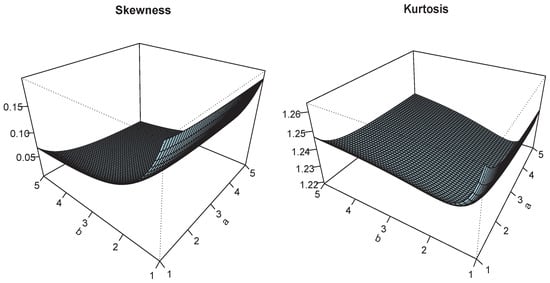
Figure 6.
Plots of and for and .
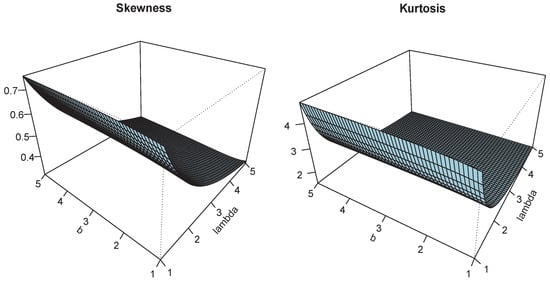
Figure 7.
Plots of and for and .
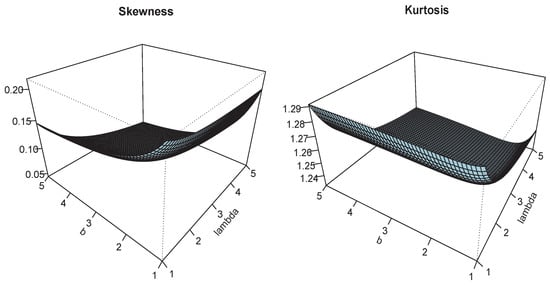
Figure 8.
Plots of and for and .
4.5. Incomplete Moments
Let us now studied the incomplete moments of X. For any , the r-th incomplete moment of X exists and it is given by
where denotes the random variable such that if is realized, and 0 otherwise. It follows from Corollary 1 that
For , we have the following sum expression for the integral term:
The first incomplete moment is given by . It is useful to define other important quantities, as the mean deviation of X about given by
the mean of X about M given by
the Bonferroni curve given by
and the Lorenz curves given by , .
4.6. Stress Strength Parameter
This subsection is devoted to the stress strength parameter, as described in [15], in the context of the TIHLIK distribution. It is defined by , when and are two independent random variables following the TIHLIK distribution with the parameters , and , and , , and , respectively.
Proposition 4.
Under the setting described above, we have
where .
Proof.
Owing to Propositions 1 and Corollary 1, we have
where and . Then, one can notice that and that the integral term can be expressed as
By putting the above equalities together, we end the proof of Proposition 4. □
Finally, we would like to mention that, when , , and , we have .
4.7. Order Statistics
Order statistics was first studied by [16] in the context of the standard normal distribution. In a more general way, order statistics naturally arise for modeling a wide variety of phenomenas, mainly in reliability and life testing. Here, we provide some useful results involving the order statistics of the TIHLIK distribution. Let be n independent random having the TIHLIK distribution as common distribution and be the i-th order statistic defined by the i-th random variable such that, by arranging in increasing order, we have . Then, a well-known result ensures that the cdf of is given by
By applying Proposition 2, we obtain the following mixture representation:
where .
Also, it is well-known that the pdf of is given by
Upon differentiation of Equation (3), one can express as a mixture of pdfs of the Lomax distribution, i.e.,
where and denotes the pdf of the Lomax distribution with parameters and 1. From this expression, one can derive some structural properties of (ordinary moments, incomplete moments…).
Let us now specially focus on the crucial first order statistic given by . The cdf and pdf of are, respectively, given by
and
The corresponding mixture expressions in terms of Lomax distribution functions are given by Equations (3) and (4), respectively, by taking .
Let us now derive the asymptotic distribution of . It follows from the equivalence results of Section 4.1 that
Hence, since , it follows from [17] (Theorem 8.3.6) that the asymptotic distribution of is the Weibull distribution with parameter b, i.e., there exist two sequence of real numbers and such that .
5. Estimation with Simulation
This section is devoted to some statistical features of the TIHLIK model, assuming that , a, and b are unknown. The estimation of , a, and b is performed by the several recognized methods of estimation. Hereafter, denote n observed values from X, and their ascending ordering values, i.e., .
5.1. Method of Maximum Likelihood Estimation
The method of maximum likelihood estimation in the context of the TIHLIK model is described below. We refer the reader to [18] for the general details. The maximum likelihood estimates (MLEs) of , a, and b can be obtained by maximizing, with respect to , a, and b, the likelihood function given by or, alternatively, the log-likelihood function for given by , i.e.,
Thus, the MLEs are obtained by solving the following equations simultaneously: , and , where
and
These equations can be solved numerically by using any mathematical software. When n is large enough, under some conditions of regularity, the subjacent distribution of the MLEs can be approximated by normal distributions, with variance given as the corresponding component of the inverse of the observed information matrix computed at those MLEs. Owing to these distributional results, confidence intervals and statistical tests for , a, and b can be defined analytically.
5.2. Methods of Least Squares and Weighted Least Squares Estimation
We now consider the methods of least squares and weighted least squares estimation introduced by [19]. The least square estimates (LSEs) of , a, and b can be determined by minimizing, with respect to , a, and b, the following function:
Thus, the LSEs are obtained by solving the following equations simultaneously: , , and , where
and
where
and
The weighted least square estimates (WLSEs) of , a, and b can be determined by minimizing, with respect to , a, and b, the following function:
Thus, the WLSEs can be determined by solving the following equations simultaneously: , , and , which are similar to those previously presented, with the weight sequence plug-in in the right place.
5.3. Method of Cramer-von Mises Minimum Distance Estimation
Another famous estimation method is the method of Cramer-von Mises minimum distance estimation introduced by [20]. By applying it in the context of the TIHLIK model, the Cramer-von Mises minimum distance estimates (CVEs) of , a, and b can be obtained by minimizing, with respect to , a, and b, the following function:
5.4. Methods of Anderson–Darling and Right-Tail Anderson–Darling Estimation
The method of Anderson–Darling estimation was introduced by [21]. Here, the Anderson–Darling estimates (ADEs) of , a, and b can be determined by minimizing, with respect to , a, and b, the following function:
This function is expressible, but we omit it to save space. Thus, the Anderson–Darling estimates are obtained by solving the following equations simultaneously: , , and , where
and
, , and are given by Equations (5)–(7), respectively.
Similarly, the right-tail Anderson–Darling estimates (RTADEs) of , a, and b, can be obtained by minimizing, with respect to and , the following function:
Thus, the RTADEs can be determined by solving the following equations simultaneously: , , and , where
and
5.5. Simulation Study
In this section, we come up with a numerical study to compare the behavior of the different estimates presented above. We generate random samples of size , and 100 from the TIHLIK distribution. Four sets of the parameters are assigned as: Set1: (), Set2: (), Set3: , and Set4: . The MLE, LSE, WLSE, CVE, and RTADE of , b, and a are determined, along with their mean estimate Est. and their mean square errors (MSEs), i.e., , where, for a given method, corresponds to , a, or b and denotes the considered estimates for obtained by using the i-th random sample. All the numerical values are set in Table 2, Table 3, Table 4 and Table 5.

Table 2.
Estimates and mean square errors (MSEs) of TIHLIK model for maximum likelihood (ML), least squares (LS), weighted least square (WLS), Cramer-von Mises minimum distance (CV), and right-tail Anderson–Darling (RTAD) estimates for the Set1, i.e., , , .

Table 3.
Estimates and MSEs of TIHLIK model for ML, LS, WLS, CV, and RTAD estimates for the Set2, i.e., , , .

Table 4.
Estimates and MSEs of TIHLIK model for ML, LS, WLS, CV, and RTAD estimates for the Set3, i.e., , , .

Table 5.
Estimates and MSEs of TIHLIK model for ML, LS, WLS, CV, and RTAD estimates for the Set4, i.e., , , .
6. Applications to Practical Data Sets
This section provides applications of the TIHLIK model to two practical data sets. We compare the TIHLIK model with some recent efficiency models: those corresponding to the IK distribution, generalized inverted Kumaraswamy (GIK) distribution proposed by [22], Marshall–Olkin extended inverted Kumaraswamy (MOEIK) distribution introduced by [23], and Topp–Leone generalized inverted Kumaraswamy (TLGIK) distribution developed by [24]. The corresponding pdfs are presented below.
- The pdf of the MOEIK distribution is given bywith .
- The pdf of the GIK distribution is given bywhere .
- The pdf of the TLGIK distribution is given bywhere .
Since they have no analytical expressions, the MLEs of the model parameters are computed using an iterative optimization technique (the so-called limited-memory Broyden–Fletcher–Goldfarb–Shanno algorithm allowing bound constraints on variables). The well-known goodness-of-fit measures minus log-likelihood , Akaike information criterion (AIC), Bayesian information criterion (BIC), Anderson–Darling (A), and Cramer-von Mises (W) values are computed. The rule is clear: the lower the values of these criteria, the better the fit. The value for the Kolmogorov Smirnov (KS) statistic along with its p-value are also provided. We recall that the required computations were carried out via the R software.
The first data set (data set 1). The first practical life data consist of 30 observations of precipitation (in inches) collected in March in Saint Paul, Minneapolis. It was originally reported by [25]. The data are: 0.77, 1.74, 0.81, 1.20, 1.95, 1.20, 0.47, 1.43, 3.37, 2.20, 3.00, 3.09, 1.51, 2.10, 0.52, 1.62, 1.31, 0.32, 0.59, 0.81, 2.81, 1.87, 1.18, 1.35, 4.75, 2.48, 0.96, 1.89, 0.90, 2.05.
The second data set (data set 2). The second data set is obtained from [26]. The data are: 3.70, 2.74, 2.73, 2.50, 3.60, 3.11, 3.27, 2.87, 1.47, 3.11, 4.42, 2.40, 3.19, 3.22, 1.69, 3.28, 3.09, 1.87, 3.15, 4.90, 3.75, 2.43, 2.95, 2.97, 3.39, 2.96, 2.53, 2.67, 2.93, 3.22, 3.39, 2.81, 4.20, 3.33, 2.55, 3.31, 3.31, 2.85, 2.56, 3.56, 3.15, 2.35, 2.55, 2.59, 2.38, 2.81, 2.77, 2.17, 2.83, 1.92.
A first analysis of the data is given in Table 6, with descriptive statistics of the two considered data sets. Figure 9 and Figure 10 present the boxplots and total test time (TTT) plots for data sets 1 and 2, respectively. In particular, we see that both TTT plots are convex, indicating that the subjacent hrf are increasing, as the hrf of the TIHLIK distribution can be for some values of the parameters. We refer the reader to [27] for more facts about the TTT plot. The use of the TIHLIK model for these data sets is pertinent at the first glance; this will be refined below.

Table 6.
Descriptive statistics for data sets 1 and 2, respectively.
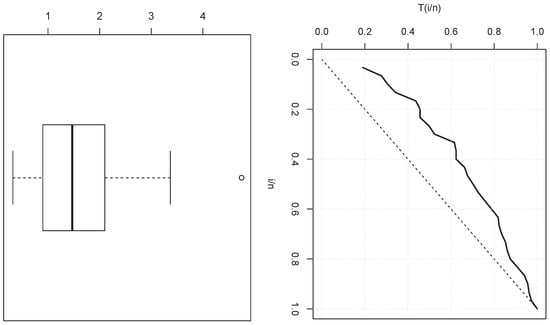
Figure 9.
Total test time (TTT) plot and boxplot for data set 1.
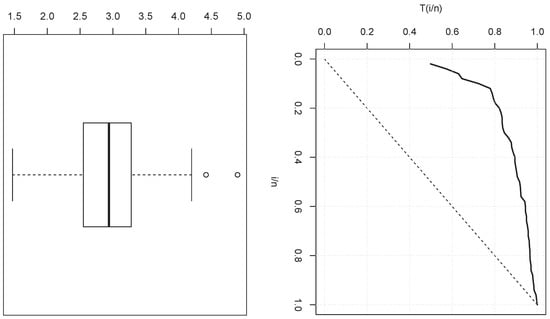
Figure 10.
TTT plot and boxplot for data set 2.
Table 7 and Table 8 show the MLEs of the considered models along with the corresponding standard errors for data set 1 and 2, respectively. The goodness-of-fit measures for the considered models are given in Table 9 and Table 10 for data set 1 and 2, respectively. Probability–Probability (P–P) plots and Quantile–Quantile (Q–Q) plots for the estimated TIHLIK model are presented in Figure 11 and Figure 12 for data sets 1 and 2, respectively. We can observe the nice adjustments of the scatter plots by the line of equation , illustrating that the TIHLIK model is adequate for the considered data. In order to observe the obtained fits, plots of the estimated pdfs over the histograms corresponding to data set 1 and 2 are shown in Figure 13 and Figure 14, respectively.

Table 7.
MLEs along with their standard errors (in parentheses) for data set 1.

Table 8.
MLEs along with their standard errors (in parentheses) for data set 2.

Table 9.
The , AIC, BIC, W, A, KS, and p-value values for data set 1.

Table 10.
The , AIC, BIC, W, A, KS, and p-value values for data set 2.
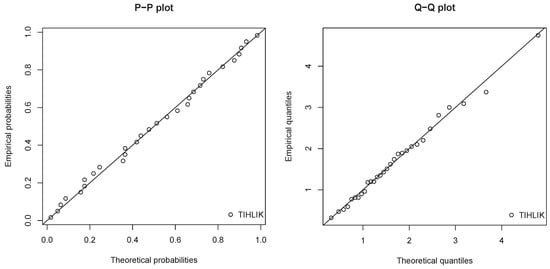
Figure 11.
Probability–Probability (P–P) plots and Quantile–Quantile (Q–Q) plot of the estimated TIHLIK model for data set 1.
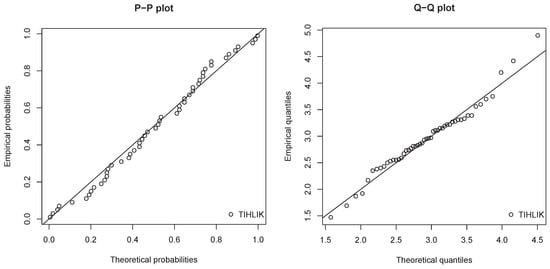
Figure 12.
P–P plot and Q–Q plot of the estimated TIHLIK model for data set 2.
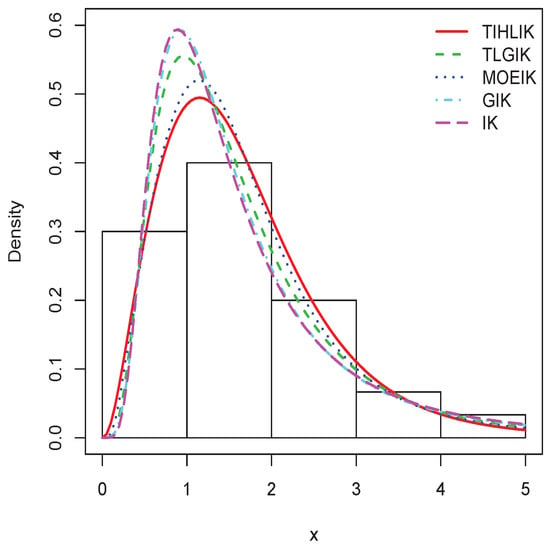
Figure 13.
Plots of the estimated pdfs for data set 1.
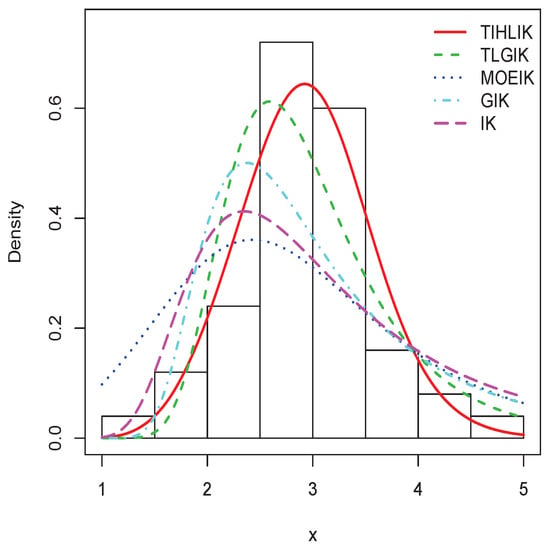
Figure 14.
Plots of the estimated pdfs for data set 2.
By observing the values of the AIC, BIC, A, and W in Table 9 and Table 10, since they are the smallest for the TIHLIK model, we conclude that it provides the best fit for the considered data sets. This is also confirmed with the p-value of the KS test. The superiority of the TIHLIK model comparing to the others is particularly flagrant for data set 2 in view of the fits in Figure 14. Last but not least, the TIHLIK model has only three parameters; it is thus less complex than the TLGIK and MOEIK models having both one more parameter.
7. Conclusions
In this paper, we introduce a new three-parameter lifetime distribution called the type I half-logistic inverted Kumaraswamy (TIHLIK) distribution, following the methodology described in Appendix A. Its main mathematical and statistical properties are derived, including mixture representations of crucial functions, shapes and asymptotes, quantile function, ordinary moments, skewness and kurtosis, incomplete moments, stress strength parameter, and order statistics. Several methods are investigated to estimate the TIHLIK model parameters, with efficiency supported by a simulation study considering varying sample sizes. We use two practical data sets to show that the new model can provide adequate fits as compared to four rivals, also based on the inverted Kumaraswamy distribution. In this setting, the smallest values for AIC, BIC, W, A, and KS are obtained for the TIHLIK model. We thus believe that it can be of interest for statisticians looking for precision in fitting various data sets extracted from sophisticated experiments, among others.
Author Contributions
R.A.Z., C.C., F.J., and M.E. have contributed equally to this work.
Funding
This work was funded by the Deanship of Scientific Research (DSR), King AbdulAziz University, Jeddah, under grant No. (DF-282-305-1441).
Acknowledgments
We thank the three reviewers for their constructive comments. This work was funded by the Deanship of Scientific Research (DSR), King AbdulAziz University, Jeddah, under grant No. (DF-282-305-1441). The authors gratefully acknowledge the DSR technical and financial support.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The main lines of the study, including contributions, are presented in the diagram of Figure A1.
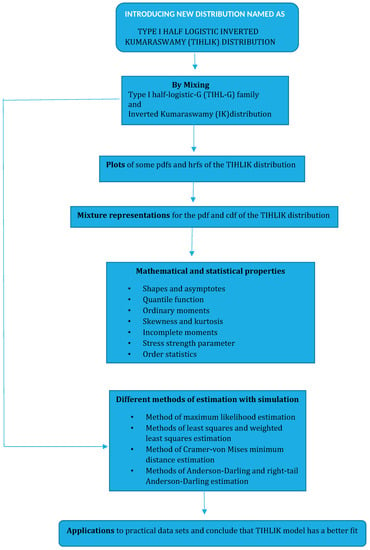
Figure A1.
Diagram summarizing the methodology and the main lines of the paper.
References
- Cordeiro, G.M.; Alizadeh, M.; Mar, E.P.R.D. The type I half-logistic family of distributions. J. Stat. Comput. Simul. 2015, 86, 707–728. [Google Scholar] [CrossRef]
- Alzaatreh, A.; Lee, C.; Famoye, F. A new method for generating families of distributions. Metron 2013, 71, 63–79. [Google Scholar] [CrossRef]
- Ghosh, I.; Bourguinon, M. A new extended burr XII distribution. Aust. J. Stat. 2017, 46, 33–39. [Google Scholar] [CrossRef]
- Anwar, M.; Bibi, A. The half-logistic generalized Weibull distribution. J. Probab. Stat. 2018, 2018, 8767826. [Google Scholar] [CrossRef]
- Anwar, M.; Zahoor, J. The half-logistic Lomax distribution for lifetime modeling. J. Probab. Stat. 2018, 2018, 3152807. [Google Scholar] [CrossRef]
- Almarashi, A.M.; Elgarhy, M.; Elsehetry, M.M.; Golam Kibria, B.M.; Algarni, A. A skew extension of the t-distribution, with applications. J. Nonlinear Sci. Appl. 2019, 12, 135–145. [Google Scholar] [CrossRef]
- El-Sherpieny, E.-S.; Elsehetry, M. Kumaraswamy Type I half-logistic family of distributions with applications. Gazi Univ. J. Sci. 2019, 32, 333–349. [Google Scholar]
- Abd Al-Fattah, A.M.; El-Helbawy, A.A.; Al-Dayian, G.R. Inverted Kumaraswamy distribution: Properties and estimation. Pak. J. Stat. 2017, 33, 37–61. [Google Scholar]
- Kumaraswamy, P. A generalized probability density function for double bounded random processes. J. Hydrol. 1980, 46, 79–88. [Google Scholar] [CrossRef]
- R Development Core Team. R- A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Austria, Vienna, 2009. [Google Scholar]
- Imani, M.; Ghoreishi, S.F.; Braga-Neto, U.M. Bayesian control of large MDPs with unknown dynamics in data-poor environments. In Proceedings of the NeurIPS 2018, Advances in Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; pp. 8156–8166. [Google Scholar]
- Xie, S.; Imani, M.; Dougherty, E.R.; Braga-Neto, U.M. Nonstationary linear discriminant analysis. In Proceedings of the 2017 51st Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 29 October–1 November 2017; pp. 161–165. [Google Scholar]
- Galton, F. Inquiries Into Human Faculty and Its Development; Macmillan and Company: London, UK, 1883. [Google Scholar]
- Moors, J.J.A. A quantile alternative for kurtosis. J. R. Stat. Soc. Ser. D (Stat.) 1988, 37, 25–32. [Google Scholar] [CrossRef]
- Kotz, S.; Lumelskii, Y.; Penskey, M. The Stress-Strength Model and Its Generalizations and Applications; World Scientific: Singapore, 2003. [Google Scholar]
- Tippett, L.H.C. On the extreme individuals and the range of samples taken from a normal population. Biometrika 1925, 17, 364–387. [Google Scholar] [CrossRef]
- Arnold, B.C.; Balakrishnan, N.; Nagaraja, H.N. First Course in Order Statistics; John Wiley: New York, NY, USA, 1992. [Google Scholar]
- Casella, G.; Berger, R.L. Statistical Inference; Brooks/Cole Publishing Company: Pacific Grove, CA, USA, 1990. [Google Scholar]
- Swain, J.J.; Venkatraman, S.; Wilson, J.R. Least-squares estimation of distribution functions in johnson’s translation system. J. Stat. Simul. 1988, 29, 271–297. [Google Scholar] [CrossRef]
- Macdonald, P.D.M. Comment on ‘An estimation procedure for mixtures of distributions’ by Choi and Bulgren. J. R. Stat. Soc. B 1971, 33, 326–329. [Google Scholar]
- Anderson, T.W.; Darling, D.A. Asymptotic theory of certain ’goodness-of- fit’ criteria based on stochastic processes. Ann. Math. Stat. 1952, 23, 193–212. [Google Scholar] [CrossRef]
- Iqbal, Z.; Tahir, M.M.; Riaz, N.; Ali, S.A.; Ahmad, M. Generalized inverted Kumaraswamy distribution: Properties and application. Open J. Stat. 2017, 7, 645–662. [Google Scholar] [CrossRef]
- Usman, R.M.; Haq, M.A.U. The Marshall-Olkin extended inverted Kumaraswamy distribution: Theory and applications. J. King Saud Univ.-Sci. 2018. [Google Scholar] [CrossRef]
- Reyad, H.; Jamal, F.; Othman, S.; Yahia, N. The Topp-Leone generalized inverted Kumaraswamy distribution: Properties and applications. Asian Res. J. Math. 2019, 13, 1–15. [Google Scholar] [CrossRef]
- Hinkley, D. On quick choice of power transformations. Appl. Stat. 1977, 26, 67–69. [Google Scholar] [CrossRef]
- Nichols, M.D.; Padgett, W.J. A bootstrap control chart for Weibull percentiles. Qual. Reliab. Eng. Int. 2005, 22, 141–151. [Google Scholar] [CrossRef]
- Aarset, M.V. How to identify bathtub hazard rate. IEEE Trans. Reliab. 1987, 36, 106–108. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).