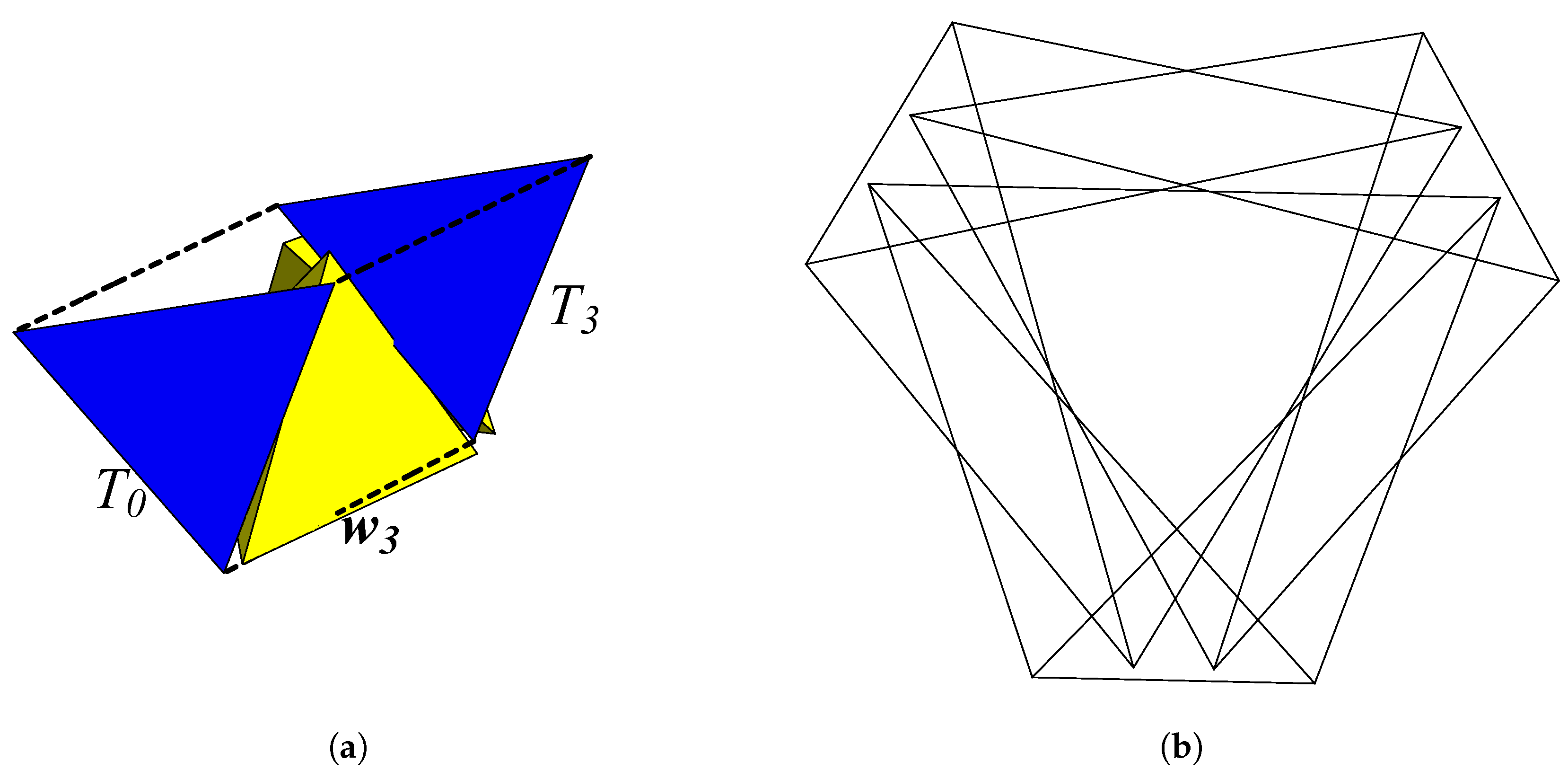
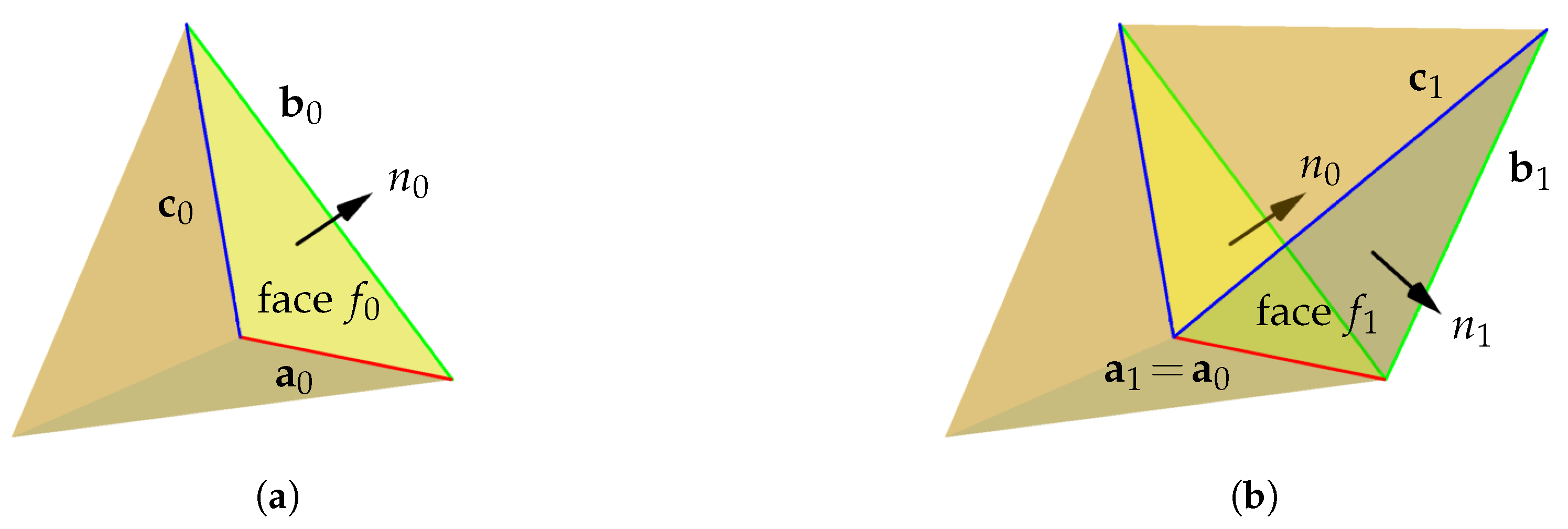3.1. Standard BC Helix, Aperiodic
On the initial tetrahedron
(
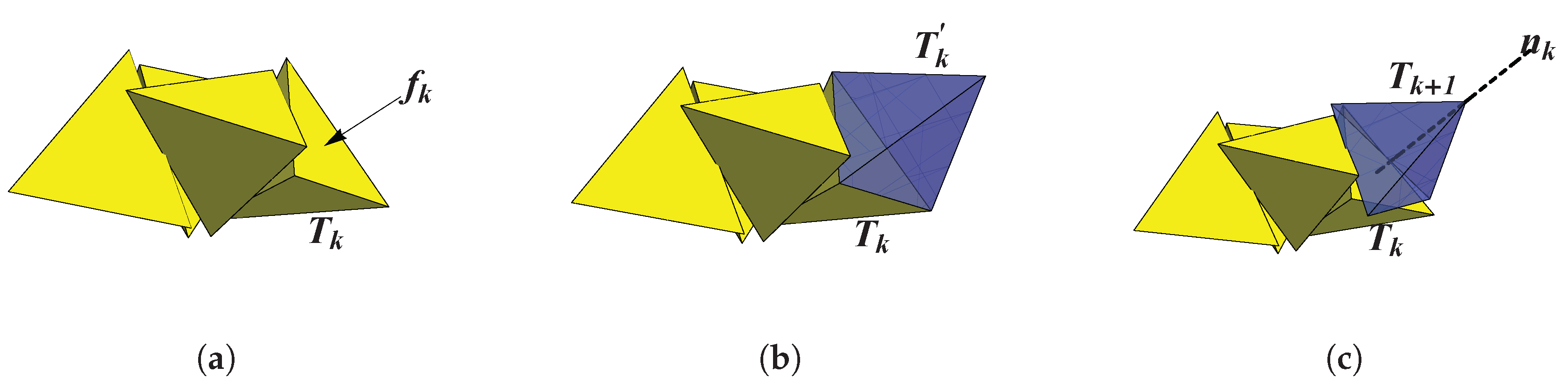
Figure 3a), select as before a face
(with unit normal
) where the next tetrahedron will be appended, and label the edges
,
,
. Then, instead of reflecting through
, rotate outward through it around
by the tetrahedron’s dihedral angle. This yields the same appended tetrahedron
as if we had reflected through
, but it transforms
to a new face
(
Figure 3b). The edges are likewise transformed to
,
, and
with, of course,
, since that was the axis of rotation.
In subsequent steps, is generated by rotating through face around one of , where the , , and are used cyclically. Thus, rotations are taken successively about , , , , , …. This sequence assures that is always the correct face across which to extend the BC helix, which will be left-/right-handed if are ordered clockwise/counterclockwise around .
Periodicity of the helix, or lack thereof, is determined by whether any tetrahedron has the same orientation as , up to the group symmetries of the tetrahedron. We can test for this most easily by ignoring the translations of the tetrahedra, locating all their centroids at the origin, and observing how they are rotated relative to .
To do so, let
be a copy of
with its centroid
translated to the origin. That is,
Let be unit vectors at the origin, parallel respectively to the edges of . The rotation about the edge by any angle can be represented as a sequence of, first, a translation taking one vertex of to the origin; next, a rotation about by the given angle; and finally, a translation taking the origin back to the vertex of . A corresponding sequence represents rotations about and . Ignoring translations, then, to compare the orientations of the , we look at the , each of which is determined simply by rotations about the vectors for .
The geometric, or Clifford, algebra
is particularly convenient for representing rotations in the Euclidean space
[
6,
7,
8], so this shall be the primary tool for our analysis. Rotation of the Euclidean vectors is a special case of the rotation of multivectors in
, where a mulitvector
M is rotated by a rotor
R and its reverse
,
R itself is a multivector subject to such transformations. Moreover, a product of rotors is another rotor, along with its reverse,
We can write a rotor, among other ways, as a bivector exponential or as the product of two vectors. Let
I be the right-handed unit trivector, and let
v and
w be arbitrary unit vectors separated by an angle
. The rotor for a rotation by
in the
-plane is
with
u another unit vector orthogonal to that plane and oriented so that
is a right-handed (though not orthogonal) triple.
is the unit bivector of the
-plane.
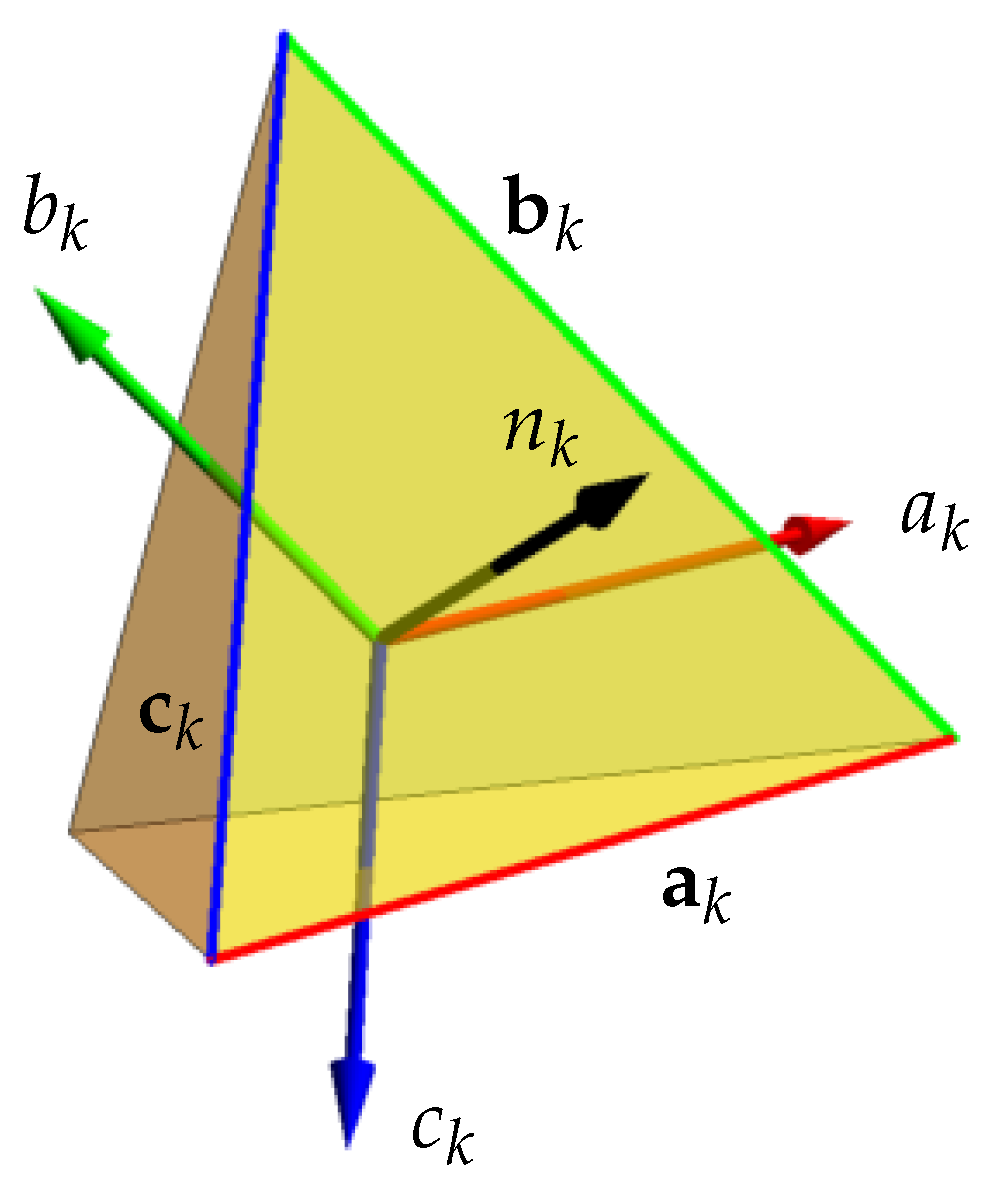
We apply this now to
. The important quantity, which shall be our focus throughout this section, is the rotor
that determines
. It is composed of a sequence of rotations about vectors
, where
represents either
a,
b, or
c, whichever is the
kth term. The angle of rotation in each case is the tetrahedron’s dihedral angle,
, so let
be the dihedral half-angle. We can therefore express the rotations in rotor form as
(This assumes a right-handed rotation about each
, so the direction of each along its specified line must be correctly chosen; we shall do that shortly). Equation (11) is an intuitive form exhibiting explicitly how
is rotated successively about the different axes, but all the distinct non-commuting bivectors in the exponents make this difficult to work with. Two simplifications will remedy this.
The first comes from the relationship between
,
, and
, which are defined to lie parallel to the sides of the equilateral triangle face
, normal to
. As mentioned in the preceding paragraph, the line on which each lies has been specified, but not the direction along that line. For Equation (11) to be valid when used in Equation (
10), choose
to be cyclically oriented in a right-handed sense relative to
(
Figure 4), such that, e.g.,
is directed from edge
to
. Hence,
Figure 4 confirms that a right-handed rotation about
is the same orientation as the rotation about edge
that takes the tetrahedron outward through face
in the direction of
, as required to correctly construct the BC helix.
Equation (
13) can be solved for
and
in terms of
as
Therefore, the sequence
,
,
, … can be written
,
,
,… with
With this first simplification we eliminate the
bs and
cs from
in Equation (11). The price is the introduction of
ns (in Equation (
15)), but it allows us to write each factor in a uniform way, distinguished only by the value of its index, whence
The second simplification is to address the fact that in Equation (15), the and of each successive transformation are themselves the results of all the previous transformations, so that has a multitude of distinct bivector exponents. Fortunately, this can be reduced to a form in terms of only and . We begin by illustrating with an example, then prove the general lemma.
Consider three rotors
,
, and
. For a general multivector
M (including the
) define
As with the tetrahedra of our BC helix, each successive rotation of
M is implemented by a rotor which is itself transformed by all the previous rotations. Now our focus is on the rotors themselves. The rotor that acts on
M to produce
is
To produce
, the rotor is
It becomes evident, then, that a sequence of rotations where each rotor is transformed by the previous ones can be expressed as a reordered sequence where each rotor is the original, untransformed rotor.
To prove the general case, begin with the following definitions. Let
represent a set of initial rotors, and define
This is just a generalization of Equation (17), though the notation here differs slightly from that example: rather than allow a proliferation of prime symbols, we use a naught subscript to denote an initial rotor, and its absence indicates a rotor transformed by all the rotors of lower index. Of course,
since the product of rotors is a rotor. We now prove the lemma, that a sequence of successively transformed rotations is equivalent to the reverse sequence of untransformed rotations.
Lemma 1. For rotors defined by Equation (20) up to any non-negative integer k, Proof. The proof is by induction. By Equation (
20a) we know the lemma holds for
. For
, assume it holds for
. Then
□
From here follows our first theorem, which presents the simple rotor form for any tetrahedron in the helix.
Theorem 1. A rotor giving the orientation of tetrahedron (relative to ) in the Boerdijk–Coxeter helix can be expressed as the kth power of a constant rotor, this constant being a compound of rotations about a face normal and the direction of an edge. Namely,where ≅ here means equivalent up to a symmetry of the tetrahedron. Proof. Begin with the definition in Equation (11) of
, and use Equation (
15) and Lemma 1.
The leading rotor in the last line is ; when acts on , this is the one that acts first. It produces a rotation around , which leaves invariant. □
The rotor product
in
is of course equivalent to a single rotation of some angle
about some axis. The cosine of
is given by the scalar part of the product, which has a simple form since the two exponents are perpendicular,
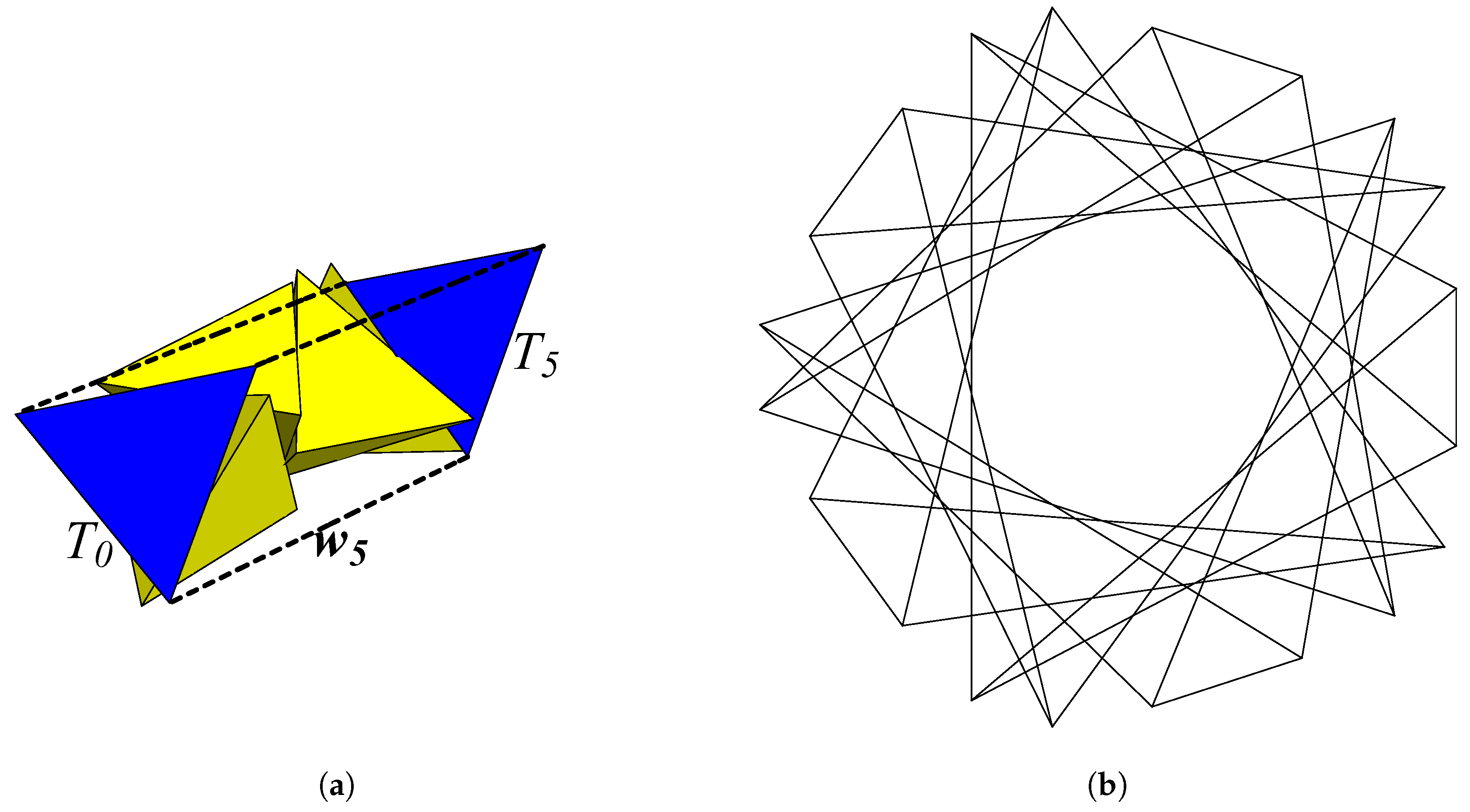
This gives , an irrational fraction of a circle, so will not return to itself for any non-zero integer k. It confirms the well-known fact that the BC helix is aperiodic. We now show, however, that modifying it with an extra twist around in each step can yield a periodic structure.
3.2. Modified BC Helix, Periodic
Theorem 2. The BC helix can be modified to have period m for any integer .
Proof. The proof is constructive. Follow the construction of the standard BC helix as above, but after each rotation about
,
, or
, insert a rotation about
by some fixed angle
. The resulting
kth rotor
for the
m-BC helix is found as in Equation (
23),
To keep
paired with the
rotation, the rearrangement in lines 4 and 5 above differs slightly from that done in Equation (
23); this results in the extra
on the end.
The modified BC helix generated by
is
m-periodic if
when acting on
. The leading and trailing rotors in
are already symmetries of
, so it remains to make the central factor one as well when
. This can be done by choosing
such that
For
this is trivial. Otherwise, for some unit vector
h and any integer
p,
This has a solution when . Numerically, , so we require (no new solutions appear if we take ). Clearly no integer p satisfies this for , but for any there is some p that does (e.g., let ). Then when acting on . □
Remark 1. β is an angle of rotation around for each tetrahedron , but a rotation around is a symmetry of , so the can therefore be dropped, This is the general formula for angles to modify a BC helix to have period m.
Remark 2. While m is the number of tetrahedra in a period, p is the number of windings. That is, for , the tetrahedra wind around repeatedly, but may not return to the original orientation until the pth winding, which occurs at the mth tetrahedron. If they do, m will not be the shortest period of that helix. In the interest of uniqueness, this motivates the following definition.
Definition 1. An m-BC helix is a BC helix modified according to Theorem 2 so as to have period m, but no shorter period.
Corollary 1. From Definition 1 and Theorem 2, an m-BC helix requires that the in be irreducible, so(The approximate inequality can be made exact by using the exact value of δ as shown in Theorem 2, which admits of slightly wider bounds.) Theorem 3. There is an m-BC helix for all integers except 6.
Proof. For , both conditions in Corollary 1 are satisfied by , so corresponding m-BC helices exist. Indeed, for , one can choose or 2, and get two distinct helices.
For , the inequality in Corollary 1 is satisfied only by , none of which is coprime with 6, so there is no 6-BC helix (periodicity of 6 only occurs as a multiple of periodicities 2 or 3).
For , a straightforward check reveals a satisfactory p for each m (usually more than one).
For
, use a lemma of D. Hanson [
9] that there is a prime between
and
for
. First define positive integers
q,
r,
n by
These can be summarized as
Since
, Hanson’s lemma applies, indicating a prime between
and
, hence between
and
. This fits it within the bounds shown in Equation (
29), slightly tighter than the exact bounds, so it satisfies the exact version of the Corollary 1 inequality. As a prime less than
m but greater than half
m, it is coprime with
m, so it satisfies the coprime condition as well. We conclude that an
m-BC helix exists for
, i.e., for
. □
From Equation (
28) with
, we find for
and 5,
In Equation (
35) we used the congruency of a
rotation to shift the angle, and in Equation (36) we used
and also
. These values confirm
given in Equation (
4).
It may be worth mentioning that the mathematics here describes abstract helix structures in which the modifying rotations do not generally avoid the intersecting of nearby tetrahedra. In a physical model with any nonzero , the extra rotation will cause to crash into and unless some extra translation is introduced to avoid it.