Global Dynamics of Leslie-Gower Competitive Systems in the Plane
Abstract
1. Introduction
- (i)
- Suppose that . If , then is globally asymptotically stable on , and attracts all points on the open semiaxis . If , then the stable manifold in is the graph of a continuous, increasing function of the first coordinate. Furthermore, a solution converges to whenever is above in South-east ordering, and converges to whenever is below in South-east ordering.
- (ii)
- Suppose that . If , then is globally asymptotically stable on , and attracts all points on the open semiaxis . If , then E is globally asymptotically stable on , attracts all points on the open semiaxis , and attracts all points on the open semiaxis .
- (i)
- Every nonzero solution to system (1) converges to an equlibrium .
- (ii)
- For every with and , the stable set is an unbounded, increasing curve with endpoint .
- (iii)
- The limiting equilibrium varies continuously with the initial condition.
2. Preliminaries
- i.
- There exists a fixed point of T in .
- ii.
- If T is strongly order preserving, then there exists a fixed point in which is stable relative to .
- iii.
- If there is only one fixed point in , then it is a global attractor in and therefore asymptotically stable relative to .
3. Global Dynamics of System (4)
- (a)
- The equilibrium solution is locally asymptotically stable if , non-hyperbolic of stable type if and a saddle point if . In each case, the eigenvectors associated with the eigenvalues and are and .
- (b)
- The equilibrium solution is locally asymptotically stable if , non-hyperbolic of stable type if and a saddle point if . In each case, the eigenvectors associated with the eigenvalues and are and .
- (c)
- The interior equilibrium solution E is a saddle point when and and is locally asymptotically stable when and .
- (d)
- The interior equilibrium solutions are non-hyperbolic of the stable type and the eigenvector which corresponds to is given as .
- (a)
- In view of (9), we havewhich implies that the eigenvalues of the Jacobian matrix are . The corresponding eigenvectors are as stated.
- (b)
- In view of (9), we havewhich implies that the eigenvalues of the Jacobian matrix are . The corresponding eigenvectors are as stated.
- (c)
- The eigenvalues of the Jacobian matrix evaluated at the equilibrium E, and , correspond to the roots of the characteristic polynomial . Note that by (9). FurthermoreConsequently, if and then and and if and then and . It follows that E is a saddle point when and and is locally asymptotically stable when and .
- (d)
- In this case, the eigenvalues of the Jacobian matrix evaluated at the equilibrium are . The eigenvector that corresponds to is , where satisfies and points towards the first quadrant.
- (a)
- If , then the equilibrium solutions are locally asymptotically stable and the interior equilibrium E is a saddle point. The separatrix , which is a graph of a continuous, non-decreasing curve, is the basin of attraction of E and the region below (resp. above) is the basin of attraction of (resp. ).
- (b)
- If , then the equilibrium solutions are saddle points and the interior equilibrium E is locally asymptotically stable. Every solution in the first quadrant which starts off the coordinate axes converges to E. Every solution which starts on the positive part of the x-axis (resp. y-axis) is attracted by (resp. ).
- (c)
- If (resp. ), then the equilibrium solution (resp. ) is locally asymptotically stable and (resp. ) is a saddle point. The basin of attraction of (resp. ) is the first quadrant of initial conditions without the positive part of the y-axis (resp. x-axis), which is attracted by (resp. ).
- (d)
- If and , then there is an infinite family of equilibrium solutions for which there exists the global stable manifold , which is the graph of a continuous, non-decreasing function asymptotic to and is exactly the basin of attraction of . The limiting equilibrium varies continuously with the initial condition.
- (e)
- If (resp. ) is non-hyperbolic and (resp. ) is locally asymptotically stable then (resp. ) attracts the first quadrant of initial conditions except the positive part of x-axis (resp. y-axis) which is attracted by (resp. ). If (resp. ) is non-hyperbolic and (resp. ) is a saddle point then (resp. ) attracts the first quadrant of initial conditions except the positive part of y-axis (resp. x-axis) which is attracted by (resp. ).
- (a)
- First we show that T does not have any period-two solutions. Our condition implies . By direct calculation one can show that a period-two solution satisfies the equationPlease note thatwhich means that both terms of such solution are complex conjugate and so there is no period-two solution in the first quadrant.Taking into account that the Jacobian matrix evaluated at E has all non-zero entries, Theorem 5 of [4] implies the existence and uniqueness of both global stable and unstable manifolds and and so . Furthermore, Theorem 5 of [4] implies that every below will satisfy for some . In view of Corollary 1, . In a similar way, we can treat the case when is above .
- (b)
- In view of Lemma 2 part (a), the eigenvectors which correspond to and point to the interior of the fourth and the second quadrant, which means that the local unstable manifolds and exist and point strictly toward E. Thus there exist points in the interior of , arbitrarily close to and such that . Now, statement iii of Theorem 3 implies that E is a global attractor in , which completes the proof.
- (c)
- Assume that which implies that is locally asymptotically stable and is a saddle point. In view of Lemma 2 part (b), the eigenvector which corresponds to points to the interior of the fourth quadrant, which means that the local unstable manifold exists and points strictly toward . Thus there exists a point u in the interior of , arbitrarily close to such that . However, then this shows that the map T has a lower solution in every neighborhood of , which in view of Theorem 6 in [6] implies that the interior of is a subset of the basin of attraction of . The result follows.The proof when is similar and will be omitted.
- (d)
- By Theorem 1 of [6], for each there exists the set passing through and asymptotic to , which is the graph of a continuous, non-decreasing function, which is exactly the basin of attraction of . The continuity of the limiting equilibrium solution as a function of initial conditions follows as in [9].
- (e)
- The proof is similar to the proof of part (c) and will be omitted.
4. Global Dynamics of System (5)
- (a)
- Every solution of system (5) satisfies ;
- (b)
- satisfies () condition on and so T has no period-two points;
- (c)
- For every , ;
- (d)
- For every , .
- (a)
- The equilibrium solution exists if . It is locally asymptotically stable if , non-hyperbolic of stable type if and a saddle point if . In each case, the eigenvectors associated with the eigenvalues and are and , respectively.
- (b)
- The equilibrium solution always exists and it is locally asymptotically stable if , non-hyperbolic of stable type if and a saddle point if . In each case, the eigenvectors associated with the eigenvalues and are and , respectively.
- (c)
- The interior equilibrium solution E exists if and it is locally asymptotically stable if and and a saddle point if and .
- (d)
- The interior equilibrium solutions exist if , and . They are non-hyperbolic of the stable type and the eigenvector associated with where is .
- (a)
- The Jacobian matrix associated with the map has the formIn view of (14), we havewhich implies that the eigenvalues of the Jacobian matrix are . The corresponding eigenvectors are as stated.
- (b)
- In view of (14), we havewhich implies that the eigenvalues of the Jacobian matrix are . The corresponding eigenvectors are as stated.
- (c)
- Denote the eigenvalues of by and , which represent the roots of the characteristic polynomial, . By Proposition 1, and are real and positive. Notice
- (d)
- For , the eigenvalues of are and . Since we clearly have that are non-hyperbolic equilibrium points of the stable type. It follows by immediate checking that the eigenvector associated with is , which points towards the first quadrant for .
- (a)
- If then is the unique equilibrium solution of system (5) and it is locally asymptotically stable. Every solution in the first quadrant which starts off of the x-axis converges to and every solution which starts on the positive x-axis converges to the singular point .
- (b)
- For , if , (resp. , ) then system (5) has equilibrium solutions and where (resp. ) is locally asymptotically stable and (resp. ) is a saddle point. The basin of attraction of (resp. ) is the first quadrant of initial conditions without the positive part of the y-axis (resp. x-axis), which is attracted by (resp. ).
- (c)
- If , , and then system (5) has equilibrium solutions , and E. The equilibrium solutions and are saddle points and E is locally asymptotically stable. Every solution in the first quadrant which starts off of the coordinate axes converges to E and every solution which starts on the positive x-axis (resp. y-axis) converges to (resp. ).
- (d)
- If , , and then system (5) has equilibrium solutions , and E. The equilibrium solutions and are locally asymptotically stable and the interior equilibrium E is a saddle point. There exists the global stable manifold and the global unstable manifold , where is the graph of a continuous, non-decreasing function and is the graph of a continuous, non-increasing function which connects all three equilibrium solutions. The region in the first quadrant above (resp. below) the curve is the basin of attraction of (resp. ) and the curve is the basin of attraction of E.
- (e)
- If , , and then there is an infinite family of equilibrium solutions for which there exists the global stable manifold for all , which is the graph of a continuous, non-decreasing function asymptotic to and is exactly the basin of attraction of . The limiting equilibrium varies continuously with the initial condition.
- (f)
- If (resp. ) is non-hyperbolic and (resp. ) is locally asymptotically stable then (resp. ) attracts the first quadrant of initial conditions except the positive part of the x-axis (resp. y-axis), which is attracted by (resp. ). If (resp. ) is non-hyperbolic and (resp. ) is a saddle point then (resp. ) attracts the first quadrant of initial conditions except the positive part of the y-axis (resp. x-axis), which is attracted by (resp. ).
- (a)
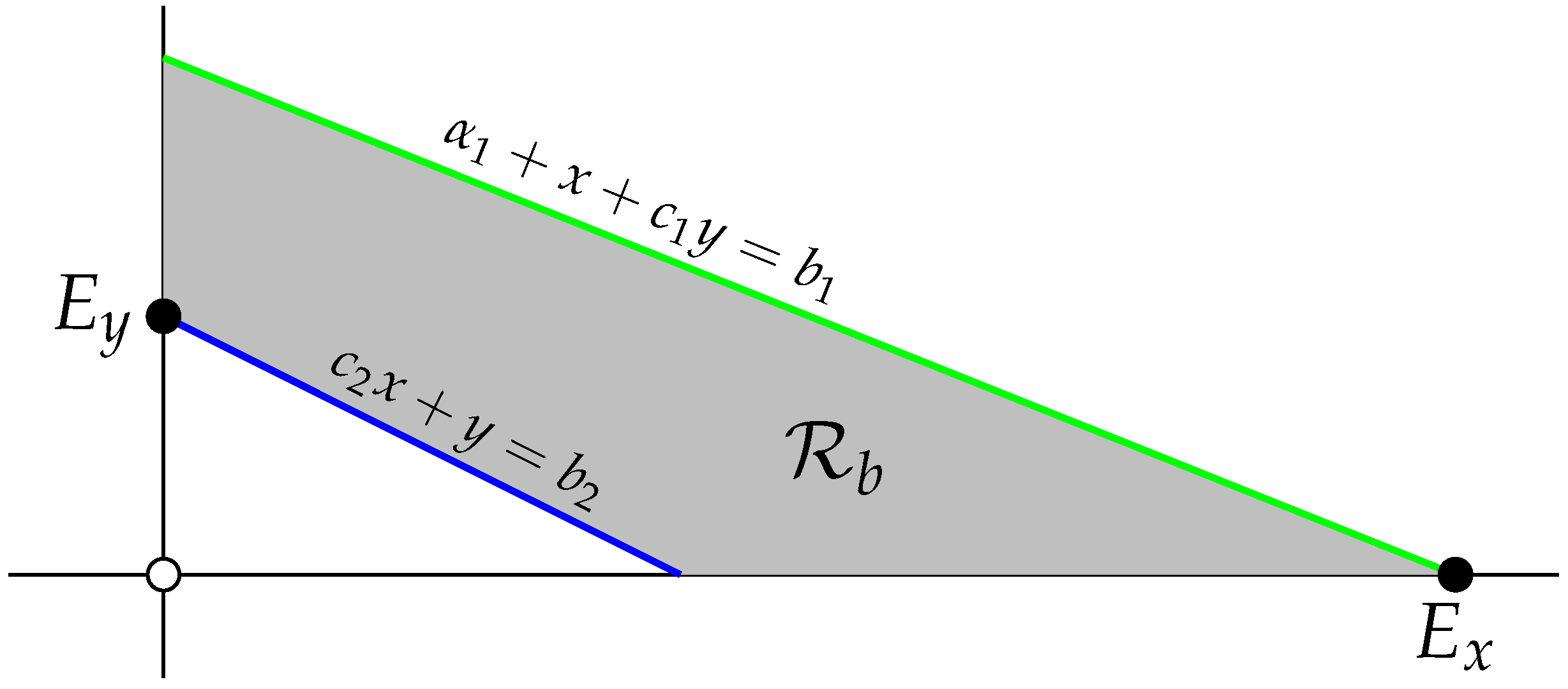
- Let . Lemma 3(c) and (d) guarantee that for initial conditions on the positive y-axis, and for initial conditions on the positive x-axis, . To treat the dynamics in the interior of , consider . By Theorem 2 of [4], is invariant. The region also attracts the interior of . To verify this, suppose that with . In this case andIt follows that there exists such that for all , and thus is attracting. To conclude the proof, suppose with . In this case , and as a consequence of the invariance of , is a decreasing sequence while is a non-decreasing sequence. Therefore, . The above arguments prove that the basins of attraction for and the singular point are and .
- (b)
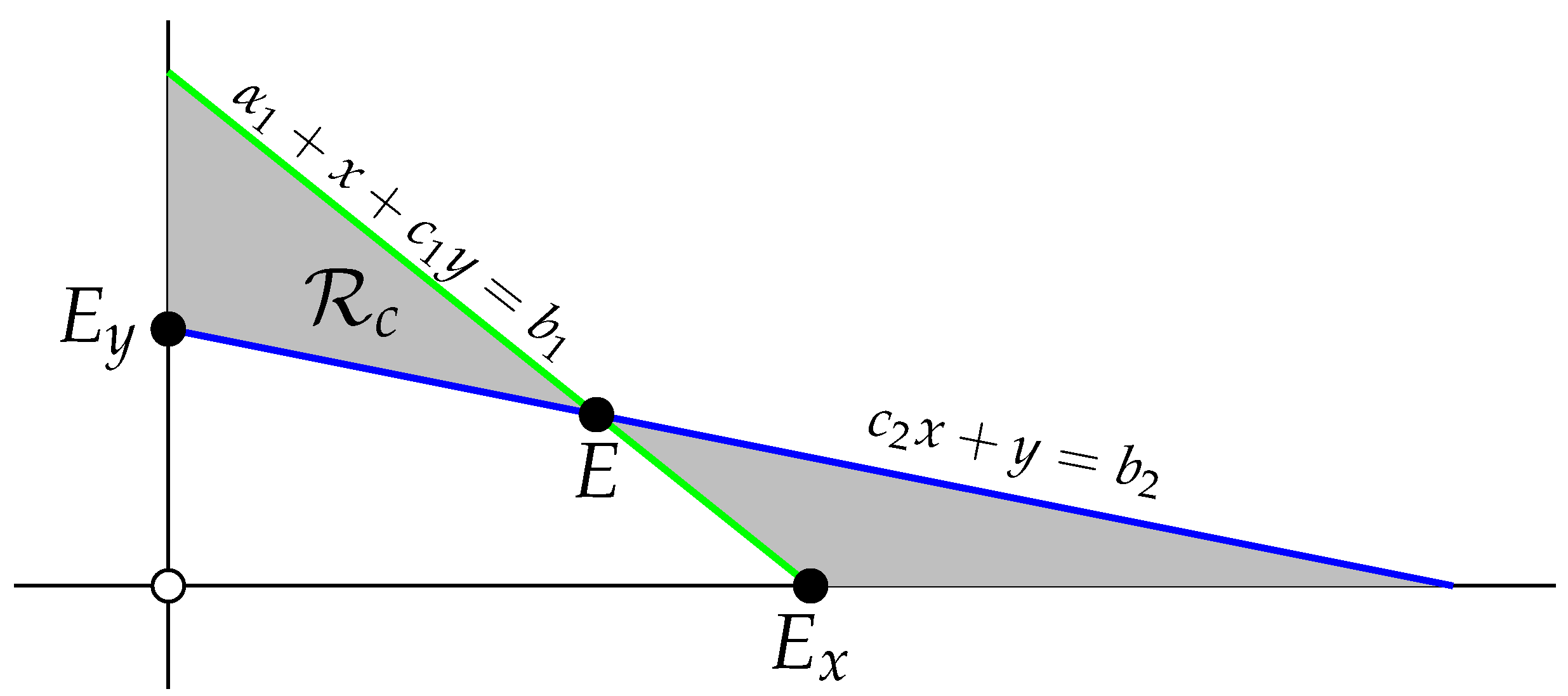
- Let , , and . Lemma 3(c) and (d) guarantee that for all initial conditions on the positive y-axis, and for all initial conditions on the positive x-axis, . To treat the interior of , consider shown in Figure 4.Please note that is an invariant region by Theorem 2 of [4]. Consider with and noticeAs a consequence of the invariance of , is a non-decreasing sequence and is a non-increasing sequence. Therefore, using basic properties of sequences and the fact that is strongly competitive, . Finally, suppose with . By Lemma 3(a), for all . Choose with such that . Since is strongly competitive, noticeTherefore, . We have arrived at the desired result that the basins of attraction for and are and .The proof for the case when , is similar and will be omitted.
- (c)
- Let , , and . As in part (b), Lemma 3(c) and (d) guarantee that the positive part of the y-axis is a subset of and the positive part of the x-axis is a subset of . To treat the interior of , consider the region shown in Figure 5.Please note that is invariant by Theorem 2 of [4]. Provided that with , monotonicity properties (similar to part (a) and (b)) along with Lemma 3(b) can be used to prove that . Suppose with . By Lemma 3(a) we know that for all . Moreover, since then for all . Consequently, there must exist an such that . Now, choose such that . Since is strongly competitive we haveTherefore, for all . We have reached the desired result that the basins of attraction for and are , and .
- (d)
- Let , , and . In light of Lemma 4(c), Theorems 1 and 5 of [6] guarantees that there exist the global stable and unstable manifolds for E, and respectively, with the above mentioned properties. An immediate checking shows that and that the interior of the ordered interval is a subset of , while the interior of the ordered interval is a subset of . Now, take any point such that (i.e., above ). Then , where . By Lemma 3(c) and the monotonicity of , for ,Since , (18) implies that enters the ordered interval and so converges to . In a similar way, one can show that the ordered interval attracts all points below , and so all such points converge to .
- (e)
- By Theorem 1 of [6], for each there exists the set passing through and asymptotic to , which is the graph of a continuous, non-decreasing function, which is exactly the basin of attraction of . The continuity of the limiting equilibrium solution as a function of initial conditions follows as in [9].
- (f)
- The proof is similar to the proof of part (b) and will be omitted here.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cushing, J.M.; Levarge, S.; Chitnis, N.; Henson, S.M. Some discrete competition models and the competitive exclusion principle. J. Differ. Equ. Appl. 2004, 10, 1139–1152. [Google Scholar] [CrossRef]
- Cushing, J.M.; Levarge, S. Some discrete competition models and the principle of competitive exclusion. In Difference Equations and Discrete Dynamical Systems; World Scientific: Hackensack, NJ, USA, 2005; pp. 283–301. [Google Scholar]
- Cushing, J.M.; Henson, S.M.; Blackburn, C.C. Multiple mixed-type attractors in a competition model. J. Biol. Dyn. 2007, 1, 347–362. [Google Scholar] [CrossRef] [PubMed]
- Kulenović, M.R.S.; Merino, O. Competitive-Exclusion versus Competitive-Coexistence for Systems in the Plane. Discret. Contin. Dyn. Syst. Ser. B 2006, 6, 1141–1156. [Google Scholar]
- Kulenović, M.R.S.; Merino, O. Global Bifurcation for Competitive Systems in the Plane. Discret. Contin. Dyn. Syst. B 2009, 12, 133–149. [Google Scholar]
- Kulenović, M.R.S.; Merino, O. Invariant Manifolds for Competitive Discrete Systems in the Plane. Int. J. Bifurc. Chaos 2010, 20, 2471–2486. [Google Scholar] [CrossRef]
- Smith, H.L. Planar Competitive and Cooperative Difference Equations. J. Differ. Equ. Appl. 1998, 3, 335–357. [Google Scholar] [CrossRef]
- Camouzis, E.; Kulenović, M.R.S.; Ladas, G.; Merino, O. Rational Systems in the Plane-Open Problems and Conjectures. J. Differ. Equ. Appl. 2009, 15, 303–323. [Google Scholar] [CrossRef]
- Burgić, D.; Kalabušić, S.; Kulenović, M.R.S. Non-hyperbolic Dynamics for Competitive Systems in the Plane and Global Period-doubling Bifurcations. Adv. Dyn. Syst. Appl. 2008, 3, 229–249. [Google Scholar]
- Sacker, R. Global stability in a multi-species periodic Leslie-Gower model. J. Biol. Dyn. 2011, 5, 549–562. [Google Scholar] [CrossRef]
- Sacker, R. An invariance theorem for mappings. J. Differ. Equ. Appl. 2012, 18, 163–166. [Google Scholar] [CrossRef]
- Sacker, R. A note: An invariance theorem for mappings II. J. Dyn. Differ. Equ. 2012, 24, 595–599. [Google Scholar] [CrossRef]
- Kulenović, M.R.S.; Ladas, G. Dynamics of Second Order Rational Difference Equations with Open Problems and Conjectures; Chapman and Hall/CRC: Boca Raton, FL, USA; London, UK, 2001. [Google Scholar]
- Clark, D.; Kulenović, M.R.S.; Selgrade, J.F. Global Asymptotic Behavior of a Two Dimensional Difference Equation Modelling Competition. Nonlinear Anal. TMA 2003, 52, 1765–1776. [Google Scholar] [CrossRef]
- Hess, P. Periodic-Parabolic Boundary Value Problems and Positivity; Pitman Research Notes in Mathematics Series, 247; Longman Scientific & Technical: Harlow, UK, 1991; pp. 619–620. [Google Scholar]
- Kalabušić, S.; Kulenović, M.R.S.; Pilav, E. Dynamics of a two-dimensional system of rational difference equations of Leslie-Gower type. Adv. Differ. Equ. 2011, 229, 29. [Google Scholar] [CrossRef]
- Kulenović, M.R.S.; Nurkanović, M. Asymptotic Behavior of a Linear Fractional System of Difference Equations. J. Inequal. Appl. 2005, 2005, 127–143. [Google Scholar] [CrossRef]
- Leonard, W.J.; May, R. Nonlinear aspects of competition between species. SIAM J. Appl. Math. 1975, 29, 243–275. [Google Scholar]
- Smale, S. On the differential equations of species in competition. J. Math. Biol. 1976, 3, 5–7. [Google Scholar] [CrossRef] [PubMed]
- de Mottoni, P.; Schiaffino, A. Competition systems with periodic coefficients: A geometric approach. J. Math. Biol. 1981, 11, 319–335. [Google Scholar] [CrossRef]
- Smith, H.L. Periodic competitive differential equations and the discrete dynamics of competitive maps. J. Differ. Equ. 1986, 64, 165–194. [Google Scholar] [CrossRef]
- Huang, Y.S.; Knopf, P.M. Global convergence properties of first-order homogeneous systems of rational difference equations. J. Differ. Equ. Appl. 2012, 18, 1683–1707. [Google Scholar] [CrossRef]
- Hirsch, M.; Smith, H. Monotone dynamical systems. In Handbook of Differential Equations: Ordinary Differential Equations; Elsevier B. V.: Amsterdam, The Netherlands, 2005; Volume II, pp. 239–357. [Google Scholar]
- Bertrand, E.; Kulenović, M.R.S. Global Dynamic Scenarios for Competitive Maps in the Plane. Adv. Differ. Equ. 2018. [Google Scholar] [CrossRef]
- Brett, A.; Kulenović, M.R.S. Two Species Competitive Model with the Allee Effect. Adv. Differ. Equ. 2014, 2014, 307. [Google Scholar] [CrossRef]

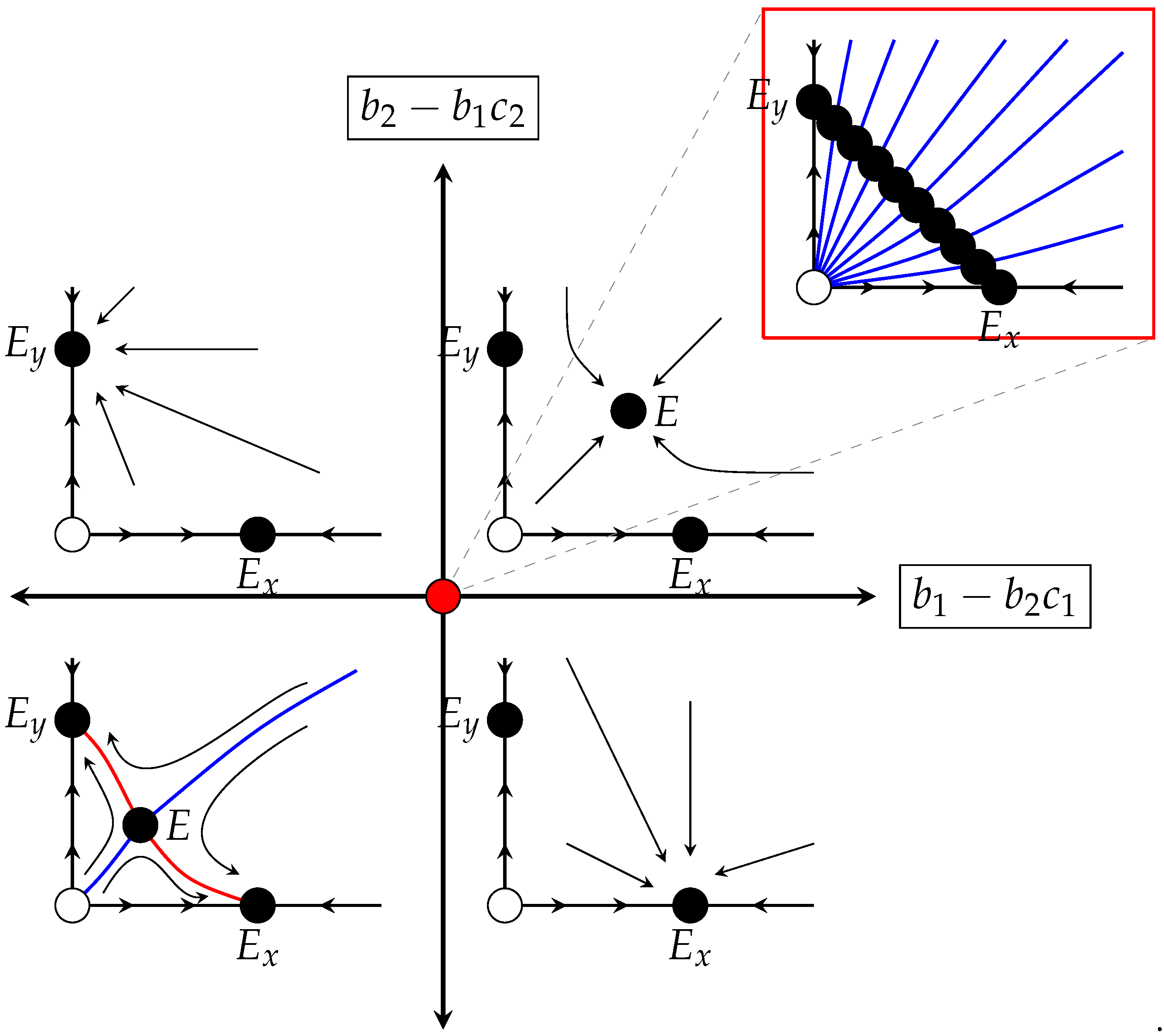
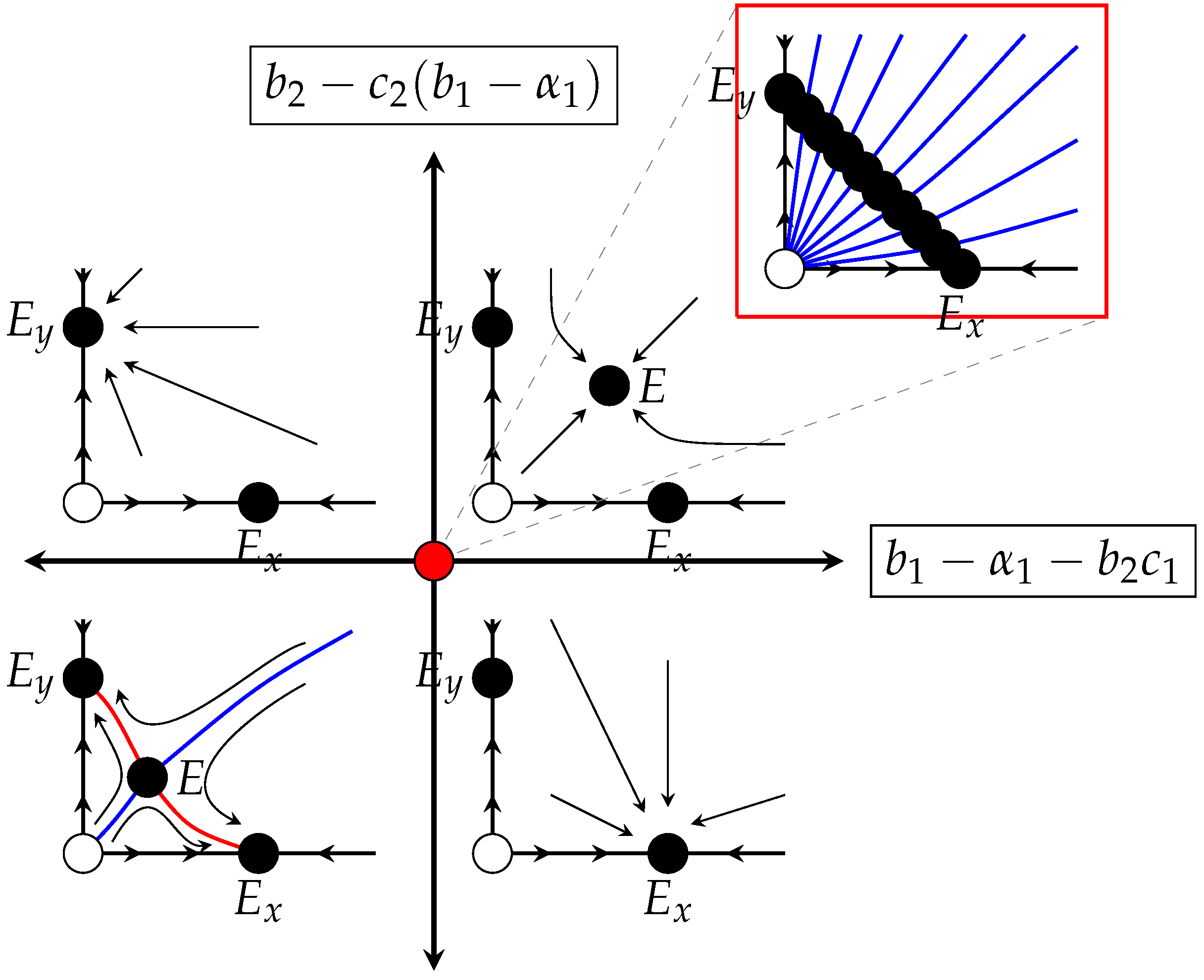
| Condition | ||
|---|---|---|
| Case 1. is a repeller is a saddle is a saddle E is an interior local attractor. | Case 2. is a repeller is a saddle attractor on No interior fixed point exists. | |
| Case 3. is a repeller is attractor on is a saddle No interior fixed point exists. | Case 4. is a repeller is a local attractor is a local attractor E is an interior saddle. |
| Condition | Equilibrium Points |
|---|---|
| , | |
| Condition | Equilibrium Points | |
|---|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kulenović, M.R.S.; McArdle, D.T. Global Dynamics of Leslie-Gower Competitive Systems in the Plane. Mathematics 2019, 7, 76. https://doi.org/10.3390/math7010076
Kulenović MRS, McArdle DT. Global Dynamics of Leslie-Gower Competitive Systems in the Plane. Mathematics. 2019; 7(1):76. https://doi.org/10.3390/math7010076
Chicago/Turabian StyleKulenović, Mustafa R. S., and David T. McArdle. 2019. "Global Dynamics of Leslie-Gower Competitive Systems in the Plane" Mathematics 7, no. 1: 76. https://doi.org/10.3390/math7010076
APA StyleKulenović, M. R. S., & McArdle, D. T. (2019). Global Dynamics of Leslie-Gower Competitive Systems in the Plane. Mathematics, 7(1), 76. https://doi.org/10.3390/math7010076





