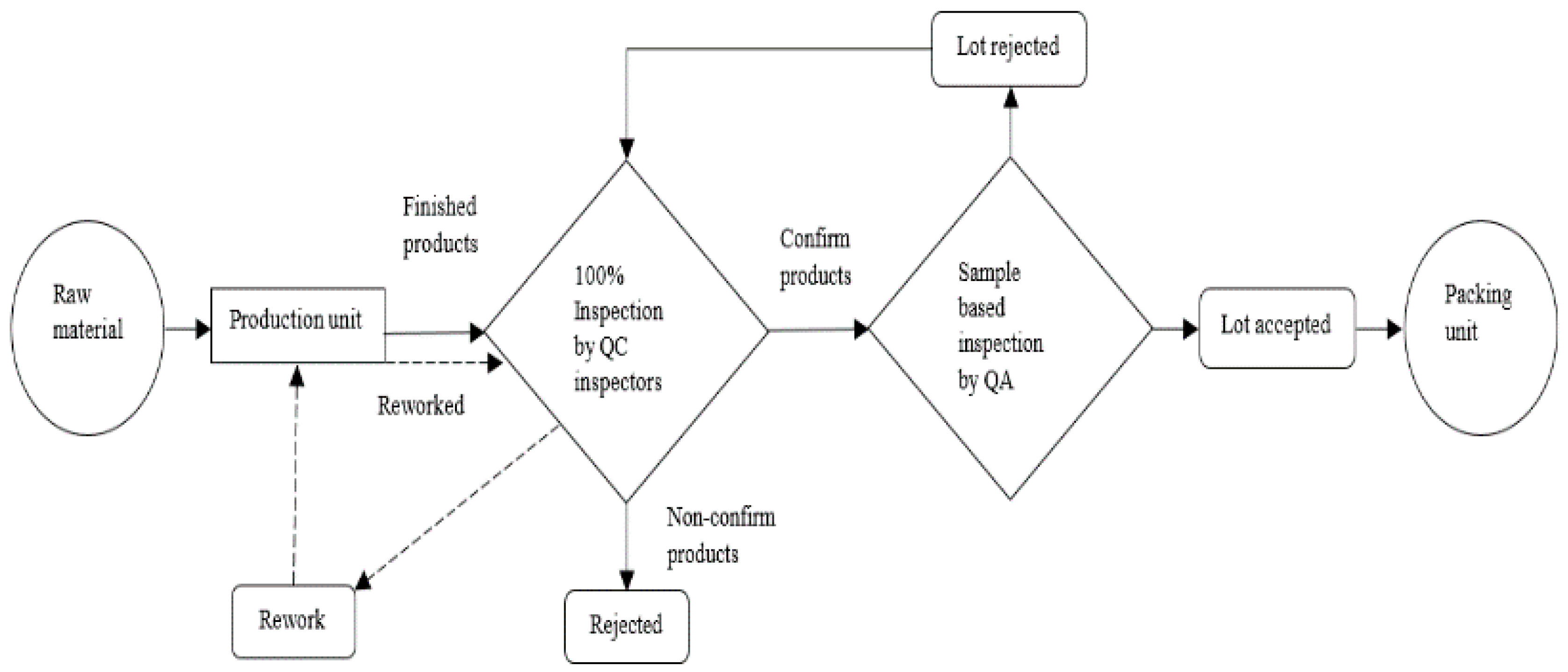
1. Introduction
Human labor and factors associated are one of the main engineering disciplines and play a vital role in maintaining good quality, manufacturing cost and productivity. Although researchers are working on automation and hybrid systems, however, the importance of human labor is not limited yet. One of the important advantage, of human labor over automation, is their decision-making ability. These type of abilities in human labor improves as skill level and experience increases. Organizations always want to utilize their manpower efficiently according to their capacity, yet there is a lack of studies that evaluate the human labor based on their skills. The present study has been conducted to fill this study gap by considering the skill level, operation time and learning behavior of human labor. For this purpose, a human-based quality control system is considered where most of the processes are carried out by human labor. Quality Control (QC) is an important part of quality management system that consists of monitoring activities along with quality planning, quality assurance and quality improvement [
1]. The main objective of QC is to maintain the good level of quality by mitigating the root causes of defective products [
2]. Inspection is the main activity of QC that is performed to decide the product’s conformance and non-conformance at different stages of manufacturing [
3]. The process of inspection is investigated here to highlight the importance of inspection skill and inspection time in a manufacturing environment where learning affects significantly. Inspection can either be online or offline where online inspect the product during the process and offline inspect the product after the completion of the process [
4,
5]. Although online inspection has been considered as an economical method, however sometimes it is not feasible. Thus inspection process has to be done offline on finished or semi-finished products [
6]. This paper also considered offline station where 100% inspection is done by human labor.
In human based manufacturing setups, learning behavior imparts significant enhancements in the performance of labor and their skill improves with the passage of time. Researchers believed that any organization that learns faster will have a competitive advantage in the future. However, this learning varies person to person within an organization and help to classify the available manpower into their respective skill levels. Six types of learning have been identified and one of them is learning by doing like inspection process performed by human labor. While planning for the new order, allocation of manpower is done once, that is, before the start of order and same labor is used until the completion of the job. However, in the actual scenario, human labor learns from their experience and improve their performance with the passage of time. Thus, they will be able to do more work with better efficiency because of their improved skills. In this situation, the organization must revise the allocation of labor that may bring advantages like better utilization of available manpower, achievement of inspection targets, reduce cost and maintain good quality. Recently, the optimal number of quality inspectors have been determined to minimize cost [
7,
8]. However, the effect of Time-Varying factors, like learning behavior, on an efficient combination of inspectors is not considered yet. This study has kept this factor in contact and the process of inspection is investigated here to determine the optimal number of quality inspectors for inspection station over different time periods.
2. Literature Review
In past, plenty of work has been done on offline inspection to reduce the overall cost, increase company profit and improve product quality. These objectives have been achieved by giving due consideration to inspection policies, inspection systems and optimization of process target values. One of the pioneering work in developing inspection policy was done by Herer and Raz [
9] to reduce the inspection cost using dynamic programming. The similar objective was also achieved by calculating optimal lot size and expected number of inspections [
10]. After that plenty of work has been conducted to improve the effectiveness of inspection policy. Anily and Grosfeld-Nir [
11] determined inspection policy and lot size for a single production run. Further investigation was done with two-time parameters and multiple productions run with rigid demand. Wang and Meng [
12] developed a joint optimization model to determine the total cost function. Their model was compared with three policies like no inspection, full inspection and disregard the first
s (DTF-
s) items policies by a numerical example. Avinadav and Perlman [
13] studied such process to minimize the cost by determining the optimal inspection interval. Sarkar and Saren [
14] developed an inspection policy for an imperfect manufacturing system that has inspection error and warranty cost to reduce the inspection cost.
Other inspection strategies have also been developed that includes inspection disposition (ID) policy and inspection disposition and rework (IDR) policy. Raz, et al. [
15] developed the first ID policy to minimize the cost function by solving the problem of economic optimization. After that their ID policy was extensively studied by other researchers with the consideration of different assumptions [
16,
17,
18,
19,
20,
21].
Continues sampling plan (CSP) is also a pioneering method of inspection in which 100% inspection and sampling inspection is alternatively conducted [
22]. The basic sampling plan known as CSP-1 was developed by Dodge [
23] to monitor the average outgoing quality level (AOQL). After that many modifications have been incorporated in the procedure of original CSP-1 by considering different assumptions [
24,
25,
26,
27,
28,
29,
30].
The studies have also been conducted to optimize the process parameters by many investigators of quality control. After the pioneering work done by Springer [
31], number of studies have been conducted to minimize the expected cost. Earlier a process target model (PTM) was proposed to optimize a single objective for three different types of screening problems [
32]. Their aim was to cancel out the effect of error in inspection through the conception of cut off points that helped to divide the products into grade one, grade two and scrap. Duffuaa, et al. [
33] proposed another PTM to increase the profit by assuming the independent characteristics of quality for a two-stage process. This PTM was also modified using acceptance sampling by Duffuaa, et al. [
34] to achieve the same objectives. Recently, Multi-Objective Optimization (MOO) problem has been explored to find out the value of process parameters: income, profit and product uniformity [
35,
36,
37]. The pioneer work on MOO was done considering 100% inspection policy to optimize the objective functions and Pareto optimal points were ranked by proposing an algorithm [
36]. Their MOO model further reviewed by considering the sampling inspection however similar results were attained [
37]. A further improvement was done considering two types of inspection errors because inspection system may be error-prone. After comparing the results of revised and previous models, it was concluded that inspection errors have a major effect on profit and uniformity. This study also worked on MOO and considered three important parameters to measure the performance of human labor while performing inspection process.
The philosophy of learning behavior is not only to improve the productivity but also look for other aspects that support the process of learning. That’s why a number of studies have found a relationship with quality control techniques and learning which was summarized by Jaber [
38]. This combination of learning and quality control was first suggested by Koulamas [
39] to evaluate the effect of product design on quality and cost. Teng and Thompson [
40] worked on the learning behavior of workers and assessed that how it affects the quality and cost of the product. Similarly, Franceschini and Galetto [
41] reduced the non-confirming quantity in production plant by improving the skill of workers. Jaber and Guiffrida [
42] worked on wright’s learning curve [
43] and proposed a quality learning curve (QLC) for a process that generates defects and required rework also. Further, this QLC was investigated by relaxing its different assumptions. Like Jaber and Guiffrida [
44] assumed that an imperfect process can be interrupted to maintain quality and improved system’s performance. Similarly, Jaber and Khan [
45] further relaxed two assumptions and considered scrap after production along with a rework of a lot. They concluded that optimal performance improves with learning and deteriorates when learning in rework becomes faster. It is observed that quantity and cost of production have a direct link with quality and this subject will have particular interest when combined with learning behavior. A number of researchers have been investigating errors in screening, however, the relationship between quality and screening need to be studied further Jaber [
38]. This study has considered learning behavior in the proposed model and its effect on inspection performance of inspectors.
Despite the above-mentioned literature, the researchers have investigated this research area with respect to the application of new trends, techniques and methodologies in the human labor selection and job assignment. It includes artificial intelligence, genetic algorithm, goal programming, fuzzy logic, data mining and data envelopment analysis [
46,
47,
48,
49]. In a human based production environment, assigning the job to workers according to their competence is an important step to keep overall cost in control and maintain production efficiency. A fuzzy logic interface method has been proposed to assign and verify production jobs to human labor. The proposed method has been applied to a discrete manufacturing system to reduce the cost due to human errors [
46]. Similarly, a synchronized job assignment model has been proposed to overcome the problem of human performance due to deviation in skill level and fluctuation of cycle time. A multi-objective simulation integrated hybrid genetic algorithm was used as a job assignment model such that it promotes teamwork and overcome the effect of varying skill level [
49]. However, there is a lack of studies in which such new trends have been applied in human-based inspection system. This study has also addressed this gap by applying multi-objective goal programming to the offline inspection station.
Table 1 has summarized the span of work done on offline inspection. It indicates that how different researchers have contributed to the field under study and compare them with the present study. Despite much work, human-based inspection system has not been studied yet considering the effect of learning on the performance of labor with different skill levels. The present study has focused this gap to contribute to the current literature and investigated that how learning behavior of different inspectors affect the inspection performance and total manpower required for inspection station. The MOO model has been presented here that can determine the group of inspectors having different skill levels such that all objectives of inspection station are achieved.
This study also incorporates the effect of learning behavior on inspection skill of human labor in terms of quality, cost and quantity. The proposed model is able to determine the optimal values of inspectors at different time periods and compares that how the requirement of manpower varies from time to time due to learning.
4. Results and Discussion
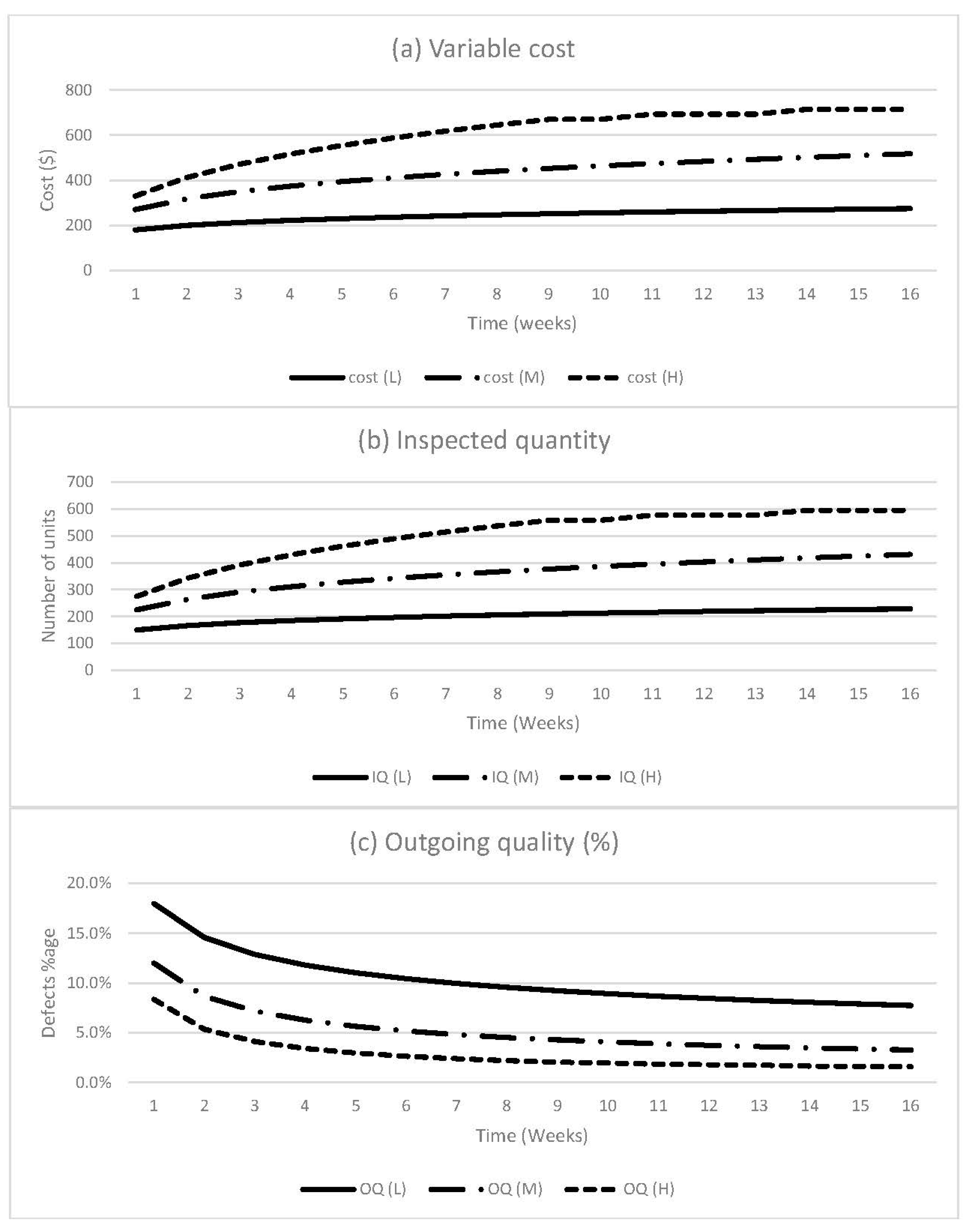
The application of the proposed model is described here with the help of an example from garment manufacturing unit and an offline station is selected where the inspection of finished products is performed by human labor. The product selected for this study is a short sleeve polo shirt and the completion of the order will take 120 days. Since this study has incorporated the concept of learning and inspection skill of human labor will improve with the passage of time. This study has considered three skill levels, that is, low, medium and high, along with the three performance measures of inspection including cost, quality and quantity.
Figure 2 indicates how these performance measures vary for three different skill levels.
At the start of order, the difference between three types of inspectors is not significant. However, the learning behavior varies person to person, that’s why some inspectors learn quickly and improve their overall skill as compared to others. To achieve the objectives of the inspection station, an efficient combination of inspectors must be maintained that utilize the available manpower according to their skill levels. Thus, the requirement of manpower with respect to the skill levels will vary until we complete the order. That’s why data were collected (
Figure 2) for three different stages, that is, at the completion of 4th week (stage A), at the completion of 8th week (stage B) and at the completion of the 12th week (stage C). Keeping this scenario in view, data are collected for the selected product after the completion of each month and summarized in
Table 2.
In order to analyze the data in
Table 2, an Optimization software, that is, Lingo 15.0, was applied by keeping the following system configuration: Intel
® Core™ i7-7500U CPU @ 2.70 GHz Intel, 8.00 GB of RAM. Min-max GP method was used to calculate the optimal values of decision variables that also gave the optimized results of objective functions. The obtained results are summarized in
Table 3 for all three stages and analysis can be divided into two parts: analysis of decision variable and analysis of objective function.
The decision variable analysis shows the optimum number of inspectors with their respective skill levels for each stage. These results ensure that all the objectives (cost, quantity and quality) have been achieved. Since the study incorporated learning behavior in this proposed model, thus the value of incoming quantity also vary along with the skill of inspectors as the order progress. At the early stage, when required targets of objective functions were low and the performance of inspectors of each skill level was also at the initial stage. The optimal combination that can achieve all targets of inspection station requires more inspectors with high inspection skill in comparison to low and medium. This is the confirmation of the fact that if an offline station consists of low skill inspectors mainly as compared to medium or high skill inspectors, the cost of inspection station may be low but the target of inspection quantity and quality level will be difficult to maintain for offline station. Therefore, the organization like to maintain an inspection station that consists of the best combination of inspectors to achieve all targets simultaneously.
As the order progress, the skill of each quality inspectors improved so as the incoming quantity which changed the targets of inspection station as well. Thus, at the second stage, the optimal results were obtained to satisfy the revised targets. However, this time, a combination of inspectors is changed and more medium skill inspectors are included. It is because of the fact that learning improves the performance of all inspectors and then the inspection station was able to achieve targets with less utilization of high skill labor. Similarly, at the last stage, the optimal combination consists of more low and medium skill quality inspectors to fulfill the revised targets. It is because of the fact that skill of both low and medium skill inspectors was improved enough meet the demands and less contribution was required from high skill inspectors.
In a labor-intensive industrial setup like garment manufacturing, where the process of inspection is mainly performed by human labor, the presence of manpower with varying skill levels develops an environment that encourages the labor to compete with each other. Such a scenario provides them an opportunity to learn quickly that improve the level of their inspection skill at a faster rate. However, product type can significantly affect the rate of improvement in inspection skill. In case of a simple or basic garment, human labor can learn the things quickly because these products consist of fewer parts, a smaller number of operations or characteristics/features that a human inspector needs to inspect. On the other hand, this learning ability not only reduce but vary from person to person as the type of product moves to slightly complex, complicated or highly fashioned garments. This is because of the fact that these have more parts, increased number of operations and tough characteristics/features that an inspector need to inspect with concentration. Such products can affect the level of inspection skill of human labor that ultimately increases the inspection costs and decrease the outgoing quality. Similarly, the required manpower also changes with respect to product type to fulfill the requirements of the inspection station.
Analysis of the objective function, on the other hand, demonstrates the variance between the target values and the actual values of each goal at different stages, where underachieved values defined as
d− and overachieved value as
d+. Min-max GP method provided optimum results of decision variables such that the set target of each objective function is attained. Even though underachieved and overachieved values are also there for different objective functions but all these deviational values do not violate the given conditions. Like in
Table 3, overachieved value of the inspection quantity (
d+) are 83, 138 and 28 for stage A, B and C respectively. However, it is still according to the constraints given in
Section 3.6. Inspection quantity per day should not be less than the set target but presented results gave over achieved value, which is a positive side of the results. Similarly in
Table 3, underachieved values of variable cost (
d−) are 48, 17 and 189 for stage A, B and C respectively. Since the constraint of the proposed model is to retain this variable cost low as much as possible so, these underachieved values also fulfill the already mentioned constraints.
In actual scenario, organization/managers allocate manpower only once, that is, at the start of the order and do not change till the completion of the order. This situation is not in favor of organizations as they are not using their labor according to their capacity. It may cause different problems like bottleneck and poor outgoing quality.
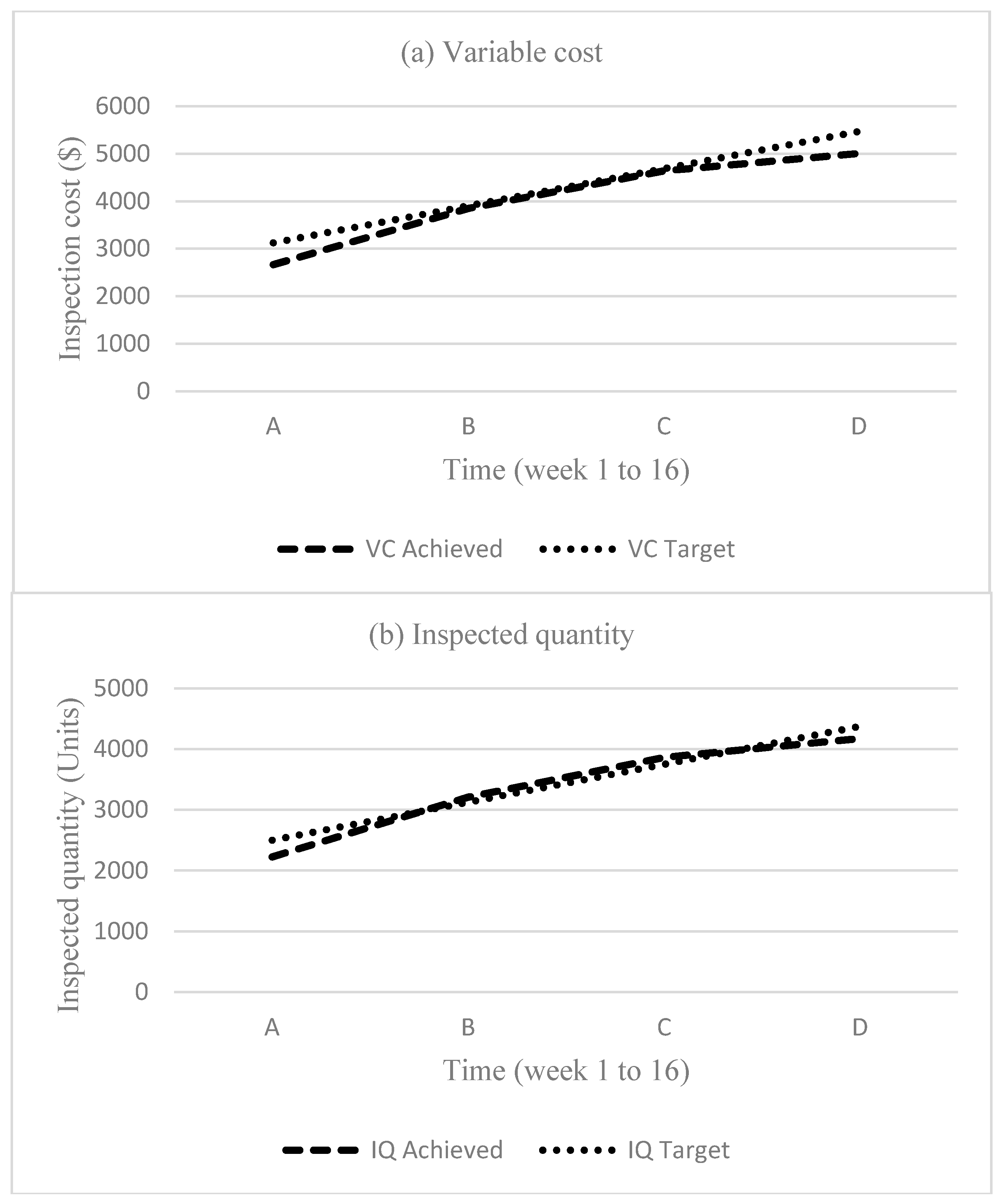
Figure 3 demonstrates this fact, where the group of inspectors with their respective skill level is kept same for a full order. Variation in achieved values and targets values was evaluated. For this purpose optimal combination obtained at stage A (
Table 3) is used here. It highlights not only the importance of skill of inspectors and learning but also explains that why it is important to revise the allocation of manpower at the periodical interval.
It is evident from the
Figure 3 that the combination of inspectors of different skill levels could not achieve the targets throughout the order even though learning is also considered. Especially, outgoing quality is not kept under control due to the high percentage of inspection error. On the other hand, inspected quantity hit the targets on some stages but underachieved as well that creates a bottleneck. Such a situation will increase the workload on inspectors, increase the chance of overtime and affect the quality of product also due to work in progress. However, in the actual scenario, the performance of labor is not the same and they improve with time due to learning and experience. Thus, revision of optimal combination of inspectors at different intervals will not only save cost and improve quality but also avoid overtime and utilize the manpower of organization efficiently. In this way, the organization will be able to use their high skill labor for inspection of complex products where more skilled labor is required. This study also provides a way how to imply the available labor and get work from them according to their skill capacity. Also, such systems provide competitive environments that will help the employee to improve their skills. However, further work must be done to explore the ways that increase the learning process and also provide some bases to establish the pay/salary scale for employees based on their improvement with time.