Forecast-Triggered Model Predictive Control of Constrained Nonlinear Processes with Control Actuator Faults
Abstract
:1. Introduction
2. Preliminaries
3. An Auxiliary Model-Based Fault-Tolerant Controller
3.1. Controller Synthesis and Analysis under Continuous State Measurements
3.2. Characterization of Closed-Loop Stability under Discretely Sampled State Measurements
4. Design and Analysis of Lyapunov-Based Fault-Tolerant MPC
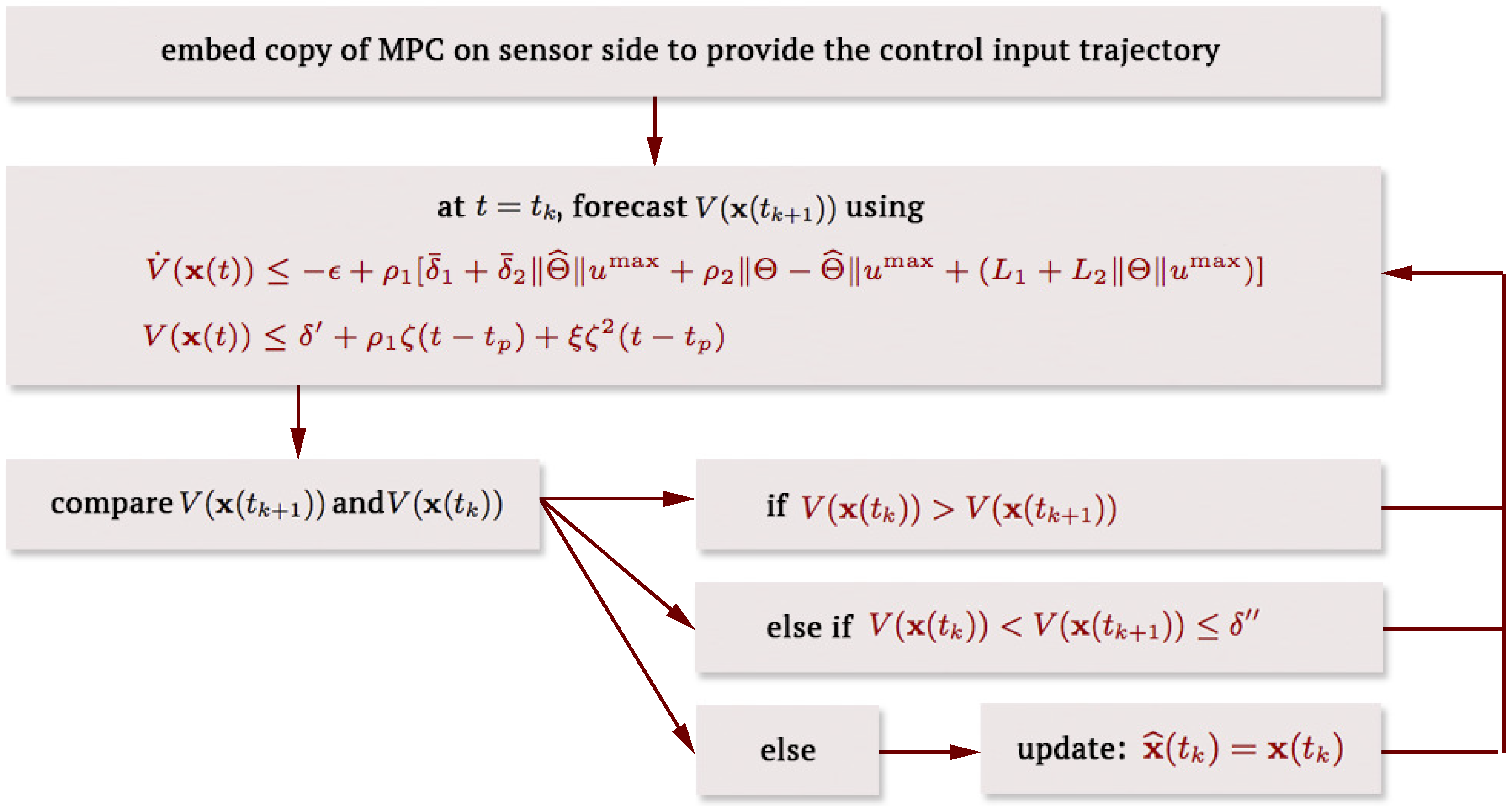
5. Fault-Tolerant MPC Implementation Using Forecast-Triggered Communication
| Algorithm 1: Forecast-triggered sensor–controller communication strategy |
| Initialize and set , |
| Solve Equation (28) for and implement the first step of the control sequence |
| if then |
| Calculate (estimate of ) using Equation (40a) and |
| else |
| Calculate (estimate of ) using Equation (40b) and |
| end if |
| if then |
| Solve Equation (28) without Equation (28d) for |
| else if and then |
| Solve Equation (28) without Equation (28d) for |
| else |
| Solve Equation (28) for and set |
| end if |
| Implement the first step of the control sequence on |
| Set and go to step 3 |
6. Simulation Case Study: Application to a Chemical Process
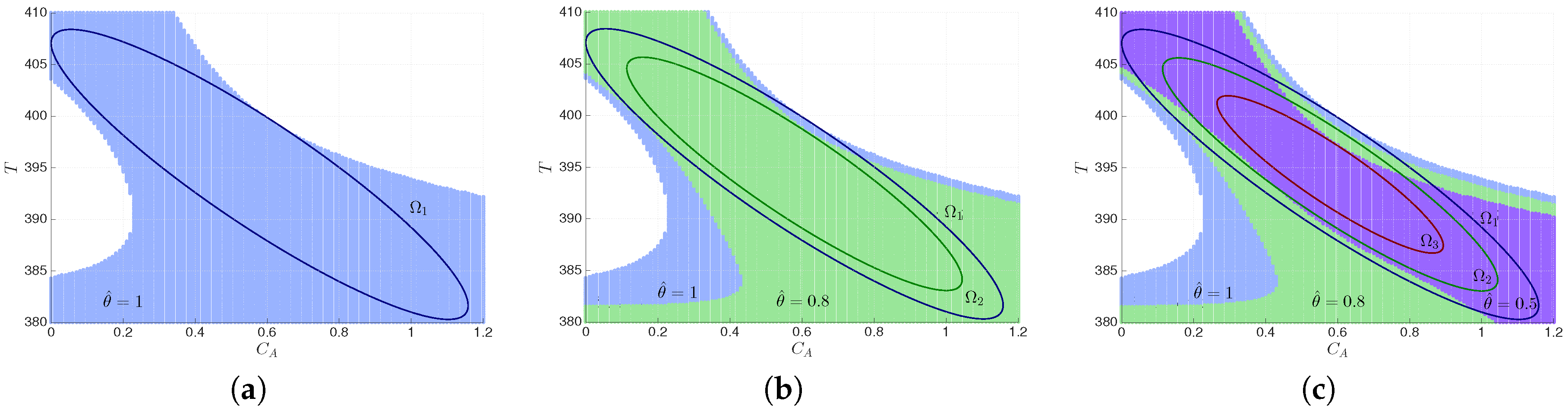
6.1. Characterization of the Fault-Tolerant Stabilization Region
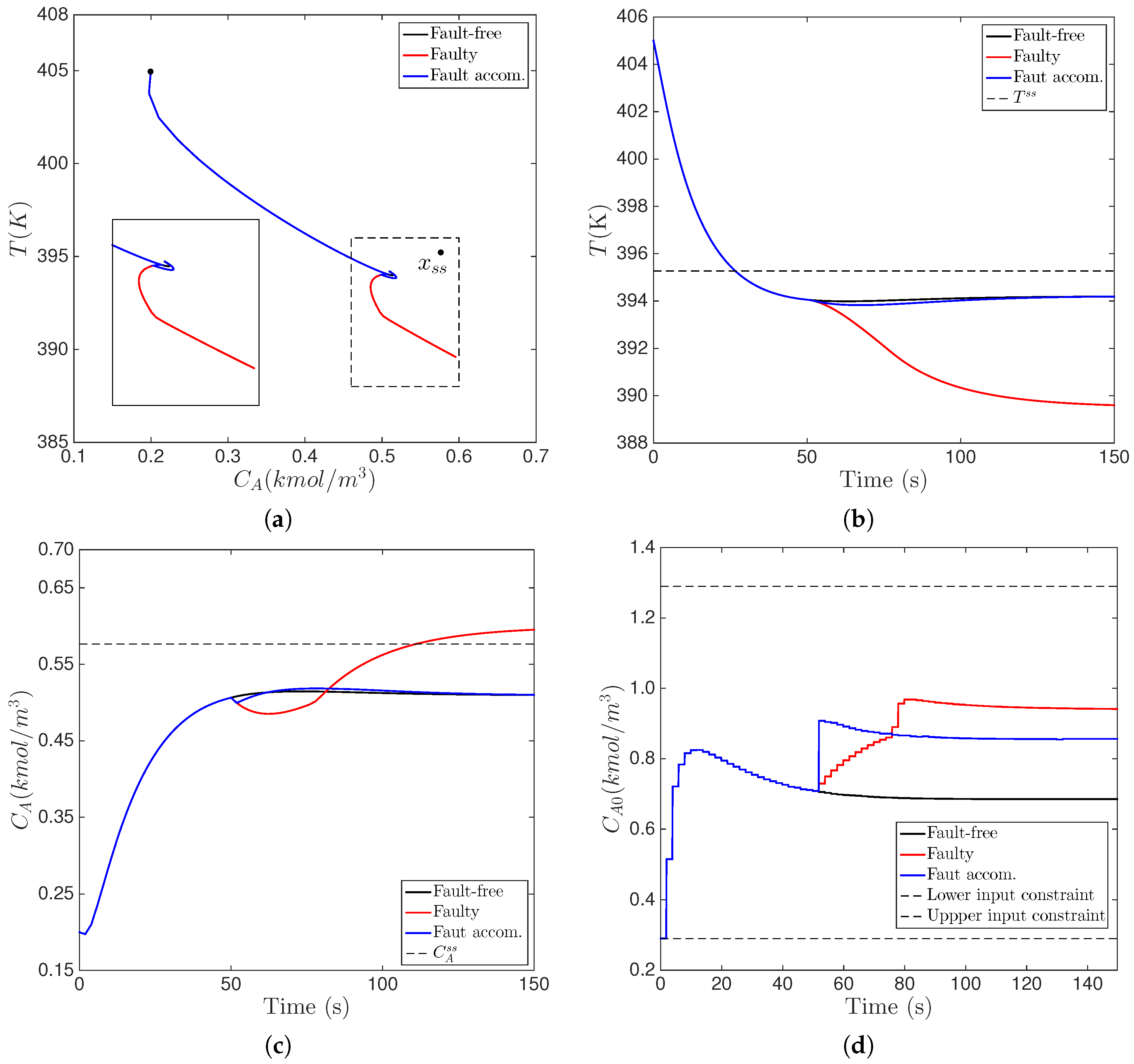
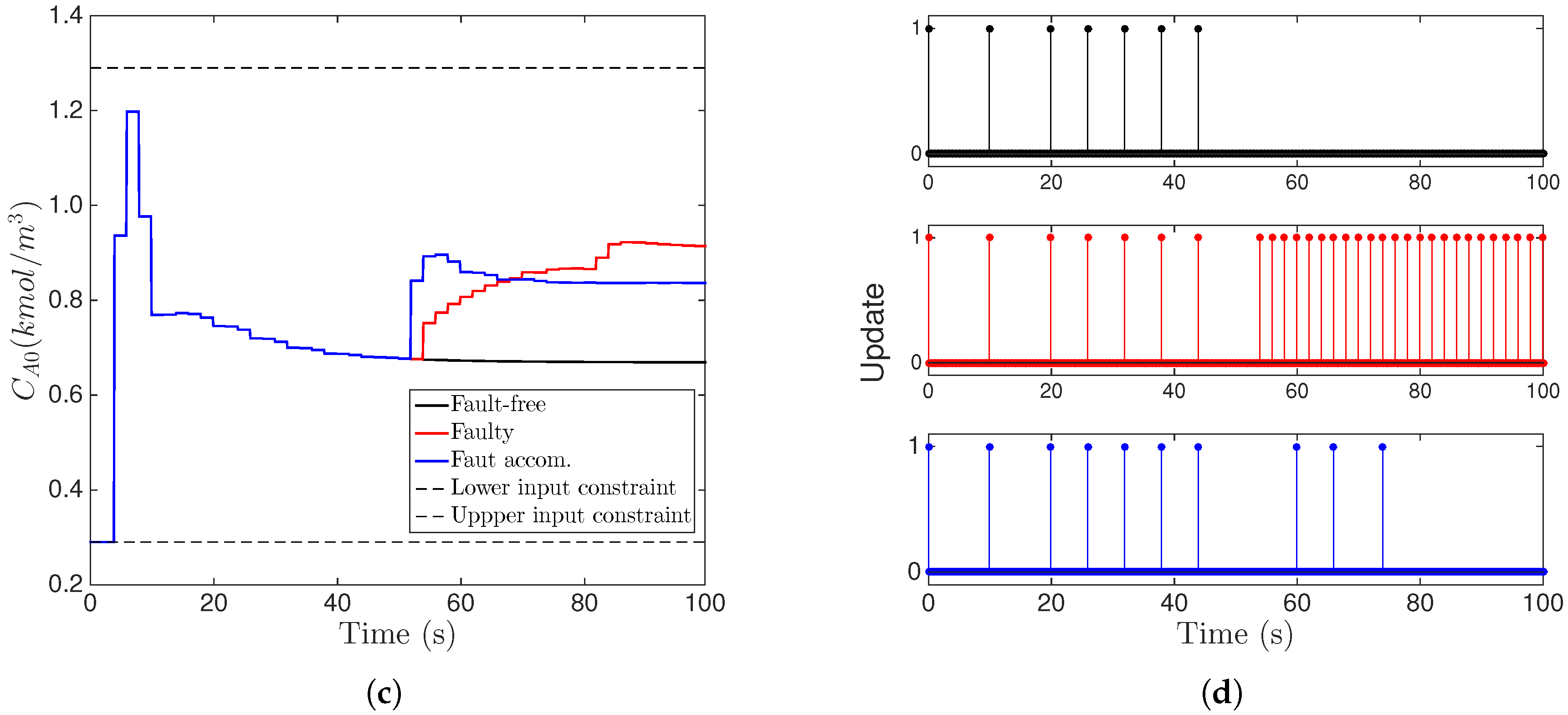
6.2. Active Fault Accommodation in the Implementation of MPC
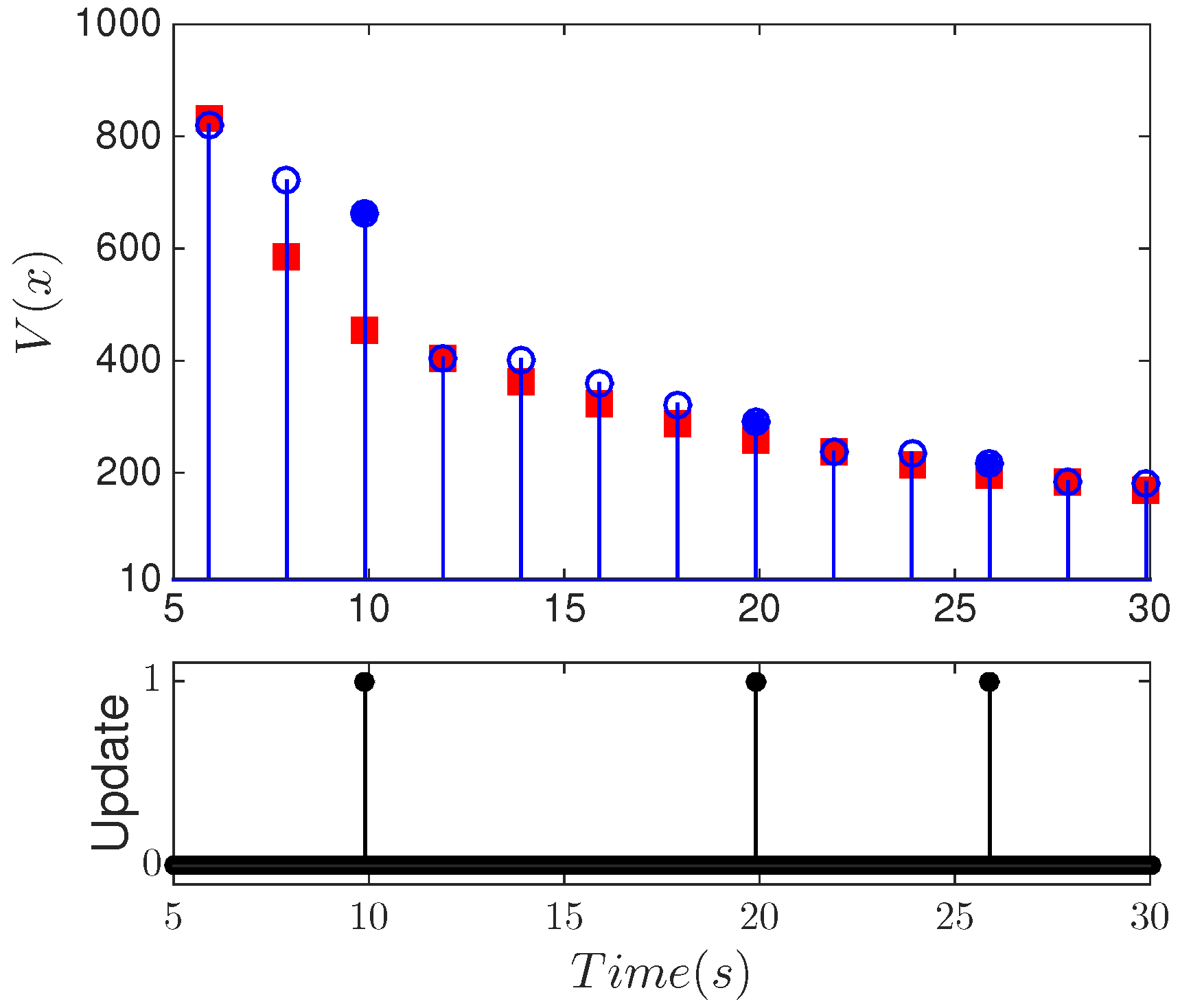
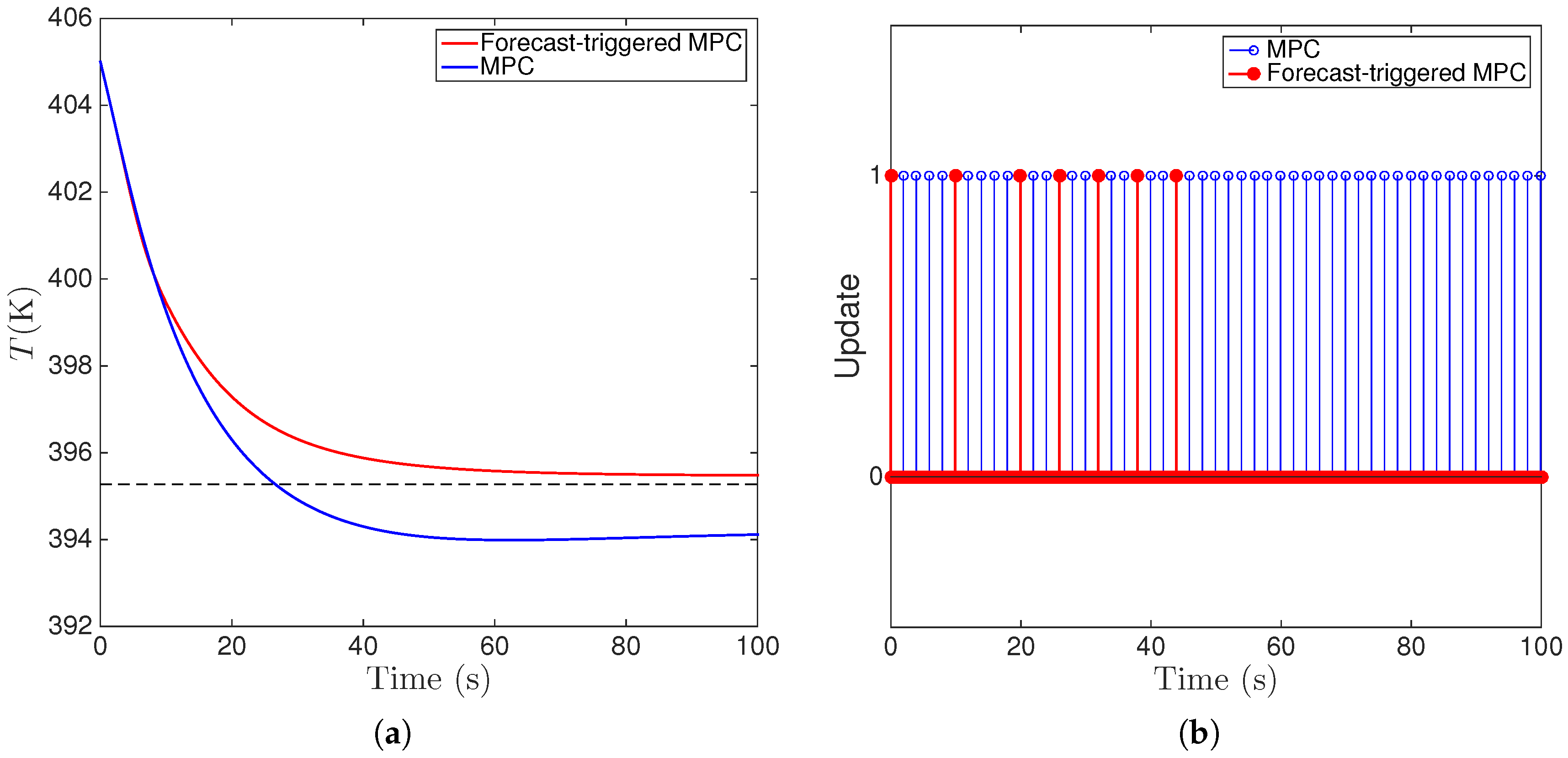
6.3. Implementation of Fault-Tolerant MPC Using Forecast-Triggered Sensor–Controller Communication
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Qin, S.J.; Badgwell, T.A. A survey of industrial model predictive control technology. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef] [Green Version]
- Rawlings, J.B.; Mayne, D.Q. Model Predictive Control: Theory and Design; Nob Hill Publishing: Madison, WI, USA, 2009. [Google Scholar]
- Christofides, P.D.; Liu, J.; de la Pena, D.M. Networked and Distributed Predictive Control: Methods and Nonlinear Process Network Applications; Springer: London, UK, 2011. [Google Scholar]
- Ellis, M.; Liu, J.; Christofides, P.D. Economic Model Predictive Control: Theory, Formulations and Chemical Process Applications; Springer: London, UK, 2017. [Google Scholar]
- Blanke, M.; Kinnaert, M.; Lunze, J.; Staroswiecki, M. Diagnosis and Fault-Tolerant Control; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Zhang, Y.; Jiang, J. Bibliographical Review on Reconfigurable Fault-Tolerant Control Systems. Annu. Rev. Control 2008, 32, 229–252. [Google Scholar] [CrossRef]
- Mhaskar, P.; Liu, J.; Christofides, P.D. Fault-Tolerant Process Control: Methods and Applications; Springer: London, UK, 2013. [Google Scholar]
- Christofides, P.D.; Davis, J.; El-Farra, N.H.; Clark, D.; Harris, K.; Gipson, J. Smart plant operations: Vision, progress and challenges. AIChE J. 2007, 53, 2734–2741. [Google Scholar] [CrossRef]
- Mhaskar, P. Robust Model Predictive Control Design for Fault-Tolerant Control of Process Systems. Ind. Eng. Chem. Res. 2006, 45, 8565–8574. [Google Scholar] [CrossRef]
- Dong, J.; Verhaegen, M.; Holweg, E. Closed-loop subspace predictive control for fault-tolerant MPC design. In Proceedings of the 17th IFAC World Congress, Seoul, Korea, 6–11 July 2008; pp. 3216–3221. [Google Scholar]
- Camacho, E.F.; Alamo, T.; de la Pena, D.M. Fault-tolerant model predictive control. In Proceedings of the IEEE Conference on Emerging Technologies and Factory Automation, Bilbao, Spain, 13–16 September 2010; pp. 1–8. [Google Scholar]
- Lao, L.; Ellis, M.; Christofides, P.D. Proactive Fault-Tolerant Model Predictive Control. AIChE J. 2013, 59, 2810–2820. [Google Scholar] [CrossRef]
- Knudsen, B.R. Proactive Actuator Fault-Tolerance in Economic MPC for Nonlinear Process Plants. In Proceedings of the 11th IFAC Symposium on Dynamics and Control of Process Systems, Trondheim, Norway, 6–8 June 2016; pp. 1097–1102. [Google Scholar]
- Hu, Y.; El-Farra, N.H. Quasi-decentralized output feedback model predictive control of networked process systems with forecast-triggered communication. In Proceedings of the American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 2612–2617. [Google Scholar]
- Hu, Y.; El-Farra, N.H. Adaptive quasi-decentralized MPC of networked process systems. In Distributed Model Predictive Control Made Easy; Springer: Dordrecht, The Netherlands, 2014; Volume 69, pp. 209–223. [Google Scholar]
- Christofides, P.D.; El-Farra, N.H. Control of Nonlinear and Hybrid Process Systems: Designs for Uncertainty, Constraints and Time-Delays; Springer: Berlin, Germany, 2005. [Google Scholar]
- Mhaskar, P.; El-Farra, N.H.; Christofides, P.D. Stabilization of Nonlinear Systems with State and Control Constraints Using Lyapunov-Based Predictive Control. Syst. Control Lett. 2006, 55, 650–659. [Google Scholar] [CrossRef]
- Allen, J.; El-Farra, N.H. A Model-based Framework for Fault Estimation and Accommodation Applied to Distributed Energy Resources. Renew. Energy 2017, 100, 35–43. [Google Scholar] [CrossRef]
- Sanchez-Sanchez, K.B.; Ricardez-Sandoval, L.A. Simultaneous Design and Control under Uncertainty Using Model Predictive Control. Ind. Eng. Chem. Res. 2013, 52, 4815–4833. [Google Scholar] [CrossRef]
- Bahakim, S.S.; Ricardez-Sandoval, L.A. Simultaneous design and MPC-based control for dynamic systems under uncertainty: A stochastic approach. Comput. Chem. Eng. 2014, 63, 66–81. [Google Scholar] [CrossRef]
- Gutierrez, G.; Ricardez-Sandoval, L.A.; Budman, H.; Prada, C. An MPC-based control structure selection approach for simultaneous process and control design. Comput. Chem. Eng. 2014, 70, 11–21. [Google Scholar] [CrossRef]

| Parameter | Process | Model |
|---|---|---|
| F (m3/h) | ||
| V (m3) | ||
| (h−1) | ||
| E (KJ/Kmol) | ||
| R (KJ/Kmol/K) | ||
| (Kg/m3) | 1000 | 1010 |
| (KJ/Kg/K) | ||
| (KJ/Kmol) | ||
| (Kmol/m3) | ||
| (K) | ||
| (KJ/h) | 0 | 0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, D.; El-Farra, N.H. Forecast-Triggered Model Predictive Control of Constrained Nonlinear Processes with Control Actuator Faults. Mathematics 2018, 6, 104. https://doi.org/10.3390/math6060104
Xue D, El-Farra NH. Forecast-Triggered Model Predictive Control of Constrained Nonlinear Processes with Control Actuator Faults. Mathematics. 2018; 6(6):104. https://doi.org/10.3390/math6060104
Chicago/Turabian StyleXue, Da, and Nael H. El-Farra. 2018. "Forecast-Triggered Model Predictive Control of Constrained Nonlinear Processes with Control Actuator Faults" Mathematics 6, no. 6: 104. https://doi.org/10.3390/math6060104
APA StyleXue, D., & El-Farra, N. H. (2018). Forecast-Triggered Model Predictive Control of Constrained Nonlinear Processes with Control Actuator Faults. Mathematics, 6(6), 104. https://doi.org/10.3390/math6060104




