Approximate Dynamic Programming Based Control of Proppant Concentration in Hydraulic Fracturing
Abstract
1. Introduction
2. Approximate Dynamic Programming
3. Application of Approximate Dynamic Programming to a Hydraulic Fracturing Process
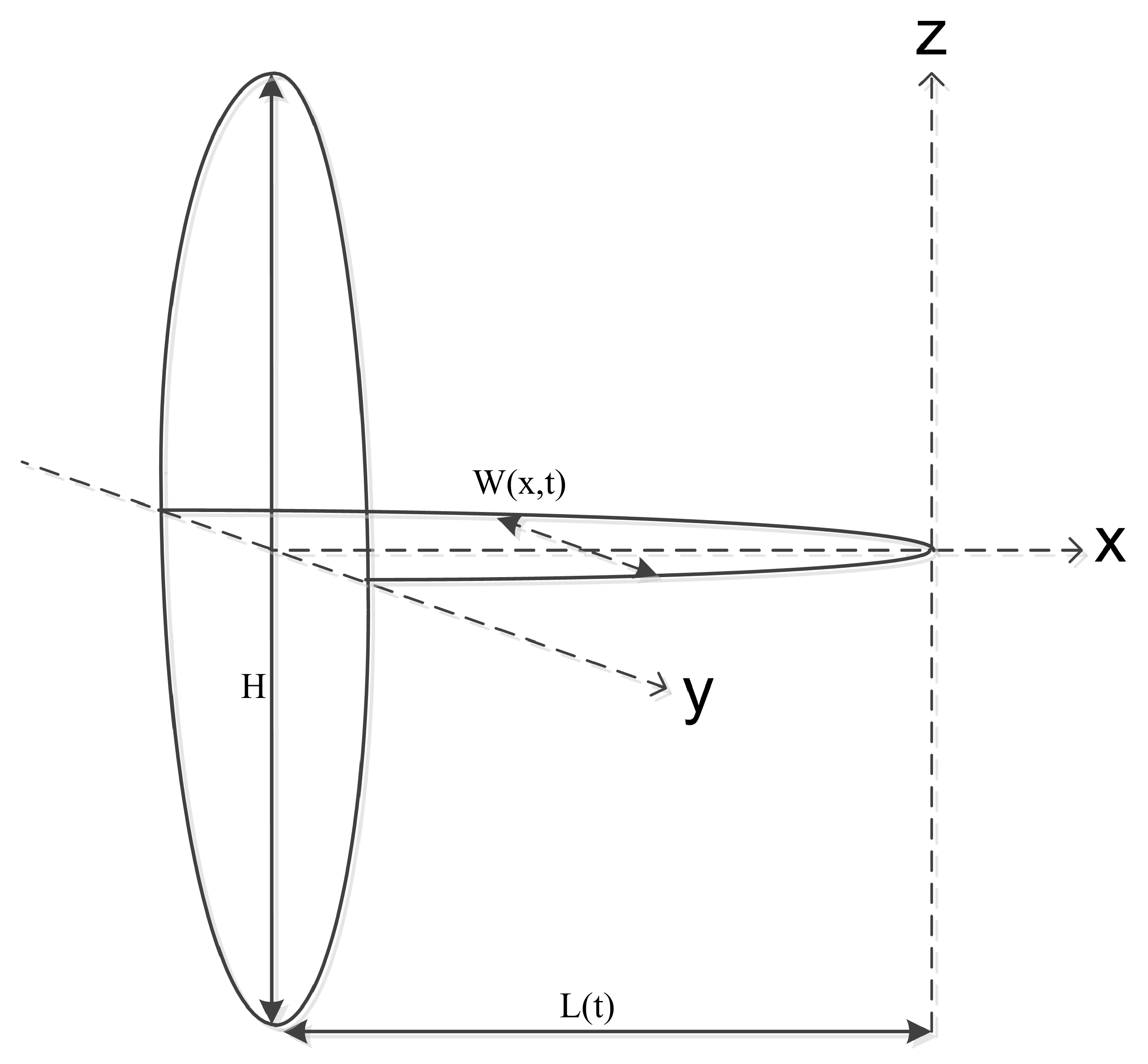
3.1. Dynamic Modeling of Hydraulic Fracturing
- At the wellbore, the fluid flow rate is specified by , where is the fluid injection rate (i.e., the manipulated variable).
- At the fracture tip, , the fracture is always closed, that is .
3.2. Obtaining Cost-to-Go Function Offline
3.2.1. Simulation of Sub-Optimal Control Policies for ADP
3.2.2. Initial Cost-to-Go Approximation
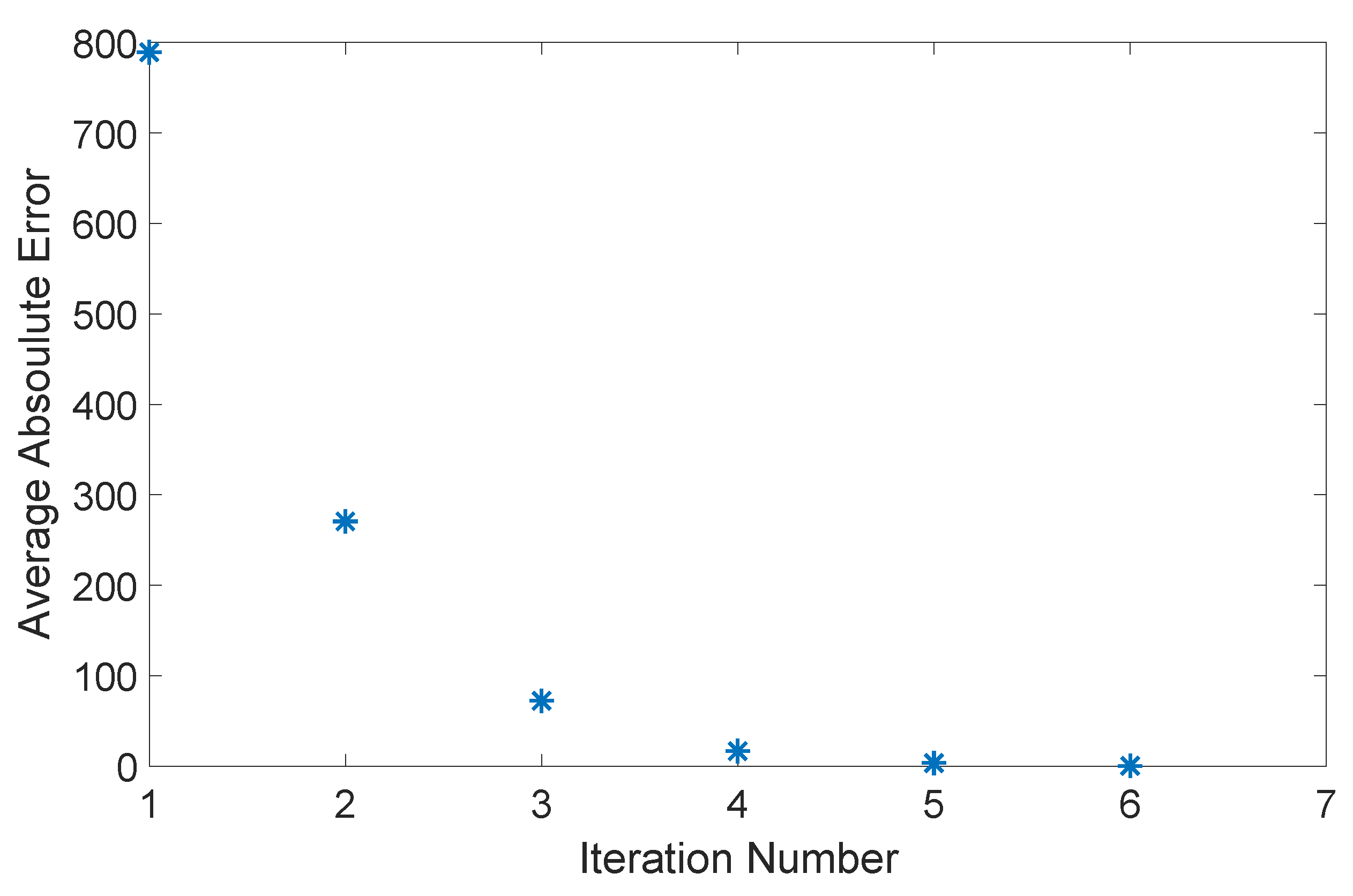
3.2.3. Bellman Iteration
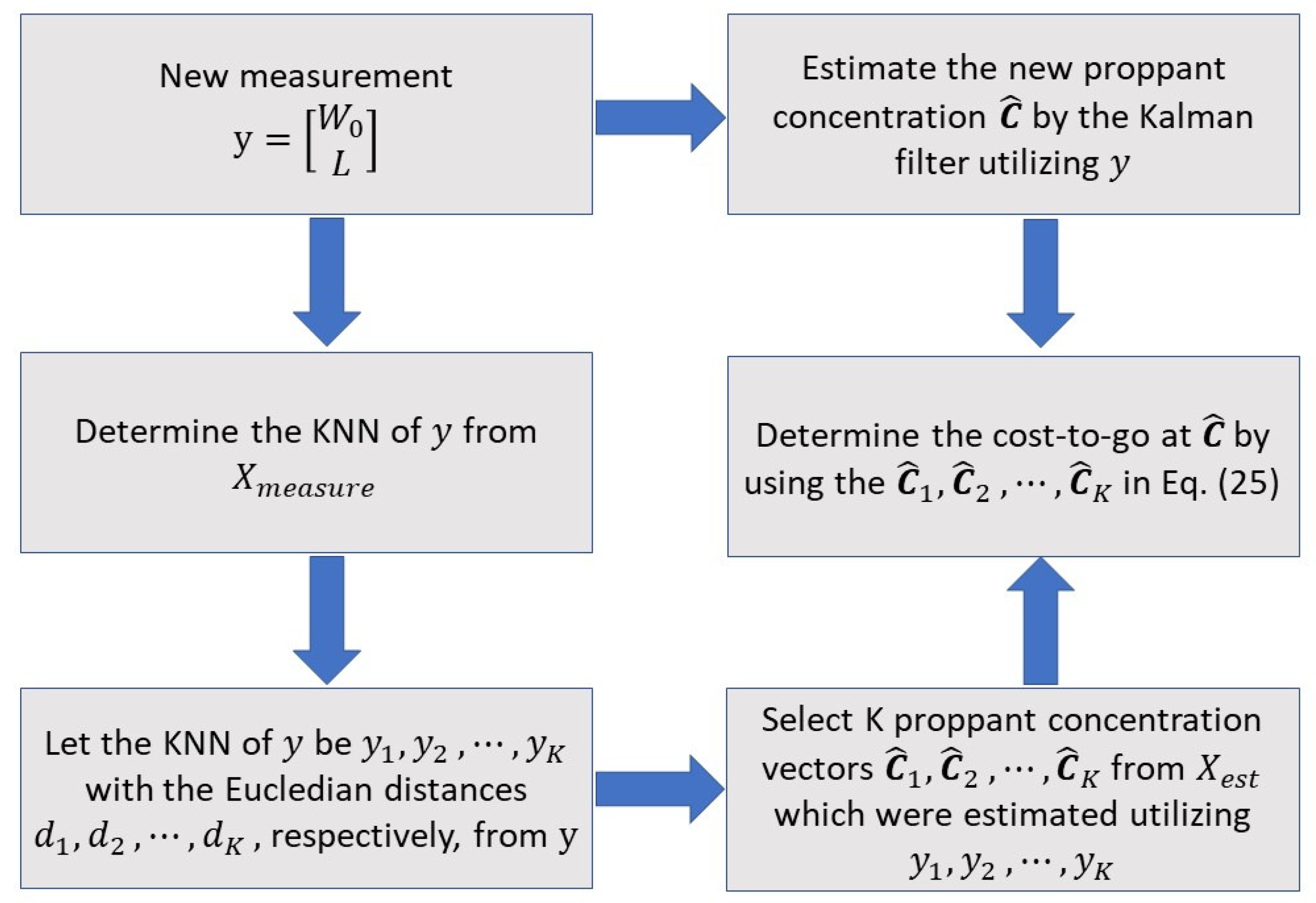
3.3. Online Optimal Control
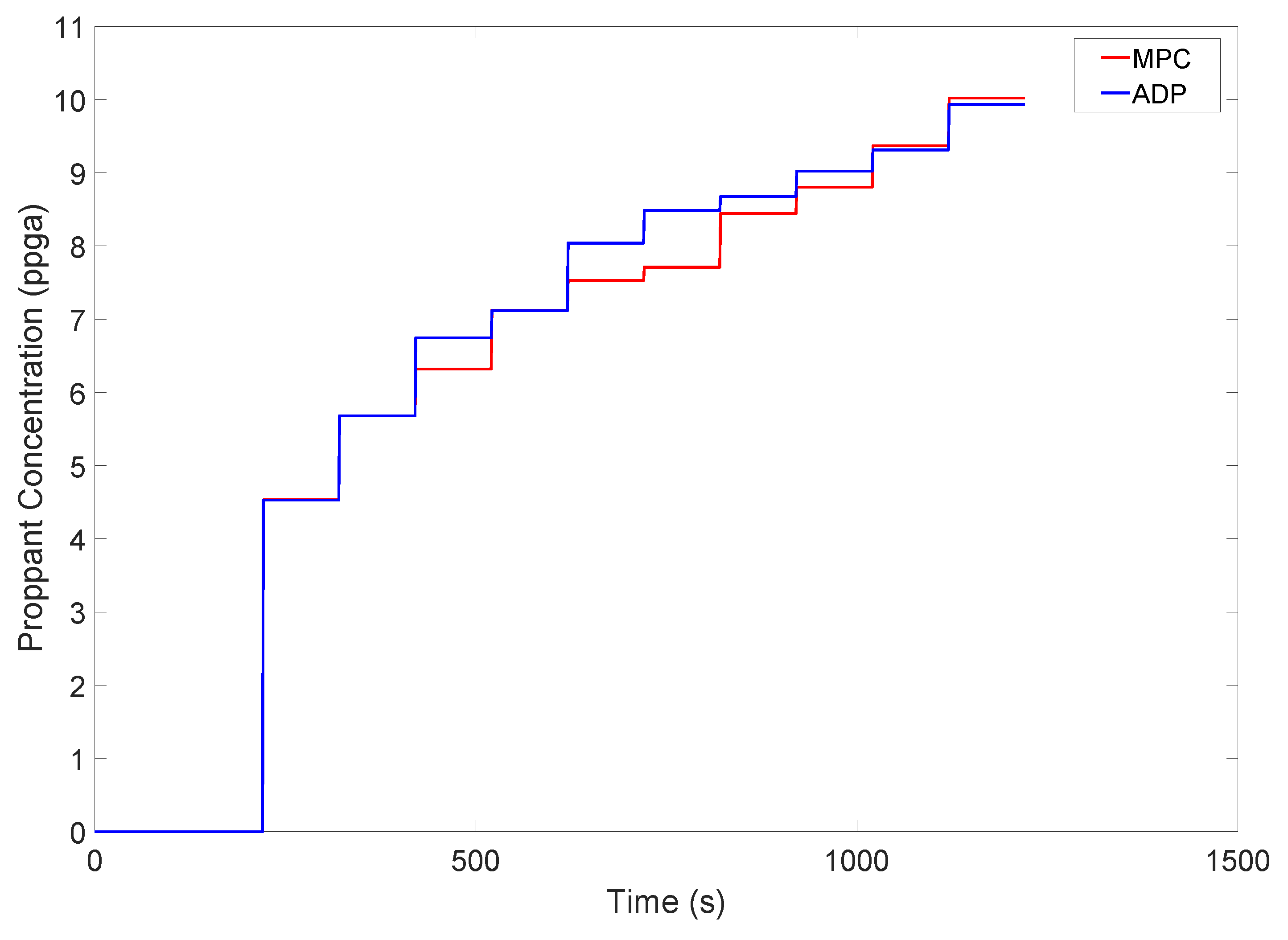
3.4. ADP-Based Control with Plant–Model Mismatch
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Economides, M.J.; Watters, L.T.; Dunn-Normall, S. Petroleum Well Construction; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Economides, M.J.; Nolte, K.G. Reservoir Stimulation; John Wiley & Sons: New York, NY, USA, 2000. [Google Scholar]
- Economides, M.J.; Martin, T. Modern Fracturing: Enhancing Natural Gas Production; ET Publishing: Houston, TX, USA, 2007. [Google Scholar]
- Nolte, K.G. Determination of proppant and fluid schedules from fracturing-pressure decline. SPE Prod. Eng. 1986, 1, 255–265. [Google Scholar] [CrossRef]
- Gu, H.; Desroches, J. New pump schedule generator for hydraulic fracturing treatment design. In Proceedings of the SPE Latin American and Caribbean Petroleum Engineering Conference, Port-of-Spain, Trinidad and Tobago, 27–30 April 2003. [Google Scholar]
- Dontsov, E.V.; Peirce, A.P. A new technique for proppant schedule design. Hydraul. Fract. J. 2014, 1, 1–8. [Google Scholar]
- Gu, Q.; Hoo, K.A. Model-based closed-loop control of the hydraulic fracturing Process. Ind. Eng. Chem. Res. 2015, 54, 1585–1594. [Google Scholar] [CrossRef]
- Siddhamshetty, P.; Yang, S.; Kwon, J.S. Modeling of hydraulic fracturing and designing of online pumping schedules to achieve uniform proppant concentration in conventional oil reservoirs. Comput. Chem. Eng. 2018, 114, 306–317. [Google Scholar] [CrossRef]
- Siddhamshetty, P.; Kwon, J.S.; Liu, S.; Valkó, P.P. Feedback control of proppant bank heights during hydraulic fracturing for enhanced productivity in shale formations. AIChE J. 2018, 64, 1638–1650. [Google Scholar] [CrossRef]
- Narasingam, A.; Siddhamshetty, P.; Kwon, J.S. Temporal clustering for order reduction of nonlinear parabolic PDE systems with time-dependent spatial domains: Application to a hydraulic fracturing process. AIChE J. 2017, 63, 3818–3831. [Google Scholar] [CrossRef]
- Narasingam, A.; Kwon, J.S. Development of local dynamic mode decomposition with control: Application to model predictive control of hydraulic fracturing. Comput. Chem. Eng. 2017, 106, 501–511. [Google Scholar] [CrossRef]
- Sidhu, H.S.; Narasingam, A.; Siddhamshetty, P.; Kwon, J.S. Model order reduction of nonlinear parabolic PDE systems with moving boundaries using sparse proper orthogonal decomposition: Application to hydraulic fracturing. Comput. Chem. Eng. 2018, 112, 92–100. [Google Scholar] [CrossRef]
- Morari, M.; Lee, J.H. Model predictive control: Past, present and future. Comput. Chem. Eng. 1999, 23, 667–682. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Rawlings, J.B.; Rao, C.V.; Scokaert, P.O. Constrained model predictive control: Stability and optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Bemporad, A.; Morari, M. Control of systems integrating logic, dynamics and constraints. Automatica 1999, 35, 407–427. [Google Scholar] [CrossRef]
- Lee, J.H.; Cooley, B. Recent advances in model predictive control and other related areas. In AIChE Symposium Series; 1971-c2002; American Institute of Chemical Engineers: New York, NY, USA, 1997; Volume 93, pp. 201–216. [Google Scholar]
- Chikkula, Y.; Lee, J.H. Robust adaptive predictive control of nonlinear processes using nonlinear moving average system models. Ind. Eng. Chem. Res. 2000, 39, 2010–2023. [Google Scholar] [CrossRef]
- Lee, J.H.; Lee, J.M. Approximate dynamic programming based approach to process control and scheduling. Comput. Chem. Eng. 2006, 30, 1603–1618. [Google Scholar] [CrossRef]
- Kaisare, N.S.; Lee, J.M.; Lee, J.H. Simulation based strategy for nonlinear optimal control: Application to a microbial cell reactor. Int. J. Robust Nonlinear Control 2003, 13, 347–363. [Google Scholar] [CrossRef]
- Lee, J.M.; Kaisare, N.S.; Lee, J.H. Choice of approximator and design of penalty function for an approximate dynamic programming based control approach. J. Process Control 2006, 16, 135–156. [Google Scholar] [CrossRef]
- Tosukhowong, T.; Lee, J.H. Approximate dynamic programming based optimal control applied to an integrated plant with a reactor and a distillation column with recycle. AIChE J. 2009, 55, 919–930. [Google Scholar] [CrossRef]
- Padhi, R.; Balakrishnan, S.N. Proper orthogonal decomposition based optimal neurocontrol synthesis of a chemical reactor process using approximate dynamic programming. Neural Netw. 2003, 16, 719–728. [Google Scholar] [CrossRef]
- Joy, M.; Kaisare, N.S. Approximate dynamic programming-based control of distributed parameter systems. Asia-Pac. J. Chem. Eng. 2011, 6, 452–459. [Google Scholar] [CrossRef]
- Munusamy, S.; Narasimhan, S.; Kaisare, N.S. Approximate dynamic programming based control of hyperbolic PDE systems using reduced-order models from method of characteristics. Comput. Chem. Eng. 2013, 57, 122–132. [Google Scholar] [CrossRef]
- Bellman, R.E. Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1957. [Google Scholar]
- Perkins, T.K.; Kern, L.R. Widths of Hydraulic Fractures. J. Pet. Technol. 1961, 13, 937–949. [Google Scholar] [CrossRef]
- Nordgren, R. Propagation of a vertical hydraulic fracture. Soc. Pet. Eng. J. 1972, 12, 306–314. [Google Scholar] [CrossRef]
- Sneddon, L.; Elliot, H. The opening of a Griffith crack under internal pressure. Q. Appl. Math. 1946, 4, 262–267. [Google Scholar] [CrossRef]
- Gudmundsson, A. Stress estimate from the length/width ratios of fractures. J. Struct. Geol. 1983, 5, 623–626. [Google Scholar] [CrossRef]
- Howard, G.C.; Fast, C.R. Optimum fluid characteristics for fracture extension. Dril. Product. Pract. 1957, 24, 261–270. [Google Scholar]
- Adachi, J.; Siebrits, E.; Peirce, A.; Desroches, J. Computer simulation of hydraulic fractures. Int. J. Rock Mech. Min. Sci. 2007, 44, 739–757. [Google Scholar] [CrossRef]
- Daneshy, A. Numerical solution of sand transport in hydraulic fracturing. J. Pet. Technol. 1978, 30, 132–140. [Google Scholar] [CrossRef]
- Barree, R.; Conway, M. Experimental and numerical modeling of convective proppant transport. J. Pet. Technol. 1995, 47, 216–222. [Google Scholar] [CrossRef]
- Gu, Q.; Hoo, K.A. Evaluating the performance of a fracturing treatment design. Ind. Eng. Chem. Res. 2014, 53, 10491–10503. [Google Scholar] [CrossRef]
- Novotny, E.J. Proppant transport. In Proceedings of the SPE Annual Fall Technical Conference and Exhibition (SPE 6813), Denver, CO, USA, 9–12 October 1977. [Google Scholar]
- Daal, J.A.; Economides, M.J. Optimization of hydraulic fracture well in irregularly shape drainage areas. In Proceedings of the SPE 98047 SPE International Symposium and Exhibition of Formation Flamage Control, Lafayette, LA, USA, 15–17 February 2006; pp. 15–17. [Google Scholar]
- Corbett, B.; Mhaskar, P. Subspace identification for data-driven modeling and quality control of batch processes. AIChE J. 2016, 62, 1581–1601. [Google Scholar] [CrossRef]
- Meidanshahi, V.; Corbett, B.; Adams, T.A., II; Mhaskar, P. Subspace model identification and model predictive control based cost analysis of a semicontinuous distillation process. Comput. Chem. Eng. 2017, 103, 39–57. [Google Scholar] [CrossRef]
- Pourkargar, D.B.; Armaou, A. Modification to adaptive model reduction for regulation of distributed parameter systems with fast transients. AIChE J. 2013, 59, 4595–4611. [Google Scholar] [CrossRef]
- Pourkargar, D.B.; Armaou, A. APOD-based control of linear distributed parameter systems under sensor/controller communication bandwidth limitations. AIChE J. 2015, 61, 434–447. [Google Scholar] [CrossRef]
- Sahraei, M.H.; Duchesne, M.A.; Yandon, R.; Majeski, A.; Hughes, R.W.; Ricardez-Sandoval, L.A. Reduced order modeling of a short-residence time gasifier. Fuel 2015, 161, 222–232. [Google Scholar] [CrossRef]
- Sahraei, M.H.; Duchesne, M.A.; Hughes, R.W.; Ricardez-Sandoval, L.A. Dynamic reduced order modeling of an entrained-flow slagging gasifier using a new recirculation ratio correlation. Fuel 2017, 196, 520–531. [Google Scholar] [CrossRef]
- Quirein, J.A.; Grable, J.; Cornish, B.; Stamm, R.; Perkins, T. Microseismic fracture monitoring. In Proceedings of the SPWLA 47th Annual Logging Symposium, Veracruz, Mexico, 4–7 June 2006. [Google Scholar]
- Narasingam, A.; Siddhamshetty, P.; Kwon, J.S. Handling Spatial Heterogeneity in Reservoir Parameters Using Proper Orthogonal Decomposition Based Ensemble Kalman Filter for Model-Based Feedback Control of Hydraulic Fracturing. Ind. Eng. Chem. Res. 2018, 57, 3977–3989. [Google Scholar] [CrossRef]
- Bertsekas, D. Dynamic Programming and Optimal Control; Athena Scientific: Belmont, MA, USA, 2005; Volume 1. [Google Scholar]
- Lee, J.M.; Lee, J.H. An approximate dynamic programming based approach to dual adaptive control. J. Process Control 2009, 19, 859–864. [Google Scholar] [CrossRef]
- Jafarpour, B. Sparsity-promoting solution of subsurface flow model calibration inverse problems. Adv. Hydrogeol. 2013, 73–94. [Google Scholar] [CrossRef]
- Daniels, J.L.; Waters, G.A.; Le Calvez, J.H.; Bentley, D.; Lassek, J.T. Contacting more of the barnett shale through an integration of real-time microseismic monitoring, petrophysics, and hydraulic fracture design. In Proceedings of the SPE Annual Technical Conference and Exhibition, Anaheim, CA, USA, 11–14 November 2007. [Google Scholar]
- King, G.E. Thirty years of gas shale fracturing: What have we learned? In Proceedings of the SPE Annual Technical Conference and Exhibition, Florence, Italy, 19–22 September 2010. [Google Scholar]
- Lucia, S.; Finkler, T.; Engell, S. Multi-stage nonlinear model predictive control applied to a semi-batch polymerization reactor under uncertainty. J. Process Control 2013, 23, 1306–1319. [Google Scholar] [CrossRef]
- Gutierrez, G.; Ricardez-Sandoval, L.A.; Budman, H.; Prada, C. An MPC-based control structure selection approach for simultaneous process and control design. Comput. Chem. Eng. 2014, 70, 11–21. [Google Scholar] [CrossRef]
- Rodriguez-Perez, B.E.; Flores-Tlacuahuac, A.; Ricardez Sandoval, L.; Lozano, F.J. Optimal Water Quality Control of Sequencing Batch Reactors Under Uncertainty. Ind. Eng. Chem. Res. 2018, 57, 9571–9590. [Google Scholar] [CrossRef]
- Lucia, S.; Tătulea-Codrean, A.; Schoppmeyer, C.; Engell, S. Rapid development of modular and sustainable nonlinear model predictive control solutions. Control Eng. Pract. 2017, 60, 51–62. [Google Scholar] [CrossRef]
| Parameter | Symbol | Value |
|---|---|---|
| Leak-off coefficient | 6.3 × m/s | |
| Maximum concentration | 0.64 | |
| Minimum concentration | 0 | |
| Young’s modulus | E | 0.5 × Pa |
| Proppant permeability | 60,000 mD | |
| Formation permeability | 1.5 mD | |
| Vertical fracture height | H | 20 m |
| Proppant particle density | 2648 kg/m | |
| Pure fluid density | 1000 kg/m | |
| Fracture fluid viscosity | 0.56 Pa·s | |
| Poisson ratio of formation | 0.2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh Sidhu, H.; Siddhamshetty, P.; Kwon, J.S. Approximate Dynamic Programming Based Control of Proppant Concentration in Hydraulic Fracturing. Mathematics 2018, 6, 132. https://doi.org/10.3390/math6080132
Singh Sidhu H, Siddhamshetty P, Kwon JS. Approximate Dynamic Programming Based Control of Proppant Concentration in Hydraulic Fracturing. Mathematics. 2018; 6(8):132. https://doi.org/10.3390/math6080132
Chicago/Turabian StyleSingh Sidhu, Harwinder, Prashanth Siddhamshetty, and Joseph S. Kwon. 2018. "Approximate Dynamic Programming Based Control of Proppant Concentration in Hydraulic Fracturing" Mathematics 6, no. 8: 132. https://doi.org/10.3390/math6080132
APA StyleSingh Sidhu, H., Siddhamshetty, P., & Kwon, J. S. (2018). Approximate Dynamic Programming Based Control of Proppant Concentration in Hydraulic Fracturing. Mathematics, 6(8), 132. https://doi.org/10.3390/math6080132






