On Short-Term Loan Interest Rate Models: A First Passage Time Approach
Abstract
:1. Introduction
2. Mathematical Background
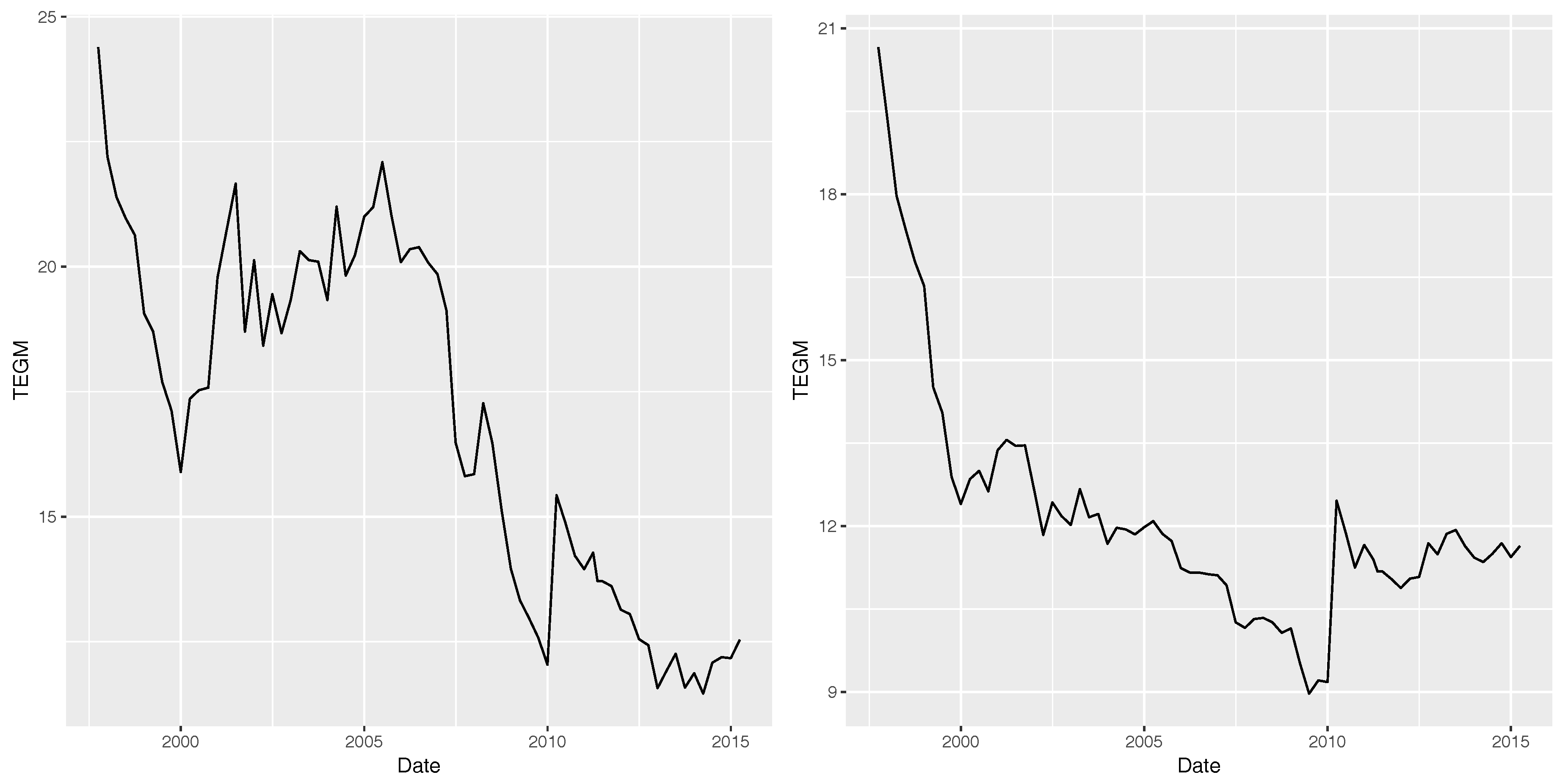
3. Modeling the Italian Loans
- Dataset A: up to 10 million lira (until 31 December 2001) and up to € 5000 (after 2002);
- Dataset B: above 10 million lire (until 31 December 2001) and above € 5000 (after 2002).
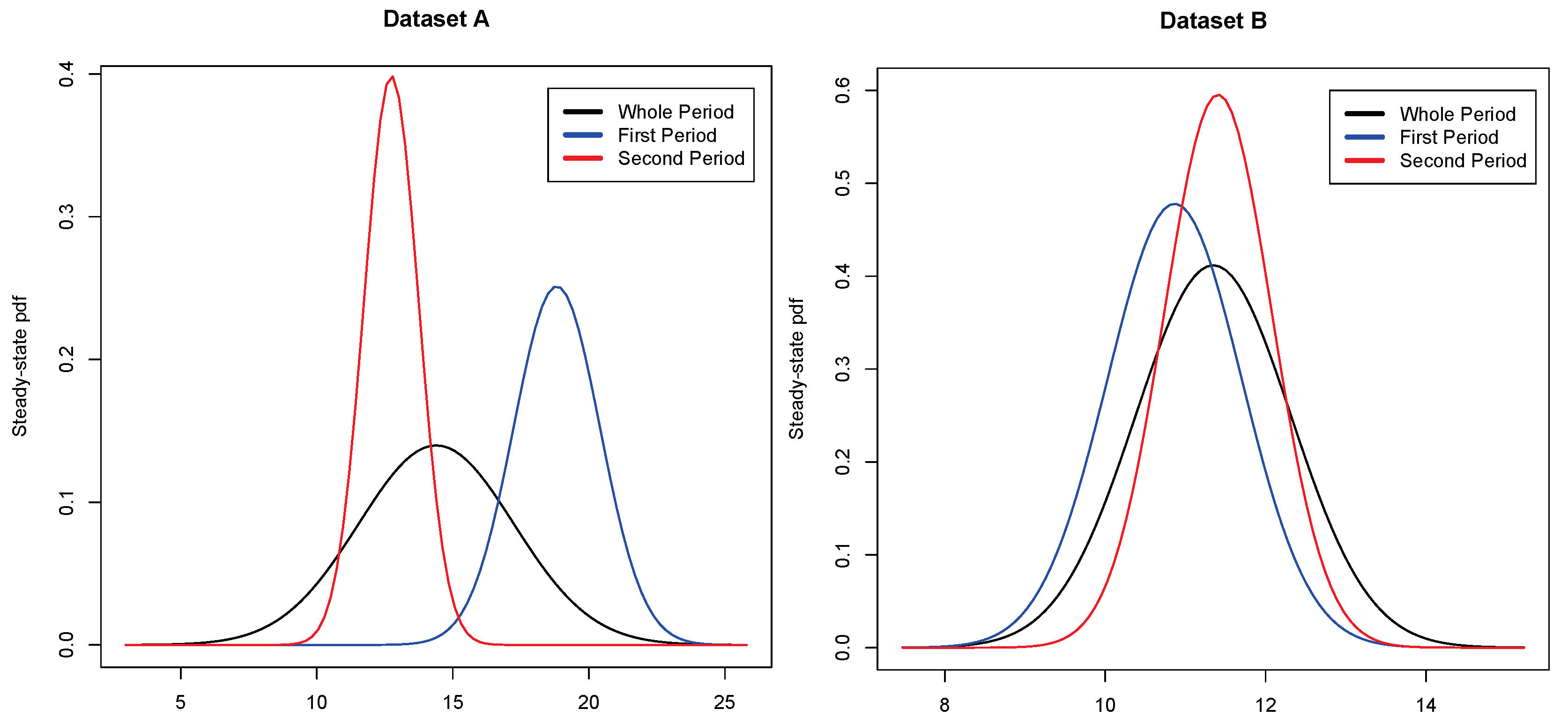
3.1. The Vasiceck Model
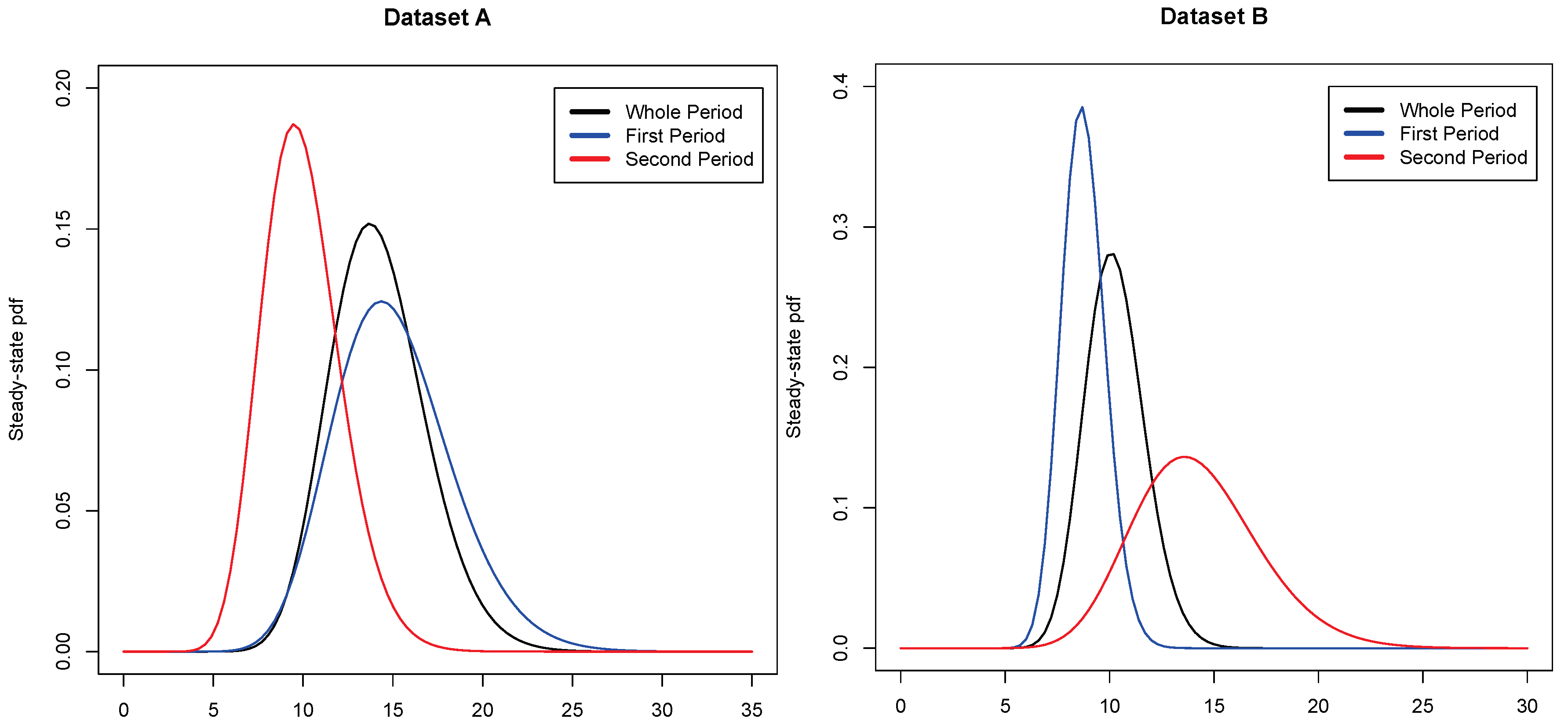
- first period: 1 July 1997–1 October 2007;
- second period: 1 January 2008–31 March 2015;
- first period: 1 July 1997–1 October 2008;
- second period: 1 January 2009–31 March 2015.
3.2. The CIR Model
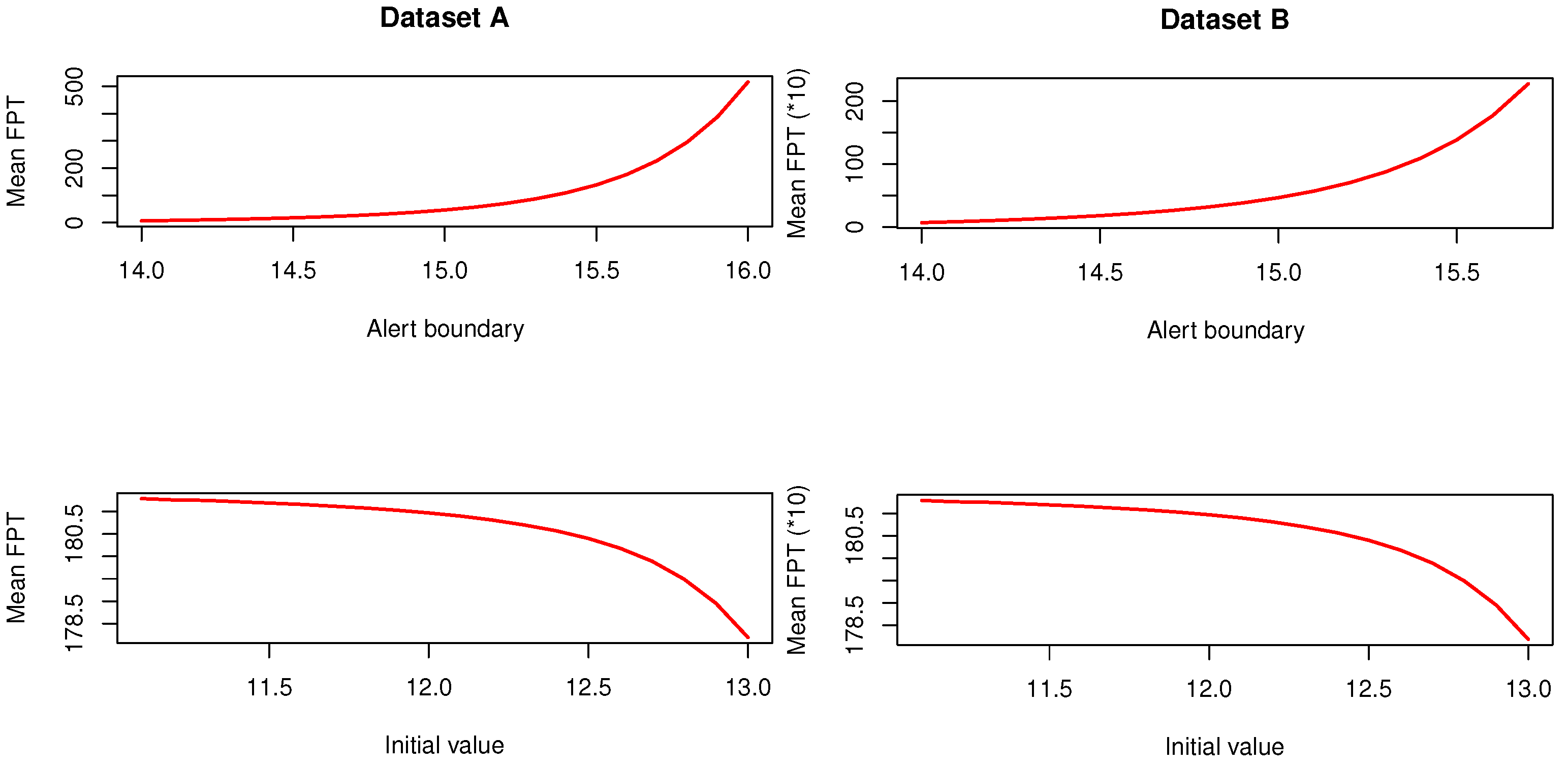
4. FPT Analysis for TEGM
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Brigo, B.; Mercurio, F. Interest Rate Models-Theory and Practice with Smile, Inflation and Credit; Springer: Berlin, Germany, 2007. [Google Scholar]
- Buetow, G.W., Jr.; Hanke, B.; Fabozzi, F.J. Impact of different interest rate models on bound value measures. J. Fixed Income 2001, 3, 41–53. [Google Scholar] [CrossRef]
- Fan, J.; Jiang, J.; Zhang, C.; Zhou, Z. Time-dependent diffusion models for term structure dynamics. Stat. Sin. 2003, 13, 965–992. [Google Scholar]
- Chen, W.; Xu, L.; Zhu, S.P. Stock loan valuation under a stochastic interest rate model. Comput. Math. Appl. 2015, 70, 1757–1771. [Google Scholar] [CrossRef]
- Di Lorenzo, E.; Orlando, A.; Sibillo, M. A Stochastic model fro loan interest rates. Banks Bank Syst. 2013, 8, 94–99. [Google Scholar]
- Cox, J.C.; Ingersoll, J.E.; Ross, S.A. A Theory of the Term Structure of Interest Rates. Econometrica 1985, 53, 385–407. [Google Scholar] [CrossRef]
- Vasicek, O. An equilibrium characterization of the term structure. J. Financ. Econ. 1977, 5, 177–188. [Google Scholar] [CrossRef]
- Khramov, V. Estimating Parameters of Short-Term Real Interest Rate Models; IMF Working Papers; International Monetary Fund: Washington, DC, USA, 2012. [Google Scholar]
- Ricciardi, L.M.; Di Crescenzo, A.; Giorno, V.; Nobile, A.G. An outline of theoretical and algorithmic approaches to first passage time problems with applications to biological modeling. Math. Jpn. 1999, 50, 247–322. [Google Scholar]
- Albano, G.; Giorno, V.; Román-Román, P.; Torres-Ruiz, F. On the effect of a therapy able to modify both the growth rates in a Gompertz stochastic model. Math. Biosci. 2013, 245, 12–21. [Google Scholar] [CrossRef] [PubMed]
- Albano, G.; Giorno, V.; Román-Román, P.; Torres-Ruiz, F. On a Non-homogeneous Gompertz-Type Diffusion Process: Inference and First Passage Time. In Computer Aided Systems Theory-EUROCAST; Moreno Diaz, R., Pichler, F., Quesada Arencibia, A., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2017; Volume 10672, pp. 47–54. [Google Scholar]
- Buonocore, A.; Nobile, A.G.; Ricciardi, L.M. A new integral equation for the evaluation of first-passage-time probability densitie. Adv. Appl. Prob. 1987, 19, 784–800. [Google Scholar] [CrossRef]
- Giorno, V.; Nobile, A.G.; Ricciardi, L.M.; Sato, S. On the evaluation of firtst-passage-time probability densities via non-singular integral equations. Adv. Appl. Prob. 1989, 21, 20–36. [Google Scholar] [CrossRef]
- Buonocore, A.; Caputo, L.; D’Onofrio, G.; Pirozzi, E. Closed-form solutions for the first-passage-time problem and neuronal modeling. Ricerche di Matematica 2015, 64, 421–439. [Google Scholar] [CrossRef]
- Di Crescenzo, A.; Giorno, V.; Nobile, A.G. Analysis of reflected diffusions via an exponential time-based transformation. J. Stat. Phys. 2016, 163, 1425–1453. [Google Scholar] [CrossRef]
- Abundo, M. The mean of the running maximum of an integrated Gauss–Markov process and the connection with its first-passage time. Stoch. Anal. Appl. 2017, 35, 499–510. [Google Scholar] [CrossRef]
- Román-Román, P.; Serrano-Pérez, J.; Torres-Ruiz, F. More general problems on first-passage times for diffusion processes: A new version of the fptdapprox r package. Appl. Math. Comput. 2014, 244, 432–446. [Google Scholar] [CrossRef]
- Román-Román, P.; Serrano-Pérez, J.; Torres-Ruiz, F. fptdapprox: Approximation of First-Passage-Time Densities for Diffusion Processes, R Package Version 2.1, 2015. Available online: http://cran.r-project.org/package=fptdApprox (accessed on 23 November 2017).
- Linetsky, V. Computing hitting time densities for CIR and OU diffusions: Applications to mean reverting models. J. Comput. Financ. 2004, 4, 1–22. [Google Scholar] [CrossRef]
- Albano, G.; Giorno, V. A stochastic model in tumor growth. J. Theor. Biol. 2006, 242, 229–236. [Google Scholar] [CrossRef] [PubMed]
- Buonocore, A.; Caputo, L.; Nobile, A.G.; Pirozzi, E. Restricted Ornstein–Uhlenbeck process and applications in neuronal models with periodic input signals. J. Comp. Appl. Math. 2015, 285, 59–71. [Google Scholar] [CrossRef]
- Dharmaraja, S.; Di Crescenzo, A.; Giorno, V.; Nobile, A.G. A continuous-time Ehrenfest model with catastrophes and its jump-diffusion approximation. J. Stat. Phys. 2015, 161, 326–345. [Google Scholar] [CrossRef]
- Giorno, V.; Spina, S. On the return process with refractoriness for non-homogeneous Ornstein–Uhlenbeck neuronal model. Math. Biosci. Eng. 2014, 11, 285–302. [Google Scholar] [PubMed]
- Iacus, S.M. Simulation and Inference for Stochastic Differential Equations with R Examples; Springer Series in Statistics: Berlin, Germany, 2008. [Google Scholar]
- Iacus, S.M. sde-Manual and Help on Using the sde R Package. 2009. Available online: http://www.rdocumentation.org/packages/sde/versions/2.0.9 (accessed on 24 October 2017).
- Giorno, V.; Lanský, P.; Nobile, A.G.; Ricciardi, L.M. Diffusion approximation and first-passage-time problem for a model neuron. III. A birth-and-death process approach. Biol. Cybern. 1988, 58, 387–404. [Google Scholar] [CrossRef] [PubMed]
- Giorno, V.; Nobile, A.G.; Ricciardi, L.M. Single neuron’s activity: On certain problems of modeling and interpretation. BioSystems 1997, 40, 65–74. [Google Scholar] [CrossRef]
- Nobile, A.G.; Pirozzi, E. On time non-homogeneous Feller-type diffusion process in neuronal modeling. In Computer Aided Systems Theory-EUROCAST 2017; Moreno Diaz, R., Pichler, F., Quesada Arencibia, A., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2015; Volume 9520, pp. 183–191. [Google Scholar]
- Karlin, S.; Taylor, H.W. A Second Course in Stochastic Processes; Academic Press: New York, NY, USA, 1981. [Google Scholar]
| Vasicek Model | ||||
|---|---|---|---|---|
| Dataset A | Dataset B | |||
| estimate | standard error | estimate | standard error | |
| 0.9473455 | 0.62502358 | 1.9016919 | 0.41732799 | |
| 0.0658379 | 0.03621181 | 0.1675858 | 0.03403613 | |
| 1.0355084 | 0.08881145 | 0.5610075 | 0.04793382 | |
| AIC | 207.8207 | 113.8432 | ||
| The Vasicek Model | ||||
|---|---|---|---|---|
| Dataset A | ||||
| First Period | Second Period | |||
| 1 July 1997–1 October 2007 | 1 January 2008–31 March 2015 | |||
| estimate | standard error | estimate | standard error | |
| 5.3865862 | 2.4412428 | 4.3464435 | 1.6780736 | |
| 0.2862057 | 0.1245413 | 0.3411949 | 0.1264711 | |
| 1.2012565 | 0.1489351 | 0.8262836 | 0.1179829 | |
| 126.2129 | 67.89682 | |||
| Dataset B | ||||
| First Period | Second Period | |||
| 1 July 1997–1 October 2008 | 1 January 2009–31 March 2015 | |||
| estimate | standard error | estimate | standard error | |
| 1.5003276 | 0.37401583 | 7.9272605 | 3.1400451 | |
| 0.1380841 | 0.02919803 | 0.6949408 | 0.2786503 | |
| 0.4386253 | 0.04613525 | 0.7898723 | 0.1424101 | |
| 54.51816 | 48.00966 | |||
| CIR Model | ||||
|---|---|---|---|---|
| Dataset A | Dataset B | |||
| estimate | standard error | estimate | standard error | |
| 0.87234371 | 0.57486263 | 0.71000000 | 0.69208186 | |
| 0.06140606 | 0.03471271 | 0.06913925 | 0.05744829 | |
| 0.24781675 | 0.02122343 | 0.16565230 | 0.01524389 | |
| 204.3006 | 123.7508 | |||
| CIR Model | ||||
|---|---|---|---|---|
| Dataset A | ||||
| before 1 January 2008 | after 1 January 2008 | |||
| estimate | standard error | estimate | standard error | |
| 0.70000000 | 1.96946686 | 0.50000000 | 1.5237235 | |
| 0.04645403 | 0.10114005 | 0.05015628 | 0.1157965 | |
| 0.25705245 | 0.02838514 | 0.21809718 | 0.0293771 | |
| 130.8434 | 73.32189 | |||
| Dataset B | ||||
| before 1 January 2009 | after 1 January 2009 | |||
| estimate | standard error | estimate | standard error | |
| 0.55000000 | 0.7378984 | 0.53234000 | 2.02364571 | |
| 0.06276713 | 0.0587019 | 0.03746054 | 0.18050398 | |
| 0.12443707 | 0.0159996 | 0.21651927 | 0.03194828 | |
| 58.07491 | 75.83153 | |||
| S | ||||
| 15 | ||||
| 16 | ||||
| 13 | ||||
| 14 |
| S | ||||
| 13 | ||||
| 14 | ||||
| 15 | ||||
| 11 | ||||
| 13 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albano, G.; Giorno, V. On Short-Term Loan Interest Rate Models: A First Passage Time Approach. Mathematics 2018, 6, 70. https://doi.org/10.3390/math6050070
Albano G, Giorno V. On Short-Term Loan Interest Rate Models: A First Passage Time Approach. Mathematics. 2018; 6(5):70. https://doi.org/10.3390/math6050070
Chicago/Turabian StyleAlbano, Giuseppina, and Virginia Giorno. 2018. "On Short-Term Loan Interest Rate Models: A First Passage Time Approach" Mathematics 6, no. 5: 70. https://doi.org/10.3390/math6050070
APA StyleAlbano, G., & Giorno, V. (2018). On Short-Term Loan Interest Rate Models: A First Passage Time Approach. Mathematics, 6(5), 70. https://doi.org/10.3390/math6050070




