A Novel Distributed Economic Model Predictive Control Approach for Building Air-Conditioning Systems in Microgrids
Abstract
:1. Introduction
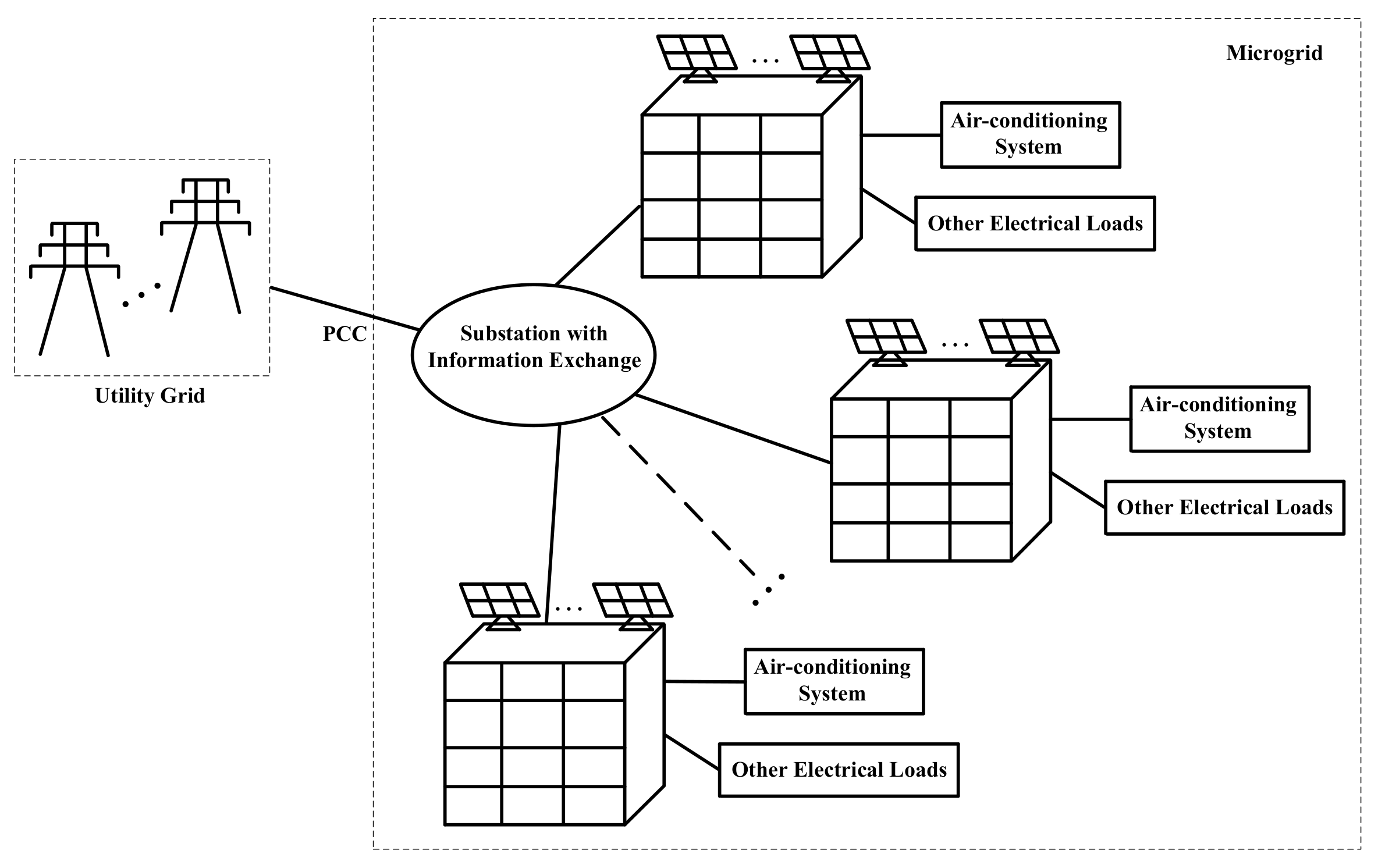
2. Buildings with Air-Conditioning and Solar Generation in Microgrids
2.1. Building Thermal Modeling
2.2. Building with Air-Conditioning and Solar Generation
2.3. State-Space Representation
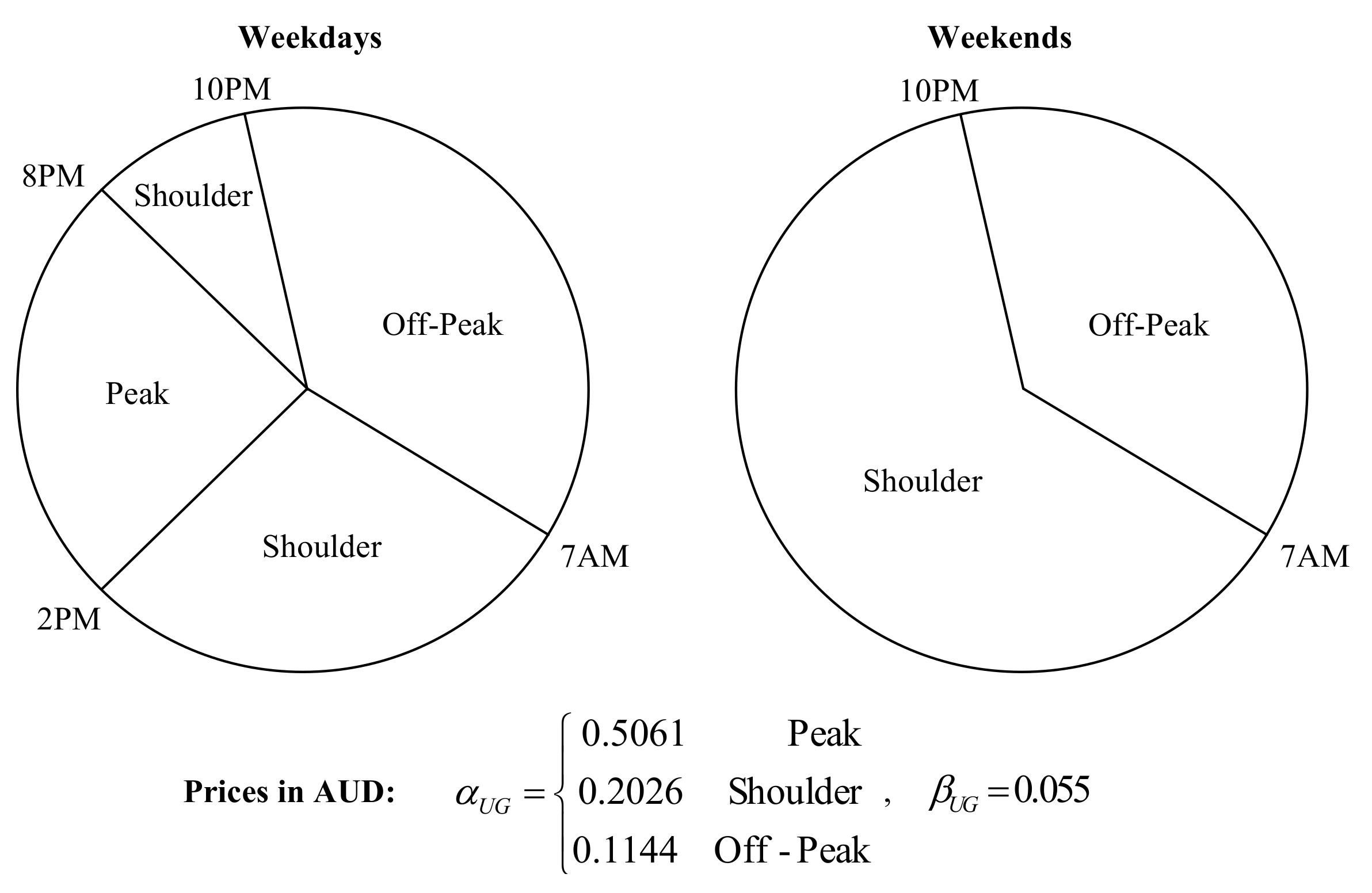
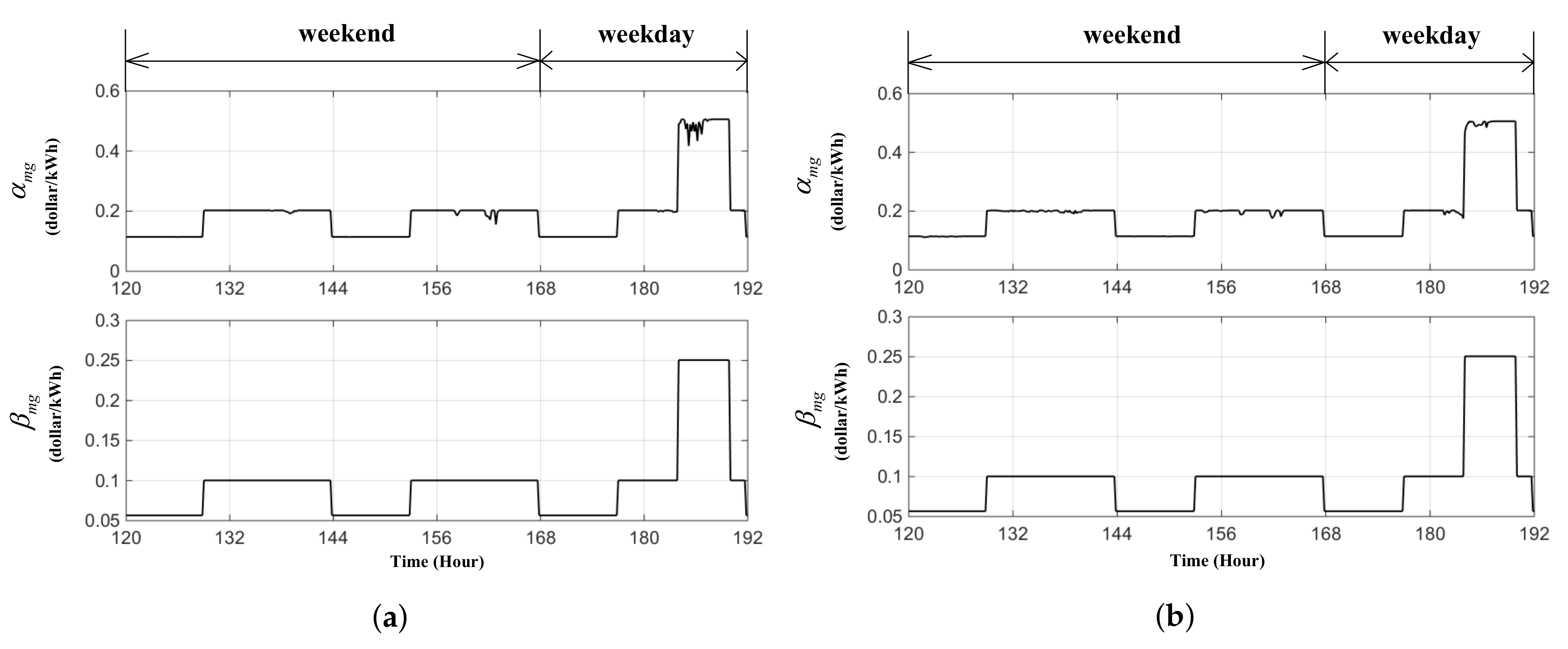
3. Electricity Price Policy for Energy Trading in Microgrids
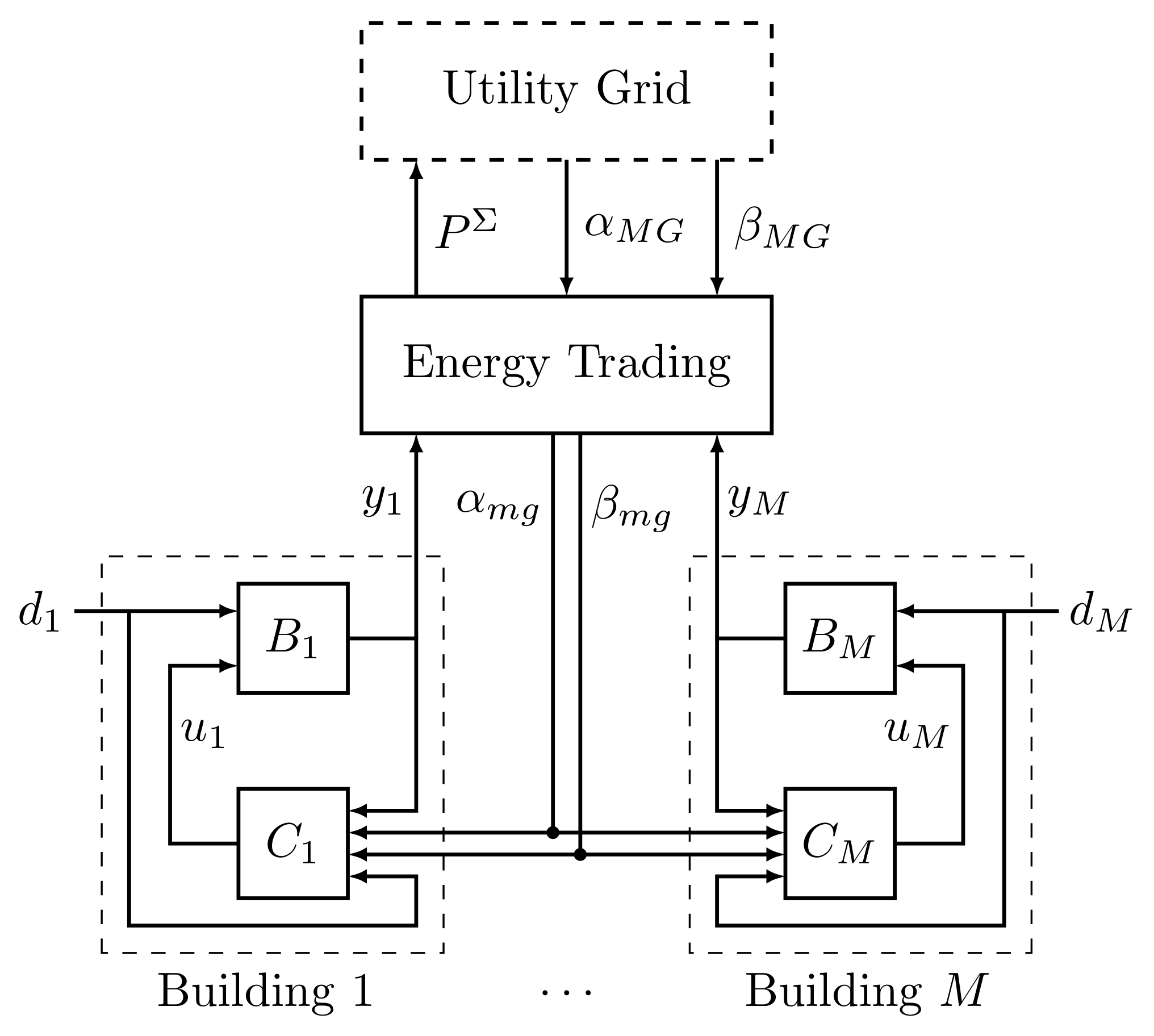
4. Dissipativity Based Distributed Control Framework
4.1. Dissipativity and Dissipative Conditions
4.2. Dissipativity Analysis of an Individual Building in the Microgrid
4.3. Dissipativity Based DEMPC
4.4. Analysis of Dissipativity of Price Controller in Microgrid
4.5. Microgrid-Wide Dissipativity Synthesis
4.6. Distributed Control Design and Implmentation
- Off-line dissipativity synthesis: The dissipativity property for a given system is not unique. A system can have different supply rates that represent different aspects of the process dynamics (e.g., the gain and phase conditions). Therefore, dissipativity conditions for all subsystems including individual buildings, BACS controllers and the pricing controller that allow the required microgrid-wide stability and performance condition in (34) need to be found during the offline design step. This is done by solving LMIs in (19) for dissipativity conditions for buildings (corresponding to the building model in (18)), feasibility conditions for individual EMPC controllers in (24), the dissipativity condition for the pricing controller in (28), and the dissipativity condition representing the microgrid-wide stability and performance in (39) simultaneously. The outcome of this step is the dissipativity conditions (more specifically, the supply rates , and for the i-th controller) that individual EMPC controllers need to satisfy.
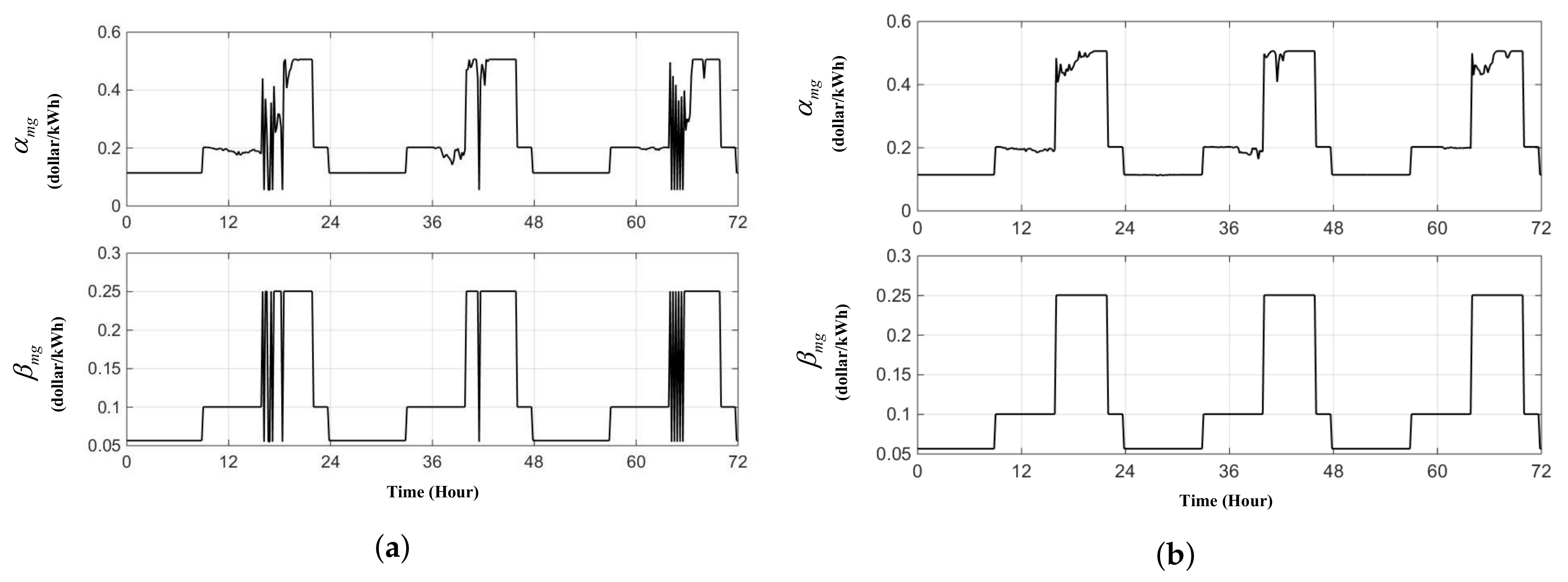
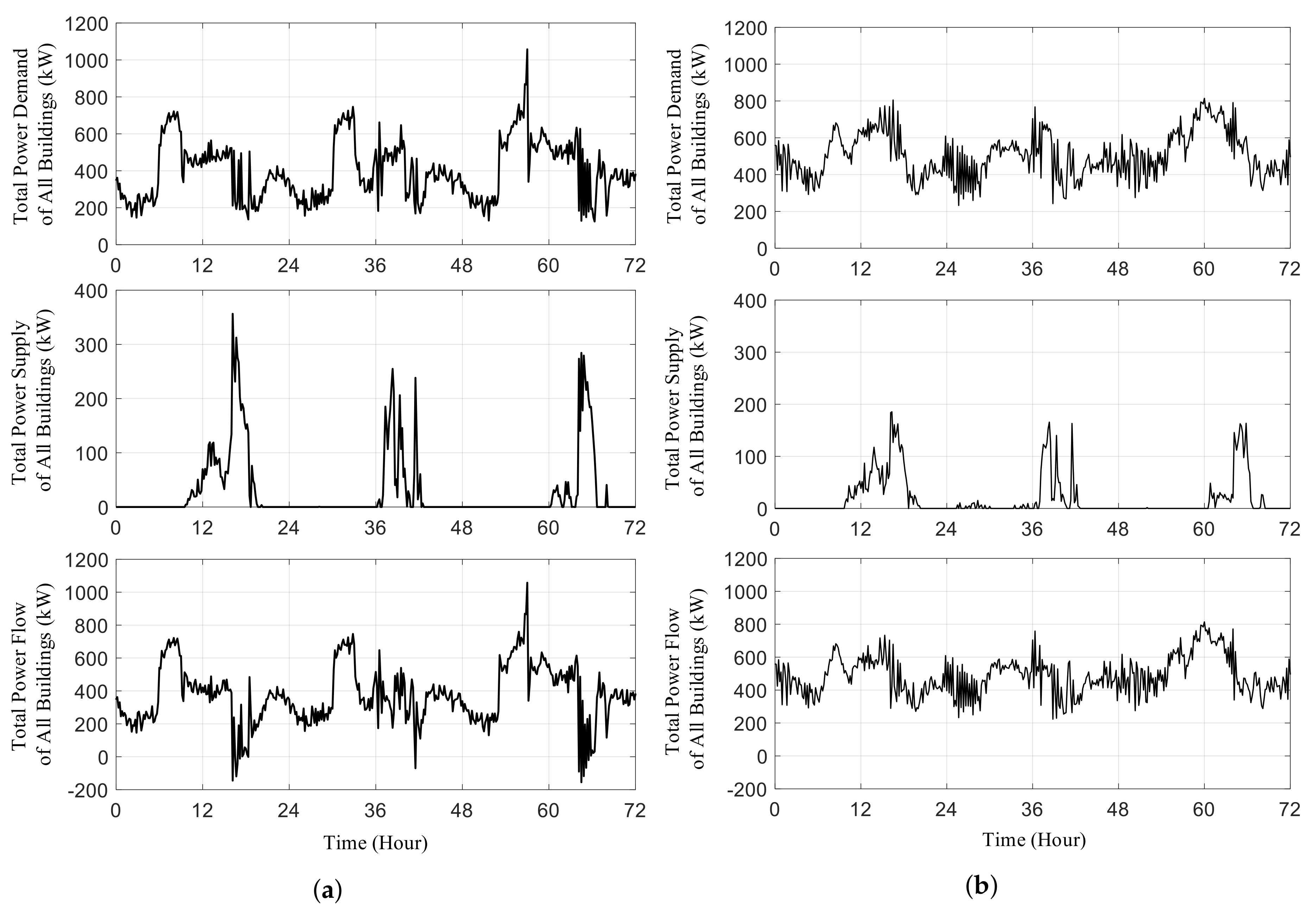
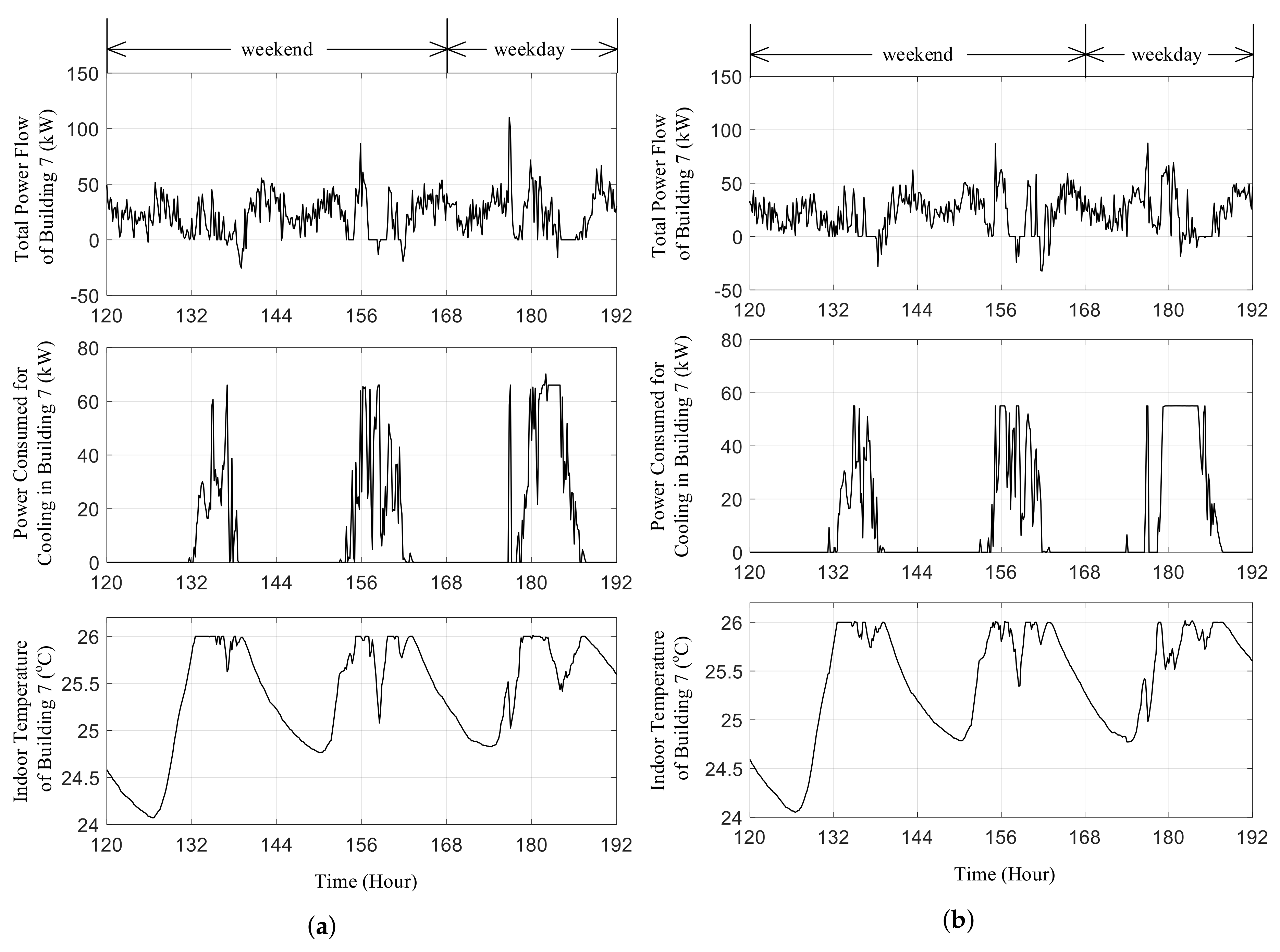
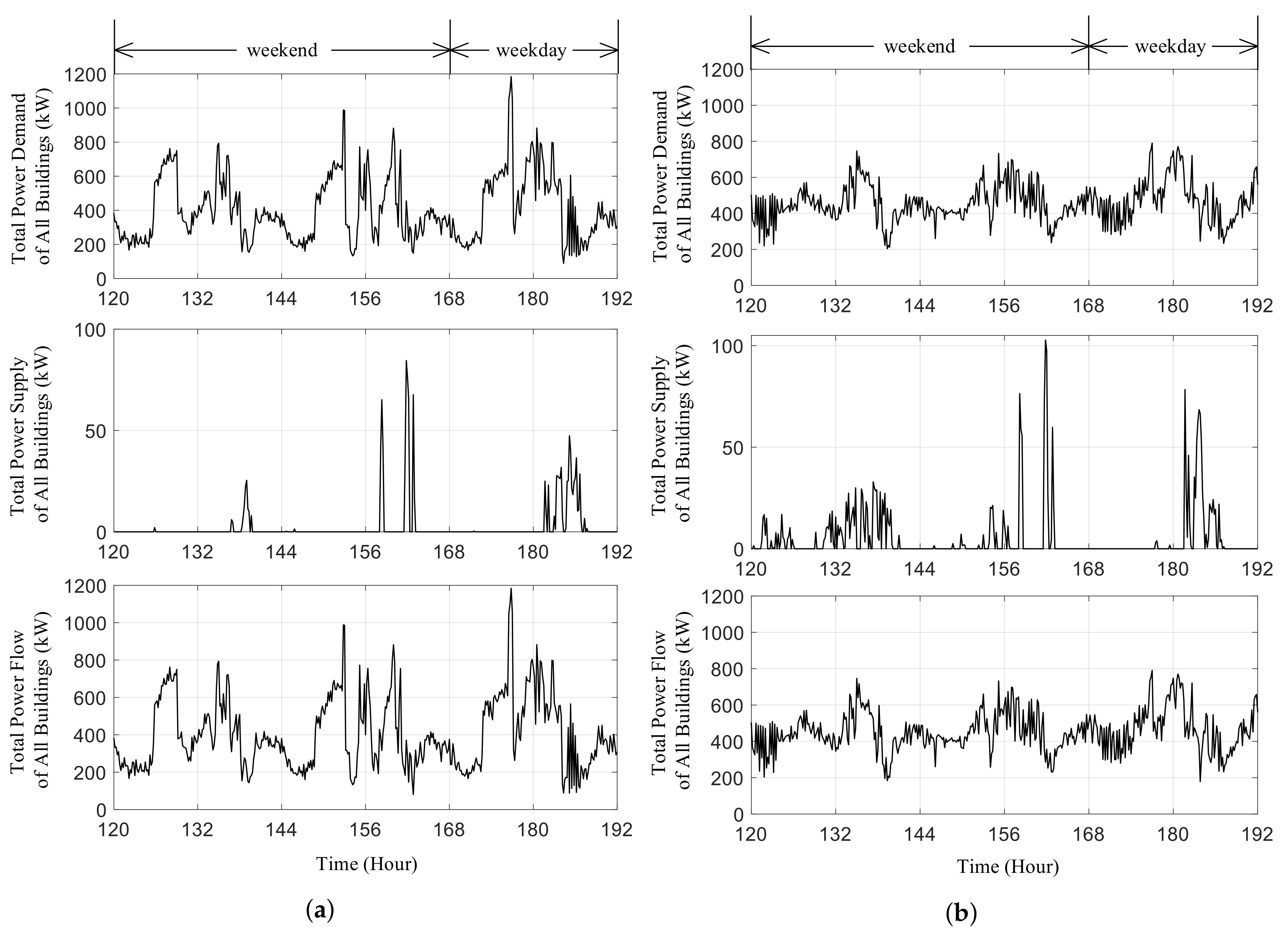
5. Simulation Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tonkoski, R.; Turcotte, D.; El-Fouly, T.H. Impact of high PV penetration on voltage profiles in residential neighborhoods. IEEE Trans. Sustain. Energy 2012, 3, 518–527. [Google Scholar] [CrossRef]
- Eftekharnejad, S.; Vittal, V.; Heydt, G.T.; Keel, B.; Loehr, J. Impact of increased penetration of photovoltaic generation on power systems. IEEE Trans. Power Syst. 2013, 28, 893–901. [Google Scholar] [CrossRef]
- Rahouma, A.; El-Azab, R.; Salib, A.; Amin, A.M. Frequency response of a large-scale grid-connected solar photovoltaic plant. In Proceedings of the SoutheastCon 2015, Fort Lauderdale, FL, USA, 9–12 April 2015; pp. 1–7. [Google Scholar]
- Wang, Y.; Zhang, P.; Li, W.; Xiao, W.; Abdollahi, A. Online overvoltage prevention control of photovoltaic generators in microgrids. IEEE Trans. Smart Grid 2012, 3, 2071–2078. [Google Scholar] [CrossRef]
- Jiang, B.; Muzhikyan, A.; Farid, A.M.; Youcef-Toumi, K. Demand side management in power grid enterprise control: A comparison of industrial & social welfare approaches. Appl. Energy 2017, 187, 833–846. [Google Scholar]
- Ramchurn, S.D.; Vytelingum, P.; Rogers, A.; Jennings, N. Agent-based control for decentralised demand side management in the smart grid. In Proceedings of the 10th International Conference on Autonomous Agents and Multiagent Systems, Taipei, Taiwan, 2–6 May 2011; Volume 1, pp. 5–12. [Google Scholar]
- Bellia, L.; Capozzoli, A.; Mazzei, P.; Minichiello, F. A comparison of HVAC systems for artwork conservation. Int. J. Refrig. 2007, 30, 1439–1451. [Google Scholar] [CrossRef]
- Lauro, F.; Moretti, F.; Capozzoli, A.; Panzieri, S. Model Predictive Control for Building Active Demand Response Systems. Energy Procedia 2015, 83, 494–503. [Google Scholar] [CrossRef]
- Xue, X.; Wang, S.; Yan, C.; Cui, B. A fast chiller power demand response control strategy for buildings connected to smart grid. Appl. Energy 2015, 137, 77–87. [Google Scholar] [CrossRef]
- Qi, W.; Liu, J.; Christofides, P.D. A distributed control framework for smart grid development: Energy/water system optimal operation and electric grid integration. J. Process Control 2011, 21, 1504–1516. [Google Scholar] [CrossRef]
- Qi, W.; Liu, J.; Chen, X.; Christofides, P.D. Supervisory predictive control of standalone wind/solar energy generation systems. IEEE Trans. Control Syst. Technol. 2011, 19, 199–207. [Google Scholar] [CrossRef]
- Qi, W.; Liu, J.; Christofides, P.D. Supervisory predictive control for long-term scheduling of an integrated wind/solar energy generation and water desalination system. IEEE Trans. Control Syst. Technol. 2012, 20, 504–512. [Google Scholar] [CrossRef]
- Qi, W.; Liu, J.; Christofides, P.D. Distributed supervisory predictive control of distributed wind and solar energy systems. IEEE Trans. Control Syst. Technol. 2013, 21, 504–512. [Google Scholar] [CrossRef]
- Maasoumy, M.; Sanandaji, B.M.; Sangiovanni-Vincentelli, A.; Poolla, K. Model predictive control of regulation services from commercial buildings to the smart grid. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 2226–2233. [Google Scholar]
- Zhang, W.; Lian, J.; Chang, C.Y.; Kalsi, K. Aggregated modeling and control of air-conditioning loads for demand response. IEEE Trans. Power Syst. 2013, 28, 4655–4664. [Google Scholar] [CrossRef]
- Bashash, S.; Fathy, H.K. Modeling and control of aggregate air-conditioning loads for robust renewable power management. IEEE Trans. Control Syst. Technol. 2013, 21, 1318–1327. [Google Scholar] [CrossRef]
- Liu, M.; Shi, Y. Model predictive control of aggregated heterogeneous second-order thermostatically controlled loads for ancillary services. IEEE Trans. Power Syst. 2016, 31, 1963–1971. [Google Scholar] [CrossRef]
- Touretzky, C.R.; Baldea, M. Integrating scheduling and control for economic MPC of buildings with energy storage. J. Process Control 2014. [Google Scholar] [CrossRef]
- Soroush, M.; Chmielewski, D.J. Process systems opportunities in power generation, storage and distribution. Comput. Chem. Eng. 2013, 51, 86–95. [Google Scholar]
- Chen, X.; Heidarinejad, M.; Liu, J.; Christofides, P.D. Distributed economic MPC: Application to a nonlinear chemical process network. J. Process Control 2012, 22, 689–699. [Google Scholar]
- Vytelingum, P.; Voice, T.D.; Ramchurn, S.D.; Rogers, A.; Jennings, N.R. Agent-based micro-storage management for the smart grid. In Proceedings of the 9th International Conference on Autonomous Agents and Multiagent Systems, Toronto, ON, Canada, 10–14 May 2010; pp. 39–46. [Google Scholar]
- Maity, I.; Rao, S. Simulation and pricing mechanism analysis of a solar-powered electrical microgrid. IEEE Syst. J. 2010, 4, 275–284. [Google Scholar]
- Stephens, E.R.; Smith, D.B.; Mahanti, A. Game theoretic model predictive control for distributed energy demand-side management. IEEE Trans. Smart Grid 2015, 6, 1394–1402. [Google Scholar]
- Willems, J.C. Dissipative dynamical systems part I: General theory. Arch. Ration. Mech. Anal. 1972, 45, 321–351. [Google Scholar]
- Weiland, S.; Willems, J.C. Dissipative dynamical systems in a behavioral context. Math. Models Methods Appl. Sci. 1991, 1, 1–25. [Google Scholar]
- Hill, D.; Moylan, P. Stability Results for Nonlinear Feedback Systems. Automatica 1977, 13, 377–382. [Google Scholar]
- Moylan, P.; Hill, D. Stability criteria for large-scale systems. IEEE Trans. Autom. Control 1978, 23, 143–149. [Google Scholar]
- Xu, S.; Bao, J. Distributed control of plantwide chemical processes. J. Process Control 2009, 19, 1671–1687. [Google Scholar]
- Xu, S.; Bao, J. Control of chemical processes via output feedback controller networks. Ind. Eng. Chem. Res. 2010, 49, 7421–7445. [Google Scholar]
- Tippett, M.J.; Bao, J. Dissipativity based distributed control synthesis. J. Process Control 2013, 23, 755–766. [Google Scholar]
- Tippett, M.J.; Bao, J. Control of plant-wide systems using dynamic supply rates. Automatica 2014, 50, 44–52. [Google Scholar]
- Willems, J.; Trentelman, H. On quadratic differential forms. SIAM J. Control Optim. 1998, 36, 1703–1749. [Google Scholar]
- Tippett, M.J.; Bao, J. Distributed model predictive control based on dissipativity. AIChE J. 2013, 59, 787–804. [Google Scholar]
- Yu, Z.; Jia, L.; Murphy-Hoye, M.C.; Pratt, A.; Tong, L. Modeling and stochastic control for home energy management. IEEE Trans. Smart Grid 2013, 4, 2244–2255. [Google Scholar]
- Hazyuk, I.; Ghiaus, C.; Penhouet, D. Optimal temperature control of intermittently heated buildings using Model Predictive Control: Part I–Building modeling. Build. Environ. 2012, 51, 379–387. [Google Scholar]
- Ghosh, S.; Reece, S.; Rogers, A.; Roberts, S.; Malibari, A.; Jennings, N.R. Modeling the Thermal Dynamics of Buildings: A Latent-Force-Model-Based Approach. ACM Trans. Intell. Syst. Technol. 2015, 6, 7. [Google Scholar]
- Ma, Y.; Anderson, G.; Borrelli, F. A distributed predictive control approach to building temperature regulation. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; pp. 2089–2094. [Google Scholar]
- Thavlov, A.; Bindner, H.W. Thermal models for intelligent heating of buildings. In Proceedings of the International Conference on Applied Energy, Suzhou, China, 5–8 July 2012. [Google Scholar]
- Haghighi, M.M. Controlling Energy-Efficient Buildings in the Context of Smart Grid: A Cyber Physical System Approach. Ph.D. Thesis, EECS Department, University of California, Berkeley, CA, USA, 2013. [Google Scholar]
- Nasution, H.; Hassan, M.N.W. Potential electricity savings by variable speed control of compressor for air-conditioning systems. Clean Technol. Environ. Policy 2006, 8, 105–111. [Google Scholar]
- Hunt, W.; Amarnath, A. Cooling Efficiency Comparison between Residential Variable Capacity and Single Speed Heat Pump. ASHRAE Trans. 2013, 119, Q1. [Google Scholar]
- Funami, K.; Nishi, H. Evaluation of power consumption and comfort using inverter control of air-conditioning. In Proceedings of the 37th Annual Conference on IEEE Industrial Electronics Society, Melbourne, VIC, Australia, 7–10 November 2011; pp. 3236–3241. [Google Scholar]
- Energy of the Environment Air Conditioners. 2016. Available online: http://www.energyrating.gov.au/products/space-heating-and-cooling/air-conditioners(Australian Government Equipment Energy Efficiency Program); (accessed on 24 April 2016).
- Lokanadham, M.; Bhaskar, K.V. Incremental conductance based maximum power point tracking (MPPT) for photovoltaic system. Int. J. Eng. Res. Appl. 2012, 2, 1420–1424. [Google Scholar]
- Ma, J.; Qin, S.J.; Salsbury, T. Experimental study of economic model predictive control in building energy systems. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 3753–3758. [Google Scholar]
- Putta, V.; Zhu, G.; Kim, D.; Hu, J.; Braun, J. Comparative evaluation of model predictive control strategies for a building HVAC system. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 3455–3460. [Google Scholar]
- Ma, J.; Qin, S.J.; Salsbury, T. Application of economic MPC to the energy and demand minimization of a commercial building. J. Process Control 2014, 24, 1282–1291. [Google Scholar]
- Brundage, M.P.; Chang, Q.; Li, Y.; Xiao, G.; Arinez, J. Energy efficiency management of an integrated serial production line and HVAC system. IEEE Trans. Autom. Sci. Eng. 2014, 11, 789–797. [Google Scholar]
- Braun, P.; Grüne, L.; Kellett, C.M.; Weller, S.R.; Worthmann, K. A real-time pricing scheme for residential energy systems using a market maker. In Proceedings of the 2015 5th Australian Control Conference (AUCC), Gold Coast, Australia, 5–6 November 2015; pp. 259–262. [Google Scholar]
- Ito, K. Nonlinear Pricing in Energy and Environmental Markets. Ph.D. Thesis, Agricultural & Resource Economics, University of California, Berkeley, CA, USA, 2011. [Google Scholar]
- Okawa, Y.; Namerikawa, T. Distributed dynamic pricing based on demand-supply balance and voltage phase difference in power grid. Control Theory Technol. 2015, 13, 90–100. [Google Scholar]
- Yang, L.; Dong, C.; Wan, C.J.; Ng, C.T. Electricity time-of-use tariff with consumer behavior consideration. Int. J. Prod. Econ. 2013, 146, 402–410. [Google Scholar]
- Rowlands, I.H.; Furst, I.M. The cost impacts of a mandatory move to time-of-use pricing on residential customers: An Ontario (Canada) case-study. Energy Effic. 2011, 4, 571–585. [Google Scholar]
- Matters, E. Feed-in Tariff for Grid-Connected Solar Power Systems. 2011. Available online: http://www.energymatters.com.au/rebates-incentives/feedintariff (accessed on 15 September 2015).
- Matters, E. Battery Storage And Solar Feed in Tariffs—State Of Play. 2015. Available online: http://www.energymatters.com.au/renewable-news/solar-fit-batteries-em5074/ (accessed on 15 September 2015).
- Muzmar, M.; Abdullah, M.; Hassan, M.; Hussin, F. Time of Use pricing for residential customers case of Malaysia. In Proceedings of the 2015 IEEE Student Conference on Research and Development (SCOReD), Kuala Lumpur, Malaysia, 13–14 December 2015; pp. 589–593. [Google Scholar]
- Zhang, X.; Bao, J.; Wang, R.; Zheng, C.; Skyllas-Kazacos, M. Dissipativity based distributed economic model predictive control for residential microgrids with renewable energy generation and battery energy storage. Renew. Energy 2017, 100, 18–34. [Google Scholar]
- Kojima, C.; Takaba, K. A generalized Lyapunov stability theorem for discrete-time systems based on quadratic difference forms. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 15 December 2005; pp. 2911–2916. [Google Scholar]
- Parrilo, P.A. Structured Semidefinite Programs and Semialgebraic Geometry Methods in Robustness and Optimization. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2000. [Google Scholar]
- Löfberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. In Proceedings of the CACSD Conference, Taipei, Taiwan, 2–4 September 2004; pp. 284–289. [Google Scholar]
- Sturm, J.F. Using SeDuMi 1.02, a MATLAB toolbox for optimization over symmetric cones. Optim. Methods Softw. 1999, 11, 625–653. [Google Scholar] [CrossRef]
- Fan, S.; Hyndman, R.J. Short-term load forecasting based on a semi-parametric additive model. IEEE Trans. Power Syst. 2012, 27, 134–141. [Google Scholar]
- Station, M.U.W. 2017. Available online: http://wwwmet.murdoch.edu.au/downloads (accessed on 24 April 2016).

| Variable | Definition | Unit |
|---|---|---|
| Temperature of building indoor air | C | |
| Temperature of building interior walls | C | |
| Temperature of building envelop | C | |
| Temperature of ambient environment | C | |
| Solar radiation | kW/m2 | |
| Heating power from air-conditioning system (positive) | kW | |
| Cooling power from air-conditioning system (negative) | kW | |
| Power consumption of indoor appliances (excluding AC system) | kW | |
| Fraction of heat generated from the operation of indoor appliances | ||
| Thermal resistance between indoor air and ambient environment | C/kW | |
| Thermal resistance between interior walls and indoor air | C/kW | |
| Thermal resistance between indoor air and building envelop | C/kW | |
| Thermal resistance between building envelop and ambient environment | C/kW | |
| Heat capacity of indoor air | kW/C | |
| Heat capacity of interior walls | kW/C | |
| Heat capacity of building envelop | kW/C | |
| A | Effective area of building envelop | m |
| Coefficient of solar radiation transferred through building envelop to heat up indoor air | ||
| Coefficient of solar radiation transferred through building envelop to heat up interior walls |
| Buildings | A | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Type 1 | 3.26 | 0.21 | 0.132 | 0.0389 | 76.02 | 874.94 | 2767.1 | 0.02 | 0.0075 | 10500 | 0.1 |
| Type 2 | 4.22 | 0.22 | 0.142 | 0.133 | 37.04 | 337 | 1465.28 | 0.02 | 0.0075 | 3600 | 0.1 |
| Type 3 | 3.95 | 0.23 | 0.146 | 0.12 | 36.72 | 300 | 1302.5 | 0.02 | 0.0075 | 3200 | 0.1 |
| Type 4 | 3.54 | 0.2 | 0.144 | 0.142 | 32.85 | 312 | 1310 | 0.02 | 0.0075 | 3200 | 0.1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Wang, R.; Bao, J. A Novel Distributed Economic Model Predictive Control Approach for Building Air-Conditioning Systems in Microgrids. Mathematics 2018, 6, 60. https://doi.org/10.3390/math6040060
Zhang X, Wang R, Bao J. A Novel Distributed Economic Model Predictive Control Approach for Building Air-Conditioning Systems in Microgrids. Mathematics. 2018; 6(4):60. https://doi.org/10.3390/math6040060
Chicago/Turabian StyleZhang, Xinan, Ruigang Wang, and Jie Bao. 2018. "A Novel Distributed Economic Model Predictive Control Approach for Building Air-Conditioning Systems in Microgrids" Mathematics 6, no. 4: 60. https://doi.org/10.3390/math6040060
APA StyleZhang, X., Wang, R., & Bao, J. (2018). A Novel Distributed Economic Model Predictive Control Approach for Building Air-Conditioning Systems in Microgrids. Mathematics, 6(4), 60. https://doi.org/10.3390/math6040060





