Prey-Predator Model with a Nonlocal Bistable Dynamics of Prey
Abstract
1. Introduction
2. Stability Analysis
2.1. Local Model
2.2. Nonlocal Model
2.3. Spatial Hopf Bifurcation
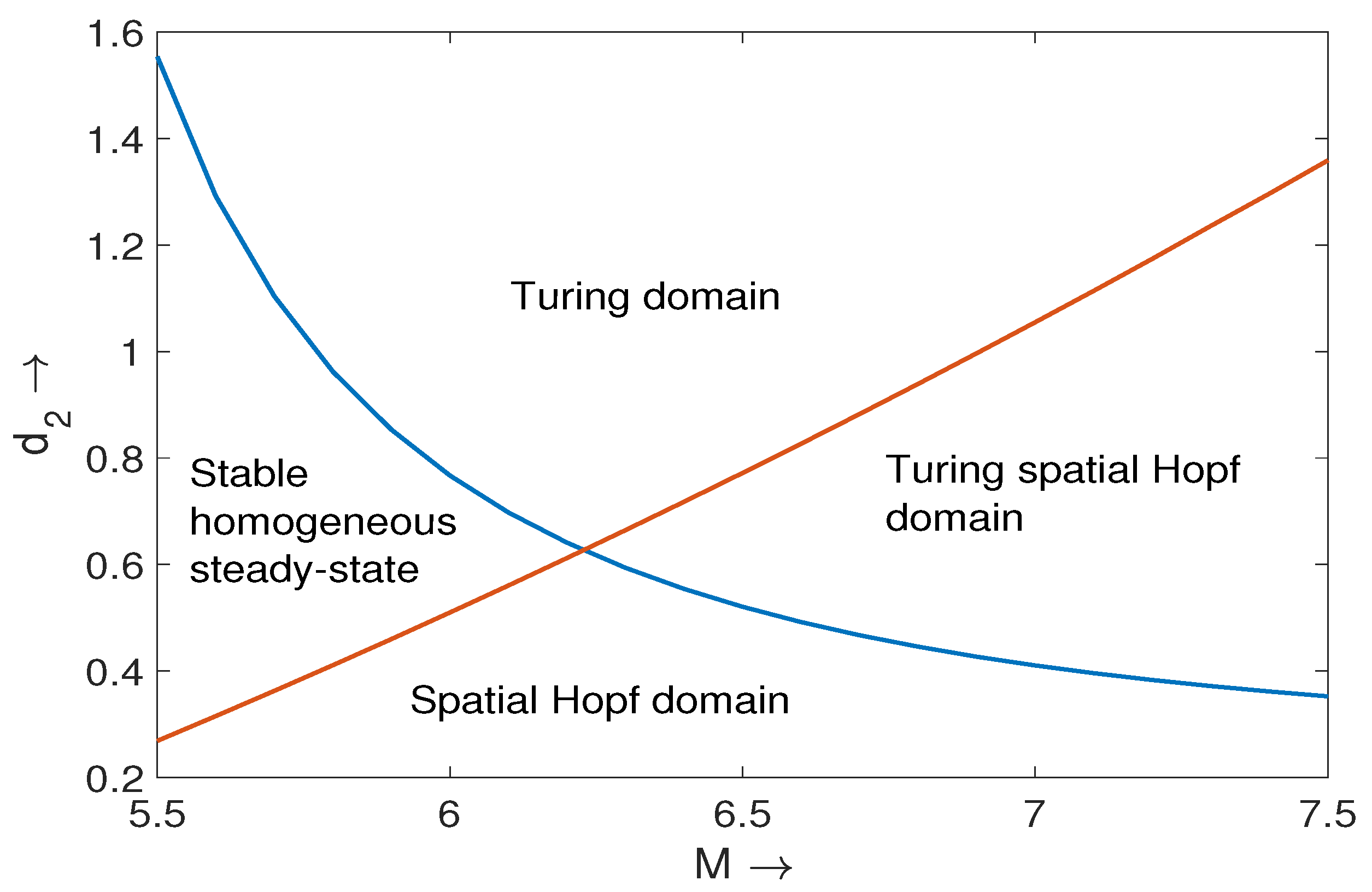
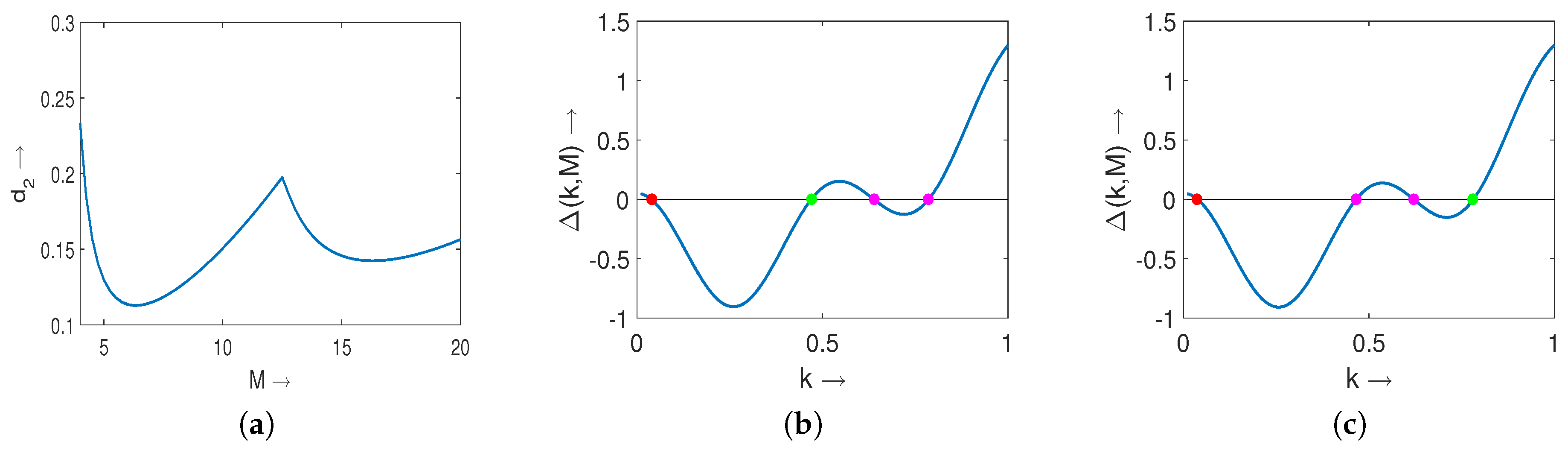
2.4. Turing Pattern for Nonlocal Prey-Predator Model
3. Spatiotemporal Patterns
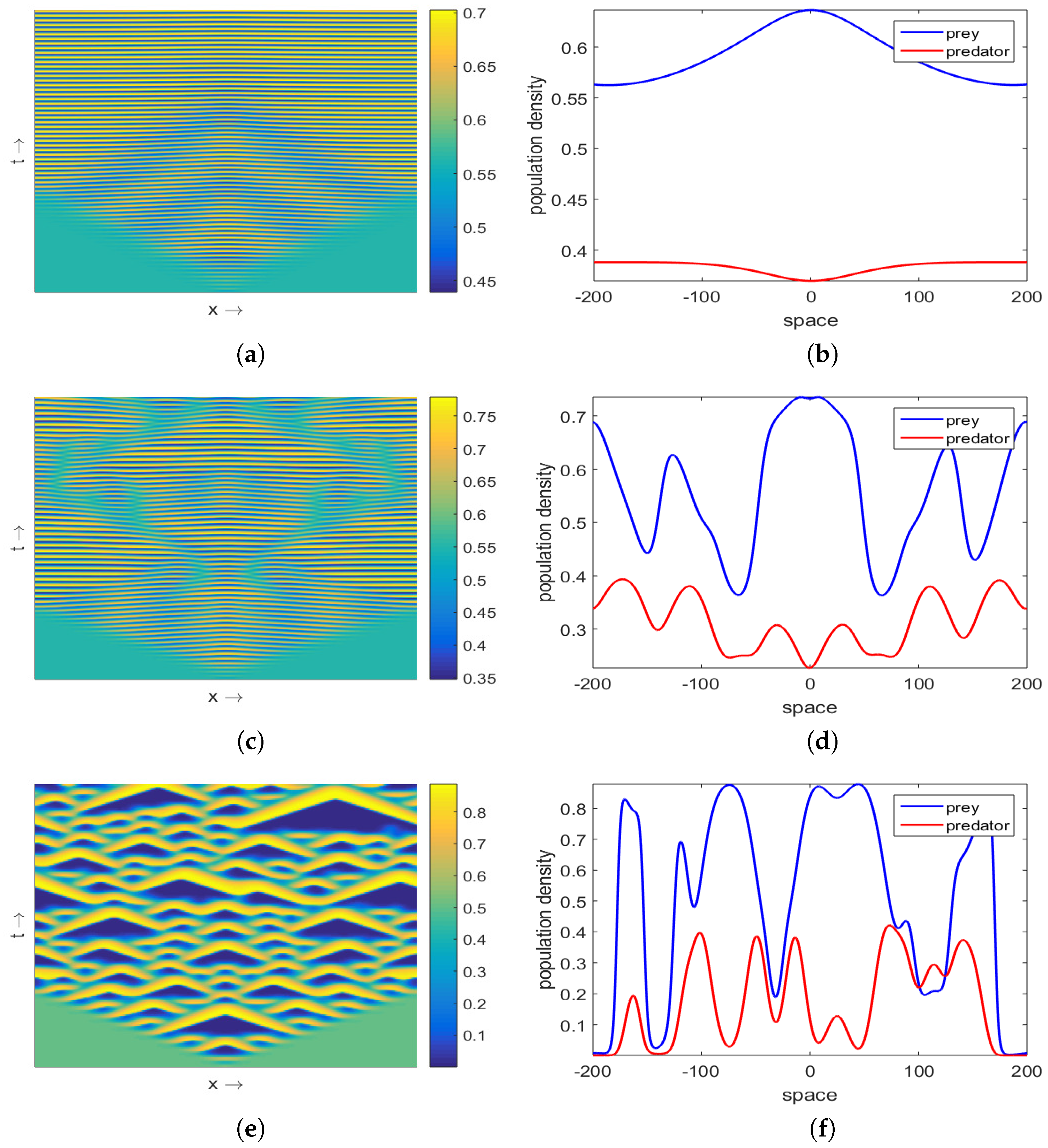
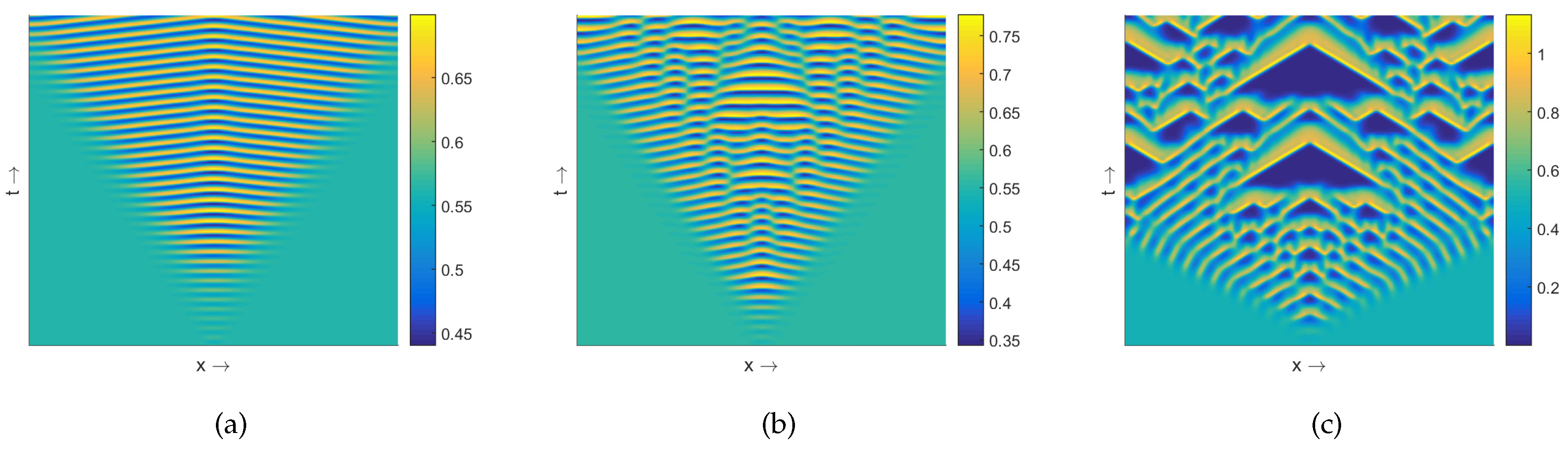
3.1. Patterns Produced by the Model (8)–(9)
3.2. Effect of Nonlocal Consumption
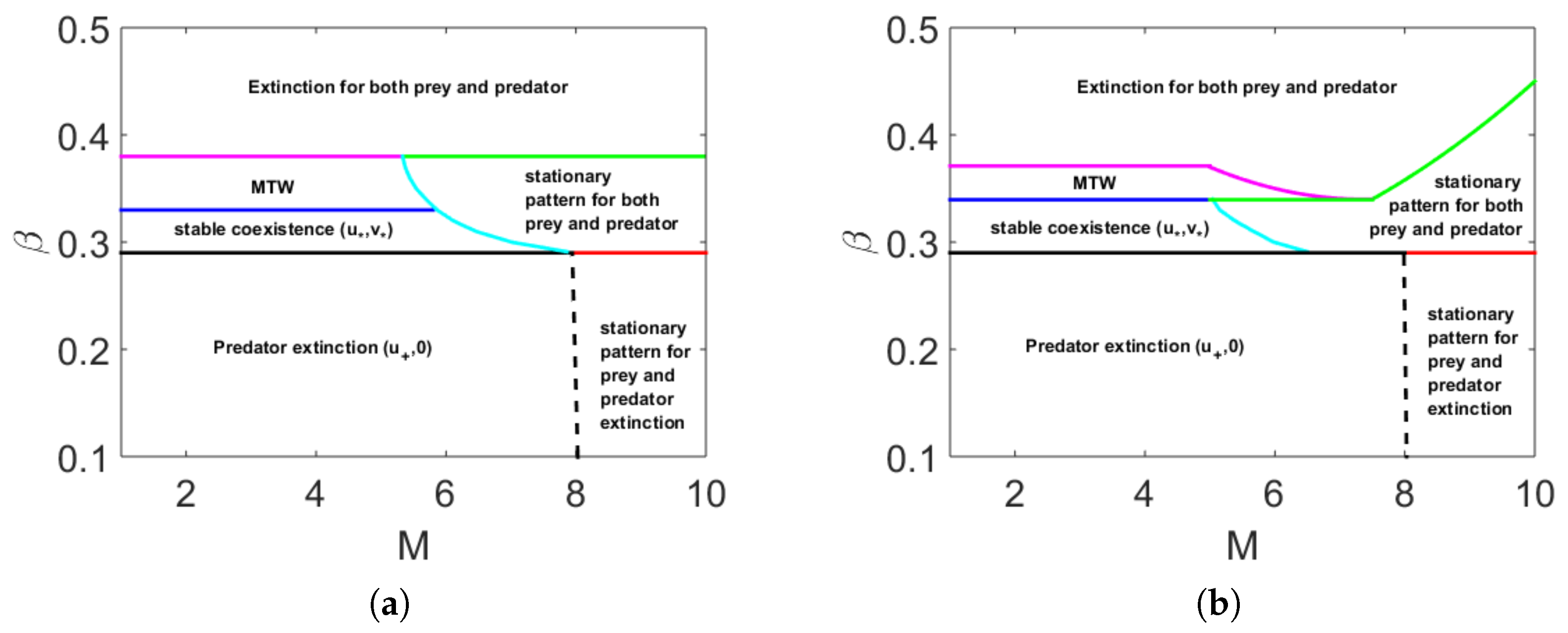
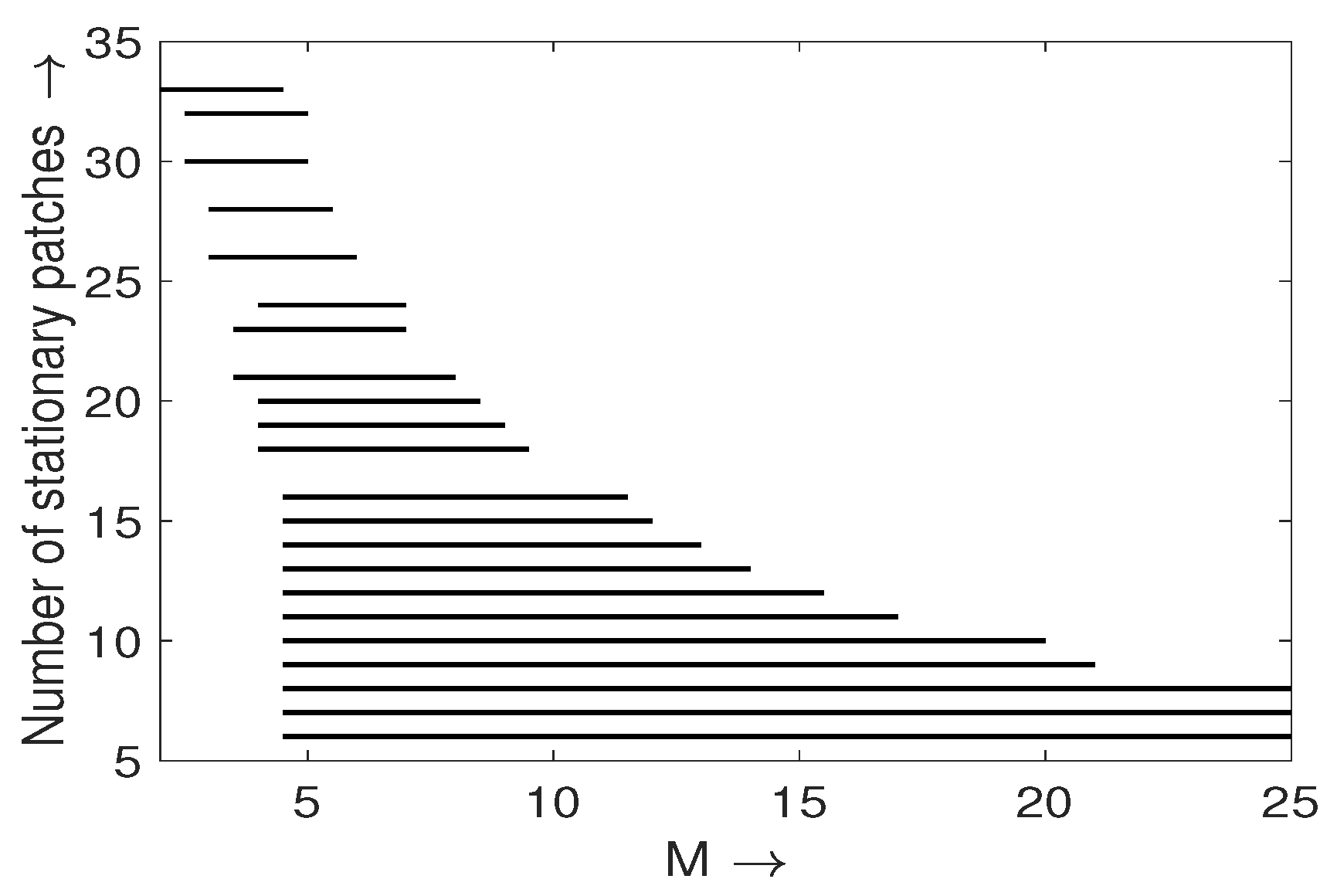
Multiplicity of Stationary Solutions
4. Discussion
Author Contributions
Conflicts of Interest
References
- Dunbar, S.R. Travelling wave solutions of diffusive Lotka-Volterra equations. J. Math. Biol. 1983, 17, 11–32. [Google Scholar] [CrossRef]
- Dunbar, S.R. Travelling waves in diffusive predator-prey equations: Periodic orbits and point-to-periodic heteroclinic orbits. SIAM J. Appl. Math. 1986, 46, 1057–1078. [Google Scholar] [CrossRef]
- Sherratt, J.A. Periodic travelling waves in cyclic predator-prey systems. Ecol. Lett. 2001, 4, 30–37. [Google Scholar] [CrossRef]
- Sherratt, J.A.; Smith, M. Periodic travelling waves in cyclic populations: Field studies and reaction diffusion models. J. R. Soc. Interface 2008, 5, 483–505. [Google Scholar] [CrossRef] [PubMed]
- Volpert, V.; Petrovskii, S.V. Reaction-diffusion waves in biology. Phys. Life Rev. 2009, 6, 267–310. [Google Scholar] [CrossRef] [PubMed]
- Petrovskii, S.V.; Malchow, H. A minimal model of pattern formation in a prey-predator system. Math. Comp. Model. 1999, 29, 49–63. [Google Scholar] [CrossRef]
- Petrovskii, S.V.; Malchow, H. Wave of chaos: New mechanism of pattern formation in spatio-temporal population dynamics. Theor. Pop. Biol. 2001, 59, 157–174. [Google Scholar] [CrossRef] [PubMed]
- Gause, G.F. The Struggle for Existence; Williams and Wilkins: Baltimore, MD, USA, 1935. [Google Scholar]
- Luckinbill, L.L. Coexistence in laboratory populations of Paramecium aurelia and its predator Didinium nasutum. Ecology 1973, 54, 1320–1327. [Google Scholar] [CrossRef]
- Luckinbill, L.L. The effects of space and enrichment on a predator-prey system. Ecology 1974, 55, 1142–1147. [Google Scholar] [CrossRef]
- Fasani, S.; Rinaldi, S. Factors promoting or inhibiting Turing instability in spatially extended prey-predator systems. Ecol. Model. 2011, 222, 3449–3452. [Google Scholar] [CrossRef]
- Huisman, J.; Weissing, F.J. Biodiversity of plankton by oscillations and chaos. Nature 1999, 402, 407–410. [Google Scholar] [CrossRef]
- Levin, S.A.; Segel, L.A. Hypothesis for origin of planktonic patchiness. Nature 1976, 259, 659. [Google Scholar] [CrossRef]
- Segel, L.A.; Jackson, J.L. Dissipative structure: An explanation and an ecological example. J. Theor. Biol. 1972, 37, 545–559. [Google Scholar] [CrossRef]
- Klausmeier, C.A. Regular and irregular patterns in semiarid vegetation. Science 1999, 284, 1826–1828. [Google Scholar] [CrossRef] [PubMed]
- Medvinsky, A.; Petrovskii, S.; Tikhonova, I.; Malchow, H.; Li, B.L. Spatiotemporal complexity of plankton and fish dynamics. SIAM Rev. 2002, 44, 311–370. [Google Scholar] [CrossRef]
- Shigesada, N.; Kawasaki, K. Biological Invasions: Theory and Practice; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Baurmann, M.; Gross, T.; Feudel, U. Instabilities in spatially extended predator-prey systems: Spatio-temporal patterns in the neighborhood of Turing-Hopf bifurcations. J. Theor. Biol. 2007, 245, 220–229. [Google Scholar] [CrossRef] [PubMed]
- Cantrell, R.S.; Cosner, C. Spatial Ecology via Reaction-Diffusion Equations; Wiley: London, UK, 2003. [Google Scholar]
- Murray, J.D. Mathematical Biology II; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Okubo, A.; Levin, S. Diffusion and Ecological Problems: Modern Perspectives; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Banerjee, M.; Banerjee, S. Turing instabilities and spatio-temporal chaos in ratio-dependent Holling-Tanner model. Math. Biosci. 2012, 236, 64–76. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, M.; Petrovskii, S. Self-organized spatial patterns and chaos in a ratio-dependent predator-prey system. Theor. Ecol. 2011, 4, 37–53. [Google Scholar] [CrossRef]
- Gourley, S.A.; Britton, N.F. A predator-prey reaction-diffusion system with nonlocal effects. J. Math. Biol. 1996, 34, 297–333. [Google Scholar] [CrossRef]
- Gourley, S.A.; Ruan, S. Convergence and travelling fronts in functional differential equations with nonlocal terms: A competition model. SIAM J. Appl. Math. 2003, 35, 806–822. [Google Scholar] [CrossRef]
- Sherratt, J.A.; Eagan, B.T.; Lewis, M.A. Oscillations and chaos behind predator-prey invasion: Mathematical artifact or ecological reality? Phils. Trans. R. Soc. Lond. B 1997, 352, 21–38. [Google Scholar] [CrossRef]
- Bessonov, N.; Reinberg, N.; Volpert, V. Mathematics of Darwin’s diagram. Math. Model. Nat. Phenom. 2014, 9, 5–25. [Google Scholar] [CrossRef]
- Genieys, S.; Bessonov, N.; Volpert, V. Mathematical model of evolutionary branching. Math. Comp. Model. 2009, 49, 2109–2115. [Google Scholar] [CrossRef]
- Genieys, S.; Volpert, V.; Auger, P. Pattern and waves for a model in population dynamics with nonlocal consumption of resources. Math. Model. Nat. Phenom. 2006, 1, 63–80. [Google Scholar] [CrossRef]
- Genieys, S.; Volpert, V.; Auger, P. Adaptive dynamics: Modelling Darwin’s divergence principle. Comp. Ren. Biol. 2006, 329, 876–879. [Google Scholar] [CrossRef] [PubMed]
- Volpert, V. Branching and aggregation in self-reproducing systems. ESAIM Proc. Surv. 2014, 47, 116–129. [Google Scholar] [CrossRef]
- Apreutesei, N.; Bessonov, N.; Volpert, V.; Vougalter, V. Spatial structures and generalized travelling waves for an integro-differential equation. DCDS B 2010, 13, 537–557. [Google Scholar] [CrossRef]
- Aydogmus, O. Patterns and transitions to instability in an intraspecific competition model with nonlocal diffusion and interaction. Math. Model. Nat. Phenom. 2015, 10, 17–19. [Google Scholar] [CrossRef]
- Volpert, V. Pulses and waves for a bistable nonlocal reaction-diffusion equation. Appl. Math. Lett. 2015, 44, 21–25. [Google Scholar] [CrossRef]
- Volpert, V. Elliptic Partial Differential Equations; Reaction-diffusion equations; Birkhäuser: Basel, Switzerland, 2014; Volume 2. [Google Scholar]
- Apreutesei, N.; Ducrot, A.; Volpert, V. Competition of species with intra-specific competition. Math. Model. Nat. Phenom. 2008, 3, 1–27. [Google Scholar] [CrossRef]
- Apreutesei, N.; Ducrot, A.; Volpert, V. Travelling waves for integro-differential equations in population dynamics. DCDS B 2009, 11, 541–561. [Google Scholar] [CrossRef]
- Bayliss, A.; Volpert, V.A. Patterns for competing populations with species specific nonlocal coupling. Math. Model. Nat. Phenom. 2015, 10, 30–47. [Google Scholar] [CrossRef]
- Banerjee, M.; Volpert, V. Prey-predator model with a nonlocal consumption of prey. Chaos 2016, 26, 083120. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, M.; Volpert, V. Spatio-temporal pattern formation in Rosenzweig-McArthur model: Effect of nonlocal interactions. Ecol. Complex. 2016, 30, 2–10. [Google Scholar] [CrossRef]
- Amarasekare, P. Interactions between local dynamics and dispersal: Insights from single species models. Theor. Popul. Biol. 1998, 53, 44–59. [Google Scholar] [CrossRef] [PubMed]
- Amarasekare, P. Allee effects in metapopulation dynamics. Am. Nat. 1998, 152, 298–302. [Google Scholar] [CrossRef] [PubMed]
- Courchamp, F.; Berec, L.; Gascoigne, J. Allee Effects in Ecology and Conservation; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Courchamp, F.; Clutton-Brock, T.; Grenfell, B. Inverse density dependence and the Allee effect. Trends. Ecol. Evol. 1999, 14, 405–410. [Google Scholar] [CrossRef]
- Lewis, M.A.; Kareiva, P. Allee dynamics and the spread of invading organisms. Theor. Popul. Biol. 1993, 43, 141–158. [Google Scholar] [CrossRef]
- Jankovic, M.; Petrovskii, S. Are time delays always destabilizing? Revisiting the role of time delays and the Allee effect. Theor. Ecol. 2014, 7, 335–349. [Google Scholar] [CrossRef]
- Petrovskii, S.; Blackshaw, R.; Li, B.L. Consequences of the Allee effect and intraspecific competition on population persistence under adverse environmental conditions. Bull. Math. Biol. 2008, 70, 412–437. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, M.; Vougalter, V.; Volpert, V. Doubly nonlocal reaction diffusion equations and the emergence of species. Appl. Math. Model. 2017, 42, 591–599. [Google Scholar] [CrossRef]
- Segal, B.L.; Volpert, V.A.; Bayliss, A. Pattern formation in a model of competing populations with nonlocal interactions. Phys. D 2013, 253, 12–23. [Google Scholar] [CrossRef]
- Petrovskii, S.V.; Li, B.L.; Malchow, H. Quantification of the spatial aspect of chaotic dynamics in biological and chemical systems. Bull. Math. Biol. 2003, 65, 425–446. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Banerjee, M.; Mukherjee, N.; Volpert, V. Prey-Predator Model with a Nonlocal Bistable Dynamics of Prey. Mathematics 2018, 6, 41. https://doi.org/10.3390/math6030041
Banerjee M, Mukherjee N, Volpert V. Prey-Predator Model with a Nonlocal Bistable Dynamics of Prey. Mathematics. 2018; 6(3):41. https://doi.org/10.3390/math6030041
Chicago/Turabian StyleBanerjee, Malay, Nayana Mukherjee, and Vitaly Volpert. 2018. "Prey-Predator Model with a Nonlocal Bistable Dynamics of Prey" Mathematics 6, no. 3: 41. https://doi.org/10.3390/math6030041
APA StyleBanerjee, M., Mukherjee, N., & Volpert, V. (2018). Prey-Predator Model with a Nonlocal Bistable Dynamics of Prey. Mathematics, 6(3), 41. https://doi.org/10.3390/math6030041






