Finite Automata Capturing Winning Sequences for All Possible Variants of the PQ Penny Flip Game
Abstract
:1. Introduction
2. Related Work
3. Preliminary Definitions
3.1. The Game
- leave the coin as is, which we denote by I, after the “identity” operator; or
- flip the coin, which we denote by F, after the “flip” operator.
- The coin is a two-dimensional quantum system. The state of the coin is represented by a ray in the two-dimensional complex Hilbert space (see [34] for details). A ray is an equivalence class of vectors whose elements differ by a multiplicative complex scalar. In the Dirac terminology and notation, which we follow in this work, vectors are called kets and are denoted by . Hence, in this case, a ray contains kets of the form , for some , and ranging over . The standard convection dictates that a normalized ket , i.e., a of unit length, is chosen as a ray representative. This representation of coin states by normalized kets greatly simplifies computations. Let us emphasize that the kets and , where , represent the same state because .
- The arbitrary state of the quantum coin can be expressed asThe fact that is normalized implies that the complex probability amplitudes a and b satisfy the relation . The kets and describe the situation where the coin is heads up or tails up, respectively. These two kets are orthogonal unit vector in the two-dimensional complex Hilbert space , and, as such, constitute an orthonormal basis of . It is customary to denote by the standard orthonormal basis of . Therefore, in this work, we shall interchangeably write instead of and instead of to emphasize that the coin is heads up or tails up, respectively. To avoid any possible source of confusion, we summarize our conventions below.
- The possible actions of the two players are represented by unitary operators. Specifically, since is two-dimensional, the operators can be represented by the following matrices:
- The state of the quantum coin is measured with respect to the orthonormal basis . After the measurement, the state of the coin will either be with probability , or with probability . In our context, this means that after the measurement the coin will turn out either heads up or tails up and this will be known to both players.
3.2. Automata
- 1.
- Q is a finite set of states,
- 2.
- Σ is a finite set of input symbols called the alphabet.
- 3.
- is the transition function.
- 4.
- is the initial state.
- 5.
- is the set of accepting states.
- 1.
- Q is a finite set of states.
- 2.
- Σ is the alphabet.
- 3.
- is the transition function.
- 4.
- is the initial state.
- 5.
- is the set of accepting states.
4. Games and Words
- The initial state of the coin is . In view of hypothesis H4, is either or .
- If , then is the 0-round trivial game (neither Picard nor Q act on the coin, which remains at its initial state).
- If , where , , then is a game that lasts n rounds and determines which of the two players moves during round i. Specifically, if then it is Picard’s turn to act on the coin, whereas if then it is Q’s turn to act on the coin.
- 1.
- , and
- 2.
- If , , , then , where if or and if .
- 1.
- , ;
- 2.
- , ; and
- 3.
- , .
- 1.
- , , and
- 2.
- For every , every , every , and every :, .
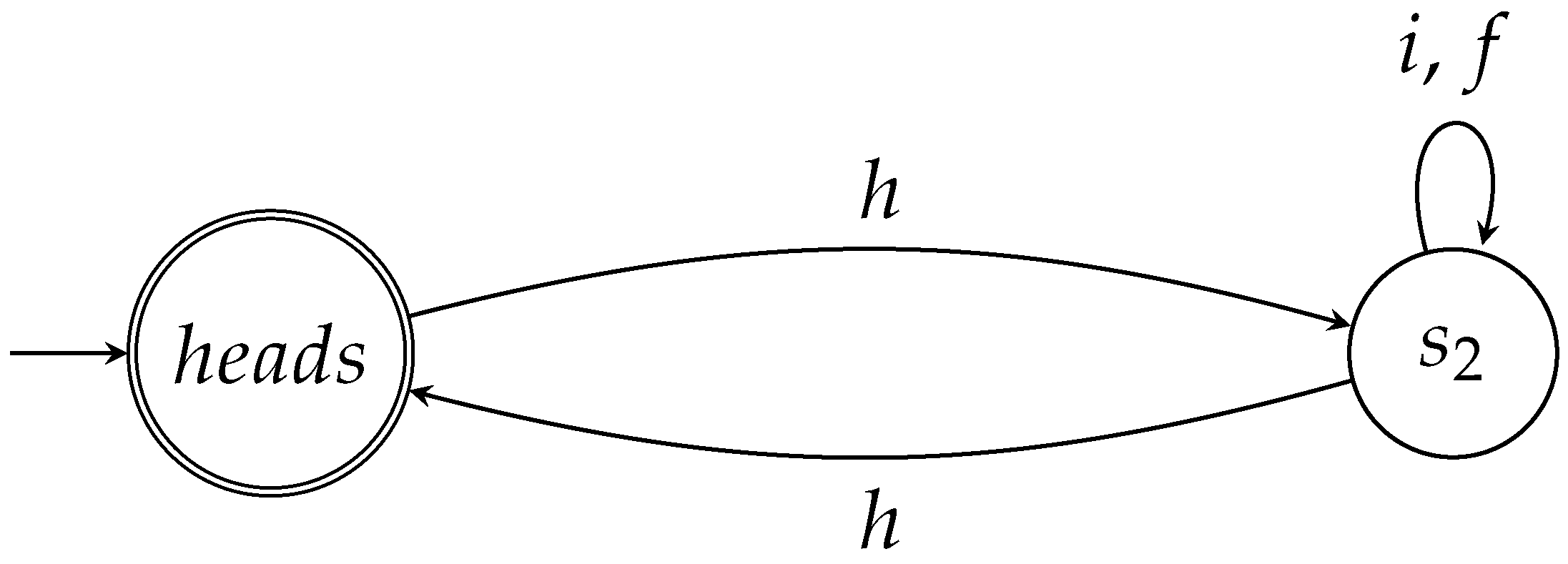
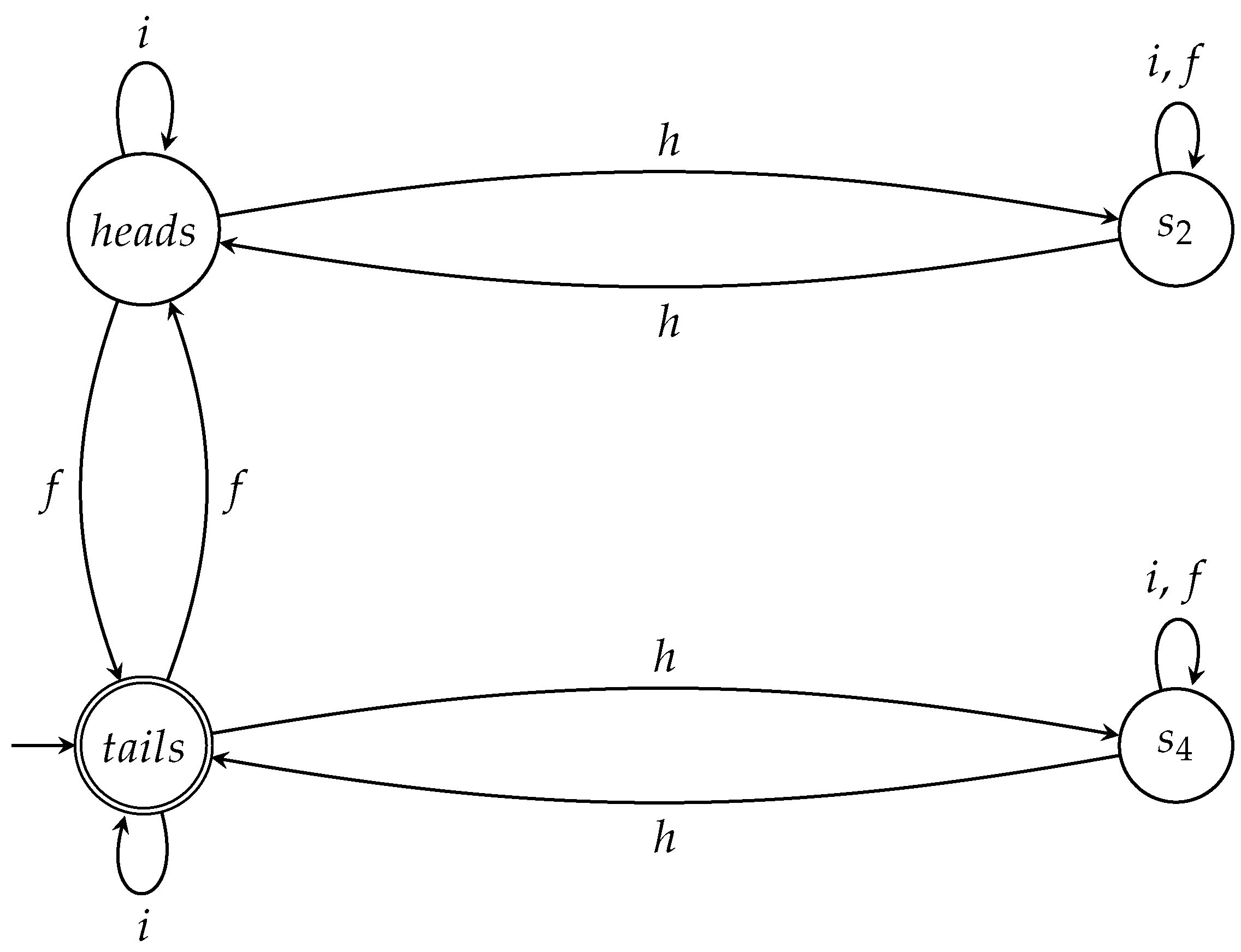
5. An Automaton for the PQ Game
- The initial state of the coin is .
- is a very special state in the sense that no matter what Picard chooses to play (Picard can act either by I or by F), after his move the coin remains in the state .
- Finally, Q wins the game by applying H one last time, which in effect sends the coin back to its initial state .
- The empty word that technically belongs to can be viewed as the representation of the trivial game, where no player gets to act on the coin, so the coin stays at its initial state and Q trivially wins.
- Words such as and , i.e., having the form , correspond to the most unfair (for Picard) games, where the game lasts exactly rounds, for some , and Q moves during each round (Picard does not get to make any move at all).
- Words of the form , where , represent games that last rounds. In these games, Q plays only during the first and last round of the game, whereas Picard plays during the n intermediate rounds. These variants give to Picard the illusion of fairness, without changing the final outcome.
- Words of the form , e.g., , correspond to more complex games. They are in effect independent repetitions of the previous category of games.
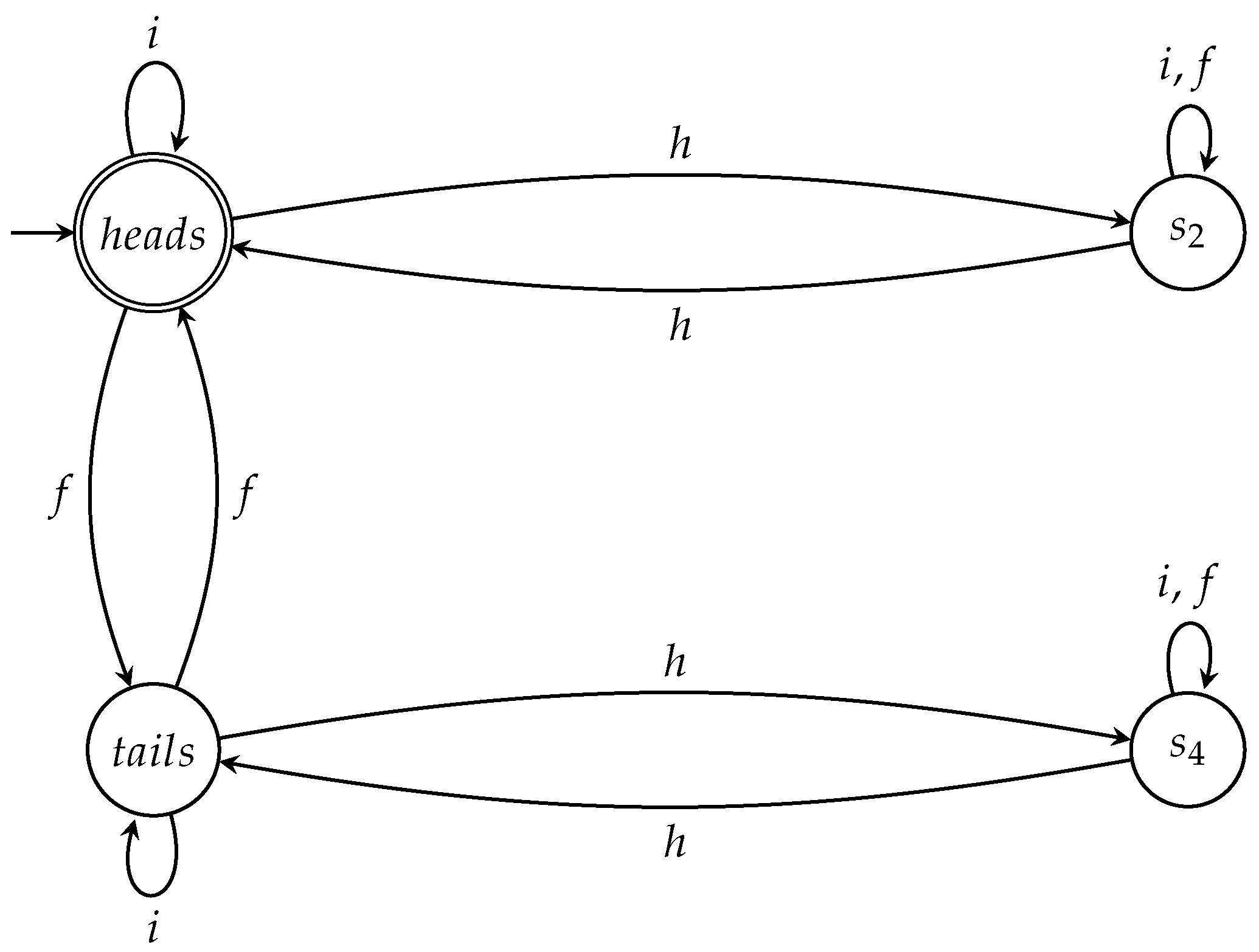
6. Variants of the Game and Their Corresponding Automata
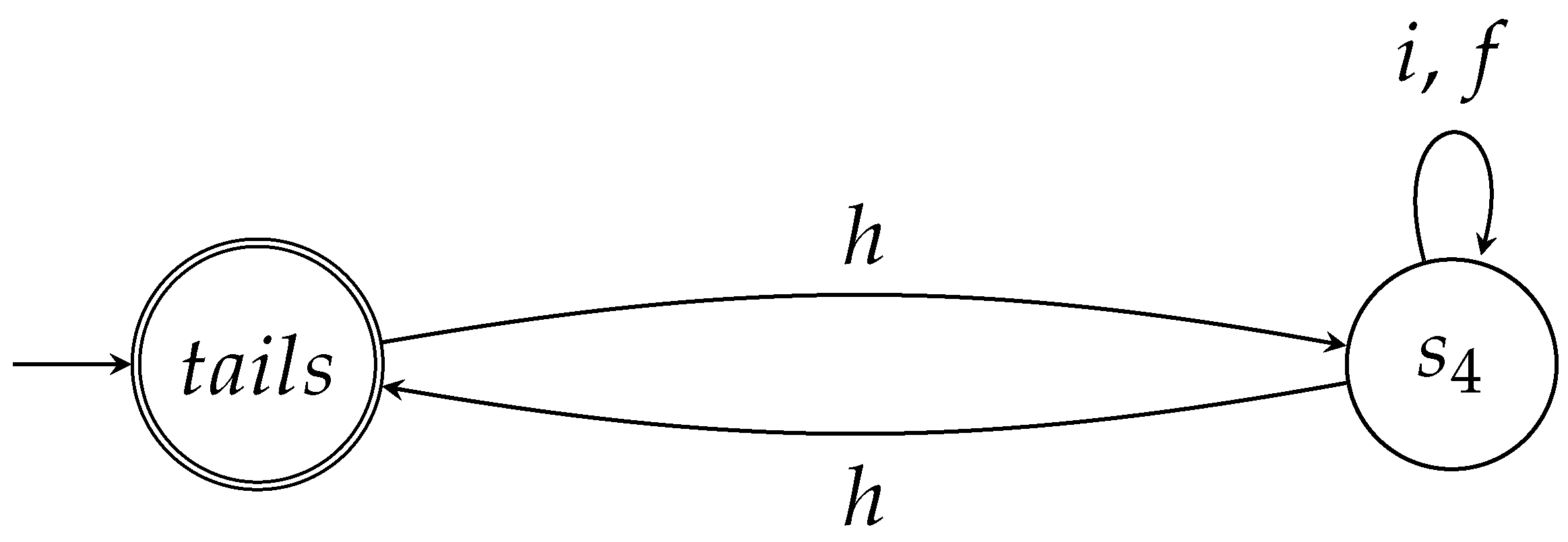
6.1. Changing the Initial State of the Coin
- The words of have the general form .
- Formally, and are the only words that correspond to valid game moves.
- Again, the empty word belongs to and can be thought of as expressing the trivial game, where Q trivially wins.
- Like before, words of the form correspond to games that last at least , , rounds, and words of the form , where , correspond to games that last rounds. Q surely wins these games no matter what Picard’s strategies are.
- Words of the form correspond to zero or more repetitions of the previous types of game. It is evident that Q also wins these complex games with probability .
6.2. Variants with More Rounds
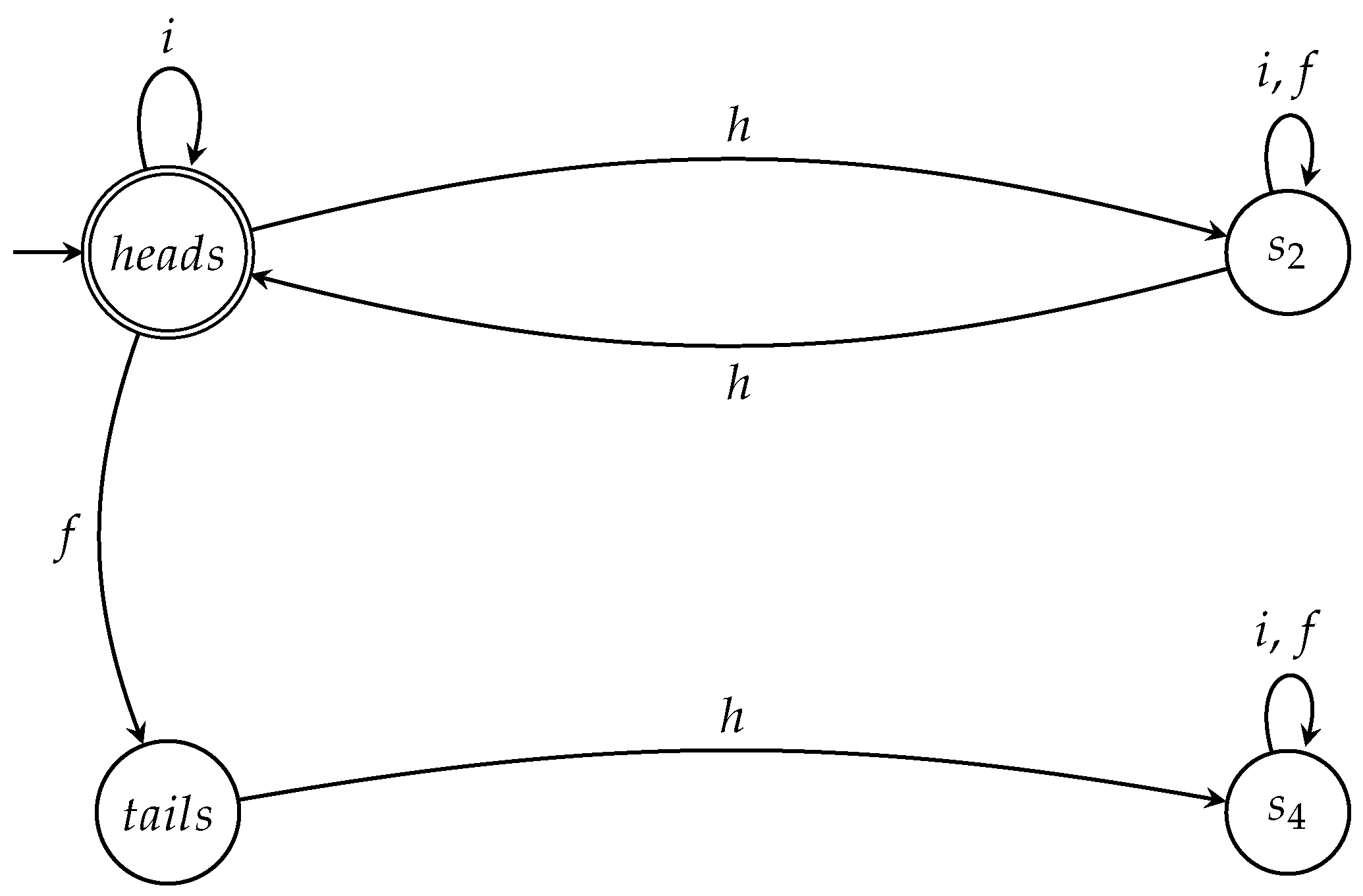
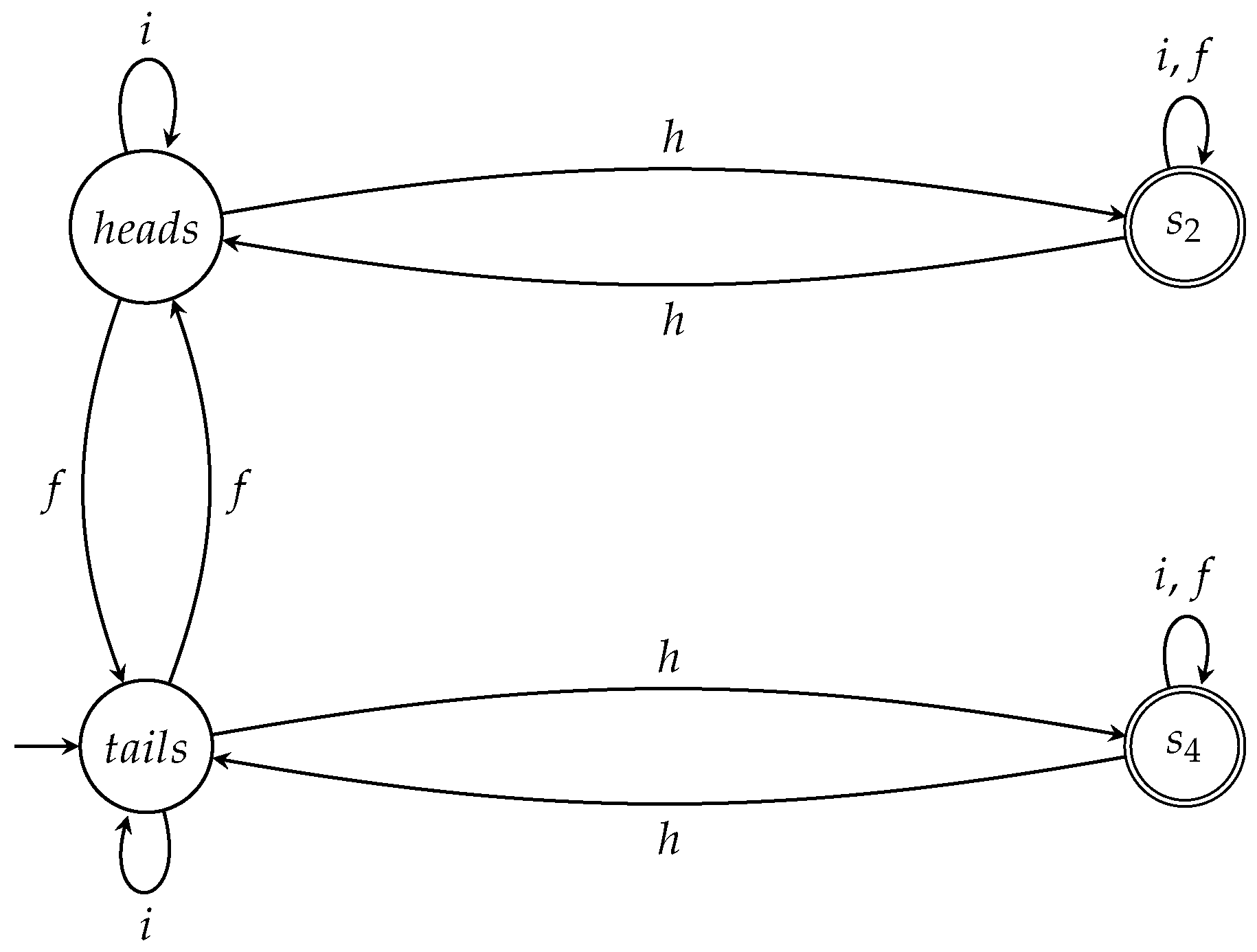
- Initially, we examine the six-round game . Clearly, after Round 3 (i.e., after Q’s second move) the coin is at state . It may remain in this state if Picard decides to use I but, if Picard decides to use F, the coin will enter state . Q’s subsequent move will send the coin to state in the first case, or to state in the second case. Thus, the coin may end up in or , irrespective of whether Picard’s final action in the 6th round is I or F (recall from our previous analysis that and represent the same state).The associated automaton is shown in Figure 3. As expected, its states correspond to the states of the coin (see Table 2) and its transitions to the actions of the players. Like the previous automata we have seen, is nondeterministic because of the rules of the game, which entail, for instance, that there is no outgoing transition labeled f from state . An important observation we can make in this case is that, by extending the duration of the game, the automata and “merge” into the .Strictly speaking, the only possible valid moves in are: , , , , , , , and . The corresponding words are: , , , , , , , and ; none of them is recognized by . This does not imply that is empty. On the contrary, is infinite. For example, belongs to . This particular word corresponds to a 7-round game and Q will surely win in this game if the corresponding sequence of actions is played by Q and Picard. is a winning automaton for Q that accepts the language . It is therefore consistent with the winning property that all the words corresponding to the action sequences that are admissible for the game are rejected because they do not guarantee that Q will surely win. As a matter of fact, with the admissible action sequences both Q and Picard have equal probability to win.
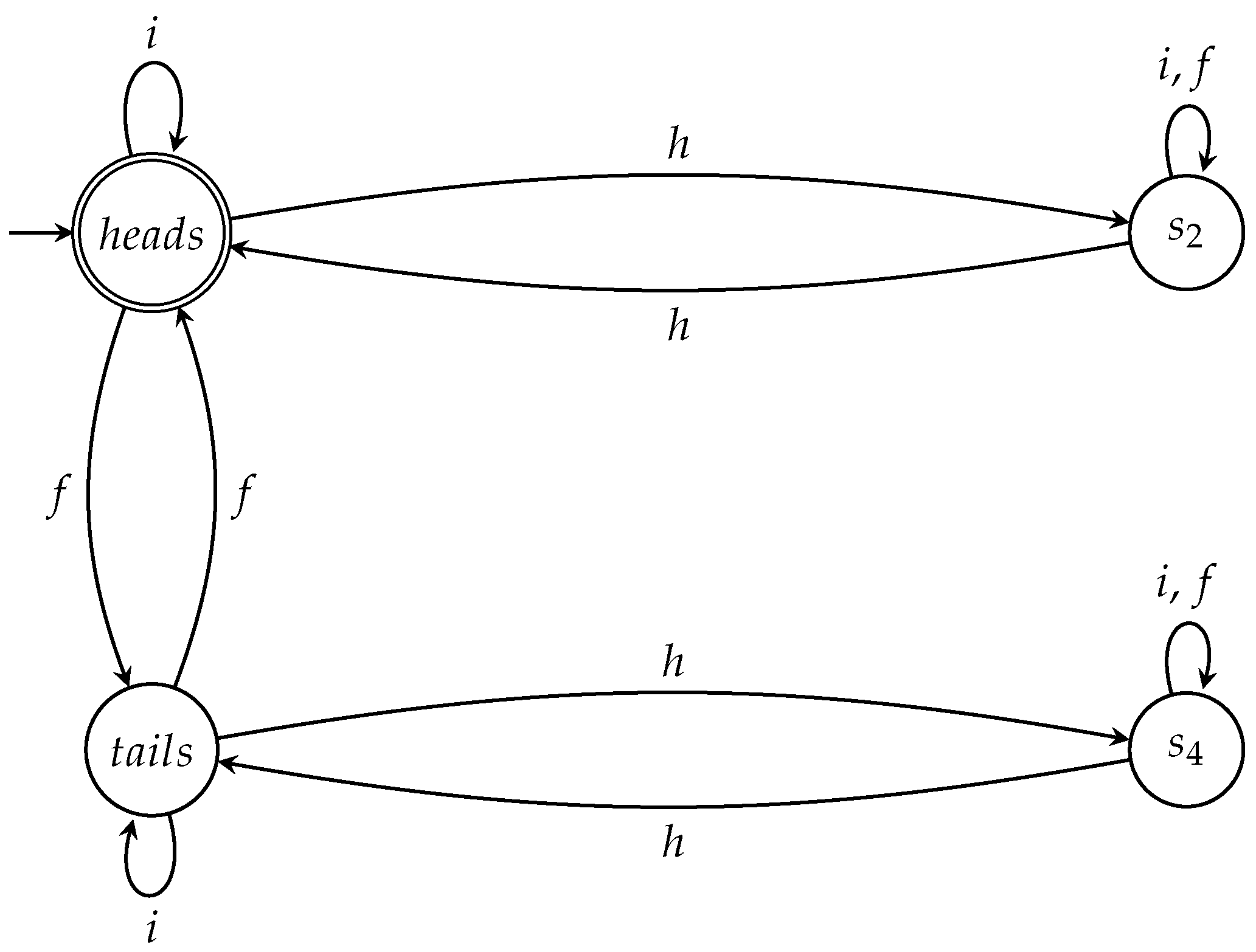
- Finally, we look at the general -round variant , for . According to our previous analysis, after Round 6, the coin may be at one of the states or . Consequently, Q’s move will send it to one of or . Picard’s action will either leave the coin to its current state or forward it to one of or ; in any case, after Picard’s move the coin will either be at or . Finally, Q’s last action will result in the coin entering one of the states or . This behavior is captured by the automaton , depicted in Figure 4. We can go on, but it should be clear by now that, no matter how many more rounds are played, no more new states will appear.Up to this point, we have constructed the automata and , shown in Figure 3 and Figure 4, respectively. They are all winning automata for Q, exactly like and . This is more or less evident, but we shall give a formal proof in the next section. We close this section with an important observation. has four states and is the biggest, in terms of number of transitions, automaton we have encountered so far. In a way, “contains” all the previous automata. The most striking difference with the previous automata is the fact that is deterministic, whereas , , and were nondeterministic. Exactly three transitions, one for each letter and h, emanate from every state. This gives a type of completeness because whatever action is taken by any player, the outcome will correspond to a state of . Hence, is able to accurately mirror the behavior of the coin.
7. Automata Capturing Sets of Games
- Picard’s actions are either I or F and Q’s action is H.
- The coin is initially at state .
- Q wins if, when the game is over and the state of the coin is measured, it is found to be in state ; otherwise, Picard wins.
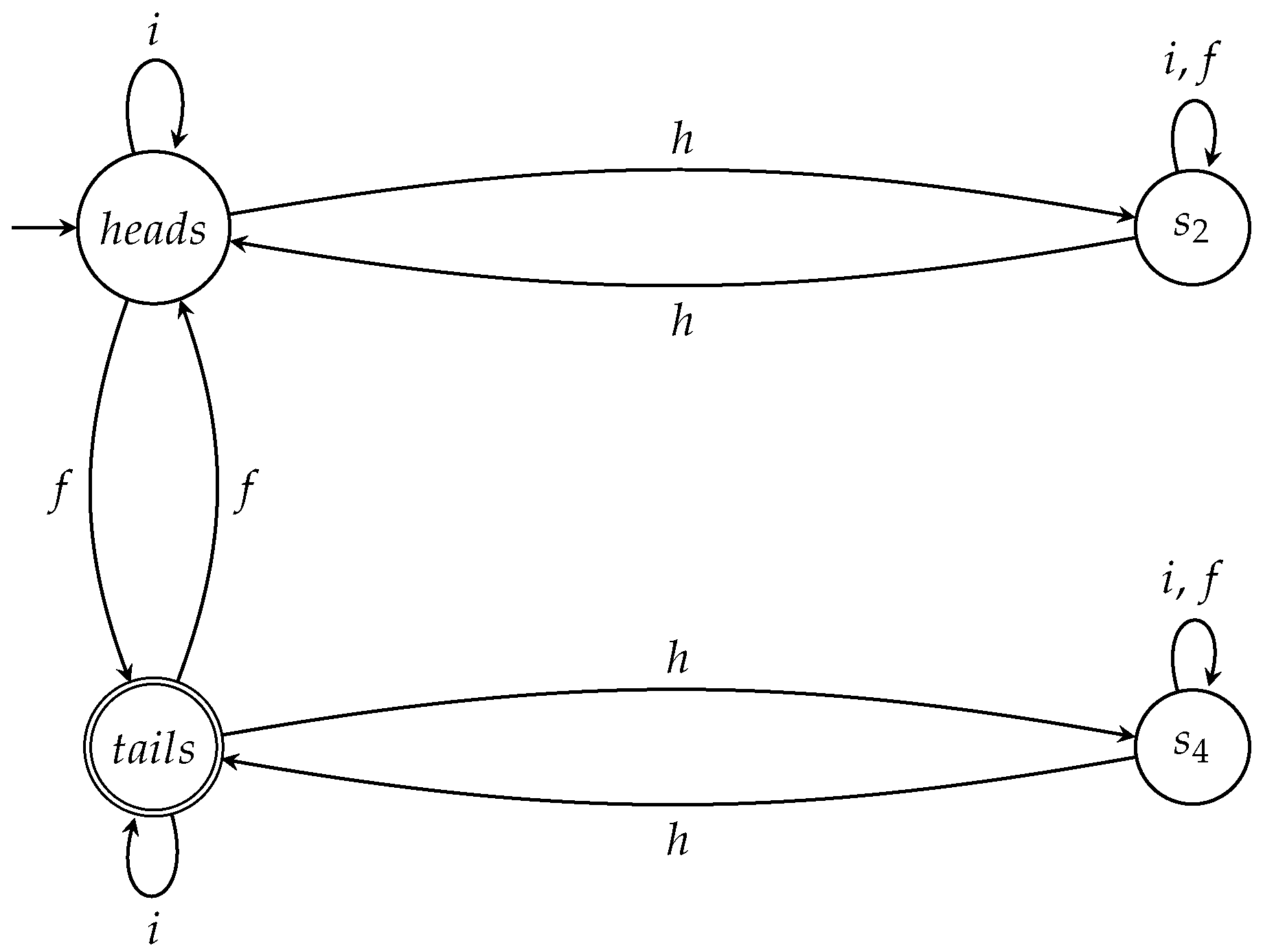
7.1. Devising Other Variants
7.1.1. Changing the Initial State of the Coin
- state as the initial state, and
- state as the only accept state.
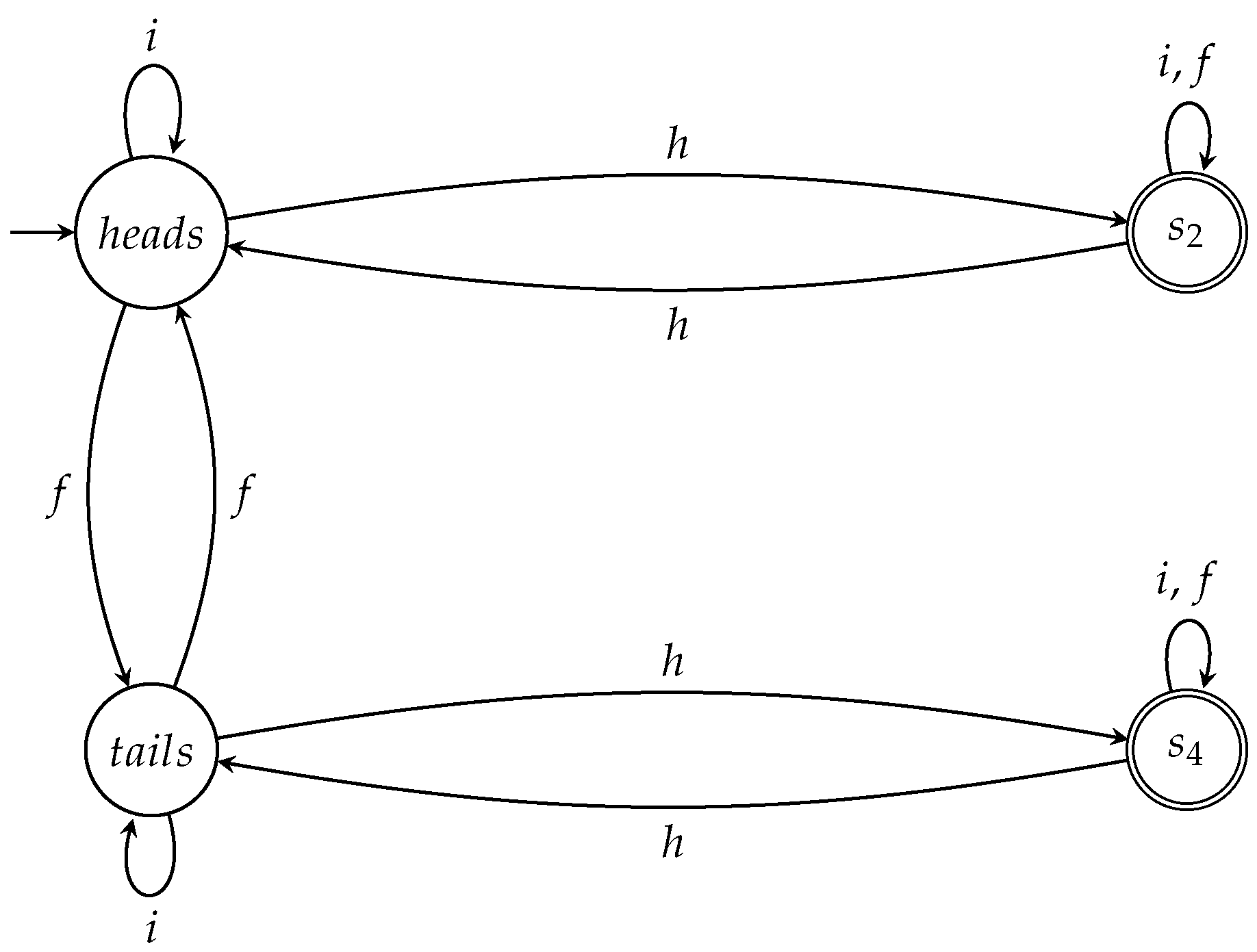
7.1.2. Picard Surely Wins
- setting as the initial state; and
- setting as the only accept state.
- set as the initial state; and
- set as the only accept state.
7.1.3. Fair Games
- setting as the initial state; and
- setting and as the accept states.
- setting as the initial state; and
- setting and as the accept states.
8. Conclusions and Further Work
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| PQ | Picard-Q |
| NFA | Nondeterministic finite automaton |
| DFA | Deterministic finite automaton |
Appendix A. Proofs of the Main Results
- When , the only word of length 0 is the empty word . In this case, by Definition 6 , by Definition A2 and, by Definition A3, . Equation (A5) then reduces to , which is trivially true.Similarly, when , is the empty action sequence , in which case (Definition 6), (Definition A2), and (Definition A3). In this special case, Equation (A6) becomes , which is of course true.
- We assume that (A5) and (A6) hold for and for all and .
- It remains to prove Equations (A5) and (A6) for .Consider an arbitrary word w over of length . w can be written as where is a word of length k and l is one of or h. By the induction hypothesis we know thatThere are three cases to consider, depending on whether , or .If , then and the transition function of (Figure 4) ensures that . At the same time, by Definition 6, and, by Definition A3, because I is the identity operator. Using , and the induction hypothesis in Equation (A7), we get . Thus, in this case, Equation (A5) holds.If , then . With respect to f the transition function of (Figure 4) is a bit more complicated, which implies that each state of must be examined separately. Let’s begin with state , that is let’s assume that . Then, the transition function requires that . Accordingly, Definition A4 implies thatBy the induction hypothesis in Equation (A7) and we can deduce thatCombining Definitions 6 and (A3) with we derive that andbecause F is the flip operator. Therefore, if , thenthat is Equation (A5) holds. It is straightforward to repeat the same reasoning for the remaining states of and verify in each case the validity of Equation (A5).If , then . As in the previous case, we have to examine each state of separately. If , then, according to the transition function, . Recalling Definition A4 we see thatBy the induction hypothesis in Equation (A7) and we conclude thatTogether, Definitions 6 and A3 and imply that andbecause H is the Hadamard operator. Hence, if , thenshowing that Equation (A5) holds. Repeating analogous arguments for the remaining states of allows us to establish the validity of Equation (A5).We proceed now to show that Equation (A6) holds. Consider an arbitrary action sequence of length : , where is the prefix action sequence of length k and U is one of the unitary operators or H. In this case the induction hypothesis becomesSince U stands for one of or H, we must distinguish three cases.If U is the identity operator I then, by Definition A3, . Hence, . The transition function of (Figure 4) guarantees that . Therefore, . Combining and , we conclude that , i.e., (A6) holds.If U is the flip operator F, then each ket of C must be examined separately. Let us begin with ket , that is let’s assume that . Then, by Definition A3, . In this case Definition A4 implies thatBy the induction hypothesis in Equation (A8) and we see thatCombining Definitions 6 and A2 with we derive that andby the transition function of transition function of (Figure 4). Consequently,that is Equation (A6) holds. It is straightforward to repeat the same reasoning for the remaining kets of C and verify in each case the validity of Equation (A6).The last case we have to examine is when U is the Hadamard operator H, in which case . As in the previous case, we have to check each ket of C. Let us consider first the case where . Then, by Definition A3, . In this case Definition A4 implies thatBy the induction hypothesis in Equation (A8) and we see thatCombining Definitions 6 and A2 with we derive that andby the transition function of transition function of (Figure 4). Finally,that is Equation (A6) holds. Using similar arguments, we can prove Equation (A6) for the remaining kets of C.
References
- Gintis, H. Game Theory Evolving: A Problem-Centered Introduction to Modeling Strategic Interaction, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Tadelis, S. Game Theory: An Introduction; Princeton University Press: Princeton, NJ, USA, 2013. [Google Scholar]
- Myerson, R. Game Theory; Harvard University Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Von Neumann, J.; Morgenstern, O. Theory of Games and Economic Behavior; Science Editions; J. Wiley: Hoboken, NJ, USA, 1944. [Google Scholar]
- Meyer, D.A. Quantum strategies. Phys. Rev. Lett. 1999, 82, 1052–1055. [Google Scholar] [CrossRef]
- Salimi, S.; Soltanzadeh, M. Investigation of quantum roulette. Int. J. Quantum Inf. 2009, 7, 615–626. [Google Scholar] [CrossRef]
- Wang, X.B.; Kwek, L.; Oh, C. Quantum roulette: An extended quantum strategy. Phys. Lett. A 2000, 278, 44–46. [Google Scholar]
- Ren, H.F.; Wang, Q.L. Quantum game of two discriminable coins. Int. J. Theor. Phys. 2008, 47, 1828–1835. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Frison, J.; Huy, K.P.; Massar, S. Experimental quantum tossing of a single coin. New J. Phys. 2008, 10, 083037. [Google Scholar] [CrossRef]
- Berlin, G.; Brassard, G.; Bussieres, F.; Godbout, N. Fair loss-tolerant quantum coin flipping. Phys. Rev. A 2009, 80, 062321. [Google Scholar] [CrossRef]
- Ambainis, A. A new protocol and lower bounds for quantum coin flipping. In Proceedings of the Thirty-Third Annual ACM Symposium on Theory of Computing, Crete, Greece, 6–8 July 2001; pp. 134–142. [Google Scholar]
- Ambainis, A.; Buhrman, H.; Dodis, Y.; Rohrig, H. Multiparty quantum coin flipping. In Proceedings of the 19th IEEE Annual Conference on Computational Complexity, Amherst, MA, USA, 24 June 2004; pp. 250–259. [Google Scholar]
- Neyman, A. Bounded complexity justifies cooperation in the finitely repeated prisoners’ dilemma. Econ. Lett. 1985, 19, 227–229. [Google Scholar] [CrossRef]
- Rubinstein, A. Finite automata play the repeated prisoner’s dilemma. J. Econ. Theory 1986, 39, 83–96. [Google Scholar] [CrossRef]
- Abreu, D.; Rubinstein, A. The structure of Nash equilibrium in repeated games with finite automata. Econometrica 1988, 56, 1259–1281. [Google Scholar] [CrossRef]
- Binmore, K.G.; Samuelson, L. Evolutionary stability in repeated games played by finite automata. J. Econ. Theory 1992, 57, 278–305. [Google Scholar]
- Ben-Porath, E. Repeated games with finite automata. J. Econ. Theory 1993, 59, 17–32. [Google Scholar] [CrossRef]
- Marks, R.E. Repeated Games and Finite Automata; Australian Graduate School of Management, University of New South Wales: Sydney, Australia, 1990. [Google Scholar]
- Eisert, J.; Wilkens, M.; Lewenstein, M. Quantum games and quantum strategies. Phys. Rev. Lett. 1999, 83, 3077. [Google Scholar]
- Benjamin, S.C.; Hayden, P.M. Comment on “Quantum Games and Quantum Strategies”. Phys. Rev. Lett. 2001, 87, 069801. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S. Quantum strategic game theory. In Proceedings of the 3rd Innovations in Theoretical Computer Science Conference, Cambridge, MA, USA, 8–10 January 2012; ACM: New York, NY, USA, 2012; pp. 39–59. [Google Scholar]
- Flitney, A.P.; Abbott, D. An introduction to quantum game theory. Fluct. Noise Lett. 2002, 2, R175–R187. [Google Scholar] [CrossRef]
- Lee, C.F.; Johnson, N. Parrondo games and quantum algorithms. arXiv, 2002; quant-ph/0203043. [Google Scholar]
- Meyer, D.A.; Blumer, H. Parrondo games as lattice gas automata. J. Stat. Phys. 2002, 107, 225–239. [Google Scholar] [CrossRef]
- Bertelle, C.; Flouret, M.; Jay, V.; Olivier, D.; Ponty, J.L. Adaptive behaviour for prisoner dilemma strategies based on automata with multiplicities. In Proceedings of the ESS 2002 Conference, Dresden, Germany, 23–26 October 2002. [Google Scholar]
- Piotrowski, E.W.; Sladkowski, J. The next stage: Quantum game theory. arXiv, 2003; quant-ph/0308027. [Google Scholar]
- Suwais, K. Assessing the Utilization of Automata in Representing Players’ Behaviors in Game Theory. Int. J. Ambient Comput. Intell. 2014, 6, 1–14. [Google Scholar] [CrossRef]
- Almanasra, S.; Suwais, K.; Rafie, M. The Applications of Automata in Game Theory. In Intelligent Technologies and Techniques for Pervasive Computing; IGI Global: Hershey, PA, USA, 2013; pp. 204–217. [Google Scholar]
- Li, L.; Feng, Y. On hybrid models of quantum finite automata. J. Comput. Syst. Sci. 2015, 81, 1144–1158. [Google Scholar] [CrossRef]
- Zheng, S.; Li, L.; Qiu, D.; Gruska, J. Promise problems solved by quantum and classical finite automata. Theor. Comput. Sci. 2017, 666, 48–64. [Google Scholar] [CrossRef]
- Li, L.; Qiu, D. Lower bounds on the size of semi-quantum finite automata. Theor. Comput. Sci. 2016, 623, 75–82. [Google Scholar] [CrossRef]
- Gainutdinova, A.; Yakaryılmaz, A. Unary probabilistic and quantum automata on promise problems. Quantum Inf. Process. 2018, 17, 28. [Google Scholar] [CrossRef]
- Giannakis, K.; Papalitsas, C.; Kastampolidou, K.; Singh, A.; Andronikos, T. Dominant Strategies of Quantum Games on Quantum Periodic Automata. Computation 2015, 3, 586–599. [Google Scholar] [CrossRef]
- Preskill, J. Quantum Information and Computation. 2017. Available online: http://www.theory.caltech.edu/preskill/ph219/ph219_2017 (accessed on 18 December 2017).
- Sipser, M. Introduction to the Theory of Computation, 2nd ed.; Course Technology: Boston, MA, USA, 2006. [Google Scholar]
- Yakhnis, A.; Yakhnis, V. Gurevich–Harrington’s games defined by finite automata. Ann. Pure Appl. Logic 1993, 62, 265–294. [Google Scholar] [CrossRef]
- Cox, E.; Schkufza, E.; Madsen, R.; Genesereth, M. Factoring general games using propositional automata. In Proceedings of the IJCAI Workshop on General Intelligence in Game-Playing Agents (GIGA), Pasadena, CA, USA, 13 July 2009; pp. 13–20. [Google Scholar]
- Rabin, M.O.; Scott, D. Finite automata and their decision problems. IBM J. Res. Dev. 1959, 3, 114–125. [Google Scholar] [CrossRef]

| (a) | (b) | (c) | |
|---|---|---|---|
| Operators vs. Letters | Letter Assignment | Operator Assignment | |
| Operators | Letters | ||
| I | i | ||
| F | f | ||
| H | h | ||
| Coin State | Automaton State |
|---|---|
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andronikos, T.; Sirokofskich, A.; Kastampolidou, K.; Varvouzou, M.; Giannakis, K.; Singh, A. Finite Automata Capturing Winning Sequences for All Possible Variants of the PQ Penny Flip Game. Mathematics 2018, 6, 20. https://doi.org/10.3390/math6020020
Andronikos T, Sirokofskich A, Kastampolidou K, Varvouzou M, Giannakis K, Singh A. Finite Automata Capturing Winning Sequences for All Possible Variants of the PQ Penny Flip Game. Mathematics. 2018; 6(2):20. https://doi.org/10.3390/math6020020
Chicago/Turabian StyleAndronikos, Theodore, Alla Sirokofskich, Kalliopi Kastampolidou, Magdalini Varvouzou, Konstantinos Giannakis, and Alexander Singh. 2018. "Finite Automata Capturing Winning Sequences for All Possible Variants of the PQ Penny Flip Game" Mathematics 6, no. 2: 20. https://doi.org/10.3390/math6020020
APA StyleAndronikos, T., Sirokofskich, A., Kastampolidou, K., Varvouzou, M., Giannakis, K., & Singh, A. (2018). Finite Automata Capturing Winning Sequences for All Possible Variants of the PQ Penny Flip Game. Mathematics, 6(2), 20. https://doi.org/10.3390/math6020020






