Four Particular Cases of the Fourier Transform
Abstract
1. Introduction
2. Preliminaries
2.1. The Fourier Transform and the Theory of Infinitely Differentiable Functions
2.2. Convolution vs. Multiplication
2.3. Discretization vs. Periodization
2.4. Poisson’s Summation Formula
2.5. Validity Statement
3. Notation
3.1. Generalized Functions
3.2. Definitions
4. Calculation Rules
4.1. Schwartz Functions
4.2. Discrete Periodic Functions
4.3. The Discrete Fourier Transform
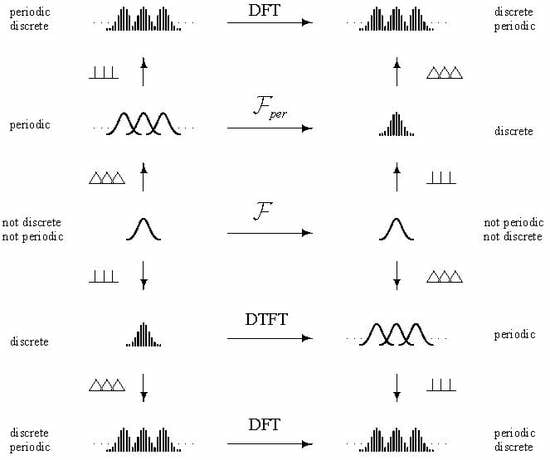
5. Four Fourier Transforms
- (27) is the Integral Fourier Transform (for non-discrete non-periodic functions) in ,
- (28) is the Integral Fourier Transform for (non-discrete) periodic functions in ,
- (29) is its inverse, the DTFT for discrete (non-per.) functions in ,
- (30) is the DFT for discrete periodic functions in ,
- (31) is its inverse, the inverse Discrete Fourier Transform (IDFT) for discrete periodic functions in
6. Discussion
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Fourier Transforms
Appendix A.1. Conventional Fourier Transforms
Appendix A.1.1. Fourier Transform
Appendix A.1.2. Fourier Transform (for Periodic Functions)
Appendix A.1.3. Fourier Transform (for Discrete Functions)
Appendix A.1.4. Fourier Transform (for Discrete Periodic Functions)
Appendix A.2. Distributional Fourier Transform
Appendix B. Derivations
- defining the Integral Fourier Transform for periodic functions via (A3) and (A4) leads to (28),
- defining the DTFT via (A5) and (A6) leads to (29) and
- defining the DFT via (A7) and (A8) leads to (30) and (31).
Appendix B.1. Fourier Transform for Periodic Functions (per)
Appendix B.2. Fourier Transform for Discrete Functions (DTFT)
Appendix B.3. Fourier Transform for Discrete Periodic Functions (DFT)
Appendix B.4. Derivation of the Inverse DFT
References
- Zayed, A.I. Handbook of Function and Generalized Function Transformations; CRC Press Inc.: Boca Raton, FL, USA, 1996. [Google Scholar]
- Woodward, P.M. Probability and Information Theory, with Applications to Radar; Pergamon Press Ltd.: Oxford, UK, 1953. [Google Scholar]
- Gasquet, C.; Witomski, P. Fourier Analysis and Applications: Filtering, Numerical Computation, Wavelets; Springer: New York, NY, USA, 1999; Volume 30. [Google Scholar]
- Panaretos, A.H.; Anastassiu, H.T.; Kaklamani, D.I. A Note on the Poisson Summation Formula and Its Application to Electromagnetic Problems Involving Cylindrical Coordinates. Turk. J. Electr. Eng. Comput. Sci. 2002, 10, 377–384. [Google Scholar]
- Benedetto, J.J.; Zimmermann, G. Sampling Multipliers and the Poisson Summation Formula. J. Fourier Anal. Appl. 1997, 3, 505–523. [Google Scholar] [CrossRef]
- Strichartz, R.S. A Guide to Distribution Theorie and Fourier Transforms; World Scientific Publishing Co. Pte Ltd.: Singapore, 2003. [Google Scholar]
- Fischer, J. Anwendung der Theorie der Distributionen auf ein Problem in der Signalverarbeitung. Diploma Thesis, Ludwig-Maximillians-Universität München, Munich, Germany, 1997. [Google Scholar]
- Kiselman, C.O. Generalized Fourier transformations: The work of Bochner and Carleman viewed in the light of the theories of Schwartz and Sato. In Microlocal Analysis and Complex Fourier Analysis; World Scientific: Singapore, 2002; pp. 166–185. [Google Scholar]
- Taylor, M.E. Pseudodifferential Operators; Princeton University Press: Princeton, NJ, USA, 1981. [Google Scholar]
- Halperin, I.; Schwartz, L. Introduction to the Theory of Distributions; University of Toronto Press, Scholarly Publishing: Toronto, ON, Canada, 1952. [Google Scholar]
- Schwartz, L. Théorie des Distributions, Tome I; Hermann: Paris, France, 1950. [Google Scholar]
- Schwartz, L. Théorie des Distributions, Tome II; Hermann: Paris, France, 1951. [Google Scholar]
- Kammler, D.W. A First Course in Fourier Analysis; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Benedetto, J.J. Harmonic Analysis and Applications; CRC Press Inc.: Boca Raton, FL, USA, 1996. [Google Scholar]
- Grafakos, L. Modern Fourier Analysis; Springer Science+Business Media: New York, NY, USA, 2009; Volume 250. [Google Scholar]
- Feichtinger, H.G.; Strohmer, T. Gabor Analysis and Algorithms: Theory and Applications; Birkhäuser: Boston, MA, USA, 1998. [Google Scholar]
- Gröchenig, K. Foundations of Time-Frequency Analysis; Birkhäuser: Basel, Switzerland, 2001. [Google Scholar]
- Brandwood, D. Fourier Transforms in Radar and Signal Processing; Artech House, Inc.: Norwood, MA, USA, 2003. [Google Scholar]
- Rahman, M. Applications of Fourier Transforms to Generalized Functions; WIT Press: Southampton, UK, 2011. [Google Scholar]
- Mallat, S.; Hwang, W.L. Singularity Detection and Processing with Wavelets. IEEE Trans. Inf. Theory 1992, 38, 617–643. [Google Scholar] [CrossRef]
- Temple, G. The Theory of Generalized Functions. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1955, 228, 175–190. [Google Scholar] [CrossRef]
- Lighthill, M.J. An Introduction to Fourier Analysis and Generalised Functions; Cambridge University Press: Cambridge, UK, 1958. [Google Scholar]
- Gelfand, I.M.; Schilow, G.E. Verallgemeinerte Funktionen (Distributionen), Teil I; VEB Deutscher Verlag der Wissenschaften: Berlin, Germany, 1960. [Google Scholar]
- Zemanian, A. Distribution Theory And Transform Analysis—An Introduction To Generalized Functions, with Applications; McGraw-Hill Inc.: New York, NY, USA, 1965. [Google Scholar]
- Trèves, F. Topological Vector Spaces, Distributions and Kernels: Pure and Applied Mathematics; Dover Publications Inc.: Mineola, NY, USA, 1967; Volume 25. [Google Scholar]
- Horváth, J. Topological Vector Spaces and Distributions; Addison-Wesley Publishing Company: Reading, MA, USA, 1966. [Google Scholar]
- Jones, D. The Theory of Generalized Functions; Cambridge University Press: Cambridge, UK, 1966. [Google Scholar]
- Zemanian, A.H. Generalized Integral Transformations; Dover Publications Inc.: Mineola, NY, USA, 1968. [Google Scholar]
- Gelfand, I.M.; Schilow, G.E. Verallgemeinerte Funktionen (Distributionen), Teil II, Zweite Auflage; VEB Deutscher Verlag der Wissenschaften: Berlin, Germany, 1969. [Google Scholar]
- Barros-Neto, J. An Introduction to the Theory of Distributions; Marcel Dekker Inc.: New York, NY, USA, 1973. [Google Scholar]
- Wagner, P. Zur Faltung von Distributionen. Math. Annalen 1987, 276, 467–485. [Google Scholar] [CrossRef]
- Hörmander, L. The Analysis of Linear Partial Differential Operators I, Die Grundlehren der mathematischen Wissenschaften; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
- Walter, W. Einführung in die Theorie der Distributionen; BI-Wissenschaftsverlag, Bibliographisches Institut & FA Brockhaus: Mannheim, Germany, 1994. [Google Scholar]
- Vladimirov, V. Methods of the Theory of Generalized Functions; CRC Press Inc.: Boca Raton, FL, USA, 2002. [Google Scholar]
- Fischer, J.V. On the Duality of Discrete and Periodic Functions. Mathematics 2015, 3, 299–318. [Google Scholar] [CrossRef]
- Fischer, J.V. On the Duality of Regular and Local Functions. Mathematics 2017, 5, 41. [Google Scholar] [CrossRef]
- Reed, M.; Simon, B. II: Fourier Analysis, Self-Adjointness; Academic Press Inc.: New York, NY, USA, 1975; Volume II. [Google Scholar]
- Constantinescu, F. Distributions and Their Applications in Physics: International Series in Natural Philosophy; Pergamon Press Ltd.: Oxford, UK, 1980. [Google Scholar]
- Glimm, J.; Jaffe, A. Quantum Physics: A Functional Integral Point of View; Springer: New York, NY, USA, 1981. [Google Scholar]
- Folland, G.B. Harmonic Analysis in Phase Space; Princeton University Press: Princeton, NJ, USA, 1989. [Google Scholar]
- Saichev, A.I.; Woyczynski, W.A. Distributions in the Physical and Engineering Sciences. Volume 2—Linear and Nonlinear Dynamics of Continuous Media; Birkhäuser-Boston: Boston, MA, USA, 2013. [Google Scholar]
- Messiah, A. Quantum Mechanics—Two Volumes Bound as One; Dover Publications, Inc.: Mineola, NY, USA, 2003. [Google Scholar]
- Debnath, L. A Short Biography of Paul A M Dirac and Historical Development of Dirac Delta Function. Int. J. Math. Educ. Sci. Technol. 2013, 44, 1201–1223. [Google Scholar] [CrossRef]
- Dirac, P. The Principles of Quantum Mechanics; Oxford University Press: Oxford, UK, 1930. [Google Scholar]
- Dierolf, P. The Structure Theorem for Linear Transfer Systems. Note di Matematica 1991, 11, 119–125. [Google Scholar]
- Smith, D.C. An Introduction to Distribution Theory for Signals Analysis. Digit. Signal Process. 2006, 16, 419–444. [Google Scholar] [CrossRef]
- Osgood, B. The Fourier transform and its applications. In Lecture Notes for EE 261; Electrical Engineering Department, Stanford University: Stanford, CA, USA, 2007. [Google Scholar]
- Boche, H.; Mönich, U.J. Distributional Behavior of Convolution Sum System Representations. IEEE Trans. Sign. Proc. 2018, 66, 5056–5065. [Google Scholar] [CrossRef]
- Unser, M. Sampling—50 Years after Shannon. Proc. IEEE 2000, 88, 569–587. [Google Scholar] [CrossRef]
- Grossmann, A.; Loupias, G.; Stein, E.M. An Algebra of Pseudodifferential Operators and Quantum Mechanics in Phase Space. Ann. Inst. Fourier 1968, 18, 343–368. [Google Scholar] [CrossRef]
- Ashino, R.; Boggiatto, P.; Wong, M.W. Advances in Pseudo-Differential Operators; Birkhäuser Verlag: Basel, Switzerland, 2012; Volume 155. [Google Scholar]
- Feichtinger, H.G. Modulation Spaces on Locally Compact Abelian Groups; Universität Wien, Mathematisches Institut: Vienna, Austria, 1983. [Google Scholar]
- Gröchenig, K.; Heil, C. Modulation Spaces and Pseudodifferential Operators. Integr. Equ. Oper. Theory 1999, 34, 439–457. [Google Scholar] [CrossRef]
- Bényi, Á.; Gröchenig, K.; Okoudjou, K.A.; Rogers, L.G. Unimodular Fourier Multipliers for Modulation Spaces. J. Funct. Anal. 2007, 246, 366–384. [Google Scholar] [CrossRef]
- Feichtinger, H.G. On a New Segal Algebra. Monatsh. Math. 1981, 92, 269–289. [Google Scholar] [CrossRef]
- Özçağ, E. Defining the k-th Powers of the Dirac-Delta Distribution for Negative Integers. Appl. Math. Lett. 2001, 14, 419–423. [Google Scholar] [CrossRef]
- Li, C. The Powers of the Dirac Delta Function by Caputo Fractional Derivatives. J. Fract. Calc. Appl. 2016, 7, 12–23. [Google Scholar]
- Bracewell, R.N. Fourier Transform and its Applications; McGraw-Hill Book Company: New York, NY, USA, 1986. [Google Scholar]
- Dierolf, P. Multiplication and Convolution Operators between Spaces of Distributions. North-Holland Math. Stud. 1984, 90, 305–330. [Google Scholar]
- Gracia-Bondía, J.M.; Varilly, J.C. Algebras of Distributions Suitable for Phase-Space Quantum Mechanics. I. J. Math. Phys. 1988, 29, 869–879. [Google Scholar] [CrossRef]
- Dubois-Violette, M.; Kriegl, A.; Maeda, Y.; Michor, P.W. Smooth*-Algebras. arXiv, 2001; arXiv:math/0106150. [Google Scholar]
- Ortner, N. On Convolvability Conditions for Distributions. Monatsh. Math. 2010, 160, 313–335. [Google Scholar] [CrossRef]
- Larcher, J. Multiplications and Convolutions in L. Schwartz’ Spaces of Test Functions and Distributions and their Continuity. Analysis 2013, 33, 319–332. [Google Scholar] [CrossRef]
- Ortner, N.; Wagner, P. On the Spaces of John Horváth. J. Math. Anal. Appl. 2014, 415, 62–74. [Google Scholar] [CrossRef]
- Katznelson, Y. Une remarque concernant la formule de Poisson. Stud. Math. 1967, 29, 107–108. [Google Scholar] [CrossRef]
- Butzer, P.L.; Stens, R. The Poisson Summation Formula, Whittaker’s Cardinal Series and Approximate Integration. In Second Edmonton Conference on Approximation Theory; American Mathematical Society: Providence, RI, USA, 1983; pp. 19–36. [Google Scholar]
- Kahane, J.P.; Lemarié-Rieusset, P.G. Remarques sur la formule sommatoire de Poisson. Stud. Math. 1994, 109, 303–316. [Google Scholar] [CrossRef]
- Gröchenig, K. An Uncertainty Principle related to the Poisson Summation Formula. Stud. Math. 1996, 121, 87–104. [Google Scholar] [CrossRef]
- Nguyen, H.Q.; Unser, M.; Ward, J.P. Generalized Poisson Summation Formulas for Continuous Functions of Polynomial Growth. J. Fourier Anal. Appl. 2017, 23, 442–461. [Google Scholar] [CrossRef]
- Lyness, J. The Calculation of Fourier Coefficients by the Möbius Inversion of the Poisson Summation Formula. I. Functions whose early derivatives are continuous. Math. Comput. 1970, 24, 101–135. [Google Scholar]
- Kerl, J. Poisson Summation and the Discrete Fourier Transform. 2008. Available online: https://johnkerl.org/doc/fourpoi.pdf (accessed on 8 October 2018).
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Feichtinger, H.G. Thoughts on Numerical and Conceptual Harmonic Analysis. In New Trends in Applied Harmonic Analysis; Birkhäuser: Cham, Switzerland, 2016; pp. 301–329. [Google Scholar]
- Susskind, L.; Friedman, A. Quantum Mechanics: The Theoretical Minimum; Pinguin Random House: Alan Lane, UK, 2014. [Google Scholar]
- Baggott, J. The Meaning of Quantum Theory: A Guide for Students of Chemistry and Physics; Oxford University Press: New York, NY, USA, 1992. [Google Scholar]
- Arici, F.; Becker, D.; Ripken, C.; Saueressig, F.; van Suijlekom, W.D. Reflection Positivity in Higher Derivative Scalar Theories. J. Math. Phys. 2018, 59, 082302. [Google Scholar] [CrossRef]
- Paule, P.; Schneider, C. Towards a Symbolic Summation Theory for Unspecified Sequences. arXiv, 2018; arXiv:1809.06578. [Google Scholar]
- Born, M. Reciprocity Theory of Elementary Particles. Rev. Mod. Phys. 1949, 21, 463. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication in the Presence of Noise. Proc. IRE 1949, 37, 10–21. [Google Scholar] [CrossRef]
- Schirman, J.D. Theoretische Grundlagen der Funkortung; Militärverlag der DDR: Berlin, Germany, 1977. [Google Scholar]
- Boyd, J.P. Construction of Lighthill’s Unitary Functions: The Imbricate Series of Unity. Appl. Math. Comput. 1997, 86, 1–10. [Google Scholar] [CrossRef]
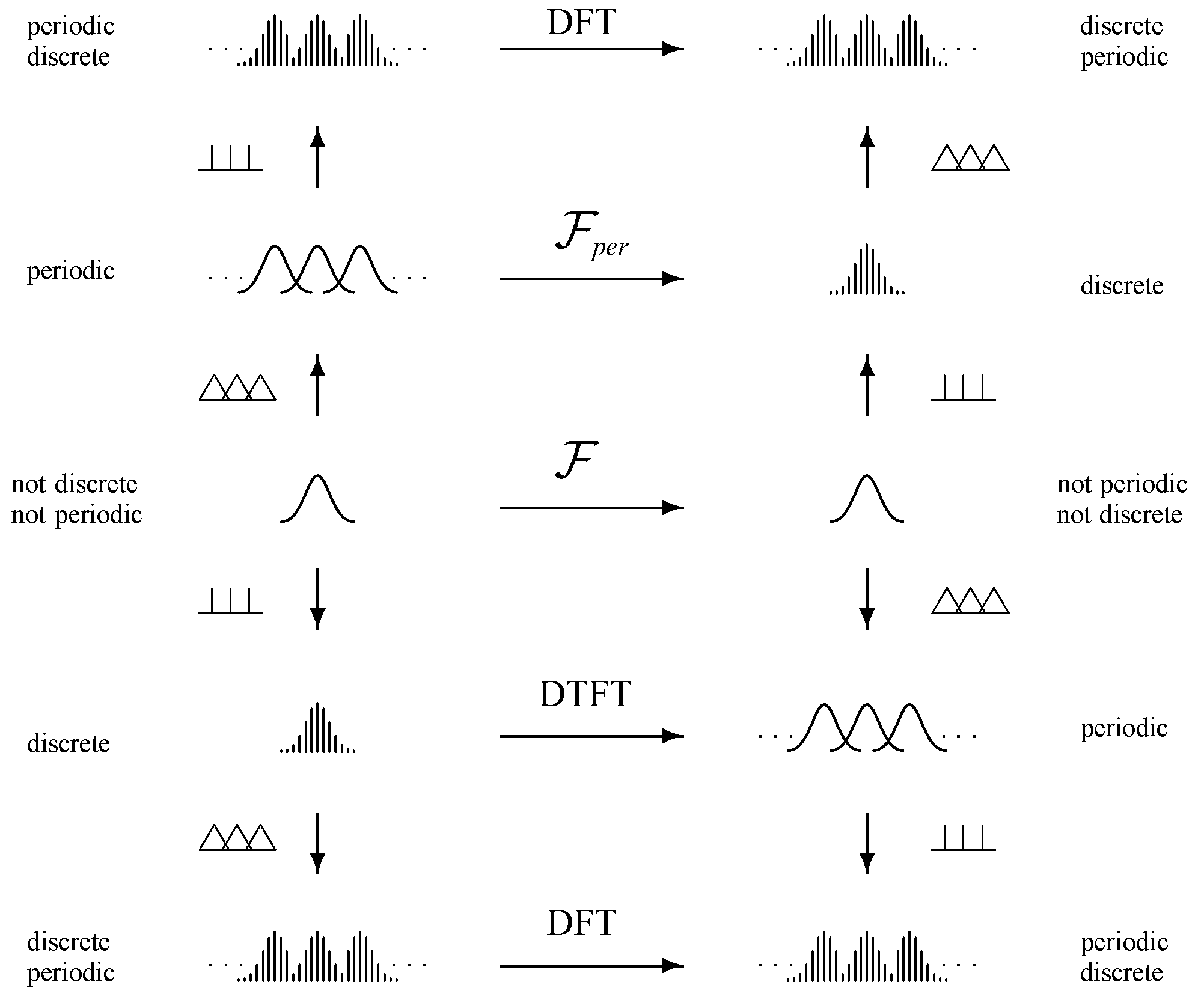
| No | Rule | Remark | Requirement |
|---|---|---|---|
| 1 | Poisson Summation Formula (generalized) | , | |
| 2 | Poisson Summation Formula (its dual) | , | |
| 3 | Rule 1, special case | ||
| 4 | Rule 2, special case | ||
| 5 | Rule 3, special case and | — | |
| 6 | Rule 4, special case and | — | |
| 7 | Rule 5 + 9, Dirac Comb Invariance | — | |
| 8 | Rule 6 + 9, Dirac Comb Invariance | — | |
| 9 | Dirac Comb Identity (by definition) | — | |
| 10 | Dirac Comb Identity (by definition) | ||
| 11 | Rule 1, , Dirac comb reciprocity | ||
| 12 | Rule 2, , Dirac comb reciprocity | ||
| 13 | Convolution vs. Multiplication | ||
| 14 | Multiplication vs. Convolution | ||
| 15 | Periodization Rule | ||
| 16 | Discretization Rule | ||
| 17 | Rule 15, , Periodization of f | ||
| 18 | Rule 16, , Discretization of f | ||
| 19 | Rule 17, , Periodization of | — | |
| 20 | Rule 18, , Discretization of | — |
| No | Waveform | Spectrum | Remark | Requirement |
|---|---|---|---|---|
| W-11 | Rule 1 in Table 1 | , | ||
| W-12 | Rule 2 in Table 1 | , |
| No | Rule | Remark | Requirement |
|---|---|---|---|
| i | Rule 1 + 2 | ||
| ii | Rule 2 + 1 | ||
| iii | Rule 3 + 2 | ||
| iv | Rule 4 + 1 | ||
| v | Rule iii | ||
| vi | Rule iv | ||
| vii | Rule x | ||
| viii | identity | ||
| ix | identity | ||
| x | commutation | ||
| xi | normalization | ||
| xii | normalization |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fischer, J.V. Four Particular Cases of the Fourier Transform. Mathematics 2018, 6, 335. https://doi.org/10.3390/math6120335
Fischer JV. Four Particular Cases of the Fourier Transform. Mathematics. 2018; 6(12):335. https://doi.org/10.3390/math6120335
Chicago/Turabian StyleFischer, Jens V. 2018. "Four Particular Cases of the Fourier Transform" Mathematics 6, no. 12: 335. https://doi.org/10.3390/math6120335
APA StyleFischer, J. V. (2018). Four Particular Cases of the Fourier Transform. Mathematics, 6(12), 335. https://doi.org/10.3390/math6120335