New Sufficient Condition for the Positive Definiteness of Fourth Order Tensors
Abstract
1. Introduction
2. New Z-Eigenvalue Localization Set for Structured Fourth Order Tensors
3. Upper Bound for the Z-Spectral Radius of Weakly Symmetric Nonnegative Tensors
4. Z-Eigenvalue Based Sufficient Condition for the Positive Definiteness of Fourth Order Tensors
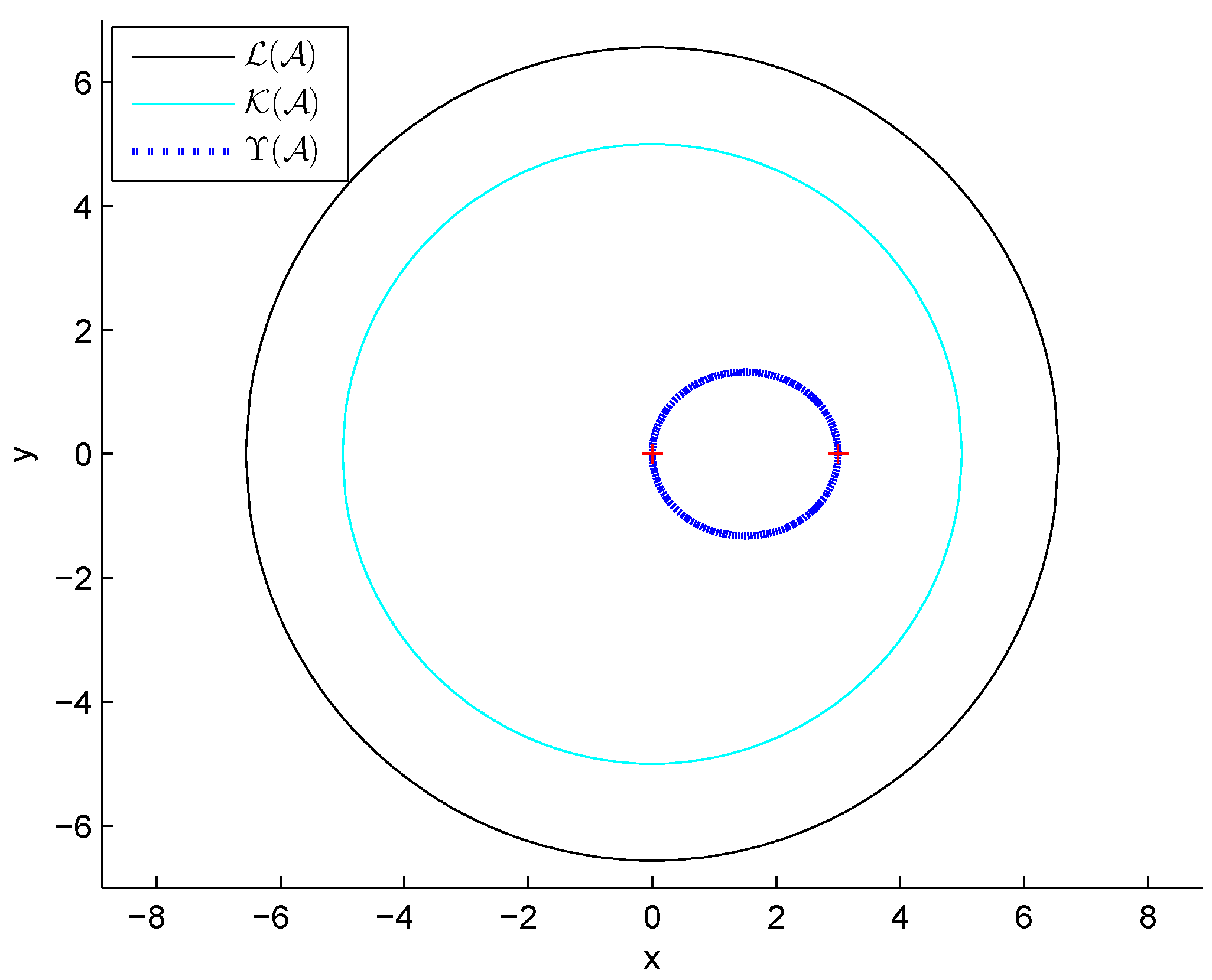
5. Numerical Examples
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lim, L.H. Singular values and eigenvalues of tensors: A variational approach. In Proceedings of the IEEE International Workshop on Computational Advances in MultiSensor Adaptive Processing, Puerto Vallarta, Mexico, 13–15 December 2005; pp. 129–132. [Google Scholar]
- Qi, L. Eigenvalues of a real supersymmetric tensor. J. Symb. Comput. 2005, 40, 1302–1324. [Google Scholar] [CrossRef]
- Li, C.; Wang, F.; Zhao, J.; Zhu, Y.; Li, Y. Criterions for the positive definiteness of real supersymmetric tensors. J. Comput. Appl. Math. 2014, 255, 1–14. [Google Scholar] [CrossRef]
- Bu, C.; Wei, Y.P.; Sun, L.; Zhou, J. Brualdi-type eigenvalue inclusion sets of tensors. Linear Algebra Appl. 2015, 480, 168–175. [Google Scholar] [CrossRef]
- Bu, C.; Jin, X.; Li, H.; Deng, C. Brauer-type eigenvalue inclusion sets and the spectral radius of tensors. Linear Algebra Appl. 2017, 512, 234–248. [Google Scholar] [CrossRef]
- Li, C.; Li, Y.; Kong, X. New eigenvalue inclusion sets for tensors. Numer. Linear Algebra Appl. 2014, 21, 39–50. [Google Scholar] [CrossRef]
- Li, C.; Jiao, A.; Li, Y. An S-type eigenvalue localization set for tensors. Linear Algebra Appl. 2016, 493, 469–483. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Q.; Qi, L. Programmable criteria for strong H-tensors. Numer. Algorithms 2017, 1, 1–23. [Google Scholar]
- Chen, Y.; Qi, L.; Wang, Q. Positive semi-definiteness and sum-of-squares property of fourth order four dimensional Hankel tensors. J. Comput. Appl. Math. 2016, 302, 356–368. [Google Scholar] [CrossRef]
- Barmpoutis, A.; Hwang, M.S.; Howland, D.; Forder, J.R.; Vemuri, B.C. Regularized positive-definite fourth order tensor filed estimation from DW-MRI. Neuroimage 2009, 45, S153–S162. [Google Scholar] [CrossRef]
- Qi, L.; Yu, G.; Wu, E.X. Higher order positive semidefinite diffusion tensor imaging. SIAM J. Imaging Sci. 2010, 3, 416–433. [Google Scholar] [CrossRef]
- Buscarino, A.; Fortuna, L.; Frasca, M.; Xibilia, M.G. Invariance of characteristic values and L∞ norm under lossless positive real transformations. J. Franklin Inst. 2016, 353, 2057–2073. [Google Scholar] [CrossRef]
- Barmpoutis, A.; Jian, B.; Vemuri, B.C.; Shepherd, T.M. Symmetric positive 4th order tensors and their estimation from diffusion weighted MRI. In Information Processing and Medical Imaging; Karssemeijer, M., Lelieveldt, B., Eds.; Springer: Berlin, Germany, 2007; pp. 308–319. [Google Scholar]
- Ghosh, A.; Descoteaux, M.; Deriche, R. Riemannian framework for estimating symmetric positive definite 4th order diffusion tensors. In Medical Image Com- puting and Computer-Assisted Intervention MICCAI 2008; Metaxas, D., Axel, L., Fichtinger, G., Szekeley, G., Eds.; Springer-Verlag: Berlin, Germany, 2008; pp. 858–865. [Google Scholar]
- Wang, G.; Zhou, G.; Caccetta, L. Z-eigenvalue inclusion theorems for tensors. Discret. Contin. Dyn. Syst. Ser. B 2017, 22, 187–198. [Google Scholar] [CrossRef]
- Song, Y.; Qi, L. Spectral properties of positively homogeneous operators induced by higher order tensors. SIAM J. Matrix Anal. Appl. 2013, 34, 1581–1595. [Google Scholar] [CrossRef]
- Li, W.; Liu, D.; Vong, S.-W. Z-eigenpair bounds for an irreducible nonnegative tensor. Linear Algebra Appl. 2015, 483, 182–199. [Google Scholar] [CrossRef]
- He, J. Bounds for the largest eigenvalue of nonnegative tensors. J. Comput. Anal. Appl. 2016, 20, 1290–1301. [Google Scholar]
- He, J.; Liu, Y.-M.; Ke, H.; Tian, J.-K.; Li, X. Bounds for the Z-spectral radius of nonnegative tensors. Springerplus 2016, 5, 1727. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Li, Y. Bounds for the Z-eigenpair of general nonnegative tensors. Open Math. 2016, 14, 181–194. [Google Scholar] [CrossRef]
- He, J.; Huang, T.-Z. Upper bound for the largest Z-eigenvalue of positive tensors. Appl. Math. Lett. 2014, 38, 110–114. [Google Scholar] [CrossRef]
- Zhao, J. A new Z-eigenvalue localization set for tensors. J. Inequal. Appl. 2017, 2017, 85. [Google Scholar] [CrossRef]
- Chang, K.C.; Pearson, K.J.; Zhang, T. Some variational principles for Z-eigenvalues of nonnegative tensors. Linear Algebra Appl. 2013, 438, 4166–4182. [Google Scholar] [CrossRef]
- Sang, C. A new Brauer-type Z -eigenvalue inclusion set for tensors. Numer. Algorithms 2018, 1, 1–14. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.; Liu, Y.; Tian, J.; Zhang, Z. New Sufficient Condition for the Positive Definiteness of Fourth Order Tensors. Mathematics 2018, 6, 303. https://doi.org/10.3390/math6120303
He J, Liu Y, Tian J, Zhang Z. New Sufficient Condition for the Positive Definiteness of Fourth Order Tensors. Mathematics. 2018; 6(12):303. https://doi.org/10.3390/math6120303
Chicago/Turabian StyleHe, Jun, Yanmin Liu, Junkang Tian, and Zhuanzhou Zhang. 2018. "New Sufficient Condition for the Positive Definiteness of Fourth Order Tensors" Mathematics 6, no. 12: 303. https://doi.org/10.3390/math6120303
APA StyleHe, J., Liu, Y., Tian, J., & Zhang, Z. (2018). New Sufficient Condition for the Positive Definiteness of Fourth Order Tensors. Mathematics, 6(12), 303. https://doi.org/10.3390/math6120303



