Strong Convergence Theorems for Fixed Point Problems for Nonexpansive Mappings and Zero Point Problems for Accretive Operators Using Viscosity Implicit Midpoint Rules in Banach Spaces

Abstract

This paper uses the viscosity implicit midpoint rule to find common points of the fixed point set of a nonexpansive mapping and the zero point set of an accretive operator in Banach space. Under certain conditions, this paper obtains the strong convergence results of the proposed algorithm and improves the relevant results of researchers in this field. In the end, this paper gives numerical examples to support the main results.

1. Introduction

Let $E$ be a Banach Space and $E^{*}$ the dual space. $J$ denotes the normalized duality mapping from $E$ to $2^{E^{*}}$ and is defined by

$$J(x)=\{f\in E^{*}:<x,f>={\Vert x\Vert }^2={\Vert f\Vert }^2\},x\in E.$$

Let $C$ be a nonempty set of $E$. A mapping $f:C\to C$ is contractive, if $\Vert f(x)-f(y)\Vert \le k\Vert x-y\Vert$, $\forall x,y\in C$, $k\in [0,1)$. A mapping $S:C\to C$ is nonexpansive, if $\Vert S(x)-S(y)\Vert \le \Vert x-y\Vert$, $\forall x,y\in C$. Let $F(S)$ denote the fixed point set of $S$.

$A:C\to E$ is called accretive operator, if there exists $j(x-y)\in J(x-y)$ such that $⟨Ax-Ay,j(x-y)⟩\ge 0$, for any $x,y\in C$. If $R(I+rA)=E$, $\forall r>0$, then $A$ is called $m$-accretive operator. $J_r:R(I+rA)\to D(A)$ is called the resolvent of $m$-accretive operator $A$ and defined by $J_r={(I+rA)}^{-1}$, $\forall r>0$. It is well known that $J_r$ is nonexpansive mapping and $N(A)=F(J_r)$, where $N(A)=\{x\in E:0\in Ax\}$ and $F(J_r)$ is the fixed point set of $J_r$. So fixed point theory of nonexpansive mappings has been applied to zero point problem of accretive operator, see [1,2,3,4,5,6] and the references therein.

The implicit midpoint rule is one of the powerful methods for solving ordinary differential equations; see [7,8,9,10,11,12] and the references therein. Moreover, viscosity iterative algorithms for finding common fixed points for nonlinear operators and solutions of variational inequality problems have been researched by many authors.

In 2009, Chang et al. [1] proposed a viscosity iterative algorithm for accretive operator and nonexpansive mapping:

$$\{\begin{array}{c}{x}_0=x\in C,\\ y_n={\beta }_n{x}_n+(1-{\beta }_n)S{J}_r{x}_n,\\ x_{n+1}={\alpha }_{n}f(x_n)+(1-{\alpha }_n)y_n,\forall n\ge 0.\end{array}$$

In 2010, Jung [13] proposed a composite iterative algorithm by viscosity method for finding the zero point of an accretive operator:

$$\{\begin{array}{c}{x}_0=x\in C,\\ y_n={\beta }_n{x}_n+(1-{\beta }_n)J_{r_n}{x}_n,\\ x_{n+1}={\alpha }_{n}f(x_n)+(1-{\alpha }_n)y_n,\forall n\ge 0.\end{array}$$

In 2016, Jung [14] extended the related results and proposed an iterative algorithm for finding common point of zero of accretive operator and fixed point of nonexpansive mapping:

$$\begin{array}{c}{x}_{n+1}=J_{r_n}({\alpha }_{n}f(x_n)+(1-{\alpha }_n)S{x}_n),\forall n\ge 0,\\ x_{n+1}=J_{r_n}({\alpha }_{n}f(x_n)+(1-{\alpha }_n)S{x}_n+e_n),\forall n\ge 0.\end{array}$$

In 2017, Li [15] introduced a new iterative algorithm in a real reflexive Banach space $E$ with the uniformly $G\widehat{a}teaux$ differentiable norm and $C$ is a nonempty closed convex subset of $E$ which has the normal structure:

$$\{\begin{array}{c}{x}_0=x\in C,\\ y_n={\beta }_{n}S{J}_{r_n}(e_n+x_n)+(1-{\beta }_n)x_n,\\ x_{n+1}={\alpha }_{n}T(x_n)+(1-{\alpha }_n)y_n,\forall n\ge 0.\end{array}$$

In 2015, Xu et al. [16] used viscosity iterative algorithm to implicit midpoint rule for nonexpansive mapping in Hilbert space and proposed viscosity implicit midpoint rule: $\left\{x_n\right\}$ was generated by the following

$$x_{n+1}={\alpha }_{n}f(x_n)+(1-{\alpha }_n)T\left(\frac{x_n+x_{n+1}}{2}\right),n\ge 0.$$

Under some conditions on $\left\{{\alpha }_n\right\}$, they obtained that $\left\{x_n\right\}$ strongly converged to $q\in F(T)$, and $q$ was the solution of variational inequality $⟨(I-f)q,x-q⟩\ge 0$, $x\in F(T)$.

In 2017, Luo et al. [17] extended the results of Xu et al. [16] from Hilbert space to uniformly smooth Banach space: $\left\{x_n\right\}$ was generated by the following

$$x_{n+1}={\alpha }_{n}f(x_n)+(1-{\alpha }_n)T\left(\frac{x_n+x_{n+1}}{2}\right),n\ge 0.$$

Under some conditions, they obtained that $\left\{x_n\right\}$ strongly converged to $q\in F(T)$, and $q$ was the solution of variational inequality $⟨(I-f)q,j(x-q)⟩\ge 0$, $x\in F(T)$.

Motivated and inspired by the above papers, this paper uses the viscosity implicit midpoint rule to find common points of the fixed point set of a nonexpansive mapping and the zero point set of an accretive operator in Banach space and obtains the strong convergence results and improves the previous results. Finally, this paper gives numerical examples to support the main results.

2. Preliminaries

For all $\epsilon \in [0,2]$, $\Vert x\Vert =\Vert y\Vert =1$, $\Vert x-y\Vert \ge \epsilon$, if there exists ${\delta }_{\epsilon }>0$ such that $\frac{\Vert x+y\Vert }{2}<1-{\delta }_{\epsilon }$, then $E$ is called uniformly convex. A Banach space is uniformly convex if and only if there exists a continuous strictly increasing convex function $g:[0,+\infty )\to [0,+\infty )$ with $g(0)=0$ such that

$${\Vert \lambda x+(1-\lambda )y\Vert }^2\le \lambda {\Vert x\Vert }^2+(1-\lambda ){\Vert y\Vert }^2-\lambda (1-\lambda )g(\Vert x-y\Vert ).$$

(1)

For each $x,y\in U$, $U=\{x\in E:\Vert x\Vert =1\}$, if $\underset{t\to 0}{\lim }\frac{\Vert x+ty\Vert -\Vert x\Vert }{t}$ exists, then $E$ is said to be have a $G\widehat{a}teaux$ differentiable norm. If for each $y\in U$, the limit is attained uniformly for $x\in U$, then $E$ is said to be have a uniformly $G\widehat{a}teaux$ differentiable norm. It is well known that if $E$ has uniformly $G\widehat{a}teaux$ differentiable norm, then $J$ is single valued and norm-to-weak* uniformly continuous on each bounded subset of $E$, see [18].

Let $C$ be a closed convex subset of $E$. If for each bounded closed convex subset $D$ of $C$ which contains at least two points, there exists one element $x\in D$ which is not a diametral point of $D$ such that $diam(D)>\sup \{\Vert x-y\Vert :y\in D\}$, where $diam(D)$ is the diameter of $D$, then $C$ is said to have normal structure.

We need the following lemmas for the proof of our main results.

Lemma 1 

[19]. For $\lambda ,\mu >0$, $x\in E$, so $J_{\lambda }x=J_{\mu }\left(\frac{\mu }{\lambda }x+\left(1-\frac{\mu }{\lambda }\right)J_{\lambda }x\right)$.

Lemma 2 

[20]. Let $\left\{a_n\right\},\left\{b_n\right\},\left\{c_n\right\}$ be three nonnegative real sequences satisfying

$$a_{n+1}\le (1-t_n)a_n+b_n+c_n,\forall n\ge 0,$$

where $\left\{t_n\right\}\subset (0,1)$. If the following conditions are satisfied ${\displaystyle \sum _{n=0}^{\infty }{t}_n}=\infty$; $b_n=o(t_n)$; ${\displaystyle \sum _{n=1}^{\infty }{c}_n}<\infty$. So $\underset{n\to \infty }{\lim }{a}_n=0$.

Lemma 3 

[4,21]. Let $E$ be a real reflexive Banach space with the uniformly $G\widehat{a}teaux$ differentiable norm and $C$ be nonempty closed convex subset of $E$ which has normal structure. Let $S:C\to C$ be a nonexpansive mapping with a fixed point and $T:C\to C$ be a fixed contraction with the coefficient $\tau \in (0,1)$. Let $\left\{x_{S,T,t}\right\}$ be an sequence defined as follows

$$x_{S,T,t}=tT{x}_t+(1-t)S{x}_{S,T,t},$$

where $t\in (0,1)$. Then $\left\{x_t\right\}$ converges strongly as $t\to 0$ to a fixed point $x^{*}$ of $S$, which is the unique solution in $F(S)$ to the following variational inequality

$$⟨T{x}^{*}-x^{*},j(x^{*}-p)⟩\ge 0,\forall p\in F(S).$$

Lemma 4 

[2]. In a Banach space $E$, there holds the inequality

$${\Vert x+y\Vert }^2\le {\Vert x\Vert }^2+2⟨y,j(x+y)⟩,\forall x,y\in E,$$

where $j(x+y)\in J(x+y)$.

3. Main Results

Theorem 1.

Let$E$be a reflexive and uniformly convex Banach space which has uniformly$G\widehat{a}teaux$differentiable norm and$C$be a nonempty closed convex subset of$E$which has normal structure. Let$f:C\to C$be a contractive mapping with$k\in [0,1)$,$A$be a$m$-accretive operator in$E$and$S:C\to C$be a nonexpansive mapping with$F(S)\cap N(A)\ne \varnothing$. For any$x_0\in C$and$\forall n\ge 0$,$\left\{x_n\right\}$is generated by

$$\{\begin{array}{l}{y}_n={\beta }_n\left(\frac{x_n+x_{n+1}}{2}\right)+(1-{\beta }_n)J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right),\hfill \\ x_{n+1}={\alpha }_{n}f{x}_n+(1-{\alpha }_n)S{y}_n,\hfill \end{array}$$

(2)

where$\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\}\subset (0,1)$and$\left\{r_n\right\}\subset (0,1)$satisfy the following conditions:

(i)$\underset{n\to \infty }{\lim }{\alpha }_n=0$,${\displaystyle \sum _{n=0}^{\infty }{\alpha }_n}=\infty$,$\left|{\alpha }_n-{\alpha }_{n-1}\right|=o({\alpha }_n)$; (ii)${\displaystyle \sum _{n=1}^{\infty }\left|{\beta }_n-{\beta }_{n-1}\right|}<\infty$; (iii)$\underset{n\to \infty }{\lim }{r}_n=r$,${\displaystyle \sum _{n=1}^{\infty }\left|r_n-r_{n-1}\right|}<\infty$.

Then$\left\{x_n\right\}$and$\left\{y_n\right\}$converge strongly to$q\in F(S)\cap N(A)$, where$q$is the unique solution of the variational inequality$⟨(I-f)q,J_{\varphi }(q-p)⟩\le 0$,$\forall p\in F(S)\cap N(A)$.

Proof. 

The proof is split into eleven steps.

Step 1: Show that $\left\{x_n\right\}$ and $\left\{y_n\right\}$ are bounded.

Take $p\in F(S)\cap N(A)$, then we have

$$\begin{array}{ll}\Vert y_n-p\Vert & \le {\beta }_n\Vert \frac{x_n+x_{n+1}}{2}-p\Vert +(1-{\beta }_n)\Vert J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)-p\Vert \\ & \le {\beta }_n\Vert \frac{x_n+x_{n+1}}{2}-p\Vert +(1-{\beta }_n)\Vert \frac{x_n+x_{n+1}}{2}-p\Vert \\ & \le \frac{1}{2}\Vert x_n-p\Vert +\frac{1}{2}\Vert x_{n+1}-p\Vert ,\end{array}$$

and then we get

$$\begin{array}{ll}\Vert x_{n+1}-p\Vert & \le {\alpha }_n\Vert f{x}_n-p\Vert +(1-{\alpha }_n)\Vert S{y}_n-p\Vert \\ & \le k{\alpha }_n\Vert x_n-p\Vert +{\alpha }_n\Vert fp-p\Vert +(1-{\alpha }_n)\Vert y_n-p\Vert \\ & \le k{\alpha }_n\Vert x_n-p\Vert +{\alpha }_n\Vert fp-p\Vert +\frac{1-{\alpha }_n}{2}\Vert x_n-p\Vert +\frac{1-{\alpha }_n}{2}\Vert x_{n+1}-p\Vert \\ & =\left(k{\alpha }_n+\frac{1-{\alpha }_n}{2}\right)\Vert x_n-p\Vert +{\alpha }_n\Vert fp-p\Vert +\frac{1-{\alpha }_n}{2}\Vert x_{n+1}-p\Vert .\end{array}$$

It follows that

$$\begin{array}{ll}\Vert x_{n+1}-p\Vert & \le \frac{k{\alpha }_n+\frac{1-{\alpha }_n}{2}}{\frac{1+{\alpha }_n}{2}}\Vert x_n-p\Vert +\frac{2{\alpha }_n}{1+{\alpha }_n}\Vert fp-p\Vert \\ & =\left[1-\frac{2{\alpha }_n(1-k)}{1+{\alpha }_n}\right]\Vert x_n-p\Vert +\frac{2{\alpha }_n(1-k)}{1+{\alpha }_n}\frac{\Vert fp-p\Vert }{1-k}\\ & \le \max \left\{\Vert x_0-p\Vert ,\frac{\Vert fp-p\Vert }{1-k}\right\}.\end{array}$$

Then $\left\{x_n\right\}$ and $\left\{y_n\right\}$ are bounded. So $\left\{f{x}_n\right\}$, $\left\{f{y}_n\right\}$, $\left\{S{x}_n\right\}$, $\left\{S{y}_n\right\}$, $\left\{J_{r_n}{x}_n\right\}$ and $\left\{J_{r_n}{y}_n\right\}$ are also bounded.

Step 2: Show that $\underset{n\to \infty }{\lim }\Vert x_{n+1}-x_n\Vert =0$.

From (2), we have

$$\begin{array}{ll}\Vert x_{n+1}-x_n\Vert & =\Vert {\alpha }_{n}f{x}_n+(1-{\alpha }_n)S{y}_n-{\alpha }_{n-1}f{x}_{n-1}-(1-{\alpha }_{n-1})S{y}_{n-1}\Vert \\ & \le {\alpha }_n\Vert f{x}_n-f{x}_{n-1}\Vert +\left|{\alpha }_n-{\alpha }_{n-1}\right|\cdot \Vert f{x}_{n-1}-S{y}_{n-1}\Vert +(1-{\alpha }_n)\Vert S{y}_n-S{y}_{n-1}\Vert \\ & \le k{\alpha }_n\Vert x_n-x_{n-1}\Vert +\left|{\alpha }_n-{\alpha }_{n-1}\right|\cdot \Vert f{x}_{n-1}-S{y}_{n-1}\Vert +(1-{\alpha }_n)\Vert y_n-y_{n-1}\Vert .\end{array}$$

(3)

From (2), we have

$$\begin{array}{ll}\Vert y_n-y_{n-1}\Vert & =\Vert {\beta }_n\left(\frac{x_n+x_{n+1}}{2}\right)+(1-{\beta }_n)J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)-{\beta }_{n-1}\left(\frac{x_{n-1}+x_n}{2}\right)\\ & -(1-{\beta }_{n-1})J_{r_{n-1}}\left(\frac{x_{n-1}+x_n}{2}\right)\Vert \\ & \le {\beta }_n\Vert \frac{x_{n+1}-x_{n-1}}{2}\Vert +\left|{\beta }_n-{\beta }_{n-1}\right|\cdot \Vert \frac{x_{n-1}+x_n}{2}-J_{r_{n-1}}\left(\frac{x_{n-1}+x_n}{2}\right)\Vert \\ & +(1-{\beta }_n)\Vert J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)-J_{r_{n-1}}\left(\frac{x_{n-1}+x_n}{2}\right)\Vert .\end{array}$$

(4)

From Lemma 1, we have

$$\begin{array}{l}\hspace{1em}\Vert J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)-J_{r_{n-1}}\left(\frac{x_{n-1}+x_n}{2}\right)\Vert \\ =\Vert J_{r_{n-1}}\left(\frac{r_{n-1}}{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)+\left(1-\frac{r_{n-1}}{r_n}\right)J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)\right)-J_{r_{n-1}}\left(\frac{x_{n-1}+x_n}{2}\right)\Vert \\ \le \Vert \frac{r_{n-1}}{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)+\left(1-\frac{r_{n-1}}{r_n}\right)J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)-\frac{x_{n-1}+x_n}{2}\Vert \\ =\Vert \frac{r_{n-1}}{r_n}\left(\frac{x_{n+1}-x_{n-1}}{2}\right)+\left(1-\frac{r_{n-1}}{r_n}\right)\left(J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)-\frac{x_{n-1}+x_n}{2}\right)\Vert \\ \le \frac{r_{n-1}}{r_n}\Vert \frac{x_{n+1}-x_{n-1}}{2}\Vert +\left|1-\frac{r_{n-1}}{r_n}\right|\cdot \Vert J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)-\frac{x_n+x_{n+1}}{2}\Vert +\left|1-\frac{r_{n-1}}{r_n}\right|\cdot \Vert \frac{x_{n+1}-x_{n-1}}{2}\Vert \\ =\Vert \frac{x_{n+1}-x_{n-1}}{2}\Vert +\left|1-\frac{r_{n-1}}{r_n}\right|\cdot \Vert J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)-\frac{x_n+x_{n+1}}{2}\Vert .\end{array}$$

(5)

Put (4) and (5) into (3), we get

$$\begin{array}{ll}\Vert x_{n+1}-x_n\Vert & \le k{\alpha }_n\Vert x_n-x_{n-1}\Vert +\left|{\alpha }_n-{\alpha }_{n-1}\right|\cdot \Vert f{x}_{n-1}-S{y}_{n-1}\Vert +(1-{\alpha }_n)\Vert \frac{x_{n+1}-x_{n-1}}{2}\Vert \\ & +(1-{\alpha }_n)\left|{\beta }_n-{\beta }_{n-1}\right|\cdot \Vert \frac{x_{n-1}+x_n}{2}-J_{r_{n-1}}\left(\frac{x_{n-1}+x_n}{2}\right)\Vert \\ & +(1-{\alpha }_n)(1-{\beta }_n)\left|1-\frac{r_{n-1}}{r_n}\right|\cdot \Vert \frac{x_n+x_{n+1}}{2}-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)\Vert \\ & \le k{\alpha }_n\Vert x_n-x_{n-1}\Vert +\frac{1-{\alpha }_n}{2}\Vert x_{n+1}-x_n\Vert +\frac{1-{\alpha }_n}{2}\Vert x_n-x_{n-1}\Vert +\left|{\alpha }_n-{\alpha }_{n-1}\right|M_1\\ & +\left[(1-{\alpha }_n)\left|{\beta }_n-{\beta }_{n-1}\right|+(1-{\alpha }_n)(1-{\beta }_n)\left|1-\frac{r_{n-1}}{r_n}\right|\right]M_2\\ & =\left(k{\alpha }_n+\frac{1-{\alpha }_n}{2}\right)\Vert x_n-x_{n-1}\Vert +\frac{1-{\alpha }_n}{2}\Vert x_n-x_{n-1}\Vert +\left|{\alpha }_n-{\alpha }_{n-1}\right|M_1\\ & +\left[(1-{\alpha }_n)\left|{\beta }_n-{\beta }_{n-1}\right|+(1-{\alpha }_n)(1-{\beta }_n)\left|1-\frac{r_{n-1}}{r_n}\right|\right]M_2.\end{array}$$

It follows that

$$\begin{array}{ll}\Vert x_{n+1}-x_n\Vert & \le \frac{k{\alpha }_n+\frac{1-{\alpha }_n}{2}}{\frac{1+{\alpha }_n}{2}}\Vert x_n-x_{n-1}\Vert +\frac{2\left|{\alpha }_n-{\alpha }_{n-1}\right|}{1+{\alpha }_n}{M}_1\\ & +\frac{2(1-{\alpha }_n)\left|{\beta }_n-{\beta }_{n-1}\right|+2(1-{\alpha }_n)(1-{\beta }_n)\left|1-\frac{r_{n-1}}{r_n}\right|}{1+{\alpha }_n}{M}_2\\ & =\left[1-\frac{2{\alpha }_n(1-k)}{1+{\alpha }_n}\right]\Vert x_n-x_{n-1}\Vert +\frac{2\left|{\alpha }_n-{\alpha }_{n-1}\right|}{1+{\alpha }_n}{M}_1\\ & +\frac{2(1-{\alpha }_n)\left|{\beta }_n-{\beta }_{n-1}\right|+2(1-{\alpha }_n)(1-{\beta }_n)\left|1-\frac{r_{n-1}}{r_n}\right|}{1+{\alpha }_n}{M}_2,\end{array}$$

where $M_1=\max \Vert f{x}_{n-1}-S{y}_{n-1}\Vert$ and $M_2=\max \Vert \frac{x_n+x_{n+1}}{2}-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)\Vert$.

Take $t_n=\frac{2{\alpha }_n(1-k)}{1+{\alpha }_n}$, then $t_n>{\alpha }_n(1-k)$. From ${\displaystyle \sum _{n=0}^{\infty }{\alpha }_n}=\infty$, so ${\displaystyle \sum _{n=0}^{\infty }{t}_n}=\infty$.

Take $b_n=\frac{2\left|{\alpha }_n-{\alpha }_{n-1}\right|}{1+{\alpha }_n}{M}_1$, then $\frac{b_n}{t_n}=\frac{\left|{\alpha }_n-{\alpha }_{n-1}\right|M_1}{{\alpha }_n(1-k)}$. From $\left|{\alpha }_n-{\alpha }_{n-1}\right|=o({\alpha }_n)$, so $b_n=o(t_n)$.

Take $c_n=\frac{2(1-{\alpha }_n)\left|{\beta }_n-{\beta }_{n-1}\right|+2(1-{\alpha }_n)(1-{\beta }_n)\left|1-\frac{r_{n-1}}{r_n}\right|}{1+{\alpha }_n}{M}_2$. From $\underset{n\to \infty }{\lim }{r}_n=r$, then $c_n<2M_2\left(\left|{\beta }_n-{\beta }_{n-1}\right|+\frac{\left|r_n-r_{n-1}\right|}{r-\epsilon }\right)$$\left(\forall \epsilon >0\right)$. From ${\displaystyle \sum _{n=1}^{\infty }\left|{\beta }_n-{\beta }_{n-1}\right|}<\infty$ and ${\displaystyle \sum _{n=1}^{\infty }\left|r_n-r_{n-1}\right|}<\infty$, so ${\displaystyle \sum _{n=1}^{\infty }{c}_n}<\infty$.

From Lemma 2, we get $\underset{n\to \infty }{\lim }\Vert x_{n+1}-x_n\Vert =0$.

Step 3: Show that $\underset{n\to \infty }{\lim }\Vert x_n-J_{r_n}{x}_n\Vert =0$.

Because ${\Vert \cdot \Vert }^2$ is convex function and (1), so we have

$$\begin{array}{ll}{\Vert x_{n+1}-p\Vert }^2& \le {\alpha }_n{\Vert f{x}_n-p\Vert }^2+(1-{\alpha }_n){\Vert S{y}_n-p\Vert }^2\\ & \le {\alpha }_n{\Vert f{x}_n-p\Vert }^2+(1-{\alpha }_n){\Vert y_n-p\Vert }^2\\ & \le {\alpha }_n{\Vert f{x}_n-p\Vert }^2+(1-{\alpha }_n)[{\beta }_n{\Vert \frac{x_n+x_{n+1}}{2}-p\Vert }^2+(1-{\beta }_n){\Vert J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)-p\Vert }^2\\ & -{\beta }_n(1-{\beta }_n)g\left(\Vert \frac{x_n+x_{n+1}}{2}-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)\Vert \right)]\\ & \le {\alpha }_n{\Vert f{x}_n-p\Vert }^2+(1-{\alpha }_n){\Vert \frac{x_n+x_{n+1}}{2}-p\Vert }^2\\ & -(1-{\alpha }_n){\beta }_n(1-{\beta }_n)g\left(\Vert \frac{x_n+x_{n+1}}{2}-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)\Vert \right)\\ & \le {\alpha }_n{\Vert f{x}_n-p\Vert }^2+\frac{1-{\alpha }_n}{2}{\Vert x_n-p\Vert }^2+\frac{1-{\alpha }_n}{2}{\Vert x_{n+1}-p\Vert }^2\\ & -(1-{\alpha }_n){\beta }_n(1-{\beta }_n)g\left(\Vert \frac{x_n+x_{n+1}}{2}-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)\Vert \right).\end{array}$$

It follows that

$$\begin{array}{ll}{\Vert x_{n+1}-p\Vert }^2& \le \frac{1-{\alpha }_n}{1+{\alpha }_n}{\Vert x_n-p\Vert }^2+\frac{2{\alpha }_n}{1+{\alpha }_n}{\Vert f{x}_n-p\Vert }^2\\ & -\frac{2(1-{\alpha }_n){\beta }_n(1-{\beta }_n)}{1+{\alpha }_n}g\left(\Vert \frac{x_n+x_{n+1}}{2}-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)\Vert \right)\\ & \le {\Vert x_n-p\Vert }^2+\frac{2{\alpha }_n}{1+{\alpha }_n}{\Vert f{x}_n-p\Vert }^2\\ & -\frac{2(1-{\alpha }_n){\beta }_n(1-{\beta }_n)}{1+{\alpha }_n}g\left(\Vert \frac{x_n+x_{n+1}}{2}-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)\Vert \right).\end{array}$$

Then we have

$$\begin{array}{ll}& \frac{2(1-{\alpha }_n){\beta }_n(1-{\beta }_n)}{1+{\alpha }_n}g\left(\Vert \frac{x_n+x_{n+1}}{2}-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)\Vert \right)-\frac{2{\alpha }_n}{1+{\alpha }_n}{\Vert f{x}_n-p\Vert }^2\\ \le & {\Vert x_n-p\Vert }^2-{\Vert x_{n+1}-p\Vert }^2.\end{array}$$

If $\frac{2(1-{\alpha }_n){\beta }_n(1-{\beta }_n)}{1+{\alpha }_n}g\left(\Vert \frac{x_n+x_{n+1}}{2}-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)\Vert \right)$$\le \frac{2{\alpha }_n}{1+{\alpha }_n}{\Vert f{x}_n-p\Vert }^2$, so from $\underset{n\to \infty }{\lim }{\alpha }_n=0$ and the boundedness of $\left\{f{x}_n\right\}$, we get $\underset{n\to \infty }{\lim }g\left(\Vert \frac{x_n+x_{n+1}}{2}-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)\Vert \right)=0$.

If $\frac{2(1-{\alpha }_n){\beta }_n(1-{\beta }_n)}{1+{\alpha }_n}g\left(\Vert \frac{x_n+x_{n+1}}{2}-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)\Vert \right)$$>\frac{2{\alpha }_n}{1+{\alpha }_n}{\Vert f{x}_n-p\Vert }^2$, so

$$\begin{array}{l}{\displaystyle \sum _{n=0}^N\left[\frac{2(1-{\alpha }_n){\beta }_n(1-{\beta }_n)}{1+{\alpha }_n}g\left(\Vert \frac{x_n+x_{n+1}}{2}-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)\Vert \right)-\frac{2{\alpha }_n}{1+{\alpha }_n}{\Vert f{x}_n-p\Vert }^2\right]}\\ \le {\Vert x_0-p\Vert }^2-{\Vert x_{N+1}-p\Vert }^2\le {\Vert x_0-p\Vert }^2.\end{array}$$

Then ${\displaystyle \sum _{n=0}^{\infty }\left[\frac{2(1-{\alpha }_n){\beta }_n(1-{\beta }_n)}{1+{\alpha }_n}g\left(\Vert \frac{x_n+x_{n+1}}{2}-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)\Vert \right)-\frac{2{\alpha }_n}{1+{\alpha }_n}{\Vert f{x}_n-p\Vert }^2\right]}<\infty$.

So we get

$$\underset{n\to \infty }{\lim }\left[\frac{2(1-{\alpha }_n){\beta }_n(1-{\beta }_n)}{1+{\alpha }_n}g\left(\Vert \frac{x_n+x_{n+1}}{2}-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)\Vert \right)-\frac{2{\alpha }_n}{1+{\alpha }_n}{\Vert f{x}_n-p\Vert }^2\right]=0,$$

and then $\underset{n\to \infty }{\lim }g\left(\Vert \frac{x_n+x_{n+1}}{2}-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)\Vert \right)=0$.

From the property of $g$, so we get $\underset{n\to \infty }{\lim }\Vert \frac{x_n+x_{n+1}}{2}-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)\Vert =0$.

We also have

$$\begin{array}{ll}\Vert x_n-J_{r_n}{x}_n\Vert & \le \Vert x_n-\frac{x_n+x_{n+1}}{2}\Vert +\Vert \frac{x_n+x_{n+1}}{2}-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)\Vert +\Vert J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)-J_{r_n}{x}_n\Vert \\ & \le \Vert x_{n+1}-x_n\Vert +\Vert \frac{x_n+x_{n+1}}{2}-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)\Vert .\end{array}$$

Then from step 2, we get $\underset{n\to \infty }{\lim }\Vert x_n-J_{r_n}{x}_n\Vert =0$.

Step 4: Show that $\underset{n\to \infty }{\lim }\Vert y_n-S{y}_n\Vert =0$.

$$\begin{array}{ll}\Vert y_n-S{y}_n\Vert & \le {\beta }_n\Vert \frac{x_n+x_{n+1}}{2}-S{y}_n\Vert +(1-{\beta }_n)\Vert J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)-S{y}_n\Vert \\ & \le \Vert \frac{x_n+x_{n+1}}{2}-S{y}_n\Vert +(1-{\beta }_n)\Vert J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)-\frac{x_n+x_{n+1}}{2}\Vert \\ & \le \Vert \frac{x_n+x_{n+1}}{2}-x_{n+1}\Vert +\Vert x_{n+1}-S{y}_n\Vert +(1-{\beta }_n)\Vert J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)-\frac{x_n+x_{n+1}}{2}\Vert \\ & =\frac{1}{2}\Vert x_n-x_{n+1}\Vert +{\alpha }_n\Vert f{x}_n-S{y}_n\Vert +(1-{\beta }_n)\Vert J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)-\frac{x_n+x_{n+1}}{2}\Vert .\end{array}$$

From steps 2 and 3, $\underset{n\to \infty }{\lim }{\alpha }_n=0$ and the boundedness of $\left\{f{x}_n\right\}$ and $\left\{S{y}_n\right\}$, we get $\underset{n\to \infty }{\lim }\Vert y_n-S{y}_n\Vert =0$.

Step 5: Show that $\underset{n\to \infty }{\lim }\Vert x_n-y_n\Vert =0$.

$$\begin{array}{ll}\Vert x_n-y_n\Vert & \le \Vert x_n-x_{n+1}\Vert +\Vert x_{n+1}-S{y}_n\Vert +\Vert S{y}_n-y_n\Vert \\ & =\Vert x_n-x_{n+1}\Vert +{\alpha }_n\Vert f{x}_n-S{y}_n\Vert +\Vert S{y}_n-y_n\Vert .\end{array}$$

From steps 2 and 4, we get $\underset{n\to \infty }{\lim }\Vert x_n-y_n\Vert =0$.

Step 6: Show that $\underset{n\to \infty }{\lim }\Vert y_n-J_{r_n}{y}_n\Vert =0$.

$$\begin{array}{ll}\Vert y_n-J_{r_n}{y}_n\Vert & \le \Vert y_n-x_n\Vert +\Vert x_n-J_{r_n}{x}_n\Vert +\Vert J_{r_n}{x}_n-J_{r_n}{y}_n\Vert \\ & \le 2\Vert y_n-x_n\Vert +\Vert x_n-J_{r_n}{x}_n\Vert .\end{array}$$

From steps 3 and 5, we get $\underset{n\to \infty }{\lim }\Vert y_n-J_{r_n}{y}_n\Vert =0$.

Step 7: Show that $\underset{n\to \infty }{\lim }\Vert x_n-S{x}_n\Vert =0$.

$$\begin{array}{ll}\Vert x_n-S{x}_n\Vert & \le \Vert x_n-y_n\Vert +\Vert y_n-S{y}_n\Vert +\Vert S{y}_n-S{x}_n\Vert \\ & \le 2\Vert x_n-y_n\Vert +\Vert y_n-S{y}_n\Vert .\end{array}$$

From steps 4 and 5, we get $\underset{n\to \infty }{\lim }\Vert x_n-S{x}_n\Vert =0$.

Step 8: Show that $\underset{n\to \infty }{\lim }\Vert y_n-J_r{y}_n\Vert =0$.

$$\begin{array}{ll}\Vert y_n-J_r{y}_n\Vert & \le \Vert y_n-J_{r_n}{y}_n\Vert +\Vert J_{r_n}{y}_n-J_r{y}_n\Vert \\ & =\Vert y_n-J_{r_n}{y}_n\Vert +\Vert J_r\left(\frac{r}{r_n}{y}_n+\left(1-\frac{r}{r_n}\right)J_{r_n}{y}_n\right)-J_r{y}_n\Vert \\ & \le \Vert y_n-J_{r_n}{y}_n\Vert +\left|1-\frac{r}{r_n}\right|\cdot \Vert J_{r_n}{y}_n-y_n\Vert .\end{array}$$

From step 6 and $\underset{n\to \infty }{\lim }{r}_n=r$, we get $\underset{n\to \infty }{\lim }\Vert y_n-J_r{y}_n\Vert =0$.

Step 9: Show that $\underset{n\to \infty }{\lim }\Vert x_n-J_r{x}_n\Vert =0$.

$$\begin{array}{ll}\Vert x_n-J_r{x}_n\Vert & \le \Vert x_n-y_n\Vert +\Vert y_n-J_r{y}_n\Vert +\Vert J_r{y}_n-J_r{x}_n\Vert \\ & \le 2\Vert x_n-y_n\Vert +\Vert y_n-J_r{y}_n\Vert .\end{array}$$

From steps 5 and 8, we get $\underset{n\to \infty }{\lim }\Vert x_n-J_r{x}_n\Vert =0$.

Step 10: Show that $\underset{n\to \infty }{\lim \sup }⟨q-fq,J(q-x_n)⟩=0$.

Let $\left\{x_t\right\}$ be defined by $x_t=tf{x}_t+(1-t)S{x}_t$. From Lemma 3, we have that $\left\{x_t\right\}$ converges strongly to $q\in P_{F(S)\cap N(A)}fq$, which is also the unique solution of the variational inequality $⟨q-fq,J(q-p)⟩\le 0$, $\forall p\in F(S)\cap N(A)$.

We have

$$\begin{array}{ll}{\Vert x_t-x_n\Vert }^2& =(1-t)⟨S{x}_t-S{x}_n+S{x}_n-x_n,J(x_t-x_n)⟩+t⟨f{x}_t-x_t+x_t-x_n,J(x_t-x_n)⟩\\ & \le (1-t){\Vert x_t-x_n\Vert }^2+(1-t)\Vert S{x}_n-x_n\Vert \cdot \Vert x_t-x_n\Vert +t{\Vert x_t-x_n\Vert }^2+t⟨f{x}_t-x_t,J(x_t-x_n)⟩\\ & ={\Vert x_t-x_n\Vert }^2+(1-t)\Vert S{x}_n-x_n\Vert \cdot \Vert x_t-x_n\Vert +t{\Vert x_t-x_n\Vert }^2+t⟨f{x}_t-x_t,J(x_t-x_n)⟩.\end{array}$$

It follows that $⟨f{x}_t-x_t,J(x_t-x_n)⟩\le \frac{1-t}{t}\Vert S{x}_n-x_n\Vert \cdot \Vert x_t-x_n\Vert$. From step 7, we get $\underset{n\to \infty }{\lim \sup }⟨q-fq,J(q-x_n)⟩=0$.

Step 11: Show that $\underset{n\to \infty }{\lim }\Vert x_n-q\Vert =0$.

From Lemma 4, we have

$$\begin{array}{ll}{\Vert x_{n+1}-q\Vert }^2& \le {(1-{\alpha }_n)}^2{\Vert S{y}_n-q\Vert }^2+2{\alpha }_n⟨f{x}_n-q,J(x_{n+1}-q)⟩\\ & \le {(1-{\alpha }_n)}^2{\Vert y_n-q\Vert }^2+2k{\alpha }_n\Vert x_n-q\Vert \cdot \Vert x_{n+1}-q\Vert +2{\alpha }_n⟨fq-q,J(x_{n+1}-q)⟩\\ & \le {(1-{\alpha }_n)}^2{\left(\frac{1}{2}\Vert x_n-q\Vert +\frac{1}{2}\Vert x_{n+1}-q\Vert \right)}^2+2k{\alpha }_n\Vert x_n-q\Vert \cdot \Vert x_{n+1}-q\Vert \\ & +2{\alpha }_n⟨fq-q,J(x_{n+1}-q)⟩\\ & ={\left(\frac{1-{\alpha }_n}{2}\right)}^2{\Vert x_n-q\Vert }^2+{\left(\frac{1-{\alpha }_n}{2}\right)}^2{\Vert x_{n+1}-q\Vert }^2+\frac{(1-{\alpha }_n{)}^2}{2}\Vert x_n-q\Vert \cdot \Vert x_{n+1}-q\Vert \\ & +2k{\alpha }_n\Vert x_n-q\Vert \cdot \Vert x_{n+1}-q\Vert +2{\alpha }_n⟨fq-q,J(x_{n+1}-q)⟩\\ & ={\left(\frac{1-{\alpha }_n}{2}\right)}^2{\Vert x_n-q\Vert }^2+{\left(\frac{1-{\alpha }_n}{2}\right)}^2{\Vert x_{n+1}-q\Vert }^2\\ & +\left[\frac{(1-{\alpha }_n{)}^2}{2}+2k{\alpha }_n\right]\Vert x_n-q\Vert \cdot \Vert x_{n+1}-q\Vert +2{\alpha }_n⟨fq-q,J(x_{n+1}-q)⟩\\ & \le {\left(\frac{1-{\alpha }_n}{2}\right)}^2{\Vert x_n-q\Vert }^2+{\left(\frac{1-{\alpha }_n}{2}\right)}^2{\Vert x_{n+1}-q\Vert }^2\\ & +\left[\frac{(1-{\alpha }_n{)}^2}{4}+k{\alpha }_n\right]\left({\Vert x_n-q\Vert }^2+{\Vert x_{n+1}-q\Vert }^2\right)+2{\alpha }_n⟨fq-q,J(x_{n+1}-q)⟩.\end{array}$$

It follows that

$$\begin{array}{ll}{\Vert x_{n+1}-q\Vert }^2& \le \frac{{\left(\frac{1-{\alpha }_n}{2}\right)}^2+\frac{(1-{\alpha }_n{)}^2}{4}+k{\alpha }_n}{1-\left[{\left(\frac{1-{\alpha }_n}{2}\right)}^2+\frac{(1-{\alpha }_n{)}^2}{4}+k{\alpha }_n\right]}{\Vert x_n-q\Vert }^2\\ & +\frac{2{\alpha }_n}{1-\left[{\left(\frac{1-{\alpha }_n}{2}\right)}^2+\frac{(1-{\alpha }_n{)}^2}{4}+k{\alpha }_n\right]}⟨fq-q,J(x_{n+1}-q)⟩\\ & =\left[1-\frac{1-2\left(\frac{(1-{\alpha }_n{)}^2}{2}+k{\alpha }_n\right)}{1-\left(\frac{(1-{\alpha }_n{)}^2}{2}+k{\alpha }_n\right)}\right]{\Vert x_n-q\Vert }^2+\frac{2{\alpha }_n}{1-\left[\frac{(1-{\alpha }_n{)}^2}{2}+k{\alpha }_n\right]}⟨fq-q,J(x_{n+1}-q)⟩.\end{array}$$

Take $t_n=\frac{1-2\left(\frac{(1-{\alpha }_n{)}^2}{2}+k{\alpha }_n\right)}{1-\left(\frac{(1-{\alpha }_n{)}^2}{2}+k{\alpha }_n\right)}$. From $\underset{n\to \infty }{\lim }{\alpha }_n=0$, we have

$$t_n\ge 1-2\left(\frac{(1-{\alpha }_n{)}^2}{2}+k{\alpha }_n\right)={\alpha }_n(2-2k-{\alpha }_n)\ge {\alpha }_n(2-2k-\epsilon )(\forall \epsilon >0).$$

From ${\displaystyle \sum _{n=0}^{\infty }{\alpha }_n}=\infty$, we get ${\displaystyle \sum _{n=0}^{\infty }{t}_n}=\infty$.

Take $b_n=\frac{2{\alpha }_n}{1-\left[\frac{(1-{\alpha }_n{)}^2}{2}+k{\alpha }_n\right]}⟨fq-q,J(x_{n+1}-q)⟩$, then we have

$$\frac{b_n}{t_n}=\frac{2{\alpha }_n⟨fq-q,J(x_{n+1}-q)⟩}{1-2\left[\frac{(1-{\alpha }_n{)}^2}{2}+k{\alpha }_n\right]}=\frac{2⟨fq-q,J(x_{n+1}-q)⟩}{2-2k-{\alpha }_n}.$$

From $\underset{n\to \infty }{\lim }{\alpha }_n=0$ and step 10, we get $b_n=o(t_n)$.

Take $c_n=0$, then we get ${\displaystyle \sum _{n=0}^{\infty }{c}_n}<\infty$.

From Lemma 2, we get $\underset{n\to \infty }{\lim }\Vert x_n-q\Vert =0$. This completes the proof. □

The results of Theorem 1 improve the related results in [13,14,16,17]. For example, this paper uses the viscosity implicit midpoint rule to find common points of the fixed point set of a nonexpansive mapping and the zero point set of an accretive operator and the results improve the related results in [13,14]; If ${\beta }_n=0$, the results of Theorem 1 can obtain the related results in [16,17].

Corollary 1.

Let$E$be a reflexive and uniformly convex Banach space which has uniformly$G\widehat{a}teaux$differentiable norm and$C$be a nonempty closed convex subset of$E$which has normal structure. Let$f:C\to C$be a contractive mapping with$k\in [0,1)$,$A$be a m-accretive operator in$E$and$S:C\to C$be a nonexpansive mapping with$F(S)\cap N(A)\ne \varnothing$. For any$x_0\in C$and$\forall n\ge 0$,$\left\{x_n\right\}$is generated by

$$\{\begin{array}{l}{y}_n={\beta }_n\left(\frac{x_n+x_{n+1}}{2}\right)+(1-{\beta }_n)J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)+e_n,\hfill \\ x_{n+1}={\alpha }_{n}f{x}_n+(1-{\alpha }_n)S{y}_n,\hfill \end{array}$$

where$\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\}\subset (0,1)$,$\left\{e_n\right\}\subset E$and$\left\{r_n\right\}\subset (0,1)$satisfy the following conditions:

(i) 

$\underset{n\to \infty }{\lim }{\alpha }_n=0$,${\displaystyle \sum _{n=0}^{\infty }{\alpha }_n}=\infty$,$\left|{\alpha }_n-{\alpha }_{n-1}\right|=o({\alpha }_n)$;

(ii) 

${\displaystyle \sum _{n=1}^{\infty }\left|{\beta }_n-{\beta }_{n-1}\right|}<\infty$;

(iii) 

$\underset{n\to \infty }{\lim }{r}_n=r$,${\displaystyle \sum _{n=1}^{\infty }\left|r_n-r_{n-1}\right|}<\infty$;

(iv) 

$\Vert e_n\Vert =o({\alpha }_n)$.

Then$\left\{x_n\right\}$and$\left\{y_n\right\}$converge strongly to$q\in F(S)\cap N(A)$, where$q$is the unique solution of the variational inequality$⟨(I-f)q,J_{\varphi }(q-p)⟩\le 0$,$\forall p\in F(S)\cap N(A)$.

Proof. 

Assume

$$\{\begin{array}{l}{w}_n={\beta }_n\left(\frac{z_n+z_{n+1}}{2}\right)+(1-{\beta }_n)J_{r_n}\left(\frac{z_n+z_{n+1}}{2}\right),\hfill \\ z_{n+1}={\alpha }_{n}f{z}_n+(1-{\alpha }_n)S{w}_n.\hfill \end{array}$$

Then we have

$$\begin{array}{ll}\Vert x_{n+1}-z_{n+1}\Vert & \le k{\alpha }_n\Vert x_n-z_n\Vert +(1-{\alpha }_n)\Vert y_n-w_n\Vert \\ & \le k{\alpha }_n\Vert x_n-z_n\Vert +(1-{\alpha }_n)\left(\Vert \frac{x_n+x_{n+1}}{2}-\frac{z_n+z_{n+1}}{2}\Vert +\Vert e_n\Vert \right)\\ & \le \left(k{\alpha }_n+\frac{1-{\alpha }_n}{2}\right)\Vert x_n-z_n\Vert +\frac{1-{\alpha }_n}{2}\Vert x_{n+1}-z_{n+1}\Vert +(1-{\alpha }_n)\Vert e_n\Vert .\end{array}$$

It follows that

$$\begin{array}{ll}\Vert x_{n+1}-z_{n+1}\Vert & \le \frac{k{\alpha }_n+\frac{1-{\alpha }_n}{2}}{\frac{1+{\alpha }_n}{2}}\Vert x_n-z_n\Vert +\frac{2(1-{\alpha }_n)}{1+{\alpha }_n}\Vert e_n\Vert \\ & =\left[1-\frac{2{\alpha }_n(1-k)}{1+{\alpha }_n}\right]\Vert x_n-z_n\Vert +\frac{2(1-{\alpha }_n)}{1+{\alpha }_n}\Vert e_n\Vert .\end{array}$$

Take $t_n=\frac{2{\alpha }_n(1-k)}{1+{\alpha }_n}$, then $t_n\ge {\alpha }_n(1-k)$. From ${\displaystyle \sum _{n=0}^{\infty }{\alpha }_n}=\infty$, we get ${\displaystyle \sum _{n=0}^{\infty }{t}_n}=\infty$.

Take $b_n=\frac{2(1-{\alpha }_n)}{1+{\alpha }_n}\Vert e_n\Vert$, then $\frac{b_n}{t_n}=\frac{(1-{\alpha }_n)\Vert e_n\Vert }{{\alpha }_n(1-k)}$. From $\Vert e_n\Vert =o({\alpha }_n)$, we get $b_n=o(t_n)$.

Take $c_n=0$, then we get ${\displaystyle \sum _{n=0}^{\infty }{c}_n}<\infty$.

From Lemma 2, we get $\underset{n\to \infty }{\lim }\Vert x_n-z_n\Vert =0$. From Theorem 1, we have $\left\{z_n\right\}$ and $\left\{w_n\right\}$ converge strongly to $q\in F(S)\cap N(A)$, where $q$ is the unique solution of the variational inequality $⟨(I-f)q,J_{\varphi }(q-p)⟩\le 0$, $\forall p\in F(S)\cap N(A)$. So $\left\{x_n\right\}$ and $\left\{y_n\right\}$ also converge strongly to $q\in F(S)\cap N(A)$. This completes the proof. □

The results of Corollary 1 improve the related results in [14,16,17].

Theorem 2.

Let$E$be a reflexive and uniformly convex Banach space which has uniformly$G\widehat{a}teaux$differentiable norm and$C$be a nonempty closed convex subset of$E$which has normal structure. Let$f:C\to C$be a contractive mapping with$k\in [0,1)$,$A$be a m-accretive operator in$E$and$S:C\to C$be a nonexpansive mapping with$F(S)\cap N(A)\ne \varnothing$. For any$x_0\in C$and$\forall n\ge 0$,$\left\{x_n\right\}$is generated by

$$\{\begin{array}{l}{y}_n={\beta }_n\left(\frac{x_n+x_{n+1}}{2}\right)+(1-{\beta }_n)J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right),\hfill \\ x_{n+1}={\alpha }_{n}f{x}_n+(1-{\alpha }_n)S{y}_n,\hfill \end{array}$$

(6)

where$\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\}\subset (0,1)$,$\left\{e_n\right\}\subset E$and$\left\{r_n\right\}\subset (0,1)$satisfy the following conditions:

(i) 

$\underset{n\to \infty }{\lim }{\alpha }_n=0$,${\displaystyle \sum _{n=0}^{\infty }{\alpha }_n}=\infty$,$\left|{\alpha }_n-{\alpha }_{n-1}\right|=o({\alpha }_n)$;

(ii) 

${\displaystyle \sum _{n=1}^{\infty }\left|{\beta }_n-{\beta }_{n-1}\right|}<\infty$;

(iii) 

$\underset{n\to \infty }{\lim }{r}_n=r$,${\displaystyle \sum _{n=1}^{\infty }\left|r_n-r_{n-1}\right|}<\infty$;

(iv) 

${\displaystyle \sum _{n=1}^{\infty }\Vert e_n\Vert }<\infty$.

Then$\left\{x_n\right\}$and$\left\{y_n\right\}$converge strongly to$q\in F(S)\cap N(A)$, where$q$is the unique solution of the variational inequality$⟨(I-f)q,J_{\varphi }(q-p)⟩\le 0$,$\forall p\in F(S)\cap N(A)$.

Proof. 

The proof is split into eleven steps.

Step 1: Show that $\left\{x_n\right\}$ and $\left\{y_n\right\}$ are bounded.

Take $p\in F(S)\cap N(A)$, then we have

$$\begin{array}{ll}\Vert y_n-p\Vert & \le {\beta }_n\Vert \frac{x_n+x_{n+1}}{2}-p\Vert +(1-{\beta }_n)\Vert J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)-p\Vert \\ & \le {\beta }_n\Vert \frac{x_n+x_{n+1}}{2}-p\Vert +(1-{\beta }_n)\Vert \frac{x_n+x_{n+1}}{2}-p\Vert +(1-{\beta }_n)\Vert e_n\Vert \\ & \le \frac{1}{2}\Vert x_n-p\Vert +\frac{1}{2}\Vert x_{n+1}-p\Vert +\Vert e_n\Vert ,\end{array}$$

and then we get

$$\begin{array}{ll}\Vert x_{n+1}-p\Vert & \le {\alpha }_n\Vert f{x}_n-p\Vert +(1-{\alpha }_n)\Vert S{y}_n-p\Vert \\ & \le k{\alpha }_n\Vert x_n-p\Vert +{\alpha }_n\Vert fp-p\Vert +(1-{\alpha }_n)\Vert y_n-p\Vert \\ & \le \left(k{\alpha }_n+\frac{1-{\alpha }_n}{2}\right)\Vert x_n-p\Vert +\frac{1-{\alpha }_n}{2}\Vert x_{n+1}-p\Vert +{\alpha }_n\Vert fp-p\Vert +(1-{\alpha }_n)\Vert e_n\Vert .\end{array}$$

It follows that

$$\begin{array}{ll}\Vert x_{n+1}-p\Vert & \le \left[1-\frac{2{\alpha }_n(1-k)}{1+{\alpha }_n}\right]\Vert x_n-p\Vert +\frac{2{\alpha }_n}{1+{\alpha }_n}\Vert fp-p\Vert +\frac{2(1-{\alpha }_n)}{1+{\alpha }_n}\Vert e_n\Vert \\ & \le \left[1-\frac{2{\alpha }_n(1-k)}{1+{\alpha }_n}\right]\Vert x_n-p\Vert +\frac{2{\alpha }_n(1-k)}{1+{\alpha }_n}\frac{\Vert fp-p\Vert }{1-k}+2\Vert e_n\Vert \\ & \le \max \left\{\Vert x_0-p\Vert ,\frac{\Vert fp-p\Vert }{1-k}+2\Vert e_n\Vert \right\}.\end{array}$$

Then $\left\{x_n\right\}$ and $\left\{y_n\right\}$ are bounded. So $\left\{f{x}_n\right\}$, $\left\{f{y}_n\right\}$, $\left\{S{x}_n\right\}$, $\left\{S{y}_n\right\}$, $\left\{J_{r_n}{x}_n\right\}$ and $\left\{J_{r_n}{y}_n\right\}$ are also bounded.

Step 2: Show that $\underset{n\to \infty }{\lim }\Vert x_{n+1}-x_n\Vert =0$.

From (6), we have

$$\begin{array}{ll}\Vert x_{n+1}-x_n\Vert & =\Vert {\alpha }_{n}f{x}_n+(1-{\alpha }_n)S{y}_n-{\alpha }_{n-1}f{x}_{n-1}-(1-{\alpha }_{n-1})S{y}_{n-1}\Vert \\ & \le {\alpha }_n\Vert f{x}_n-f{x}_{n-1}\Vert +\left|{\alpha }_n-{\alpha }_{n-1}\right|\cdot \Vert f{x}_{n-1}-S{y}_{n-1}\Vert +(1-{\alpha }_n)\Vert S{y}_n-S{y}_{n-1}\Vert \\ & \le k{\alpha }_n\Vert x_n-x_{n-1}\Vert +\left|{\alpha }_n-{\alpha }_{n-1}\right|\cdot \Vert f{x}_{n-1}-S{y}_{n-1}\Vert +(1-{\alpha }_n)\Vert y_n-y_{n-1}\Vert .\end{array}$$

(7)

From (6), we have

$$\begin{array}{ll}\Vert y_n-y_{n-1}\Vert & \le {\beta }_n\Vert \frac{x_{n+1}-x_{n-1}}{2}\Vert +\left|{\beta }_n-{\beta }_{n-1}\right|\cdot \Vert \frac{x_{n-1}+x_n}{2}-J_{r_{n-1}}\left(\frac{x_{n-1}+x_n}{2}+e_{n-1}\right)\Vert \\ & +(1-{\beta }_n)\Vert J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)-J_{r_{n-1}}\left(\frac{x_{n-1}+x_n}{2}+e_{n-1}\right)\Vert .\end{array}$$

(8)

From Lemma 1, we have

$$\begin{array}{l} \Vert J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)-J_{r_{n-1}}\left(\frac{x_{n-1}+x_n}{2}+e_{n-1}\right)\Vert \\ =\Vert J_{r_{n-1}}\left(\frac{r_{n-1}}{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)+\left(1-\frac{r_{n-1}}{r_n}\right)J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\right)-J_{r_{n-1}}\left(\frac{x_{n-1}+x_n}{2}+e_{n-1}\right)\Vert \\ \le \Vert \frac{r_{n-1}}{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)+\left(1-\frac{r_{n-1}}{r_n}\right)J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)-\left(\frac{x_{n-1}+x_n}{2}+e_{n-1}\right)\Vert \\ \le \frac{r_{n-1}}{r_n}\Vert \frac{x_{n+1}-x_{n-1}}{2}+e_n-e_{n-1}\Vert +\left|1-\frac{r_{n-1}}{r_n}\right|\cdot \Vert J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)-\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert \\ +\left|1-\frac{r_{n-1}}{r_n}\right|\cdot \Vert \frac{x_{n+1}-x_{n-1}}{2}+e_n-e_{n-1}\Vert \\ =\Vert \frac{x_{n+1}-x_{n-1}}{2}+e_n-e_{n-1}\Vert +\left|1-\frac{r_{n-1}}{r_n}\right|\cdot \Vert J_{r_n}\left(\frac{x_n+x_{n+1}}{2}\right)-\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert .\end{array}$$

(9)

Put (8) and (9) into (7), we get

$$\begin{array}{ll}\Vert x_{n+1}-x_n\Vert & \le k{\alpha }_n\Vert x_n-x_{n-1}\Vert +\left|{\alpha }_n-{\alpha }_{n-1}\right|M_1+(1-{\alpha }_n)\Vert \frac{x_{n+1}-x_{n-1}}{2}\Vert \\ & +(1-{\alpha }_n)\left|{\beta }_n-{\beta }_{n-1}\right|M_3+(1-{\alpha }_n)(1-{\beta }_n)\Vert e_n-e_{n-1}\Vert \\ & +(1-{\alpha }_n)(1-{\beta }_n)\left|1-\frac{r_{n-1}}{r_n}\right|M_4\\ & \le \left(k{\alpha }_n+\frac{1-{\alpha }_n}{2}\right)\Vert x_n-x_{n-1}\Vert +\frac{1-{\alpha }_n}{2}\Vert x_{n+1}-x_n\Vert +\left|{\alpha }_n-{\alpha }_{n-1}\right|M_1\\ & +(1-{\alpha }_n)\left|{\beta }_n-{\beta }_{n-1}\right|M_3+(1-{\alpha }_n)(1-{\beta }_n)\Vert e_n-e_{n-1}\Vert \\ & +(1-{\alpha }_n)(1-{\beta }_n)\left|1-\frac{r_{n-1}}{r_n}\right|M_4.\end{array}$$

It follows that

$$\begin{array}{ll}\Vert x_{n+1}-x_n\Vert =& \left[1-\frac{2{\alpha }_n(1-k)}{1+{\alpha }_n}\right]\Vert x_n-x_{n-1}\Vert +\frac{2\left|{\alpha }_n-{\alpha }_{n-1}\right|}{1+{\alpha }_n}{M}_1+\frac{2(1-{\alpha }_n)}{1+{\alpha }_n}\left|{\beta }_n-{\beta }_{n-1}\right|M_3\\ & +\frac{2(1-{\alpha }_n)(1-{\beta }_n)}{1+{\alpha }_n}\left(\Vert e_n\Vert +\Vert e_{n-1}\Vert \right)+\frac{2(1-{\alpha }_n)(1-{\beta }_n)\left|r_n-r_{n-1}\right|}{(1+{\alpha }_n)r_n}{M}_4,\end{array}$$

where

$$M_3=\max \Vert \frac{x_n+x_{n+1}}{2}-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert ,M_4=\max \Vert J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)-\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert .$$

Take $t_n=\frac{2{\alpha }_n(1-k)}{1+{\alpha }_n}$, then $t_n>{\alpha }_n(1-k)$. From ${\displaystyle \sum _{n=0}^{\infty }{\alpha }_n}=\infty$, so ${\displaystyle \sum _{n=0}^{\infty }{t}_n}=\infty$.

Take $b_n=\frac{2\left|{\alpha }_n-{\alpha }_{n-1}\right|}{1+{\alpha }_n}{M}_1$, then $\frac{b_n}{t_n}=\frac{\left|{\alpha }_n-{\alpha }_{n-1}\right|M_1}{{\alpha }_n(1-k)}$. From $\left|{\alpha }_n-{\alpha }_{n-1}\right|=o({\alpha }_n)$, so $b_n=o(t_n)$.

Take

$$c_n=\frac{2(1-{\alpha }_n)}{1+{\alpha }_n}\left|{\beta }_n-{\beta }_{n-1}\right|M_3+\frac{2(1-{\alpha }_n)(1-{\beta }_n)}{1+{\alpha }_n}\left(\Vert e_n\Vert +\Vert e_{n-1}\Vert \right)+\frac{2(1-{\alpha }_n)(1-{\beta }_n)\left|r_n-r_{n-1}\right|}{(1+{\alpha }_n)r_n}{M}_4,$$

then $c_n<2\left|{\beta }_n-{\beta }_{n-1}\right|M_3+2\left(\Vert e_n\Vert +\Vert e_{n-1}\Vert \right)+\frac{2\left|r_n-r_{n-1}\right|M_4}{r+\epsilon }$$(\forall \epsilon >0)$.

From ${\displaystyle \sum _{n=1}^{\infty }\left|{\beta }_n-{\beta }_{n-1}\right|}<\infty$, ${\displaystyle \sum _{n=1}^{\infty }\Vert e_n\Vert }<\infty$, $\underset{n\to \infty }{\lim }{r}_n=r$ and ${\displaystyle \sum _{n=1}^{\infty }\left|r_n-r_{n-1}\right|}<\infty$, so ${\displaystyle \sum _{n=1}^{\infty }{c}_n}<\infty$.

From Lemma 2, we get $\underset{n\to \infty }{\lim }\Vert x_{n+1}-x_n\Vert =0$.

Step 3: Show that $\underset{n\to \infty }{\lim }\Vert x_n-J_{r_n}{x}_n\Vert =0$.

Because ${\Vert \cdot \Vert }^2$ is convex function and (1), so we have

$$\begin{array}{ll}{\Vert x_{n+1}-p\Vert }^2& \le {\alpha }_n{\Vert f{x}_n-p\Vert }^2+(1-{\alpha }_n){\Vert S{y}_n-p\Vert }^2\\ & \le {\alpha }_n{\Vert f{x}_n-p\Vert }^2+(1-{\alpha }_n){\Vert y_n-p\Vert }^2\\ & \le {\alpha }_n{\Vert f{x}_n-p\Vert }^2+(1-{\alpha }_n){\beta }_n{\Vert \frac{x_n+x_{n+1}}{2}-p\Vert }^2\\ & +(1-{\alpha }_n)(1-{\beta }_n){\Vert J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)-p\Vert }^2\\ & ={\alpha }_n{\Vert f{x}_n-p\Vert }^2+(1-{\alpha }_n)[{\beta }_n{\Vert \frac{x_n+x_{n+1}}{2}-p\Vert }^2\\ & +(1-{\beta }_n){\Vert J_{\frac{r_n}{2}}\left(\frac{1}{2}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)+\frac{1}{2}{J}_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\right)-p\Vert }^2]\\ & \le {\alpha }_n{\Vert f{x}_n-p\Vert }^2+(1-{\alpha }_n){\beta }_n{\Vert \frac{x_n+x_{n+1}}{2}-p\Vert }^2\\ & +(1-{\alpha }_n)(1-{\beta }_n){\Vert \frac{1}{2}\left(\frac{x_n+x_{n+1}}{2}+e_n-p\right)+\frac{1}{2}\left(J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)-p\right)\Vert }^2\\ & \le {\alpha }_n{\Vert f{x}_n-p\Vert }^2+(1-{\alpha }_n){\beta }_n{\Vert \frac{x_n+x_{n+1}}{2}-p\Vert }^2\\ & +(1-{\alpha }_n)(1-{\beta }_n){\Vert \frac{x_n+x_{n+1}}{2}+e_n-p\Vert }^2\\ & -\frac{(1-{\alpha }_n)(1-{\beta }_n)}{4}g\left(\Vert \frac{x_n+x_{n+1}}{2}+e_n-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert \right)\\ & \le {\alpha }_n{\Vert f{x}_n-p\Vert }^2+(1-{\alpha }_n){\beta }_n{\Vert \frac{x_n+x_{n+1}}{2}-p\Vert }^2\\ & +(1-{\alpha }_n)(1-{\beta }_n){\Vert \frac{x_n+x_{n+1}}{2}+e_n-p\Vert }^2\\ & -\frac{(1-{\alpha }_n)(1-{\beta }_n)}{4}g\left(\Vert \frac{x_n+x_{n+1}}{2}+e_n-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert \right)\\ & \le {\alpha }_n{\Vert f{x}_n-p\Vert }^2+(1-{\alpha }_n){\beta }_n{\Vert \frac{x_n+x_{n+1}}{2}-p\Vert }^2{}^2\\ & +(1-{\alpha }_n)(1-{\beta }_n)\Vert \frac{x_n+x_{n+1}}{2}+e_n-p\Vert \\ & +(1-{\alpha }_n)(1-{\beta }_n)\left({\Vert \frac{x_n+x_{n+1}}{2}-p\Vert }^2+2⟨e_n,J\left(\frac{x_n+x_{n+1}}{2}+e_n-p\right)⟩\right)\\ & -\frac{(1-{\alpha }_n)(1-{\beta }_n)}{4}g\left(\Vert \frac{x_n+x_{n+1}}{2}+e_n-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert \right)\\ & ={\alpha }_n{\Vert f{x}_n-p\Vert }^2+(1-{\alpha }_n){\Vert \frac{x_n+x_{n+1}}{2}-p\Vert }^2\\ & +2(1-{\alpha }_n)(1-{\beta }_n)⟨e_n,J\left(\frac{x_n+x_{n+1}}{2}+e_n-p\right)⟩\\ & -\frac{(1-{\alpha }_n)(1-{\beta }_n)}{4}g\left(\Vert \frac{x_n+x_{n+1}}{2}+e_n-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert \right)\\ & \le {\alpha }_n{\Vert f{x}_n-p\Vert }^2+\frac{1-{\alpha }_n}{2}{\Vert x_n-p\Vert }^2+\frac{1-{\alpha }_n}{2}{\Vert x_{n+1}-p\Vert }^2\\ & +2(1-{\alpha }_n)(1-{\beta }_n)⟨e_n,J\left(\frac{x_n+x_{n+1}}{2}+e_n-p\right)⟩\\ & -\frac{(1-{\alpha }_n)(1-{\beta }_n)}{4}g\left(\Vert \frac{x_n+x_{n+1}}{2}+e_n-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert \right).\end{array}$$

It follows that

$$\begin{array}{ll}{\Vert x_{n+1}-p\Vert }^2& \le \frac{1-{\alpha }_n}{1+{\alpha }_n}{\Vert x_n-p\Vert }^2+\frac{2{\alpha }_n}{1+{\alpha }_n}{\Vert f{x}_n-p\Vert }^2+\frac{(1-{\alpha }_n)(1-{\beta }_n)}{1+{\alpha }_n}\Vert e_n\Vert \cdot \Vert \frac{x_n+x_{n+1}}{2}+e_n-p\Vert \\ & -\frac{(1-{\alpha }_n)(1-{\beta }_n)}{4}g\left(\Vert \frac{x_n+x_{n+1}}{2}+e_n-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert \right)\\ & \le {\Vert x_n-p\Vert }^2+\frac{2{\alpha }_n}{1+{\alpha }_n}{\Vert f{x}_n-p\Vert }^2+\frac{(1-{\alpha }_n)(1-{\beta }_n)}{1+{\alpha }_n}\Vert e_n\Vert \cdot \Vert \frac{x_n+x_{n+1}}{2}+e_n-p\Vert \\ & -\frac{(1-{\alpha }_n)(1-{\beta }_n)}{4}g\left(\Vert \frac{x_n+x_{n+1}}{2}+e_n-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert \right).\end{array}$$

Then we have

$$\begin{array}{l}\frac{(1-{\alpha }_n)(1-{\beta }_n)}{4}g\left(\Vert \frac{x_n+x_{n+1}}{2}+e_n-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert \right)-\frac{2{\alpha }_n}{1+{\alpha }_n}{\Vert f{x}_n-p\Vert }^2-\\ \frac{(1-{\alpha }_n)(1-{\beta }_n)}{1+{\alpha }_n}\Vert e_n\Vert \cdot \Vert \frac{x_n+x_{n+1}}{2}+e_n-p\Vert \le {\Vert x_n-p\Vert }^2-{\Vert x_{n+1}-p\Vert }^2.\end{array}$$

If $\frac{(1-{\alpha }_n)(1-{\beta }_n)}{4}g\left(\Vert \frac{x_n+x_{n+1}}{2}+e_n-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert \right)\le$$\frac{2{\alpha }_n}{1+{\alpha }_n}{\Vert f{x}_n-p\Vert }^2+$ $\frac{(1-{\alpha }_n)(1-{\beta }_n)}{1+{\alpha }_n}\Vert e_n\Vert \cdot \Vert \frac{x_n+x_{n+1}}{2}+e_n-p\Vert$, so from $\underset{n\to \infty }{\lim }{\alpha }_n=0$, step 1 and ${\displaystyle \sum _{n=0}^{\infty }\Vert e_n\Vert }<\infty$, we get $\underset{n\to \infty }{\lim }g\left(\Vert \frac{x_n+x_{n+1}}{2}+e_n-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert \right)=0$.

If $\frac{(1-{\alpha }_n)(1-{\beta }_n)}{4}g\left(\Vert \frac{x_n+x_{n+1}}{2}+e_n-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert \right)\ge \frac{2{\alpha }_n}{1+{\alpha }_n}{\Vert f{x}_n-p\Vert }^2+$ $\frac{(1-{\alpha }_n)(1-{\beta }_n)}{1+{\alpha }_n}\Vert e_n\Vert \cdot \Vert \frac{x_n+x_{n+1}}{2}+e_n-p\Vert$, so

$$\begin{array}{l}{\displaystyle \sum _{n=0}^N[\frac{(1-{\alpha }_n)(1-{\beta }_n)}{4}g\left(\Vert \frac{x_n+x_{n+1}}{2}+e_n-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert \right)-\frac{2{\alpha }_n}{1+{\alpha }_n}{\Vert f{x}_n-p\Vert }^2}-\\ \frac{(1-{\alpha }_n)(1-{\beta }_n)}{1+{\alpha }_n}\Vert e_n\Vert \cdot \Vert \frac{x_n+x_{n+1}}{2}+e_n-p\Vert ]\le {\Vert x_0-p\Vert }^2-{\Vert x_{N+1}-p\Vert }^2\le {\Vert x_0-p\Vert }^2.\end{array}$$

Then

$$\begin{array}{l}{\displaystyle \sum _{n=0}^{\infty }[\frac{(1-{\alpha }_n)(1-{\beta }_n)}{4}g\left(\Vert \frac{x_n+x_{n+1}}{2}+e_n-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert \right)-\frac{2{\alpha }_n}{1+{\alpha }_n}{\Vert f{x}_n-p\Vert }^2}-\\ \frac{(1-{\alpha }_n)(1-{\beta }_n)}{1+{\alpha }_n}\Vert e_n\Vert \cdot \Vert \frac{x_n+x_{n+1}}{2}+e_n-p\Vert ]<\infty .\end{array}$$

So we get

$$\begin{array}{l}\underset{n\to \infty }{\lim }[\frac{(1-{\alpha }_n)(1-{\beta }_n)}{4}g\left(\Vert \frac{x_n+x_{n+1}}{2}+e_n-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert \right)-\frac{2{\alpha }_n}{1+{\alpha }_n}{\Vert f{x}_n-p\Vert }^2-\\ \frac{(1-{\alpha }_n)(1-{\beta }_n)}{1+{\alpha }_n}\Vert e_n\Vert \cdot \Vert \frac{x_n+x_{n+1}}{2}+e_n-p\Vert ]=0\end{array}$$

and then $\underset{n\to \infty }{\lim }g\left(\Vert \frac{x_n+x_{n+1}}{2}+e_n-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert \right)=0$.

From the property of $g$, so we get $\underset{n\to \infty }{\lim }\Vert \frac{x_n+x_{n+1}}{2}+e_n-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert =0$.

We also have

$$\begin{array}{ll}\Vert x_n-J_{r_n}{x}_n\Vert & \le \Vert x_n-\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert +\Vert \frac{x_n+x_{n+1}}{2}+e_n-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert \\ & +\Vert J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)-J_{r_n}{x}_n\Vert \\ & \le 2\Vert x_n-\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert +\Vert \frac{x_n+x_{n+1}}{2}+e_n-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert \\ & \le \Vert x_n-x_{n+1}\Vert +2\Vert e_n\Vert +\Vert \frac{x_n+x_{n+1}}{2}+e_n-J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert .\end{array}$$

Then from step 2 and ${\displaystyle \sum _{n=0}^{\infty }\Vert e_n\Vert }<\infty$, we get $\underset{n\to \infty }{\lim }\Vert x_n-J_{r_n}{x}_n\Vert =0$.

Step 4: Show that $\underset{n\to \infty }{\lim }\Vert y_n-S{y}_n\Vert =0$.

$$\begin{array}{ll}\Vert y_n-S{y}_n\Vert & \le {\beta }_n\Vert \frac{x_n+x_{n+1}}{2}-S{y}_n\Vert +(1-{\beta }_n)\Vert J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)-S{y}_n\Vert \\ & \le \Vert \frac{x_n+x_{n+1}}{2}-S{y}_n\Vert +(1-{\beta }_n)\Vert e_n\Vert \\ & +(1-{\beta }_n)\Vert J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)-\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert \\ & \le \Vert \frac{x_n+x_{n+1}}{2}-x_{n+1}\Vert +\Vert x_{n+1}-S{y}_n\Vert +(1-{\beta }_n)\Vert e_n\Vert \\ & +(1-{\beta }_n)\Vert J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)-\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert \\ & \le \frac{1}{2}\Vert x_n-x_{n+1}\Vert +{\alpha }_n\Vert f{x}_n-S{y}_n\Vert +(1-{\beta }_n)\Vert e_n\Vert \\ & +(1-{\beta }_n)\Vert J_{r_n}\left(\frac{x_n+x_{n+1}}{2}+e_n\right)-\left(\frac{x_n+x_{n+1}}{2}+e_n\right)\Vert .\end{array}$$

From step 1, step 2, step 3, $\underset{n\to \infty }{\lim }{\alpha }_n=0$ and ${\displaystyle \sum _{n=0}^{\infty }\Vert e_n\Vert }<\infty$, we get $\underset{n\to \infty }{\lim }\Vert y_n-S{y}_n\Vert =0$.

Step 5: Show that $\underset{n\to \infty }{\lim }\Vert x_n-y_n\Vert =0$.

$$\begin{array}{ll}\Vert x_n-y_n\Vert & \le \Vert x_n-x_{n+1}\Vert +\Vert x_{n+1}-S{y}_n\Vert +\Vert S{y}_n-y_n\Vert \\ & =\Vert x_n-x_{n+1}\Vert +{\alpha }_n\Vert f{x}_n-S{y}_n\Vert +\Vert S{y}_n-y_n\Vert .\end{array}$$

From step1, step 2, step 4 and $\underset{n\to \infty }{\lim }{\alpha }_n=0$, we get $\underset{n\to \infty }{\lim }\Vert x_n-y_n\Vert =0$.

Step 6: Show that $\underset{n\to \infty }{\lim }\Vert y_n-J_{r_n}{y}_n\Vert =0$.

$$\begin{array}{ll}\Vert y_n-J_{r_n}{y}_n\Vert & \le \Vert y_n-x_n\Vert +\Vert x_n-J_{r_n}{x}_n\Vert +\Vert J_{r_n}{x}_n-J_{r_n}{y}_n\Vert \\ & \le 2\Vert y_n-x_n\Vert +\Vert x_n-J_{r_n}{x}_n\Vert .\end{array}$$

From steps 3 and 5, we get $\underset{n\to \infty }{\lim }\Vert y_n-J_{r_n}{y}_n\Vert =0$.

Step 7: Show that $\underset{n\to \infty }{\lim }\Vert x_n-S{x}_n\Vert =0$.

$$\begin{array}{ll}\Vert x_n-S{x}_n\Vert & \le \Vert x_n-y_n\Vert +\Vert y_n-S{y}_n\Vert +\Vert S{y}_n-S{x}_n\Vert \\ & \le 2\Vert x_n-y_n\Vert +\Vert y_n-S{y}_n\Vert .\end{array}$$

From steps 4 and 5, we get $\underset{n\to \infty }{\lim }\Vert x_n-S{x}_n\Vert =0$.

Step 8: Show that $\underset{n\to \infty }{\lim }\Vert y_n-J_r{y}_n\Vert =0$.

$$\begin{array}{ll}\Vert y_n-J_r{y}_n\Vert & \le \Vert y_n-J_{r_n}{y}_n\Vert +\Vert J_{r_n}{y}_n-J_r{y}_n\Vert \\ & =\Vert y_n-J_{r_n}{y}_n\Vert +\Vert J_r\left(\frac{r}{r_n}{y}_n+\left(1-\frac{r}{r_n}\right)J_{r_n}{y}_n\right)-J_r{y}_n\Vert \\ & \le \Vert y_n-J_{r_n}{y}_n\Vert +\left|1-\frac{r}{r_n}\right|\cdot \Vert J_{r_n}{y}_n-y_n\Vert .\end{array}$$

From step 6 and $\underset{n\to \infty }{\lim }{r}_n=r$, we get $\underset{n\to \infty }{\lim }\Vert y_n-J_r{y}_n\Vert =0$.

Step 9: Show that $\underset{n\to \infty }{\lim }\Vert x_n-J_r{x}_n\Vert =0$.

$$\begin{array}{ll}\Vert x_n-J_r{x}_n\Vert & \le \Vert x_n-y_n\Vert +\Vert y_n-J_r{y}_n\Vert +\Vert J_r{y}_n-J_r{x}_n\Vert \\ & \le 2\Vert x_n-y_n\Vert +\Vert y_n-J_r{y}_n\Vert .\end{array}$$

From steps 5 and 8, we get $\underset{n\to \infty }{\lim }\Vert x_n-J_r{x}_n\Vert =0$.

Step 10: Show that $\underset{n\to \infty }{\lim \sup }⟨q-fq,J(q-x_n)⟩=0$.

From Theorem 1, we have that $\left\{x_t\right\}$ converges strongly to $q\in P_{F(S)\cap N(A)}fq$, which is also the unique solution of the variational inequality $⟨q-fq,J(q-p)⟩\le 0$, $\forall p\in F(S)\cap N(A)$.

We have

$$\begin{array}{ll}{\Vert x_t-x_n\Vert }^2& =(1-t)⟨S{x}_t-S{x}_n+S{x}_n-x_n,J(x_t-x_n)⟩+t⟨f{x}_t-x_t+x_t-x_n,J(x_t-x_n)⟩\\ & \le (1-t){\Vert x_t-x_n\Vert }^2+(1-t)\Vert S{x}_n-x_n\Vert \cdot \Vert x_t-x_n\Vert +t{\Vert x_t-x_n\Vert }^2+t⟨f{x}_t-x_t,J(x_t-x_n)⟩\\ & ={\Vert x_t-x_n\Vert }^2+(1-t)\Vert S{x}_n-x_n\Vert \cdot \Vert x_t-x_n\Vert +t{\Vert x_t-x_n\Vert }^2+t⟨f{x}_t-x_t,J(x_t-x_n)⟩.\end{array}$$

It follows that $⟨f{x}_t-x_t,J(x_t-x_n)⟩\le \frac{1-t}{t}\Vert S{x}_n-x_n\Vert \cdot \Vert x_t-x_n\Vert$. From step 1 and step 7, we get $\underset{n\to \infty }{\lim \sup }⟨q-fq,J(q-x_n)⟩=0$.

Step 11: Show that $\underset{n\to \infty }{\lim }\Vert x_n-q\Vert =0$.

From Lemma 4, we have

$$\begin{array}{ll}{\Vert x_{n+1}-q\Vert }^2& \le {(1-{\alpha }_n)}^2{\Vert S{y}_n-q\Vert }^2+2{\alpha }_n⟨f{x}_n-q,J(x_{n+1}-q)⟩\\ & \le {(1-{\alpha }_n)}^2{\Vert y_n-q\Vert }^2+2k{\alpha }_n\Vert x_n-q\Vert \cdot \Vert x_{n+1}-q\Vert +2{\alpha }_n⟨fq-q,J(x_{n+1}-q)⟩\\ & \le {(1-{\alpha }_n)}^2{\left(\frac{1}{2}\Vert x_n-q\Vert +\frac{1}{2}\Vert x_{n+1}-q\Vert +\Vert e_n\Vert \right)}^2+2k{\alpha }_n\Vert x_n-q\Vert \cdot \Vert x_{n+1}-q\Vert \\ & +2{\alpha }_n⟨fq-q,J(x_{n+1}-q)⟩\\ & ={\left(\frac{1-{\alpha }_n}{2}\right)}^2{\Vert x_n-q\Vert }^2+{\left(\frac{1-{\alpha }_n}{2}\right)}^2{\Vert x_{n+1}-q\Vert }^2+(1-{\alpha }_n{)}^2{\Vert e_n\Vert }^2\\ & +\frac{(1-{\alpha }_n{)}^2}{2}\Vert x_n-q\Vert \cdot \Vert x_{n+1}-q\Vert +(1-{\alpha }_n{)}^2\Vert x_n-q\Vert \cdot \Vert e_n\Vert \\ & +(1-{\alpha }_n{)}^2\Vert x_{n+1}-q\Vert \cdot \Vert e_n\Vert +2k{\alpha }_n\Vert x_n-q\Vert \cdot \Vert x_{n+1}-q\Vert \\ & +2{\alpha }_n⟨fq-q,J(x_{n+1}-q)⟩\\ & \le {\left(\frac{1-{\alpha }_n}{2}\right)}^2{\Vert x_n-q\Vert }^2+{\left(\frac{1-{\alpha }_n}{2}\right)}^2{\Vert x_{n+1}-q\Vert }^2\\ & +\left[\frac{(1-{\alpha }_n{)}^2}{4}+k{\alpha }_n\right]\left({\Vert x_n-q\Vert }^2+{\Vert x_{n+1}-q\Vert }^2\right)+(1-{\alpha }_n{)}^2{\Vert e_n\Vert }^2\\ & +(1-{\alpha }_n{)}^2\Vert e_n\Vert \left(\Vert x_n-q\Vert +\Vert x_{n+1}-q\Vert \right)+2{\alpha }_n⟨fq-q,J(x_{n+1}-q)⟩.\end{array}$$

It follows that

$$\begin{array}{ll}{\Vert x_{n+1}-q\Vert }^2& \le \frac{{\left(\frac{1-{\alpha }_n}{2}\right)}^2+\frac{(1-{\alpha }_n{)}^2}{4}+k{\alpha }_n}{1-\left[{\left(\frac{1-{\alpha }_n}{2}\right)}^2+\frac{(1-{\alpha }_n{)}^2}{4}+k{\alpha }_n\right]}{\Vert x_n-q\Vert }^2\\ & +\frac{2{\alpha }_n}{1-\left[{\left(\frac{1-{\alpha }_n}{2}\right)}^2+\frac{(1-{\alpha }_n{)}^2}{4}+k{\alpha }_n\right]}⟨fq-q,J(x_{n+1}-q)⟩\\ & +\frac{(1-{\alpha }_n{)}^2\Vert e_n\Vert }{1-\left[{\left(\frac{1-{\alpha }_n}{2}\right)}^2+\frac{(1-{\alpha }_n{)}^2}{4}+k{\alpha }_n\right]}\left(\Vert x_n-q\Vert +\Vert x_{n+1}-q\Vert +\Vert e_n\Vert \right)\\ & =\left[1-\frac{1-2\left(\frac{(1-{\alpha }_n{)}^2}{2}+k{\alpha }_n\right)}{1-\left(\frac{(1-{\alpha }_n{)}^2}{2}+k{\alpha }_n\right)}\right]{\Vert x_n-q\Vert }^2\\ & +\frac{2{\alpha }_n}{1-\left[\frac{(1-{\alpha }_n{)}^2}{2}+k{\alpha }_n\right]}⟨fq-q,J(x_{n+1}-q)⟩\\ & +\frac{(1-{\alpha }_n{)}^2\Vert e_n\Vert }{1-\left[\frac{(1-{\alpha }_n{)}^2}{2}+k{\alpha }_n\right]}\left(\Vert x_n-q\Vert +\Vert x_{n+1}-q\Vert +\Vert e_n\Vert \right).\end{array}$$

Take $t_n=\frac{1-2\left(\frac{(1-{\alpha }_n{)}^2}{2}+k{\alpha }_n\right)}{1-\left(\frac{(1-{\alpha }_n{)}^2}{2}+k{\alpha }_n\right)}$. From $\underset{n\to \infty }{\lim }{\alpha }_n=0$, we have

$$t_n\ge 1-2\left(\frac{(1-{\alpha }_n{)}^2}{2}+k{\alpha }_n\right)={\alpha }_n(2-2k-{\alpha }_n)\ge {\alpha }_n(2-2k-\epsilon )(\forall \epsilon >0).$$

From ${\displaystyle \sum _{n=0}^{\infty }{\alpha }_n}=\infty$, we get ${\displaystyle \sum _{n=0}^{\infty }{t}_n}=\infty$.

Take $b_n=\frac{2{\alpha }_n}{1-\left[\frac{(1-{\alpha }_n{)}^2}{2}+k{\alpha }_n\right]}⟨fq-q,J(x_{n+1}-q)⟩$, then we have

$$\frac{b_n}{t_n}=\frac{2{\alpha }_n⟨fq-q,J(x_{n+1}-q)⟩}{1-2\left[\frac{(1-{\alpha }_n{)}^2}{2}+k{\alpha }_n\right]}=\frac{2⟨fq-q,J(x_{n+1}-q)⟩}{2-2k-{\alpha }_n}.$$

From $\underset{n\to \infty }{\lim }{\alpha }_n=0$ and step 10, we get $b_n=o(t_n)$.

Take $c_n=\frac{(1-{\alpha }_n{)}^2\Vert e_n\Vert }{1-\left[\frac{(1-{\alpha }_n{)}^2}{2}+k{\alpha }_n\right]}\left(\Vert x_n-q\Vert +\Vert x_{n+1}-q\Vert +\Vert e_n\Vert \right)$, then

$$c_n=\frac{2(1-{\alpha }_n{)}^2\Vert e_n\Vert }{1+{\alpha }_n(2-2k-{\alpha }_n)}\left(\Vert x_n-q\Vert +\Vert x_{n+1}-q\Vert +\Vert e_n\Vert \right).$$

From $k\in (0,1)$ and ${\alpha }_n\in (0,1)$, we get ${\alpha }_n(2-2k-{\alpha }_n)>0$, and then $c_n<2\left(\Vert x_n-q\Vert +\Vert x_{n+1}-q\Vert +\Vert e_n\Vert \right)\Vert e_n\Vert$. From ${\displaystyle \sum _{n=0}^{\infty }\Vert e_n\Vert }<\infty$, we get ${\displaystyle \sum _{n=0}^{\infty }{c}_n}<\infty$.

From Lemma 2, we get $\underset{n\to \infty }{\lim }\Vert x_n-q\Vert =0$. This completes the proof. □

The results of Theorem 2 improve the related results in [15,16,17]. For example, the results of Theorem 2 is can obtain the related results in [15,16,17]; the rate of convergence and computational accuracy is better than their in [15,16,17].

4. Numerical Examples

We give four numerical examples to support the main results.

Example 1.

Let$R$be the real line with Euclidean norm,$f:R\to R$be defined by$f(x)=\frac{x}{6}$,$S:R\to R$be defined by$S(x)=\frac{x}{4}$and$J_{r_n}x=\frac{r_{n}x}{2}$. So$F(T)=\left\{0\right\}$. Let${\alpha }_n=\frac{1}{n}$,${\beta }_n=\frac{1}{n}$and$r_n=1-\frac{1}{n}$, then they satisfy the conditions of Theorem 1.$\left\{x_n\right\}$is generated by (2). From Theorem 1, we can obtain$\left\{x_n\right\}$converges strongly to 0.

Next, we simplify the form of (2) and get

$$x_{n+1}=\frac{3-9n+9n^2+3n^3-14n^4}{-3+9n-9n^2-51n^3+6n^4}{x}_n.$$

(10)

Next, we take $x_1=1$ into (10). Finally, we get the following numerical results in Figure 1.

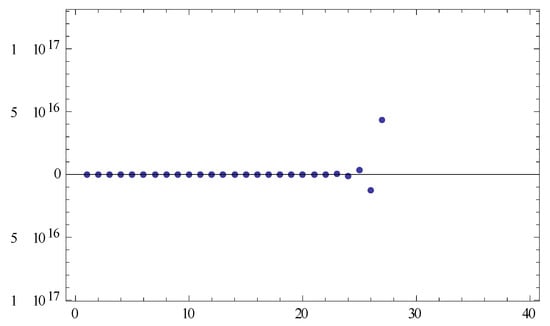
Figure 1. Numerical results.

Example 2.

Let$R$be the real line with Euclidean norm,$f:R\to R$be defined by$f(x)=\frac{x}{6}$,$S:R\to R$be defined by$S(x)=\frac{x}{4}$and$J_{r_n}x=\frac{r_{n}x}{2}$. So$F(T)=\left\{0\right\}$. Let${\alpha }_n=\frac{1}{n}$,${\beta }_n=\frac{1}{n}$,$r_n=1-\frac{1}{n}$and$e_n=\frac{1}{n^2}$, then they satisfy the conditions of Theorem 2.$\left\{x_n\right\}$is generated by (6). From Theorem 2, we can obtain$\left\{x_n\right\}$converges strongly to 0.

Next, we simplify the form of (6) and get

$$x_{n+1}=-\frac{2{(n-1)}^2{n}^4}{-1+3n-3n^2-17n^3+2n^4}{x}_n.$$

(11)

Next, we take $x_1=1$ into (11). Finally, we get the following numerical results in Figure 2.

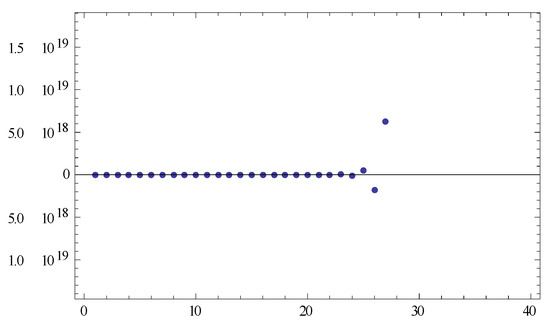
Figure 2. Numerical results.

Example 3.

Let$⟨\cdot ,\cdot ⟩:R^3\times R^3\to R$be the inner product and defined by

$$⟨x,y⟩=x_1{y}_1+x_2{y}_2+x_2{y}_3.$$

Let$\Vert \cdot \Vert :R^3\to R$be the usual norm and defined by$\Vert x\Vert =\sqrt{x_1^2+x_2^2+x_3^2}$for any$x=(x_1,x_2,x_3)$.

For any$x\in R^3$, let$f:R^3\to R^3$be defined by$f(x)=\frac{x}{6}$,$S:R^3\to R^3$be defined by$S(x)=\frac{x}{4}$and$J_{r_n}x=\frac{r_{n}x}{2}$. So$F(T)=\left\{0\right\}$. Let${\alpha }_n=\frac{1}{n}$,${\beta }_n=\frac{1}{n}$and$r_n=1-\frac{1}{n}$, then they satisfy the conditions of Theorem 1.$\left\{x_n\right\}$is generated by (2). From Theorem 1, we can obtain$\left\{x_n\right\}$converges strongly to 0.

Next, we simplify the form of (2) and get

$$x_{n+1}=\frac{3-9n+9n^2+3n^3-14n^4}{-3+9n-9n^2-51n^3+6n^4}{x}_n.$$

(12)

Next, we take $x_1=(1,2,3)$ into (12). Finally, we get the following numerical results in Figure 3.

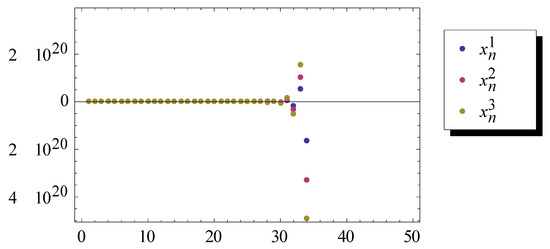
Figure 3. Numerical results.

Example 4.

Let$⟨\cdot ,\cdot ⟩:R^3\times R^3\to R$be the inner product and defined by

$$⟨x,y⟩=x_1{y}_1+x_2{y}_2+x_2{y}_3.$$

Let$\Vert \cdot \Vert :R^3\to R$be the usual norm and defined by$\Vert x\Vert =\sqrt{x_1^2+x_2^2+x_3^2}$for any$x=(x_1,x_2,x_3)$.

For any$x\in R^3$, let$f:R^3\to R^3$be defined by$f(x)=\frac{x}{6}$,$S:R^3\to R^3$be defined by$S(x)=\frac{x}{4}$and$J_{r_n}x=\frac{r_{n}x}{2}$. So$F(T)=\left\{0\right\}$. Let${\alpha }_n=\frac{1}{n}$,${\beta }_n=\frac{1}{n}$,$r_n=1-\frac{1}{n}$and$e_n=\frac{1}{n^2}$, then they satisfy the conditions of Theorem 2.$\left\{x_n\right\}$is generated by (6). From Theorem 2, we can obtain$\left\{x_n\right\}$converges strongly to 0.

Next, we simplify the form of (6) and get

$$x_{n+1}=-\frac{2{(n-1)}^2{n}^4}{-1+3n-3n^2-17n^3+2n^4}{x}_n.$$

(13)

Next, we take $x_1=(1,10,100)$ into (13). Finally, we get the following numerical results in Figure 4.

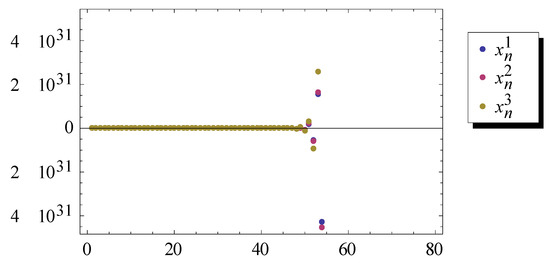
Figure 4. Numerical results.