Price and Treatment Decisions in Epidemics: A Differential Game Approach
Abstract
1. Introduction
2. The Epidemic Model
3. The Decision Problem
Cost Functions
- , linear state independent cost (LSI);
- , linear state dependent cost (LSD);
- , quadratic state independent cost (QSI);
- , quadratic state dependent cost (QSD).
- , linear;
- , quadratic;
- , blow-up;
4. Cooperative Solution
- What is the most reasonable way to represent the cartel’s payoff?
- How should the players’ cooperation gains be divided among all players?
4.1. Necessary Conditions
- 1.
- Linear case.H is constant with respect to p. The following can be immediately verified:
- (a)
- If , then H obtains its maximum at
- (b)
- If , then H obtains its maximum at any point
- (c)
- If , then H obtains its maximum at
- 2.
- Quadratic case.The following proposition holds.Proposition 1.The inequality (9) is true for all . It follows that the maximum of H, whenever it exists, belongs to the set or to the set .Proof.See Appendix. □It is
- (a)
- Let It is
- i.
- If , then H obtains its maximum at
- ii.
- If , then H obtains its maximum at any point
- iii.
- If , then decreases with respect to u andIt follows that , but H fails to have a maximum.
- (b)
- Let It is
- i.
- If , then H obtains its maximum at
- ii.
- If , then H obtains its maximum at any point
- iii.
- If , then decreases with respect to u andIt follows that , but H fails to have a maximum.
- 3.
- Blow-up case.The following proposition holds.Proposition 2.The inequality (9) is true for all . It follows that the maximum of H, whenever it exists, belongs to the set or to the set .Proof.See Appendix. □It is Moreover,
- (a)
- If , then H obtains its maximum at
- (b)
- If , then H obtains its maximum at any point
- (c)
- If , then decreases with respect to u andIt follows that , but H fails to have a maximum.
4.2. Individual Rationality
4.3. Sufficient Conditions
4.4. One Time-Switch Treatments
- If , then , and the value of does not matter.
- If , then
- If , then , and the value of does not matter.
- If , then
- If , then , and the value of does not matter.
- If , then
- If , then
- If , then
5. Stackelberg Equilibria
- If (linear cost function), then no interior maxima of occurs, and the best response of the follower is a corner solution (bang-bang control).
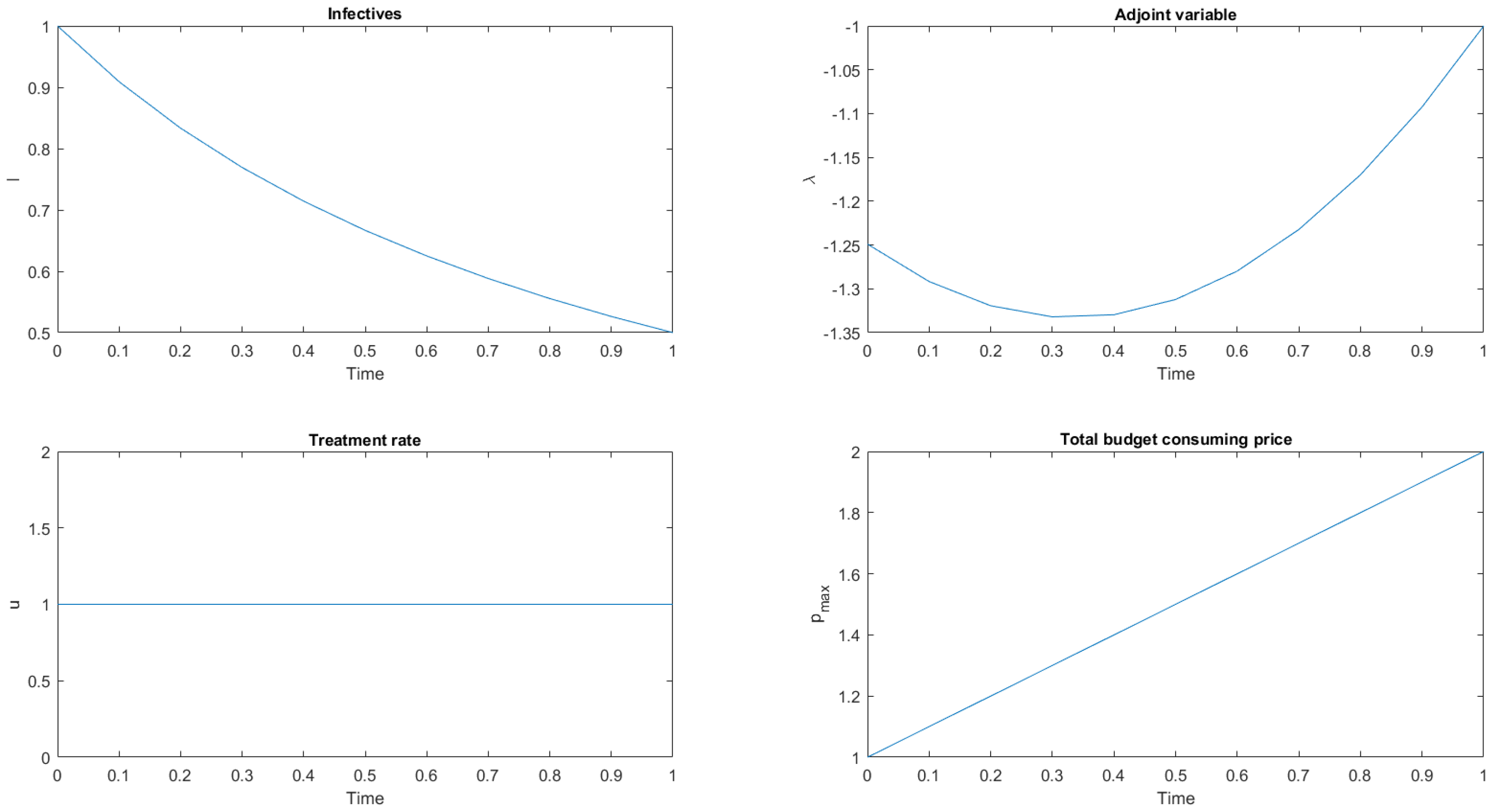
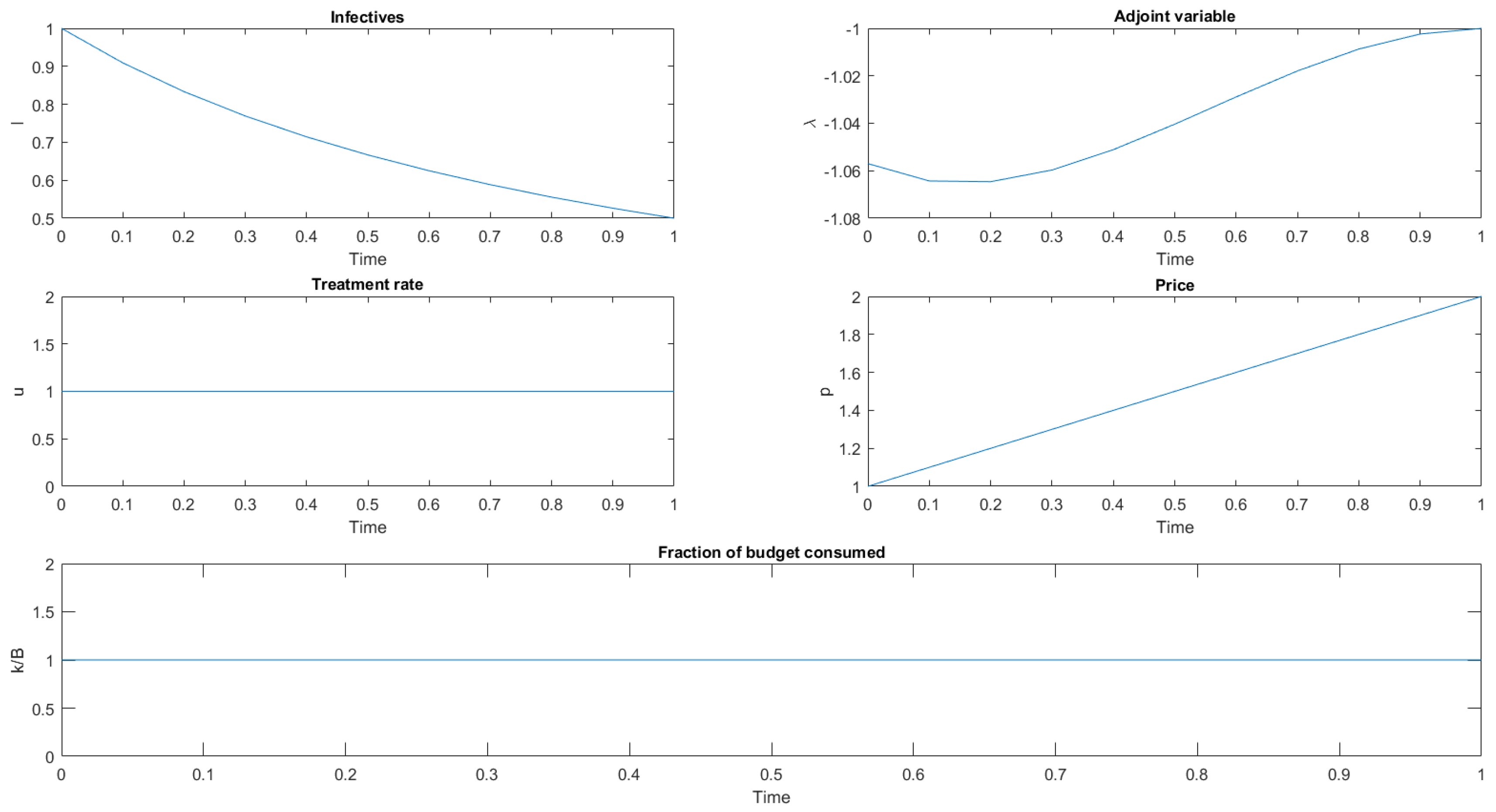
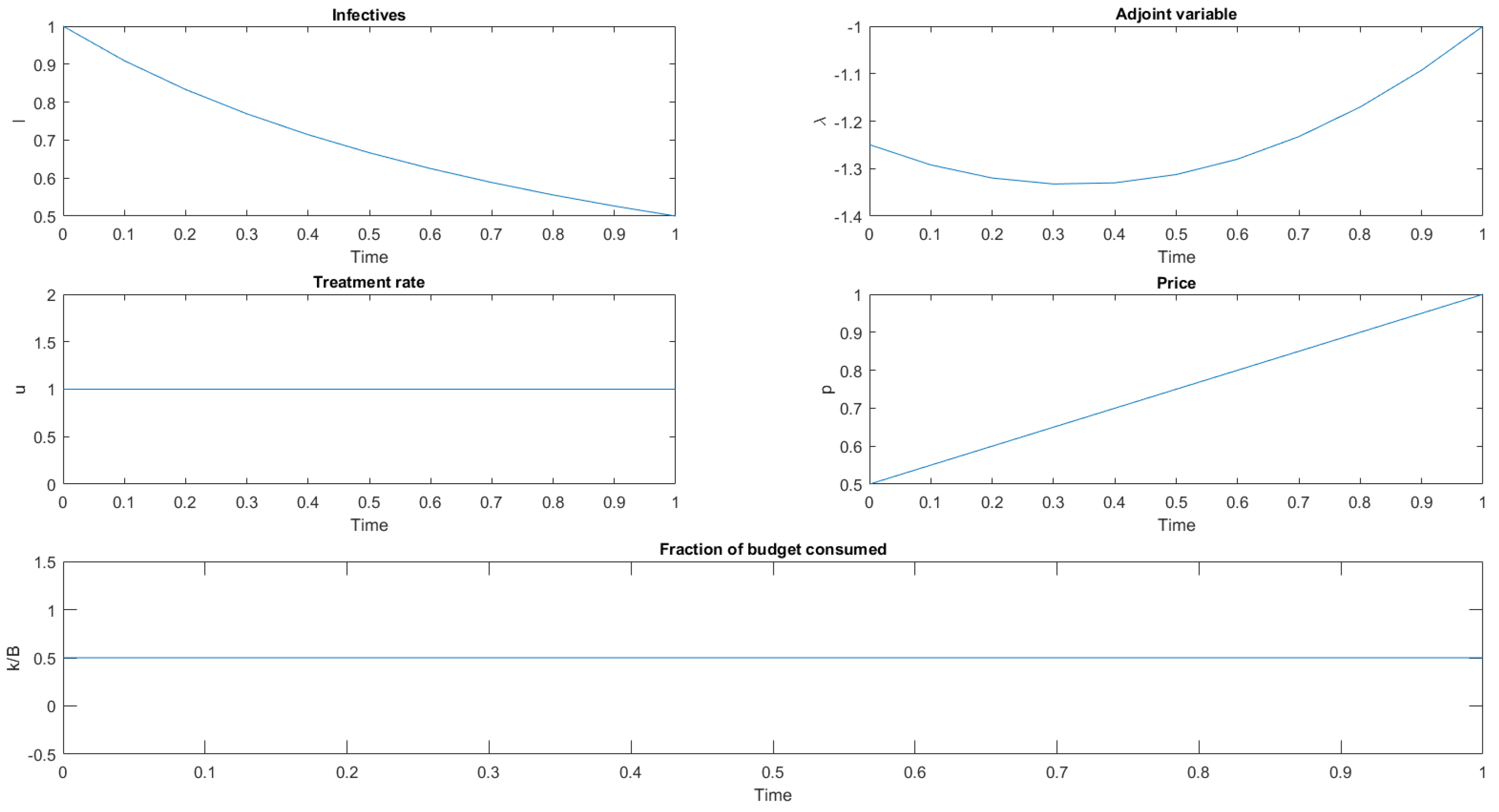
- If (quadratic cost function), then a local maximum of the Hamiltonian isand it is the best response of the social planner, provided that it satisfies the budget constraint.Moreover, the adjoint variable satisfies the differential equation . From inserting the value of u given by Equation (17), we havewith the transversality condition .The leader, foreseeing the the follower’s decision, maximizes the functionalsubject to the constraints (15) and (16). From inserting into Equation (18), we have that the leader maximizessubject to the constraintsThe leader’s Hamiltonian iswhere and are the adjoint variables. By maximizing with respect to p, we obtainand substituting in Equation (17) givesThe adjoint variables and satisfy the differential equations , respectively, and the transversality conditions , .Inserting into the state and adjoint equations leads to the following two-point boundary value problems:System (19) can be solved numerically to give the solution of the Stackelberg game, provided that , , , where
- If (blow-up cost function) then a local maximum of the Hamiltonian isBy substituting (20) into the leader Hamiltonian and differentiating with respect to p, we obtain that is the solution of the cubic equationAs in the quadratic case, it is argued that the solution of the Stackelberg game is characterized by the following two-point boundary value problems:
6. Concluding Remarks
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Theorems
- If , then .
- If , then , where .
- If , then , where .
- If , then .
- If , then .
- If , then , where .
- If , then .
- If , then .
- If , then .
- If , then .
- If , then , where .
- If , then .
- let ; then, for , where ;
- let ; then for .
- Let , then for and for where .
- Let , then for .
- Let , then and for and for where .
- Let , then for .
- let . Then .
- Let , then .
- Let , then .
References
- Kermack, W.; McKendrick, A. Contributions to the mathematical theory of epidemics. Part I. Proc. R. Soc. A 1927, 115, 700–721. [Google Scholar] [CrossRef]
- Brauer, F.; van den Driessche, P.; Wu, J. Mathematical Epidemiology; Springer: Berlin, Germany, 2008. [Google Scholar]
- Busenberg, S.; Cooke, K. Vertically Transmitted Diseases: Models and Dynamics; Springer: Berlin/Heidelberg, Germnay, 1993. [Google Scholar]
- Capasso, V. Mathematical Structures of Epidemic Systems; Springer: Berlin, Germnay, 1993. [Google Scholar]
- Anderson, R.M.; May, R.M. Infectious Diseases of Humans. Dynamics and Control; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Martcheva, M. An Introduction to Mathematical Epidemiology; Springer: New York, NY, USA, 2015. [Google Scholar]
- Bailey, N.T.J. The Mathematical Theory of Infectious Diseases; Griifin: London, UK, 1975. [Google Scholar]
- Bhatia, H.K.; Singh, H.; Grewal, N.; Natt, N.K. Sofosbuvir: A novel treatment option for chronic hepatitis C infection. J. Pharmacol. Pharmacother. 2014, 5, 278–284. [Google Scholar] [PubMed]
- Di Liddo, A. Optimal Control and Treatment of Infectious Diseases. The Case of Huge Treatment Costs. Mathematics 2016, 4, 21. [Google Scholar] [CrossRef]
- Hethcote, H.W. Three basic epidemiological models. In Applied Mathematical Ecology; Levin, S.A., Hallam, T.G., Gross, L.J., Eds.; Springer: Berlin/Heidelberg, Germnay, 1989; pp. 119–144. [Google Scholar]
- Neilan, R.L.M.; Schaefer, E.; Gaff, H.; Fister, K.R. Modeling Optimal Intervention Strategies for Cholera. Bull. Math. Biol. 2010, 72, 2004–2018. [Google Scholar]
- Posny, D.; Wang, J.; Mukandavire, Z.; Modnak, C. Analyzing transmission dynamics of cholera with public health. Math. Biosci. 2015, 264, 38–53. [Google Scholar] [CrossRef] [PubMed]
- Francis, P.J. Optimal tax/subsidy combinations for the flu season. J. Econ. Dyn. Control 2004, 28, 2037–2054. [Google Scholar] [CrossRef]
- Jana, S.; Haldar, P.; Kar, T.K. Optimal control and stability analysis of an epidemic model. Chaos Solitons Fractals 2016, 83, 67–81. [Google Scholar] [CrossRef]
- Jung, E.; Iwami, S.; Takeuci, Y.; Jo, T.C. Optimal control strategy for prevention of avian influenza pandemic. J. Theor. Biol. 2009, 260, 220–229. [Google Scholar] [CrossRef] [PubMed]
- Lashari, A.A.; Zaman, G. Optimal control of a vector borne disease with horizontal transmission. Nonlinear Anal. Real World Appl. 2012, 13, 203–212. [Google Scholar] [CrossRef]
- Rodrigues, H.S.; Monteiro, M.T.T.; Torres, D.F.M. Vaccination models and optimal control startegies to dengue. Math. Biosci. 2014, 247, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Jørgensen, S.; Zaccour, G. Differential Games in Marketing; Kluwer Academic Publishers: Boston, MA, USA, 2004. [Google Scholar]
- Leitmann, G. Cooperative and Non-Cooperative Many Players Differential Games; Springer: New York, NY, USA, 1974. [Google Scholar]
- Seierstad, A.; Sydsaeter, J.K. Optimal Control Theory with Economic Applications; Elsevier: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Lenhart, S.; Workman, J.T. Optimal Control Applied to Biological Models; Chapman & Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Liddo, A. Price and Treatment Decisions in Epidemics: A Differential Game Approach. Mathematics 2018, 6, 190. https://doi.org/10.3390/math6100190
Di Liddo A. Price and Treatment Decisions in Epidemics: A Differential Game Approach. Mathematics. 2018; 6(10):190. https://doi.org/10.3390/math6100190
Chicago/Turabian StyleDi Liddo, Andrea. 2018. "Price and Treatment Decisions in Epidemics: A Differential Game Approach" Mathematics 6, no. 10: 190. https://doi.org/10.3390/math6100190
APA StyleDi Liddo, A. (2018). Price and Treatment Decisions in Epidemics: A Differential Game Approach. Mathematics, 6(10), 190. https://doi.org/10.3390/math6100190




