Abstract
A nonrenewable resource extraction game model is analyzed in a differential game theory framework with random duration. If the cumulative distribution function (c.d.f.) of the final time is discontinuous, the related subgames are differentiated based on the position of the initial instant with respect to the jump. We investigate properties of optimal trajectories and of imputation distribution procedures if the game is played cooperatively.
1. Introduction
Modern mathematical game theory solves problems of modeling, research and analysis of various conflict-controlled processes. Of particular interest are the processes developing over time [1]. Differential games allow us to describe such dynamic processes in the sense of a conflict.
In a differential game of extraction, the standard scenario involves a dynamic competition among players (or, more precisely, companies) which exert effort aimed at extracting a natural resource. If the resource does not regenerate over time, such as natural gas or earth minerals, it is called exhaustible or nonrenewable.
Economic literature has been dealing with effects and characteristics of exhaustible resource extraction since 1817, when Ricardo [2] addressed the issue in his essay The principles of political economy and taxation. In the 20th century, the debate was relaunched by Hotelling [3], and then subsequently a vast stream of static and dynamic models was conceived and developed over the years (see, for example [4]).
If we only focus on models described through differential games, the basic framework includes a population of companies extracting the same resource, having the extraction effort levels as their strategic variables, which directly affect their respective payoffs, which increase as the extracted quantity increases. On the other hand, the state variables represent the stocks of resources, which are depleted over time by extraction. In the easiest representation, there is a unique resource and all companies aim to pick it up as much as possible. To describe a more realistic economic behavior, a key element was introduced in economic literature: the random duration of the game.
The seminal paper on this extension of the standard optimal control problem is due to Yaari [5] in 1965. At the same time, in Russia, in 1966, Petrosyan and Murzov [6] first studied differential zero-sum games with terminal payoff at random time horizon. Subsequently, further studies have been provided: in the work of Boukas et al. [7] in 1990, an optimal control problem with random duration was studied in general terms. Cooperative differential games with random time horizon were first studied by Petrosyan and Shevkoplyas [8] in 2000, whereas the concept of time consistency in differential games with prescribed duration was introduced in [9].
Such a concept is particularly relevant because most literature treats stability of the cooperative solutions in static cooperative settings. On the other hand, stable cooperation in the problem is a key requirement when the scenario is dynamic as well. In cooperative differential games, cooperating players wish to establish a dynamically stable (time-consistent) cooperative agreement (e.g., the dynamic versions of the Shapley Value, core, etc.).
Time consistency implies that, as cooperation evolves, cooperating partners are guided by the same optimality principle at each instant of time and hence do not have any incentive to deviate from the previously adopted cooperative behavior.
After Petrosyan’s seminal paper in 1977, such topic was actively developed by a number of researchers. In a paper by Jorgensen et al. [10], the problem of time-consistency and agreeability of the solution in linear-state class of differential games was investigated. In a paper by Petrosjan and Zaccour [11], a similar problem of ecological management was studied as well as in the more recent paper by Zaccour [12] and book by Petrosyan and Yeung [13]. Recently, the notion of time consistency was extended to the case of discrete games (see, e.g., [14]). An extension of the time consistency problem to the case of differential games with random duration was first undertaken in [8], subsequently further investigation and results were accomplished in [15,16,17,18,19]. In [20], a random time horizon hybrid (see also [21] for a general treatment of hybrid differential games) differential game was considered such that the probability distribution can change over time. Differential games with discrete random variable of time horizon and corresponding time-consistency problem were considered recently in [22]. Time-consistency notation for multistage games with vector payoffs was introduced in [23]. The regularization of a cooperative solution for the case of Core and the Shapley value had been done for a multistage game with random time horizon in [24]. The present contribution locates itself in this line of research.
In this paper, we intend to propose a description and an analysis of a scenario which differs from the previous treatments: the random variable which indicates the stopping time of extraction has a c.d.f. which is not continuous over the whole time interval. Specifically, we assume that there is a jump at an internal point, and we carry out an analysis which is differentiated based on the initial time of the game, i.e., before or after the jump. This formulation can represent any situation in which the distribution of the random variable is affected by external factors such as a Parliament bill which makes an extraction technique illegal. An example may be provided by the controversial fracking process for gas extraction.
In this setting, standard models take into account an oligopolistic competition among firms, where each firm aims to maximize its own profit. However, there exist some different approaches in the literature which also involve the possibility of cooperation among agents.
Because of the depletion of oil and gas resources on the mainland, the active development of oil-and-gas fields on continental shelves is to begin in the near future. Today, there are about seventy developing and potential oil-and-gas fields on continental shelves of Azerbaijan, Canada, Kazakhstan, Mexico, Norway, Russia, Saudi Arabia, the USA, etc. For example, today the firms which are involved in the development of Sakhalin oil-and-gas fields (Russia) are Gazprom, Shell, Mitsui, and Mitsubishi.
Moreover, the task of oil and gas exploitation in the Arctic is a key issue nowadays, especially relevant for Canada, Denmark, Norway, Russia and the USA. We believe that the source of economic success of the development of pool in Arctic should bring about a cooperative collaboration of participating countries. Collaboration in the Arctic is important at least in the sense that an accident at one borehole could lead to serious problems or complete stoppage of resource exploitation for all neighbors. Thus, the involved countries have to collaborate to provide security for oil and gas exploitation in the Arctic, otherwise environmental disasters and huge economic losses for all participants might occur. This is the main motivation to consider the cooperative form of the non-renewable resource extraction game.
However, despite all the above, the oil and gas extraction on a continental shelf is a high-risk economic activity and reconsideration of existing models of non-renewable resource extraction is required. Stochastic framework may be useful in the sense that it increases the validity of models (see, for example, [25]). As usual, game-theoretical models with infinite or fixed time horizon are used for modeling of renewable or exhausted resource exploitation. Although they provide numerous insights for equilibrium and stability, such an approach is not very realistic. Namely, the contract date is never equal to the real period of field exploitation, because either exploitation is prematurely finished by accident or unprofitability or the period of exploitation is extended.
Here, we specifically consider the occurrence of a cooperative game structure, where companies agree on a collective strategy to maximize the aggregate payoff. The agreement establishes that, after maximization, the total payoff is supposed to be redistributed among the cooperating firms. As in standard theory of cooperative games, the distribution of the total worth is the problem to be addressed (see, for example, [8]). In a differential game, the total worth simply corresponds to the sum of the integral payoffs of all players, and the distribution of the total worth has to be implemented by using a suitable solution concept. Our main focus is on the cooperative setup, where we describe the determination of an IDP (imputation distribution procedure, which was first introduced by Petrosyan in [9]), which is a dynamic way to attribute players their respective shares gained in the game. We also determine the relations to explicitly calculate IDPs in the above different cases, also discussing the issue of time consistency. Finally, we outline a complete example where N companies compete over extraction of a unique exhaustible resource, comparing the results in the non-cooperative and cooperative scenarios.
The paper is organized as follows. Section 2 introduces the notation of the game, whose non-cooperative setup is exposed. The cooperative setup is proposed in Section 3, where the main findings, including a theorem which establishes the existence of a time-consistent imputation, are laid out in detail. In Section 4, we propose a model to employ the above-mentioned procedure. Section 5 concludes and proposes some possible future developments.
2. Notation and Non-Cooperative Setup
2.1. Problem Statement
Consider the following standard notation for the N-players differential game , starting at initial time instant and at initial state :
- are the extraction effort levels of the N companies involved in pulling out M exhaustible resources. More precisely, is the effort exerted by firm i to extract resource j. The only requirement for the control sets , for , , concerns the non-negativity of effort levels, so we can assume , for all . (We do not impose any other constraint both on the control sets and on the state set, thus admitting any possible level. Because such sets are not compact in principle, maximum points may fail to exist, hence the choice of the payoff functions is crucial to have an equilibrium structure.)
- is the state vector indicating the quantities of the exhaustible resources available to be extracted by the companies. We assume .
- The M dynamic constraints of the game are given by:where , , and is a vector-valued function. The state equations in Equation (1) are ODEs whose solutions satisfy the standard existence and uniqueness requirements (the standard requirements are simply satisfied when dealing with a linear-quadratic structure such as the one we consider in Section 4).
- The interval over which the game is played is , where and .
- The final instant of the game, i.e., the exact time at which all companies stop the extraction, is described by the random variable . The cumulative distribution function (c.d.f.) of is given by , which is assumed to have a break (jump) of length . The jump occurs at instant , i.e., it can be described as follows (Figure 1):where is a sufficiently regular function. By construction, there exists such that
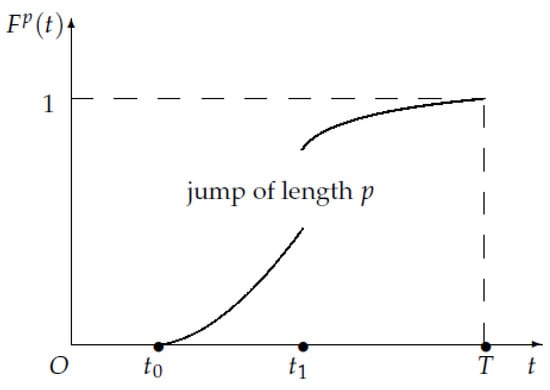 Figure 1. An example of a c.d.f. in the interval .
Figure 1. An example of a c.d.f. in the interval . - The instantaneous payoff of the i-th player at the moment is defined as . To shorten the notation, we writeThe i-th related integral function is:
- The i-th objective function is represented by the following integral payoff to be maximized:
The transformation of integral functional in the form of double integral (Equation (3)) to the standard for dynamic programming form is important for further study of the game (see also [26]).
Proposition 1.
The integral payoff in Equation (3) has the following form:
Proof.
Keeping in mind that , , , the payoffs can be rearranged by a simple manipulation:
☐
It can be helpful to provide a piece of justification for this model. Namely, this problem statement intends to take into account a common situation that there are certain events that happen at fixed time instants and that can be decisive for the game to stop or to proceed.
For instance, political activity or controversy may affect the situation: suppose that the Parliament passes a bill, or the outcome of a referendum establishes that would seriously impede or forbid the extraction activity (for example, prohibition of the fracking process). Obviously, companies know that the decision will be taken on a certain day and they can also estimate the probability of a negative outcome. Hence, it can be readily embedded into the ex-ante estimation of the terminal time probability distribution. Furthermore, the interpretation of such a scenario can also be extended towards other dynamic models involving environmental aspects. For example, even settings where the objective is pollution reduction can be affected by temporary shocks which modify the p.d.f. of some relevant variable: if the state variable is the pollution stock and we have a p.d.f. of its diffusion over the environment ex ante, a natural event may cause a jump in the distribution and, consequently, the need for a change of strategy. Other applications in other fields (such as insurance theory) can be hypothesized as well, but that goes far beyond the scope of our paper.
Back to our modeling, the jump in the probability distribution can also occur at the initial time, and this implies that there is a finite probability that the game does not start at all. Such a situation can be very interesting from the theoretical point of view as this corresponds to a non-proper probability function, i.e., a situation that was never addressed before in literature.
Finally, an interesting interpretation can be attached to the c.d.f. : basically, , suggesting that it can represent the probability that the jump occurs. Namely, if the game stops immediately after the start, and since , . On the other hand, p decreases as time goes on, because is increasing: if , no jump occurs and , so .
2.2. Problem Statement for a Subgame
The important notation in dynamic (differential) games is a notion of subgame [13] which takes non-trivial form for our problem statement for the reason of stochastic elements relating to time of a game duration. In dynamic (differential) games, there is a key notion of subgame [13], which takes a non-standard form, due to the stochastic time duration of the game.
Let the game evolves along the trajectory . To better identify subgames of , we are going to distinguish two main cases, which are differentiated based on the payoff flows: when the subgame starts before the jump instant and after .
Subgame starting at : Consider a subgame such that . The conditional c.d.f. in the considered subgame takes the following form:
where
Therefore, recalling that , the expected integral payoff accruing to the player i in this subgame is given by the following formula:
Subgame starting at : Consider a subgame such that . The conditional cumulative distribution function in the considered subgame takes the following form:
Therefore, player i’s expected integral payoff is provided by the formula:
Thus, we prove the following proposition.
Proposition 2.
The expected integral payoff of player i in the subgame , has the following form:
2.3. Open-loop Nash equilibrium
To find the equilibrium in the non-cooperative setup of the game, we use the definition of a time-consistent Nash equilibrium from [13] adopted for the new problem statement as defined in Section 2.1. Let us consider case of (the definition can be easily extended for the case with several resources).
3. Main Results in the Cooperative Setup
Suppose that the game is played in a cooperative scenario. Generally speaking, cooperation means that a group of companies agree to form a coalition before starting the game. In this case, we assume that such a group is the grand coalition, i.e., the totality of the involved players. Clearly, any dynamic model in which players form coalitions that are subgroups of the grand coalition deserves a special attention as well, but it is outside the scope of this paper (for the construction of the value functions in cooperative games, see, for example, [27,28] for cooperative differential games).
From now on, to simplify the notation and to reconcile the ongoing discussion with a standard case, we assume a unique exhaustible resource, which is extracted by N different companies, hence and are the effort levels. The cooperating players decide to use optimal strategies , which are defined as the strategies maximizing the sum of all payoffs, i.e.,
As is standard in cooperative games, all players in the coalition jointly agree on a distribution method to share the total payoff. It is possible that, in some instant, the solution of the current game is not optimal according to the optimality principle which was initially selected, meaning that the optimality principle may lose time-consistency. Because we are investigating a dynamic setting, it is necessary to define and to determine an imputation distribution procedure which is supposed to be compliant with the payoff in the form of Equation (4).
Before proceeding, we briefly recall the notion of imputation: in an N-players cooperative game, an imputation is a distribution among players such that the sum of its coordinates is equal to the value of the grand coalition and each assigns to the i-th player a quantity which is not smaller than the one she would achieve by playing as a singleton. In other words, if N is the set of players and is the characteristic function of the game, is an imputation if and for all . The first property is called efficiency and guarantees that the imputation is a method of distribution of the total gain among all players (for an exhaustive overview on cooperative games, see [29]). Different imputations are usually employed in cooperative games, because not all solution concepts fit all models. However, the most useful one seems to be the Shapley value, first introduced by Nobel laureate L.S. Shapley in [30] in 1953, and which has been utilized in a huge number of economic and financial applications. (An extensive treatment of the Shapley value and of other relevant solution concepts can be found in [29].)
Definition 2.
Given an imputation in a game , such that for all we have that:
then the vector function is called an imputation distribution procedure (IDP).
The next Definition intends to expose the property of time-consistency for imputations.
Definition 3.
An imputation in a game is time-consistent if there exists an IDP such that:
- 1.
- for all the vector , wherefor all , belongs to the same optimality principle in the subgame , i.e., is an imputation in ;
- 2.
- for all the vector wherefor all , belongs to the same optimality principle in the subgame , i.e., is an imputation in .
The next step consists in the determination of a relation between and . In addition, in this case, we have to distinguish the cases when the subgame starts before or after the jump at instant . Firstly, we prove a lemma which is helpful to reformulate imputation . The subsequent Proposition intend to explicitly outline the forms for the IDPs of the game.
Lemma 1.
If , for all , the coordinates of imputation ξ can be written as follows:
Proof.
Proposition 3.
If , then for all , the i-th coordinate of the IDP is given by:
If , then for all , the i-th coordinate of the IDP is given by:
Proof.
When , we can differentiate Equation (6) with respect to , thus obtaining:
Then, solving for yields:
When , we can differentiate Equation (7) with respect to , thus obtaining:
Then, solving for yields:
☐
The above results can be collected as follows:
Theorem 1.
Let the imputation of the game be an absolutely continuous function of t, . If the IDP has one of the following forms:
- 1.
- if ,
- 1.
- if
The problem of stable cooperation in differential games with random duration where c.d.f. is continuous ( without any breaks) was studied by in [8,16,18]. Assuming in our model p is equal to zero, the obtained results coincide with the results in the above-mentioned work. Moreover, new results cover the framework for a fully deterministic models. Namely, for the problem with prescribed duration for in Equations (10) and (11), we obtain the results published in [9]. For the problem with constant discounting, see work [11] and Equation (10) with .
4. An Example
We are going to consider a simple model of common-property nonrenewable resource extraction published in [31] in 2000, and then further investigated in successive papers (e.g., [15,32]).
In addition, in this case, , that is we have a unique state variable indicating the stock of a nonrenewable resource at time t. The companies’ strategic variables , for denote the rates of extraction, or extraction efforts, at time t. The state equation has the form:
the initial condition, i.e., the amount of resource at time is The differential Equation (12) is the most standard and simple dynamics in nonrenewable resource extraction games, where all players concur to extract and deplete the resource with the same intensity. When the involved resource is renewable, it also regenerates at a growth rate , hence a positive linear term in the state variable also appears in Equation (12), and the model must be treated differently (see for example [33] or the survey [34]).
Back to the model, we suppose that the game ends at the random time instant t, a random variable having exponential distribution on the interval (Figure 2), i.e., we are investigating the first case, before the jump in the distribution. We also assume that the jump takes place in the end of the interval , i.e., . Hence, the discontinuity occurs at the terminal time. The c.d.f. of the random variable t is given by:
which turns into for . From now on, we consider this case, i.e., .
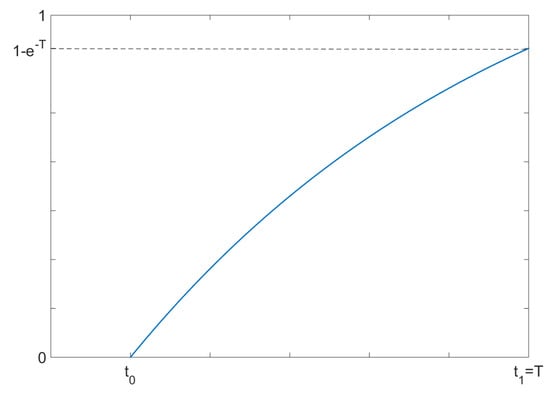
Figure 2.
The exponential c.d.f. in the interval .
Note that we can provide the complete formulation of the discontinuous c.d.f. as in the previous section:
meaning that, in this case, .
In this game, each player i has a utility function
where and are positive constants depending on the specific scenario and on the companies’ characteristics.
The expected integral payoff of player (to lighten the notation, we omit redundant arguments whenever possible):
We are going to find noncooperative open-loop optimal trajectories of state and controls in relation to the noncooperative form of the game using Pontryagin’s maximum principle, which is one of the two major procedures for equilibrium structure in differential games [31]. In this model, this method is suitable, because the open-loop trajectories are easily visualized in . Each company aims to solve the following problem:
Each player has a Hamiltonian function of the form:
where is the i-th adjoint variable attached by company i to the resource dynamics or, in line with a standard economic interpretation, the related shadow price.
Differentiating each Hamiltonian with respect to and then equating to 0 yields the first order conditions:
then, solving for , we obtain:
The second order conditions hold, because for all :
The adjoint equations and the related transversality conditions read as:
hence the optimal costates are , for all .
Plugging into the FOCs yields the optimal controls, i.e.,
To determine the optimal state , it suffices to substitute Equation (14) into the state dynamics in Equation (12) and subsequently integrate both sides, employing the initial condition:
so the optimal stock of resource amounts to:
Now, we are going to take into account a cooperative version of the game, that is a scenario where all companies agree to play strategies such that their aggregate payoff is maximized. The sum of all payoffs is:
The approach for the determination of the open-loop equilibrium structure is analogous to the one adopted in the noncooperative case. From now on, we are going to use the notation , to avoid confusion with the previous quantities.
The comparison between the resource stocks in the two scenarios can be illustrated by a simple inequality, highlighting that the noncooperative resource stock exceeds the cooperative one (Figure 3 and Figure 4). Namely, at all , we have that:
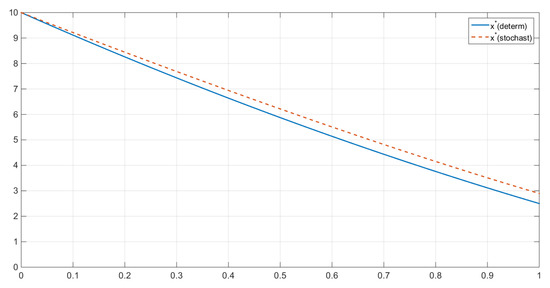
Figure 3.
Comparison between deterministic and stochastic settings for state .
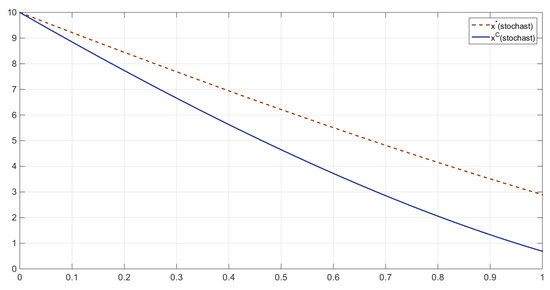
Figure 4.
Comparison between Nash equilibrium and cooperative equilibrium for .
Such an estimate always holds for , because
An investigation of a suitable IDP requires the definition of an imputation in this model. If we choose an egalitarian distribution, we can define the shares of the imputation as fractions of the total payoff equally divided by the number of players, i.e.,
The case we are taking into account is the first one in the previous section, i.e., , where constant . Furthermore, the exponential c.d.f. at hand has a relevant property: since , the ratio , hence Equation (8) for IDP takes the form:
Evaluating at the optimal controls and states amount to:
By employing in , we can determine the expression of the expected integral payoff of company i for a subgame starting at :
Subsequently, we have to determine , by a simple differentiation:
Finally, employing the found forms for and , we get:
Thus, IDP takes form
Figure 5, which was created with Matlab R2016a, portrays a sketch of the behavior of the imputation and of the IDP over time. The numerical simulation was performed for the following parameters: , , , , , and .
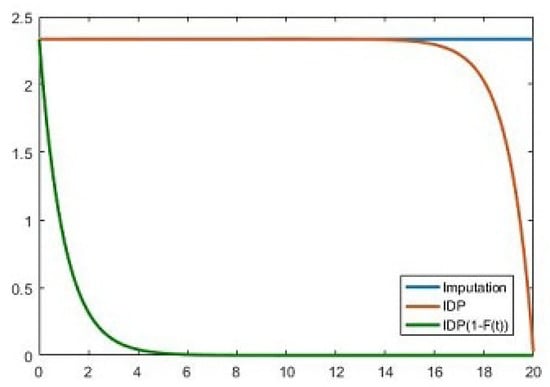
Figure 5.
IDP and Imputation for one player.
On this figure, we can see that the amount of imputation is equal to the integral of IDP multiplied by discount probability factor.
5. Conclusions and Further Developments
We proposed an analysis of a class of extraction differential games with uncertain duration possibly involving a discontinuous c.d.f. for the random variable indicating the duration of the game. Then, we focused our attention on the cooperative aspects of the game to identify the appropriate IDP and applied such a theory to a standard nonrenewable resource extraction model.
There exists a number of possible improvements, both from theoretical and applied viewpoints, regarding the feedback information structure of such a class of games, the solution concepts (i.e., Shapley value, Banzhaf value, and core) to be employed, the models which represent scenarios different from the extraction of an exhaustible resource and also models of processes with more complex and realistic c.d.f. All of them are left for future research.
Author Contributions
Conceptualization, E.G. and A.M.; Methodology, E.G.; Validation, E.G., A.M. and A.P.; Formal Analysis, E.G., A.M. and A.P.; Investigation, E.G., A.M. and A.P.; Writing—Original Draft Preparation, E.G., A.M. and A.P.; Writing—Review & Editing, A.M.; Visualization, E.G., A.M. and A.P.
Funding
Ekaterina Gromova acknowledges the grant from Russian Science Foundation 17-11-01079.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Isaacs, R. Differential Games; John Wiley and Sons: New York, NY, USA, 1965. [Google Scholar]
- Ricardo, D. On the Principles of Political Economy and Taxation; John Murray: London, UK, 1817. [Google Scholar]
- Hotelling, H. The economics of exhaustible resources. J. Polit. Econ. 1931, 39, 137–175. [Google Scholar] [CrossRef]
- Tsiropoulou, E.E.; Vamvakas, P.; Katsinis, G.K.; Papavassiliou, S. Combined Power and Rate Allocation in Self- Optimized Multi-Service Two-Tier Femtocell Networks. Comput. Commun. 2015, 72, 38–48. [Google Scholar] [CrossRef]
- Yaari, M.E. Uncertain lifetime, life insurance, and the theory of the consumer. Rev. Econ. Stud. 1965, 32, 137–150. [Google Scholar] [CrossRef]
- Petrosyan, L.A.; Murzov, N.V. Game-theoretic problems of mechanics. Litovsk. Math. Sb. 1966, 7, 423–433. [Google Scholar]
- Boukas, E.K.; Haurie, A.; Michael, P. An optimal control problem with a random stopping time. J. Optim. Theory Appl. 1990, 64, 471–480. [Google Scholar] [CrossRef]
- Petrosyan, L.A.; Shevkoplyas, E.V. Cooperative solutions for games with random duration. Game Theory Appl. 2003, 9, 125–139. [Google Scholar]
- Petrosyan, L.A. Time-consistency of solutions in multi-player differential games. Vestn. Leningr. State Univ. Math. 1977, 4, 46–52. [Google Scholar]
- Jorgensen, S.; Martin-Herran, G.; Zaccour, G. Agreeability and Time Consistency in Linear-State Differential Games. J. Optim. Theory Appl. 2003, 119, 49–63. [Google Scholar] [CrossRef]
- Petrosjan, L.A.; Zaccour, G. Time-consistent Shapley value allocation of pollution cost reduction. J. Econ. Dyn. Control 2003, 27, 381–398. [Google Scholar] [CrossRef]
- Zaccour, G. Time consistency in cooperative differential games: A tutorial. Inf. Syst. Oper. Res. 2008, 46, 81. [Google Scholar] [CrossRef]
- Yeung, D.W.K.; Petrosyan, L.A. Subgame Consistent Cooperation; Springer: New York, NY, USA, 2016. [Google Scholar]
- Reddy, P.V.; Shevkoplyas, E.V.; Zaccour, G. Time-consistent Shapley value for games played over event trees. Automatica 2013, 49, 1521–1527. [Google Scholar] [CrossRef]
- Kostyunin, S.; Palestini, A.; Shevkoplyas, E.V. On a nonrenewable resource extraction game played by asymmetric firms. J. Optim. Theory Appl. 2014, 163, 660–673. [Google Scholar] [CrossRef]
- Marin-Solano, J.; Shevkoplyas, E.V. Non-constant discounting and differential games with random time horizon. Automatica 2011, 47, 2626–2638. [Google Scholar] [CrossRef]
- Parilina, E.M.; Zaccour, G. Node-Consistent Shapley Value for Games Played over Event Trees with Random Terminal Time. J. Optim. Theory Appl. 2017, 175, 236–254. [Google Scholar] [CrossRef]
- Shevkoplyas, E.V. Stable cooperation in differential games with random duration. Control Soc. Econ. Syst. 2010, 2, 79–105. [Google Scholar]
- Shevkoplyas, E.V. The Hamilton-Jacobi-Bellman equation for a class of differential games with random duration. Autom. Remote Control 2014, 75, 959–970. [Google Scholar] [CrossRef]
- Gromov, D.; Gromova, E. Differential games with random duration: A hybrid systems formulation. Contrib. Game Theory Manag. 2014, 7, 104–119. [Google Scholar]
- Gromov, D.; Gromova, E. On a Class of Hybrid Differential Games. Dyn. Games Appl. 2017, 7, 266–288. [Google Scholar] [CrossRef]
- Malakhova, A.P.; Gromova, E.V. Strongly Time-Consistent Core in Differential Games with Discrete Distribution of Random Time Horizon. Math. Appl. 2018, 46, 197–209. [Google Scholar]
- Kuzyutin, D.; Nikitina, M. Time consistent cooperative solutions for multistage games with vector payoffs. Op. Res. Lett. 2017, 45, 269–274. [Google Scholar] [CrossRef]
- Gromova, E.; Plekhanova, T. On the regularization of a cooperative solution in a multistage game with random time horizon. Discret. Appl. Math. 2018. [Google Scholar] [CrossRef]
- Feliz, R.A. The optimal extraction rate of a natural resource under uncertainty. Econ. Lett. 1993, 43, 231–234. [Google Scholar] [CrossRef]
- Gromova, E.V.; Malakhova, A.P.; Tur, A.V. On the conditions on the integral payoff function in the games with random duration. Contrib. Game Theory Manag. 2017, 10, 94–99. [Google Scholar]
- Reddy, P.V.; Zaccour, G. A friendly computable characteristic function. Math. Soc. Sci. 2016, 82, 18–25. [Google Scholar] [CrossRef]
- Gromova, E.V.; Petrosyan, L.A. On an approach to constructing a characteristic function in cooperative differential games. Autom. Remote Control 2017, 78, 1680–1692. [Google Scholar] [CrossRef]
- Owen, G. Game Theory, 3nd ed.; Academic Press: New York, NY, USA, 1995. [Google Scholar]
- Shapley, L.S. A Value for n-person Games. In Contributions to the Theory of Games; Kuhn, H.W., Tucker, A.W., Eds.; Princeton University Press: Princeton, NJ, USA, 1953; Volume II, pp. 307–317. [Google Scholar]
- Dockner, E.J.; Jorgensen, S.; Long, N.V.; Sorger, G. Differential Games in Economics and Management Science; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Rubio, S.J. On the coincidence of feedback Nash equilibria and Stackelberg equilibria in economic applications of differential games. J. Optim. Theory Appl. 2006, 128, 203–220. [Google Scholar] [CrossRef]
- Jorgensen, S.; Yeung, D.W. Stochastic differential game model of a common property fishery. J. Optim. Theory Appl. 1996, 90, 381–403. [Google Scholar] [CrossRef]
- Van Long, N. Dynamic games in the economics of natural resources: a survey. Dyn. Games Appl. 2011, 1, 115–148. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).