1. Introduction
The structural properties of quasi-cyclic (QC) [
1,
2] and generalized quasi-cyclic (GQC) codes [
3,
4,
5] have been reported. On the other hand, cyclic codes can be extended to pseudo-cyclic (PC) and generalized pseudo-cyclic (GPC) codes [
6]. Similar constructions for the rational integer ring
are known as integer codes and generalized integer codes [
7]. We can summarize the module structure of these codes as follows:
where
is a one-variable polynomial ring over a
q-element finite field
with a prime power
q,
is the ideal of
generated by
,
is their quotient ring,
denotes the direct sum of the
- or
-modules and
is the integer residue ring modulo
. Note that both
and
are Euclidean domains [
8,
9]; we say that a commutative integral domain
R is a Euclidean domain if there exists a function
such that, for any
with
,
and
or
are valid for some
, where
denotes the set of non-negative integers. Finding
with
and
or
is called Euclidean division, and
are called a quotient and a remainder of
a by
b, respectively. If
, then
is the degree function, and if
, then
is the absolute value. However, no theory has yet been reported concerning the unified treatment of codes over the quotient rings of the general Euclidean domains.
In this study, we deal with the above codes uniformly, which can be constructed by any Euclidean domain
R. Let
be the ring of
l-by-
l matrices with entries in
R. We denote:
where
denotes the diagonal matrix whose
i-th entry is
for all
; for
,
denotes the
R-module consisting of
for all
; and for two
R-modules
,
denotes their quotient
R-module. We investigate
R-submodules of
, and we denote one of them by
. If
, then
R-submodules are equivalent to the GPC codes, and if
, then
R-submodules are equivalent to the generalized integer codes.
To indicate the
R-modules explicitly, let us define their generator matrices. Let
be a natural surjective map of the
R-modules and
be the inverse image of an
R-submodule
. If
satisfies
, then we say that
G is a generator matrix of
. For an arbitrary given
, there exists an
R-module
such that
G is its generator matrix if and only if
, and this condition is equivalent to:
for some
. Then, we have
.
Under the above preparation, if
, then we can reveal the multiplicative structure of generator matrices of
R-submodules in the following manner. Hereafter, we set
. Let
be the identity matrix. In this case, we have
and:
For two R-modules and , if and , we have . If we set and , then determines an R-module in . Our results can be divided into two parts. The first result asserts that this correspondence by the multiplication of generator matrices is surjective, i.e., all R-modules in can be obtained by this correspondence. The second result asserts that, if , then this correspondence is injective, i.e., and are both uniquely determined for each . The latter assertion corresponds to the explicit version of Chinese remainder theorem in our theory of R-submodules. Because we can express its composition and decomposition through the multiplication of generator matrices effectively, our results can be applied to the fast enumeration of the generator matrices of efficient R-modules in . The above results we obtain here are valid for the codes over the quotient rings of arbitrary Euclidean domains.
In general, the result of the Euclidean division is not unique; for
with
, the quotient
s and the remainder
r are not always unique in
and
or
. For example, if
, the result is unique, but if
,
. One way to impose the uniqueness for the result of the Euclidean division in
is to indicate
, where, for a real number
x,
denotes a unique
such that
. It is shown that, if
, then
is equivalent to
, and
or
follows from
. In this study, for the other cases of Euclidean domains
R such as the ring of Gaussian integers
, the ring of Eisenstein integers
, the
p-adic integer ring
and the ring of the formal power series
, namely,
where
,
and
p denotes a rational prime, we determine a unique pair of the quotient and remainder similar to
and
of
. We apply this uniqueness to show the uniqueness of the Euclidean division by a class of matrices over
R.
Let
be the group of invertible matrices in
. Then, for two generator matrices
of an
R-module
, there exists
such that
. Among these
’s, we can algorithmically find a simple form of
G, which is called the reduced generator matrix, which generalizes the Hermite normal form [
10,
11] of
. Then, we apply the uniqueness of the Euclidean divisions to show that there exists a unique reduced generator matrix for each
R-module in
. This standard expression of the generator matrix is useful for enumerating and searching for efficient
R-modules in
.
Furthermore, we apply our theory of generator matrices to Hecke rings of matrices over the prescribed Euclidean domains. Hecke rings or Hecke algebras we consider here are the rings of the formal finite sums
of the double cosets
with
, where
,
denotes the matrix determinant, and
. Hecke rings are commonly used as Hecke operators to the number theory, especially, the theory of modular forms [
12,
13]. In this study, we show that the generator matrices of
R-modules in
are deeply concerned with the theory of Hecke rings. We describe in terms of the generator matrices the definition of Hecke rings, the homomorphism “ind
”, the prime decompositions and a generating function of ind
. Although these results on Hecke rings are not new (cf. [
13]), the argument in this study shows that the concept of reduced generator matrices simplifies the theory of Hecke rings and makes it computable.
The rest of this paper is organized as follows.
Section 2 gives the basic definitions and the one-to-one correspondence between
R-modules in
and certain
R-modules in
.
Section 3 gives a division algorithm, which is similar to the Euclidean division in
R, for a class of matrices with a pair of quotient and remainder matrices.
Section 4 defines generator matrices of
R-modules in
and shows their existence constructively.
Section 5 shows the multiplicative structure among the generator matrices in the case of
.
Section 6 treats the cases where Euclidean divisions have a uniqueness property, which can deduce the uniqueness of the reduced generator matrix. Finally,
Section 7 applies our theory of generator matrices to Hecke rings and shows a generating function which is useful for counting the reduced generator matrices with a fixed determinant.
Section 8 concludes the study.
2. -Modules in
Throughout this section, R is used to denote any commutative ring. The purposes of this section are to define R-modules in and to show a one-to-one correspondence between R-modules in and a class of lattices.
Let
be positive and
. Consider the quotient ring
for
. For any
, we denote the corresponding element in
by
. If we define:
then
has the natural structure of an
R-module. If
, then we write:
We denote the projection map of the
R-modules by:
Hereafter, if is considered, then is assumed to be for all .
Let be a subset. In this study, we consider R-submodules of the form .
For example, let . Then, can be also viewed as a vector space of dimension over . If is an R-module, then determines a linear code of length n over , whose dimension will be stated later in Proposition 5. If and , then is called a cyclic code. If and is arbitrary, then is called a PC code. If , l divides n, and , then is called a QC code. If for all and , then is called a GQC code.
For the other example, let . Then, an R-module is called a generalized integer code. If , then is called an integer code.
Let
be an
R-module. Consider
R-module
. Then,
includes
l elements of the form:
where
. Note that:
where:
and
for
. Conversely, let
be an
R-module with
. Then,
is an
R-module. It is proven below that this correspondence between
with
and
is one-to-one and onto.
Proposition 1. The set of R-modules with and the set of R-modules are bijective through the correspondences and which are the inverse maps of one another.
Proof. follows from the surjectivity of F. Thus, we only need to show that . For , implies that . Conversely, from , there exists such that . Then, , and there exists such that . Thus, and . ☐
In [
5], the author identified
with
and expressed them using the same notation
. In this study, we distinguish them and use the notation
only for an
R-module in
.
6. Unique Euclidean Division Cases
In this section, we focus on the Euclidean domain R described above specifically. First, we will show that the Euclidean division in R satisfies the following condition.
To validate this condition for the Euclidean division by a nonzero , one may choose a complete system of representatives of such that for all . Then, the above condition is valid because with and implies and . However, for each b, it is not always easy to choose . Thus, in this section, we show that a convenient can be taken in each case of R’s.
The case of . The Euclidean function has the uniqueness properties, i.e., are uniquely determined in with and because, if , then , and it follows from and that .
The case of
. For
with
, the results
of Euclidean division
with
and
are not unique as stated in Introduction. Hence, we decide
by
with
. In other words, we have
with
, or equivalently, with
, because:
Then,
are unique because of the expression
. (Alternatively, if
, then
and it follows from
and
that
and
.) There are some choices to indicate unique
, e.g.,
where, for
,
denotes a unique
such that
. We adopt
for simplicity.
The case of
. For
with
, the results
of Euclidean division
with
and
are not unique because
. We decide
with
and
by
(Similarly,
is also satisfactory. On the other hand,
dose not satisfy
in general, e.g.,
and
.)
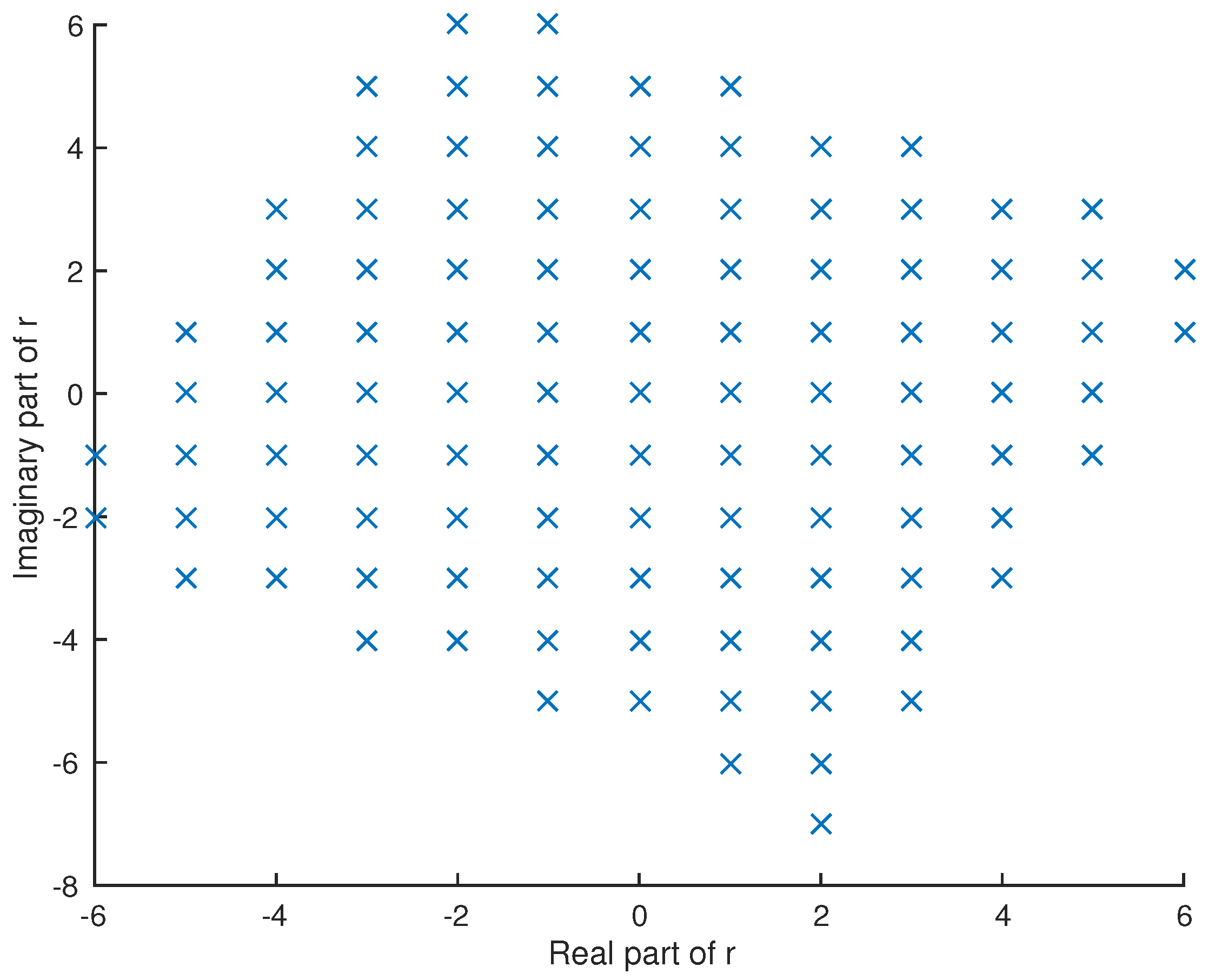
Because:
(
16) deduces
and
of (
4). Moreover, (
16) is equivalent to the property on
r, through the equation
,
Then,
are unique because of the expression (
16) on
s. Alternatively, if
, then
and it follows from
that:
and
deduces
, and similarly,
.
Thus, we take (
16) or (
17) as “the additional property” to indicate unique quotient and remainder in Euclidean division in
R. A numerical example is shown in
Figure 1.
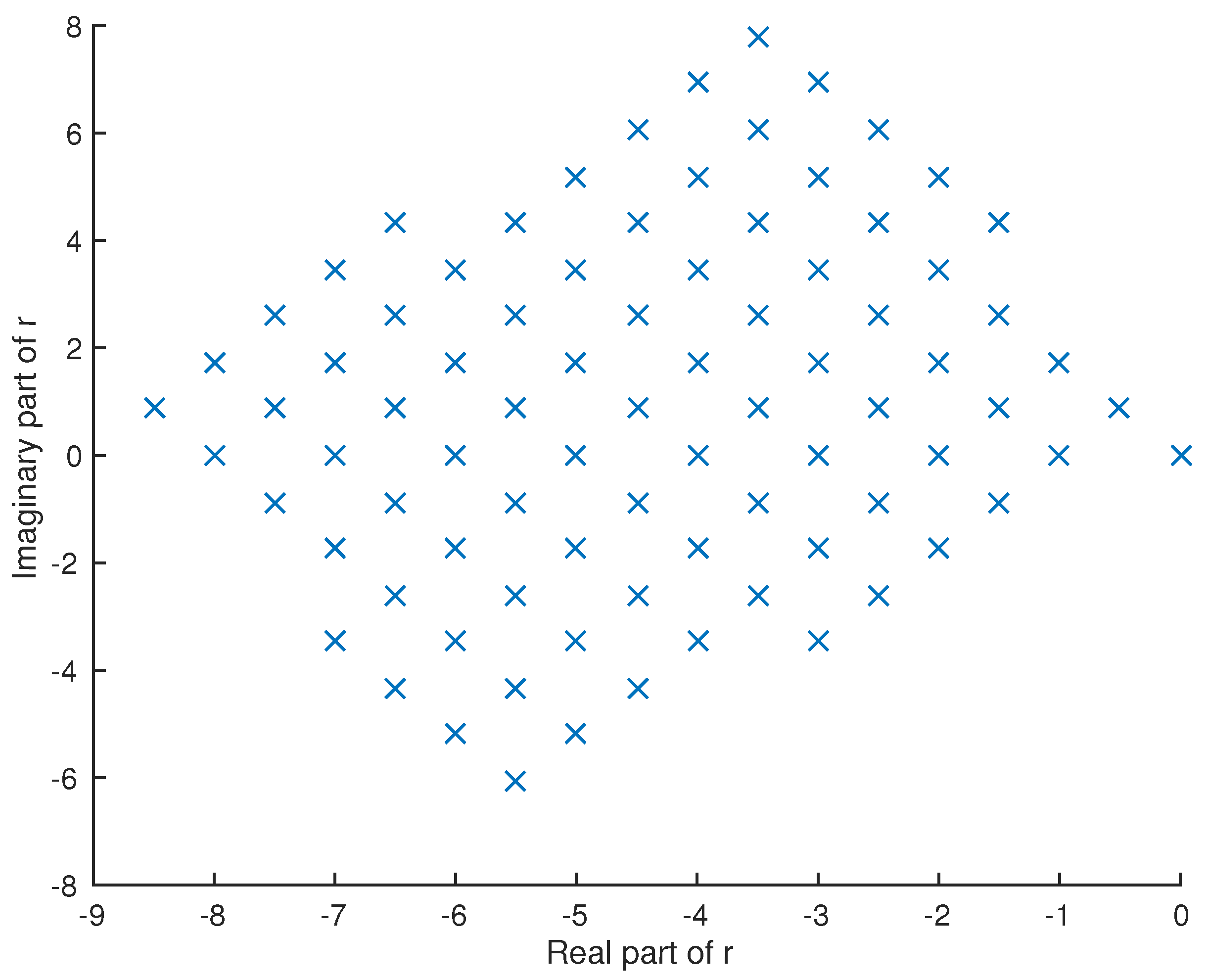
The case of
. For
with
, the results
of Euclidean division
with
and
are not unique because
. Similarly to
, we may decide
with
and
by
if
, which is equivalent to
if
. (Similarly,
is also satisfactory.) However, unlike
, we can decide
with
and
by:
Because (
18) deduces
and
,
where the last inequality follows from the fact that
takes the maximum on
only at
and that, for
,
. Moreover, (
18) is equivalent to the property on
r, through the equation
,
Then,
are unique because of the expression (
18) on
s. Thus, we take (
18) or (
19) as “the additional property” to indicate unique quotient and remainder in Euclidean division in
R. A numerical example is shown in
Figure 2.
The case of
. For
with
, the results
of Euclidean division
with
and
or
are not unique because
for
. Let
be the field of fractions of
R. For
, there exists
such that
with
. For
, we uniquely define
and
such that
. Then, for
with
, we decide
by
with
. In other words, we have
with
because:
Moreover, implies because . Finally, we show the uniqueness of such . Suppose that, for with , and . Then, from , we say . In view of , the uniqueness of and implies that and .
The case of
. For
with
, the results
of Euclidean division
with
are not unique because
for
and
or
. Let
be the field of fractions of
R. For
, there exists
such that
with
. For
, we uniquely define
and
such that
. Then, for
with
, we decide
by
with
. In other words, we have
with
because:
Moreover, implies because . The uniqueness of such can be shown similarly to the case of .
Hereafter, we denote the quotient field of R by . For any , with are uniquely determined up to units because implies and .
Definition 3. For , we define by In the case of , this definition is well-defined because, if with , , , and , then and deduce .
Lemma 2. For any , if and , then .
Proof. In the case of , let and with , , , and . Then, deduces . The other cases follow from the argument in each case. ☐
Hereafter, for with , the quotient s and the remainder r of the Euclidean division with are determined uniquely such that , or equivalently, . Note that follows from .
Proposition 6. Let be upper triangular. Then, for any , there exist unique such that , i.e.,with for all . In other words, the result of the division in Proposition 2 is unique. Proof. Suppose that satisfy and for all . Then, subtracting one expression for a from the other, we obtain , which is equivalent to for all . For , we have , which deduces by Lemma 2. Supposing for all , we have , which deduces by Lemma 2. By induction on i, we obtain , which completes the proof. ☐
Reduced Generator Matrices of -Modules in
Definition 4. For , we say that a is monic if and only if and a satisfies the following condition: If for with monic and invertible e, then we have and .
Definition 5. We say that is reduced if and only if G is upper triangular, is monic for all and for all .
If a generator matrix
G of
is given, then the reduced generator matrix
with
is obtained through the row operations for
G, cf. [
14]. In fact, the result of the row operations is written as
for some
.
Example 5. (Continued from Example 1.) is not reduced because and . From , is reduced.
In the case where
, the reduced
of
G is called the Hermite normal form of
G, which is unique for each
R-module
, according to Theorem 4.2 in [
11]. Here, we prove the uniqueness of the reduced generator matrix in the cases of Euclidean domains with unique Euclidean division.
Proposition 7. There exists a unique reduced generator matrix of each .
Proof. Let
be two reduced generator matrices of
. Then, it follows from
that there exists an upper triangular
such that
. Note that:
Then,
is invertible in
R for all
because
is invertible in
R. If
, then
implies that
and
because
and
are monic. If
, then:
Because of
,
, and Lemma 2, we have
and
. If
, then:
Because of , , and Lemma 2, we have and . It follows from induction on j that , which completes the proof. ☐
Example 6. (Continued from Remark 2.) Let , , , , and . Then, and are explicitly given as: Thus, all G with can be obtained by . Although is not always reduced, e.g., , we can find such that is reduced.
Example 7. In [15], an ideal generated by in a ring is considered, where divides in and is a root of . This ideal is called the two-adic lift of the binary [7,4] Hamming code because agrees with its generator polynomial. Moreover, it is pointed out that -module , where:can be called a self-dual code over because is all-zero, where denotes the transpose matrix of U. Then, there exists such that: We say for . Note that holds for any positive , where and . Then, various notable codes appear as the image of by , where , and Proposition 7assures that their unique reduced generator matrices can be computed from for some . For example, If , then is equal to the binary [8,4] extended Hamming code and there exists such that its unique reduced generator matrix satisfies , where: If , then is equal to the octacode, cf. [15], and there exists such that its unique reduced generator matrix satisfies 8. Conclusions
In this study, we have found various useful properties of the codes over some Euclidean residue rings and proven that many characteristics of the generator matrices of GQC codes (in particular, the uniqueness of the reduced generator matrices) remain valid for the case analyzed here. If the moduli of the codes are equal among all symbols, i.e., for some nonzero , then we have shown that the product of the generator matrices constructs all generator matrices. In addition, if the moduli of the codes are relatively prime, then this construction has been shown to be a one-to-one correspondence among the classes of generator matrices.
In the case of QC and GQC codes, the results in [
2,
3] have a similarity with ours in the sense of producing codes of a modulus from those of factored moduli. We compare these results as follows.
Table 1 is supplementally explained as follows. For the classes of codes, we have treated the codes
with Euclidean domain
R, which generalize the case of QC codes with
. Whereas, in [
2,
3], the producing methods is the concatenation which is represented by, e.g., Turyn’s
-method, our producing method is the multiplication
of generator matrices in Theorems 1,2. In [
2,
3], the self-duality is preserving, i.e., roughly speaking, if codes mod
and mod
are self-dual in a sense, then the produced code mod
is also self-dual. Unfortunately, our producing method does not have this preserving property of self-duality. From the viewpoint of computational complexity, our method can have an advantage over those of [
2,
3] because, whereas Turyn-type methods require overall combination of codewords in the worst case, our method requires only multiplying two
l-by-
l matrices. Consequently, it is important to use different methods according to the desired types of codes. For example, for GQC or self-dual codes, the methods of [
2,
3] should be chosen, and for high-rate QC codes, where “high-rate” means that the ratio
of dimension
k and length
n is greater than 1/2, our method is appropriate because of its less computational complexity.
As an application, for specified standard Euclidean domains, we have applied the theory of reduced generator matrices to Hecke rings, and we have shown the enumeration formulae of the number of a certain types of generator matrices. Future work will focus on developing a method for the efficient enumeration of general GPC codes. Another area of research will involve the establishment of the theory of parity-check matrices for these codes, especially a formula for extracting them from the equalities such as in [
5,
7].