Global Analysis and Optimal Control of a Periodic Visceral Leishmaniasis Model
Abstract
:1. Introduction
2. Model Formulation
Invariant Region
3. Analysis of the Model
3.1. Mathematical Properties
3.2. Global Stability of the Disease-Free Equilibrium
3.3. Basic Reproduction Number
- 1.
- if and only if .
- 2.
- if and only if .
- 3.
- if and only if .
3.4. Existence and Permanence of the Endemic Periodic Solution
- 1.
- and f has a global attractor A.
- 2.
- There exists a finite sequence of disjoint, compact, and isolated invariant sets in such that
- = ;
- no subset of forms a cycle in ;
- is isolated in X;
- for each .
3.5. Global Stability of the Positive Periodic Solution
4. The Optimal Control Problem
4.1. Constructing the Problem
4.2. Analysis of the Optimal Control Problem
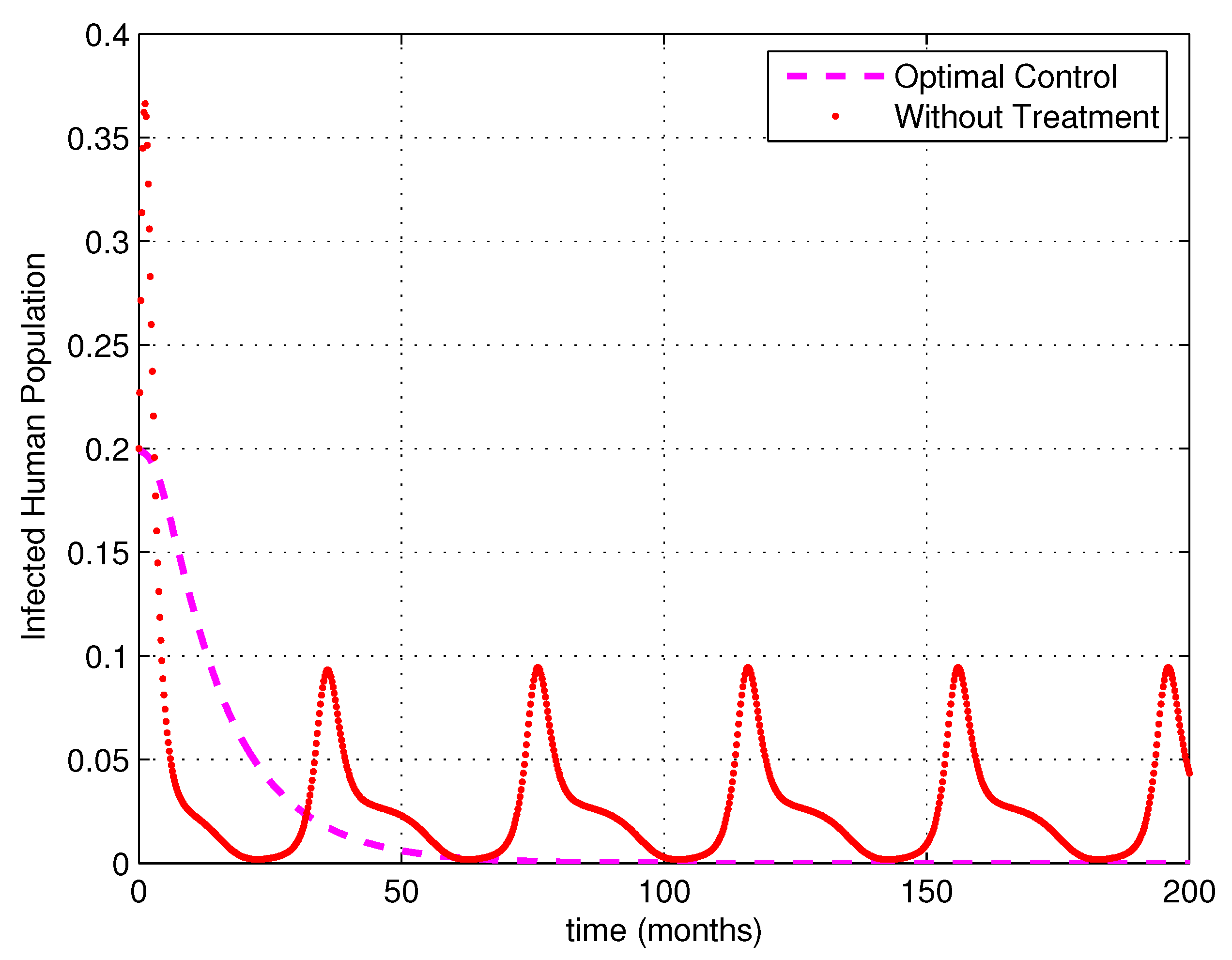
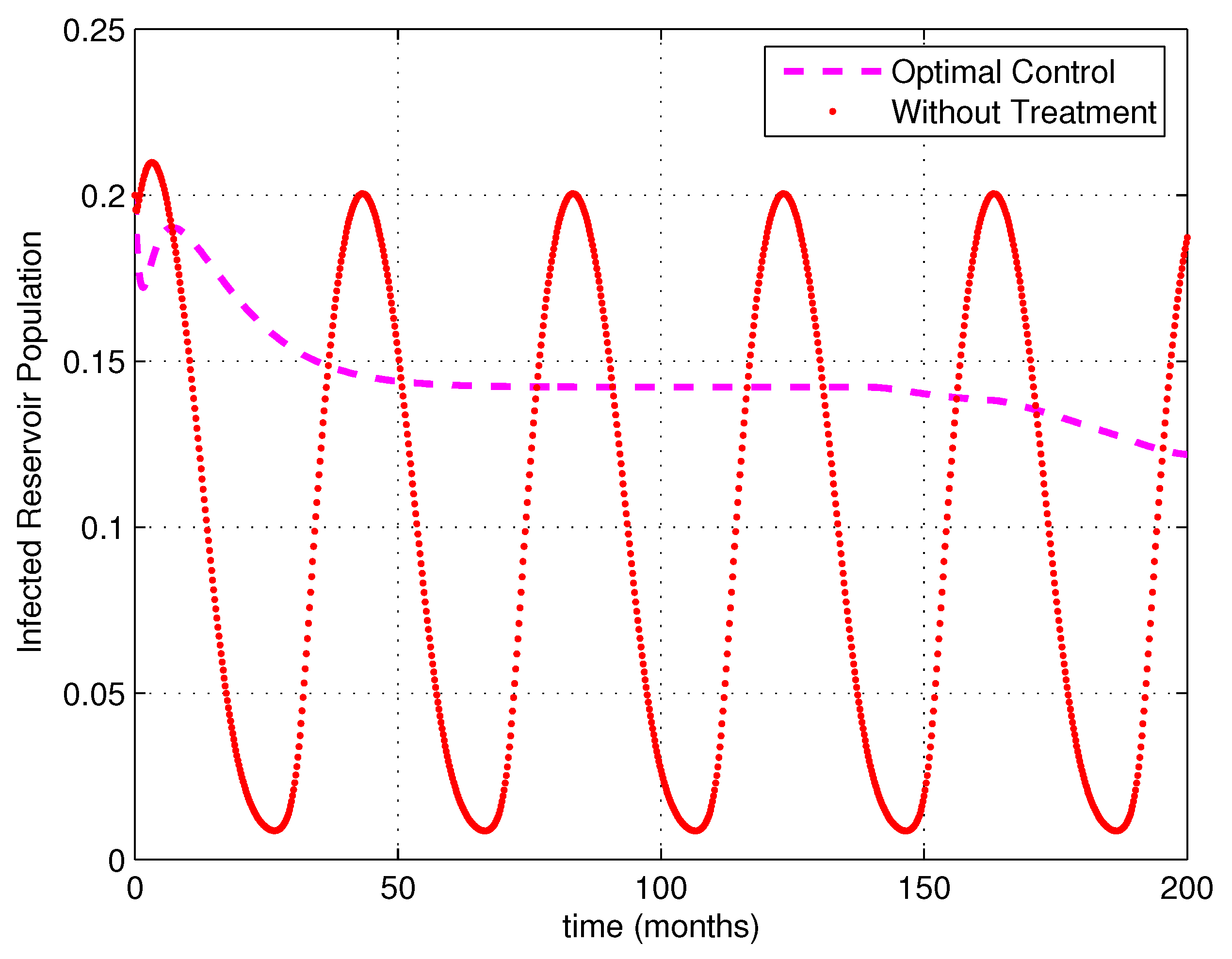
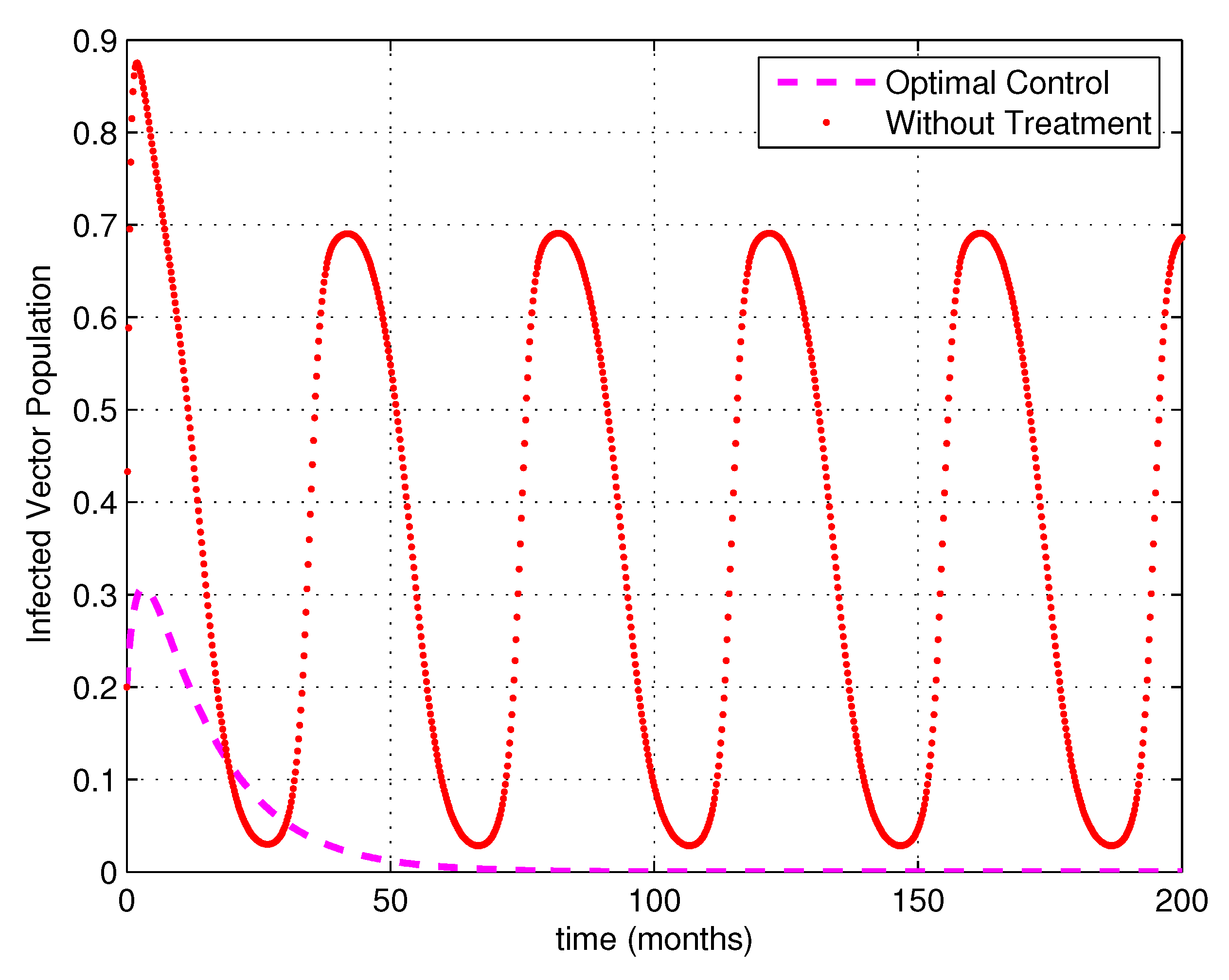
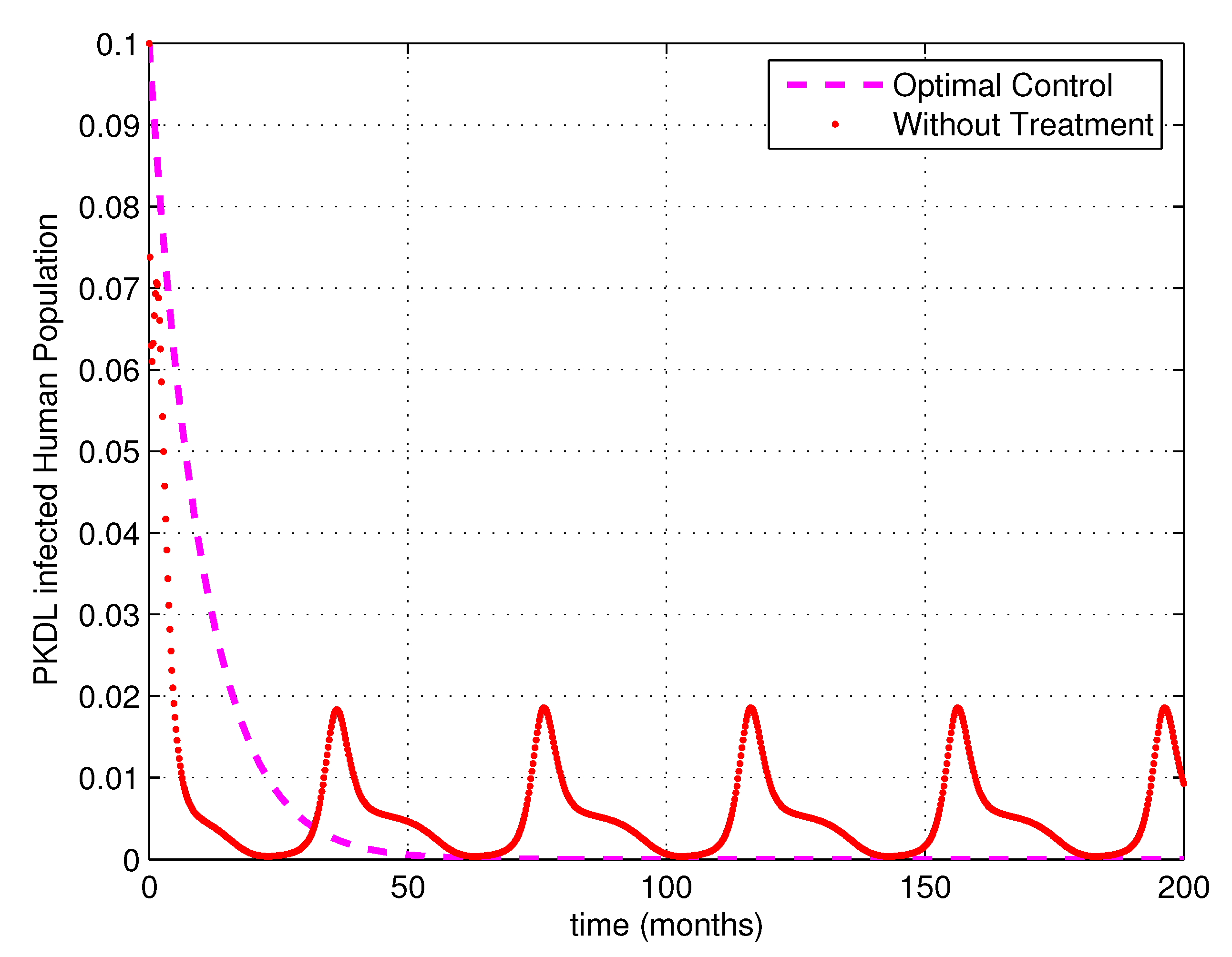
5. Numerical Simulations
6. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chaves, L.F.; Pascual, M. Climate Cycles and Forecasts of Cutaneous Leishmaniasis, a Nonstationary Vector-Borne Disease. PLoS Med. 2006, 3, 1320–1328. [Google Scholar] [CrossRef] [PubMed]
- Reithinger, R.; Jean-Claude, D.; Hechmi, L.; Claude, P.; Bruce, A.; Simon, B. Cutaneous leishmaniasis. Lancet Infect. Dis. 2007, 7, 581–596. [Google Scholar] [CrossRef]
- Zijlstra, E.E.; Musa, A.M.; Khalil, E.A.; el-Hassan, I.M.; el-Hassan, A.M. Post-kala-azar dermal leishmaniasis. Lancet Infect. Dis. 2003, 3, 87–98. [Google Scholar] [CrossRef]
- Schriefer, A.; Luiz, H.G.; Paulo, R.L.M.; Marcus, L.; Hélio, A.L.; Ednaldo, L.; Guilherme, R.; Aristóteles, G.-N.; Ana, L.F.S.; Lee, W.R.; et al. Geographic Clustering of Leishmaniasis in Northeastern Brazil. Emerg. Infect. Dis. 2009, 15, 871–876. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, A.A.; Abdoon, M.A.A. Distribution and population dynamics of phlebotomus Sandflies in an endemic area of cutaneous leishmaniasis in Asir Region. J. Entomol. 2005, 2, 102–108. [Google Scholar]
- Al-Tawfiq, J.A.; Abu-Khams, A. Cutaneous leishmaniasis: A 46-year study of the epidemiology and clinical features in Saudi Arabia (1956–2002). Int. J. Infect. Dis. 2004, 8, 244–250. [Google Scholar] [CrossRef] [PubMed]
- Cardenas, R.; Claudia, M.; Alfonso, J.; Franco-Paredes, C. Studied impact of climate change variability in the occurrence of leishmaniasis in Northeastern Colombia. Am. J. Trop. Med. Hyg. 2006, 75, 273–277. [Google Scholar] [PubMed]
- Cross, E.R.; Newcomb, W.W.; Tucker, C.J. Use of weather data and remote sensing to predict the geographic and seasonal distribution of phlebotomus papatasi in Southwest Asia. Am. J. Trop. Med. Hyg. 1996, 56, 530–536. [Google Scholar] [CrossRef]
- Tiwary, P.; Kumar, D.; Mishra, M.; Singh, R.P.; Rai, M.; Sundar, S. Seasonal Variation in the Prevalence of Sand Flies Infected with Leishmania donovani. PLoS ONE 2013, 8, e61370. [Google Scholar] [CrossRef] [PubMed]
- Turki, K.F.; Iain, R.L. The Seasonality of Cutaneous Leishmaniasis in Asir Region, Saudi Arabia. Int. J. Environ. Sustain. 2014, 3, 1–13. [Google Scholar]
- Beaumier, C.M.; Gillespie, P.M.; Hotez, P.J.; Bottazzi, M.E. New vaccines for neglected parasitic diseases and dengue. Transl. Res.: J. Lab. Clin. Med. 2013, 162, 144–155. [Google Scholar] [CrossRef] [PubMed]
- Dye, C. The Logic of Visceral Leishmaniasis control. Am. J. Trop. Med. Hyg. 1996, 55, 125–130. [Google Scholar] [CrossRef] [PubMed]
- Dye, C.; Williams, B.G. Malnutrition, age and risk of parasitic disease: Visceral leishmaniasis revisited. Proc. R. Soc. Lond. Ser. B 1993, 254, 33–39. [Google Scholar] [CrossRef] [PubMed]
- Lysenko, A.J.; Beljaev, A.E. Quantitative Approaches to Epidemiology; Peters, W., Killick-Kendrick, R., Eds.; The Leishmaniasis in Biology and Medicine; Academic Press: London, UK, 1987; pp. 263–290. [Google Scholar]
- Rabinovich, J.E.; Feliciangeli, M.D. Arameters of leishmania braziliensis transmission by indoor Lutzomyia ovallesi in Venezuela. Am. J. Trop. Med. Hyg. 2004, 70, 373–382. [Google Scholar] [PubMed]
- Burattini, M.N.; Coutinho, F.A.B.; Lopez, L.F.; Massad, E. Modeling the dynamics of leishmaniasis considering human, animal host and vector populations. J. Biol. Syst. 1998, 6, 337–356. [Google Scholar] [CrossRef]
- Osman, O.F.; Kager, P.A.; Oskam, L. Lieshmaniasis in the Sudan: A literature review with emphasis on clinical aspects. Trop. Med. Int. Health 2000, 5, 553–562. [Google Scholar] [CrossRef] [PubMed]
- Elmojtaba, I.M.; Mugisha, J.Y.T.; Hashim, M.H.A. Mathematical analysis of the dynamics of visceral leishmaniasis in the Sudan. Appl. Math. Comput. 2010, 217, 2567–2578. [Google Scholar] [CrossRef]
- Elmojtaba, I.M.; Mugisha, J.Y.T.; Hashim, M.H.A. Modeling the role of cross immunity between two different strains of leishmania. Nonlinear Anal.: Real World Appl. 2010, 11, 2175–2189. [Google Scholar] [CrossRef]
- Elmojtaba, I.M. Mathematical model for the dynamics of visceral leishmaniasis–malaria co-infection. Math. Methods Appl. Sci. 2016, 39, 4334–4353. [Google Scholar] [CrossRef]
- Elmojtaba, I.M.; Mugisha, J.Y.T.; Hashim, M.H.A. Vaccination Model for Visceral Leishmaniasis with infective immigrants. Math. Methods Appl. Sci. 2013, 36, 216–226. [Google Scholar] [CrossRef]
- Zhang, F.; Zhao, X.-Q. A periodic epidemic model in patchy environment. J. Math. Anal. Appl. 2007, 325, 496–516. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, X.-Q. Threshold Dynamics for compartmental Epidemic Models in Periodic Environments. J. Dyn. Diff. Equ. 2008, 20, 699–717. [Google Scholar] [CrossRef]
- Smith, H.L.; Waltman, P. The Theory of the Chemostat: Dynamics of Microbial Competition; Cambridge University Press: London, UK, 1995. [Google Scholar]
- Thieme, H.R. Convergence results and Poincare-Bendixson trichotomy for asymptomatically autonomous differential equations. J. Math. Biol. 1992, 30, 755–763. [Google Scholar] [CrossRef]
- Zhao, X.-Q. Dynamical Systems in Population Biology; Springer: New York, NY, USA, 2003. [Google Scholar]
- Hale, J.K. Asymptotic Behavior of Dissipative Systems; American Mathematical Society: Providence, RI, USA, 1988. [Google Scholar]
- Zhu, Y.; Wang, K. Existence and global attractivity of positive periodic solutions for a predator-prey model with modified Laslie-Gower Holling-type II schemes. J. Math. Anal. Appl. 2011, 384, 400–408. [Google Scholar] [CrossRef]
- Gemperli, A.; Vounatsou, P.; Sogoba, N.; Smith, T. Malaria mapping using transmission models: Application to survey data from Mali. Am. J. Epidemiol. 2006, 163, 289–297. [Google Scholar] [CrossRef] [PubMed]
- Kasap, O.E.; Alten, B. Comparative demography of the sand fly Phlebotomus papatasi (Diptera: Psychodidae) at constant temperatures. J. Vect. Ecol. 2006, 31, 378–385. [Google Scholar] [CrossRef]
- Coutinho, F.A.B.; Burattini, M.N.; Lopez, L.F.; Massad, E. An approximate threshold condition for non-autonomous system: An application to a vector-borne infection. Math. Comput. Simul. 2005, 70, 149–158. [Google Scholar] [CrossRef]
- Lainson, R.; Ryan, L.; Shaw, J.J. Infective stages of Leishmania in the sandfly vector and some observations on the mechanism of transmission. Memórias Inst. Oswaldo Cruz 1987, 82, 421–424. [Google Scholar] [CrossRef]
- Gasim, S.; Elhassan, A.M.; Kharazmi, A.; Khalil, E.A.G.; Ismail, A.; Theander, T.G. The development of post-kala-azar dermal leishmaniasis (PKDL) is associated with acquisition of Leishmania reactivity by peripheral blood mononuclear cells (PBMC). Clin. Exp. Immunol. 2000, 119, 523–529. [Google Scholar] [CrossRef] [PubMed]
- Sundar, S.; Lockwood, D.N.J.; Agrawal, G.; Rai, M.; Makharia, M.K.; Murray, H.W. Treatment of Indian visceral leishmaniasis with single or daily infusions of low dose liposomal amphotericin B: Randomised trial Commentary: Cost and resistance remain issues. BMJ 2001, 323, 419–422. [Google Scholar] [CrossRef] [PubMed]
- Pontryagin, L.S. Mathematical Theory of Optimal Processes; CRC Press: Boca Raton, FL, USA, 1987. [Google Scholar]
- Yusuf, T.T.; Benyah, F. Optimal control of vaccination and treatment for an SIR epidemiological model. World J. Model. Simul. 2008, 8, 194–204. [Google Scholar]
- Lenhart, S.; Workman, J.T. Optimal Control Applied to Biological Models; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Fleming, W.H.; Rishel, R.W. Deterministic and Stochastic Optimal Control; Springer: New York, NY, USA, 2012. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
ELmojtaba, I.M.; Biswas, S.; Chattopadhyay, J. Global Analysis and Optimal Control of a Periodic Visceral Leishmaniasis Model. Mathematics 2017, 5, 80. https://doi.org/10.3390/math5040080
ELmojtaba IM, Biswas S, Chattopadhyay J. Global Analysis and Optimal Control of a Periodic Visceral Leishmaniasis Model. Mathematics. 2017; 5(4):80. https://doi.org/10.3390/math5040080
Chicago/Turabian StyleELmojtaba, Ibrahim M., Santanu Biswas, and Joydev Chattopadhyay. 2017. "Global Analysis and Optimal Control of a Periodic Visceral Leishmaniasis Model" Mathematics 5, no. 4: 80. https://doi.org/10.3390/math5040080
APA StyleELmojtaba, I. M., Biswas, S., & Chattopadhyay, J. (2017). Global Analysis and Optimal Control of a Periodic Visceral Leishmaniasis Model. Mathematics, 5(4), 80. https://doi.org/10.3390/math5040080




