Emergence of an Aperiodic Dirichlet Space from the Tetrahedral Units of an Icosahedral Internal Space
Abstract
:1. Introduction
Organization of the Paper
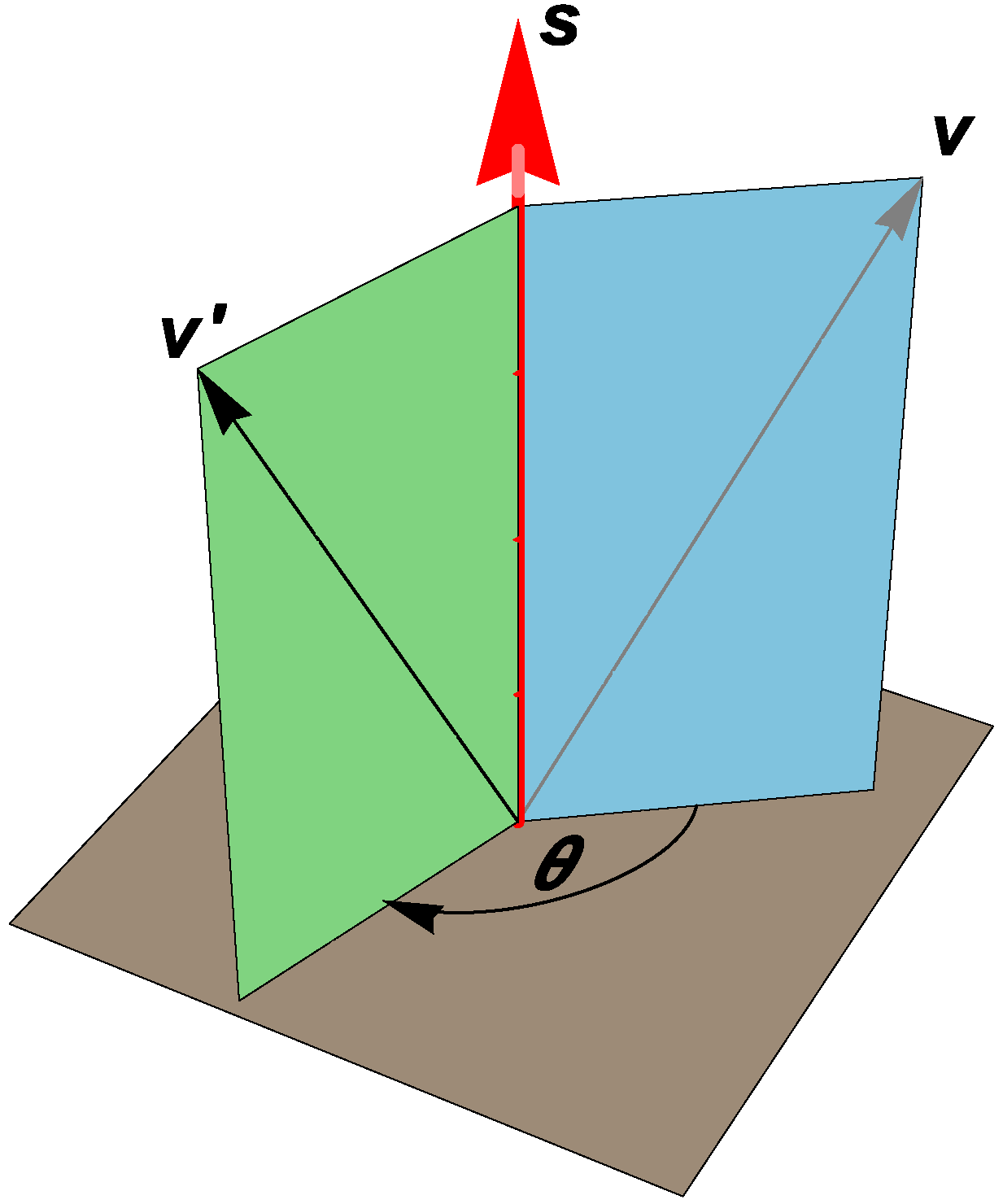
2. Aperiodic Internal Space and Clifford Motors
- (1)
- (2)
- (3)
- The bridge between the Dirichlet quantized lattice and the physical Minkowski space is illustrated through the language of Cartan sub-algebra and Dynkin–Coxeter graphs [11]. The comprehension of quasicrystalline forms through non-crystallographic Dynkin–Coxeter graphs and Lie algebras has been discussed in detail in the work of Koca et al. [12]
2.1. Clifford Spinors in Dirichlet Coordinates
2.1.1. Spinors of
2.1.2. Dirichlet Coordinates
2.1.3. Spinors in Dirichlet Coordinates
2.2. Emergence of the 20G by the Action of Clifford Motors
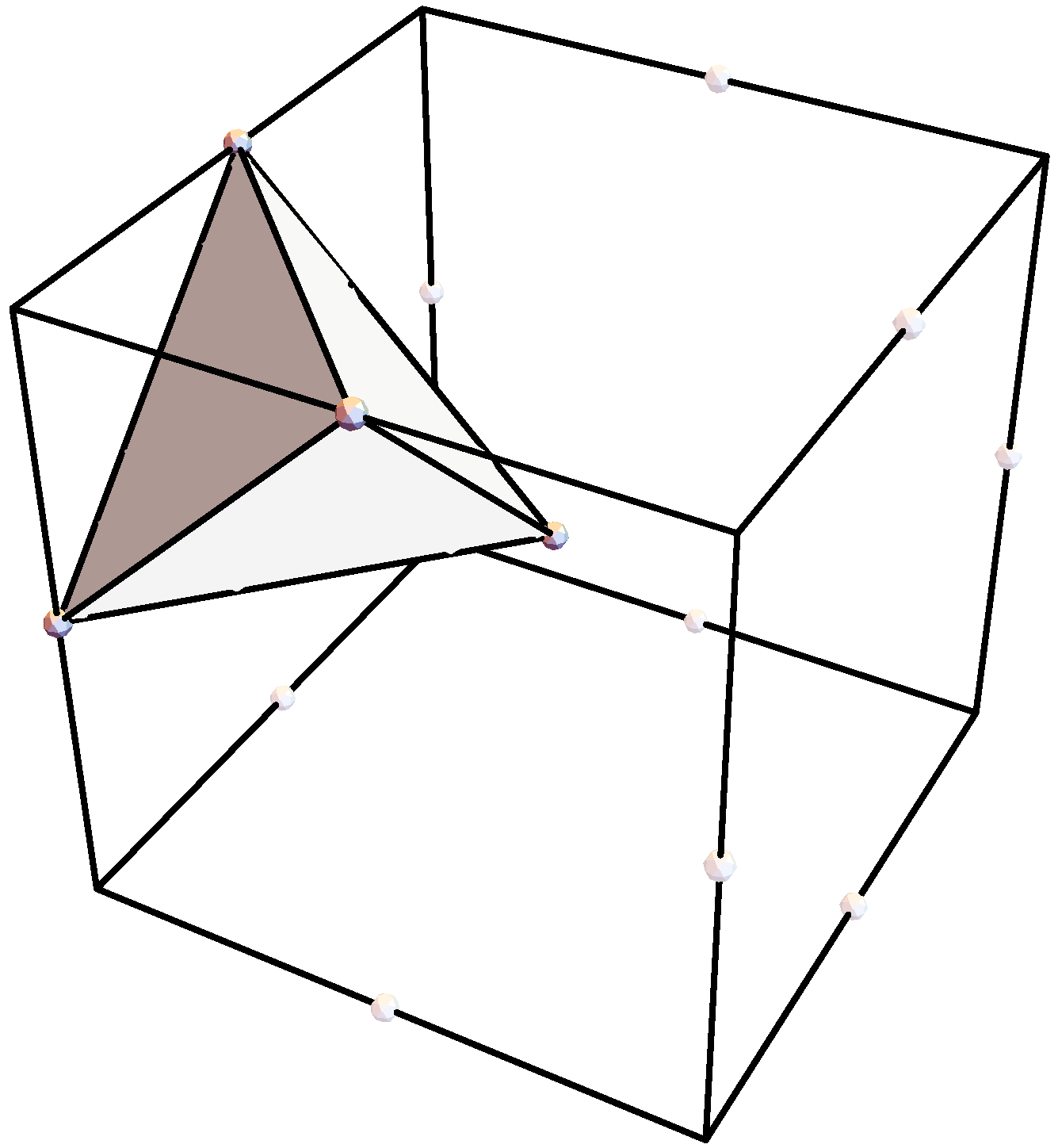
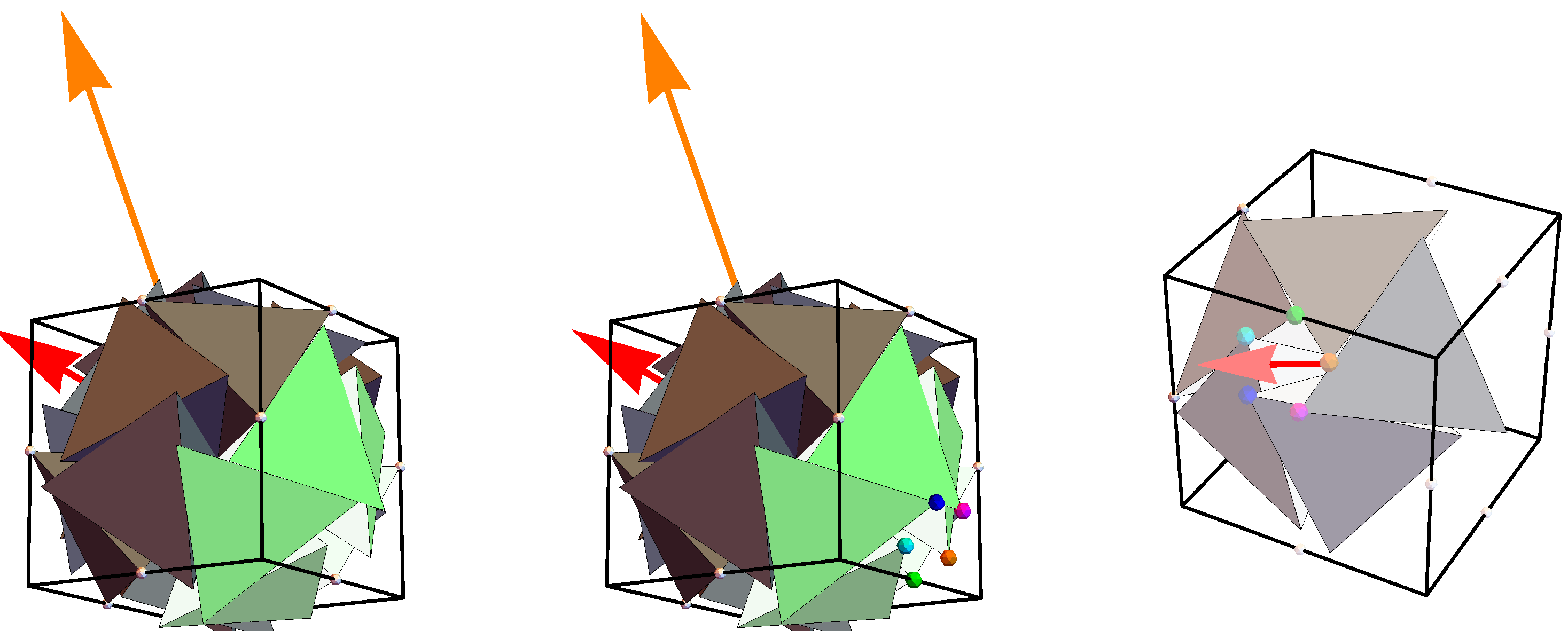
2.2.1. The Primal Five-Group
- (1)
- The primal 5G is the simplest unit of the 20G icosahedral cluster that fixes the chirality of the 20G as has been mentioned earlier.
- (2)
- The pentagonal gap associated with the primal 5G (as well as the other 5Gs), as seen in the rightmost graphic in Figure 3, is a direct consequence of the fact that the 20G built from it has the minimal number of plane classes (see discussion in [1]). This makes the 5Gs canonical building blocks of the 20G.
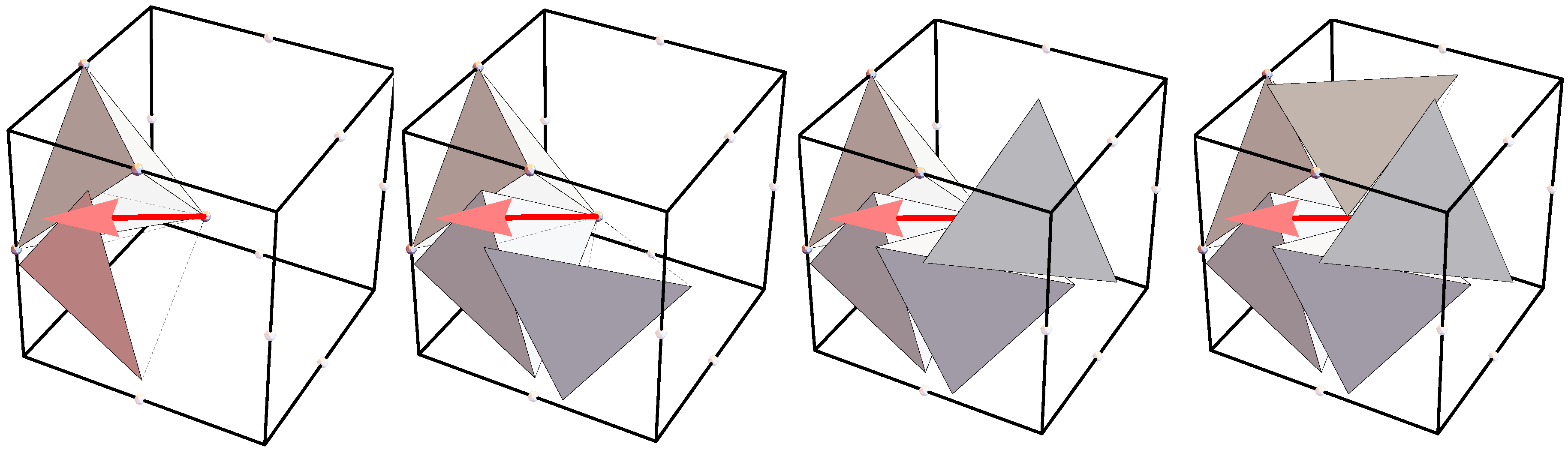
2.2.2. Generation of the Auxiliary 5Gs
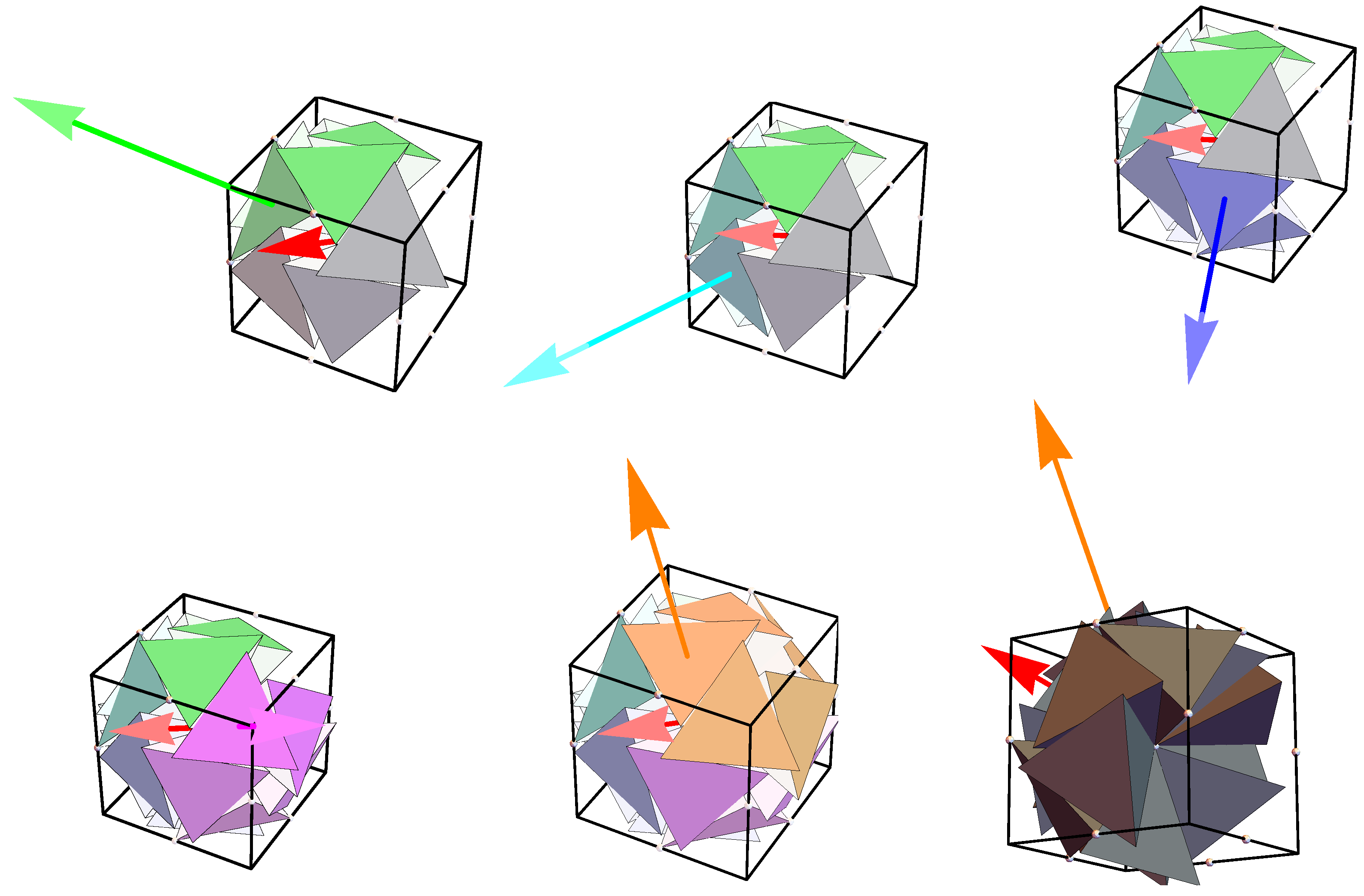
2.3. Emergence of the Dirichlet Quantized Quasicrystal
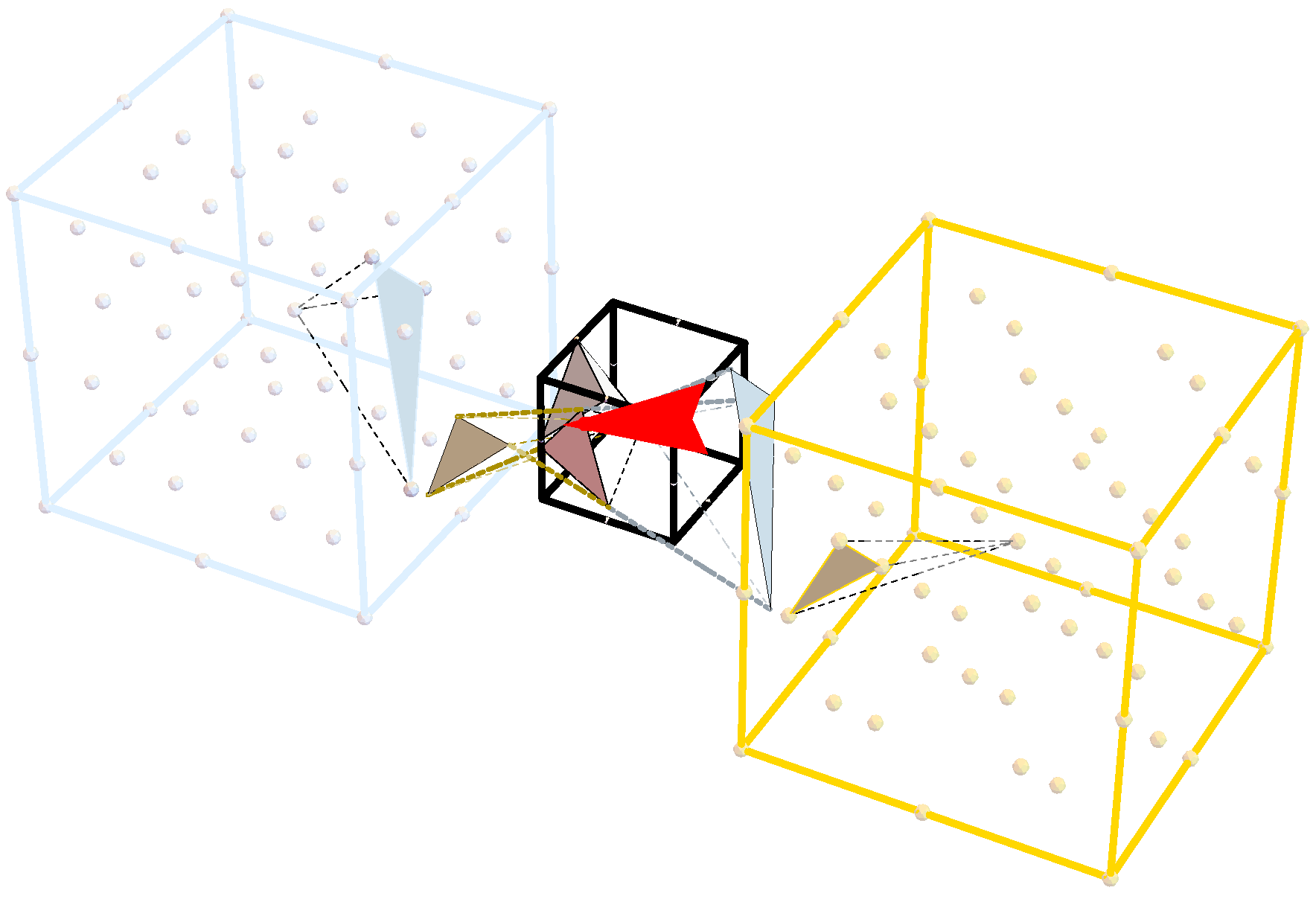
3. Emergence of the 6D Dirichlet Quantized Host,
3.1. Vertices of 20G as Embeddings in Lattice
3.2. Representation of and Its Root System
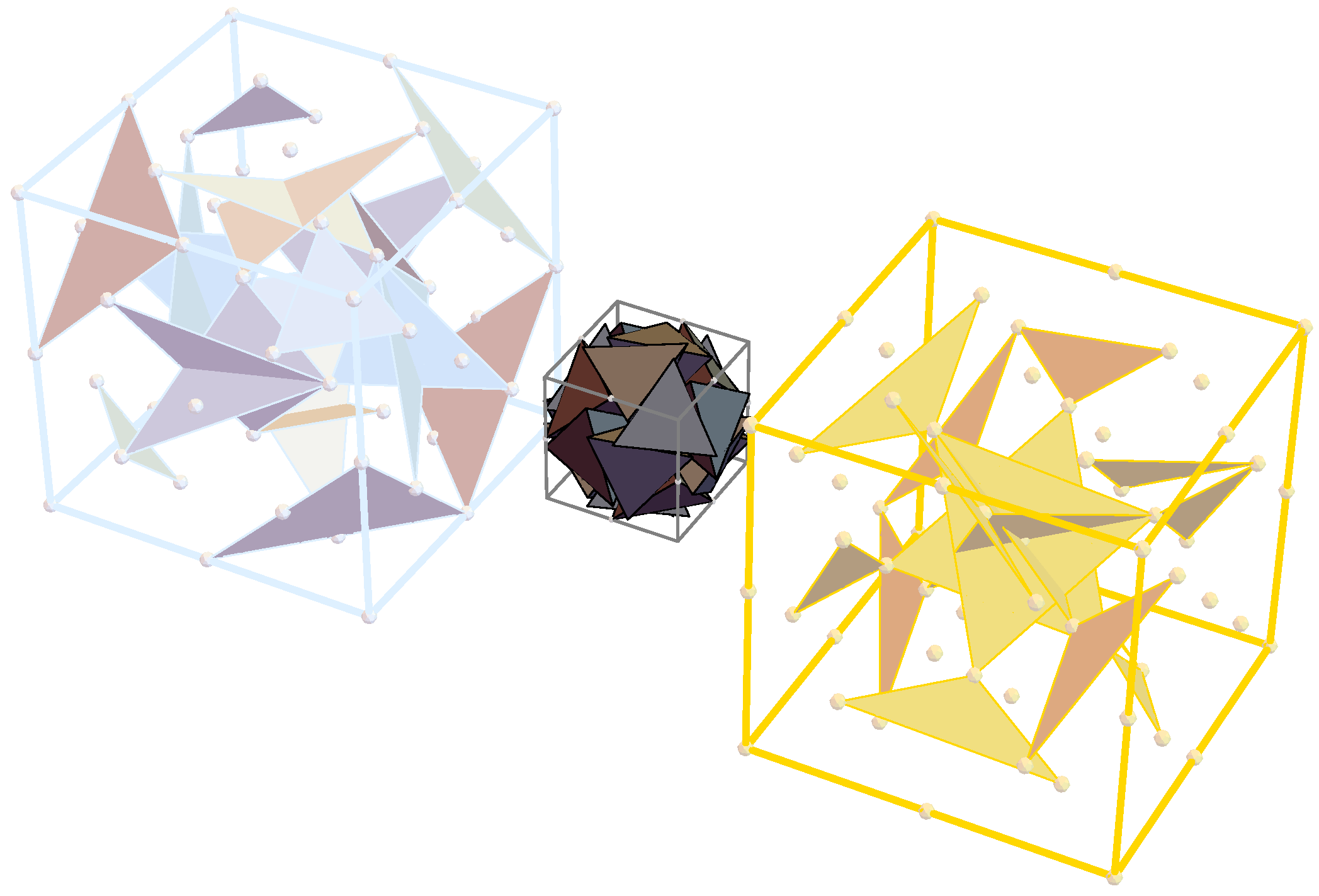
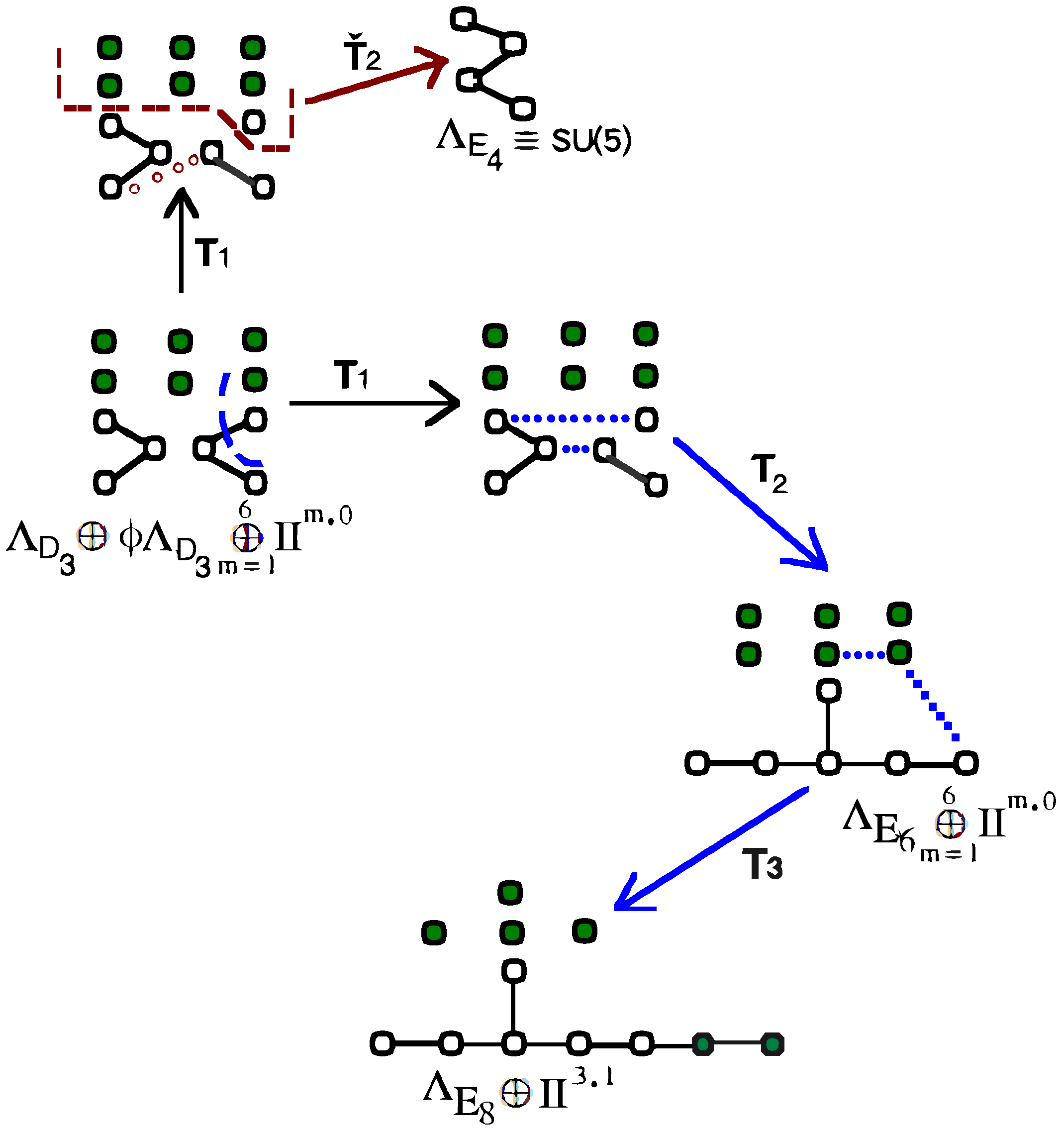
4. Emergence of and from
4.1. Transformations that Encode Emergence of Spacetime Fabric
4.2. Spectral Norm of Transformation Matrices
4.2.1. Physical Interpretation of the Spectral Norms
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| x | y | z | |||||
|---|---|---|---|---|---|---|---|
| 0 | −2 | 2 | 0 | 0 | 0 | 0 | 0 |
| −2 | 0 | 2 | 0 | 0 | 0 | 0 | 0 |
| −2 | −2 | 0 | −4 | 0 | 0 | 0 | 0 |
| −2 | −1 | 1 | −2 | 1 | −1 | 0 | 0 |
| −1 | 1 | 0 | 0 | 1 | −2 | −1 | −2 |
| −1 | 0 | −1 | −2 | 2 | −1 | 1 | 2 |
| 2 | −1 | −1 | 0 | −1 | −1 | 0 | −2 |
| 1 | 1 | 0 | 2 | −1 | −2 | 1 | −2 |
| 1 | 0 | 1 | 2 | −2 | −1 | −1 | −4 |
| 2 | −1 | 1 | 2 | −1 | −1 | 0 | −2 |
| 1 | −1 | 2 | 2 | 1 | 0 | −1 | 0 |
| 1 | −2 | 1 | 0 | 0 | 1 | 1 | 2 |
| −1 | 1 | 0 | 0 | 1 | −2 | 1 | 0 |
| 1 | 2 | 1 | 4 | 0 | −1 | 1 | 0 |
| 0 | 1 | −1 | 0 | −1 | −1 | 2 | 0 |
| 0 | 2 | −2 | 0 | 0 | 0 | 0 | 0 |
| −2 | 2 | 0 | 0 | 0 | 0 | 0 | 0 |
| −2 | 0 | −2 | −4 | 0 | 0 | 0 | 0 |
| 2 | 1 | −1 | 2 | −1 | 1 | 0 | 0 |
| 1 | 2 | −1 | 2 | 0 | −1 | −1 | −2 |
| 1 | 1 | −2 | 0 | 1 | 0 | 1 | 2 |
| −2 | 1 | 1 | 0 | 1 | 1 | 0 | 2 |
| −1 | 2 | 1 | 2 | 0 | −1 | 1 | 0 |
| −1 | 1 | 2 | 2 | −1 | 0 | −1 | −2 |
| −2 | 1 | −1 | −2 | 1 | 1 | 0 | 2 |
| −1 | 0 | 1 | 0 | 2 | 1 | −1 | 2 |
| −1 | −1 | 0 | −2 | 1 | 2 | 1 | 4 |
| 1 | −1 | 0 | 0 | −1 | 2 | −1 | 0 |
| 2 | 1 | 1 | 4 | −1 | 1 | 0 | 0 |
| 1 | 0 | −1 | 0 | −2 | 1 | 1 | 0 |
| 2 | −2 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | −2 | 0 | 0 | 0 | 0 | 0 |
| 0 | −2 | −2 | −4 | 0 | 0 | 0 | 0 |
| −1 | −2 | 1 | −2 | 0 | 1 | 1 | 2 |
| 1 | −1 | 0 | 0 | −1 | 2 | 1 | 2 |
| 0 | −1 | −1 | −2 | 1 | 1 | 2 | 4 |
| 1 | −2 | −1 | −2 | 0 | 1 | −1 | 0 |
| −1 | −1 | 0 | −2 | 1 | 2 | −1 | 2 |
| 0 | −1 | 1 | 0 | −1 | 1 | −2 | −2 |
| 1 | 0 | −1 | 0 | −2 | −1 | 1 | −2 |
| −1 | 1 | −2 | −2 | −1 | 0 | 1 | 0 |
| 0 | −1 | −1 | −2 | −1 | 1 | 2 | 2 |
| −2 | −1 | −1 | −4 | 1 | −1 | 0 | 0 |
| −1 | −2 | −1 | −4 | 0 | 1 | −1 | 0 |
| −1 | −1 | −2 | −4 | −1 | 0 | 1 | 0 |
| 2 | 0 | 2 | 4 | 0 | 0 | 0 | 0 |
| 0 | 2 | 2 | 4 | 0 | 0 | 0 | 0 |
| 2 | 2 | 0 | 4 | 0 | 0 | 0 | 0 |
| −1 | −1 | 2 | 0 | −1 | 0 | −1 | −2 |
| 0 | 1 | 1 | 2 | −1 | −1 | −2 | −4 |
| 1 | 0 | 1 | 2 | −2 | 1 | −1 | −2 |
| 1 | −1 | −2 | −2 | 1 | 0 | 1 | 2 |
| 0 | 1 | −1 | 0 | 1 | −1 | 2 | 2 |
| −1 | 0 | −1 | −2 | 2 | 1 | 1 | 4 |
| 1 | 1 | 0 | 2 | −1 | −2 | −1 | −4 |
| 0 | 1 | 1 | 2 | 1 | −1 | −2 | −2 |
| −1 | 2 | −1 | 0 | 0 | −1 | −1 | −2 |
| −1 | 0 | 1 | 0 | 2 | −1 | −1 | 0 |
| 1 | 1 | 2 | 4 | 1 | 0 | −1 | 0 |
| 0 | −1 | 1 | 0 | 1 | 1 | −2 | 0 |
References
- Fang, F.; Irwin, K. An Icosahedral Quasicrystal as a Golden Modification of the Icosagrid and its Connection to the E8 Lattice. 2015. Available online: http://arxiv.org/pdf/1511.07786.pdf (accessed on 24 June 2016).
- Dechant, P. The birth of E8 out of the spinors of the icosahedron. Proc. R. Soc. A 2015, 472, 20150504. [Google Scholar] [CrossRef] [PubMed]
- Kanatani, K. Understanding Geometric Algebra: Hamilton, Grassmann, and Clifford for Computer Vision and Graphics; Taylor & Francis Group: Boca Raton, FL, USA, 2015. [Google Scholar]
- Jaric, M.V. Quasicrystals and Geometry; Academic Press Inc.: San Diego, CA, USA, 1988. [Google Scholar]
- Senechal, M. Introduction to QUASICRYSTALS; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Fang, F.; Kovacs, J.; Sadler, G.; Irwin, K. An Icosahedral Quasicrystal as a Packing of Regular Tetrahedra. Acta Phys. Pol. A 2014, 126, 458–460. [Google Scholar] [CrossRef]
- Muralidhar, K. Algebra of Complex Vectors and Applications in Electromagnetic Theory and Quantum Mechanics. Mathematics 2015, 3, 781–842. [Google Scholar] [CrossRef]
- Dirichlet, J.P.G.L. Mémoire sur l’impossibilité de quelques équations indéterminées du cinquième degré. J. Reine Angew. Math. 1828, 3, 354–375. [Google Scholar] [CrossRef]
- Kronecker, L. Dirichlet, P.G. Lejeune: Werke; Reimer: Berlin, Germany, 1889; Volume 1. [Google Scholar]
- Kronecker, L.; Fuchs, L. Dirichlet, P.G. Lejeune: Werke; Reimer: Berlin, Germany, 1897; Volume 2. [Google Scholar]
- Gilmore, R. Lie Groups, Lie Algebras, and Some of their Applications; John Wiley and Sons Inc.: Hoboken, NJ, USA, 1974. [Google Scholar]
- Koca, M.; Koca, N.O.; Koc, R. Quaternionic Roots of E8 Related Coxeter Graphs and Quasicrystals. Turk. J. Phys. 1998, 22, 421–435. [Google Scholar]
- Penrose, R. The Road to Reality; Alfred A. Knopf: New York, NY, USA, 2005. [Google Scholar]
- Mauldin, T. Philosophy of Physics: Space and Time; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Coxeter, H.S.M. Regular Polytopes; Dover Publications, Inc.: New York, NY, USA, 1973. [Google Scholar]
- Lounesto, P. Clifford Algebras and Spinors; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- De Bruijn, N.G. Algebraic theory of Penrose’s non-periodic tilings of the plane. Math. Proc. A 1981, 84, 39–52. [Google Scholar] [CrossRef]
- Castro, C. Fractal strings as an alternative justification for El Naschie’s Cantorian spacetime and the fine structure constant. Chaos Solitons Fractals 2002, 14, 1341–1351. [Google Scholar] [CrossRef]
- Sirag, S.-P. ADEX Theory: How the ADE Coxeter Graphs Unify Mathematics and Physics; World Scientific: Singapore, 2016. [Google Scholar]
- Humphreys, J.E. Reflection Groups and Coxeter Groups; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Fuchs, J.; Schweigert, C. Symmetries, Lie Algebras and Representations; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Das, A.; Okubo, S. Lie Groups and Lie Algebras for Physicists; Hindustan Book Agency: Gurugram, Haryana, India, 2014. [Google Scholar]
- Georgi, H. Lie Algebras in Particle Physics; Perseus Books Group: New York, NY, USA, 1999. [Google Scholar]
- Keller, J. Spinors and Multivectors as a Unified Tool for Spacetime Geometry and for Elementary Particle Physics. Int. J. Theor. Phys. 1991, 30, 137–184. [Google Scholar] [CrossRef]
- Nesti, F. Standard model and gravity from spinors. Eur. Phys. J. C 2009, 59, 723–729. [Google Scholar] [CrossRef]
- Lisi, A.G.; Smolin, L.; Speziale, S. Unification of gravity, gauge fields and Higgs bosons. J. Phys. A Math. Theor. 2010, 43, 445401. [Google Scholar] [CrossRef]
- Lisi, A.G. An Explicit Embedding of Gravity and the Standard Model in E8. 2010. Available online: http://arxiv.org/pdf/1006.4908.pdf (accessed on 25 June 2010).
- Georgi, H.; Glashow, S.L. Unity of All Elementary Particle Forces. Phys. Rev. Lett. 1974, 32, 438–441. [Google Scholar] [CrossRef]
- Dimopoulos, S.; Raby, S.A.; Wilczek, F. Unification off Couplings. Phys. Today 1991, 25–33. [Google Scholar] [CrossRef]
- Robinson, M. Symmetry and the Standard Model; Springer: New York, NY, USA, 2011. [Google Scholar]
- Gorsey, F.; Ramond, P. A Universal Gauge Theory Model based on E6. Phys. Lett. B 1976, 60, 177–180. [Google Scholar] [CrossRef]
- Breit, J.D.; Ovrut, B.A.; Segré, G.C. E6 symmetry breaking in the superstring theory. Phys. Letts. B 1985, 158, 33–39. [Google Scholar] [CrossRef]
- Hofkirchner, W. Emergent Information—A Unified Theory of Information Framework; World Scientific: Singapore, 2013. [Google Scholar]
- Knuth, K.H.; Bahreyni, N. A potential foundation for emergent space-time. J. Math. Phys. 2014, 55, 112501. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Kleinert, H. Gauge Fields in Condensed Matter, Vol II: Stresses and Defects; World Scientific: Singapore, 1989. [Google Scholar]
- Kleinert, H. Non-Abelian Bosonization as a Nonholonomic Transformation from a Flat to a Curved Field Space. Ann. Phys. 1997, 253, 121–176. [Google Scholar] [CrossRef]
- Kleinert, H. Nonholonomic Mapping Principle for Classical and Quantum Mechanics in Spaces with Curvature and Torsion. Gen. Relativ. Gravit. 2000, 32, 769–839. [Google Scholar] [CrossRef]
- Kleinert, H. Emerging gravity from defects in world crystal. Braz. J. Phys. 2005, 35, 359–361. [Google Scholar] [CrossRef]
- Ruggiero, M.L.; Tartaglia, A. Einstein-Cartan theory as a theory of defects in space-time. Am. J. Phys. 2003, 71, 1303–1313. [Google Scholar] [CrossRef]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sen, A.; Aschheim, R.; Irwin, K. Emergence of an Aperiodic Dirichlet Space from the Tetrahedral Units of an Icosahedral Internal Space. Mathematics 2017, 5, 29. https://doi.org/10.3390/math5020029
Sen A, Aschheim R, Irwin K. Emergence of an Aperiodic Dirichlet Space from the Tetrahedral Units of an Icosahedral Internal Space. Mathematics. 2017; 5(2):29. https://doi.org/10.3390/math5020029
Chicago/Turabian StyleSen, Amrik, Raymond Aschheim, and Klee Irwin. 2017. "Emergence of an Aperiodic Dirichlet Space from the Tetrahedral Units of an Icosahedral Internal Space" Mathematics 5, no. 2: 29. https://doi.org/10.3390/math5020029
APA StyleSen, A., Aschheim, R., & Irwin, K. (2017). Emergence of an Aperiodic Dirichlet Space from the Tetrahedral Units of an Icosahedral Internal Space. Mathematics, 5(2), 29. https://doi.org/10.3390/math5020029





