Abstract
We present the emergence of a root system in six dimensions from the tetrahedra of an icosahedral core known as the 20-group (20G) within the framework of Clifford’s geometric algebra. Consequently, we establish a connection between a three-dimensional icosahedral seed, a six-dimensional (6D) Dirichlet quantized host and a higher dimensional lattice structure. The 20G, owing to its icosahedral symmetry, bears the signature of a 6D lattice that manifests in the Dirichlet integer representation. We present an interpretation whereby the three-dimensional 20G can be regarded as the core substratum from which the higher dimensional lattices emerge. This emergent geometry is based on an induction principle supported by the Clifford multi-vector formalism of three-dimensional (3D) Euclidean space. This lays a geometric framework for understanding several physics theories related to , , Lie algebras and their composition with the algebra associated with the even unimodular lattice in . The construction presented here is inspired by Penrose’s three world mode.
1. Introduction
This paper investigates the emergence of higher dimensional lattice geometry from the spatially-physical three-dimensional (3D) world of icosahedral space. This mathematical structure is encoded here within the language of Lie algebra.
We begin by presenting here the induction of a six-dimensional (6D) embedding of lattice geometry, , from the icosahedral symmetry group of a 20-tetrahedra—20-group (20G)—cluster that is at the core of a newly-discovered 3D quasi-crystalline structure called the quasicrystalline spin network [1]. This 6D composite lattice forms the core of an eight-dimensional (8D) internal space. This internal space manifests physically in a four-dimensional (4D) Minkowski spacetime, represented here by the unimodular lattice , and together constitutes an aperiodic Dirichlet space. The subscripts in this notation denote the dimension of the root system, and the superscripts denote the base dimensions from which the higher root system is deduced. The presence of the golden mean, , is a result of Dirichlet decomposition of 3D space and is elucidated in subsequent sections. Moreover, the notation denotes the lattice associated with the Lie algebra .
The purpose of the current paper is to demonstrate an inductive framework for the creation of a higher dimensional lattice from the simple components of 3D quasicrystalline forms. This approach is distinct from the one by Dechant [2] where the birth of is deduced through the non-crystallographic intermediary root systems, and , but is inspired by Dechant’s use of Clifford spinors as an induction tool for creating higher dimensional forms from 3D icosahedra. In this paper, the induction is presented through an intermediary host structure. The precise representation of this intermediary host is , but will often be represented in a concise manner as , where the representation of the physical dimensions is suppressed, and only the 6D embedding of the internal space is referred to as the intermediary host.
Organization of the Paper
Following the introductory section, we define spinors and shifters in the language of Clifford’s geometric algebra in Section 2. Dirichlet coordinates are also introduced in Section 2. The construction of the 20G is explained in detail in Section 2. In Section 3, we show the emergence of the Dirichlet quantized host in 6D as a consequence of the spawning of dimensions within the Dirichlet integer representation. In Section 4, we present a pathway to connect the Dirichlet host with a higher dimensional lattice through a series of transformations of Cartan matrices within the framework of Lie theory. We also comment on the properties of these transformations that reveal the emergent geometry. Finally, in Section 5, we provide concluding remarks and discuss the direction of future research.
2. Aperiodic Internal Space and Clifford Motors
In this section, we demonstrate that an icosahedral core comprising a group of twenty tetrahedra is constructed from the vertices of a tetrahedron hosted by a Face Centered Cubic (FCC) lattice by using Clifford motors—motors are the composition of rotors/spinors and translators/shifters— (cf. p. 132 in [3]) with Dirichlet integer coefficients. This is followed by dilation of the inter-tetrahedral gaps based on a metric prescribed by an infinite Fibonacci word. The resulting structure has icosahedral symmetry and a quasicrystalline diffraction pattern with a finite number of vertex-types [1,4,5,6]. The crux of the mathematics presented in this paper relies on three key machinery.
- (1)
- The use of spinors as an induction mechanism [2]. The complexification process, in general, provides a pathway for generating higher dimensional geometric algebra from lower dimensions. This is explicitly illustrated through examples in the work of Muralidhar [7]
- (2)
- Expressing coefficients of the spinor as an ordered pair in Dirichlet space [8,9,10] allows one to mathematically grasp the imagery of higher dimensional space in the language of geometric algebra
- (3)
- The bridge between the Dirichlet quantized lattice and the physical Minkowski space is illustrated through the language of Cartan sub-algebra and Dynkin–Coxeter graphs [11]. The comprehension of quasicrystalline forms through non-crystallographic Dynkin–Coxeter graphs and Lie algebras has been discussed in detail in the work of Koca et al. [12]
Surely, a strong hypothesis is made in the constructive presentation of this paper, viz., about the a priori existence of an internal space [13] and a physical Minkowski spacetime [14]. This is rather a matter of philosophical ontology and is beyond the scope of this paper.
2.1. Clifford Spinors in Dirichlet Coordinates
Simply speaking, spinors are rotors. The action of a spinor on a vector results in a rotation of the vector in Euclidean space. In this section, we formally introduce Clifford spinors as our primary rotor mechanism for the geometric construction discussed subsequently.
2.1.1. Spinors of
The icosahedral core is generated from the simplest Platonic solid [15] by the action of spinors. Spinors are pure rotors, i.e., the action of a spinor on a vector results in the rotation of the vector by a desired angle around the axis defined by the spinor. As mentioned, the starting point of our inductive framework is the 3D Euclidean space defined by . In the language of Clifford’s geometric algebra, we work within the algebra of of . Therefore, we use the 3D spinor, s, defined by the elements of the even sub-algebra of over the subspace [16]. Thus:
where the axis of rotation (of the spinor) is defined by the axis-vector and the bivector . We note that . The magnitude (length) of the bivector (hence that of the spinor) is proportional to the angle by which it rotates the object-vector, . This is evident by re-writing the spinor in Equation (1) as follows:
where is the unit vector that denotes the direction of the spinor-axis and the angle of rotation, (Compare the role of the bivector of in and in in the exponential form demonstrating a rotation. Here, .). Finally, the rotation of the vector, , is given by:
because . Moreover, s is a two-fold covering, which means that the action of s and on by the way of and is identical. The action of the spinor s on a vector is graphically illustrated in Figure 1.
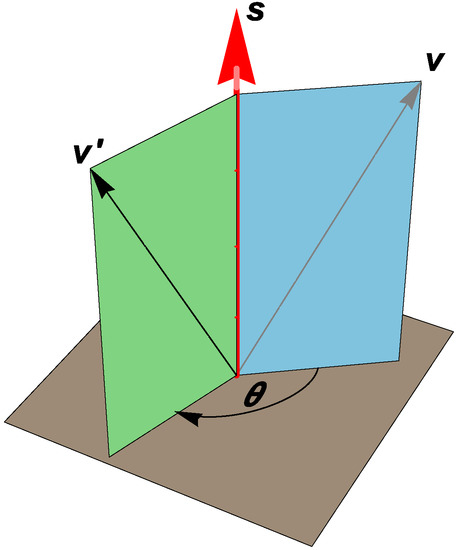
Figure 1.
The action of a spinor s, with the axis given by , on the vector rotates the latter by an angle resulting in the vector . The length of is proportional to the angle of rotation . In this figure, the planes containing vectors (, ) and (, ) are orthogonal to the plane of rotation. Moreover, the spinor-axis denoted by the vector is also normal to the plane of rotation.
2.1.2. Dirichlet Coordinates
Recall that our objective is to generate an icosahedral core that has a characteristic five-fold rotational symmetry. This entails a representation of the coordinate frame by quadratic integers in the quadratic field . defines the quadratic integer ring with five-fold symmetry (Note that the three-fold symmetry corresponding to the rotations has the axes of rotation passing through the vertices of a dodecahedron that have coordinates in the Dirichlet frame. Hence, the Dirichlet integer decomposition used in this paper follows entirely from pentagonal symmetry and the implications of the three-fold symmetry in the coordinate representation is accounted for automatically). The units of this ring corresponding to the solution of Pell’s equation ( with ) are of the form , and is the golden ratio when . Thus, the quadratic integer ring corresponding to the desired pentagonal rotational symmetry has algebraic integers of the form , which are known as Dirichlet integers. The Dirichlet coordinate frame is defined as a set of coordinates that span the ring of Dirichlet integers [8,9,10] (this ring has also been studied in the context of other objects with five fold symmetry like the Penrose tilings (pp. 60–64 in [17])). This decomposition of the coordinates into two orthogonal golden and non-golden parts lies at the core of the doubling of dimensions representative of an emergent geometry, as explained in subsequent sections. We use the notations and interchangeably, both implying the presence of two orthogonal coordinate frames, viz. non-golden (first component) and golden (second component) coordinate frames. Therefore, the symmetry group of the icosahedron ensures, a priori, that the Dirichlet coordinates are sufficient to host all of the vertices of the 20G and the quasicrystalline spin network (QSN). Consequently, the spinor axes and the spinors, defined in the next section, are Dirichlet quantized (normalized).
2.1.3. Spinors in Dirichlet Coordinates
For the construction of the icosahedrally symmetric , we use a family of two successive spinors with with axes of fold and fold rotations (p. 47 in [15]). Here, , as evident by the Schläfli notation for the icosahedron, i.e., . The origin is located at the center of a cubic section of an FCC lattice that hosts tetrahedrons in eight corners in such a way that all eight tetrahedra share a common vertex at this origin. The starting point of our geometric construction using spinors is one of these eight tetrahedra, as will be discussed in the next section. The spinor-axis corresponding to the rotations is given in Dirichlet coordinates as follows:
It is important to note that the axis defined above is Dirichlet normalized in the sense that the coefficients are Dirichlet numbers (denoted by ˚ here). Likewise, the spinor-axis corresponding to the first set of rotations is given in Dirichlet coordinates as follows:
We also note that:
and:
To demonstrate this natural occurrence of the Dirichlet coordinates in the expression of the spinor defined by Equation (2), we note that where is the golden ratio. Next, we examine the bivector components of the spinor, i.e., the terms ,
Thus, the Dirichlet normalized spinor corresponding to the rotations is defined as follows:
with the spinor axis defined by Equation (4). It is noteworthy to compare Equations (6) and (8), which define this spinor in the Dirichlet coordinates (the multiplying factor of 2 in Equation (8) ensures that the spinor is Dirichlet normalized, i.e., the coefficients in the definition of the spinor are Dirichlet integers (and not made of fractional numbers) of the minimum unit value permissible). Likewise, the Dirichlet normalized spinor corresponding to the first set of rotations is defined below:
with the spinor axis defined by Equation (5). The Dirichlet normalized spinors for the subsequent set of rotations are obtained by successive rotations of by . Summarizing, we use one spinor and a family of spinors obtained by successive rotations by starting with the first spinor defined by Equation (9).
2.2. Emergence of the 20G by the Action of Clifford Motors
In this section, we demonstrate the action of the spinors and on the vertices of successive tetrahedra starting with a tetrahedron hosted by a cubic section of an FCC lattice, which bears the crystallographic root system, . A cubic section of an FCC lattice hosts eight different tetrahedra in each of its eight corners. These eight tetrahedra belong to two different families of either right- or left-handed chiral groups. However, once we pick one of these tetrahedra as the origin of our construction (see Figure 2 below), the chirality of the ensuing collection of tetrahedra remains invariant under the action of the Clifford spinors.
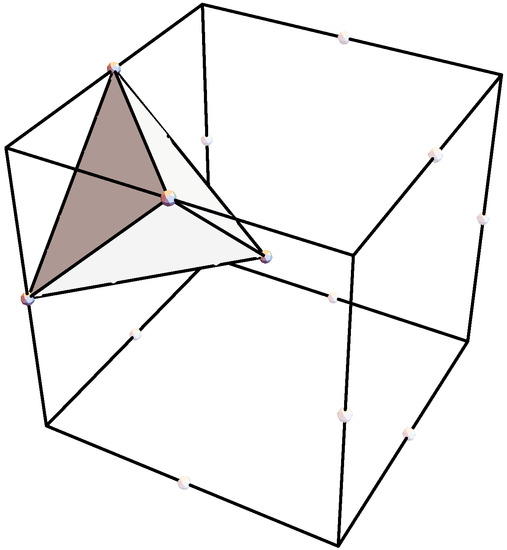
Figure 2.
The tetrahedron hosted by a cubic section of a Face Centered Cubic (FCC) lattice is the simplest platonic solid that forms the base of our construction of the icosahedral 20-group (20G). The spherical nodes are some of the lattice points of an FCC lattice. The node at the center of the cubic section forms the central vertex (center) of the 20G. All tetrahedra that constitute the 20G share one of their vertices at this center.
2.2.1. The Primal Five-Group
In Figure 3, we show the construction of the primal five-group (5G) (the primal 5G is of fundamental importance, as we show subsequently that this 5G is the generator of the remaining tetrahedral clusters and, hence, can be regarded as the generator of the 20G by the action of the Clifford motors) by the action of the spinor on the successive tetrahedra (specifically, the vertices of the tetrahedra that are position vectors with reference to the central vertex, called the center) starting with the originating tetrahedron shown in Figure 2. The primal 5G (along with the four other 5Gs) are the canonical units of the 20G for two reasons.
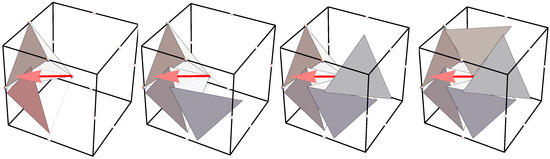
Figure 3.
Construction of the first five-group (5G), known as the primal 5G, by the action of the spinor on successively generated tetrahedra. The spinor is denoted here by the red arrow.
- (1)
- The primal 5G is the simplest unit of the 20G icosahedral cluster that fixes the chirality of the 20G as has been mentioned earlier.
- (2)
- The pentagonal gap associated with the primal 5G (as well as the other 5Gs), as seen in the rightmost graphic in Figure 3, is a direct consequence of the fact that the 20G built from it has the minimal number of plane classes (see discussion in [1]). This makes the 5Gs canonical building blocks of the 20G.
2.2.2. Generation of the Auxiliary 5Gs
The generation of the remaining 5Gs is described below by the combined action of a family of spinors followed by the action of a family of Clifford shift vectors upon the primal 5G. This sequence of rotations followed by a set of translations (shifts) together constitute the action of Clifford motors (spinors followed by shifters).
Action of spinors on the primal 5G: the primal 5G is rotated by the spinor given by Equation (9). This means each vertex (and hence, their position vectors with respect to the center) of each tetrahedron of the primal 5G is rotated by . The resulting tetrahedral cluster, along with the newly generated 5G shaded in green, is shown in the top left graphic of Figure 4. Consequently, other new sets of 5Gs are generated by the successive action of spinors, which are themselves generated by the rotation of their predecessors by the spinor as shown in the sequence of graphics in Figure 4. It must be noted that each generation of 5Gs shares some tetrahedral units with its predecessor.
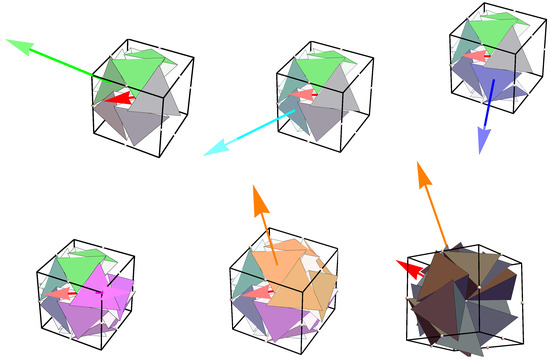
Figure 4.
Construction of the auxiliary 5Gs by the action of the family of spinors on the primal 5G is shown here beginning with top left and moving row wise. The last graphic at the bottom right shows a gap diametrically opposite to the primal 5G. The family of spinors is designed by successive rotation of the spinors by the spinors starting with the first spinor defined by Equation (9). The family of spinors is shown here by the non-red arrows.
This process of producing auxiliary 5G clusters may be continued in this manner until production of the 20G. Clearly, something more efficient can be done to accomplish this. In the last graphic of Figure 4, we observe that upon the completion of the sixth generation of 5G clusters, a gap befitting a 5G is created that is diametrically opposite to the primal 5G. This means that a reflection of the primal 5G, by a suitable plane passing through the center and parallel to the plane containing the primal pentagonal gap, followed by an appropriate chirality correction, can be used to fill the aforementioned gap and complete the generation of the 20G.
Action of Clifford shifters on the primal 5G: the strategy described in the previous paragraph to fill the gap and complete the generation of the 20G is analogous to a simple shift operation of the primal 5G by a family of Clifford shifters along an appropriate direction. We begin with the first tetrahedron (the one shown in Figure 2 above) of the primal 5G and shift it along the shift vector:
by a magnitude . The direction of the shift vector is determined by the edge of the first tetrahedron of the primal 5G that is closest to the spinor or, equivalently, by the edge containing the center and the vertex that forms the pentagonal gap of the primal 5G. The magnitude of the shift is determined by the distance between the shaded face of the starting tetrahedron shown in Figure 2 and the plane containing the center with a normal vector given by . This choice of the shift operation guarantees the symmetry of the newly-generated final 5G, as well as its chirality. We repeat this shift operation for each of the tetrahedra of the primal 5G. The 20G thus created is shown in Figure 5. The 20G has icosahedral symmetry and is the fundamental unit of the aperiodic quasicrystal described in the next section. The vertices of the 20G lie on the Dirichlet coordinate frame and are hosted by two orthogonal lattices, as described in a later section. The interested reader is referred to the article by Fang et al. [1] for further discussions about the 20G.
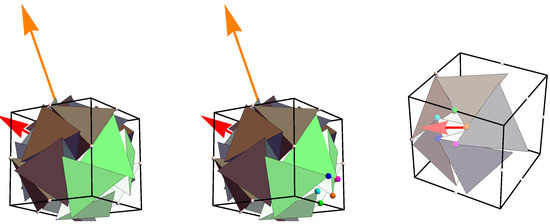
Figure 5.
The graphic on the left shows the closure of the gap in the last graphic of Figure 4 by action of the Clifford shifter on the primal 5G. The middle and right graphics show the correspondence of the vertices of the pentagonal gap of the primal 5G and the newly created 5G. These color-matched vertex pairs form the direction axis for the shift operations on the corresponding tetrahedra of the primal 5G.
2.3. Emergence of the Dirichlet Quantized Quasicrystal
The 20G does not have aperiodic order and is therefore not a quasicrystal. Aperiodicity is included by spacing the plane sets (classes) of the 20G prescribed by a family of Fibonacci chains made of binary units 1 and as described in [1] (Fang et al. refer to this Fibonacci spaced quasi-lattice as the Quasicrystalline Spin Network (QSN) with the goal of encoding the quantum geometry of space with a suitable language. One of such attempts towards this goal of prescribing a suitable language in terms of Clifford’s geometric algebra in Dirichlet space is an underlying objective of this current manuscript). The resulting object is a quasicrystal (cf. Figure 6) and its vertices form a point set that also lives in the Dirichlet coordinate frame (Since the space of Dirichlet integers is closed under addition and multiplication, the spacing of tetrahedral vertices by 1 or in the appropriate direction, prescribed by Dirichlet normalized shift vectors, map them to Dirichlet coordinate points). This can be illustrated mathematically by recalling from Section 2.1.2 that the units of the Dirichlet quadratic ring are given by and noting the following relation [18]:
where are the set of Fibonacci numbers. Equation (11) clearly shows that the Fibonacci numbers are a special case of Dirichlet numbers, and hence, the space of vertex points generated by the aforementioned Fibonacci spacing is embedded in the Dirichlet space. This Dirichlet quantized quasi-lattice has a finite set of vertex types that are cataloged in detail in [1]. The detailed geometric construction and properties of this emergent quasicrystalline structure are also described in [1].

Figure 6.
The Dirichlet quantized quasicrystal referred to by Fang et al. [1] as theQuasicrystalline Spin Network (QSN).
The topology defined by the vertices of the 20G, along with additional properties such as handedness, vertex types and the quasicrystalline diffraction pattern of the quasicrystal (see Fang et al. [1]) invokes further understanding of the emergent geometry that is hosted by the Dirichlet coordinate frame. We present a detailed exploration of the emergent Dirichlet geometry, accompanied by a two-fold spawning of dimensions, in the following section.
3. Emergence of the 6D Dirichlet Quantized Host,
Recall that the vertices of the 20G (and the QSN) are Dirichlet coordinates, i.e., they are of the form where . This is by construction true as described in Section 2.1.2 and Section 2.1.3 above and inherently linked to the icosahedral symmetry of the 20G. Subsequently, the Dirichlet coordinates are written as ordered pairs of the form resulting in a collection of 6D coordinates (two sets of orthogonal 3D coordinates). The pairing is comprised of a non-golden part and a golden part (the non-golden part of is a, and the golden part is b), each embedded in one of two orthogonal 3D coordinate frames respectively. This is illustrated in detail in Figure 7, Figure 8 and Figure 9.
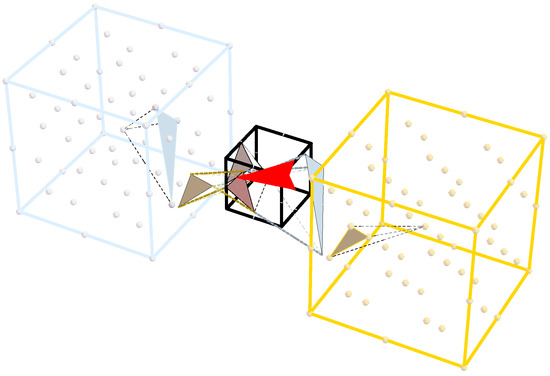
Figure 7.
The graphic depicts the doubling of dimensions by the action of the Dirichlet quantized spinor, where successively generated tetrahedra have vertices with Dirichlet coordinates with non-golden and golden parts, each being hosted by the three-dimensional crystallographic root system . In this figure, the newly-generated tetrahedron has a golden (colored brown) and non-golden component (colored cyan). Each of their vertices are at a distance and one units from the corresponding vertices of tetrahedra hosted by the original FCC lattice (middle), respectively. For the sake of visual clarity, the lattice hosting these golden and non-golden components are translated in space and shown on the sides of the original lattice.
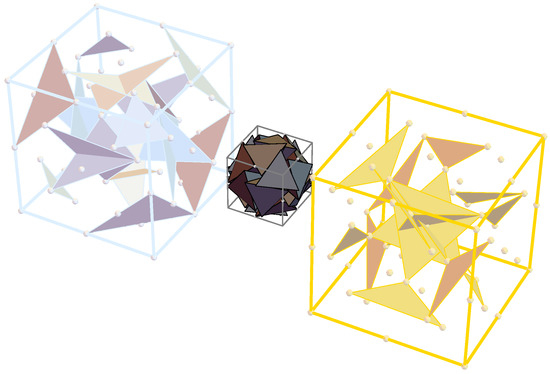
Figure 8.
The six-dimensional (6D) Dirichlet quantized lattice hosting the 20G. In other words, the geometric fabric of the icosahedral object (20G) is unraveled and presented as a 6D host .

Figure 9.
Superposition of the golden and non-golden components of the Dirichlet coordinate frames revealing the orthogonal relationship between them.
The mapping between the 20G (vertices) that is embedded in the original lattice and the inductively-generated component lattices embedded in the root system is bijective, as the vertex pair uniquely associates with the corresponding vertex of the 20G in the original lattice. It is important to note that the resultant six-dimensional structure comprising the golden and non-golden elements of the tetrahedral vertices is embedded in the root system, but does not entirely fill the lattice space of . The embedding is simple (the embedding is the marginal identity map that maps all points in the embedded space to itself; is the embedded space with Dirichlet coordinates) and is topologically invariant of . We refer to as the Dirichlet quantized host (here, the word host is used to emphasize the important fact that the 6D hosts the 3D quasicrystalline substrate as depicted pictorially in Figure 8).
3.1. Vertices of 20G as Embeddings in Lattice
We present a brute force proof that the vertices of the 20G are embeddings in the lattice. The geometry of the lattice is such that the sum of the coordinate points of a lattice is even [19]. This requirement demands that the vertices of the 20G with coordinates must satisfy the following criteria:
where is read as follows: a is congruent to b modulo n. In the Appendix, we provide data of all of the coordinate points of the vertices of the 20G where it can be easily verified that the conditions listed in Equation (12) are satisfied. A more elegant proof will require a better understanding of why the action of spinors on the tetrahedra results in new tetrahedra with vertices satisfying the above conditions and will entail rigorous investigation using tools from the theory of algebraic rings and combinatoric approaches. This is beyond the scope of the current manuscript.
In an identical manner, it can be verified that the coordinates of the QSN are embedded in the lattice. It is also essential to emphasize that the vertices of the 20G and the QSN are embeddings in the lattice. This means not all lattice points of are vertices of the 20G and the QSN. Moreover, while the QSN is aperiodic in its point space, the golden and the non-golden parts of its vertex coordinates are each embedded in a periodic lattice.
3.2. Representation of and Its Root System
The Dirichlet quantized host, , has the following representation in Lie theory using Dynkin graphs [20,21,22] as shown in Figure 10. The Dynkin diagram is clearly representative of the fact that the 6D Dirichlet host lattice is comprised of two independent component lattices.
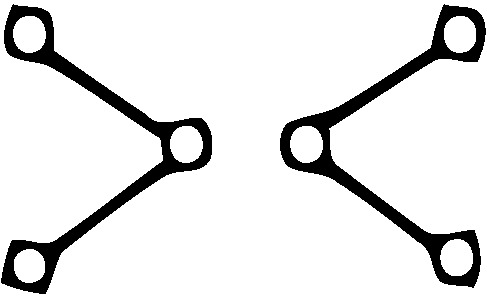
Figure 10.
Dynkin graph of .
Consequently, the Cartan matrix [20,21,22] can be deduced from the Dynkin graph shown in Figure 10 as follows:
which can be easily recognized as a block diagonal form of two Cartan matrices. The roots of can be easily computed from the Cartan matrix [23] (Any set of roots is not unique. The ones mentioned here are the ones that can be easily computed from the Cartan matrix). The simple roots can be read off from the rows of the matrix and are listed below:
The remaining roots are and the negative copies of each of the roots listed above. In total, there are 24 roots of . In subsequent sections, we present the action of a sequence of bounded linear operators (transformations) on the Cartan matrix of and the concomitant changes in the topology of the Dynkin graphs and the corresponding root system. We show that the response to this action (sequel) spans the root system of higher dimensional lattice spaces, viz., and .
4. Emergence of and from
Several higher dimensional theories are of importance in theoretical physics. In this context, we consider specifically and [24,25,26,27,28,29,30,31,32,33,34]. To understand the emergent role of the aperiodic Dirichlet quantized host, introduced in earlier sections, in connection with these higher dimensional spaces, we restrict ourselves to the framework of Cartan sub-algebra [11].
We begin by presenting a flow chart (see Figure 11 below) depicting the emergence of a 6D Dirichlet quantized host. The isolated green nodes associated with the Dynkin graphs for each of the intermediary lattices, starting with that of the Dirichlet host and except for the graph of , are hidden dimensions and can be regarded as the reflection of the internal Dirichlet space. These hidden dimensions manifest as the physical Minkowski space that coincides with the connection of the reflection space to the internal space, as shown schematically in Figure 11. The action of the Dirichlet spinors and the transformation matrices shown in Figure 11 is invariant in time.
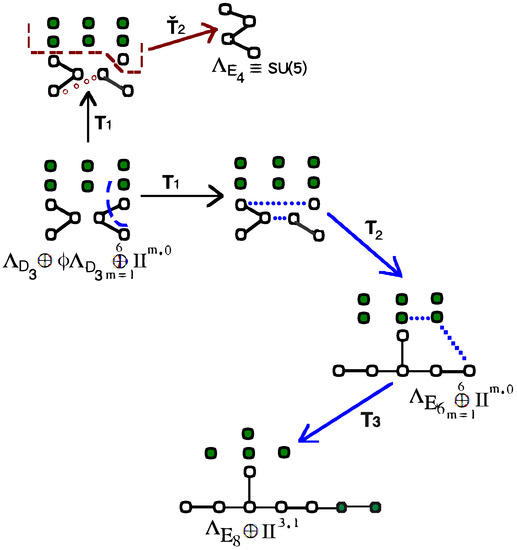
Figure 11.
A graphical representation of the emergence of lattices that constitute the unified world space beginning with the Dirichlet quantized host lattice, . The solid dotted (dashed) lines denote the addition of edges between (removal of) nodes (edges and/or nodes). Note: In Dynkin graphs, nodes represent root vectors. Each hollow dotted line denotes the merging of two nodes. The solid green circles represent the six physical dimensions that are hidden in the internal space; subsequently, two of these hidden dimensions bridge the internal space and the physical Minkowski spacetime. The hollow circles represent nodes in the Euclidean (non-curved) space. The transformations act on the corresponding Cartan matrices and regulate the emergence of higher dimensional lattices.
4.1. Transformations that Encode Emergence of Spacetime Fabric
The emergence of is brought about by the action of a sequence of transformations on the respective Cartan matrices as follows:
where ∘ refers to a composition operation, and the Cartan matrices are given below. Furthermore, note that in terms of their Cartan representation. The associated Cartan matrix is given below:
where:
The transformation matrices are listed as follows:
and:
The transformations given by the notation and encode all of the information about the evolution of the root-vectors and, hence, that of the emerging geometrical fabric of the spacetime coordinates. In other words, they regulate the setting of the Dirichlet quantized host , thereby determining which geometry manifests itself.
4.2. Spectral Norm of Transformation Matrices
The spectral norm of an operator L is defined as:
where is the conjugate transpose of L and denotes the maximum eigenvalue of L. The spectral norms of the transformation matrices are given as follows:
The norm of is an order of magnitude larger than the norms of all other transformation matrices.
4.2.1. Physical Interpretation of the Spectral Norms
Recall that the spectral norm of a transformation matrix reflects the largest singular value of the matrix that entails the maximum extent of allowable deformation (stretching) of vectors in the corresponding vector space [35]. Kleinert [36,37,38,39] used a linear perturbation of the coordinate frame by a displacement field generating strain and consequently revealed that space-time with torsion and curvature can be generated from a flat Euclidean space-time using singular coordinate transformations. He argued in favor of comparing the above to a crystallographic medium filled with dislocations and disclinations. Ruggiero and Tartaglia [40] showed that Kleinert’s singular coordinate transformations are the spacetime equivalent of the plastic deformations, which lead to incompatible defect states corresponding to the generation of mass, mass current and spin.
In our analysis presented above, is a representation in the Cartan sub-algebra and coincides with the bridging of the internal host lattice with that of the 4D Minkowski spacetime denoted by . The aforementioned spike in the spectral norm of is a signature of the linear deformations (these singular value deformations are a combination of rotation and stretching/scaling processes) in lattice geometry proposed by Kleinert to account for gravity. The spike in the spectral norm coincides with the link between the internal world and the Minkowski physical world denoted by the unimodular lattice .
5. Conclusions
In this paper, we have described a rigorous pathway for the emergence of the 12-dimensional (12D) lattice from a 3D aperiodic substrate through an intermediary crystallographic host lattice of the internal space in 6D. The mathematical framework is set in the language of Clifford’s geometric algebra and representations from Lie theory. We have demonstrated that the spawning of the new dimensions is inherently related to the symmetries of our base object, viz. the 20G that has icosahedral symmetry. This has been possible by utilizing the concept of Dirichlet integers from the theory of algebraic rings. Consequently, we have presented a sequence of transformations to illustrate the emergence of spacetime geometry through the use of Dynkin graphs and Cartan algebra. The norms of these transformation matrices have a special significance in relation to the underlying geometry they induce.
Future work will include investigating the links between the quasicrystalline base and the higher dimensional geometry from a dynamical point of view. This will enable the possibility of mapping our understanding of dynamics in the measurable three dimensions with the dynamics encompassed by the Lie group. In a subsequent paper, we propose to perform detailed investigation of the Dirichlet host from the perspective of the theory of algebraic rings. This will shed further light on the importance of this intermediary host contributing toward a better understanding of the interconnections between group symmetries of higher dimensions.
Acknowledgments
The first author would like to acknowledge several useful suggestions and discussions with Carlos Castro Perelman.
Author Contributions
Amrik Sen formulated the research problem, designed the mathematical framework of the scientific inquiry and wrote the paper, Raymond Aschheim performed computer calculations and generated most of the figures, and Klee Irwin envisioned and initiated the research program, revised and edited the manuscript and arranged all necessary financial and computational resources for the scientific work.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Vertex Coordinates of the 20G, .
Table A1.
Vertex Coordinates of the 20G, .
| x | y | z | |||||
|---|---|---|---|---|---|---|---|
| 0 | −2 | 2 | 0 | 0 | 0 | 0 | 0 |
| −2 | 0 | 2 | 0 | 0 | 0 | 0 | 0 |
| −2 | −2 | 0 | −4 | 0 | 0 | 0 | 0 |
| −2 | −1 | 1 | −2 | 1 | −1 | 0 | 0 |
| −1 | 1 | 0 | 0 | 1 | −2 | −1 | −2 |
| −1 | 0 | −1 | −2 | 2 | −1 | 1 | 2 |
| 2 | −1 | −1 | 0 | −1 | −1 | 0 | −2 |
| 1 | 1 | 0 | 2 | −1 | −2 | 1 | −2 |
| 1 | 0 | 1 | 2 | −2 | −1 | −1 | −4 |
| 2 | −1 | 1 | 2 | −1 | −1 | 0 | −2 |
| 1 | −1 | 2 | 2 | 1 | 0 | −1 | 0 |
| 1 | −2 | 1 | 0 | 0 | 1 | 1 | 2 |
| −1 | 1 | 0 | 0 | 1 | −2 | 1 | 0 |
| 1 | 2 | 1 | 4 | 0 | −1 | 1 | 0 |
| 0 | 1 | −1 | 0 | −1 | −1 | 2 | 0 |
| 0 | 2 | −2 | 0 | 0 | 0 | 0 | 0 |
| −2 | 2 | 0 | 0 | 0 | 0 | 0 | 0 |
| −2 | 0 | −2 | −4 | 0 | 0 | 0 | 0 |
| 2 | 1 | −1 | 2 | −1 | 1 | 0 | 0 |
| 1 | 2 | −1 | 2 | 0 | −1 | −1 | −2 |
| 1 | 1 | −2 | 0 | 1 | 0 | 1 | 2 |
| −2 | 1 | 1 | 0 | 1 | 1 | 0 | 2 |
| −1 | 2 | 1 | 2 | 0 | −1 | 1 | 0 |
| −1 | 1 | 2 | 2 | −1 | 0 | −1 | −2 |
| −2 | 1 | −1 | −2 | 1 | 1 | 0 | 2 |
| −1 | 0 | 1 | 0 | 2 | 1 | −1 | 2 |
| −1 | −1 | 0 | −2 | 1 | 2 | 1 | 4 |
| 1 | −1 | 0 | 0 | −1 | 2 | −1 | 0 |
| 2 | 1 | 1 | 4 | −1 | 1 | 0 | 0 |
| 1 | 0 | −1 | 0 | −2 | 1 | 1 | 0 |
| 2 | −2 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | −2 | 0 | 0 | 0 | 0 | 0 |
| 0 | −2 | −2 | −4 | 0 | 0 | 0 | 0 |
| −1 | −2 | 1 | −2 | 0 | 1 | 1 | 2 |
| 1 | −1 | 0 | 0 | −1 | 2 | 1 | 2 |
| 0 | −1 | −1 | −2 | 1 | 1 | 2 | 4 |
| 1 | −2 | −1 | −2 | 0 | 1 | −1 | 0 |
| −1 | −1 | 0 | −2 | 1 | 2 | −1 | 2 |
| 0 | −1 | 1 | 0 | −1 | 1 | −2 | −2 |
| 1 | 0 | −1 | 0 | −2 | −1 | 1 | −2 |
| −1 | 1 | −2 | −2 | −1 | 0 | 1 | 0 |
| 0 | −1 | −1 | −2 | −1 | 1 | 2 | 2 |
| −2 | −1 | −1 | −4 | 1 | −1 | 0 | 0 |
| −1 | −2 | −1 | −4 | 0 | 1 | −1 | 0 |
| −1 | −1 | −2 | −4 | −1 | 0 | 1 | 0 |
| 2 | 0 | 2 | 4 | 0 | 0 | 0 | 0 |
| 0 | 2 | 2 | 4 | 0 | 0 | 0 | 0 |
| 2 | 2 | 0 | 4 | 0 | 0 | 0 | 0 |
| −1 | −1 | 2 | 0 | −1 | 0 | −1 | −2 |
| 0 | 1 | 1 | 2 | −1 | −1 | −2 | −4 |
| 1 | 0 | 1 | 2 | −2 | 1 | −1 | −2 |
| 1 | −1 | −2 | −2 | 1 | 0 | 1 | 2 |
| 0 | 1 | −1 | 0 | 1 | −1 | 2 | 2 |
| −1 | 0 | −1 | −2 | 2 | 1 | 1 | 4 |
| 1 | 1 | 0 | 2 | −1 | −2 | −1 | −4 |
| 0 | 1 | 1 | 2 | 1 | −1 | −2 | −2 |
| −1 | 2 | −1 | 0 | 0 | −1 | −1 | −2 |
| −1 | 0 | 1 | 0 | 2 | −1 | −1 | 0 |
| 1 | 1 | 2 | 4 | 1 | 0 | −1 | 0 |
| 0 | −1 | 1 | 0 | 1 | 1 | −2 | 0 |
References
- Fang, F.; Irwin, K. An Icosahedral Quasicrystal as a Golden Modification of the Icosagrid and its Connection to the E8 Lattice. 2015. Available online: http://arxiv.org/pdf/1511.07786.pdf (accessed on 24 June 2016).
- Dechant, P. The birth of E8 out of the spinors of the icosahedron. Proc. R. Soc. A 2015, 472, 20150504. [Google Scholar] [CrossRef] [PubMed]
- Kanatani, K. Understanding Geometric Algebra: Hamilton, Grassmann, and Clifford for Computer Vision and Graphics; Taylor & Francis Group: Boca Raton, FL, USA, 2015. [Google Scholar]
- Jaric, M.V. Quasicrystals and Geometry; Academic Press Inc.: San Diego, CA, USA, 1988. [Google Scholar]
- Senechal, M. Introduction to QUASICRYSTALS; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Fang, F.; Kovacs, J.; Sadler, G.; Irwin, K. An Icosahedral Quasicrystal as a Packing of Regular Tetrahedra. Acta Phys. Pol. A 2014, 126, 458–460. [Google Scholar] [CrossRef]
- Muralidhar, K. Algebra of Complex Vectors and Applications in Electromagnetic Theory and Quantum Mechanics. Mathematics 2015, 3, 781–842. [Google Scholar] [CrossRef]
- Dirichlet, J.P.G.L. Mémoire sur l’impossibilité de quelques équations indéterminées du cinquième degré. J. Reine Angew. Math. 1828, 3, 354–375. [Google Scholar] [CrossRef]
- Kronecker, L. Dirichlet, P.G. Lejeune: Werke; Reimer: Berlin, Germany, 1889; Volume 1. [Google Scholar]
- Kronecker, L.; Fuchs, L. Dirichlet, P.G. Lejeune: Werke; Reimer: Berlin, Germany, 1897; Volume 2. [Google Scholar]
- Gilmore, R. Lie Groups, Lie Algebras, and Some of their Applications; John Wiley and Sons Inc.: Hoboken, NJ, USA, 1974. [Google Scholar]
- Koca, M.; Koca, N.O.; Koc, R. Quaternionic Roots of E8 Related Coxeter Graphs and Quasicrystals. Turk. J. Phys. 1998, 22, 421–435. [Google Scholar]
- Penrose, R. The Road to Reality; Alfred A. Knopf: New York, NY, USA, 2005. [Google Scholar]
- Mauldin, T. Philosophy of Physics: Space and Time; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Coxeter, H.S.M. Regular Polytopes; Dover Publications, Inc.: New York, NY, USA, 1973. [Google Scholar]
- Lounesto, P. Clifford Algebras and Spinors; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- De Bruijn, N.G. Algebraic theory of Penrose’s non-periodic tilings of the plane. Math. Proc. A 1981, 84, 39–52. [Google Scholar] [CrossRef]
- Castro, C. Fractal strings as an alternative justification for El Naschie’s Cantorian spacetime and the fine structure constant. Chaos Solitons Fractals 2002, 14, 1341–1351. [Google Scholar] [CrossRef]
- Sirag, S.-P. ADEX Theory: How the ADE Coxeter Graphs Unify Mathematics and Physics; World Scientific: Singapore, 2016. [Google Scholar]
- Humphreys, J.E. Reflection Groups and Coxeter Groups; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Fuchs, J.; Schweigert, C. Symmetries, Lie Algebras and Representations; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Das, A.; Okubo, S. Lie Groups and Lie Algebras for Physicists; Hindustan Book Agency: Gurugram, Haryana, India, 2014. [Google Scholar]
- Georgi, H. Lie Algebras in Particle Physics; Perseus Books Group: New York, NY, USA, 1999. [Google Scholar]
- Keller, J. Spinors and Multivectors as a Unified Tool for Spacetime Geometry and for Elementary Particle Physics. Int. J. Theor. Phys. 1991, 30, 137–184. [Google Scholar] [CrossRef]
- Nesti, F. Standard model and gravity from spinors. Eur. Phys. J. C 2009, 59, 723–729. [Google Scholar] [CrossRef]
- Lisi, A.G.; Smolin, L.; Speziale, S. Unification of gravity, gauge fields and Higgs bosons. J. Phys. A Math. Theor. 2010, 43, 445401. [Google Scholar] [CrossRef]
- Lisi, A.G. An Explicit Embedding of Gravity and the Standard Model in E8. 2010. Available online: http://arxiv.org/pdf/1006.4908.pdf (accessed on 25 June 2010).
- Georgi, H.; Glashow, S.L. Unity of All Elementary Particle Forces. Phys. Rev. Lett. 1974, 32, 438–441. [Google Scholar] [CrossRef]
- Dimopoulos, S.; Raby, S.A.; Wilczek, F. Unification off Couplings. Phys. Today 1991, 25–33. [Google Scholar] [CrossRef]
- Robinson, M. Symmetry and the Standard Model; Springer: New York, NY, USA, 2011. [Google Scholar]
- Gorsey, F.; Ramond, P. A Universal Gauge Theory Model based on E6. Phys. Lett. B 1976, 60, 177–180. [Google Scholar] [CrossRef]
- Breit, J.D.; Ovrut, B.A.; Segré, G.C. E6 symmetry breaking in the superstring theory. Phys. Letts. B 1985, 158, 33–39. [Google Scholar] [CrossRef]
- Hofkirchner, W. Emergent Information—A Unified Theory of Information Framework; World Scientific: Singapore, 2013. [Google Scholar]
- Knuth, K.H.; Bahreyni, N. A potential foundation for emergent space-time. J. Math. Phys. 2014, 55, 112501. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Kleinert, H. Gauge Fields in Condensed Matter, Vol II: Stresses and Defects; World Scientific: Singapore, 1989. [Google Scholar]
- Kleinert, H. Non-Abelian Bosonization as a Nonholonomic Transformation from a Flat to a Curved Field Space. Ann. Phys. 1997, 253, 121–176. [Google Scholar] [CrossRef]
- Kleinert, H. Nonholonomic Mapping Principle for Classical and Quantum Mechanics in Spaces with Curvature and Torsion. Gen. Relativ. Gravit. 2000, 32, 769–839. [Google Scholar] [CrossRef]
- Kleinert, H. Emerging gravity from defects in world crystal. Braz. J. Phys. 2005, 35, 359–361. [Google Scholar] [CrossRef]
- Ruggiero, M.L.; Tartaglia, A. Einstein-Cartan theory as a theory of defects in space-time. Am. J. Phys. 2003, 71, 1303–1313. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).