A Two-Stage Method for Piecewise-Constant Solution for Fredholm Integral Equations of the First Kind
Abstract
:1. Introduction
2. The Objective Functionals
2.1. Discretization
- (1)
- The discretization of is given by:where denotes the vector two-norm.
- (2)
- Let be the i-th column of the identity matrix, and let:and:
- (3)
- As for , we simply approximate it by:Here, we omit the factor for the sake of simplicity.
3. Numerical Implementation
| Algorithm 1: Damped Newton (DN) method for the minimization of . |
| Input an initial guess ; ; Begin iterations Compute and ; Solve to obtain ; Obtain the minimum point of the one-dimensional nonnegative function by using line search to get ; Update the approximate solution: ; Check the termination condition: If , break; ; End iterations Output . |
| Algorithm 2: Weighted total variation Modica-Mortola (WTVMM) method for estimating piecewise-constant solution of Equation (2). |
| Obtain the minimizer of by using the MGN method or the DN method; Obtain a minimizer of by using the DN method with as the initial guess; Output . |
4. Numerical Examples
- (1)
- Since we use as an approximation of , we set β to a very small positive number. We note that if β is significantly larger than , then:As a result, the regularization term leads to an -like regularization.
- (2)
- If θ is much larger than , then the weighting function is close to one, i.e.,It follows that the weighted TV regularization is about the same as the traditional TV regularization. Therefore, we should not choose a large value for θ.
- (3)
- We choose the value for α by the help of the discrepancy principle and observe if the numerical solution is near piecewise-constant. After choosing a value for α, we consider adjustment of β and θ: if the numerical solution is over-smooth, we choose a smaller value for β or θ; on the other hand, if the numerical solution is oscillating, we choose a larger value for β or θ.
- (1)
- For the WTVMM method, the main cost lies in obtaining the numerical solution , i.e., minimization of defined by (8).
- (2)
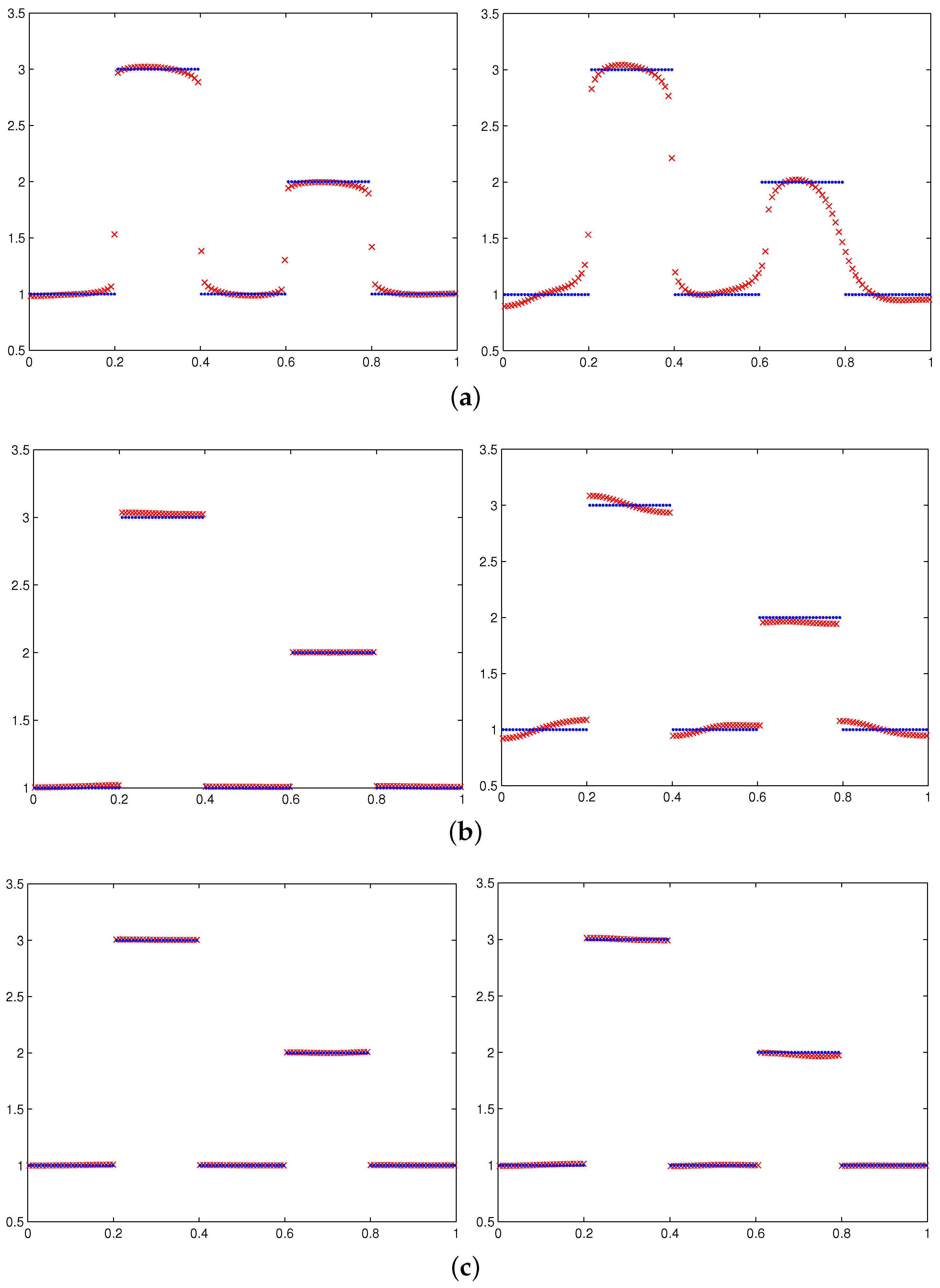
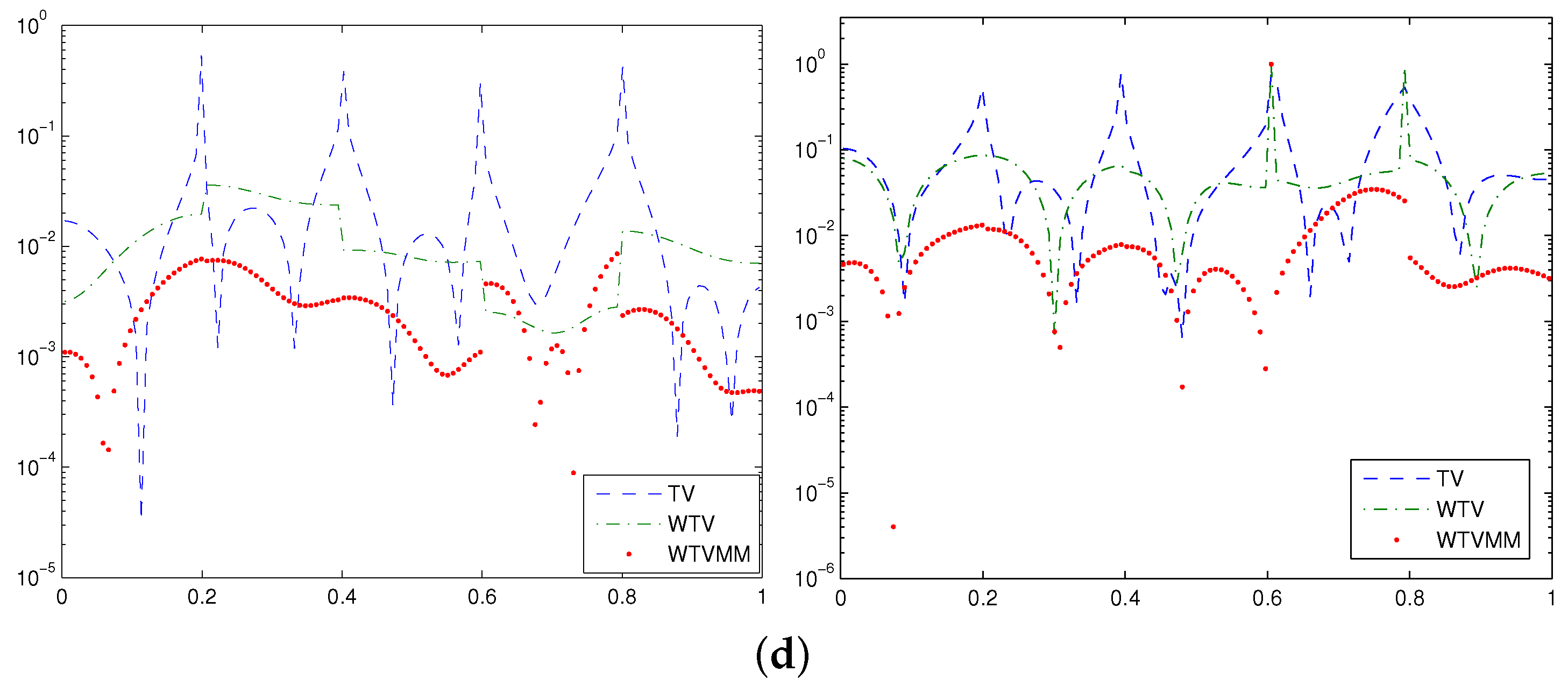
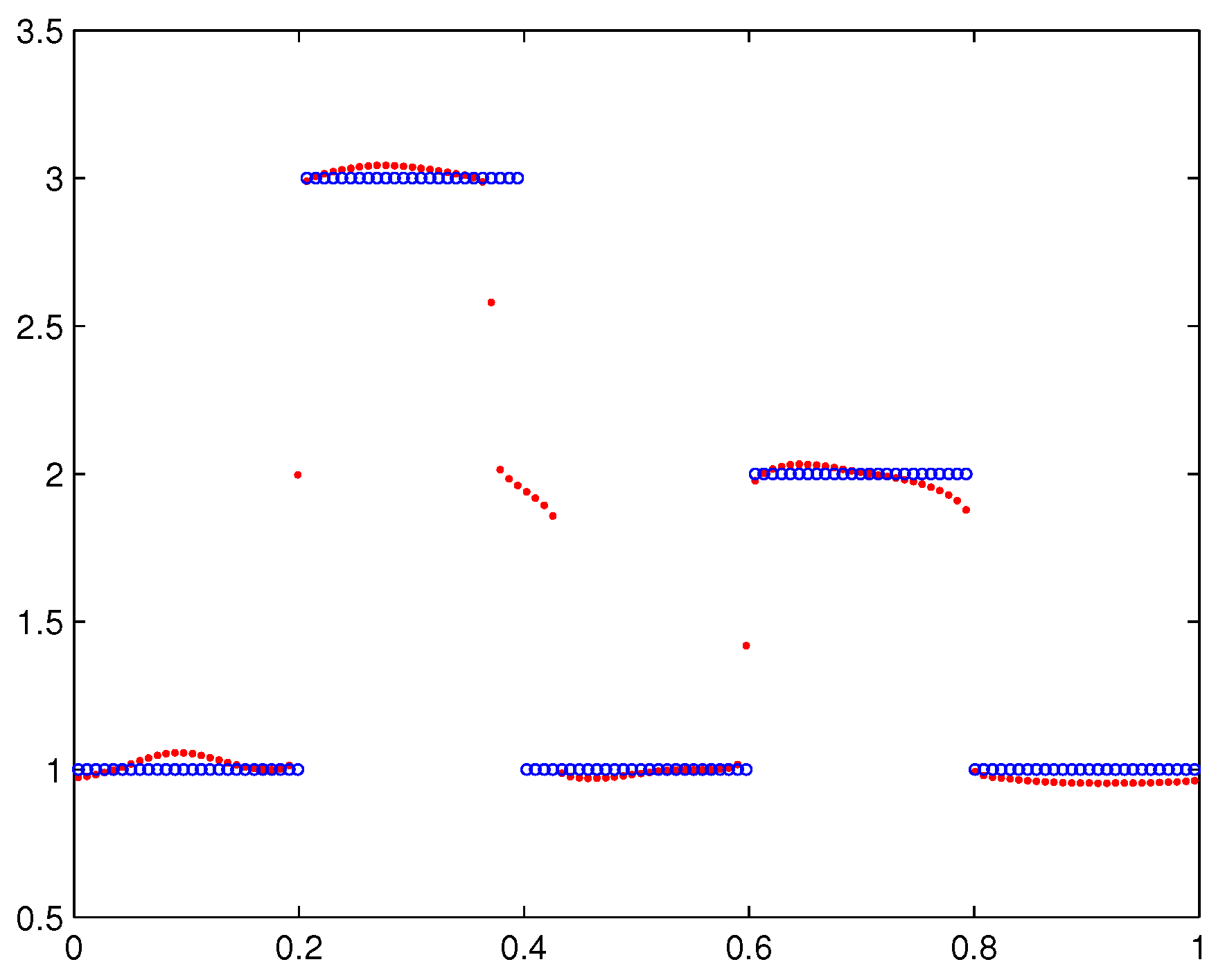
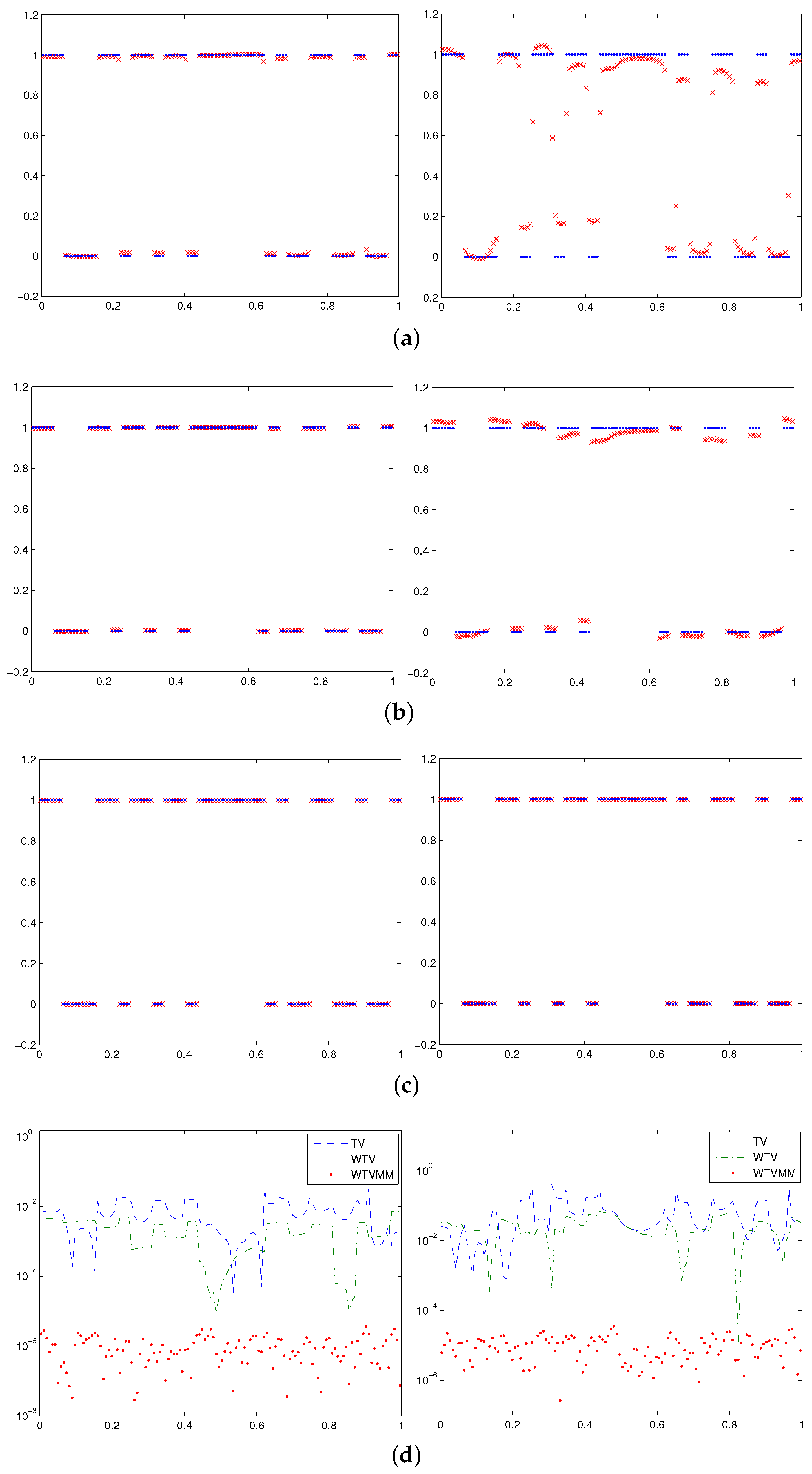
- The numerical solutions obtained by using the WTV method are better than those obtained by the TV method. The numerical solutions obtained by using the WTVMM method can be quite accurate, which can be clearly seen from the relative errors shown in Table 1 and Table 2, the numerical solutions shown in Figure 2c and the point-wise errors shown in Figure 2d.
- (3)
- If the position of the break points in the solution can be identified by the previous step, the approximate solution obtained by the WTVMM method can be very accurate. In the other hand, since the local minimizer of obtained by the DN method is sensitive to the initial guess, we may not be able to obtain a good numerical solution if the approximate solution obtained in the previous step cannot identify the break points well.
5. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hansen, P.C. Discrete Inverse Problems: Insight and Algorithms; SIAM: Philadelphia, PA, USA, 2010. [Google Scholar]
- Delves, L.M.; Mohamed, J.L. Computational Methods for Integral Equations; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Dehghan, M.; Saadatmandi, A. Chebyshev finite difference method for Fredholm integro-differential equation. Int. J. Comput. Math. 2008, 85, 123–130. [Google Scholar]
- Ghasemi, M.; Babolian, E.; Kajani, M.T. Numerical solution of linear Fredholm integral equations using sinecosine wavelets. Int. J. Comput. Math. 2007, 84, 979–987. [Google Scholar]
- Koshev, N.; Beilina, L. An adaptive finite element method for Fredholm integral equations of the first kind and its verification on experimental data. CEJM 2013, 11, 1489–1509. [Google Scholar]
- Koshev, N.; Beilina, L. A posteriori error estimates for Fredholm integral equations of the first kind. In Applied Inverse Problems, Springer Proceedings in Mathematics and Statistics; Springer: New York, NY, USA, 2013; Volume 48, pp. 75–93. [Google Scholar]
- Zhang, Y.; Lukyanenko, D.V.; Yagola, A.G. Using Lagrange principle for solving linear ill-posed problems with a priori information. Numer. Methods Progr. 2013, 14, 468–482. (In Russian) [Google Scholar]
- Vogel, C.R. Computational Methods for Inverse Problems; SIAM: Philadelphia, PA, USA, 2002. [Google Scholar]
- Tikhonov, A.N. Regularization of incorrectly posed problems. Sov. Math. Dokl. 1964, 4, 1624–1627. [Google Scholar]
- Hansen, P.C. The truncated SVD as a method for regularization. BIT Numer. Math. 1987, 27, 534–553. [Google Scholar]
- Hansen, P.C.; Sekii, T.; Shibahashi, H. The modified truncated SVD method for regularization in general form. SIAM J. Sci. Stat. Comput. 1992, 13, 1142–1150. [Google Scholar]
- Rashed, M.T. Numerical solutions of the integral equations of the first kind. Appl. Math. Comput. 2003, 145, 413–420. [Google Scholar]
- Lin, S.; Cao, F.; Xu, Z. A convergence rate for approximate solutions of Fredholm integral equations of the first kind. Positivity 2012, 16, 641–652. [Google Scholar]
- Wang, K.; Wang, Q. Taylor collocation method and convergence analysis for the Volterra-Fredholm integral equations. J. Comput. Appl. Math. 2014, 260, 294–300. [Google Scholar]
- Neggal, B.; Boussetila, N.; Rebbani, F. Projected Tikhonov regularization method for Fredholm integral equations of the first kind. J. Inequal. Appl. 2016. [Google Scholar]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Physica 1992, 60, 259–268. [Google Scholar]
- Acar, R.; Vogel, C.R. Analysis of bounded variation penalty methods for ill-posed problems. Inverse Probl. 1994, 10, 1217–1229. [Google Scholar]
- Wang, Y.; Yang, J.; Yin, W.; Zhang, Y. A new alternating minimization algorithm for total variation image reconstruction. SIAM J. Imaging Sci. 2008, 1, 248–272. [Google Scholar]
- Defrise, M.; Vanhove, C.; Liu, X. An algorithm for total variation regularization in high-dimensional linear problems. Inverse Probl. 2011, 27, 065002. [Google Scholar]
- Fadili, J.M.; Peyré, G. Total variation projection with first order schemes. IEEE Trans. Image Process. 2011, 20, 657–669. [Google Scholar]
- Micchelli, C.A.; Shen, L.; Xu, Y. Proximity algorithms for image models: Denoising. Inverse Probl. 2011, 27, 045009. [Google Scholar]
- Chan, R.H.; Liang, H.X.; Ma, J. Positively constrained total variation penalized image restoration. Adv. Adapt. Data Anal. 2011, 3, 1–15. [Google Scholar]
- Strong, D.M.; Blomgren, P.; Chan, T.F. Spatially adaptive local feature-driven total variation minimizing image restoration. Proc. SPIE 1997, 222–233. [Google Scholar]
- Chantas, G.; Galatsanos, N.P.; Molina, R.; Katsaggelos, A.K. Variational Bayesian image restoration with a product of spatially weighted total variation image priors. IEEE Trans. Image Process. 2010, 19, 351–362. [Google Scholar]
- Chen, Q.; Montesinos, P.; Sun, Q.S.; Heng, P.A.; Xia, D.S. Adaptive total variation denoising based on difference curvature. Image Vision Comput. 2010, 28, 298–306. [Google Scholar]
- Chopra, A.; Lian, H. Total variation, adaptive total variation and nonconvex smoothly clipped absolute deviation penalty for denoising blocky images. Pattern Recognit. 2010, 43, 2609–2619. [Google Scholar]
- El Hamidi, A.; Ménard, M.; Lugiez, M.; Ghannam, C. Weighted and extended total variation for image restoration and decomposition. Pattern Recognit. 2010, 43, 1564–1576. [Google Scholar]
- Hansen, P.C.; Mosegaard, K. Piecewise polynomial solutions to linear inverse problems. Lect. Notes Earth Sci. 1996, 63, 284–294. [Google Scholar]
- Jin, B.T.; Zou, J. Numerical estimation of piecewise constant Robin coefficient. SIAM J. Control Optim. 2009, 48, 1977–2002. [Google Scholar]
- Bogosel, B.; Oudet, É. Qualitative and numerical analysis of a spectral problem with perimeter constraint. SIAM J. Control Optim. 2016, 54, 317–340. [Google Scholar]
- Chan, R.H.; Ng, M.K. Conjugate gradient method for Toeplitz systems. SIAM Rev. 1996, 38, 427–482. [Google Scholar]
- Groetsch, C.W. Integral equations of the first kind, inverse problems and regularization: A crash course. J. Phys. Conf. Ser. 2007, 73, 012001. [Google Scholar]
- Goncharskii, A.V.; Leonov, A.S.; Yagola, A.G. A generalized discrepancy principle. USSR Comput. Math. Math. Phys. 1973, 13, 25–37. [Google Scholar]
- Bakushinsky, A.; Kokurin, M.Y.; Smirnova, A. Iterative Methods for Ill-posed Problems: An Introduction. Inverse and Ill-Posed Problems Series 54. De Gruyter: Berlin, Germany; New York, NY, USA, 2011. [Google Scholar]

| Error | |||
|---|---|---|---|
| TV | (, , -, -) | 24 | |
| WTV | (, , , -) | 11 | |
| WTVMM | (, , , 1) | 11 + 4 |
| Error | |||
|---|---|---|---|
| TV | (, , -, -) | 10 | |
| WTV | (, , , -) | 13 | |
| WTVMM | (, , , 1) | 10+11 |
| 5.0 | (, , ) | (, , ) | (, , ) | |
| (, , ) | (, , ) | (, , ) | ||
| (, , ) | (, , ) | (, , ) | ||
| (, , ) | (, , ) | (, , ) | ||
| (, , ) | (, , ) | (, , ) | ||
| (, , ) | (, , ) | (, , ) | ||
| Error | |||
|---|---|---|---|
| TV | (, , -, -) | 14 | |
| WTV | (, , , -) | 8 | |
| WTVMM | (, , , 1) | 8+3 |
| Error | |||
|---|---|---|---|
| TV | (, , -, -) | 16 | |
| WTV | (, , , -) | 11 | |
| WTVMM | (, , , 1) | 11+4 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, F.-R.; Yang, S.-W. A Two-Stage Method for Piecewise-Constant Solution for Fredholm Integral Equations of the First Kind. Mathematics 2017, 5, 28. https://doi.org/10.3390/math5020028
Lin F-R, Yang S-W. A Two-Stage Method for Piecewise-Constant Solution for Fredholm Integral Equations of the First Kind. Mathematics. 2017; 5(2):28. https://doi.org/10.3390/math5020028
Chicago/Turabian StyleLin, Fu-Rong, and Shi-Wei Yang. 2017. "A Two-Stage Method for Piecewise-Constant Solution for Fredholm Integral Equations of the First Kind" Mathematics 5, no. 2: 28. https://doi.org/10.3390/math5020028
APA StyleLin, F.-R., & Yang, S.-W. (2017). A Two-Stage Method for Piecewise-Constant Solution for Fredholm Integral Equations of the First Kind. Mathematics, 5(2), 28. https://doi.org/10.3390/math5020028





