Deterministic Seirs Epidemic Model for Modeling Vital Dynamics, Vaccinations, and Temporary Immunity
Abstract
:1. Introduction
2. Epidemiological Model
3. Local Stability
3.1. Disease-Free Equilibrium
3.2. Endemic Equilibrium
4. Experimental Methodology
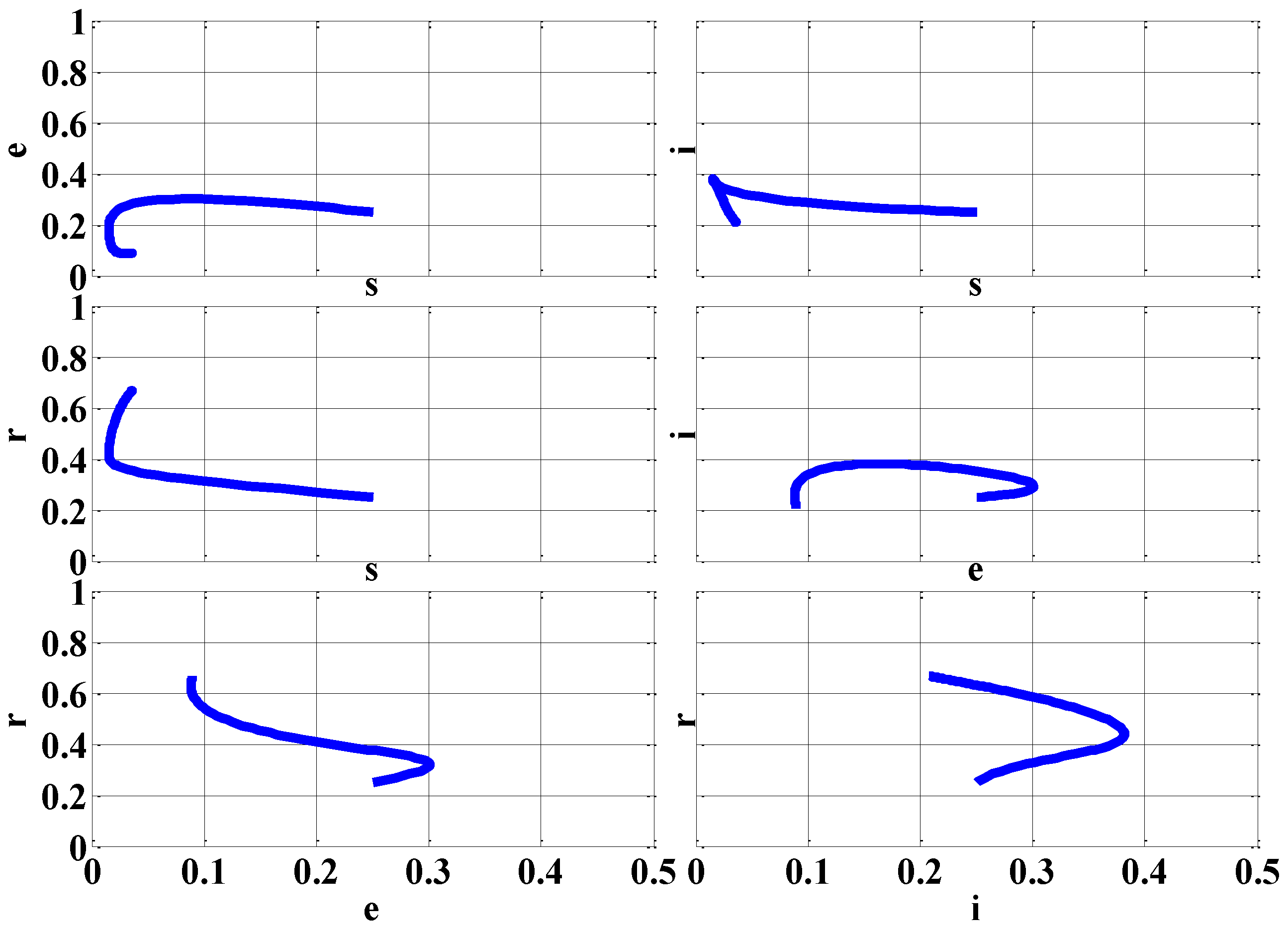
5. Experimental Results
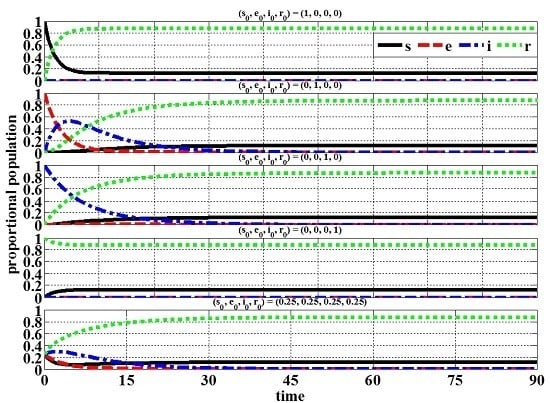
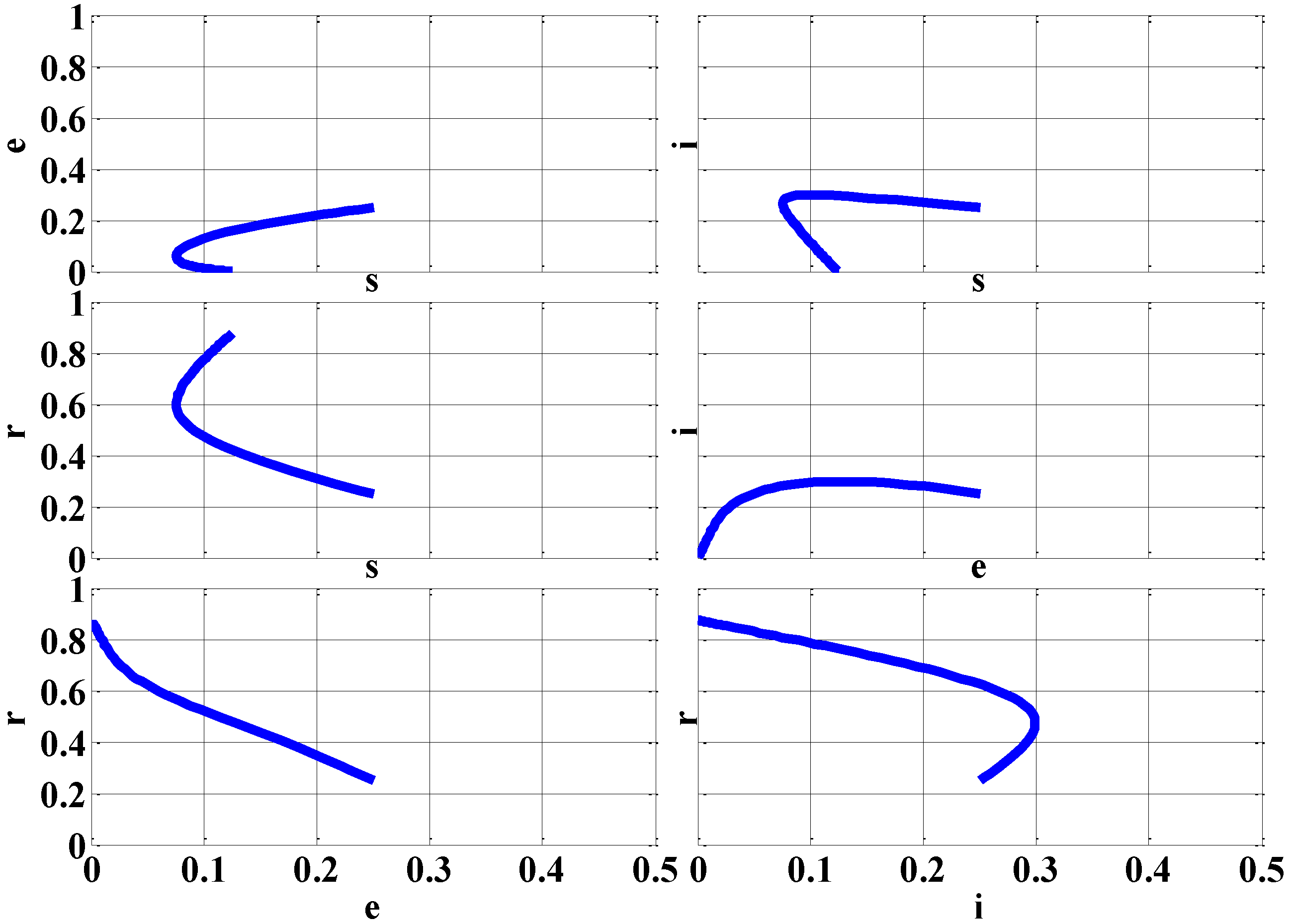
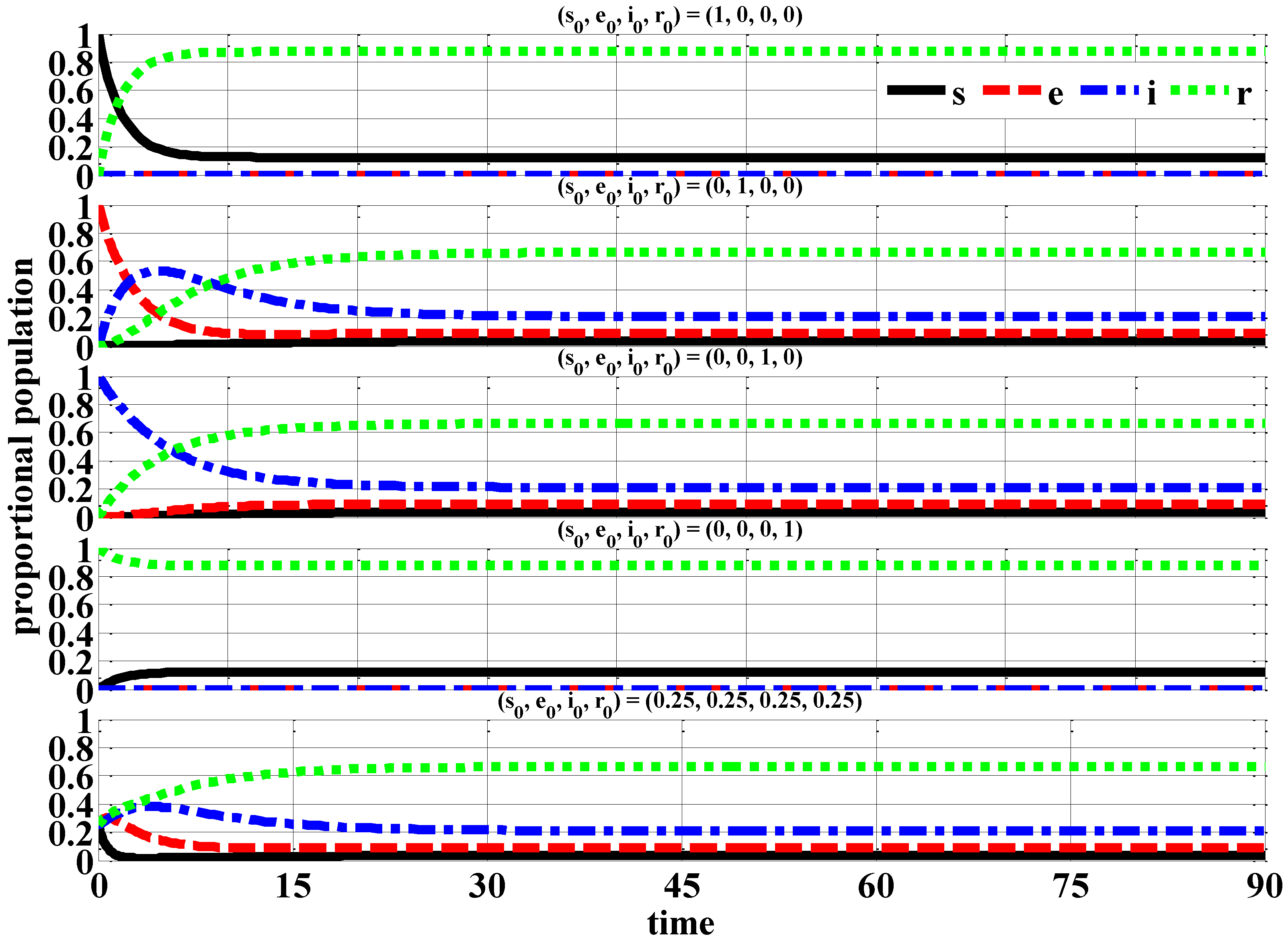
5.1. No Epidemic
5.2. Epidemic
6. Conclusions
Conflicts of Interest
Appendix A
References
- Brauer, F.; Van den Driessche, P.; Wu, J. Mathematical Epidemiology; Springer: New York, NY, USA, 2008; p. 415. [Google Scholar]
- Ma, Z.; Li, J. Dynamic Modeling and Analysis of Epidemics; World Scientific: Singapore, Singapore, 2009; p. 513. [Google Scholar]
- Murray, J.D. Mathematical Biology I. An Introduction, 3rd ed.; Springer: New York, NY, USA, 2002; p. 576. [Google Scholar]
- Sontag, E.D. Lecture Notes on Mathematical Systems Biology; Rutgers University: New Brunswick, NJ, USA, 2014; Available online: http://www.math.rutgers.edu/~sontag/FTPDIR/systems_biology_notes.pdf (accessed on 16 January 2017).
- Kermack, W.O.; McKendrick, A.G. A Contribution to the Mathematical Theory of Epidemics. Proc. R. Soc. A 1927, 115, 700–721. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. Contributions to the Mathematical Theory of Epidemics. II. The Problem of Endemicity. Proc. R. Soc. A 1932, 138, 55–83. [Google Scholar] [CrossRef]
- Hethcote, H. Qualitative Analyses of Communicable Disease Models. Math. Biosci. 1976, 28, 335–356. [Google Scholar] [CrossRef]
- Hethcote, H. The Mathematics of Infectious Diseases. Soc. Ind. Appl. Math. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M. Population biology of infectious diseases: Part I. Nature 1979, 280, 361–367. [Google Scholar] [CrossRef] [PubMed]
- Anderson, R.M.; May, R.M. Population biology of infectious diseases: Part II. Nature 1979, 280, 455–461. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M. Directly Transmitted Infectious Diseases: Control by Vaccination. Science 1982, 215, 1053–1060. [Google Scholar] [CrossRef] [PubMed]
- Anderson, R.M.; May, R.M. Vaccination and herd immunity to infectious diseases. Nature 1985, 318, 323–329. [Google Scholar] [CrossRef] [PubMed]
- D’Onofrio, A. On pulse vaccination strategy in the SIR epidemic model with vertical transmission. Appl. Math. Lett. 2005, 18, 729–732. [Google Scholar] [CrossRef]
- Buonomo, B.; d’Onofrio, A.; Lacitignola, D. Global stability of an SIR epidemic model with information dependent vaccination. Math. Biosci. 2008, 216, 9–16. [Google Scholar] [CrossRef] [PubMed]
- Li, M.Y.; Muldowney, J.S. Global Stability for the SEIR Model in Epidemiology. Math. Biosci. 1994, 28, 155–164. [Google Scholar] [CrossRef]
- D’Onofrio, A. Stability properties of pulse vaccination strategy in SEIR epidemic model. Math. Biosci. 2002, 179, 57–72. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, Z. Global dynamics of an SEIR epidemic model with saturating contact rate. Math. Biosci. 2003, 30, 15–32. [Google Scholar] [CrossRef]
- Li, M.Y.; Graef, J.R.; Wang, L.; Karsai, J. Global dynamics of a SEIR model with varying total population size. Math. Biosci. 1999, 160, 191–213. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J.; Ma, Z. Global Dynamics of an SEIR Epidemic Model with Immigration of Different Compartments. Acta Math. Sci. 2006, 26, 551–567. [Google Scholar] [CrossRef]
- Zhao, Z.; Chen, L.; Song, X. Impulsive vaccination of SEIR epidemic model with time delay and nonlinear incidence rate. Math. Comput. Simul. 2008, 79, 500–510. [Google Scholar] [CrossRef]
- Li, G.; Jin, Z. Global stability of a SEIR epidemic model with infectious force in latent, infected and immune period. Chaos Solitons Fractals 2005, 25, 1177–1184. [Google Scholar] [CrossRef]
- Li, G.; Wang, W.; Jin, Z. Global stability of an SEIR epidemic model with constant immigration. Chaos Solitons Fractals 2006, 30, 1013–1019. [Google Scholar] [CrossRef]
- Feng, Z. Final and Peak Epidemic Sizes for SEIR Models with Quarantine and Isolation. Math. Biosci. Eng. 2007, 4, 675–686. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Cui, N. Dynamic Analysis of an SEIR Model with Distinct Incidence for Exposed and Infectives. Sci. World J. 2013, 2013, 871393. [Google Scholar] [CrossRef] [PubMed]
- Safi, M.A.; Imran, M.; Gumel, A.B. Threshold dynamics of a non-autonomous SEIRS model with quarantine and isolation. Theory Biosci. 2012, 131, 19–30. [Google Scholar] [CrossRef] [PubMed]
- Safi, M.A.; Garba, S.M. Global Stability Analysis of SEIR Model with Holling Type II Incidence Function. Comput. Math. Methods Med. 2012, 2012, 826052. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Teng, Z. On a Nonautonomous SEIRS Model in Epidemiology. Bull. Math. Biol. 2007, 69, 2537–2559. [Google Scholar] [CrossRef] [PubMed]
- Rost, G.; Huang, S.Y.; Szekely, L. On a SEIR Epidemic Model with Delay. Dynam. Syst. Appl. 2012, 21, 33–48. [Google Scholar]
- Smith, H.L.; Wang, L.; Li, M.Y. Global Dynamics of an SEIR Epidemic Model with Vertical Transmission. SIAM J. Appl. Math. 2001, 62, 58–69. [Google Scholar] [CrossRef]
- Yan, P.; Liu, S. SEIR Epidemic Model with Delay. Aust. N. Z. Ind. Appl. Math. J. 2006, 48, 119–134. [Google Scholar] [CrossRef]
- Li, X.Z.; Fang, B. Stability of an Age-structured SEIR Epidemic Model with Infectivity in Latent Period. Appl. Appl. Math. 2009, 1, 218–236. [Google Scholar]
- Yi, N.; Zhang, Q.; Mao, K.; Yang, D.; Li, Q. Analysis and control of an SEIR epidemic system with nonlinear transmission rate. Math. Comput. Model. 2009, 50, 1498–1513. [Google Scholar] [CrossRef]
- Sun, C.; Hsieh, Y.H. Global analysis of an SEIR model with varying population size and vaccination. Appl. Math. Model. 2010, 34, 2685–2697. [Google Scholar] [CrossRef]
- Gao, S.; Chen, L.; Teng, Z. Impulsive Vaccination of an SEIRS Model with Time Delay and Varying Total Population Size. Bull. Math. Biol. 2007, 69, 731–745. [Google Scholar] [CrossRef] [PubMed]
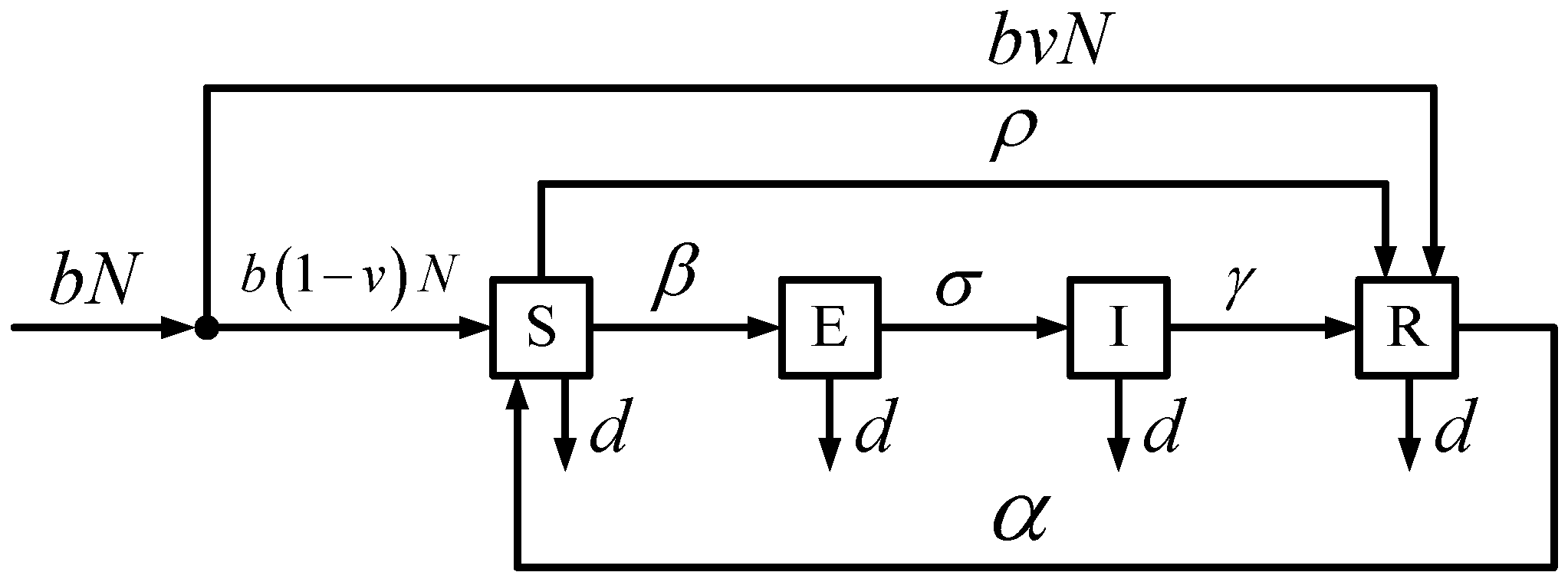

| Parameter | Name | Units | Meaning |
|---|---|---|---|
| S | Susceptible Individuals | Number of Individuals | Individuals susceptible to infection who can contract the disease if they are exposed to it |
| E | Exposed Individuals | Number of Individuals | Individuals exposed to infection who are infected but have not yet become infectious and cannot pass the infection to other susceptible individuals |
| I | Infected Individuals | Number of Individuals | Individuals infected by infection who are capable of transmitting the infection to any susceptible individuals |
| R | Recovered Individuals | Number of Individuals | Individuals recovered from infection who are temporarily immune from the infection |
| Parameter | Name | Units | Meaning |
|---|---|---|---|
| b | Birth Rate | Birth rate of newborns each year | |
| d | Death Rate | Death rate of susceptible, exposed, infected, and recovered individuals each year | |
| ν | Vaccination Proportion (Newborns) | Dimensionless | Proportion of vaccinated newborns |
| ρ | Vaccination Rate (Susceptible) | days−1 | Rate at which susceptible individuals are vaccinated and leave susceptible class and enter recovered class to gain temporary immunity |
| α | Transmission Rate (Recovered to Susceptible) | days−1 | Rate at which recovered individuals lose temporary immunity and leave recovered class and enter susceptible class |
| β | Transmission Rate (Susceptible to Infected) | days−1 | Rate at which susceptible individuals become exposed by infected individuals and leave susceptible class and enter exposed class |
| σ | Transmission Rate (Exposed to Infected) | days−1 | Rate at which exposed individuals become infected by incubating infection and leave exposed class and enter infected class |
| γ | Recovery Rate (Infected to Recovered) | days−1 | Rate at which infected individuals leave infected class and enter recovered class |
| Parameter | Name | Units | Meaning |
|---|---|---|---|
| Mean Susceptibility Period (Pre-Vaccination of Susceptible Individuals) | days | Time for susceptible individuals to become recovered individuals | |
| Mean Temporary Immunity Period | days | Time for recovered individuals to become susceptible individuals | |
| Mean Susceptibility Period (Pre-Exposed Individuals) | days | Time for susceptible individuals to become exposed individuals | |
| Mean Latency Period | days | Time for exposed individuals to become infected individuals | |
| Mean Infectious Period | days | Time for infected individuals to become recovered individuals |
| Parameter | Value | |
|---|---|---|
| b | ||
| d | ||
| ν | 0.8 | |
| 2 days | ||
| 14 days | ||
| 4 days (No Epidemic) | ¼ days (Epidemic) | |
| 3 days | ||
| 7 days | ||
| Parameter | Value | |
|---|---|---|
| 0.07140 | ||
| 0.57150 | ||
| 0.33340 | ||
| 0.14290 | ||
| 0.07150 | ||
| 0.21865 (No Epidemic) | 3.49840 (Epidemic) | |
| Point | s | e | i | λ1 | λ2 | λ3 | Stability |
|---|---|---|---|---|---|---|---|
| DFE | 0.12501 | 0 | 0 | −0.57148 | −0.37775 | −0.09855 | Stable |
| EE | 0.57173 | −0.44677 | −1.0421 | −0.44276 +i0.14310 | −0.44276 −i0.14310 | 0.09826 | Unstable |
| Point | s | e | i | λ1 | λ2 | λ3 | Stability |
|---|---|---|---|---|---|---|---|
| DFE | 0.12501 | 0 | 0 | −0.57148 | −0.65737 | 0.18107 | Unstable |
| EE | 0.03573 | 0.08928 | 0.20825 | −1.3929 | −0.34731 | −0.14062 | Stable |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trawicki, M.B. Deterministic Seirs Epidemic Model for Modeling Vital Dynamics, Vaccinations, and Temporary Immunity. Mathematics 2017, 5, 7. https://doi.org/10.3390/math5010007
Trawicki MB. Deterministic Seirs Epidemic Model for Modeling Vital Dynamics, Vaccinations, and Temporary Immunity. Mathematics. 2017; 5(1):7. https://doi.org/10.3390/math5010007
Chicago/Turabian StyleTrawicki, Marek B. 2017. "Deterministic Seirs Epidemic Model for Modeling Vital Dynamics, Vaccinations, and Temporary Immunity" Mathematics 5, no. 1: 7. https://doi.org/10.3390/math5010007
APA StyleTrawicki, M. B. (2017). Deterministic Seirs Epidemic Model for Modeling Vital Dynamics, Vaccinations, and Temporary Immunity. Mathematics, 5(1), 7. https://doi.org/10.3390/math5010007