Zoology of Atlas-Groups: Dessins D’enfants, Finite Geometries and Quantum Commutation

Abstract

Every finite simple group P can be generated by two of its elements. Pairs of generators for P are available in the Atlas of finite group representations as (not necessarily minimal) permutation representations $\mathcal{P}$. It is unusual, but significant to recognize that a $\mathcal{P}$ is a Grothendieck’s “dessin d’enfant” $\mathcal{D}$ and that a wealth of standard graphs and finite geometries $\mathcal{G}$—such as near polygons and their generalizations—are stabilized by a $\mathcal{D}$. In our paper, tripods $\mathcal{P}-\mathcal{D}-\mathcal{G}$ of rank larger than two, corresponding to simple groups, are organized into classes, e.g., symplectic, unitary, sporadic, etc. (as in the Atlas). An exhaustive search and characterization of non-trivial point-line configurations defined from small index representations of simple groups is performed, with the goal to recognize their quantum physical significance. All of the defined geometries ${\mathcal{G}}^{\prime }s$ have a contextuality parameter close to its maximal value of one.

1. Introduction

Over the last few years, it has been recognized that the detailed investigation of commutation between the elements of generalized Pauli groups—the qudits and arbitrary collections of them [1]—is useful for a better understanding of the concepts of quantum information, such as error correction [2,3], entanglement [4,5] and contextuality [6,7,8], that are cornerstones of quantum algorithms and quantum computation. Only recently, the first author observed that much of the information needed is encapsulated in permutation representations, of rank larger than two, available in the Atlas of finite group representations [9]. The coset enumeration methodology of the Atlas was used by us for deriving many finite geometries underlying quantum commutation and the related contextuality [10,11,12,13]. As a bonus, the two-generator permutation groups and their underlying geometries may luckily be considered as dessins d’enfants [14], although this topological and algebraic aspect of the finite simple (or not simple) groups is barely mentioned in the literature. Ultimately, it may be that the Monster group and its structure fits our quantum world, as in Dyson’s words [13]. More cautiously, in Section 2 of the present paper, we briefly account for the group concepts involved in our approach by defining a tripod $\mathcal{P}-\mathcal{D}-\mathcal{G}$. One leg $\mathcal{P}$ is a desired two-generator permutation representation of a finite group P [9]. Another leg $\mathcal{D}$ signs the coset structure of the used subgroup H of the two-generator free group G (or of a quotient group $G^{\prime }$ of G with relations), whose finite index $[G,H]=n$ is the number of edges of $\mathcal{D}$, and at the same time, the size of the set on which $\mathcal{P}$ acts, as in [11]. Finally, $\mathcal{G}$ is the geometry with n vertices that is defined/stabilized by $\mathcal{D}$ [10]. Then, in Section 3, we organize the relevant $\mathcal{P}-\mathcal{D}-\mathcal{G}$ tripods taken from the classes of the Atlas and find that many of them reflect quantum commutation, specifically the symplectic, unitary and orthogonal classes. The geometries of other (classical and sporadic) classes are investigated similarly with the goal to recognize their possible physical significance. A physically-oriented survey of simple groups is [15].

2. Group Concepts for the $\mathcal{P}-\mathcal{D}-\mathcal{G}$ Puzzle

2.1. Groups, Dessins and Finite Geometries

Following the impetus given by Grothendieck [16], it is now known that there are various ways to dress a group P generated by two permutations: (i) as a connected graph drawn on a compact oriented two-dimensional surface, a bicolored map (or hypermap) with n edges, B black points, W white points, F faces, genus g and Euler characteristic $2-2g=B+W+F-n$ [17]; (ii) as a Riemann surface X of the same genus equipped with a meromorphic function f from X to the Riemann sphere $\overline{\mathbb{C}}$ unramified outside the critical set $\{0,1,\infty \}$, the pair $(X,f)$ called a Belyi pair, and in this context, hypermaps are called dessins d’enfants [14,16]; (iii) as a subgroup H of the free group $G=⟨a,b⟩$ (or of a two-generator group $G^{\prime }=⟨a,b|\mathrm{rels}⟩$) where P encodes the action of (right) cosets of H on the two generators a and b; the Coxeter–Todd algorithm does the job [11]; and finally (iv), when P is of rank at least three, that is of a point stabilizer with at least three orbits, as a non-trivial finite geometry [10,11,12,13]. Finite simple groups are generated by two of their elements [18], so that it is useful to characterize them as members of the categories just described.

There are many mathematical papers featuring the correspondence between items (i) and (ii) in view of a better understanding of the action of the absolute Galois group $\mathrm{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})$, the automorphism group of the field $\overline{\mathbb{Q}}$ of algebraic numbers, on the hypermaps [16,17,19]. Coset enumeration featured in Item (iii) is at work in the permutation representations of finite groups found in the Atlas [9]. Item (i) in conjunction to (iii) and (iv) allowed us to arrive at the concept of geometric contextuality as a lack of commutativity of cosets on the lines of the finite geometry stabilized by P [11].

Item (iv) may be further clarified thanks to the concept of the rank of a permutation group P. First it is expected that P acts faithfully and transitively on the set $\mathsf{\Omega }=\{1,2,\cdots ,n\}$ as a subgroup of the symmetric group $S_n$. The action of P on a pair of distinct elements of Ω is defined as ${(\alpha ,\beta )}^p=({\alpha }^p,{\beta }^p)$, $p\in P$, $\alpha \ne \beta$. The orbits of P on $\mathsf{\Omega }\times \mathsf{\Omega }$ are called orbitals, and the number of orbits is called the rank r of P on Ω. The rank of P is at least two, and the two-transitive groups identify the rank two permutation groups. Second the orbitals for P are in one to one correspondence with the orbits of the stabilizer subgroup $P_{\alpha }=\{p\in P|{\alpha }^p=\alpha \}$ of a point α of Ω. This means that r is also defined as the number of orbits of $P_{\alpha }$. The orbits of $P_{\alpha }$ on Ω are called the sub-orbits of P, and their lengths are the sub-degrees of P. A complete classification of permutation groups of rank at most five is in the book [20]. Next, selecting a pair $(\alpha ,\beta )\in \mathsf{\Omega }\times \mathsf{\Omega }$, $\alpha \ne \beta$, one introduces the two-point stabilizer subgroup $P_{(\alpha ,\beta )}=\{p\in P|{(\alpha ,\beta )}^p=(\alpha ,\beta )\}$. There exist $1<m\le r$ such non-isomorphic (two-point stabilizer) subgroups $S_m$ of P. Selecting the largest one with $\alpha \ne \beta$, one defines a point/line incidence geometry $\mathcal{G}$ whose points are the elements of Ω and whose lines are defined by the subsets of Ω sharing the same two-point stabilizer subgroup. Thus, two lines of $\mathcal{G}$ are distinguished by their (isomorphic) stabilizers acting on distinct subsets of Ω. A non-trivial geometry arises from P as soon as the rank of the representation $\mathcal{P}$ of P is $r>2$, and simultaneously, the number of non isomorphic two-point stabilizers of $\mathcal{P}$ is $m>2$.

2.2. Geometric Contextuality

Let $G^{\prime }$ be the two-generator group defined by a set of relations on its generators and H a subgroup of $G^{\prime }$ of index n. As shown in Section 2.1, the permutation representation $\mathcal{P}$ associated with the pair $(G^{\prime },H)$ is a dessin d’enfant $\mathcal{D}$ whose edges are encoded by the representative of cosets of H in $G^{\prime }$. A graph/geometry $\mathcal{G}$ may be defined by taking the n vertices of $\mathcal{G}$ as the edges of $\mathcal{D}$ and the edges of $\mathcal{G}$ as the distinct (but isomorphic) two-point stabilizer subgroups of $\mathcal{P}$.

Further, $\mathcal{G}$ is said to be contextual if at least one of its lines/edges corresponds to a set/pair of vertices encoded by non-commuting cosets [11]. A straightforward measure of contextuality can be taken as the ratio $\kappa =E_c/E$ between the number $E_c$ of lines/edges of $\mathcal{G}$ with non-commuting cosets and the whole number E of lines/edges of $\mathcal{G}$. Of course, lines/edges passing through the identity coset e have commuting vertices, so that one always as $\kappa <1$.

In Section 3 below, the contextuality parameter κ corresponding to the collinear graph of the relevant geometry $\mathcal{G}$ is displayed in the right column of the tables. In order to compute κ, one needs the finite presentation of the corresponding subgroup H in $G^{\prime }$ leading to the permutation representation $\mathcal{P}$, but this information is not always available in the Atlas.

We can also quote two other approaches of quantum contextuality. The first one consists of computing the Lovasz number of the incidence graph of the geometry in question, e.g., [21], the second one is based on cohomological concepts [22].

2.3. Illustrating the Concepts

2.3.1. The Mermin Square

We first show how to recover the geometry of the well-known Mermin square, a $(3\times 3)$ grid, that is the basic model of two-qubit contextuality [23] (see Figure 7 in [10] and Figure 3i in [11]). Starting with group $G^{\prime }=⟨a,b|b^2⟩$ and making use of a mathematical software, such as Magma, one derives the (unique) subgroup H of $G^{\prime }$ that is of index nine and possesses a permutation representation $\mathcal{P}$ isomorphic to the finite group $P_{36}={\mathbb{Z}}_3^2\times {\mathbb{Z}}_2^2$ reflecting the symmetry of the grid. The permutation representation is as follows:

$$\mathcal{P}=⟨9\left|\right(1,2,4,8,7,3\left)\right(5,9,6),(2,5\left)\right(3,6\left)\right(4,7\left)\right(8,9)⟩,$$

where the list $[1,...,9]$ means the list of coset representatives $[e,a,a^{-1},a^2,ab,a^{-1}b,a^{-2},a^3,aba]$. The permutation representation $\mathcal{P}$ can be seen as a dessin d’enfant drawn on a torus (as in Figure 1i) [10,11]. Next, we apply the procedure described in Item (iv) of Section 2.1. There are two types of two-point stabilizer subgroups that are isomorphic to the single element group ${\mathbb{Z}}_1$ or to the two-element group ${\mathbb{Z}}_2$. Both define the geometry of a $(3\times 3)$ grid comprising six lines identified, but their non-identical, but isomorphic two-point stabilizers $s_1$ to $s_6$, made explicit in the caption of Figure 1. The first grid (not shown) is non-contextual in the sense that the cosets on a line are commuting. In the second grid, shown in Figure 1j, the (group theoretical) commutator for the points on a line is the identity element e except for the one associated with the right-hand side column where it is $(a^{-1}b,ab,aba)=a^{-1}$ (which is not the class e of the identity element). The non-commuting cosets on this line reflect the contextuality that occurs when one takes two-qubit coordinates for the points of the grid; see [11,12] for more details about the relationship between non-commuting cosets and geometric contextuality.

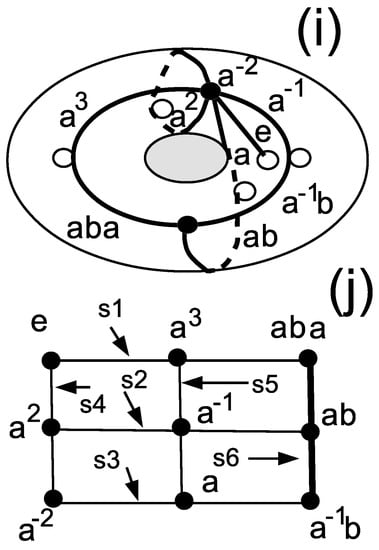
Figure 1. The dessin d’enfant (i) leading to Mermin’s square (j). The two-point stabilizer subgroups of the permutation representation $\mathcal{P}$ corresponding to the dessin (one for each line) are as follows: $s_1=(2,3)(4,7)(5,6)$, $s_2=(1,7)(2,8)(6,9)$, $s_3=(1,4)(3,8)(5,9)$, $s_4=(2,6)(3,5)(8,9)$, $s_5=(1,9)(4,5)(6,7)$, $s_6=(1,8)(2,7)(3,4)$, where the points of the square (resp. the edges of the dessin d’enfant) are labeled as $[1,..,9]=[e,a,a^{-1},a^2,ab,a^{-1}b,a^{-2},a^3,aba]$.

2.3.2. A Modular Geometry

Now, we deal with a contextual configuration $\mathcal{G}$ arising from a modular dessin d’enfant, that is that follows from a subgroup $H\cong {\mathsf{\Gamma }}^{\prime }$ of the modular group $G^{\prime }=⟨a,b|b^2,a^3⟩\cong \mathsf{\Gamma }=PSL(2,\mathbb{Z})$.

Let us remind how to pass from the topological structure of a modular dessin $\mathcal{D}$ to that of a hyperbolic polygon $\mathcal{P}$ ([13], Section 3). There are ${\nu }_2$ elliptic points of order two (resp. ${\nu }_3$ elliptic points of order three) of $\mathcal{P}$; these points are white points (resp. black points) of $\mathcal{D}$. The genus of $\mathcal{P}$ equals that of $\mathcal{D}$; a cusp of $\mathcal{P}$ follows from a face of $\mathcal{D}$; the number B of black (resp. the number W of white) points of $\mathcal{D}$ is given by the relation $B=f+{\nu }_2-1$ (resp. $W=n+2-2g-B-c$), where f is the number of fractions and c the number of cusps in $\mathcal{P}$.

Now, we pass to a specific example by selecting a subgroup H of index 12 whose permutation representation $\mathcal{P}$ is isomorphic to the finite group ${\mathbb{Z}}_2^2⋊({\mathbb{Z}}_3^2⋊{\mathbb{Z}}_2)$ of order 72 ([12], Figure 4). The dessin of Figure 2i has of course trivalent black points; it corresponds to a subgroup of the modular group Γ that is recognized to be the congruence subgroup ${\mathsf{\Gamma }}_0\left(6\right)$ of Γ depicted in Figure 2j. The normalizer of ${\mathsf{\Gamma }}_0\left(6\right)$ in Γ is the moonshine group ${\mathsf{\Gamma }}_0^{+}\left(6\right)$ [13]. The configuration $\mathcal{G}={[{12}_6,{24}_3]}_{\left(4\right)}$ is of rank four, comprises 12 points and 24 lines/triangles with six lines through each point. It is pictured in Figure 2k. The group of automorphisms of $\mathcal{G}$ is isomorphic to ${\mathbb{Z}}_2^4⋊P_{36}$, where $P_{36}$ was encountered in Figure 1 as the symmetry group of the Mermin square. The complement of the collinearity graph of $\mathcal{G}$ is the $(3\times 4)$-grid that physically corresponds to the geometry of the 12 maximum sets of commuting operators in a qubit-qutrit system [24]. Two points on a line of the grid correspond to maximum sets having one point in common, while the triangles in (k) correspond to maximum sets of (three) mutually unbiased bases.

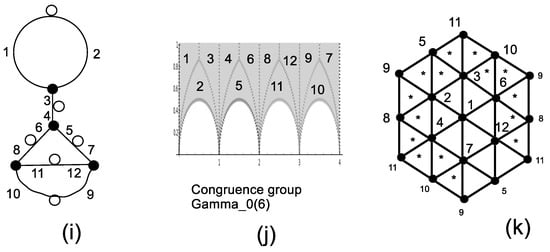
Figure 2. The contextual dessin d’enfant (i) with permutation group of order 72; it corresponds to the congruence subgroup ${\mathsf{\Gamma }}_0\left(6\right)$ of modular group Γ, as shown in (j); the stabilized configuration is in (k). Triangles with a star inside have non-commuting cosets.

2.4. A Few Significant Geometries

There exist layers in the organization of finite geometries; see [25] for an introduction and [26,27,28] for advanced material. A partial linear space is an incidence structure $\mathsf{\Gamma }(P,L)$ of points P and lines L satisfying axioms (i) any line has at least two points and (ii) any pair of distinct points is incident with at most one line. In our context, the geometry $\mathcal{G}$ that is defined by a two-generator permutation group $\mathcal{P}$, alias its dessin d’enfant $\mathcal{D}$, has order $(s,t)$, meaning that every line has $s+1$ points and every point is on $t+1$ lines. Thus, $\mathcal{G}$ is the geometric configuration ${[p_{s+1},l_{t+1}]}_{\left(r\right)}$, with p and l the number of points and lines. The extra index r denotes the rank of $\mathcal{P}$ from which $\mathcal{D}$ arises.

We introduce a first layer of organization that is less restrictive than that of a near polygon to be defined below [28] and that of a symplectic polar space encountered in Section 3.3. We denote by ${\mathcal{G}}_u=\mathcal{G}(s,t;u)$ a connected partial linear space with the property that, given a line L and a point x not on L, there exist a constant number u of points of L nearest to x. A near polygon (or near $2d$-gon) is a partial linear space, such that the maximum distance between two points (the so-called diameter) is d, and given a line L and a point x not on L, there exists “a unique point” on L that is nearest to x. A graph (whose lines are edges) is of course of type ${\mathcal{G}}_1$. A near polygon is, by definition, of type ${\mathcal{G}}_1$. Symplectic polar spaces are of the form ${\mathcal{G}}_u$, possibly with $u>1$, but not all ${\mathcal{G}}_u$ with $u>1$, are polar spaces. A generalized polygon (or generalized N-gon) is a near polygon whose incidence graph has diameter N (the distance between its furthest points) and girth $2N$ (the length of a shortest path from a vertex to itself) [27]. According to the Feit–Higman theorem [26], finite generalized N-gons with $s>1$ and $t>1$ may exist only for $N\in \{2,3,4,6,8\}$. They consist of projective planes with $N=3$ and generalized quadrangles GQ$(s,t)$, generalized hexagons GH$(s,t)$ and generalized octagons GO$(s,t)$ when $N=4,6,8$, respectively.

Many ${\mathcal{G}}^{\prime }s$ have a collinearity graph that is a strongly regular graph (denoted srg). These graphs are partial geometries pg$(s,t;\alpha )$ of order $(s,t)$ and (constant) connection number α. By definition, α is the number of points of a line L joined to a selected point P by a line. The partial geometries pg listed in our tables are those associated with srg graphs found in [29].

2.5. A Few Small Examples

Let us illustrate our concepts by selecting a rank three (or higher) representation for the group of the smallest cardinality in each class of simple groups. The notation for the simple groups and their representations are taken from the Atlas [9].

2.5.1. Alternating

The smallest non-cyclic simple group is the alternating group $A_5$ whose finite representation is $H=⟨a,b|a^2=b^3={\left(ab\right)}^5=1⟩$.

The permutation representations of $A_5$ are obtained by taking the subgroups of the finite index of the free group $G=⟨a,b⟩$ whose representation is H.

Table 1 lists the rank r and the number m of two-point stabilizer subgroups for the permutation representations $\mathcal{P}$ up to rank 15. The only non-trivial permutation group has index 10, rank three, sub-degrees $1,3,6$ with $\mathcal{P}=⟨10\left|\right(2,3,4\left)\right(5,7,8\left)\right(6,9,10),(1,2\left)\right(3,5\left)\right(4,6\left)\right(7,10)⟩$.

Table 1. Parameters r and s for small index representations of $A_5$.

${\mathit{A}}_5$ Index	5	6	10	12	15
r	2	2	3	4	5
m	2	2	3	1	1

The dessin d’enfant $\mathcal{D}$ corresponding to $\mathcal{P}$ is pictured in our previous papers (see [10], Figure 10, [11], Figure 3j, [13], Figure 4). The geometries that are stabilized are the Petersen graph PG or Mermin’s pentagram MP, depending on the choice of the two-point stabilizer subgroup. Thus, $A_5$ features three-qubit “3QB” contextuality.

2.5.2. Symplectic

The smallest (simple) symplectic group is $S_4^{\prime }\left(2\right)=A_6$, whose finite representation is $H=⟨a,b|a^2=b^4={\left(ab\right)}^5={\left(a{b}^2\right)}^5=1⟩$. Table 2 lists the rank r and the number m of two-point stabilizer subgroups for the permutation representations $\mathcal{P}$ up to rank 30.

Table 2. Parameters r and s for the small index representations of $A_6$.

${\mathit{A}}_6$ Index	6	10	15	20	30
r	2	2	3	4	7
m	2	2	3	2	3

The smallest non-trivial permutation group $\mathcal{P}$ has index 15, rank three and sub-degrees $1,6,8$, as shown in Table 2.

The geometry that is stabilized by $\mathcal{P}$ is the (self-dual) generalized quadrangle $GQ(2,2)$, alias the graph $\widehat{L}\left(K_6\right)$ (the complement of the line graph of the complete graph $K_6$). It is known that $GQ(2,2)$ is a model of two-qubit “2QB” commutation; see [11], Figure 12. The permutation representation of index 30 of $S_4^{\prime }\left(2\right)$ stabilizes the configuration $[{30}_{16},{160}_3]$ of rank seven that turns out to be a geometry of type ${\mathcal{G}}_2$.

As for two-qutrit commutation, one uses the $S_4\left(3\right)$ permutation representation $\mathcal{P}$ of rank three and index ${40}_b$ found in the Atlas. The dessin d’enfant picturing $\mathcal{P}$ is found in Figure 3. The dessin has signature $(B,W,F,g)=(8,28,6,0)$.

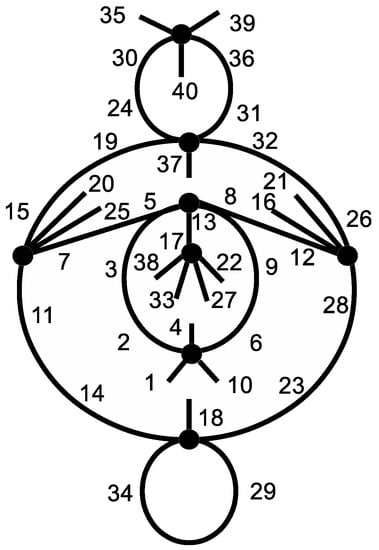
Figure 3. The dessin d’enfant stabilizing the generalized quadrangle $GQ(3,3)$ (a model of two-qutrit “2QT” commutation). The dessin corresponds to the Sp$(4,3)$ permutation representation of index ${40}_b$ found in the Atlas. Only black points are shown: white points are implicit at the mid-edges or at the ends of half-edges.

2.5.3. Unitary

The smallest (simple) unitary group is $U_3\left(3\right)$. Representations of $U_3\left(3\right)$ of index 28 (rank two), 36 (rank four), 63 (rank four) and 63 (rank five) may be found in the Atlas (denoted ${63}_a$ and ${63}_b$, respectively). The most interesting ones are the ${63}_a$, of sub-degrees $1,6,24,32$, and the ${63}_b$, of sub-degrees $1,6,{16}^2,24$. These representations stabilize the split Cayley hexagon $GH(2,2)$ (with ${63}_b$) and its dual (with ${63}_a$). The hexagon $GH(2,2)$ is a configuration of type $\left[{63}_3\right]$ with 63 points on three lines and 63 lines with three points. It may be used as a model of $3QB$contextuality; see [11], Figures 5 and 6, for details and plots of the corresponding dessins d’enfants.

2.5.4. Orthogonal

The smallest (simple) orthogonal group is $O_7\left(3\right)$. The Atlas lists four representations of rank three and index 351, 364, 378 and 1080. We could recognize that the first representation is associated with the strongly regular graph srg($351,126,45,45$) and the geometry $N{O}^{-}(7,3)$; the second representation is associated with srg($364,120,38,40$) and the geometry of the symplectic polar space $W_5\left(3\right)$; the third representation is associated with srg($378,117,36,36$) and presumably the partial geometry pg$(13,18,4)$; and the fourth representation is associated with srg($1080,351,126,108$) and the geometry $N{O}^{+}(8,3)$; see [29] for details about the undefined acronyms. The second representation corresponds to the commutation of the 364 three-qutrit “3QT” observables [1]. It is found to be of type ${\mathcal{G}}_4$. The representation of index 1120 and rank four of $O_7\left(3\right)$ found in the Atlas is associated with the dual of $W_5\left(3\right)$ that is the dense near hexagon $DQ(6,3)$. See below Table 9 for further details.

2.5.5. Exceptional and Twisted

The smallest (simple) twisted exceptional group is Sz$\left(8\right)$. The representation of index 520 listed in the Atlas leads to an unconnected graph. The representation of index 560 of rank 17 and sub-degrees $1,{13}^3,{26}^6,{52}^7$ leads to a configuration of type $[{560}_{13},{1820}_4]$ (i.e., every point is on 13 lines, and there are 1820 lines of size four). The Atlas also provides a representation of index 1456 and rank 79 that leads to another geometry, of order $(3,4)$, with again 1820 lines of size four (see also the relevant item in Table 10). The physical meaning of both representations, if any, has not been discovered.

2.6. Sporadic

The smallest sporadic group is $M_{11}$. The Atlas provides representations of rank 3 and index 55, rank 4 and index 66 and rank 8 and index 165. The first representation leads to the triangular graph $T\left(11\right)=L\left(K_{11}\right)$. The second one leads two a non-strongly regular graph with 495 edges, of girth 4 and diameter 2. The third representation leads to a partial linear space of order $(2,3)$ with 220 lines/triangles.

Brief Summary

The results of this subsection are summarized in Table 3. Observe that the smallest simple linear group is equivalent to $A_5$ and that the smallest untwisted group $G_2{\left(2\right)}^{\prime }$ is similar to $U_3\left(3\right)$. Except for $M_{11}$ and Sz$\left(8\right)$, all of these “small” groups occur in the commutation of quantum observables. Further relations between the geometry of simple groups and the commutation of multiple qudits are given in the next section.

Table 3. A few characteristics of a index m and rank $r=3$ (or higher) representation of the simple group of smallest cardinality in each class. The characteristics of the Sp$(4,3)$ representation for two qutrits is added to this list. The question marks point out that a physical interpretation is lacking.

Type	Group	m	r	$\mathcal{G}$	Physics	κ
alternating	$A_5$	10	3	PG $=\widehat{L}\left(K_5\right)$	MP in 3QB	0.767
linear	$L_2\left(5\right)=A_5$	.	.	.	.	.
symplectic	$S_4^{\prime }\left(2\right)$	15	3	$GQ(2,2)=\widehat{L}\left(K_6\right)$	2QB	.
.	$S_4\left(3\right)$	40	3	$GQ(3,3)$	2QT	0.704
unitary	$U_3\left(3\right)$	63	4	$GH(2,2)$	3QB	0.846
orthogonal	$O_7\left(3\right)$	364	3	$W_5\left(3\right)$, ${\mathcal{G}}_4$	3QT	.
except.untwist.	$G_2{\left(2\right)}^{\prime }=U_3\left(3\right)$	.	.	.	.	0.846
except. twist.	Sz$\left(8\right)$	560	17	${[{560}_{13},{1820}_4]}_{\left(17\right)}$	?	0.971
sporadic	$M_{11}$	55	3	$T\left(11\right)=L\left(K_{11}\right)$	?	.

3. Atlas Classes and the Related Geometries

3.1. Alternating

The non-trivial configurations that are stabilized by (low rank) small simple alternating groups are listed in Table 4. The alternating group $A_7$ is missing because no non-trivial geometry has been recognized. Permutation groups for alternating groups $A_n$, $n>8$ are those listed in the Atlas.

Table 4. The non-trivial configurations stabilized by small simple alternating groups and their rank r given as an index. The notation $T\left(n\right)=L\left(K_n\right)$ means the triangular graph, and $S(2,k,v)$ means a Steiner system, that is a $2-(v,k,1)$ design [29]. The symbol srg is for a strongly regular graph. A description of the $A_8$ configuration on 35 points is given in the text.

${\mathit{A}}_{\mathit{n}}$	Geometries ${}_{\left(\mathbf{rank}\right)}$    ${\mathcal{G}}_{\left(\mathit{r}\right)}$	κ
$A_5$	MP, $\widehat{T}{\left(5\right)}_{\left(3\right)}$	0.767, 0.666
$A_6$	$GQ(2,2)$, $\widehat{T}{\left(6\right)}_{\left(3\right)}$	0.800
$A_8$	$T{\left(8\right)}_{\left(3\right)}$, (${[{35}_6,{30}_7]}_{\left(3\right)}$: srg, ${\mathcal{G}}_3$, $S(2,3,15)$, lines in $PG(3,2)$, $O^{+}(6,2)$)	0.684, 0.737
$A_9$	$T{\left(9\right)}_{\left(3\right)}$, ${[{126}_5,{315}_2]}_{\left(5\right)}$, ${[{280}_3,{84}_{10}]}_{\left(5\right)}$, ${[{840}_4,{1120}_3]}_{\left(12\right)}$	-
$A_{10}$	$T{\left(10\right)}_{\left(3\right)}$, ${[{126}_{10},{210}_6]}_{\left(4\right)}$: srg), ${[{210}_{15},{1575}_2]}_{\left(5\right)}$, ${[{945}_{10},{3150}_3]}_{\left(7\right)}$	-
$A_{11}$	$T{\left(11\right)}_{\left(3\right)}$, ${[{165}_8,{330}_4]}_{\left(4\right)}$, ${[{462}_6,{1386}_2]}_{\left(6\right)}$	-
$A_{12}$	$T{\left(12\right)}_{\left(3\right)}$, ${[{220}_9,{495}_4]}_{\left(4\right)}$, ${[{462}_{12},{792}_7]}_{\left(4\right)}$	-
$A_{13}$	$T{\left(13\right)}_{\left(3\right)}$	-
$A_{14}$	$T{\left(14\right)}_{\left(3\right)}$, ${[{364}_{11},{1001}_4]}_{\left(4\right)}$	-
$A_{15}$	$T{\left(15\right)}_{\left(3\right)}$, ${[{1365}_{11},{3003}_5]}_{\left(5\right)}$	-

The $A_8$ Configuration on 35 Points

It has been shown in the previous section that $A_5$ and $A_6$ are associated with three-qubit contextuality (via Mermin’s pentagram) and two-qubit commutation (via the generalized quadrangle of order two $GQ(2,2)$), respectively. Since $A_8$ encodes the 35 lines in $PG(3,2)$, the corresponding configuration may be seen as a model of four-qubit contextuality; see [11], Section 4, for the recognition of $PG(3,2)$ as a model of a 4QB maximum commuting set and [30] for an explicit reference to the $O^{+}(6,2)$ polarity.

As the permutation representation is not in the Atlas, we provide a few details below. The permutation representation on 35 points of $A_8$ is:

$$\begin{array}{c}\mathcal{P}=<35\left|\right(3,4,6,12,10,5\left)\right(7,13,19,23,15,9\left)\right(8,14,21,24,16,11\left)\right(17,25,26)\\ (18,27,28)(20,22,30)(29,33,35,34,32,31),(1,2,3)(4,7,8)(5,9,11)(12,17,18)\\ (13,20,14)(15,22,16)(19,29,21)(23,31,24)(25,32,27)(26,33,28)>.\end{array}$$

The representation is of rank three, with sub-orbit lengths $(1,16,18)$, and corresponds to a dessin $\mathcal{D}$ of signature $(B,W,F,G)=(9,15,5,4))$, that is of genus four, and cycles $[6^4{3}^3{1}^2,3^{10}{1}^5,7^5]$. The two-point stabilizer subgroups are of order 32 and 36. The group of order 36 is isomorphic to the symmetry group ${\mathbb{Z}}_3^2\times {\mathbb{Z}}_2^2$ of the Mermin square (a $(3\times 3)$ grid); see [10], Section 4.4. The edges of the collinearity graph of the putative geometry $\mathcal{G}$ are defined as sharing the same stabilizer subgroup of order 36, up to isomorphism, but acting on different subsets. The graph is srg of spectrum $[{16}^1,2^{20},-4^{14}]$ and can be found in [29]. The lines of $\mathcal{G}$ are defined as the maximum cliques of the collinearity graph. In the present case, the lines do not all share the same stabilizer subgroup. One gets $\mathcal{G}={[{35}_8,{56}_5]}_{\left(3\right)}$, a finite geometry of type ${\mathcal{G}}_2$. The collinearity graph associated with the stabilizer subgroup of order 32 is the complement of the collinearity graph of $\mathcal{G}$, and the corresponding geometry is $\overline{\mathcal{G}}={[{35}_6,{30}_7]}_{\left(3\right)}$, a configuration of type ${\mathcal{G}}_3$ and a model of the $O^{+}(6,2)$ polarity.

3.2. Linear

The non-trivial configurations that are stabilized by (low rank) small simple linear groups are listed in Table 5.

Table 5. The non-trivial configurations stabilized by small simple linear groups and their rank. The configuration ${[{21}_2,{14}_3]}_{\left(6\right)}$ corresponds to the thin generalized hexagon GO$(2,1)$ (see Figure 6 of [31]).

Group ${\mathit{L}}_{\mathit{n}}\left(\mathit{m}\right)$	Geometries ${}_{\left(\mathbf{rank}\right)}$ ${\mathcal{G}}_{\left(\mathit{r}\right)}$	κ
$L_2\left(4\right)=L_2\left(5\right)=A_5$	MP, $\widehat{T}{\left(5\right)}_{\left(3\right)}$	0.767, 0.666
$L_2\left(7\right)$	(${[{21}_2,{14}_3]}_{\left(6\right)}$: GH(2,1)), ${[{28}_3,{21}_4]}_{\left(7\right)}$	0.857, 0.893
$L_2\left(8\right)$	${[{36}_7,{63}_4]}_{\left(5\right)}$: srg	-
$L_2\left(9\right)=A_6$	$GQ(2,2)$, ${(\widehat{T}(6))}_{\left(3\right)}$	0.800
$L_2\left(11\right)$	${\left[{55}_3\right]}_{\left(9\right)}$	-
$L_2\left(19\right)$	${[{37}_6,{171}_2]}_{\left(4\right)}$, ${[{171}_5,{285}_3]}_{\left(15\right)}$, ${[{190}_{108},{5130}_4]}_{\left(16\right)}$	-
$L_2\left(32\right)$	$\widehat{T}{\left(33\right)}_{\left(17\right)}$: srg	0.968
$L_3\left(2\right)=L_2\left(7\right)$	.	.
$L_3\left(3\right)$	${[{144}_{78},{2308}_4]}_{\left(8\right)}$	-
$L_3\left(4\right)$	${[{56}_{10},{280}_2]}_{\left(3\right)}$: srg, Sims-Gewirtz graph	0.911
$L_5\left(2\right)$	${\left[{155}_7\right]}_{\left(3\right)}$: srg, $S(2,3,31)$, lines in $PG(4,2)$	-

As for a relation to physics, we already know that the linear group $L_2\left(4\right)=L_2\left(5\right)=A_5$ is associated with a 3QB pentagram and that $L_2\left(9\right)=A_6$ is associated with 2QB commutation. Then, the group $L_5\left(2\right)$ is associated with $5QB$ contextuality through the lines in $PG(4,2)$. The other configurations in Table 5 lack a physical meaning.

3.3. Symplectic

The symplectic class of simple groups is a very useful one for modeling quantum commutation of multiple qudits. In the previous section, we already met groups $S_4^{\prime }\left(2\right)$ and $S_4\left(3\right)$ associated with two-qubits and two-qutrits, respectively.

3.3.1. The Group $S_4\left(3\right)$

Let us go back to the group $S_4\left(3\right)$, whose finite representation is $H=⟨a,b|a^2=b^5={\left(ab\right)}^9={[a,b]}^3={[a,bab]}^2=1⟩$. Apart from $GQ(3,3)$ associated with two-qutrits, other geometries exist for this group, as shown in Table 6.

Table 6. Characteristics of small index representations of $S_4\left(3\right)$ and their geometry. The bold notation corresponds to geometries that are “stabilized” by the corresponding permutation representation $\mathcal{P}$. The other geometries are only “defined” from the collinearity graph associated with $\mathcal{P}$.

${\mathit{S}}_4\left(3\right)$ Index	$\mathcal{D}$-Signature	Spectrum	Geometry	κ
27	$(7,15,3,2)$	$[{10}^1,1^{20},-5^6]$	${[{27}_5,{45}_3]}_{\left(3\right)}$: GQ(2,4)	0.785
36	$(8,24,4,1)$	$[{15}^1,3^{15},-3^{20}]$	${[{36}_{15},{135}_4]}_{\left(3\right)}$: OA(6,3)	0.833
${40}_b$	$(8,28,6,0)$	$[{12}^1,2^{24},-4^{15}]$	${\left[{40}_4\right]}_{\left(3\right)}$: GQ(3,3)	0.704
${40}_a$	$(8,24,8,1)$	$[{12}^1,2^{24},-4^{15}]$	${\left[{40}_4\right]}_{\left(3\right)}$: GQ(3,3) dual	0.825
45	$(9,29,7,1)$	$[{12}^1,3^{20},-3^{24}]$	${[{45}_3,{27}_5]}_{\left(4\right)}$: GQ(4,2)	0.855

A few remarks are in order. Stricto sensu, only the generalized quadrangles $GQ(2,4)$ and $GQ(3,3)$ are “stabilized” by the corresponding permutation representations $\mathcal{P}$ (and dessins d’enfants $\mathcal{D}$; their signature is given at the second column). The lines of each of the two geometries are defined as having two-stabilizer subgroups acting on the same subsets of points. In a weaker sense, the permutation representation for index 36, ${40}_a$ and 45 “define” the geometries $OA(6,3)$, the dual of $GQ(3,3)$ and $GQ(4,2)$ from the collinearity graph, its srg spectrum (shown at the third column) and the structure of its maximum cliques. In these last cases, not all lines of the geometry have their pair of points corresponding to the same two-stabilizer subgroup. Observe that case ${40}_a$ and case ${40}_b$ are isospectral, but with a distinct $\mathcal{D}$-signature.

3.3.2. The Group $S_6\left(2\right)$

Another group of rich structure is the symplectic group $S_6\left(2\right)$ whose finite representation is $H=⟨a,b|a^2=b^7={\left(ab\right)}^9={\left[a{b}^2\right]}^{12}={[a,b]}^3,{[a,b^2]}^2=1⟩$. The smallest non-trivial permutation representation $\mathcal{P}$ of $S_6\left(2\right)$ stabilizes the symplectic polar space $W_5\left(3\right)$ associated with three-qubits [1]. The small permutation representations of $S_6\left(2\right)$ are shown in Table 7. The one of index 135 is associated with the near quadrangle DQ$(6,2)$ ([28], Chapter 6).

Table 7. Characteristics of small index representations of $S_6\left(2\right)$ and their geometry. The meaning of the bold notation is as in Table 6. The * symbol means that the triangles of the configuration are “stabilized”, but not the full lines.

${\mathit{S}}_6\left(2\right)$	$\mathcal{D}$-Signature	Spectrum	Geometry	κ
63	$(9,47,7,1)$	$[{30}^1,3^{35},-5^{27}]$	${[{63}_{15},{135}_7]}_{\left(3\right)}$: ${\mathcal{G}}_3$, ${\mathbf{W}}_{\mathbf{5}}\left(\mathbf{2}\right)$ *	0.787
120	$(16,60,14,15)$	$[{56}^1,8^{35},-4^{84}]$	${[{\mathbf{120}}_{\mathbf{28}},{\mathbf{1120}}_{\mathbf{3}}]}_{\left(\mathbf{3}\right)}$	0.847
126	$(18,64,14,16)$	$[{64}^1,8^{27},0^{63},-8^{35}]$	${[{126}_{64},{2688}_3]}_{\left(5\right)}$	0.766
135	$(21,75,15,13)$	$[{14}^1,5^{35},-1^{84},-7^{15}]$	${[{135}_7,{315}_3]}_{\left(4\right)}$: DQ(6,2)	0.794
240	$(36,120,28,29)$	$[{126}^1,6^{84},0^{120},-{18}^{35}]$	${[{240}_{17280},{518400}_8]}_{\left(5\right)}$	0.894
315	$(45,195,37,20)$	$[{18}^1,9^{35},3^{84},-3^{195}]$	${[{\mathbf{315}}_{\mathbf{3}},{\mathbf{135}}_{\mathbf{7}}]}_{\left(\mathbf{5}\right)}$ *	0.909
336	$(48,216,40,17)$	$[{20}^1,8^{35},2^{168},-4^{105},-8^{27}]$	${[{\mathbf{336}}_{\mathbf{10}},{\mathbf{1120}}_{\mathbf{3}}]}_{\left(\mathbf{5}\right)}$	0.918
960	$(138,480,114,115)$	$[{56}^1,8^{385},-4^{504},-{16}^{70}]$	${[{960}_{28},{8960}_3]}_{\left(6\right)}$	0.961

3.3.3. The Geometry of Multiple Qudits

We define the multiple qudit Pauli group ${\mathcal{P}}_q(q=p^n)$ as the n-fold tensor product between single p-dit Pauli operators with $\omega =exp\left(\frac{2i\pi }{p}\right)$ and p a prime number. Observables of ${\mathcal{P}}_q/Center\left({\mathcal{P}}_q\right)$ are seen as the elements of the $2n$-dimensional vector space $V(2n,p)$ defined over the field ${\mathbb{F}}_p$. The commutator $[.,.]:V(2n,p)\times V(2n,p)\to {\mathcal{P}}_q^{\prime }$ induces a non-singular alternating bilinear form on $V(2n,p)$ and simultaneously a symplectic form on the projective space $PG(2n-1,p)$ over ${\mathbb{F}}_p$.

The $\left|V(2n,q)\right|=p^{2n}$ observables of ${\mathcal{P}}_q/\mathrm{Center}\left({\mathcal{P}}_q\right)$ are mapped to the points of the symplectic polar space $W_{2n-1}\left(p\right)$ of cardinality $|W_{2n-1}\left(p\right)|=\frac{p^{2n}-1}{p-1}\equiv \sigma (p^{2n-1})$ (where $\sigma (.)$ is the sum of the divisor function of the argument), and two elements of $[{\mathcal{P}}_q/\mathrm{Center}\left({\mathcal{P}}_q\right),\times ]$ commute if and only if the corresponding points of the polar space $W_{2n-1}\left(p\right)$ are collinear [1].

A subspace of $V(2n,p)$ is called totally isotropic if the symplectic form vanishes identically on it. The number of such totally isotropic subspaces/generators $g_e$ (of dimension $p^n-1$) is $\Sigma \left(n\right)={\prod }_{i=1}^n(1+p^i).$ A spread $s_p$ of a vector space is a set of generators partitioning its points. One has $|s_p|=p^n+1$ and $\left|V(2n,p)\right|-1=|s_p|\times |g_e|=(p^n+1)\times (p^n-1)=p^{2n}-1$. A generator $g_e$ corresponds to a maximal commuting set, and a spread $s_p$ corresponds to a maximum (and complete) set of disjoint maximal commuting sets. Two generators in a spread are mutually disjoint, and the corresponding maximal commuting sets are mutually unbiased.

The symplectic polar spaces $W_{2n-1}\left(p\right)$ at work, alias the commutation structure of n p-dits, may be constructed by taking the permutation representation of index $\sigma (p^{2n-1})$ of the symplectic (rank three) group $S_{2n}\left(p\right)$ available in the Atlas. The special cases of two-qubits [with $S_4^{\prime }\left(2\right)$], two-qutrits [with $S_4\left(3\right)$] and three qubits [with $S_6\left(2\right)$] can be found in Table 4, Table 5 and Table 6. For the group $S_6\left(3\right)$, one finds two permutation representations of index 364 and 1120 that are similar to the ones of the same index found for the group $O_7\left(3\right)$ (see Section 2.5, item “Orthogonal” and Table 9) The representation of index 364 corresponds to the commutation structure of three qutrits, and the one of index 1120 is the dual geometry encoding the non-intersection of the 1120 maximum commuting sets of size 26 built with the three-qutrit observables.

The collinearity graph of the polar space $W_{2n-1}\left(p\right)$ is an srg$(a,pb,b-2,b)$, with $a=a\left(n\right)=\sigma (p^{2n-1})$ and $b=b\left(n\right)=\sigma (p^{2n-3})$. The corresponding geometric configuration is of the form $[a{\left(n\right)}_{\Sigma (n-1)},\Sigma {\left(n\right)}_{(p^n-1)/(p-1)}]$.

3.4. Unitary

The unitary class of simple groups is a very rich one. It defines many generalized quadrangles, the hexagons $GH(2,2)$ associated with three-qubit contextuality (as shown in Section 2, Table 3), and two near hexagons, including the largest of “slim dense” near hexagons on 891 points, as shown in Table 8 [28]. Whether such configurations have a physical relevance is unknown at the present time. Since unitary groups play a role as normalizers of Pauli groups, it may be expected that some of these geometries occur in the context of quantum error correction and Clifford groups [3].

Table 8. The non-trivial configuration “stabilized” (bold) or “defined” by unitary groups with their corresponding $\mathcal{D}$ signature. ${}^{†}$ Groups $U_4\left(3\right)$ and $U_6\left(2\right)$ define two large near hexagons of order $(2,14)$ and of order $(2,20)$, respectively; see [28] for details about the notation.

Group	$\mathcal{D}$-Signature	Geometry	κ
$U_3\left(3\right)$	$(8,24,6,0)$	${[{36}_{28},{336}_3]}_{\left(4\right)}$	-
	$(13,39,9,2)$	${\left[{63}_3\right]}_{\left(5\right)}$: GH(2,2)	0.846
	$(15,35,9,3)$	${\left[{63}_3\right]}_{\left(4\right)}$: GH(2,2) dual	0.820
$U_3\left(4\right)$	$(70,112,16,6)$	${[{208}_6,{416}_3]}_{\left(5\right)}$: conf.over ${\mathbb{F}}_{16}$ [32]	0.970
$U_3\left(5\right)$	$(10,20,8,7)$	${[{50}_7,{175}_2]}_{\left(3\right)}$: Hoffman–Singleton	-
$U_3\left(7\right)$	$(703,1075,49,141)$	${[{2107}_{21},{14749}_3]}_{\left(8\right)}$	0.991
$U_4\left(2\right)$	$S_4\left(3\right)$ in Table 6	Table 6: GQ(2,4), GQ(3,3), etc.	-
$U_4\left(3\right)$	$(24,64,16,5)$	${[{112}_{10},{280}_4]}_{\left(3\right)}$: srg, $GQ(3,3^2)$	-
	$(30,90,24,10)$	${[{162}_{280},{15120}_3]}_{\left(3\right)}$: srg	-
	$(101,303,81,42)$	${[{567}_{15},{2835}_3]}_{\left(5\right)}$: NH$(2,14;(2,4\left)\right)$${}^{†}$	-
$U_4\left(4\right)$	$(87,165,17,29)$	${[{325}_{17},{1105}_5]}_{\left(3\right)}$: srg, $GQ(4,4^2)$	-
$U_4\left(5\right)$	$(204,396,84,37)$	${[{756}_{26},{3276}_6]}_{\left(3\right)}$: srg, $GQ(5,5^2)$	-
$U_5\left(2\right)$	$(33,101,15,9)$	${[{165}_9,{297}_5]}_{\left(3\right)}$: srg, $GQ(4,8)$	0.950
	$(36,112,16,7)$	${[{176}_{40},{1408}_5]}_{\left(3\right)}$: srg	0.923
	$(61,153,27,29)$	${[{297}_5,{165}_9]}_{\left(3\right)}$: srg, $GQ(8,4)$	0.953
$U_6\left(2\right)$	$(96,416,62,50)$	${[{672}_{1408},{157696}_6]}_{\left(3\right)}$: srg, $pg(11,15,3)?$	-
	$(99,437,63,48)$	${[{693}_{27},{891}_{21}]}_{\left(3\right)}$: srg, $pg(20,8,5)?$	-
	$(129,459,81,112)$	${[{891}_{21},{6237}_3]}_{\left(4\right)}$: NH$(2,20;4)$${}^{†}$	-

Let us feature the $U_3\left(4\right)$ configuration. One defines the three-dimensional unitary space U over the field ${\mathbb{F}}_{16}$, the projective space $\mathbb{P}\left(U\right)$ and a nondegenerate Hermitian form $(.,.)$ on U. The space $\mathbb{P}\left(U\right)$ consists of 65 isotropic points x satisfying $(x,x)=0$, $x\ne (0,0,0)$ and 208 non-isotropic points satisfying $(x,x)\ne 0$. There exist 416 orthogonal bases, that is triples of mutually orthogonal non-isotropic points. The resulting configuration ${[{208}_6,{416}_3]}_{\left(5\right)}$ has been shown to be related to a $3-(66,16,21)$ design used to construct the Suzuki sporadic group Suz [32] (see also Table 12 below).

In passing, it is noticeable to feature the hyperplane structure of the $U_3\left(4\right)$ configuration. A basic hyperplane is defined from the points of the collinearity graph that are either at minimum or maximal distance from a selected vertex. There are 208 such hyperplanes. The other hyperplanes may be easily built from Velkamp sums $H\oplus H^{\prime }$ of the basic hyperplanes H and $H^{\prime }$, where the set theoretical operation ⊕ means the complement of the symmetric difference $(H\cup H^{\prime })\backslash (H\cap H^{\prime })$ (as in [33]). One finds 10 distinct classes of hyperplanes totaling $2^{16}$ hyperplanes.

3.5. Orthogonal

The geometries carried by orthogonal simple groups of a small index are listed in Table 9. It is noticeable that some representations are associated with the non-intersection of maximum commuting sets for three qubits [from $O_8^{+}\left(2\right):2$)] and three qutrits [from $O_7\left(3\right)$ or $O_8^{+}\left(3\right)$]. These geometries are introduced in [1], Table 2. The srg’s are identified in [29].

Table 9. The non-trivial configuration “defined” by orthogonal groups with their corresponding $\mathcal{D}$ signature. The notation 3QB${}^{\ast }$ (resp. 3QT${}^{\ast }$) means that we are dealing with the geometry associated with the non-intersection of the maximum commuting sets built with the three-qubit (resp. three-qutrit) observables. Several configurations are of type ${\mathcal{G}}_i$. The near hexagon $O_8^{-}\left(2\right)$ on 765 points is described in the text.

Group	$\mathcal{D}$-Signature	Geometry	κ
$O_7\left(3\right)$	$(51,239,27,18)$	${[{351}_{567},{28431}_7]}_{\left(3\right)}$, srg, $N{O}^{-}(7,3)$	-
	$(28,58,24,238)$	${[{364}_{40},{1120}_{13}]}_{\left(3\right)}$, srg, ${\mathcal{G}}_4$, $W_5\left(3\right)$, 3QT	-
	$(54,252,30,22)$	${[{378}_{3159},{199017}_6]}_{\left(3\right)}$, srg, pg$(13,8,4)$?	-
	$(156,540,84,151)$	${[{1080}_{28431},{3838185}_8]}_{\left(3\right)}$, srg, $N{O}^{+}(8,3)$	-
	$(160,560,88,157)$	${[{1120}_{13},{3640}_4]}_{\left(4\right)}$, srg, DQ$(6,3)$, 3QT${}^{\ast }$	-
$O_8^{+}\left(2\right):2$	$(12,92,12,3)$	${[{120}_{28},{1120}_3]}_{\left(3\right)}$, srg, $N{O}^{+}(8,2)$, pg$(7,8,4)$	0.817
	$(15,99,11,6)$	${[{135}_{64},{960}_9]}_{\left(3\right)}$, srg, ${\mathcal{G}}_4$, pg$(8,7,4)$, 3QB${}^{\ast }$	0.770
	$(96,624,72,85)$	${[{960}_{36},{4320}_8]}_{\left(4\right)}$	0.923
$O_8^{-}\left(2\right)$	$(41,63,7,5)$	${[{119}_{45},{765}_7]}_{\left(3\right)}$, $O_8^{-}\left(2\right)$ polar srg, ${\mathcal{G}}_3$, pg$(6,8,3)$?	-
	$(46,72,8,6)$	${[{136}_{135},{2295}_8]}_{\left(3\right)}$, srg, NO${}^{-}(8,2)$	-
	$(267,389,45,33)$	${[{765}_7,{1071}_5]}_{\left(4\right)}$, ${\mathcal{G}}_1$: NH$(4,6)$	-
	$(552,832,96,77)$	${[{1632}_{280},{152320}_3]}_{\left(5\right)}$	-
$O_8^{+}\left(3\right)$	$(216,604,84,89)$	as for $O_7\left(3\right)$, index 1080	-
	$(224,616,88,97)$	as for $O_7\left(3\right)$, index 1120	-
$O_8^{-}\left(3\right)$	$(274,598,26,85)$	${[{1066}_{280},{22960}_{13}]}_{\left(3\right)}$, $O_8^{-}\left(3\right)$ polar srg, ${\mathcal{G}}_4$, pg$(12,27,4)$?	-
$O_{10}^{+}\left(2\right)$	$(38,376,16,34)$	index 496, srg, NO${}^{+}(10,2)$, pg$(15,16,8)$	0.836
	$(45,391,15,39)$	index 527, srg, pg$(16,15,8)$	0.759
	$(135,1335,117,355)$	index 2295, rank 3, 4QB${}^{\ast }$	-
$O_{10}^{-}\left(2\right)$	$(99,303,15,40)$	${[{495}_{765},{25245}_{15}]}_{\left(3\right)}$, $O_{10}^{-}\left(2\right)$ polar srg, ${\mathcal{G}}_7$, pg$(14,16,7)$	-
	$(108,336,16,35)$	${[{528}_{2295},{75735}_{16}]}_{\left(3\right)}$, srg, ${\mathcal{G}}_8$, NO${}^{-}(10,2)$	-

Several of the configurations arising from simple orthogonal groups are of type ${\mathcal{G}}_i$, for some $i\ge 1$. This includes the configurations attached to polar (strongly regular) graphs of $O_8^{-}\left(2\right)$ (on 119 points), $O_8^{-}\left(3\right)$ (on 1066 points) and $O_{10}^{-}\left(2\right)$ (on 495 points).

The Near Hexagon $O_8^{-}\left(2\right)$

There exists a near polygon (thus of type ${\mathcal{G}}_1$) built from $O_8^{-}\left(2\right)$ (on 765 points) that seems to have been unnoticed. The configuration is of the type ${[{765}_7,{1071}_5]}_{\left(4\right)}$ with a collinearity graph of spectrum $[{28}^1,{11}^{84},1^{476},-7^{204}]$ and an incidence graph of diameter six and girth eight corresponding to a near hexagon of order $(4,6)$. Since the permutation representation is a subgroup of the modular group $\mathsf{\Gamma }=PSL(2,\mathbb{Z})$, it is possible to see the dessin $\mathcal{D}$ as an hyperbolic polygon ${\mathcal{D}}^H$. As in [11,13], the genus g of $\mathbb{D}$ equals that of the hyperbolic polygon ${\mathcal{D}}^H$; a face of $\mathbb{D}$ corresponds to a cusp of ${\mathcal{D}}^H$; the number of black points (resp. of white points) of $\mathbb{D}$ is $B=f+{\nu }_3-1$ (resp. $W=n+2-2g-B-c$), where f is the number of fractions; c is the number of cusps; ${\nu }_2$ and ${\nu }_3$ are the number of elliptic points of order two and three of ${\mathcal{D}}^H$, respectively. In the present case, the polygon ${\mathcal{D}}^H$ is associated with a non-congruence subgroup of level 17 of Γ and $(n,g,{\nu }_2,{\nu }_3,c,f)=(765,33,13,18,45,250)$. A schematic of ${\mathcal{D}}^H$ is shown in Figure 4.

Figure 4. A schematic of the hyperbolic polygon on 765 tiles corresponding to the near polygon arising from the permutation group of $O_8^{-}\left(2\right)$. Pairs of edges of the same color have to be identified. The drawing is performed by using the software Sage that allows one to visualize (in the hyperbolic half-plane) the permutation representation of a subgroup of $PSL(2,\mathbb{Z})$ ([13], p. 752).

3.6. Exceptional

A few exceptional groups of low index and low rank are defining well-known generalized polygons GH$(2,2)$ and its dual, GH$(4,4)$ and its dual, GH$(2,8)$, the Ree–Tits octagon GO$(2,4)$, as well as two extra ${\mathcal{G}}_1$ geometries [coming from Sz$\left(8\right)$]. This is summarized in Table 10.

Table 10. Small non-trivial configurations “defined” by exceptional groups of the Lie type. The most remarkable configurations are generalized hexagons, their duals and generalized octagon GO$(2,4)$.

Group	$\mathcal{D}$-Signature	Geometry	κ
$G_2{\left(2\right)}^{\prime }$	$U_3\left(3\right)$ in Table 8	srg, $\left[{63}_3\right]$; GH$(2,2)$, GH$(2,2)$ dual	0.846, 0.820
$G_2\left(4\right)$	$(88,224,32,37)$	${[{416}_{8400},{698830}_5]}_{\left(3\right)}$: srg, part of Suz graph	-
	$(273,725,105,132)$	${\left[{1365}_5\right]}_{\left(4\right)}$: GH$(4,4)$	-
	$(277,693,105,146)$	${\left[{1365}_5\right]}_{\left(4\right)}$: GH$(4,4)$ dual	-
${}^2{F}_4{\left(2\right)}^{\prime }$	$(585,923,135,57)$	${[{1755}_5,{2925}_3]}_{\left(5\right)}$: GO$(2,4)$ (Ree–Tits)	0.988
Sz$\left(8\right)$	(146,288,112,8)	${[{560}_{13},{1820}_4]}_{\left(17\right)}$	0.971
	(370,736,292,30)	${[{1456}_5,{1820}_4]}_{\left(79\right)}$	0.980
$3D_4\left(2\right)$	(95,419,63,122)	${[{819}_9,{2457}_3]}_{\left(4\right)}$: GH$(2,8)$	-

3.7. Sporadic

Finally, small index representations of small sporadic groups lead to geometries of various types. The results are split into three tables: configurations arising from Mathieu groups in Table 11, from Leech lattice groups in Table 12 and the remaining ones—small sections of the Monster group and pariahs—in Table 13. Noticeable geometries arising from sporadic groups are the $M_{24}$ near hexagon $NH(2,14)$ on 759 points, the $J_2$ near octagon $NO(2,4)$ on 315 points and Tits generalized octagon $GO(2,4)$ on 1755 points. Another remarkable geometry is the one built from the McLgraph on 275 points, which is found to be of type ${\mathcal{G}}_2$; see also https://www.win.tue.nl/∼aeb/graphs/McL.html for details about the McL graph.

Table 11. Small non-trivial configurations “defined” by Mathieu groups. A noticeable geometry is the $M_{24}$ near hexagon on 759 points.

Group	$\mathcal{D}$-Signature	Geometry	κ
$M_{11}$	$(17,31,5,2)$	${[{55}_9,{165}_3]}_{\left(3\right)}$: srg, $T\left(11\right)$	-
	$(20,38,6,2)$	${[{66}_{15},{495}_2]}_{\left(4\right)}$	-
	$(45,89,15,9)$	${[{165}_4,{220}_3]}_{\left(8\right)}$	-
$M_{12}$	$(22,38,6,1)$	srg, ${[{66}_{10},{220}_3]}_{\left(3\right)}$: $T\left(12\right)$	-
$M_{22}$	$(25,45,7,1)$	srg, ${[{77}_{16},{616}_2]}_{\left(3\right)}$: srg, $S(3,6,22)$	0.891
	$(48,96,16,9)$	${[{176}_{210},{9320}_4]}_{\left(3\right)}$: srg, $S(4,7,23)\setminus S(3,6,22)$ [29]	0.953
	$(65,127,21,10)$	${[{231}_{10},{330}_7]}_{\left(4\right)}$: srg, $M_{22}$ graph [29]	0.955
	$(92,178,30,16)$	${[{330}_{77},{1155}_2]}_{\left(5\right)}$	0.961
	$(162,320,56,40)$	${[{616}_2,{77}_{16}]}_{\left(5\right)}$	0.973
$M_{23}$	$(73,141,11,15)$	${[{253}_{21},{1771}_3]}_{\left(3\right)}$: srg, $T\left(23\right)$	0.971
	$(140,274,22,36)$	${[{506}_{15},{3795}_2]}_{\left(4\right)}$	0.984
	$(338,672,56,112)$	${[{1288}_{165},{106260}_2]}_{\left(4\right)}$	0.993
	$(469,931,77,148)$	${[{1771}_{20},{17710}_2]}_{\left(8\right)}$	0.992
$M_{24}$	$(102,144,12,10)$	${[{276}_{22},{2024}_3]}_{\left(3\right)}$: srg, $T\left(24\right)$	0.972
	$(267,387,33,37)$	${[{759}_{15},{3795}_3]}_{\left(4\right)}$: NH$(2,14;2)$	0.990
	$(436,668,56,65$)	index 1288: srg, pg$(22,35,14)?$	0.994

Table 12. Small non-trivial configurations “defined” by Leech lattice groups. Noticeable geometries are the $J_2$ near octagon on 315 points and the Co${}_2$ geometry that is locally the $U_6\left(2\right)$ near hexagon. Another remarkable configuration of type ${\mathcal{G}}_2$ is attached to the permutation representation on 275 points of the McLgroup.

Group	$\mathcal{D}$-Signature	Geometry	κ
HS	$(20,60,10,6)$	${[{100}_{22},{1100}_2]}_{\left(3\right)}$: srg	0.903
	$(220,580,100,101)$	${[{1100}_2,{10}_{22}]}_{\left(5\right)}$	-
$J_2$	$(36,50,16,0)$	${[{100}_{336},{8400}_4]}_{\left(3\right)}$: srg, Hall–Janko graph	0.930
	$(196,146,40,0)$	${[{280}_{12},{840}_4]}_{\left(4\right)}$: srg	-
	$(105,165,45,1)$	${[{315}_5,{525}_3]}_{\left(6\right)}$: NO$(2,4)$ [34]	-
	$(179,265,75,4)$	${[{525}_3,{315}_5]}_{\left(6\right)}$	-
	$(286,428,120,4)$	${[{840}_5,{1050}_4]}_{\left(7\right)}$	-
	$(336,522,144,4)$	${[{1008}_6,{2016}_3]}_{\left(11\right)}$	-
	$(604,910,258,15)$	${[{1800}_{70},{42000}_3]}_{\left(18\right)}$	-
Co${}_2$	$(460,1292,96,227)$	srg$(2300,891,378,324)$ [35]	0.992
McL	$(55,155,25,21)$	${[{275}_{280},{15400}_5]}_{\left(3\right)}$: srg, ${\mathcal{G}}_2$ [36]	0.974
	$(405,1065,185,186)$	${[{2025}_{1155},{779625}_3]}_{\left(4\right)}$	-
Suz	$(594,912,138,70)$	${[{1782}_{1365},{405405}_6]}_{\left(3\right)}$: srg [32,37]	-

Table 13. Non-trivial configurations “defined” by small sections of the Monster group, the Pariah groups $J_1$ and $Ru$ and Tits group T.

Group	$\mathcal{D}$-Signature	Geometry	κ
He	$(294,1106,122,269)$	${[{2058}_{4896},{3358656}_3]}_{\left(5\right)}$	0.984
Fi${}_{22}$	$(270,2102,320,410)$	${[{3510}_{891},{142155}_{22}]}_{\left(3\right)}$: srg	0.997
Fi${}_{23}$	$(10575,16183,1163,1876)$	srg, index 31671	-
Fi${}_{24}^{\prime }$	$(102312,155224,10584,19409)$	srg, index 306936	-
$J_1$	$(92,138,38,0)$	${[{266}_{11},{1463}_2]}_{\left(5\right)}$: Livingstone graph	-
	$(355,525,151,8)$	${[{1045}_8,{4180}_2]}_{\left(11\right)}$	-
	$(491,747,209,9)$	${[{1463}_6,{2926}_3]}_{\left(22\right)}$	-
	$(780,520,220,11)$	${[{1540}_{19},{14630}_2]}_{\left(21\right)}$	-
	$(532,804,228,17)$	${[{1596}_{11},{8778}_2]}_{\left(19\right)}$	-
Ru	$(1054,2030,316,331)$	srg, index 4060	-
T=${}^2{F}_4{\left(2\right)}^{\prime }$	$(585,923,135,57)$	${[{1755}_5,{2925}_3]}_{\left(5\right)}$: GO$(2,4)$ [26]	0.988
	$(774,1152,180,100)$	${[{2304}_{26},{14976}_4]}_{\left(7\right)}$	0.988

This closes our investigation between simple groups and finite geometries. The contextuality parameter κ, when it is known, is the highest (exceeding $0.97$) for graphs associated with standard representations of $L_2\left(32\right)$, $U_3\left(4\right)$, $U_3\left(7\right)$, exceptional groups $2F_4^{\prime }\left(2\right)$ and $Sz\left(8\right)$ and sporadic groups, such $M_{23}$, $M_{24}$, $C{o}_2$, $McL$, $He$, $F{i}_{22}$, T, etc.

4. Conclusions

We explored two-generator permutation representations of simple groups, as listed in the Atlas [9], with the viewpoint of Grothendieck’s dessins d’enfants and the finite geometries associated with them, as started in our earlier work. A strong motivation for this work is the understanding of commutation structures in quantum information and their contextuality [10,11,12,13,30,31]. A wealth of known and new point-line configurations $\mathcal{G}$ and, as much as possible, their contextuality parameter κ are defined from permutation representations $\mathcal{P}$ and their corresponding dessin $\mathcal{D}$, using the methodology described in Section 2. It is intriguing that the concept of a near polygon, defined in Section 2.3, may be usefully expanded to that of a geometry of type ${\mathcal{G}}_i$ ($i>1$) to qualify some of the new configurations we found. Looking at the unitary groups of Table 8, one observes that most configurations we obtained are of the near polygon type (that is of type ${\mathcal{G}}_1$) or have a strongly regular collinearity graph. However, we do not know how to unify both aspects. To some extent, orthogonal simple groups, as well as exceptional groups of the Lie type, have this common feature (as shown in Table 9 and Table 10, respectively).

It is much more involved to recognize the regularities of geometries defined from (small) sporadic groups (see Table 11, Table 12 and Table 13). Many sporadic groups (including the Monster) are subgroups of the modular group or even of the Hurwitz group $G=⟨a,b|a^2=b^3={\left(ab\right)}^7⟩$ [38]. It is a challenging question to relate the symmetric genus of such structures to the (much smaller) genus of the corresponding dessin d’enfant (and modular polygon) [13]. Our down-to-earth approach of understanding quantum commutation and contextuality from representations of some simple groups is of course far from the concept of a VOA (vertex operator algebra), which is related to string theory and generalized moonshine [39]. Let us mention F. J.Dyson again: So far as we know, the physical universe would look and function just as it does whether or not the sporadic groups existed. But we should not be too sure that there is no connection ⋯ We have strong evidence that the creator of the universe loves symmetry, and if he loves symmetry, what lovelier symmetry could he find than the symmetry of the Monster? [40].