Data Clustering with Quantum Mechanics
Abstract
:1. Introduction
- (1)
- Assume in advance the number of clusters;
- (2)
- Generate random seeds;
- (3)
- Assume at least one seed “hits” every cluster;
- (4)
- Clusters “grow” in the neighborhood of each seed;
- (5)
- Cluster regions grow until saturation.
2. Methods
2.1. Theoretical Background
2.1.1. Preliminaries: Definitions of Metrics
2.1.2. Spectral Clustering: Meila–Shi Algorithm
- Let and be vectors defined by and where is given by Equation (4):
- and are diagonal matrices.
- The matrices and are related to each other by a similarity transformation according to:
2.1.3. Quantum Clustering
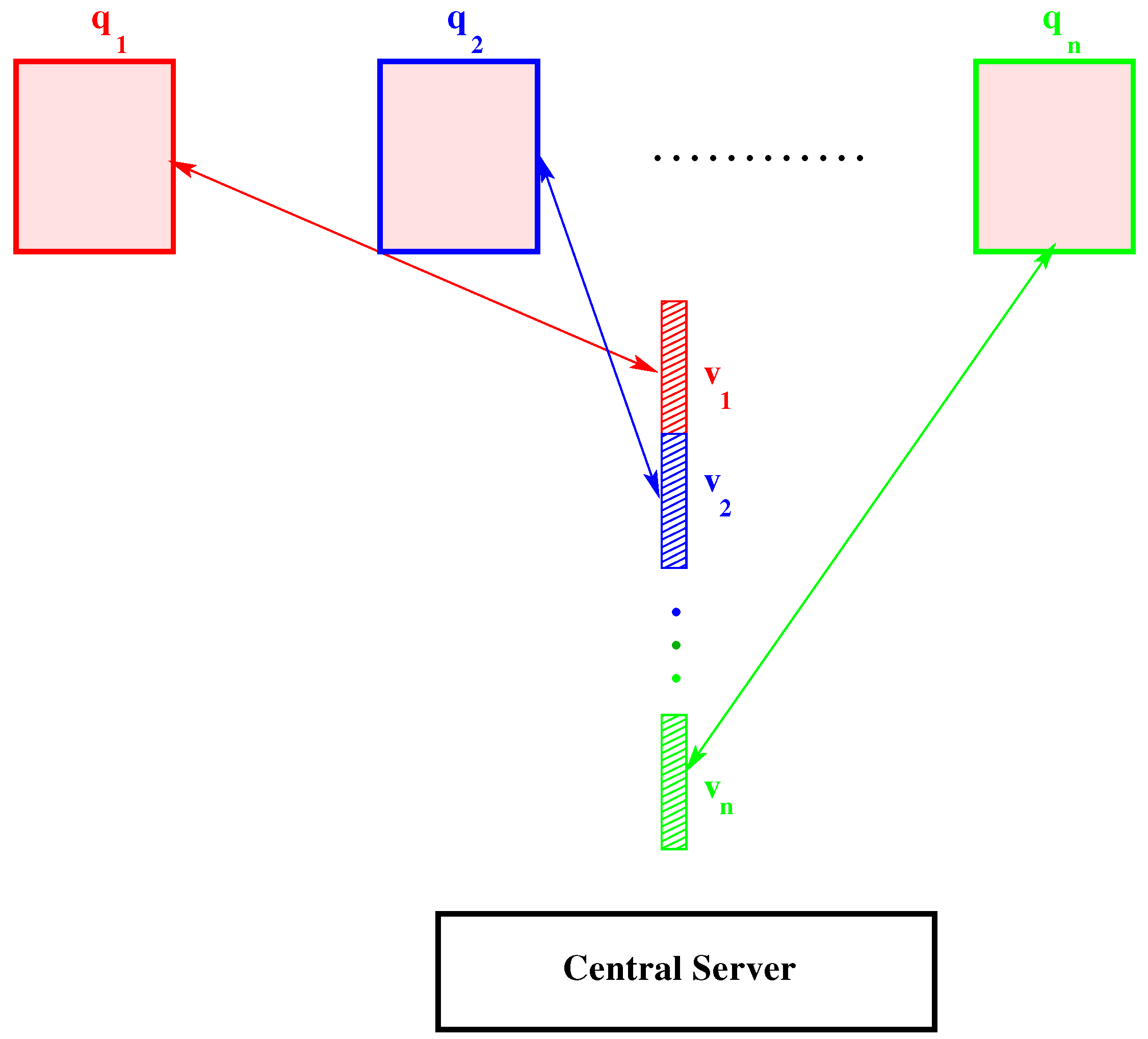
2.2. Computational Aspects
2.2.1. Dimensional Reduction
- SVD:
- For a matrix, the complexity of a full SVD is (this is quoted more often in its “optimized” version as , e.g., see [30], which has a lower complexity for thinner SVDs), and K is expected to be very large for text data, easily the size of a thesaurus of a hundred thousand words. The complexity is roughly cubic in behavior when (note that we rarely need, e.g., in Equation (12) for clustering only the vectors and the eigenvalues , unless we desire to reconstitute ; in this respect, the SVD is overkill).
- Meila–Shi:
- For various cases, the complexity for getting the eigenvalues of the matrix is:where c is the product cost (cost of a scalar multiplication plus a scalar addition).
- Returning to the standard SVD on as defined in Equation (12), we define a symmetric matrix from the non-symmetric matrix as:The eigenvectors of have the form ([36] (p. 3)):where will contain the leading eigenvectors (equal to ) of the matrix . is then subjected to the eigenpair solver. The above also applies for the eigenpairs of , since we have established the connection between , , and in Equations (11) and (12) in Section 2.1.2 on the Meila–Shi algorithm. The eigenvalues of (which are the same as those for ) are the square root of the eigenvalues of , normalized so that the first (or zeroth eigenvalue) is unity. We call this the “B method”, as tabulated in Table 1.
- Since it is the eigenpairs of Λ that we want, the matrix-vector multiplication routine is done in two steps:where is a temporary vector. This two-step process performs . We call this the “ method” as also tabulated it in Table 1.
2.2.2. Finding the Minima of Quantum Potential
3. Results
3.1. Examples
3.1.1. K-Means vs. Quantum Clustering
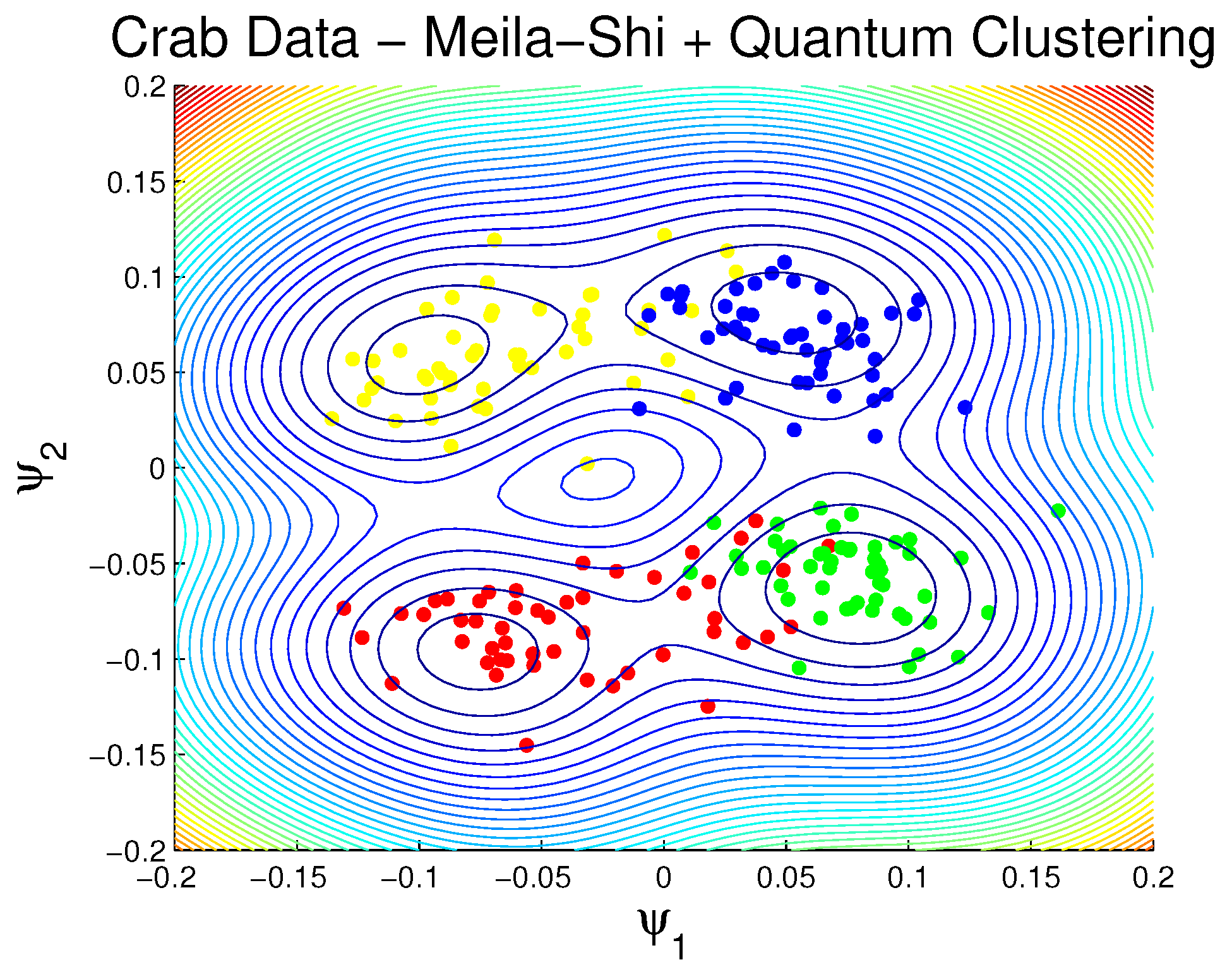
3.1.2. Rock Crabs
3.1.3. Finding Clues of a Disease
- (1)
- stress is associated with migraines;
- (2)
- stress can lead to loss of magnesium;
- (3)
- calcium channel blockers prevent some migraines;
- (4)
- magnesium is a natural calcium channel blocker;
- (5)
- Spreading Cortical Depression (SCD) is implicated in some migraines;
- (6)
- high levels of magnesium inhibit SCD;
- (7)
- migraine patients have high platelet aggregability;
- (8)
- magnesium can suppress platelet aggregability.
- (1)
- Documents 5 and 6: high levels of magnesium inhibit spreading cortical depression (SCD), which is implicated in some migraines.
- (2)
- Documents 3 and 4: magnesium is a natural calcium channel blocker that prevents some migraines.
- (3)
- Documents 1, 2, 7 and 8:
- (a)
- tress is associated with migraines and can lead to loss of magnesium.
- (b)
- migraine patients have high platelet aggregability, which can be suppressed by magnesium.
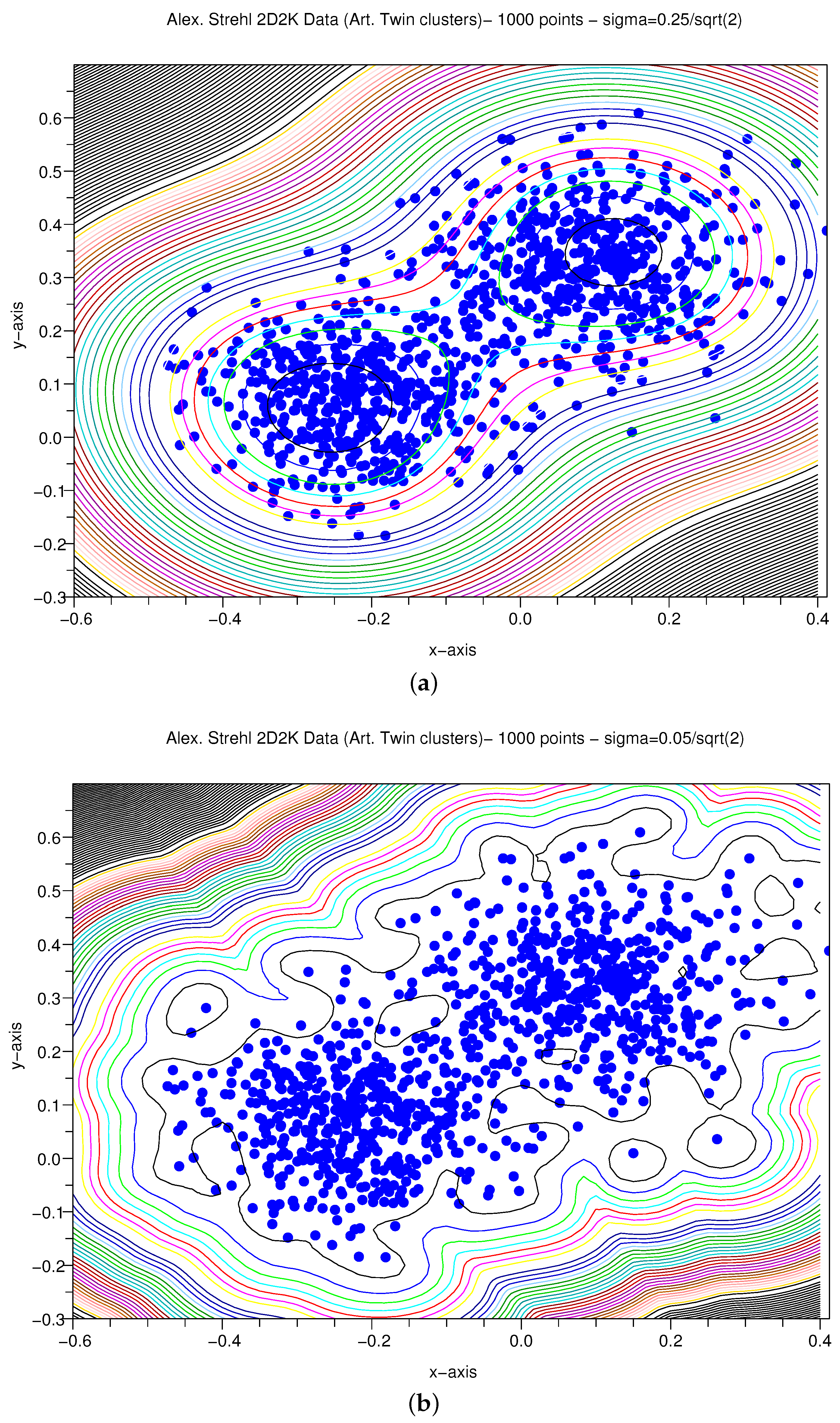
3.1.4. Artificial X–Y Pairs with Gaussian Variance
3.1.5. Engineering Data Demo
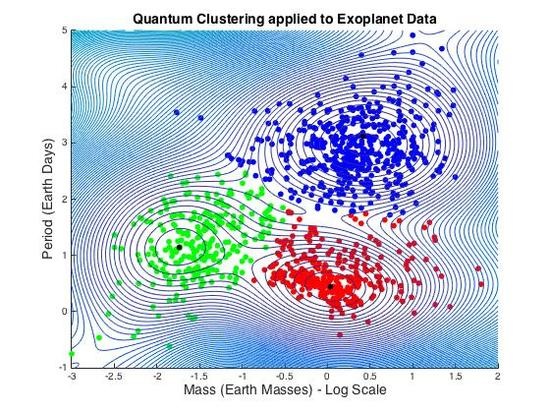
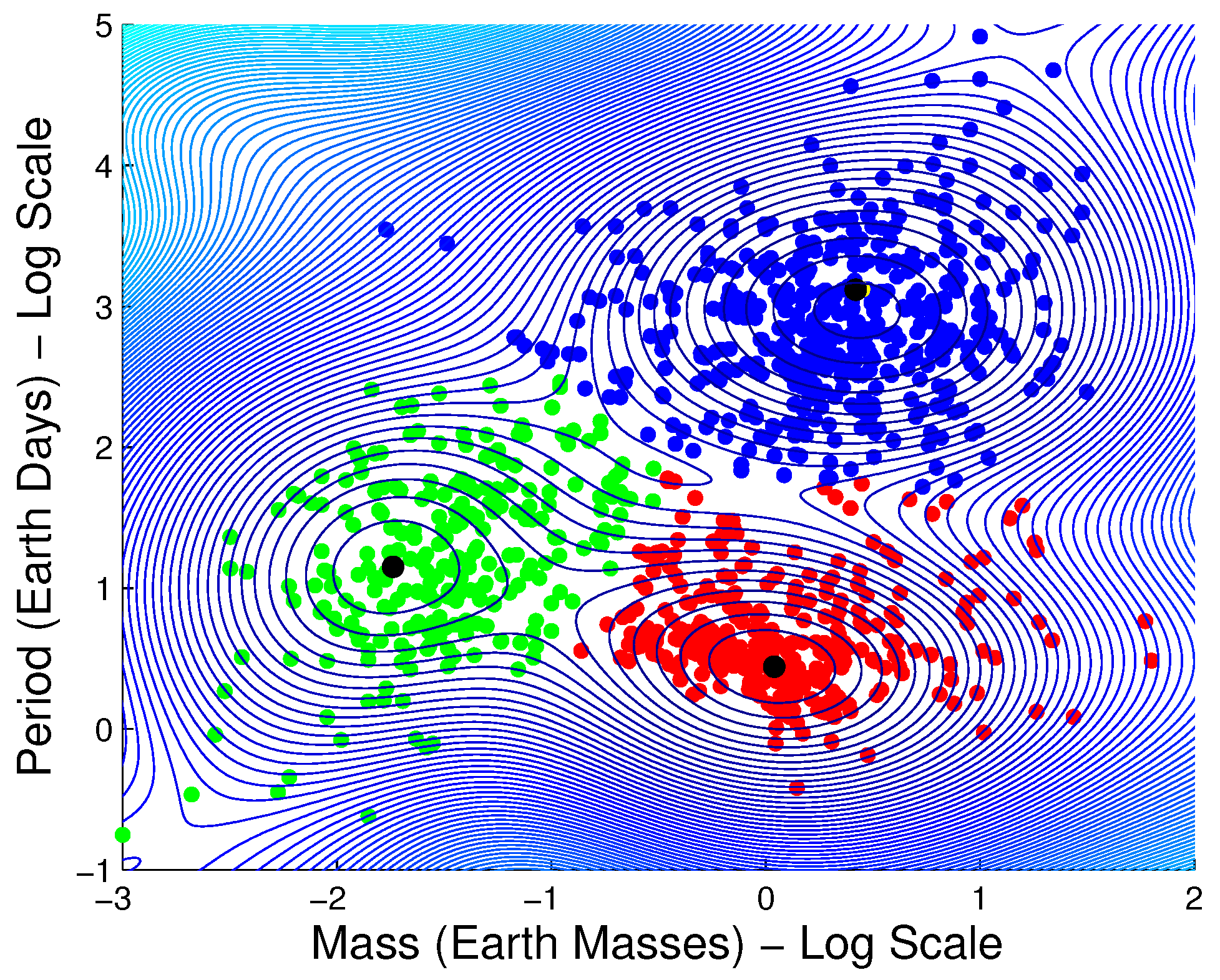
3.1.6. Exoplanet Data
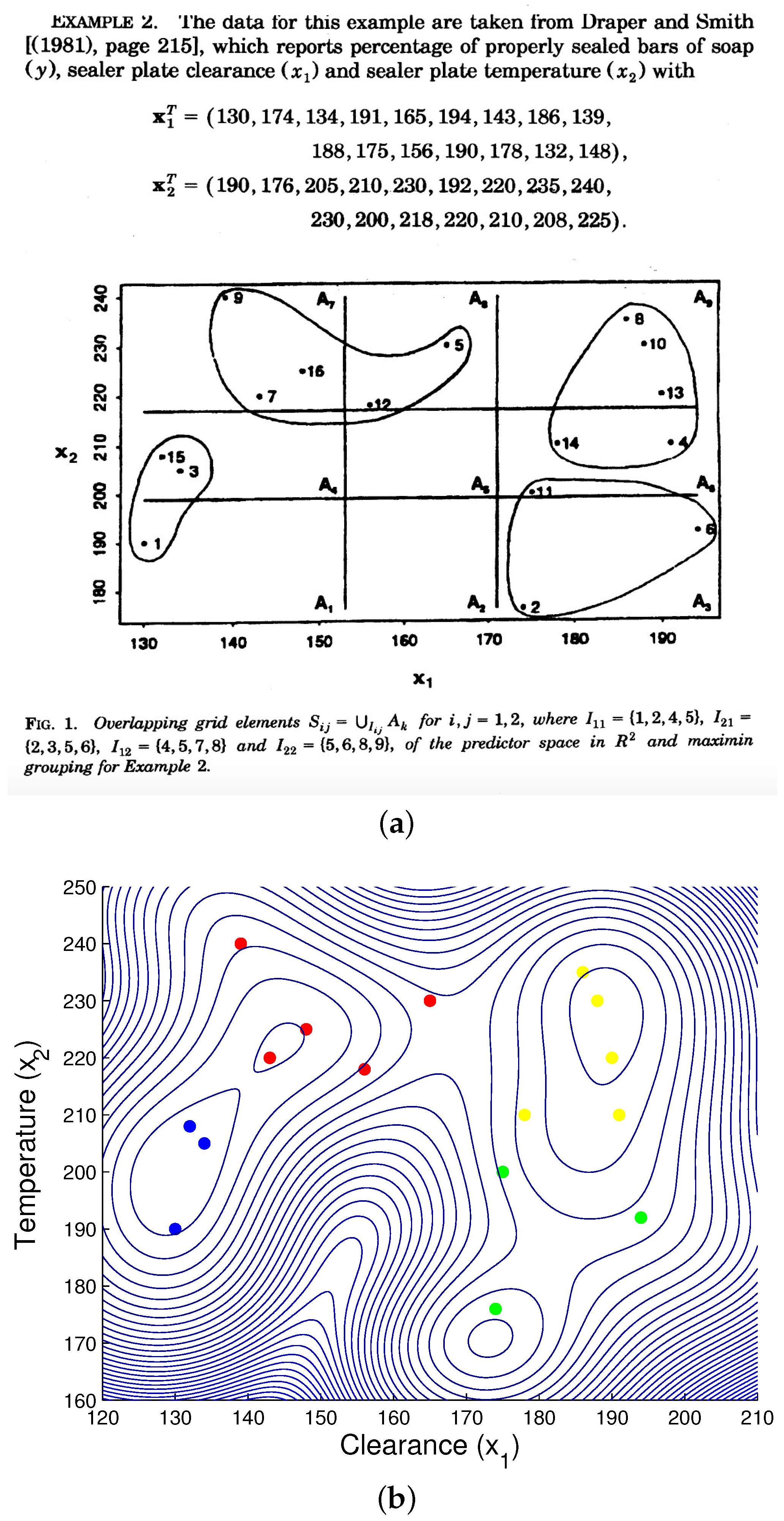
3.2. PRIMME Test Cases of the Meila–Shi algorithm
- Reuters:
- 2742 articles from Reuters, 21,578 test set.
- Enron:
- 55,365 email documents, 121,415 distinct terms, sparse data matrix of eight million non-zero entries (density is ).
- user60784:
- documents from website search on a particular person.
- Bill mark:
- test case for web-search on keywords “bill mark” [53].
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lloyd, S.P. Least squares quantization in PCM. IEEE Trans. Inform. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Huang, M.; Yu, L.; Chen, Y. Improved K-Means Clustering Center Selecting Algorithm. In Information Engineering and Applications, Proceedings of the International Conference on Information Engineering and Applications (IEA 2011), Chongqing, China, 21–24 October 2011; Zhu, R., Ma, Y., Eds.; Springer: London, UK, 2012; pp. 373–379. [Google Scholar]
- Girisan, E.; Thomas, N.A. An Efficient Cluster Centroid Initialization Method for K-Means Clustering. Autom. Auton. Syst. 2012, 4, 1. [Google Scholar]
- Dunn, J.C. A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters. J. Cybernet. 1973, 3, 32–57. [Google Scholar] [CrossRef]
- Brillouin, L. Science and Information Theory; Academic Press: Dover, UK, 1956. [Google Scholar]
- Georgescu-Roegencholas, N. The Entropy Law and the Economic Process; Harvard University Press: Cambridge, MA, USA, 1971. [Google Scholar]
- Chen, J. The Physical Foundation of Economics—An Analytical Thermodynamic Theory; World Scientific: London, UK, 2005. [Google Scholar]
- Lin, S.K. Diversity and Entropy. Entropy 1999, 1, 101–104. [Google Scholar] [CrossRef]
- Buhmann, J.M.; Hofmann, T. A Maximum Entropy Approach to Pairwise Data Clustering. In Conference A: Computer Vision & Image Processing, Proceedings of the 12th IAPR International Conference on Pattern Recognition, Jerusalem, Israel, 9–13 October 1994; IEEE Computer Society Press: Hebrew University, Jerusalem, Israel, 1994; Volume II, pp. 207–212. [Google Scholar]
- Hofmann, T.; Buhmann, J.M. Pairwise Data Clustering by Deterministic Annealing. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 1–14. [Google Scholar] [CrossRef]
- Zhu, S.; Ji, X.; Xu, W.; Gong, Y. Multi-labelled Classification Using Maximum Entropy Method. In Proceedings of the 28th Annual International ACM SIGIR Conference on Research and Development in Information (SIGIR’05), Salvador, Brazil, 15–19 August 2005; pp. 207–212.
- Coifman, R.R.; Lafon, S.; Lee, A.B.; Maggioni, M.; Nadler, B.; Warner, F.; Zucker, S. Geometric Diffusions as a Tool for Harmonic Analysis and Structure Definition of Data: Diffusion Maps. Proc. Natl. Acad. Sci. USA 2005, 102, 7426–7431. [Google Scholar] [CrossRef] [PubMed]
- Meila, M.; Shi, J. Learning Segmentation by Random Walks. Neural Inform. Process. Syst. 2001, 13, 873–879. [Google Scholar]
- Markov Chains. Applied Probability and Queues; Springer: New York, NY, USA, 2003; pp. 3–38. [Google Scholar]
- Hammond, B.L.; Lester, W.A.; Reynolds, P.J. EBSCOhost. In Monte Carlo Methods in Ab Initio Quantum Chemistry; World Scientific: Singapore; River Edge, NJ, USA, 1994; pp. 287–304. [Google Scholar]
- Lüchow, A. Quantum Monte Carlo methods. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 388–402. [Google Scholar] [CrossRef]
- Park, J.L. The concept of transition in quantum mechanics. Found. Phys. 1970, 1, 23–33. [Google Scholar] [CrossRef]
- Louck, J.D. Doubly stochastic matrices in quantum mechanics. Found. Phys. 1997, 27, 1085–1104. [Google Scholar] [CrossRef]
- Lafon, S.; Lee, A.B. Diffusion maps and coarse-graining: a unified framework for dimensionality reduction, graph partitioning, and data set parameterization. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1393–1403. [Google Scholar] [CrossRef] [PubMed]
- Nadler, B.; Lafon, S.; Coifman, R.R.; Kevrekidis, I.G. Diffusion maps, spectral clustering and eigenfunctions of fokker-planck operators. In Advances in Neural Information Processing Systems 18; MIT Press: Cambridge, MA, USA, 2005; pp. 955–962. [Google Scholar]
- Bogolyubov, N., Jr.; Sankovich, D.P. N. N. Bogolyubov and Statistical Mechanics. Russ. Math. Surv. 1994, 49, 19. [Google Scholar]
- Brics, M.; Kaupuzs, J.; Mahnke, R. How to solve Fokker-Planck equation treating mixed eigenvalue spectrum? Condens. Matter Phys. 2013, 16, 13002. [Google Scholar] [CrossRef]
- Lüchow, A.; Scott, T.C. Nodal structure of Schrüdinger wavefunction: General results and specific models. J. Phys. B: At. Mol. Opt. Phys. 2007, 40, 851. [Google Scholar] [CrossRef]
- Lüchow, A.; Petz, R.; Scott, T.C. Direct optimization of nodal hypersurfaces in approximate wave functions. J. Chem. Phys. 2007, 126, 144110. [Google Scholar] [CrossRef] [PubMed]
- Cheng, D.; Vempala, S.; Kannan, R.; Wang, G. A Divide-and-merge Methodology for Clustering. In Proceedings of the Twenty-fourth ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems (PODS ’05), Baltimore, MD, USA, 13–17 June 2015; ACM: New York, NY, USA, 2005; pp. 196–205. [Google Scholar]
- Golub, G.H.; Van Loan, C.F. Matrix Computations. In Johns Hopkins Studies in the Mathematical Sciences; The Johns Hopkins University Press: Baltimore, MD, USA; London, UK, 1996. [Google Scholar]
- Horn, D.; Gottlieb, A. Algorithm for data clustering in pattern recognition problems based on quantum mechanics. Phys. Rev. Lett. 2002, 88, 18702. [Google Scholar]
- COMPACT Software Package. Available online: http://adios.tau.ac.il/compact/ (accessed on 3 January 2017).
- Jones, M.; Marron, J.; Sheather, S. A brief survey of bandwidth selection for density estimation. J. Am. Stat. Assoc. 1996, 91, 401–407. [Google Scholar] [CrossRef]
- Brand, M. Fast low-rank modifications of the thin singular value decomposition. Linear Algebra Appl. 2006, 415, 20–30. [Google Scholar] [CrossRef]
- Sleipjen, G.L.G.; van der Vorst, H.A. A Jacobi-Davidson iteration method for linear eigenvalue problems. SIAM J. Matrix Anal. Appl. 1996, 17, 401–425. [Google Scholar]
- Steffen, B. Subspace Methods for Large Sparse Interior Eigenvalue Problems. Int. J. Differ. Equ. Appl. 2001, 3, 339–351. [Google Scholar]
- Voss, H. A Jacobi–Davidson Method for Nonlinear Eigenproblems. In Proceedings of the 4th International Conference on Computational Science (ICCS 2004), Kraków, Poland, 6–9 June 2004; Bubak, M., van Albada, G.D., Sloot, P.M.A., Dongarra, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 34–41. [Google Scholar]
- Stathopoulos, A. PReconditioned Iterative MultiMethod Eigensolver. Available online: http://www.cs.wm.edu/~andreas/software/ (accessed on 3 January 2017).
- Stathopoulos, A.; McCombs, J.R. PRIMME: Preconditioned Iterative Multimethod Eigensolver—Methods and Software Description. ACM Trans. Math. Softw. 2010, 37, 1–29. [Google Scholar] [CrossRef]
- Larsen, R.M. Computing the SVD for Large and Sparse Matrices, SCCM & SOI-MDI. 2000. Available online: http://sun.stanford.edu/~rmunk/PROPACK/talk.pdf (accessed on 3 January 2017).
- Chen, W.Y.; Song, Y.; Bai, H.; Lin, C.J.; Chang, E.Y. Parallel Spectral Clustering in Distributed Systems. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 568–586. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Estrada, T.; Cicotti, P.; Taufer, M. On Efficiently Capturing Scientific Properties in Distributed Big Data without Moving the Data: A Case Study in Distributed Structural Biology using MapReduce. In Proceedings of the 16th IEEE International Conferences on Computational Science and Engineering (CSE), Sydney, Australia, 3–5 December 2013; Available online: http://mapreduce.sandia.gov/ (accessed on 3 January 2017).
- Ripley, B. Pattern Recognition and Neural Networks; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Ripley, B. CRAB DATA, 1996. Available online: http://www.stats.ox.ac.uk/pub/PRNN/ (accessed on 3 January 2017).
- Jaccard, P. Etude comparative de la distribution florale dans une portion des Alpes et des Jura. Bull. Soc. Vaud. Sci. Nat. 1901, 37, 547–579. [Google Scholar]
- Hearst, M. Untangling Text Data Mining, 1999. Available online: http://www.ischool.berkeley.edu/~hearst/papers/acl99/acl99-tdm.html (accessed on 3 January 2017).
- Wang, S. Thematic Clustering and the Dual Representations of Text Objects; Sherman Visual Lab. Available online: http://shermanlab.com/science/CS/IR/ThemCluster.pdf (accessed on 2 January 2017).
- Wang, S.; Dignan, T.G. Thematic Clustering. U.S. Patent 888,665,1 B1, 11 November 2014. [Google Scholar]
- Strehl, A. strehl.com. Available online: http://strehl.com/ (accessed on 3 January 2017).
- Ben-Hur, A.; Horn, D.; Siegelmann, H.T.; Vapnik, V. Support Vector Clustering. J. Mach. Learn. Res. 2002, 2, 125–137. [Google Scholar] [CrossRef]
- Dietterich, T.G.; Ghahramani, Z. (Eds.) The Method of Quantum Clustering. In Advances in Neural Information Processes; MIT Press: Cambridge, MA, USA, 2002.
- Draper, N.; Smith, H. Applied Regression Analysis, 2nd ed.; Wiley: New York, NY, USA, 1981. [Google Scholar]
- Miller, F.R.; Neill, J.W.; Sherfey, B.W. Maximin Clusters from near-replicate Regression of Fit Tests. Ann. Stat. 1998, 26, 1411–1433. [Google Scholar]
- Expoplanet.eu—Extrasolar Planets Encyclopedia. Exoplanet Team, Retrieved 16 November 2015. Available online: http://exoplanet.eu/ (accessed on 2 January 2017).
- Yaqoob, T. Exoplanets and Alien Solar Systems; New Earth Labs (Education and Outreach): Baltimore, MD, USA, 16 November 2011. [Google Scholar]
- Fertik, M.; Scott, T.; Dignan, T. Identifying Information Related to a Particular Entity from Electronic Sources, Using Dimensional Reduction and Quantum Clustering. U.S. Patent 8,744,197, 3 June 2014. [Google Scholar]
- Bekkerman, R.; McCallum, A. Disambiguating Web Appearances of People in a Social Network. 2005. Available online: https://works.bepress.com/andrew_mccallum/47/ (accessed on 3 January 2017).
- Zeimpekis, D.; Gallopoulos, E. TMG: A MATLAB Toolbox for Generating Term-Document Matrices from Text Collections. 2005. Available online: http://link.springer.com/chapter/10.1007%2F3-540-28349-8_7 (accessed on 3 January 2017).
- Ding, J.; Zhou, A. Eigenvalues of rank-one updated matrices with some applications. Appl. Math. Lett. 2007, 20, 1223–1226. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian-09 Revision E.01, Gaussian Inc.: Wallingford, CT, USA, 2009.

| Dataset | Row Dim. | Col.Dim. | No. Non-Zero Entries | Time (s) | Time (s) |
|---|---|---|---|---|---|
| N | K | nz | Method | B Method | |
| Bill Mark | 94 | 10,695 | 33,693 | 0.010820 | 0.115671 |
| Reuters | 2742 | 12,209 | 129,793 | 0.054852 | 0.201204 |
| Enron | 55,365 | 121,415 | 7,989,058 | 1.765044 | 5.741161 |
| user60784 | 2478 | 492,947 | 2,329,810 | 0.462936 | 4.790335 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scott, T.C.; Therani, M.; Wang, X.M. Data Clustering with Quantum Mechanics. Mathematics 2017, 5, 5. https://doi.org/10.3390/math5010005
Scott TC, Therani M, Wang XM. Data Clustering with Quantum Mechanics. Mathematics. 2017; 5(1):5. https://doi.org/10.3390/math5010005
Chicago/Turabian StyleScott, Tony C., Madhusudan Therani, and Xing M. Wang. 2017. "Data Clustering with Quantum Mechanics" Mathematics 5, no. 1: 5. https://doi.org/10.3390/math5010005
APA StyleScott, T. C., Therani, M., & Wang, X. M. (2017). Data Clustering with Quantum Mechanics. Mathematics, 5(1), 5. https://doi.org/10.3390/math5010005