On Some Extended Block Krylov Based Methods for Large Scale Nonsymmetric Stein Matrix Equations
Abstract
:1. Introduction
2. The Extended Block Krylov Subspace Algorithm
| Algorithm 1. The Extended Block Arnoldi (EBA) Algorithm |
|
3. Galerkin-Based Methods
3.1. The Case: Both A and B Are Large Matrices
| Algorithm 2. Galerkin Approach (GA) for the Stein Matrix Equations |
|
3.2. The Case: A Large and B Small
4. Minimal Residual Method for Large Scale Stein Matrix Equations
4.1. The Case: Both A and B Are Large
4.2. The Preconditioned Global CG Method for Solving the Reduced Minimization Problem
| Algorithm 3. The Preconditioned Global Conjugate Gradient (PGCG) Algorithm. |
|
| Algorithm 4. The Minimal Residual (MR) Method for Nonsymmetric Stein Matrix Equations |
4.3. The Case: A Large and B Small
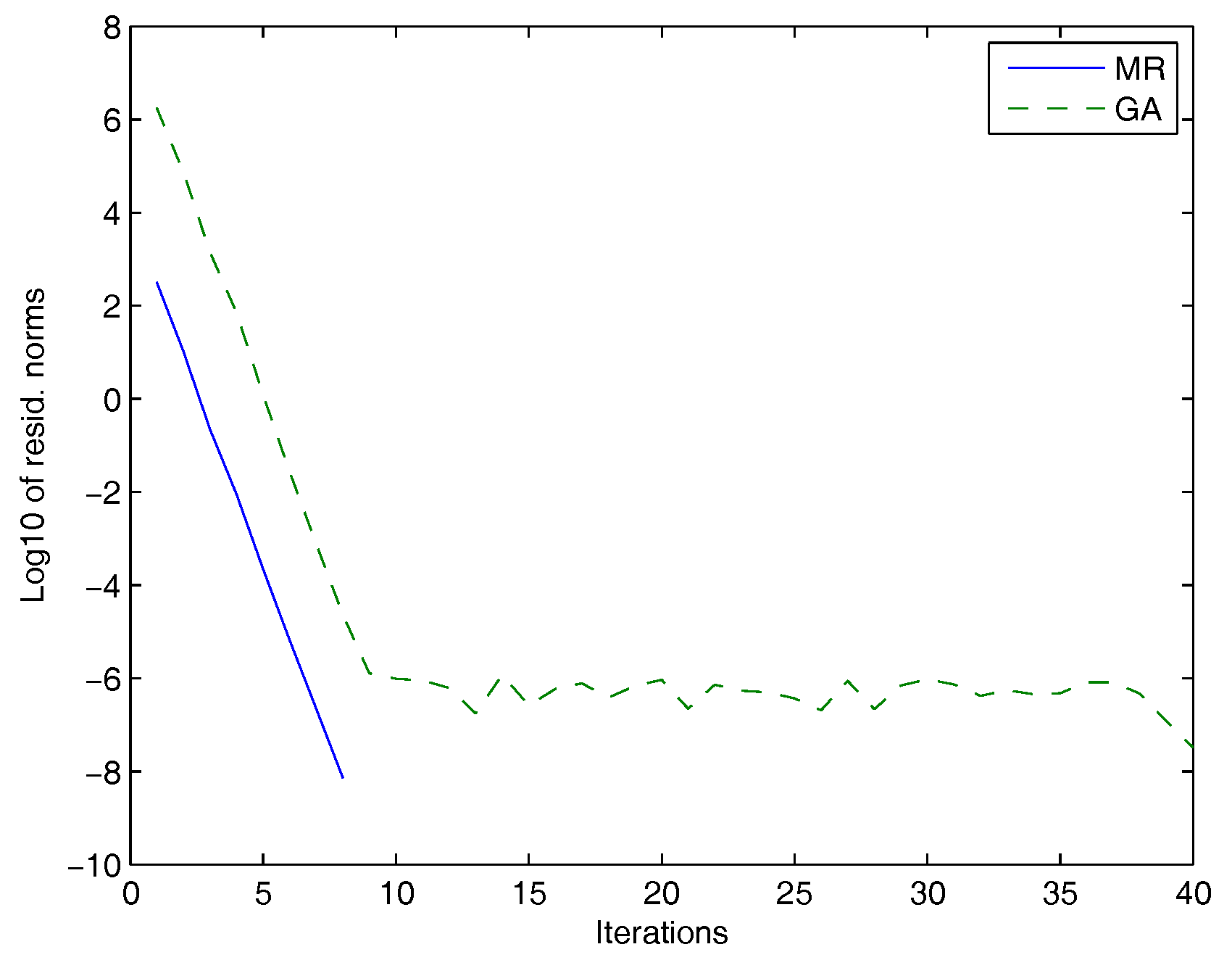
5. Numerical Experiments
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Bouhamidi, A.; Heyouni, M.; Jbilou, K. Block Arnoldi-based methods for large scale discrete-time algebraic Riccati equations. J. Comput. Appl. Math. 2011, 236, 1531–1542. [Google Scholar] [CrossRef]
- Bouhamidi, A.; Jbilou, K. Sylvester Tikhonov-regularization methods in image restoration. J. Comput. Appl. Math. 2007, 206, 86–98. [Google Scholar] [CrossRef]
- Zhou, B.; Lam, J.; Duan, G.-R. On Smith-type iterative algorithms for the Stein matrix equation. Appl. Math. Lett. 2009, 22, 1038–1044. [Google Scholar] [CrossRef]
- Zhou, B.; Lam, J.; Duan, G.-R. Toward solution of matrix equation X = Af (X)B + C. Linear Algebra Appl. 2011, 435, 1370–1398. [Google Scholar] [CrossRef]
- Zhou, B.; Duan, G.-R.; Lam, J. Positive definite solutions of the nonlinear matrix equation. Appl. Math. Comput. 2013, 219, 7377–7391. [Google Scholar] [CrossRef]
- Li, Z.-Y.; Zhou, B.; Lam, J. Towards positive definite solutions of a class of nonlinear matrix equations. Appl. Math. Comput. 2014, 237, 546–559. [Google Scholar] [CrossRef]
- Van Dooren, P. Gramian Based Model Reduction of Large-Scale Dynamical Systems. In Numerical Analysis; Chapman and Hall/CRC Press: London, UK, 2000; pp. 231–247. [Google Scholar]
- Datta, B.N. Numerical Methods for Linear Control Systems; Academic Press: New York, NY, USA, 2003. [Google Scholar]
- Datta, B.N.; Datta, K. Theoretical and computational aspects of some linear algebra problems in control theory. In Computational and Combinatorial Methods in Systems Theory; Byrnes, C.I., Lindquist, A., Eds.; Elsevier: Amsterdam, The Netherlands, 1986; pp. 201–212. [Google Scholar]
- Calvetti, D.; Levenberg, N.; Reichel, L. Iterative methods for X − AXB = C. J. Comput. Appl. Math. 1997, 86, 73–101. [Google Scholar] [CrossRef]
- Bartels, R.H.; Stewart, G.W. Solution of the matrix equation A X + X B = C, Algorithm 432. Commun. ACM 1972, 15, 820–826. [Google Scholar] [CrossRef]
- Golub, G.H.; Nash, S.; van Loan, C. A Hessenberg Schur method for the problem AX + XB = C. IEEE Trans. Autom. Control 1979, 24, 909–913. [Google Scholar] [CrossRef]
- Simoncini, V. Computational methods for linear matrix equations. SIAM Rev. 2016, 58, 377–441. [Google Scholar] [CrossRef]
- Agoujil, S.; Bentbib, A.H.; Jbilou, K.; Sadek, E.L.M. A minimal residual norm method for large-scale Sylvester matrix equations. Elect. Trans. Numer. Anal. 2014, 43, 45–59. [Google Scholar]
- Bentbib, A.H.; Jbilou, K.; Sadek, E.M. On some Krylov subspace based methods for large-scale nonsymmetric algebraic Riccati problems. Comput. Math. Appl. 2015, 2555–2565. [Google Scholar] [CrossRef]
- Druskin, V.; Knizhnerman, L. Extended Krylov subspaces: Approximation of the matrix square root and related functions. SIAM J. Matrix Anal. Appl. 1998, 19, 755–771. [Google Scholar] [CrossRef]
- El Guennouni, A.; Jbilou, K.; Riquet, A.J. Block Krylov subspace methods for solving large Sylvester equations. Numer. Algorithms 2002, 29, 75–96. [Google Scholar] [CrossRef]
- Heyouni, M. Extended Arnoldi methods for large low-rank Sylvester matrix equations. Appl. Numer. Math. 2010, 60, 1171–1182. [Google Scholar] [CrossRef]
- Jaimoukha, I.M.; Kasenally, E.M. Krylov subspace methods for solving large Lyapunov equations. SIAM J. Numer. Anal. 1994, 31, 227–251. [Google Scholar] [CrossRef]
- Jbilou, K. Low-rank approximate solution to large Sylvester matrix equations. Appl. Math. Comput. 2006, 177, 365–376. [Google Scholar] [CrossRef]
- Jbilou, K.; Riquet, A.J. Projection methods for large Lyapunov matrix equations. Linear Algebra Appl. 2006, 415, 344–358. [Google Scholar] [CrossRef]
- Lin, Y.; Simoncini, V. Minimal residual methods for large scale Lyapunov equations. Appl. Numer. Math. 2013, 72, 52–71. [Google Scholar] [CrossRef]
- Simoncini, V. A new iterative method for solving large-scale Lyapunov matrix equations. SIAM J. Sci. Comput. 2007, 29, 1268–1288. [Google Scholar] [CrossRef]
- Jagels, C.; Reichel, L. Recursion relations for the extended Krylov subspace method. Linear Algebra Appl. 2011, 434, 1716–1732. [Google Scholar] [CrossRef]
- Heyouni, M.; Jbilou, K. An extended Block Arnoldi algorithm for large-scale solutions of the continuous-time algebraic Riccati equation. Elect. Trans. Numer. Anal. 2009, 33, 53–62. [Google Scholar]
- Saad, Y. Numerical solution of large Lyapunov equations. In Signal Processing, Scattering, Operator Theory and Numerical Methods; Kaashoek, M.A., van Shuppen, J.H., Ran, A.C., Eds.; Birkhaser: Boston, MA, USA, 1990; pp. 503–511. [Google Scholar]
- Bouhamidi, A.; Hached, M.; Heyouni, M.; Jbilou, K. A preconditioned block Arnoldi method for large Sylvester matrix equations. Numer. Linear Algebra Appl. 2011, 20, 208–219. [Google Scholar] [CrossRef]
- Saad, Y. Iterative Methods for Sparse Linear Systems, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2003. [Google Scholar]
- Saad, Y.; Yeung, M.; Erhel, J.; Guyomarc’h, F. A deflated version of the conjugate gradient algorithm. SIAM J. Sci. Comput. 2000, 21, 1909–1926. [Google Scholar] [CrossRef]
- Penzl, T. LYAPACK A MATLAB Toolbox for Large Lyapunov and Riccati Equations, Model Reduction Problems, and Linear-Quadratic Optimal Control Problems. Available online: http://www.tu-chemintz.de/sfb393/lyapack (Accessed on 10 June 2016).
- Davis, T. The University of Florida Sparse Matrix Collection, NA Digest, Volume 97, No. 23, 7 June 1997. Available online: http://www.cise.ufl.edu/research/sparse/matrices (Accessed on 10 June 2016).


| Test Problem | Method | Iterations | Residual Norm | Times (s) |
|---|---|---|---|---|
| , , | GA | 43 | 7.56 × 10 | 4.80 |
| MR | 3 | 1.87 | ||
| 10,000, , | GA | 45 | 26.52 | |
| MR | 3 | 3.75 | ||
| 12,100, , | GA | 49 | 12.96 | |
| MR | 3 | 3.63 |
| Test Problem | Method | Iterations | Residual Norm | Time (s) |
|---|---|---|---|---|
| , , , A = pde2961 | GA | 45 | 3.7440 | |
| and B = fdm | MR | 7 | 1.0296 | |
| , , , A = Thermal | GA | 40 | 10.1245 | |
| and B = fdm | MR | 8 | 7.3008 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bentbib, A.H.; Jbilou, K.; Sadek, E.M. On Some Extended Block Krylov Based Methods for Large Scale Nonsymmetric Stein Matrix Equations. Mathematics 2017, 5, 21. https://doi.org/10.3390/math5020021
Bentbib AH, Jbilou K, Sadek EM. On Some Extended Block Krylov Based Methods for Large Scale Nonsymmetric Stein Matrix Equations. Mathematics. 2017; 5(2):21. https://doi.org/10.3390/math5020021
Chicago/Turabian StyleBentbib, Abdeslem Hafid, Khalide Jbilou, and EL Mostafa Sadek. 2017. "On Some Extended Block Krylov Based Methods for Large Scale Nonsymmetric Stein Matrix Equations" Mathematics 5, no. 2: 21. https://doi.org/10.3390/math5020021
APA StyleBentbib, A. H., Jbilou, K., & Sadek, E. M. (2017). On Some Extended Block Krylov Based Methods for Large Scale Nonsymmetric Stein Matrix Equations. Mathematics, 5(2), 21. https://doi.org/10.3390/math5020021





