1. Introduction
In the early 1970s, Black and Scholes [
1,
2] and, independently, Merton [
3] introduced a mathematical model for the pricing of European options. The Black-Scholes-Merton (BS) Model is described by an
evolution equation. The mathematical expression of the BS equation is
in which
t is time,
S is the current value of the underlying asset, for example a stock price,
r is the rate of return on a safe investment, such as government bonds and
is the value of the option. The solution of Equation (
1) is subject to the satisfaction of the terminal condition
, when
.
For the prices of commodities, Schwartz [
4] proposed three models which study the stochastic behaviour of the prices of commodities that take into account several aspects of possible influence on the prices. In the simplest model he assumed that the logarithm of the spot price followed a mean-reversion process of Ornstein-Uhlenbeck type. This is termed the one-factor model. The one-factor model is described by the equation:
where
measures the degree of reversion to the long-run mean log price,
λ is the market price of risk,
μ is the drift rate of
S and
is the current value of the futures contract. The solution of Equation (
2) satisfies the initial condition
The BS Equation (
1) and the one-factor Equation (
2) are of the same equivalence class as the Schrödinger equation and the Heat diffusion equation. All four equations model random phenomena of different contexts. The two first are in financial mathematics, the third in quantum physics and the fourth in dispersion.
It has been proven that all four equations are maximally symmetric and invariant under the same group of invariant transformations of dimension
which span the Lie algebra
, where
is a representation of the three-dimensional Weyl–Heisenberg Group, (in the Mubarakzyanov Classification Scheme [
5,
6,
7,
8] this is
). This means that there exists a point transformation which transforms one equation to another. The Lie symmetries of the BS Equation (
1) have been found in [
9], whereas the Lie symmetries of the one-factor model (
2) were found in [
10].
The parameters of the models (
1) and (
2) are generally assumed to be constant. However, in real problems they may vary with time if the time-span of the model is sufficiently long. In [
11] it has been shown that, when the parameters
σ, and
r of the BS equation are time-dependent,
i.e.,
and
, the time-dependent BS equation is invariant under the same group of invariant transformations as that of the “static” BS equation. The same result has been found for the time-dependent one-factor model of commodities [
12]. Hence the autonomous and the nonautonomous Equations (
1) and (
2) are maximally symmetric and equivalent under point transformations.
In Classical Mechanics the slowly lengthening pendulum with equation of motion in the linear approximation,
in which the time dependence in the "spring constant" is due to the length of the pendulum’s string increasing slowly [
13], admits the conservation law [
14,
15] (note that the case of a slowly shortening pendulum is quite different [
16]),
where
, is a solution of the second-order differential equation,
This result is independent of the rate of change of the length of the pendulum.
The latter equation is the well-known Ermakov-Pinney equation [
17]. The solution was given by Pinney in [
18] and it is:
subject to a constraint on the three constants,
A,
B and
C. Functions
are two linearly independent solutions of Equation (
3) .
Equation (
3) is invariant under the action of the group invariant transformations in which the generators of the infinitesimal transformations form the
algebra. This is the Lie algebra admitted by the harmonic oscillator,
, and the equation of the free particle,
[
19,
20,
21]. The transformation which connects the nonautonomous linear Equation (
3) with the autonomous oscillator is a time-dependent linear canonical transformation of the form:
where
ρ is given by Equation (
6).
The connection of the number of symmetries of the corresponding Schrödinger Equation with the Noether point symmetries of the classical Lagrangian [
22,
23] was seen to extend to the time-dependent case [
24] and, indeed, be seen to be the same as the equivalent autonomous systems [
25] and in the case of maximal symmetry is
which is that of the
classical heat equation.
In this context we wish to see what happens when we pass from an autonomous evolution equation to the corresponding nonautonomous case. For that we study the Lie symmetries of the nonautonomous models of: (a) the two-factor model of commodities and (b) the two-dimensional BS equation.
We find that, for the two-factor model, the autonomous and the nonautonomous equations are invariant under the same group of invariant transformations . However, that it is not true for the two-dimensional BS equation. The reason for that is that the Lie symmetries of the two-factor model follow from the translation group of the two-dimensional Euclidian space (except the homogeneous and the infinite number of solution symmetries). The translation group generates Lie symmetries for both the autonomous system and for the nonautonomous system.
On the other hand the autonomous two-dimensional BS equation is maximally symmetric,
i.e., it admits nine Lie symmetries plus the infinite number of solution symmetries, which form the
Lie algebra. This result completes the analysis of [
26] in which they found that the two-dimensional BS equation admits seven Lie point symmetries plus the
.
The nonautonomous two-dimensional BS equation is invariant under the Lie algebra , that is, the subalgebra is lost. The reason for that is that the Lie symmetries of the autonomous two-dimensional BS equation arise from the homothetic algebra of the two-dimensional Euclidian space which defines the Laplace operator of the evolution equation and, when the parameters in the second derivatives are not constants, the homothetic algebra of the Euclidian space does not generate Lie symmetries. Moreover, in the case for which the parameters of the second derivatives are time-indepedent, the two-dimensional BS equation is maximally symmetric, i.e., it is invariant under the same group of point transformations as the (1 + 2) autonomous BS and Heat conduction equations.
The plan of the paper is as follows. In
Section 2 we study the Lie symmetries of the two-factor model of commodities for the autonomous and nonautonomous cases. We show that in both cases the two-factor model is invariant under the
Lie algebra. The Lie symmetries of the two-dimensional BS equation, the autonomous and the nonautonomous, are studied in
Section 3. Finally in
Section 4 we give some applications and we draw our conclusions.
3. The Two-Dimensional Black-Scholes Equation
Consider a basket containing two assets the prices of which are
and
and that the the prices of the underlying assets obey the system of stochastic differential equations,
where
,
, and
are two independent standard Brownian motions. Let
be the payoff function on a European option on this two-asset basket. Then the evolution equation which
u satisfies is an
linear evolution equation given by [
29]
with the terminal condition
, when
Equation (
34) is a generalisation of the BS equation and it is called the two-dimensional BS equation. The Lie symmetry analysis of Equation (
1) has been presented in [
9] and recently a Lie symmetry analysis for Equation (
1), with a general potential function, was performed in [
30]. The algebraic properties of the autonomous form of Equation (
34) have been studied in [
26] and it was found that Equation (
34) is invariant under a seven-dimensional Lie algebra, plus the infinite number of solution symmetries. As we see below, the analysis of the autonomous Equation (
34) in [
26] is not complete. In particular we find that it is maximally symmetric,
i.e., invariant under a nine-dimensional Lie algebra, plus the infinite number of solution symmetries. In [
26] the authors considered the following equation
which reduces to Equation (
34) when
Below we determine the Lie symmetries of Equation (
35) for the autonomous and nonautonomous system.
3.1. Lie Symmetries of the Autonomous Equation
We introduce the coordinate transformation
under which Equation (
35) becomes
where now the new constants,
and
, are
On application of the Lie symmetry condition (
18) for (
37) we find that the Lie symmetry vectors are
and
which are
symmetries. This is the admitted group invariant algebra of the two-dimensional Heat Equation, that is,
. Hence the two-dimensional BS Equation (
35) is maximally symmetric and equivalent with the two-dimensional Heat and Schrödinger equations [
31]. This result does not hold for the two-factor model of commodities. An analysis does hold when in Equation (
35),
; that is, for Equation (
34).
When we apply the transformations
and
to Equation (
37), the equation becomes
which is the two-dimensional Heat conduction equation.
We proceed to the determination of the Lie symmetries for the nonautonomous Equation (
35).
3.2. Lie Symmetries of the Nonautonomous Equation
We take the parameters,
and
of Equation (
35) to be well-defined functions of time. Moreover without loss of generality we select
We apply the time-dependent transformation Equation (
36) to Equation (
35) and we have
in which
and
From the symmetry condition (
18) for Equation (
47) we find that the generic Lie symmetry vector has the following mathematical expression
where
is a constant,
and
which given by the system of differential equations of
Appendix B. Furthermore, from Equation (
51) and the system of
Appendix B, we observe that the nonautonomous Equation (
34) is invariant under the group of transformations in which the generators form the
Lie algebra. Below we consider a special case for which
and
Special Case: and
As a special case of the nonautonomous Equation (
35) we consider
, where
is a constant and
is a constant. The nonautonomous two-dimensional BS equation becomes
where without loss of generality we can select
. Under the transformation Equations (
36) and (
52) becomes
where the new functions
are defined as
and
From the symmetry condition (
18) for Equation (
47) the following symmetry vectors arise
and
Hence the nonautonomous Equation (
52) is maximally symmetric, just as the autonomous two-dimensional BS equation, in contrast to the nonautonomous Equation (
47) which is invariant under another group of point transformations.
Moreover Equation (
53) can be written in the form of Equation (
46) and the transformation which does that is
and
Below we discuss our results and draw our conclusions.
4. Conclusions
The purpose of this work is to study the algebraic properties of nonautonomous evolution equations in financial mathematics. Specifically, we examined the relation among the admitted group of invariant transformations between the autonomous and the nonautonomous equations of the two-factor model of commodities and of the two-dimensional BS equation was performed.
For the two-factor model of commodities we proved that the autonomous and the nonautonomous equations are invariant under the same group of point transformations in which the generators form the Lie algebra.
As far as the autonomous two-dimensional BS equation is concerned, we proved that it is maximally symmetric and admits as Lie symmetries the generators of the Lie algebra This corrects the existing result in the literature. However, the admitted Lie symmetries of the nonautonomous two-dimensional BS equation form a different Lie algebra than that of the autonomous equation and is of lower dimension. Specifically the admitted Lie algebra is . That result differs from that for the model of commodities for which the autonomous and the nonautonomous equations are invariant under the same group of transformations, namely
In the case for which and , the two-dimensional BS equation is maximally symmetric. In order to understand why we have this special case consider the general evolution equation ( We use the Einstein summation convention).
If
is the generator of a Lie symmetry vector, one of the symmetry conditions can be written as
where
ψ is a function of
t only, and
. Therefore from Equation (
66) we know that
From Equation (
67) we know that, when
, the Lie symmetries of Equation (
65) are generated by the Homothetic Algebra of
. However, that is not true when
and new possible generators arise. In the
equations,
i.e., Equations (
1) and (
2), when
, as we discussed above, we can always perform a time (coordinate) transformation and cause the second derivatives to be time-independent. Therefore, in order to apply this method to the two-dimensional systems, we have to select
and
so that at the end the components of the second derivatives can be seen as time-independent.
Furthermore, we remark that we performed a reduction on the two nonautonomous Equations (
8) and (
34) by using the Lie symmetries (
32) and (
51), respectively, for
. We found that the reduced equations, which are
evolution equations, are maximally symmetric. This is the same result as is to be found in the case of the autonomous two-factor model [
10].
As a final application consider the nonautonomous two-dimensional BS Equation (
53). From the application of the invariant functions of the Lie symmetries
we have the solution
, where
In the case for which
and
,
ω,
ε and
are constants, the solution of the nonautonomous two-dimensional BS equation for the “
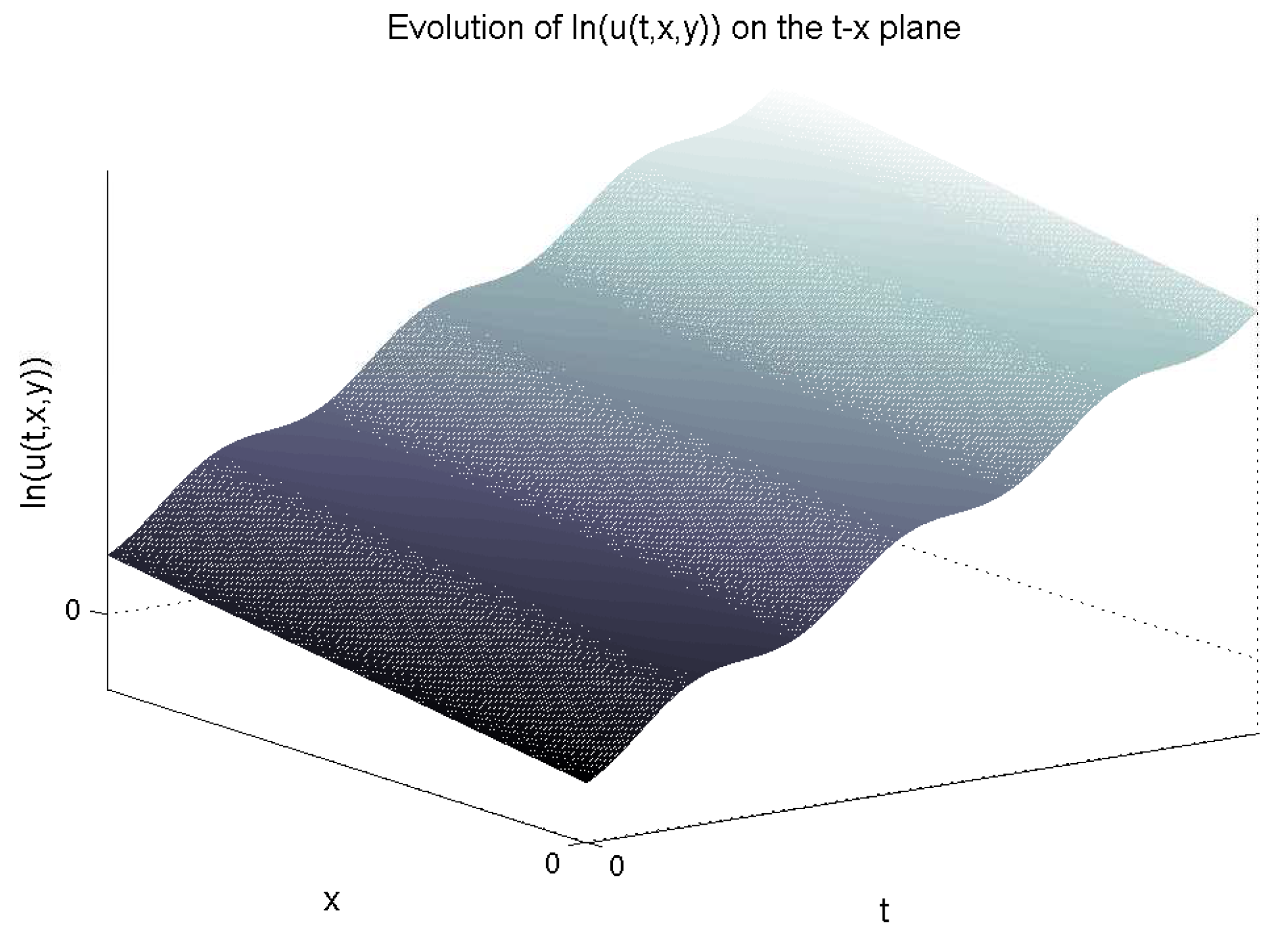
” plane is given in
Figure 1. We observe that in the
direction, function
has periodic behavior along the line
with period
ω.
The implication of the results of the present analysis is that for the two-factor model of commodities, the autonomous and the nonautonomous problem share the same static solutions, that is, the differences follow only from the time-dependent terms of the solution. However, that is not true for the two-dimensional Black-Scholes Equation in which the nonautonomous equation in general is not maximally symmetric and does not share the same number of static solutions with that of the autonomous equation. On the other hand we found that if and only if the time-dependence of the two volatilities are the same, i.e., , and if the correlation factor ρ is constant then the nonautonomous Black-Scholes shares the same static solutions, i.e., static evolution, with the autonomous equation.
The results of this analysis are important in the sense that by starting from the autonomous equation and with the use of coordinate transformations and only someone can analyse models with time-varying constants. On the other hand starting from real data and with the use of coordinate transformations to see if the data are well described from the autonomous system, and vice verca. The situation is not different from that which one finds on the relation between the free particle and harmonic oscillator. In order to demonstrate that, if we plot the time-position diagram of the mathematical pendulum, where we measure the distance and the time with nonlinear instruments, the graph will be a straight line, which describes the motion of the free particle.
In a forthcoming work we intend to extend our analysis to the case where the free parameters of the models are space-dependent. Such an analysis is in progress and will be published elsewhere.