Microtubules Nonlinear Models Dynamics Investigations through the exp(−Φ(ξ))-Expansion Method Implementation
Abstract
:1. Introduction
- (i)
- The model of nonlinear dynamics of microtubules assuming a single longitudinal degree of freedom per tubulin dimer is described by the nonlinear PDE (see [59]),where and are positive parameters, , is the mass of the dimer, , is the traveling wave, is the magnitude of intrinsic electric field, , is the MT length, , is the excess charge within the dipole, , is the viscosity coefficient and, , is a harmonic constant describing the nearest-neighbor interaction between the dimers belonging to the same PFs. In [48], authors have used the Jacobi elliptic function method to find the exact solutions of Equation (1), the physical details and derivations of which were discussed there, although omitted here for obvious reasons.
- (ii)
- The nonlinear PDE describing the nonlinear dynamics of radially dislocated MTs:Here, , is the corresponding angular displacement when the whole dimer rotates and, , is the MT length, is the magnitude of intrinsic electric field, , stands for inter-dimer bonding interaction within the same PFs, , is the moment of inertia of the single dimer and is the viscosity coefficient. In [57], authors have used the simple equation method to find the exact solutions of Equation (2), after relating physical aspects and equation derivation being omitted here.
2. Description of the -Expansion Method
3. Applications
3.1. Exact Solutions of the NPDE Equation(1)
3.2. Exact Solutions of the NPDE Equation (2)
4. Comparison
5. Physical Interpretations of Some Obtained Solutions
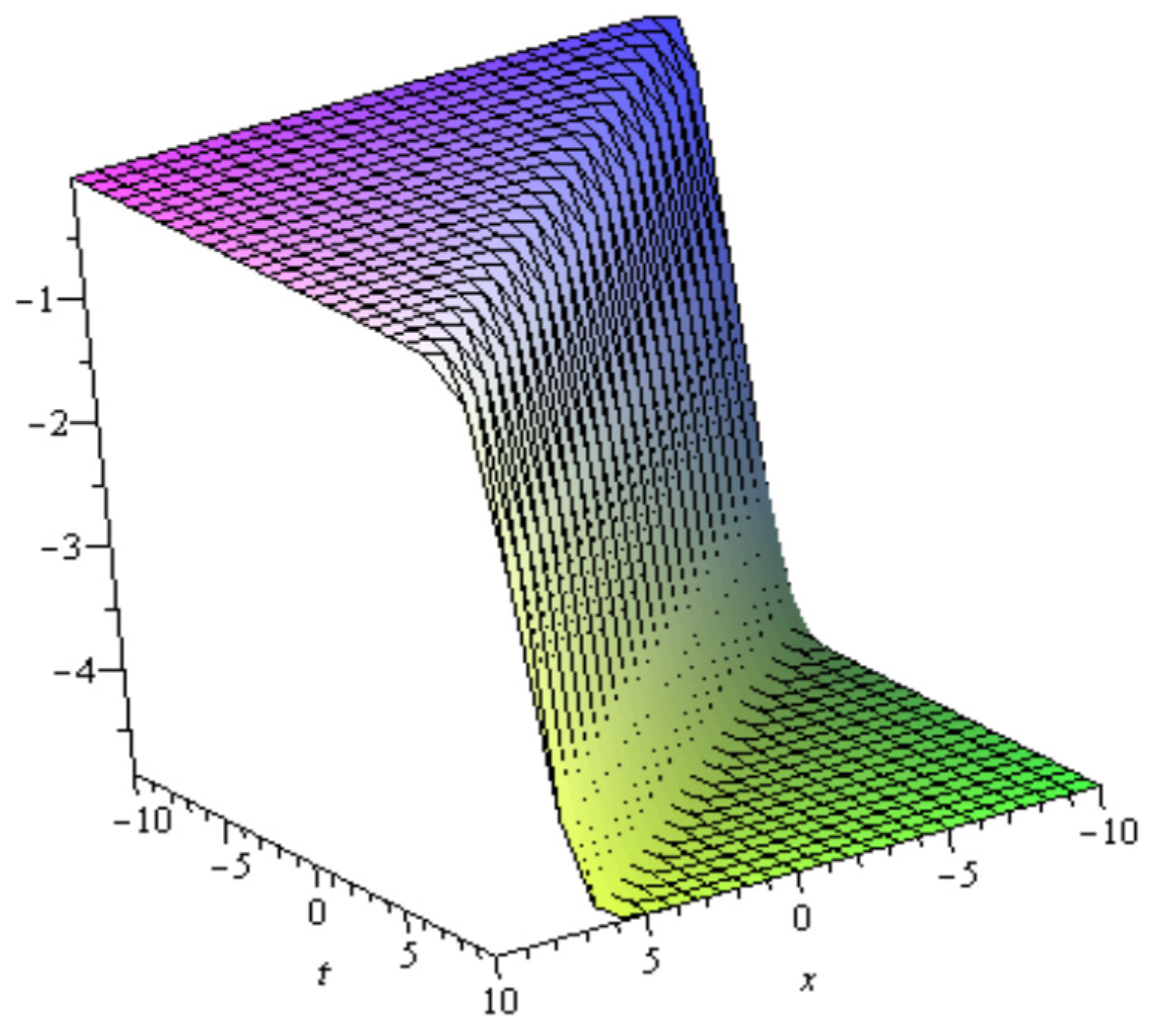

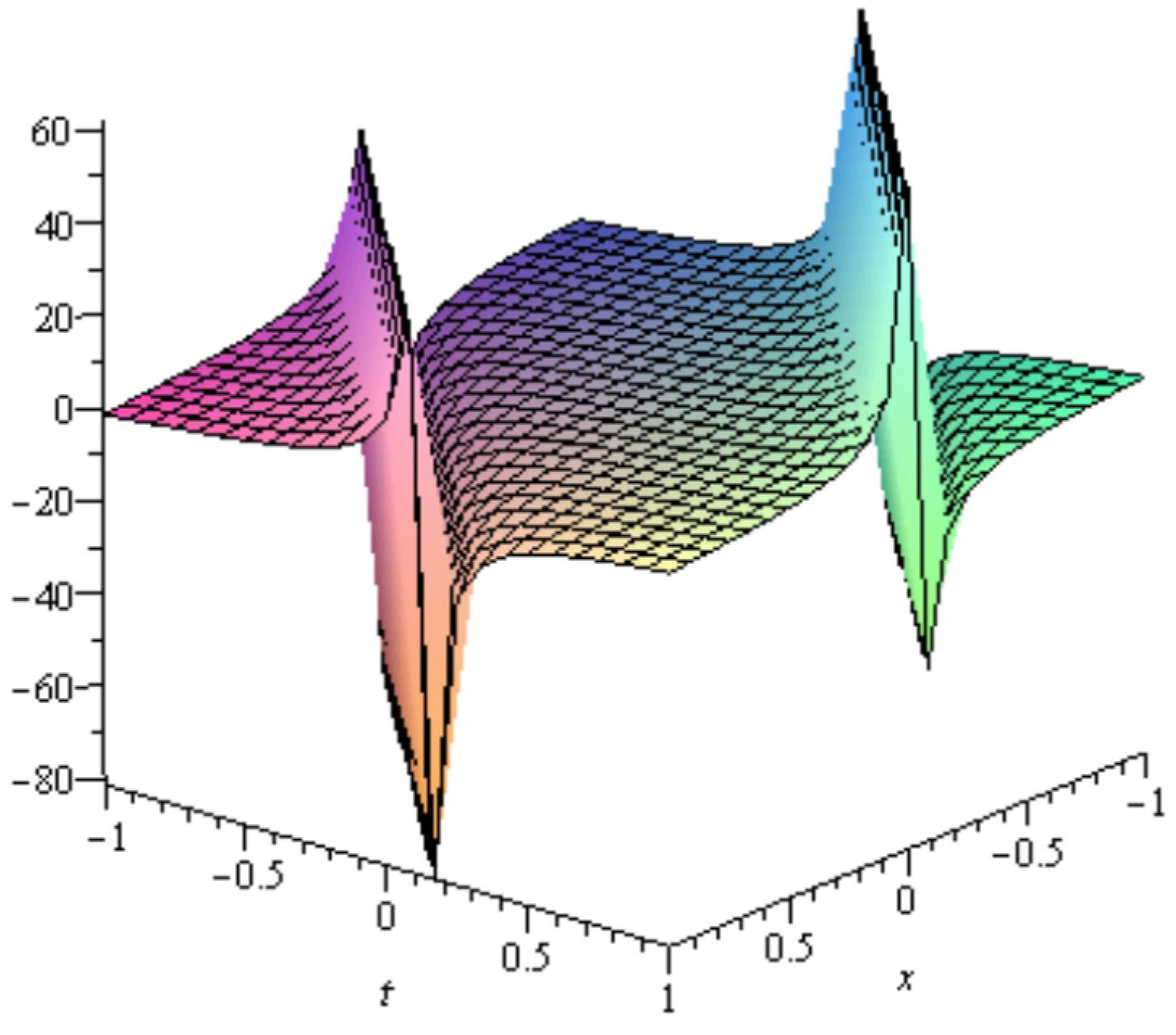
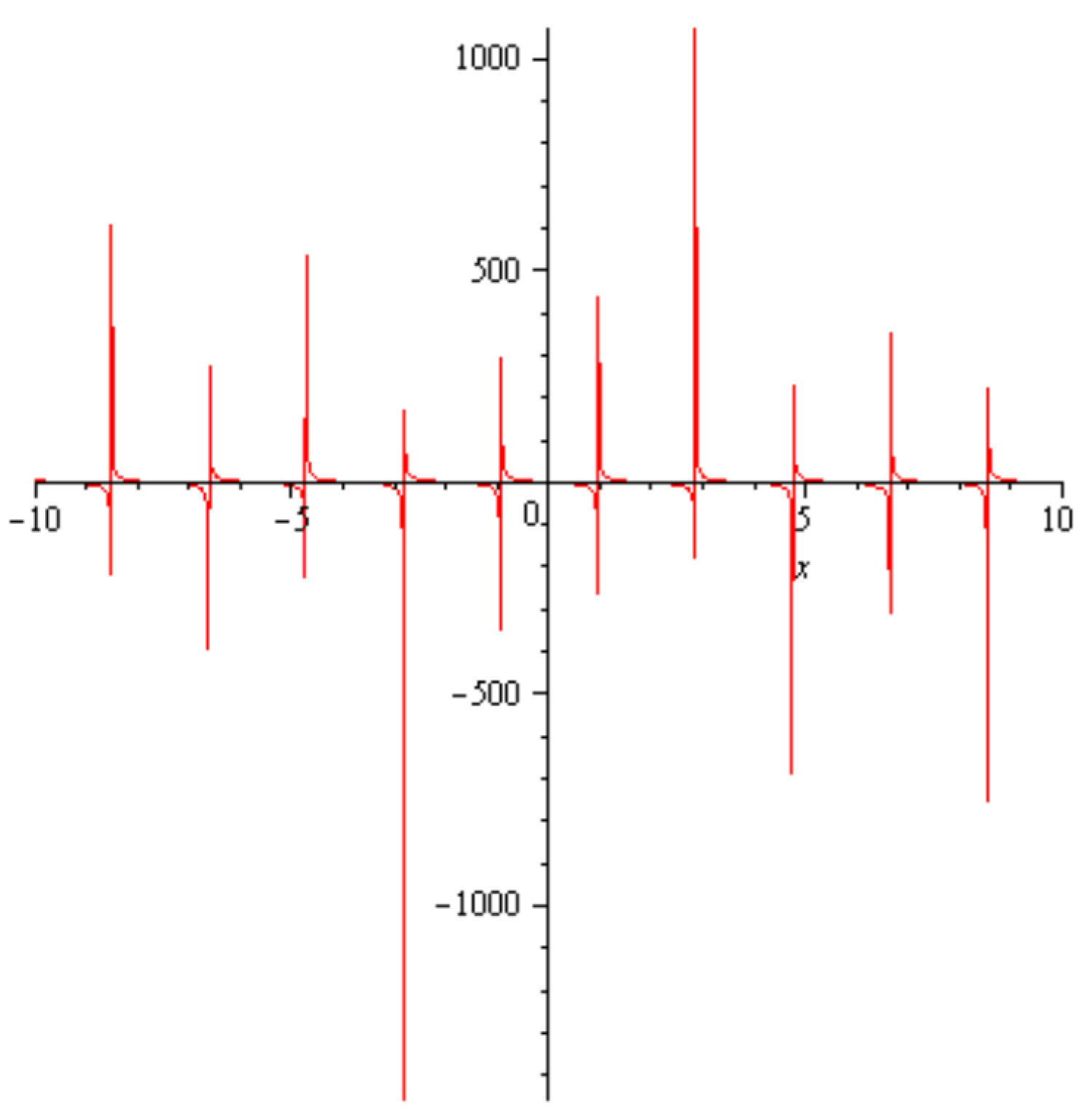

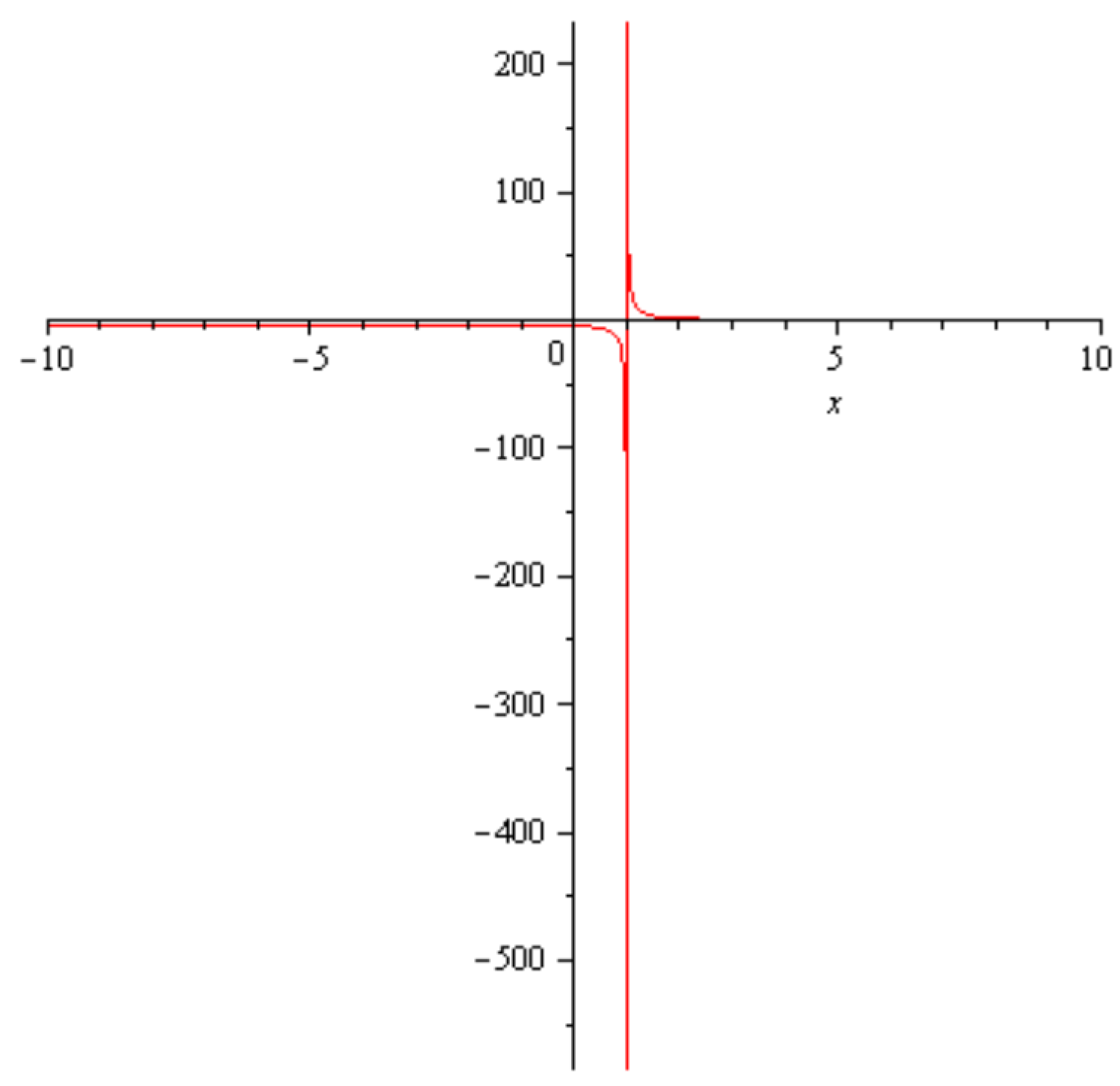
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
References
- Alam, M.A.; Akbar, M.A.; Mohyud-Din, S.T. General traveling wave solutions of the strain wave equation in microstructured solids via the new approach of generalized (G′/G)-Expansion method. Alex. Eng. J. 2014, 53, 233–241. [Google Scholar] [CrossRef]
- Alam, M.N.; Akbar, M.A.; Hoque, M.F. Exact traveling wave solutions of the (3+1)-dimensional mKdV-ZK equation and the (1+1)-dimensional compound KdVB equation using new approach of the generalized (G′/G)-expansion method. PramanJ. Phys. 2014, 83, 317–329. [Google Scholar] [CrossRef]
- Alam, M.N.; Akbar, M.A. A new (G′/G)-expansion method and its application to the Burgers equation. Walailak J. Sci. Technol. 2014, 11, 643–658. [Google Scholar]
- Hafez, M.G.; Alam, M.N.; Akbar, M.A. Exact traveling wave solutions to the Klein-Gordon equation using the novel (G′/G)-expansion method. Results Phys. 2014, 4, 177–184. [Google Scholar] [CrossRef]
- Alam, M.N.; Akbar, M.A. The new approach of generalized (G′/G)-expansion method for nonlinear evolution equations. Ain Shams Eng. 2014, 5, 595–603. [Google Scholar] [CrossRef]
- Younis, M.; Rizvi, S.T.R. Dispersive dark optical soliton in (2+1)-dimensions by G′/G-expansion with dual-power law nonlinearity. Opt. Int. J. Light Electron Opt. 2015, 126, 5812–5814. [Google Scholar] [CrossRef]
- Ma, W.X.; Wu, H.Y.; He, J.S. Partial differential equations possessing Frobeniusintegrable decomposition technique. Phys. Lett. A 2007, 364, 29–32. [Google Scholar] [CrossRef]
- Yang, Y.J.; Baleanu, D.; Yang, X.J. A Local fractional variational iteration method for Laplace equation within local fractional operators. Abstr. Appl. Anal. 2013, 2013, 202650. [Google Scholar] [CrossRef]
- Yang, A.M.; Yang, X.J.; Li, Z.B. Local fractional series expansion method for solving wave and diffusion equations on cantor sets. Abstr. Appl. Anal. 2013, 2013, 351057. [Google Scholar] [CrossRef]
- Ma, W.X.; Zhu, Z. Solving the (3+1)-dimensional generalized KP and BKP equations by the multiple exp-function algorithm. Appl. Math. Comput. 2012, 218, 11871–11879. [Google Scholar] [CrossRef]
- Ma, W.X.; Huang, T.; Zhang, Y. A multiple exp-function method for nonlinear differential equations and its application. Phys. Scr. 2010, 82, 065003. [Google Scholar] [CrossRef]
- Ma, W.X.; Lee, J.H. A transformed rational function method and exact solutions to the (3+1) dimensional Jimbo-Miwa equation. Chaos Solitons Fractals 2009, 42, 1356–1363. [Google Scholar] [CrossRef]
- He, J.H.; Wu, X.H. Exp-function method for nonlinear wave equations. Chaos Solitons Fractals 2006, 30, 700–708. [Google Scholar] [CrossRef]
- Younis, M.; Rizvi, S.T.R.; Ali, S. Analytical and soliton solutions: Nonlinear model of an obioelectronics transmission lines. Appl. Math. Comput. 2015, 265, 994–1002. [Google Scholar] [CrossRef]
- Zhang, Z.Y. New exact traveling wave solutions for the nonlinear Klein-Gordonequation. Turk. J. Phys. 2008, 32, 235–240. [Google Scholar]
- Ablowitz, M.J.; Segur, H. Solitions and Inverse Scattering Transform; SIAM: Philadelphia, PA, USA, 1981. [Google Scholar]
- Fan, E.; Zhang, H. A note on the homogeneous balance method. Phys. Lett. A 1998, 246, 403–406. [Google Scholar] [CrossRef]
- Wang, M.L. Exact solutions for a compound KdV-Burgers equation. Phys. Lett. A 1996, 213, 279–287. [Google Scholar] [CrossRef]
- Moosaei, H.; Mirzazadeh, M.; Yildirim, A. Exact solutions to the perturbed nonlinear Schrodinger equation with Kerr law nonlinearity by using the first integral method. Nonlinear Anal. Model. Control 2011, 16, 332–339. [Google Scholar]
- Bekir, A.; Unsal, O. Analytic treatment of nonlinear evolution equations using the first integral method. Pramana J. Phys. 2012, 79, 3–17. [Google Scholar] [CrossRef]
- Lu, B.H.Q.; Zhang, H.Q.; Xie, F.D. Traveling wave solutions of nonlinear partial differential equations by using the first integral method. Appl. Math. Comput. 2010, 216, 1329–1336. [Google Scholar] [CrossRef]
- Feng, Z.S. The first integral method to study the Burgers–KdVequation. J. Phys. A Math. Gen. 2002, 35, 343–349. [Google Scholar] [CrossRef]
- Abdou, M.A. The extended F-expansion method and its application for a class of nonlinear evolution equations. Chaos Solitons Fractals 2007, 31, 95–104. [Google Scholar] [CrossRef]
- Ren, Y.J.; Zhang, H.Q. A generalized F-expansion method to find abundant families of Jacobi elliptic function solutions of the (2+1)-dimensional Nizhnik-Novikov-Veselovequation. Chaos Solitons Fractals 2006, 27, 959–979. [Google Scholar] [CrossRef]
- Zhang, J.L.; Wang, M.L.; Wang, Y.M.; Fang, Z.D. The improved F-expansion method and its applications. Phys. Lett. A 2006, 350, 103–109. [Google Scholar] [CrossRef]
- Dai, C.Q.; Zhang, J.F. Jacobian elliptic function method for nonlinear differential-difference equations. Chaos Solitons Fractals 2006, 27, 1042–1049. [Google Scholar] [CrossRef]
- Fan, E.; Zhang, J. Applications of the Jacobi elliptic function method to special-type nonlinear equations. Phys. Lett. A 2002, 305, 383–392. [Google Scholar] [CrossRef]
- Liu, S.; Fu, Z.; Liu, S.; Zhao, Q. Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations. Phys. Lett. A 2001, 289, 69–74. [Google Scholar] [CrossRef]
- Zhao, X.Q.; Zhi, H.Y.; Zhang, H.Q. Improved Jacobi elliptic function method with symbolic computation to construct new double-periodic solutions for the generalized Ito system. Chaos Solitons Fractals 2006, 28, 112–126. [Google Scholar] [CrossRef]
- Belgacem, F.B.M. Sumudu Transform Applications to Bessel Functions and Equations. Appl. Math. Sci. 2010, 4, 3665–3686. [Google Scholar]
- Belgacem, F.B.M.; Karaballi, A.A. Sumudu transform Fundamental Properties investigations and applications. J. Appl. Math. Stoch. Anal. 2006, 2006, 1–23. [Google Scholar] [CrossRef]
- Belgacem, F.B.M. Sumudu Applications to Maxwell’s Equations. PIERS Online 2009, 5, 1–6. [Google Scholar] [CrossRef]
- Younis, M.; Ali, S. Bright, dark and singular solitons in magneto-electro-elastic circular rod. Waves Random Complex Media 2015, 25, 549–555. [Google Scholar] [CrossRef]
- Younis, M.; Ali, S. Solitary wave and shock wave solutions to the transmission line model for nano-ionic currents along microtubules. Appl. Math. Comput. 2014, 246, 460–463. [Google Scholar] [CrossRef]
- Ali, S.; Rizvi, S.T.R.; Younis, M. Traveling wave solutions for nonlinear dispersive water wave systems with time dependent coefficients. Nonlinear Dyn. 2015, 82, 1755–1762. [Google Scholar] [CrossRef]
- Younis, M.; Ali, S.; Mahmood, S.A. Solitons for compound KdV-Burgers’ equation with variable coefficients and power law nonlinearity. Nonlinear Dyn. 2015, 81, 1191–1196. [Google Scholar] [CrossRef]
- Alam, M.N.; Belgacem, F.B.M. Application of the Novel (G′/G)-Expansion Method to the Regularized Long Wave Equation. Waves Wavelets Fractals Adv. Anal. 2015, 1, 51–67. [Google Scholar] [CrossRef]
- Alam, M.N.; Hafez, M.G.; Belgacem, F.B.M.; Akbar, M.A. Applications of the novel (G′/G)-expansion method to find new exact traveling wave solutions of the nonlinear coupled Higgs field equation. Nonlinear Stud. 2015, 22, 613–633. [Google Scholar]
- Alam, M.N.; Belgacem, F.B.M.; Akbar, M.A. Analytical treatment of the evolutionary (1+1) dimensional combined KdV-mKdV equation via novel (G′/G)-expansion method. J. Appl. Math. Phys. 2015, 3, 61765. [Google Scholar] [CrossRef]
- Alam, M.N.; Belgacem, F.B.M. New generalized (G𠄲/G)-expansion method applications to coupled Konno-Oono and right-handed noncommutative Burgers equations. Adv. Pure Math 2016, in press. [Google Scholar]
- Alam, M.N.; Hafez, M.G.; Akbar, M.A.; Belgacem, F.B.M. Application of new generalized (G′/G)-expansion method to the (3+1)-dimensional Kadomtsev-Petviashvili equation. Ital. J. Pure Appl. Math 2016, in press. [Google Scholar]
- Alam, M.N.; Belgacem, F.B.M. Traveling Wave Solutions for the (1+1)-Dim Compound KdVB Equation by the Novel (G′/G)-Expansion Method. Int. J. Mod. Nonlinear Theory Appl. 2016, in press. [Google Scholar]
- Younis, M.; Rehman, H.; Iftikhar, M. Travelling wave solutions to some nonlinear evolution equations. Appl. Math. Comput. 2014, 249, 81–88. [Google Scholar] [CrossRef]
- Hereman, W.; Banerjee, P.P.; Korpel, A.; Assanto, G.; van Immerzeele, A.; Meerpoel, A. Exact solitary wave solutions of nonlinear evolution and wave equations using a direct algebraic method. J. Phys. A: Math. Gen. 1986, 19, 607. [Google Scholar] [CrossRef]
- Hafez, M.G.; Alam, M.N.; Akbar, M.A. Traveling wave solutions for some important coupled nonlinear physical models via the coupled Higgs equation and the Maccarisystem. J. King Saud Univ.Sci. 2015, 27, 105–112. [Google Scholar] [CrossRef]
- Hafez, M.G.; Alam, M.N.; Akbar, M.A. Application of the -expansion method to find exact solutions for the solitary wave equation in an un-magnetized dusty plasma. World Appl. Sci. J. 2014, 32, 2150–2155. [Google Scholar]
- Alam, M.N.; Hafez, M.G.; Akbar, M.A.; Roshid, H.O. Exact traveling wave solutions to the (3+1)-dimensionalmKdV-ZK and the (2+1)-dimensional Burgers equations via -expansion method. Alex. Eng. J. 2015, 54, 635–644. [Google Scholar]
- Alam, M.N.; Hafez, M.G.; Akbar, M.A.; Roshid, H.O. Exact Solutions to the (2+1)-Dimensional Boussinesq Equation via -Expansion Method. J. Sci. Res. 2015, 7, 1–10. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Amer, Y.A.; Shohid, R.M.A. The (G′/G)-expansion method and the -Expansion Method with applications to a higher order dispersive nonlinear schrodingerequation. Sci. Res. Essays 2015, 10, 218–231. [Google Scholar]
- Zekovic, S.; Muniyappan, A.; Zdravkovic, S.; Kavitha, L. Employment of Jacobian elliptic functions for solving problems in nonlinear dynamics of microtubules. Chin. Phys. B 2014, 23, 020504. [Google Scholar] [CrossRef]
- Sataric, M.V.; Sekulic, D.L.; Sataric, B.M.; Zdravkovic, S. Role of nonlinear localized Ca2+ pulses along microtubules in tuning the mechano-Sensitivity of hair cells. Prog. Biophys. Mol. Biol. 2015, 119, 162–174. [Google Scholar] [CrossRef] [PubMed]
- Sekulic, D.; Sataric, M.V. An improved nanoscale transmission line model of microtubules: The effect of nonlinearity on the propagation of electrical signals. Facta Univ. Ser. Electron. Energ. 2015, 28, 133–142. [Google Scholar] [CrossRef]
- Sekulic, D.L.; Sataric, B.M.; Tuszynski, J.A.; Sataric, M.V. Nonlinear ionic pulses along microtubules. Eur. Phys. J. E Soft Matter 2011, 34, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Sekulic, D.; Sataric, M.V.; Zivanov, M.B. Symbolic computation of some new nonlinear partial differential equations of nanobiosciences using modified extended tanh-function method. Appl. Math. Comput. 2011, 218, 3499–3506. [Google Scholar] [CrossRef]
- Sataric, M.V.; Sekulic, D.; Zivanov, M.B. Solitoniclonic currents along microtubules. J. Comput. Theor. Nanosci. 2010, 7, 2281–2290. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Alurrfi, K.A.E. The generalized projective riccati equations method and its applications for solving two nonlinear PDEs describing microtubules. Int. J. Phys. Sci. 2015, 10, 391–402. [Google Scholar]
- Sekulic, D.L.; Sataric, M.V. Microtubule as Nanobioelectronic nonlinear circuit. Serbian J. Electr. Eng. 2012, 9, 107–119. [Google Scholar] [CrossRef]
- Zdravkovic, S.; Sataric, M.V.; Maluckov, A.; Balaz, A. A nonlinear model of the dynamics of radial dislocations in microtubules. Appl. Math. Comput. 2014, 237, 227–237. [Google Scholar] [CrossRef]
- Zdravkovic, S.; Sataric, M.V.; Zekovic, S. Nonlinear Dynamics of Microtibules—A longitudinal Model. Europhys. Lett. 2013, 102, 38002. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alam, N.; Belgacem, F.B.M. Microtubules Nonlinear Models Dynamics Investigations through the exp(−Φ(ξ))-Expansion Method Implementation. Mathematics 2016, 4, 6. https://doi.org/10.3390/math4010006
Alam N, Belgacem FBM. Microtubules Nonlinear Models Dynamics Investigations through the exp(−Φ(ξ))-Expansion Method Implementation. Mathematics. 2016; 4(1):6. https://doi.org/10.3390/math4010006
Chicago/Turabian StyleAlam, Nur, and Fethi Bin Muhammad Belgacem. 2016. "Microtubules Nonlinear Models Dynamics Investigations through the exp(−Φ(ξ))-Expansion Method Implementation" Mathematics 4, no. 1: 6. https://doi.org/10.3390/math4010006
APA StyleAlam, N., & Belgacem, F. B. M. (2016). Microtubules Nonlinear Models Dynamics Investigations through the exp(−Φ(ξ))-Expansion Method Implementation. Mathematics, 4(1), 6. https://doi.org/10.3390/math4010006






