A Note on Burg’s Modified Entropy in Statistical Mechanics
Abstract
:1. Introduction
1.1. Clausius’s Entropy
1.2. Boltzmann’s Entropy
1.3. Information Theory andShannon’s Entropy
- (i)
- is a continuous function of
- (ii)
- is a symmetric function of its arguments.
- (iii)
- , i.e., it should not change if there is an impossible outcome to the probability.
- (iv)
- Its minimum is 0 when there is no uncertainty about the outcome. Thus, it should vanish when one of the outcomes is certain to happen so that
- (v)
- It is the maximum when there is maximum uncertainty, which arises when the outcomes are equally likely so that is the maximum when .
- (vi)
- The maximum value of increases with .
- (vii)
- For two independent probability distributions and , the uncertainty of the joint scheme should be the sum of their uncertainties:
2. Discussion
2.1. Jaynes’ Maximum Entropy (MaxEnt) Principle
2.2. Formulation of MEPD in Statistical Mechanics Using Shannon’s Measure of Entropy
2.3. Burg’s Entropy Measure and MEPD
2.4. d Burg’s Modifie Entropy (MBE) Measure and MEPD
2.4.1. Monotonic Character of MBE
2.4.2. MBE and Its Relation with Burg’s Entropy
2.4.3. MBE and Its Concavity of under Prescribed Mean
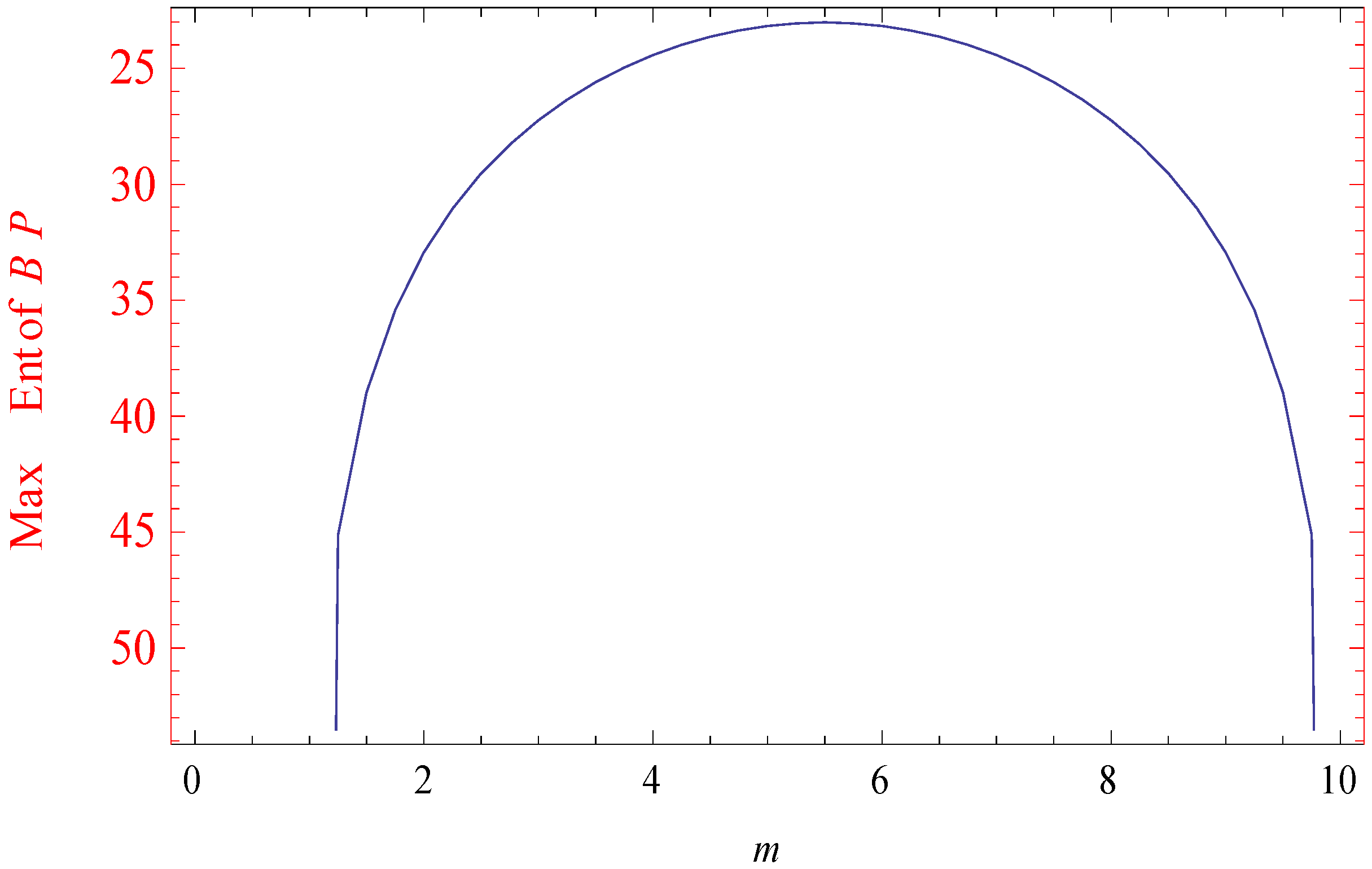
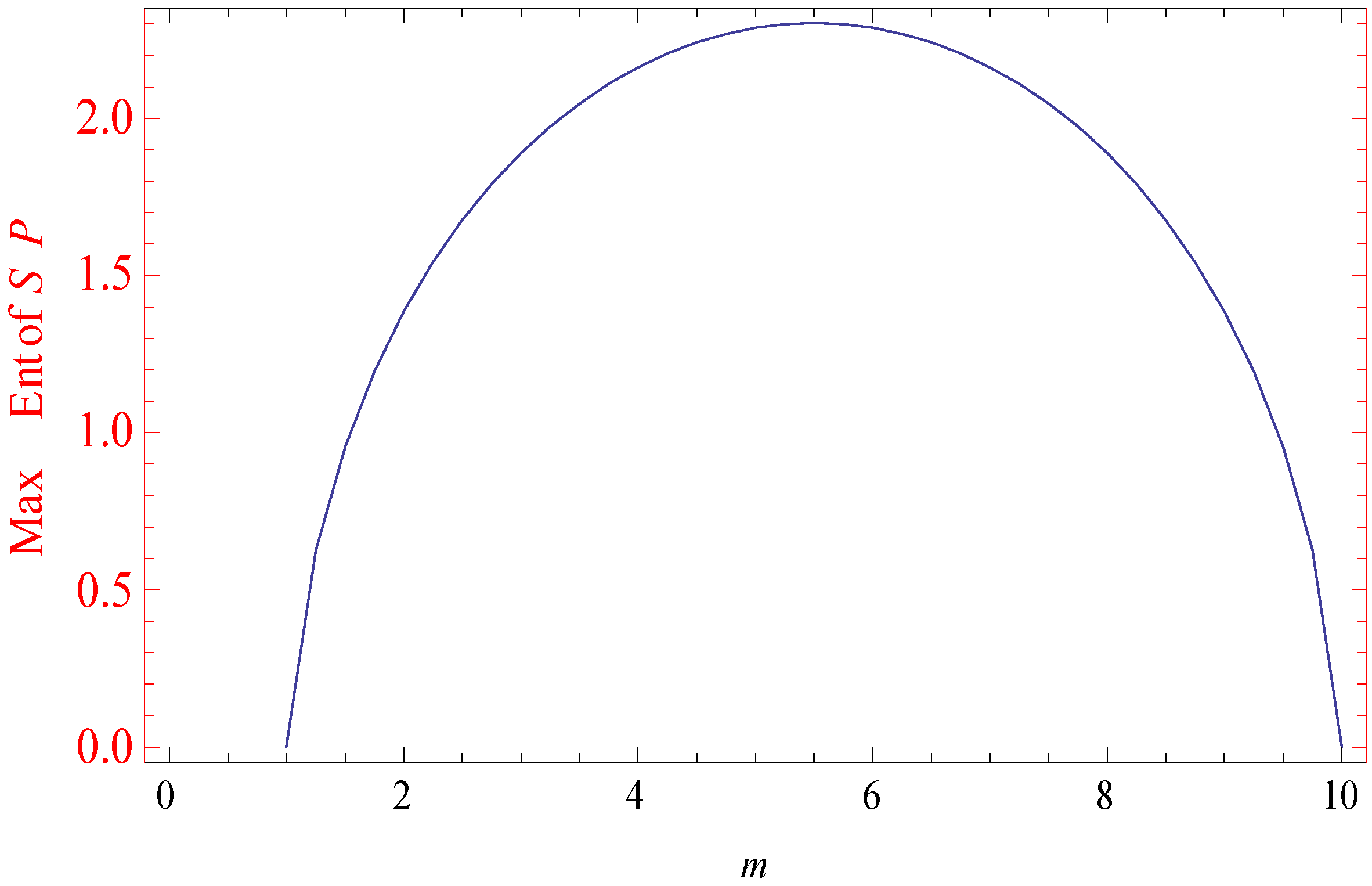
3. An Illustrative Example in Statistical Mechanics
3.1. Example
3.2. Simulated Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
- = Entropy
- , probability of th event
- = Information entropy
- = Shannon’s entropy
- = Burg’s entropy
- = Burg’s modified entropy
- = Number of energy levels/number of possible outcome
- = Boltzmann constant
- = Absolute temperature
- = Identical particle of ideal gas
- = Increase of entropy
- = Change in entropy
- = Greatest integer value of
- Where is the mean value:
- = Expectation
- = Change in volume
- = Union of two sets
- , ranges from 1 to 10 with step length of 0.25
- = Maximum entropy
- = Maximum value under the given probability distribution
- MBE=Modified Burg’s Entropy
Greek Symbols
- = The maximum number of microscopic ways in the macroscopic state
- = Position of the molecule
- = Momentum of the molecule
- =Lagrangian constant
- =Different energy levels
- =Mean energy
Subscripts
- B=Boltzmann
- max =Maximum
- mod =modified
Superscript
- =New constant different from
References
- Andreas, G.; Keller, G.; Warnecke, G. Entropy; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Phil, A. Thermodynamics and Statistical Mechanics: Equilibrium by Entropy Maximisation; Academic Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Rudolf, C. Ueber verschiedene für die Anwendung bequeme Formen der Hauptgleichungen der mechanischen Wärmetheorie. Annalen der Physik 1865. (In German) [Google Scholar] [CrossRef]
- Wu, J. Three Factors Causing the Thermal Efficiency of a Heat Engine to Be Less than Unity and Their Relevance to Daily Life. Eur. J. Phys. 2015, 36, 015008. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Shamekhi, L. Entropy Generation Analysis of the Revised Cheng-Minkowycz Problem for Natural Convective Boundary Layer Flow of Nanofluid in a Porous Medium. J. Thermal Sci. 2015, 19. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Mohammadi, F. Entropy Generation Analysis for Stagnation Point Flow in a Porous Medium over a Permeable Stretching Surface. J. Appl. Fluid Mech. 2014, 8, 753–763. [Google Scholar]
- Rashidi, M.M.; Mahmud, S. Analysis of Entropy Generation in an MHD Flow over a Rotating Porous Disk with Variable Physical Properties. Int. J. Energy 2014. [Google Scholar] [CrossRef]
- Abolbashari, M.H.; Freidoonimehr, N. Analytical Modeling of Entropy Generation for Casson Nano-Fluid Flow Induced by a Stretching Surface. Adv. Powder Technol. 2015, 231. [Google Scholar] [CrossRef]
- Baag, S.S.R.; Dash, M.G.C.; Acharya, M.R. Entropy Generation Analysis for Viscoelastic MHD Flow over a Stretching Sheet Embedded in a Porous Medium. Ain Shams Eng. J. 2016, 23. [Google Scholar] [CrossRef]
- Shi, Z.; Tao, D. Entropy Generation and Optimization of Laminar Convective Heat Transfer and Fluid Flow in a Microchannel with Staggered Arrays of Pin Fin Structure with Tip Clearance. Energy Convers. Manag. 2015, 94, 493–504. [Google Scholar] [CrossRef]
- Hossein, A.M.; Ahmadi, M.A.; Mellit, A.; Pourfayaz, F.; Feidt, M. Thermodynamic Analysis and Multi Objective Optimization of Performance of Solar Dish Stirling Engine by the Centrality of Entransy and Entropy Generation. Int. J. Electr. Power Energy Syst. 2016, 78, 88–95. [Google Scholar] [CrossRef]
- Giovanni, G. Statistical Mechanics: A Short Treatise; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Reif, F. Fundamentals of Statistical and Thermal Physics; Waveland Press: Long Grove, IL, USA, 2009. [Google Scholar]
- Rudolf, C.; Shimony, A. Two Essays on Entropy; University of California Press: Berkeley, CA, USA, 1977. [Google Scholar]
- Shu-Cherng, F.; Rajasekera, J.R.; Tsao, H.S.J. Entropy Optimization and Mathematical Programming; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Robert, M.G. Entropy and Information Theory; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Silviu, G. Information Theory with New Applications; MacGraw-Hill Books Company: New York, NY, USA, 1977. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. SigmobileMob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- Thomas, M.C.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Christodoulos, A.F.; Pardalos, P.M. Encyclopedia of Optimization; Springer Science & Business Media: New York, NY, USA, 2008. [Google Scholar]
- Arash, M.; Azarnivand, A. Application of Integrated Shannon’s Entropy and VIKOR Techniques in Prioritization of Flood Risk in the Shemshak Watershed, Iran. Water Resour. Manag. 2015, 30, 409–425. [Google Scholar] [CrossRef]
- Liu, L.; Miao, S.; Liu, B. On Nonlinear Complexity and Shannon’s Entropy of Finite Length Random Sequences. Entropy 2015, 17, 1936–1945. [Google Scholar] [CrossRef]
- Karmeshu. Entropy Measures, Maximum Entropy Principle and Emerging Applications; Springer: Berlin, Germany; Heidelberg, Germany, 2012. [Google Scholar]
- Jaynes, E.T. Information Theory and Statistical Mechanics. II. Phys. Rev. 1957, 108, 171–190. [Google Scholar] [CrossRef]
- Jaynes, E.T. On the Rationale of Maximum-Entropy Methods. Proc. IEEE 1982, 70, 939–952. [Google Scholar] [CrossRef]
- Jaynes, E.T. Prior Probabilities. IEEE Trans. Syst. Sci. Cybernet. 1968, 4, 227–241. [Google Scholar] [CrossRef]
- Kapur, J.N. Maximum-Entropy Models in Science and Engineering; John Wiley & Sons: New York, NY, USA, 1989. [Google Scholar]
- Kapur, J.N. Maximum-Entropy Probability Distribution for a Continuous Random Variate over a Finite Interval. J. Math. Phys. Sci. 1982, 16, 693–714. [Google Scholar]
- Ray, A.; Majumder, S.K. Concavity of maximum entropy through modified Burg’s entropy subject to its prescribed mean. Int. J. Math. Oper. Res. 2016, 8. to appear. [Google Scholar]
- Kapur, J.N. Measures of Information and Their Applications; Wiley: New York, NY, USA, 1994. [Google Scholar]
- Burg, J. The Relationship between Maximum Entropy Spectra and Maximum Likelihood Spectra. Geophysics 1972, 37, 375–376. [Google Scholar] [CrossRef]
- Narain, K.J.; Kesavan, H.K. Entropy Optimization Principles with Applications; Academic Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Solomon, K. Information Theory and Statistics; Courier Corporation: North Chelmsford, MA, USA, 2012. [Google Scholar]
- Amritansu, R.; Majumder, S.K. Derivation of some new distributions in statistical mechanics using maximum entropy approach. Yugoslav J. Oper. Res. 2013, 24, 145–155. [Google Scholar]
- Ulrych, T.J.; Bishop, T.N. Maximum Entropy Spectral Analysis and Autoregressive Decomposition. Rev. Geophys. 1975, 13, 183–200. [Google Scholar] [CrossRef]
- Michele, P.; Ferrante, A. On the Geometry of Maximum Entropy Problems. 2011. arXiv:1112.5529. [Google Scholar]
- Ke, J.-C.; Lin, C.-H. Maximum Entropy Approach to Machine Repair Problem. Int. J. Serv. Oper. Inform. 2010, 5, 197–208. [Google Scholar] [CrossRef]

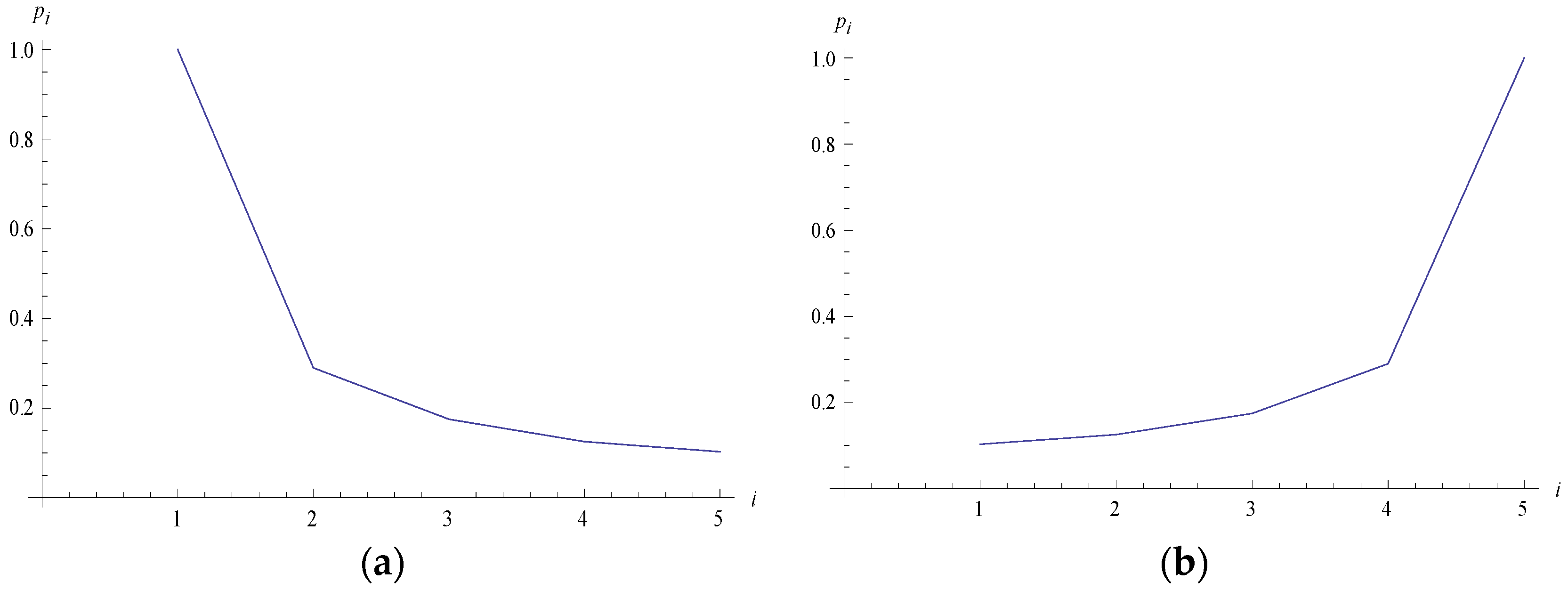
| 0.5 | 0.04082 |
| 1.0 | 0.11778 |
| 1.5 | 0.20294 |
| 2.0 | 0.28768 |
| 5.0 | 0.71376 |
| 10.0 | 1.1856 |
| 20.0 | 1.7512 |
| 30.0 | 2.1111 |
| 40.0 | 2.3754 |
| 50.0 | 2.5843 |
| m | Maximum Entropy Value of | Maximum Entropy Value of | Maximum Entropy Value of |
|---|---|---|---|
| 1.00 | 0 | −158.225 | 0 |
| 1.25 | 0.0896122 | −45.13505 | 0.6255029 |
| 1.50 | 0.1345336 | −38.98478 | 0.9547543 |
| 1.75 | 0.1633092 | −35.43113 | 1.194875 |
| 2.00 | 0.1836655 | −32.94620 | 1.385892 |
| 2.25 | 0.1989097 | −31.05219 | 1.542705 |
| 2.50 | 0.2107459 | −29.53735 | 1.675885 |
| 2.75 | 0.2201939 | −28.28982 | 1.790029 |
| 3.00 | 0.2279397 | −27.24394 | 1.888477 |
| 3.25 | 0.2344146 | −26.35851 | 1.973503 |
| 3.50 | 0.2399041 | −25.60649 | 2.046725 |
| 3.75 | 0.24461 | −24.96958 | 2.109324 |
| 4.00 | 0.248682 | −24.43512 | 2.162186 |
| 4.25 | 0.252127 | −23.99419 | 2.205980 |
| 4.50 | 0.2549453 | −23.64047 | 2.241209 |
| 4.75 | 0.257137 | −23.36942 | 2.268253 |
| 5.00 | 0.2587024 | −23.17789 | 2.287386 |
| 5.25 | 0.2596416 | −23.06376 | 2.298794 |
| 5.50 | 0.2599546 | −23.02585 | 2.302585 |
| 5.75 | 0.2596416 | −23.06376 | 2.298794 |
| 6.00 | 0.2587024 | −23.17789 | 2.287386 |
| 6.25 | 0.257137 | −23.36942 | 2.268253 |
| 6.50 | 0.2549453 | −23.64047 | 2.241209 |
| 6.75 | 0.252127 | −23.99419 | 2.205980 |
| 7.00 | 0.248682 | −24.43512 | 2.162186 |
| 7.25 | 0.24461 | −24.96958 | 2.109324 |
| 7.50 | 0.2399041 | −25.60649 | 2.046725 |
| 7.75 | 0.2344146 | −26.35851 | 1.973503 |
| 8.00 | 0.2279397 | −27.24394 | 1.888477 |
| 8.25 | 0.2201939 | −28.28982 | 1.790029 |
| 8.50 | 0.2107459 | −29.53735 | 1.675885 |
| 8.75 | 0.1989097 | −31.05219 | 1.542705 |
| 9.00 | 0.1836655 | −32.94620 | 1.385892 |
| 9.25 | 0.1633092 | −35.43113 | 1.194875 |
| 9.50 | 0.1345336 | −38.98478 | 0.9547543 |
| 9.75 | 0.0896122 | −45.13505 | 0.6255029 |
| 10.0 | 0 | −141.25285 | 0 |
| 1 | 1.000000 |
| 2 | 0.2899575 |
| 3 | 0.1747893 |
| 4 | 0.1253783 |
| 5 | 0.1027619 |
| 6 | 0.1027620 |
| 7 | 0.1253782 |
| 8 | 0.1747891 |
| 9 | 0.2899574 |
| 10 | 1.000000 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ray, A.; Majumder, S.K. A Note on Burg’s Modified Entropy in Statistical Mechanics. Mathematics 2016, 4, 10. https://doi.org/10.3390/math4010010
Ray A, Majumder SK. A Note on Burg’s Modified Entropy in Statistical Mechanics. Mathematics. 2016; 4(1):10. https://doi.org/10.3390/math4010010
Chicago/Turabian StyleRay, Amritansu, and S. K. Majumder. 2016. "A Note on Burg’s Modified Entropy in Statistical Mechanics" Mathematics 4, no. 1: 10. https://doi.org/10.3390/math4010010
APA StyleRay, A., & Majumder, S. K. (2016). A Note on Burg’s Modified Entropy in Statistical Mechanics. Mathematics, 4(1), 10. https://doi.org/10.3390/math4010010






