Understanding Visceral Leishmaniasis Disease Transmission and its Control—A Study Based on Mathematical Modeling
Abstract
:1. Introduction
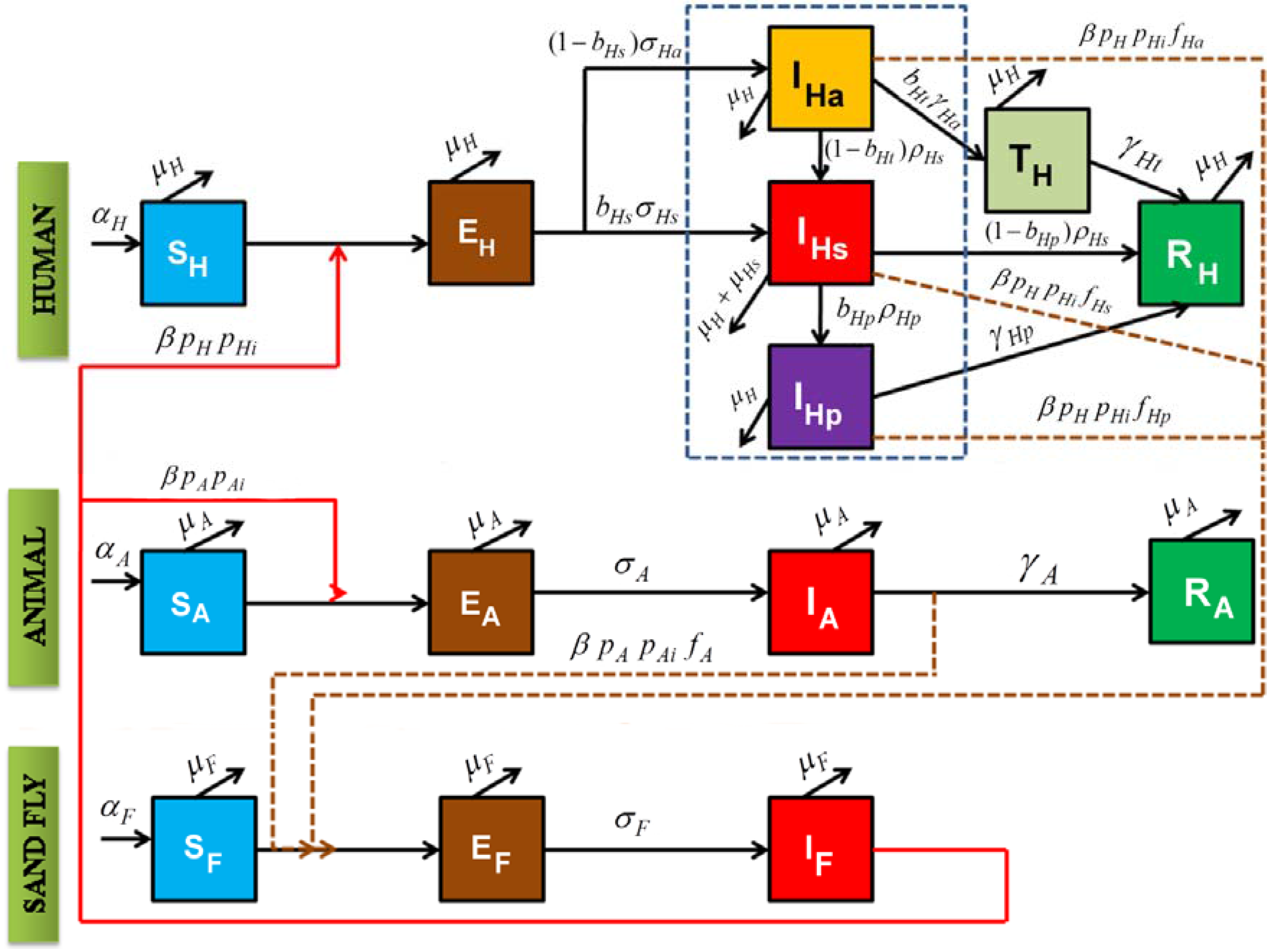
2. Model Construction
| Parameters | Symbols | Values | References |
|---|---|---|---|
| Natural birth/mortality rate of human | αH, μH | 7.95 × 10−5 day−1 | [31] |
| Biting rate of infected sandfly (kept constant for both human and animal infection spread) | β | 0.2856 day−1 | [15] |
| Natural birth, mortality rate of animal | αA, μA | 0.00167 day−1 | [18] |
| Natural birth, mortality rate of sandfly | αF, μF | 0.07 day−1 | [18] |
| Incubation period of sandfly | σF | 1 day−1 | [18] |
| Latent period of infection through animals | σA | 0.005 day−1 | [18] |
| Recovery rate of the animal population | γA | 0.015 day−1 | [18] |
| Probability of sandfly biting a human host according to availability of human blood meal | pH | 0.4 | Assumed |
| Probability of sandfly biting an animal host according to availability of animal blood meal | pA=1-pH | 0.6 | Assumed |
| Probability that an infected sandfly transmits infection to susceptible human host | pHi | 1 | Assumed |
| Probability that an infected fly transmits infection to susceptible animal host | pAi | 1 | Assumed |
| Proportion of humans who become symptomatically infected | bHs | 0.3 | Assumed |
| Duration between developing symptoms and becoming PKDL | ρHp | 0.001 day−1 | Assumed |
| Duration between asymptomatic infection and onset of symptoms | ρHs | 0.01 day−1 | Assumed |
| Duration of the latent stage in asymptomatically infected humans | σHa | 0.03333 day−1 | Assumed |
| Duration of the latent stage in symptomatically infected humans | σHs | 0.01 day−1 | [32] |
| Proportion of asymptomatic infections which recover directly (via transient state) | bHt | 0.001 | Assumed |
| Proportion of symptomatic infected who develop PKDL | bHp | 0.1 | [33] |
| Duration of the infectious period in asymptomatic patients leading to a delayed transition period | γHa | 0.01 day−1 | Assumed |
| Recovery rate of asymptomatic patients | γHt | 0.01 day−1 | Assumed |
| Recovery rate of symptomatic patients | γHs | 0.01 day−1 | [34] |
| Recovery rate of PKDL patients | γHp | 0.0055 day−1 | [35] |
| Weight for infection of flies from human asymptomatic patients | fHa | 0.001 | Assumed |
| Weight for infection of flies from human symptomatic patients | fHs | 0.299 | Assumed |
| Weight for infection of flies from human PKDL patients | fHp | 0.3 | Assumed |
| Weight for infection of flies from animal | fAb = 1 − (fHa + fHs + fHp) | 0.4 | Assumed |
3. Results and Discussion
3.1. Positivity and Boundedness
3.2. Deriving the Equilibrium Points from the Model
3.2.1. Disease Free Equilibrium
- (a)
- Absence of infected sandflies: In order to create the situation during which there were no infected sandflies, for calculations of equilibrium point (SH*, EH*, IHa*, IHs*, IHp*, TH*, RH*, SA*, EA*, IA*, RA*, SF*, EF*, IF*), the infected fly population IF was set to zero. This led all infected populations to become zero, without which the disease could not sustain in the populations considered. Hence, total population consisted of susceptible individuals alone with respect to each group. Therefore,
- (b)
- Absence of infected animal population: In this situation, only disease transmission between human and sandfly populations was considered but animal populations remained non-infected. To calculate equilibrium point (SH**, EH**, IHa**, IHs**, IHp**, TH**, RH**, SA**, EA**, IA**, RA**, SF**, EF**, IF**) in this scenario, EA**, IA** and RA** were set to zero. When animal populations were not infected, the disease transmission was between human and sandfly population alone. Therefore total animal population would be equal to susceptible animal population. The equilibriums of all other variables were found by substituting value of IF**. Hence,
- (c)
- Absence of infected humans: In this situation, only disease transmission between animal and sandfly populations was considered but human populations remained non-infected. To calculate the equilibrium point (SH***, EH***, IHa***, IHs***, IHp***, TH***, RH***, SA***, EA***, IA***, RA***, SF***, EF***, IF***), EH***, IHa***, IHs***, IHp***, RH*** were set to be zero. Therefore, the total human population would be equal to susceptible human population. The equilibriums of all other variables were found by substituting value of IF***. Hence,
3.2.2. Endemic Equilibrium
3.3. Basic Reproduction Number
3.4. Stability Analysis
3.4.1. Stability Analysis around Disease-Free Equilibrium
- (a)
- Absence of infected sandflies: The behavior of system could be understood by finding eigenvalues of J1 and J2 matrix. The eigenvalues were found after substituting the equilibrium points which were calculated for the sandfly uninfected case. As there was no infection in sandfly population, implies that there would be no infection through other population group. We obtained eigenvalues for this condition from the model as -µH, -µA, -µF, 0,0,0,0,0,0,0,0,0,0,0. When there is no disease transmission throughout the population, the system would be stable ifTheorem 4. The system (Equations (1)–(14)) is locally, asymptotically stable around the disease free equilibrium points (SH*, EH*, IHa*, IHs*, IHp*, TH*, RH*, SA*, EA*, IA*, RA*, SF*, EF*, IF*) if < 1, otherwise unstable.Proof: From the above eigenvalue analysis using Theorems 2 and 3, the proof of Theorem 4 is obvious if the inequality, < 1 holds true.
- (b)
- Absence of infected animal populations: The previously calculated equilibrium points were incorporated into the aforementioned matrices (J1 and J3). The following eigenvalues were obtainedTheorem 5. The system (Equations (1)–(14)) is locally asymptotically stable around the infected animal free equilibrium points (SH**, EH**, IHa**, IHs**, IHp**, TH**, RH**, SA**, EA**, IA**, RA**, SF**, EF**, IF**), if bHpγHs < γHs + bHpρHp + μH and bHtρHs < ρHs + bHtμHa + μH, otherwise unstable.Proof: From the above eigenvalue analysis it is clear that if bHpγHs < γHs + bHpρHp +μH and bHtρHs < ρHs + bHtμHa + μH holds true, only then the system is locally asymptotically stable, otherwise, it is unstable.
- (c)
- Absence of infected humans: The previously calculated equilibrium point (SH***, EH***, IHa***, IHs***, IHp***, TH***, RH***, SA***, EA***, IA***, RA***, SF***, EF***, IF***) were then incorporated into the aforementioned matrices (J1 and J3). The following eigenvalues were obtainedSince the obtained eigenvalues from matrix J1 and J3 were not all real and negative, the system is locally unstable.
3.4.2. Stability Analysis around Endemic Equilibrium
3.5. Numerical Analysis of the Model
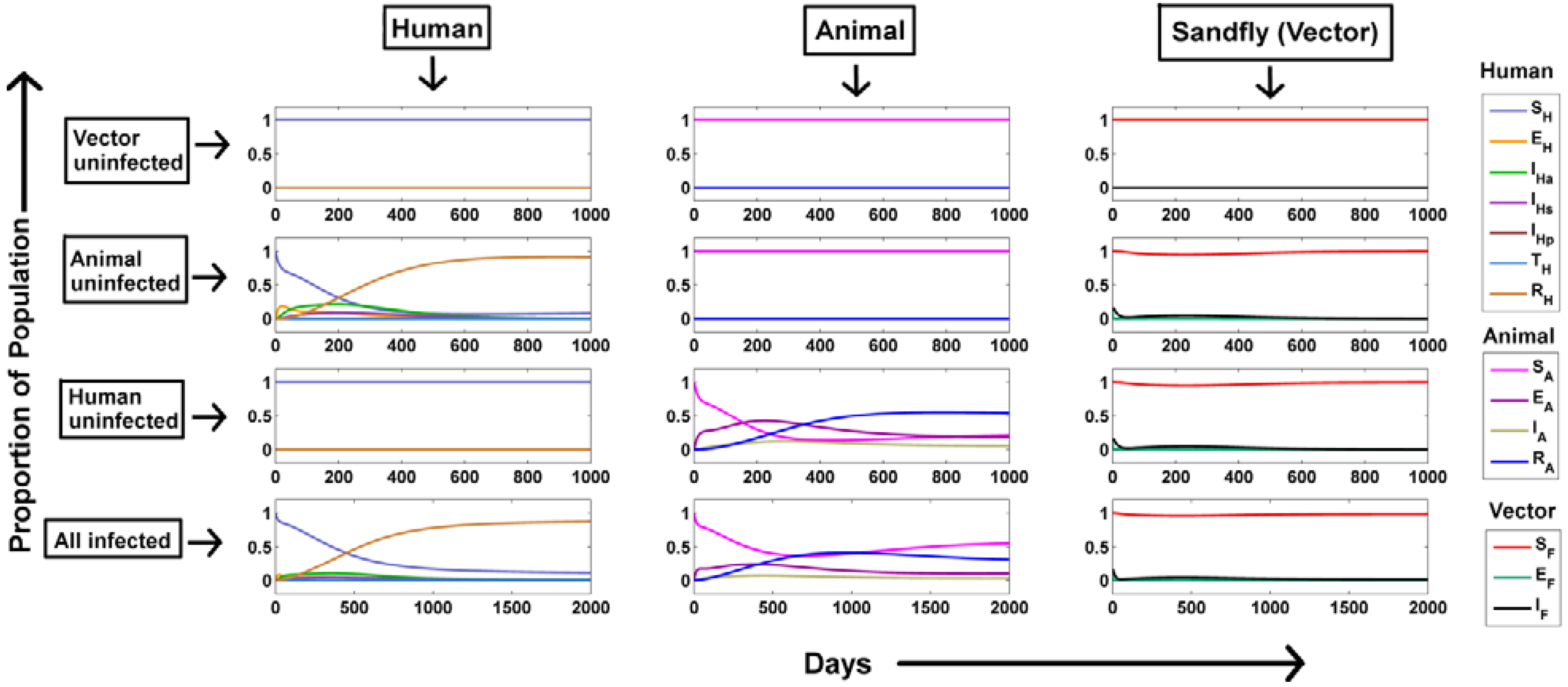
Dynamics of Visceral Leishmaniasis Transmission:
- (a)
- Vector populations remain uninfected: In order to create this situation, IF was kept to be zero. Hence, it is evident that absence of infected sandflies in the population would lead to no disease transmission. This could be captured from the model simulations as well (vector uninfected, Figure 2). The susceptible population stabilized around 1 and other populations stabilized around 0. As no infection persists in the population, the equilibrium prevalence of all population fractions remains same as the initial value justifying our analytical observation.
- (b)
- No infections through the animal population: When there were no infected animals, the disease transmission was restricted to humans and sandflies alone (animal uninfected, Figure 2). In order to create this situations, the preference of sandfly blood meal to animal (pA) and human population (pH) was changed from their default values to 0 and 1.The infected fly population shows a transient increase within a few days as disease load is totally dependent on a single host population that is the human population, avoiding delay in infection spread as opposed to distribution within two hosts where the infection would be lost by clearance of infection from each host. Hence the corresponding infected human populations also show a transient increase. As the susceptible human population (SH) becomes continually infected, SH shows a rapid decrease until it is totally transported. In addition, with respect to immunity of individual the recovered class shows a similar increase.
- (c)
- No infections through the human population: When there were no infected humans, the disease transmission was restricted to animals and sandflies alone (human uninfected, Figure 2). Similar to the non-infected animal scenario, the preference of sandfly blood meal to animal (pA) and human population (pH) was changed from their default values to 1 and 0 respectively to maintain infection only through animals. The infected fly population shows an increase similar to the animal uninfected case for the initial few days after which a rapid decline is observed. However, comparing both the situations, it can be observed that steady state of IF is around 100 fold higher in the situation when only animals are present as compared to situation when they are absent. This suggests that the animal population act as the major contributor for continual infection.
- (d)
- All populations were infected: Under the influence of both the host populations (human and animal), the dynamics of infected sandfly population demonstrated a combinatorial effect where the initial population rise resembled the infection under presence of only the human infected population and the latter persistent infected population resembled the infection under presence of only the animal infected population (all infected, Figure 2). Another observation was that the steady state of recovered animal population decreased further in presence of both animals and human populations as compared to situation where only animals were present suggesting an increased flow of infection from animals to humans via the increase in proportion of infected sandflies. A similar behavior of each population considered in our model was also observed in a previous study [17].
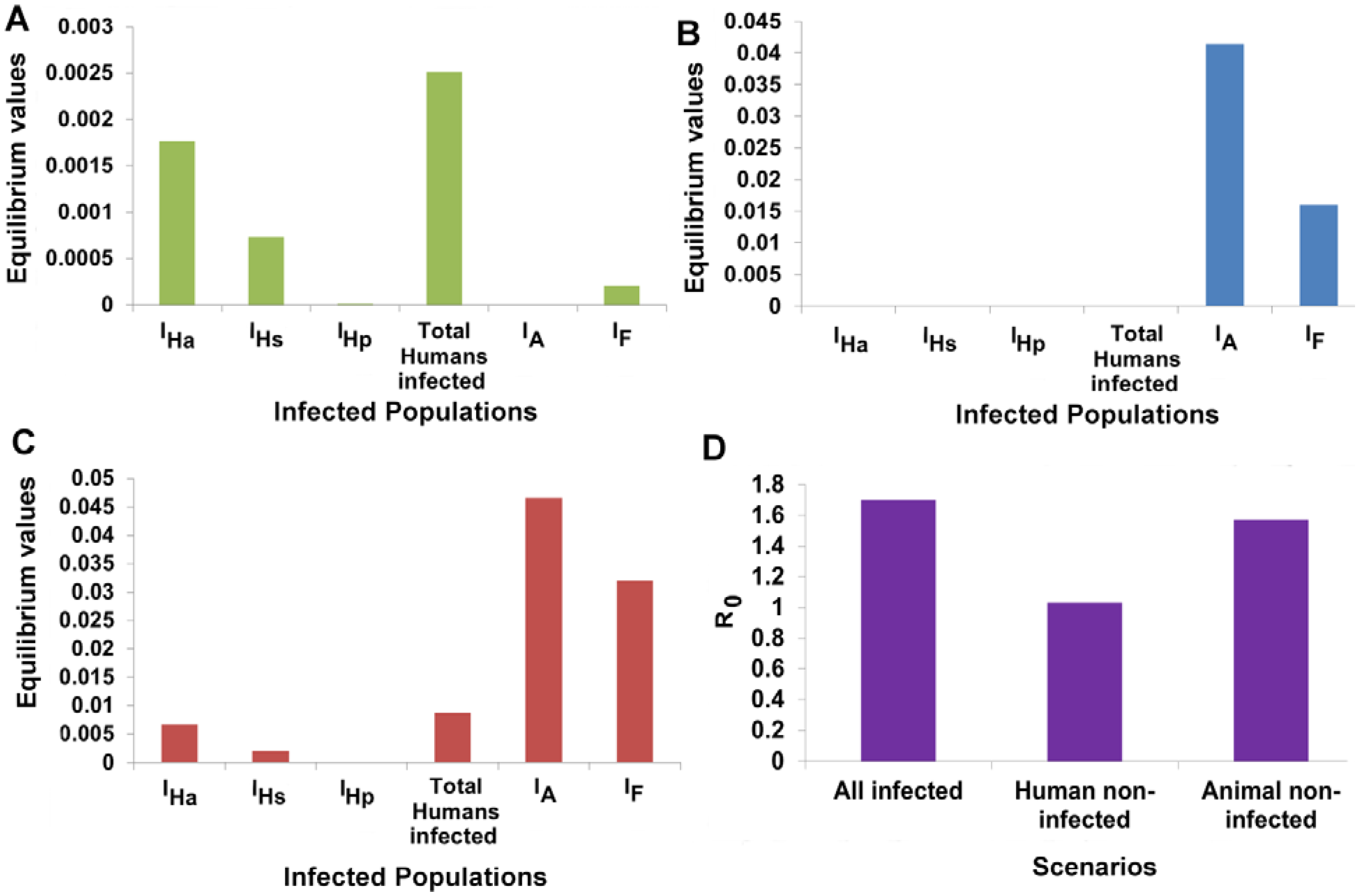
3.6. Animal Populations Act as a Reservoir of VL Infection
3.7. Designing Disease Control Strategies from Model Predictions
3.7.1. Identification of Important Parameters that Control VL Infection
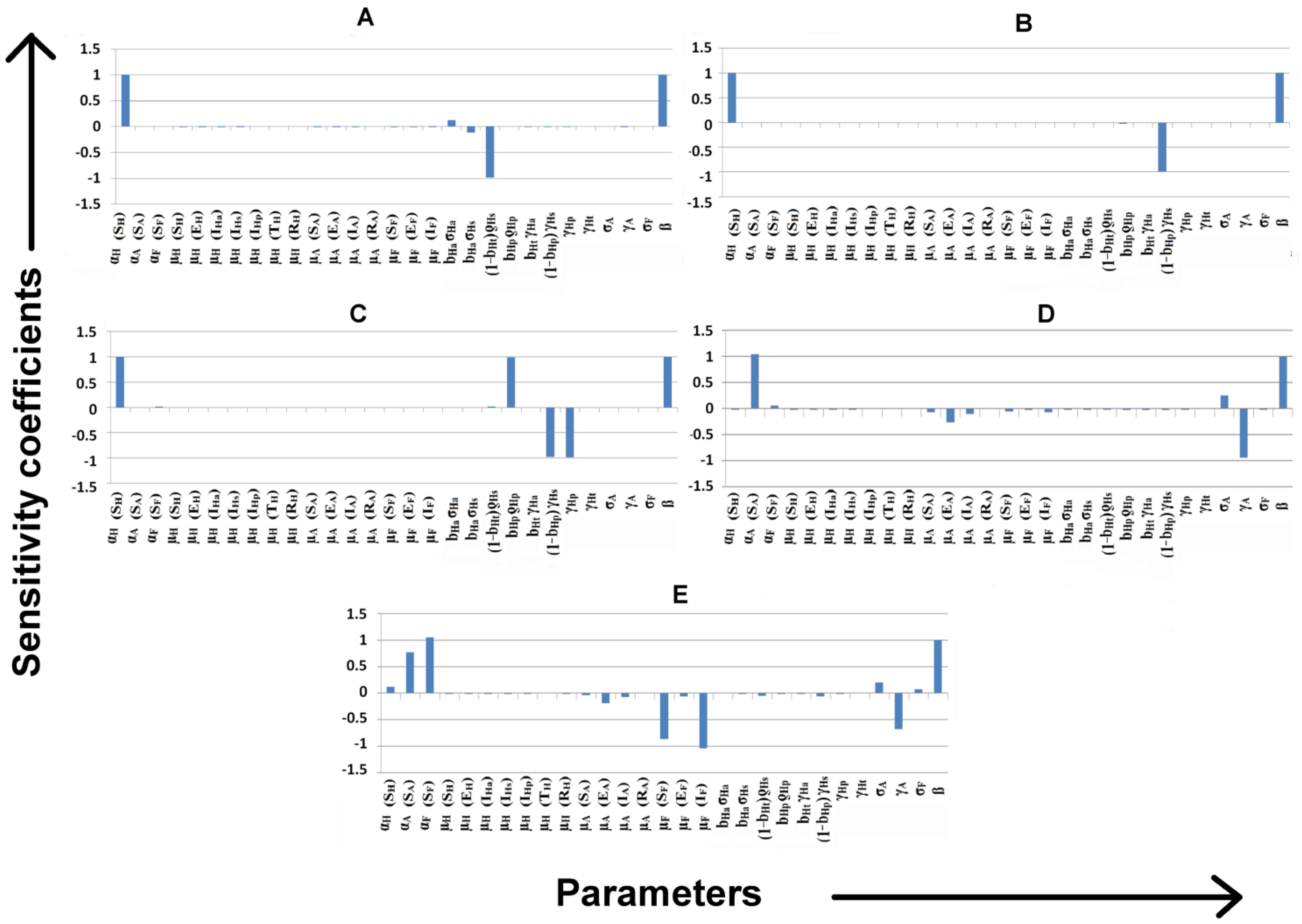
3.7.2. Variation of Parameters to Control VL Infection Spread
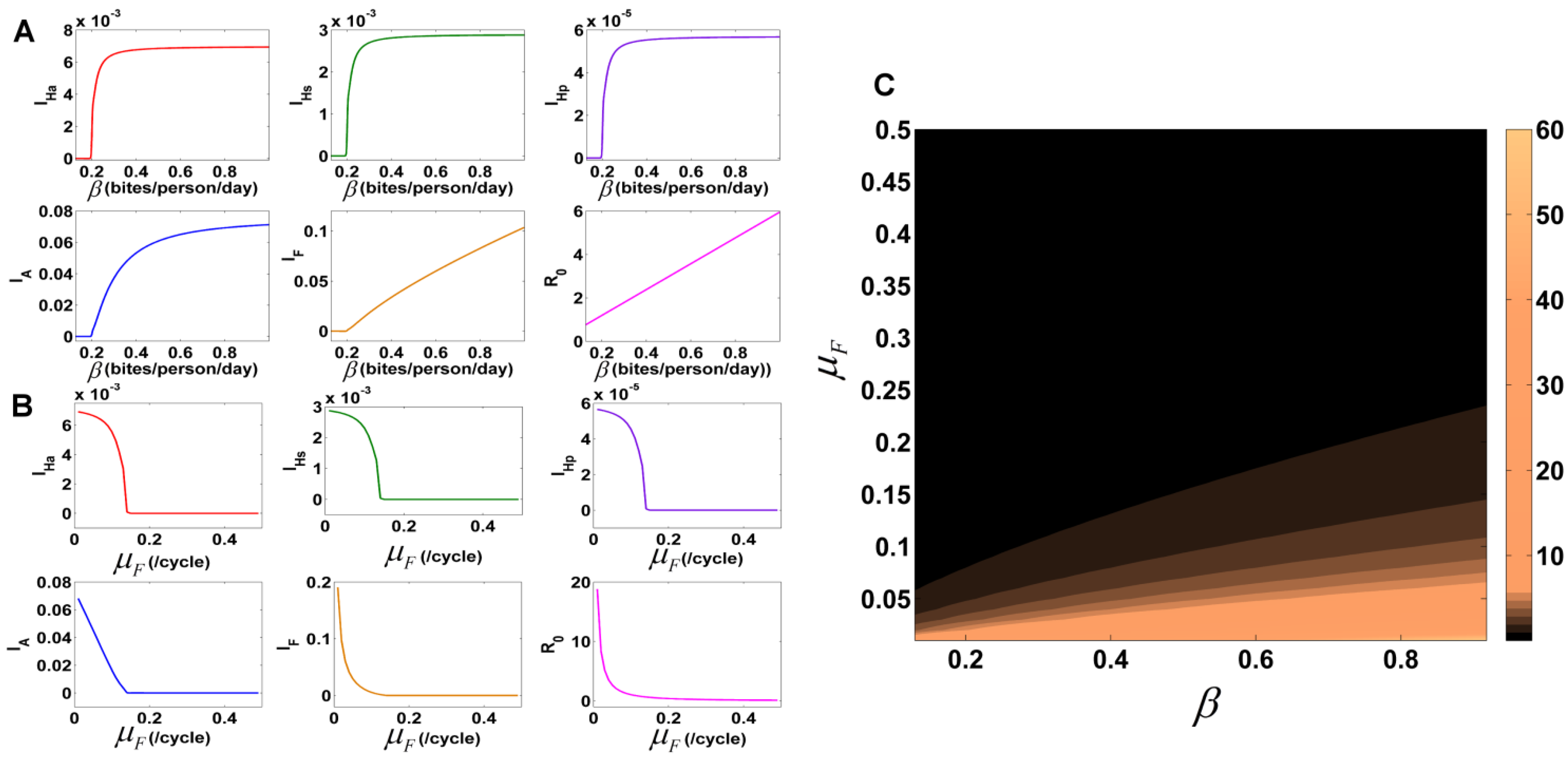
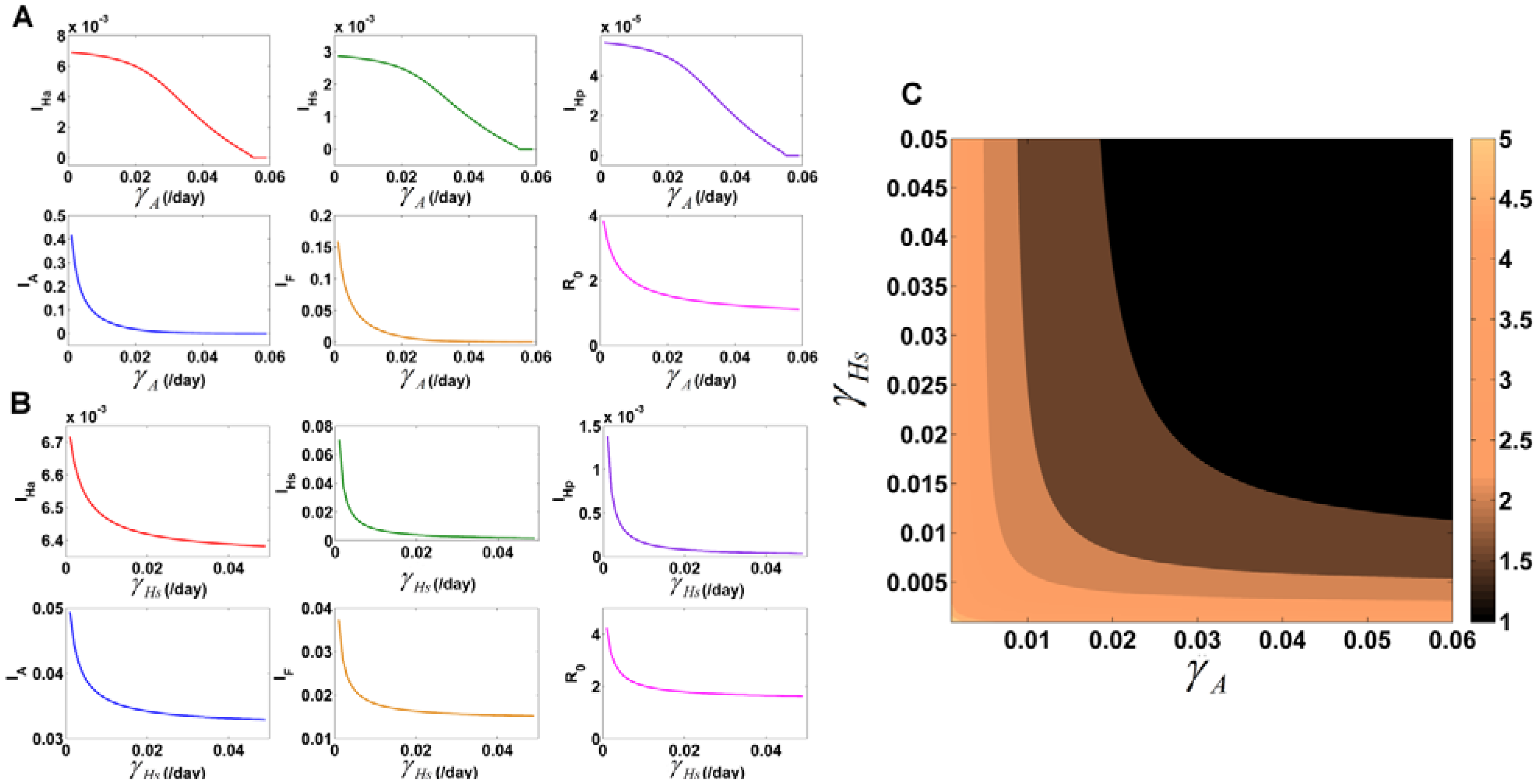
3.8. Testing the Model with Real Data
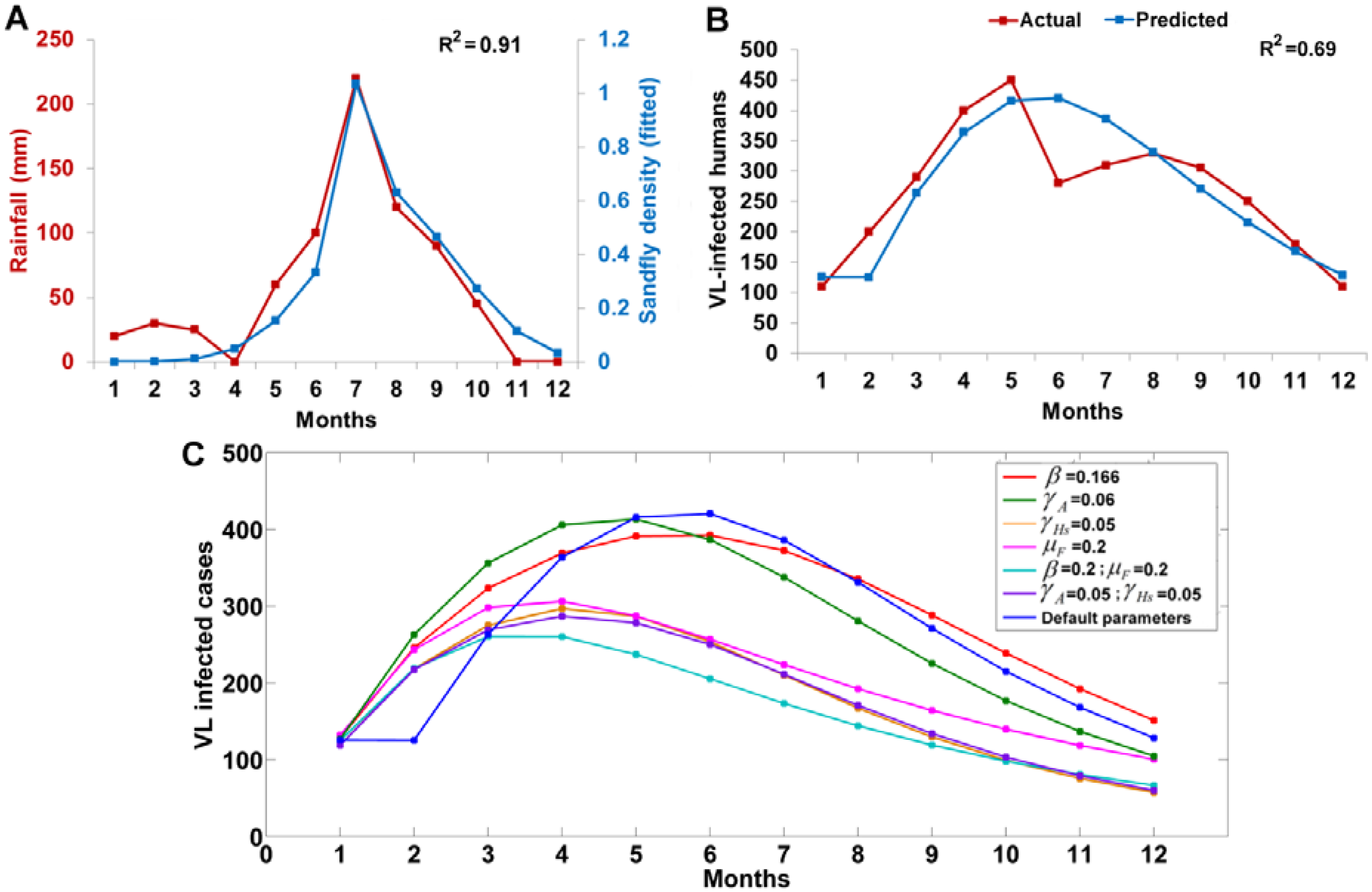
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Leishmaniasis fact sheet. Available online: http://www.who.int/mediacentre/factsheets/fs375/en/ (accessed on 10 September 2014).
- Research to Support Elimination of Visceral Leishmaniasis (WHO Annual Report 2009); WHO: Geneva, Switzerland, 2009.
- Desjeux, P. Global control and Leishmania HIV co-infection. Clin. Dermatol. 1993, 17, 317–325. [Google Scholar] [CrossRef]
- Sundar, S.; Mondal, D.; Rijal, S.; Bhattacharya, S.; Ghalib, H.; Kroeger, A.; Boelaert, M.; Desjeux, P.; Richter-Airijoki, H.; Harms, G. Implementation research to support the initiative on the elimination of kala azar from Bangladesh, India and Nepal—The challenges for diagnosis and treatment. Trop. Med. Int. Health 2008, 13, 2–5. [Google Scholar] [CrossRef] [PubMed]
- Mubayi, A.; Castillo-Chavez, C.; Chowell, G.; Kribs-Zaleta, C.; Ali Siddiqui, N.; Kumar, N.; Das, P. Transmission dynamics and underreporting of Kala-azar in the Indian state of Bihar. J. Theor. Biol. 2010, 262, 177–185. [Google Scholar] [CrossRef] [PubMed]
- Ashford, R.W. The leishmaniases as emerging and reemerging zoonoses. Int. J. Parasitol. 2000, 30, 1269–1281. [Google Scholar] [CrossRef]
- Lewis, D.J. The biology of Phlebotomidae in relation to leishmaniasis. Annu. Rev. Entomol. 1974, 19, 363–384. [Google Scholar] [CrossRef] [PubMed]
- Lewis, D.J. Phlebotomid sandflies. Bull. World Health Organ. 1971, 44, 535–551. [Google Scholar] [PubMed]
- Lewis, D.J.; Hitchocock, J.C. Phlebotomine sandflies of Chad. Ann. Trop. Med. Parasitol. 1968, 62, 117–121. [Google Scholar] [PubMed]
- Claborn, D.M. The biology and control of leishmaniasis vectors. J. Glob. Infect. Dis. 2010, 2, 127–134. [Google Scholar] [CrossRef] [PubMed]
- Chappuis, F.; Sundar, S.; Hailu, A.; Ghalib, H.; Rijal, S.; Peeling, R.W.; Alvar, J.; Boelaert, M. Visceral leishmaniasis: What are the needs for diagnosis, treatment and control? Nat. Rev. Microbiol. 2007, 5, 873–882. [Google Scholar] [CrossRef] [PubMed]
- Romero, G.A.S.; Boelaert, M. Control of visceral leishmaniasis in Latin America—A systematic review. PLoS Negl. Trop. Dis. 2010, 4, e584. [Google Scholar] [CrossRef] [PubMed]
- Mandal, S.; Sarkar, R.R.; Sinha, S. Mathematical models of malaria—A review. Malar. J. 2011, 10, 202. [Google Scholar] [CrossRef] [PubMed]
- Agyingi, E.O.; Ross, D.S.; Bathena, K. A model of the transmission dynamics of leishmaniasis. J. Biol. Syst. 2011, 19, 237–250. [Google Scholar] [CrossRef]
- ELmojtaba, I.M.; Mugisha, J.Y.T.; Hashim, M.H.A. Mathematical analysis of the dynamics of visceral leishmaniasis in the Sudan. Appl. Math. Comput. 2010, 217, 2567–2578. [Google Scholar] [CrossRef]
- Palatnik-de-sousa, C.B.; Renata, W.; Santos, D.O.S.; Teodoro, R.; Costa, D.A.; Reis, A.B.; Palatnik, M. Impact of canine control on the epidemiology of canine and human. Am. J. Trop. Med. Hyg. 2001, 65, 510–517. [Google Scholar] [PubMed]
- Burattini, M.N.; Coutinho, F.A.B.; Lopez, L.F.; Massad, E. Modelling the dynamics of leishmaniasis considering human, animal host and vector populations. J. Biol. Syst. 1998, 6, 337–356. [Google Scholar] [CrossRef]
- Dye, C. The logic of visceral leishmaniasis control. Am. J. Trop. Med. Hyg. 1996, 55, 125–130. [Google Scholar] [PubMed]
- Stauch, A.; Sarkar, R.R.; Picado, A.; Ostyn, B.; Sundar, S.; Rijal, S.; Boelaert, M.; Dujardin, J.C.; Duerr, H.P. Visceral leishmaniasis in the Indian subcontinent: Modelling epidemiology and control. PLoS Negl. Trop. Dis. 2011, 5, e1405. [Google Scholar] [CrossRef] [PubMed]
- Stauch, A.; Duerr, H.-P.; Picado, A.; Ostyn, B.; Sundar, S.; Rijal, S.; Boelaert, M.; Dujardin, J.C.; Eichner, M. Model-based investigations of different vector-related intervention strategies to eliminate visceral leishmaniasis on the Indian subcontinent. PLoS Negl. Trop. Dis. 2014, 8, e2810. [Google Scholar] [CrossRef] [PubMed]
- Bacaër, N.; Guernaoui, S. The epidemic threshold of vector-borne diseases with seasonality. J. Math. Biol. 2006, 53, 421–436. [Google Scholar] [CrossRef] [PubMed]
- Chaves, L.F.; Hernandez, M.-J. Mathematical modelling of American cutaneous leishmaniasis: Incidental hosts and threshold conditions for infection persistence. Acta Trop. 2004, 92, 245–252. [Google Scholar] [CrossRef] [PubMed]
- Das, P.; Mukherjee, D.; Sarkar, A.K. Effect of delay on the model of American cutaneous leishmaniasis. J. Biol. Syst. 2007, 15, 139–147. [Google Scholar] [CrossRef]
- Hasibeder, G.; Dye, C.; Carpenter, J. Mathematical modelling and theory for estimating the basic reproduction number of canine leishmaniasis. Parasitology 1992, 105, 43–53. [Google Scholar] [CrossRef] [PubMed]
- Dye, C. Leishmaniasis epidemiology: The theory catches up. Parasitology 1992, 104, S7–S18. [Google Scholar] [CrossRef] [PubMed]
- Malaviya, P.; Picado, A.; Singh, S.P.; Hasker, E.; Singh, R.P.; Boelaert, M.; Sundar, S. Visceral leishmaniasis in Muzaffarpur district, Bihar, India from 1990 to 2008. PLoS ONE 2011, 6, e14751. [Google Scholar] [CrossRef] [PubMed]
- ELmojtaba, I.M.; Mugisha, J.Y.T.; Hashim, M.H.A. Vaccination model for visceral leishmaniasis with infective immigrants. Math. Methods Appl. Sci. 2013, 36, 216–226. [Google Scholar] [CrossRef]
- Ribas, L.M.; Zaher, V.L.; Shimozako, H.J.; Massad, E. Estimating the Optimal Control of Zoonotic Visceral Leishmaniasis by the Use of a Mathematical Model. 2013; 2013. [Google Scholar] [CrossRef]
- Heffernan, J.M.; Smith, R.J.; Wahl, L.M. Perspectives on the basic reproductive ratio. J. R. Soc. Interface 2005, 2, 281–293. [Google Scholar] [CrossRef] [PubMed]
- Brauer, F.; Castillo-chavez, C. Texts in Applied Mathematics Mathematical Models in Population Biology and Epidemiology, 2nd ed.; Springer: Berlin, Germany; Heidelberg, Germany, 2011; pp. 345–464. [Google Scholar]
- Trade India. Available online: http://www.tradingeconomics.com/india/birth-rate-crude-per-1-000-people-wb-data.html (accessed on 10 September 2014).
- Malla, N.; Mahajan, R.C. Pathophysiology of visceral leishmaniasis—Some recent concepts. Indian J. Med. Res. 2006, 123, 267–274. [Google Scholar] [PubMed]
- Dye, C.; Wolpert, D.M. Earthquakes, influenza and cycles of Indian kala-azar. Trans. R. Soc. Trop. Med. Hyg. 1988, 82, 843–850. [Google Scholar] [CrossRef]
- Grevelink, S.A.; Lerner, E.A. Leishmaniasis. J. Am. Dermatol. Acad. 1996, 34, 257–272. [Google Scholar] [CrossRef]
- Gasim, S.; Elhassan, A.M.; Kharazmi, A.; Khalil, E.A.G.; Ismail, A.; Theander, T.G. The development of post-kala-azar dermal leishmaniasis (PKDL) is associated with acquisition of Leishmania reactivity by peripheral blood mononuclear cells (PBMC). Clin. Exp. Immunol. 2000, 119, 523–529. [Google Scholar] [CrossRef] [PubMed]
- Birkhoff, G.; Rota, G.C. Ordinary Differential Equations, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Garba, S.M.; Gumel, A.B.; Abu Bakar, M.R. Backward bifurcations in dengue transmission dynamics. Math. Biosci. 2008, 215, 11–25. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berman, A.; Hershkowitz, D. Matrix diagonal stability and its implications. SIAM J. Algebr. Discret. Methods 1983, 4, 377–382. [Google Scholar] [CrossRef]
- Rinaldi, F. Global stability results for epidemic models with latent period. Math. Med. Biol. 1990, 7, 69–75. [Google Scholar] [CrossRef]
- Brown, R.C.; Hinton, D.B. Lyapunov inequalities and their applications. In Survey on Classical Inequalities; Springer: Berlin, Germany; Heidelberg, Germany, 2000; pp. 1–25. [Google Scholar]
- Tapaswi, P.K.; Ghosh, A.K.; Mukhopadhyay, B.B. Transmission of Japanese encephalitis in a 3-population model. Ecol. Model. 1995, 83, 295–309. [Google Scholar] [CrossRef]
- Hoops, S.; Sahle, S.; Gauges, R.; Lee, C.; Pahle, J.; Simus, N.; Singhal, M.; Xu, L.; Mendes, P.; Kummer, U. COPASI—A complex pathway simulator. Bioinformatics 2006, 22, 3067–3074. [Google Scholar] [CrossRef] [PubMed]
- Lord, C.C.; Woolhouse, M.E.J.; Heesterbeek, J.A.P.; Mellor, P.S. Vector-borne diseases and the basic reproduction number: A case study of African horse sickness. Med. Vet. Entomol. 1996, 10, 19–28. [Google Scholar] [CrossRef] [PubMed]
- Hamby, D.M. A review of techniques for parameter sensitivity analysis of environmental models. Environ. Monit. Assess. 1994, 32, 135–154. [Google Scholar] [CrossRef] [PubMed]
- Srinivasan, R.; Panicker, K.N.; Dhanda, V. Population dynamics of Phlebotomus papatasi (Diptera:Phlebotomidae) in Pondicherry, India. Acta Trop. 1993, 54, 125–130. [Google Scholar] [CrossRef]
- Ghosh, K.; Mukhopadhyay, J.; Desai, M.M.; SenRoy, S.; Bhattacharya, A. Population ecology of Phlebotomus argentipes (Diptera: Psychodidae) in West Bengal, India. J. Med. Entomol. 1999, 36, 588–594. [Google Scholar] [CrossRef] [PubMed]
- Singh, N.; Mishra, J.; Singh, R.; Singh, S. Animal reservoirs of visceral leishmaniasis in India. J. Parasitol. 2013, 99, 64–67. [Google Scholar] [CrossRef] [PubMed]
- Costa, D.N.C.C.; Silva, M.A.; Werneck, G.L. Culling Dogs in Scenarios of Imperfect Control: Realistic Impact on the Prevalence of Canine Visceral Leishmaniasis. PLoS Negl. Trop. Dis. 2013, 7, e2355. [Google Scholar] [CrossRef] [PubMed]
- Courtenay, O.; Quinnell, R.J.; Garcez, L.M.; Shaw, J.J.; Dye, C. Infectiousness in a cohort of brazilian dogs: Why culling fails to control visceral leishmaniasis in areas of high transmission. J. Infect. Dis. 2002, 186, 1314–1320. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Subramanian, A.; Singh, V.; Sarkar, R.R. Understanding Visceral Leishmaniasis Disease Transmission and its Control—A Study Based on Mathematical Modeling. Mathematics 2015, 3, 913-944. https://doi.org/10.3390/math3030913
Subramanian A, Singh V, Sarkar RR. Understanding Visceral Leishmaniasis Disease Transmission and its Control—A Study Based on Mathematical Modeling. Mathematics. 2015; 3(3):913-944. https://doi.org/10.3390/math3030913
Chicago/Turabian StyleSubramanian, Abhishek, Vidhi Singh, and Ram Rup Sarkar. 2015. "Understanding Visceral Leishmaniasis Disease Transmission and its Control—A Study Based on Mathematical Modeling" Mathematics 3, no. 3: 913-944. https://doi.org/10.3390/math3030913
APA StyleSubramanian, A., Singh, V., & Sarkar, R. R. (2015). Understanding Visceral Leishmaniasis Disease Transmission and its Control—A Study Based on Mathematical Modeling. Mathematics, 3(3), 913-944. https://doi.org/10.3390/math3030913





