A Practical CNN–Transformer Hybrid Network for Real-World Image Denoising

Abstract

Real-world image denoising faces a critical trade-off: Convolutional Neural Network (CNN)-based methods are computationally efficient but limited in capturing long-range dependencies, while Transformer-based approaches achieve superior global modeling at prohibitive computational costs (>100 G Multiply–Accumulate Operations, MACs). This presents significant challenges for deployment in resource-constrained environments. We present a practical CNN–Transformer hybrid network that systematically balances performance and efficiency under practical deployment constraints for real-world image denoising. By integrating key components from NAFNet (Nonlinear Activation Free Network) and Restormer, our method employs three design strategies: (1) strategic combination of CNN and Transformer blocks enabling performance–efficiency trade-offs; (2) elimination of nonlinear operations for hardware compatibility; and (3) architecture search under explicit resource constraints. Experimental results demonstrate competitive performance with significantly reduced computational cost: our models achieve 39.98–40.05 dB Peak Signal-to-Noise Ratio (PSNR) and 0.958–0.961 Structural Similarity Index Measure (SSIM) on the SIDD dataset, and 39.73–39.91 dB PSNR and 0.959–0.961 SSIM on the DND dataset, while requiring 7.18–16.02 M parameters and 20.44–44.49 G MACs. Cross-validation results show robust generalization without significant performance degradation across diverse scenes, demonstrating a favorable trade-off among performance, efficiency, and practicality.

1. Introduction

Recent research on image processing techniques aimed at enhancing the quality of old or low-quality videos has been attracting significant attention, with image denoising playing a crucial role in the image restoration process. Traditional image processing methods rely on filtering and mathematical operations to remove noise, but they have limitations when dealing with various types and patterns of noise [1]. In contrast, deep learning-based approaches can adaptively remove noise by automatically learning its characteristics [2]. CNN-based models have significantly improved denoising performance and have demonstrated successful results in various image restoration processes. Recently, Transformer-based architectures have further advanced the field by introducing self-attention mechanisms that enable global context modeling, achieving state-of-the-art performance on benchmark datasets [3,4,5].

Convolutional Neural Networks (CNNs) have become a core technology in computer vision because they capture local patterns and efficiently extract image features. Likewise, image denoising models, such as DnCNN and FFDNet [6,7], are primarily based on CNNs. Recently, the state-of-the-art NAFNet model—a CNN-based denoising model optimized to reduce unnecessary computations while maintaining performance—has also shown excellent results in image restoration tasks [8]. Building upon NAFNet’s success, PA-NAFNet by Zhang et al. [9,10] further improved performanceby incorporating pyramid attention mechanisms [11] into the NAFNet framework. PA-NAFNet has demonstrated state-of-the-art results in various image restoration tasks and continues to be widely cited, with subsequent research building upon its architectural innovations. This demonstrates that NAFNet’s efficiency-focused approach remains highly relevant and continues to inspire ongoing developments in the field. The advantages of CNN-based image processing models are as follows:

• Excellent feature extraction capability: Convolution operations effectively extract local features of an image.
• Low computational cost: The computation scales linearly with the input size, making the overall model lightweight.

Due to these advantages, various image denoising models are designed based on CNNs. However, CNNs have the following drawbacks:

• Long-range dependency: Due to the inherent structure of CNNs, learning relationships between distant pixels is challenging, limiting the ability to capture global patterns and overall context.
• Low generalization performance: Due to their inductive biases and limited receptive fields, CNNs may struggle to capture long-range dependencies and generalize to domains that differ significantly from the training distribution.

For example, several studies have demonstrated critical cross-dataset generalization failures in CNN-based denoisers. Research has shown that deep learning methods including DnCNN, FFDNet, and MIRNet [6,7,12], when trained on the SIDD dataset, fail to outperform methods such as BM3D and NLM [13,14] on other real-world datasets like PolyU and CC, largely due to their inability to generalize across different camera sensors and noise characteristics [15]. This fundamental limitation stems from CNNs’ reliance on local receptive fields. Specifically, NAFNet, despite achieving computational efficiency (16.11 G MACs) and strong performance on standard benchmarks (39.96 dB PSNR, 0.960 SSIM on SIDD), employs Simplified Channel Attention (SCA) that operates primarily on channel-wise global pooling without explicit spatial global modeling. While this design proves effective within the training distribution, the lack of explicit global context modeling renders it may experience performance variation when deployed across different camera systems, ISO settings, and imaging conditions. These limitations make it difficult to deploy CNN-based models in real-world environments where noise characteristics inevitably vary, even if they achieve excellent performance on their training datasets.

To overcome these limitations, Transformer modules have been applied to computer vision, introducing a new paradigm. Originally used in the field of NLP, Transformers leverage the self-attention mechanism to effectively utilize global information in an image and model complex noise. The strengths of the Transformer module are as follows:

• Superior global feature extraction capability: Unlike CNNs, which primarily extract local features, the self-attention mechanism in Transformers computes and integrates global image information across the entire spatial domain, achieving superior performance on benchmark datasets (e.g., Restormer: 40.03 dB PSNR on SIDD).

However, Transformer modules have the following drawbacks:

• High computational cost: The self-attention mechanism exhibits quadratic complexity O (N²) with image resolution, making it difficult to deploy on edge devices or in real-time processing environments.
• Increased memory usage: Transformer-based models generally require more computations than CNNs, leading to higher memory usage, which makes real-time processing of high-resolution images challenging.

In implementation, when comparing the computational cost for a 256 × 256 image, Restormer with width 32 requires approximately 64.46 G MACs, which is approximately 4 times higher than NAFNet with width 32’s 16.11 G MACs. This indicates that Transformer-based models are not suitable for deployment in resource-constrained environments such as mobile devices or embedded systems.

To overcome the limitations of existing CNN and Transformer models, this paper proposes a practical hybrid model that leverages the strengths of both modules. In designing the model, we considered the following conditions:

• The model should perform well across diverse real-world environments beyond the training dataset, ensuring high practical applicability.
• The structure should have reasonable computational requirements and architecture that allows for efficient deployment on hardware platforms.

To meet these conditions, this study proposes a hybrid model that integrates CNN and Transformer architecture. By combining the lightweight algorithm structure of NAFNet and incorporating the Transformer module from Restormer to reinforce global information integration, we have developed a practical hybrid model that balances computational efficiency and denoising performance.

2. Related Works

2.1. Image Denoising Dataset

The selection of appropriate datasets for developing deep learning image denoising algorithms is a crucial factor in model performance evaluation and training. Datasets for image denoising can be categorized into synthetic noise datasets and real-world datasets. Synthetic noise datasets are generated by adding artificial noise such as Gaussian noise to clean images, while real-world noise datasets consist of noisy images captured with actual cameras. This paper collected and investigated Real-World Denoising Datasets to implement deep learning algorithms that can operate in real-world scenarios.

Table 1. Comparison of Image Denoising Datasets.

Dataset	No. of Scenes	No. of Images Pairs	Data Format
Real-World Dataset
SIDD	160	30,000	Raw, s-RGB
PolyU Dataset	40	100	Raw, s-RGB
RENOIR Dataset	120	500	Raw, sRGB
DnD	50	50	Raw, sRGB
Synthetic Datasets
Set12	12	12	Grayscale
BSD68	68	68	Grayscale
CBSD68	68	68	sRGB
Kodak24	24	24	sRGB

shows the comparison of real-world and synthetic image denoising datasets used in this study.

Real-world datasets contain authentic noise captured from actual camera sensors, reflecting the complex characteristics of real photography conditions. Each of these real-world datasets has distinct characteristics:

• SIDD (Smartphone Image Denoising Dataset) [16]: Contains 160 scenes captured from 5 smartphone cameras under various lighting conditions. Provides Small (160 pairs), Medium (320 pairs for training), and Full (30,000 pairs for official benchmarking).
• PolyU Dataset [17]: Generates ground truth by capturing the same scene multiple times with different cameras and computing the average values. It comprises 40 scenes with 80 images and 100 cropped images.
• RENOIR [18]: Consists of approximately 100 scenes and over 400 images, provided in pixel- and brightness-aligned format. Furthermore, this dataset focuses on real-world denoising under low-light conditions.
• DnD [19]: Consists of 50 pairs of noisy-clean image pairs and provides 50 noisy images for benchmarking. Also, it extracts 20 patches of 512 × 512 size from each image to provide a total of 1000 patches for real-world photography applications.

Synthetic datasets are generated by artificially adding statistical noise to clean images. The most used is Additive White Gaussian Noise (AWGN), which follows a normal distribution with zero mean and specified variance. While Gaussian noise is widely adopted due to its well-defined mathematical properties and ability to represent thermal noise components, real-world camera noise involves additional complexities including signal-dependent Poisson noise, spatially correlated patterns, and sensor-specific artifacts. The synthetic datasets used in denoising research have the following characteristics:

• Set12 [20]: Consists of 12 grayscale images with 12 scenes. It is widely used for evaluation of image denoising with artificially added Additive White Gaussian Noise (AWGN) at various noise levels.
• BSD68 [21]: Contains 68 grayscale images from the Berkeley Segmentation Dataset. It represents a diverse collection of natural scenes and is commonly used for benchmarking denoising algorithms with synthetic Gaussian noise.
• CBSD68 [22]: The color version of BSD68 dataset, containing 68 color images with the same resolutions. It is specifically designed for testing color image denoising algorithms on various real-world image content with artificially added noise.
• Kodak24 [23]: Comprises 24 high-quality color images, featuring fine details and rich textures.

In this study, we focus on real-world image denoising to develop models suitable for practical deployment in smartphones and cameras. Models trained on synthetic noise often suffer performance degradation when applied to real-world images due to the distribution gap between Gaussian noise assumptions and the more complex characteristics of real-world sensor noise, which includes various types of noise, such as signal-dependent components, spatially correlated patterns, and sensor artifacts. To address this fundamental challenge, we selected SIDD and DnD as our primary datasets because they are the most widely adopted real-world benchmarks with comprehensive published results, enabling fair comparison and reproducible research outcomes. By focusing exclusively on real-world datasets for both training and evaluation, we ensure that our hybrid architecture demonstrates genuine practical applicability for real-world deployment. Figure 1 and Figure 2 show sample images from real-world denoising datasets, illustrating the diverse characteristics of authentic camera noise.

2.2. Image Denoising Network

2.2.1. Convolutional Neural Network-Based Model

In the field of image processing, including denoising, research has primarily focused on developing models based on CNN architecture. DnCNN, proposed by Zhang et al., demonstrated superior performance in Gaussian noise removal by incorporating residual learning and batch normalization [24]. Subsequently, CBDNet by Guo et al. [25] proposed a dual network structure consisting of a noise estimation subnetwork and a non-blind denoising subnetwork to address real-world noise.

PRIDNet by Zhao et al. [26] improved adaptability to various noise types through multi-scale feature extraction and a kernel selection module [27], while RIDNet [28] demonstrated the capability to perform precise denoising regardless of noise variance by utilizing feature attention modules [29]. DRUNet [30] achieved high performance by combining residual blocks [31] with a U-Net-based structure and integrating it with the half-quadratic splitting algorithm.

Many CNN-based image denoising studies have improved performance by stacking layers deeply and designing complex model architectures to achieve sophisticated results [32,33,34]. However, Chen et al. proposed NAFNet, which achieved state-of-the-art performance in both computational efficiency and denoising quality by reducing unnecessary nonlinear activation functions and simplifying the model structure.

2.2.2. Transformer-Based Model

Transformers, based on self-attention [35], have the advantage of effectively utilizing global information and were primarily used in natural language processing. They have recently been applied to computer vision and have begun to be introduced in image processing fields by achieving good performance [36,37,38].

Wang et al. proposed Uformer, which presents a U-shaped Transformer architecture for image restoration. Uformer introduces locally enhanced window (LeWin) Transformer blocks that perform non-overlapping window-based self-attention to reduce computational cost while using depth-wise convolution in the feed-forward network to improve local feature capture capability. The hierarchical encoder–decoder structure with skip connections enables effective information flow between different scales, making it suitable for various image restoration tasks including denoising, deblurring, and deraining.

Xformer [39] presented by Zhang et al. features an X-shaped architecture that processes spatial and channel-wise Transformer blocks in separate branches. The X-shape design attempts to decompose attention computation to reduce complexity while maintaining global modeling capability, and the spatial unit Transformer block performs fine-grained local patch polymerization at a scale defined by the spatial size, while the channel unit Transformer block performs coarse-grained broadband replication at a scale defined by the channel size.

The biggest problem of Transformer-based models is their large computational cost, which makes them unsuitable for image processing. Zamir et al.’s Restormer mitigates the computational cost of existing Transformers through MDTA (Multi-Dconv Head Transposed Attention) and GDFN (Gated-Dconv Feed-Forward Network) modules, achieving higher generalization performance compared to CNN models. Restormer includes the transposed attention mechanism that operates in the channel dimension rather than the spatial dimension, significantly reducing computational complexity from O ((HW)²) to O (C²).

2.2.3. CNN–Transformer Hybrid Model

To address the limitations of single-module-based algorithms, recent research has also focused on hybrid models that combine the advantages of CNNs and Transformers [40].

Various hybrid models have been developed, including TECDNet [41], which combines a Transformer-based encoder with a CNN-based decoder; HTCNet [42], which specializes in speckle noise removal for SAR images; and Hcformer [43], which is specifically designed for low-dose CT medical imaging.

TECDNet (Transformer-Encoder CNN-Decoder Network) proposed by Wang et al. represents an early attempt at combining these architectures through a dual-pathway design. TECDNet employs a Transformer-based encoder for global feature extraction followed by a CNN-based decoder for detailed reconstruction. TECDNet employs a hierarchical network architecture where a Swin Transformer-based encoder equipped with a novel Radial Basis Function (RBF) attention mechanism serves as the primary feature extractor to capture global contextual dependencies, while a residual CNN-based decoder is subsequently utilized to perform detailed image reconstruction with significantly reduced computational complexity compared to pure Transformer-based approaches.

HTCNet (Hybrid Transformer–CNN Network) by Huang et al. is specifically designed for speckle noise removal in SAR (Synthetic Aperture Radar) images. HTCNet introduces a parallel processing approach where CNN and Transformer branches operate simultaneously on different aspects of the input. The CNN branch focuses on local speckle pattern recognition, while the Transformer branch captures global statistical dependencies.

Hcformer (Hybrid CNN–Transformer) developed by Zhang et al. targets low-dose CT medical imaging applications. Hcformer employs a multi-scale hybrid architecture where different resolution levels are processed by either CNN or Transformer modules based on the spatial dimensions.

2.2.4. Contribution of Our Study

Despite the individual success of CNN-based and Transformer-based approaches in image denoising, the application of hybrid CNN–Transformer architecture specifically to real-world image denoising remains limited. Most existing hybrid models have been developed for synthetic noise scenarios or specialized domains (medical imaging, SAR processing), with limited focus on the complex noise characteristics inherent in real-world photography captured by consumer devices such as smartphones and digital cameras.

Real-world noise challenges, such as spatially diverse noise patterns, sensor-specific artifacts, and complex noise correlations, require different optimization strategies than synthetic noise. While synthetic noise can be effectively handled with conventional CNN methods, real-world noise requires both preserving local details and understanding global context. Therefore, hybrid architecture is particularly promising in this area.

This motivated our work to develop a hybrid CNN–Transformer model designed for practical deployment in real-world denoising scenarios, with explicit consideration of computational efficiency constraints.

The main differentiating characteristics of the proposed model compared to existing hybrid approaches are as follows:

• Strategic Architecture Design: Unlike existing methods that apply Transformersacross the entire network or employ complex multi-branch architectures, we achieve computational efficiency by utilizing a streamlined U-Net structure with Transformer blocks strategically positioned at the bottleneck level, thereby obtaining the benefits of global feature extraction while minimizing computational overhead.
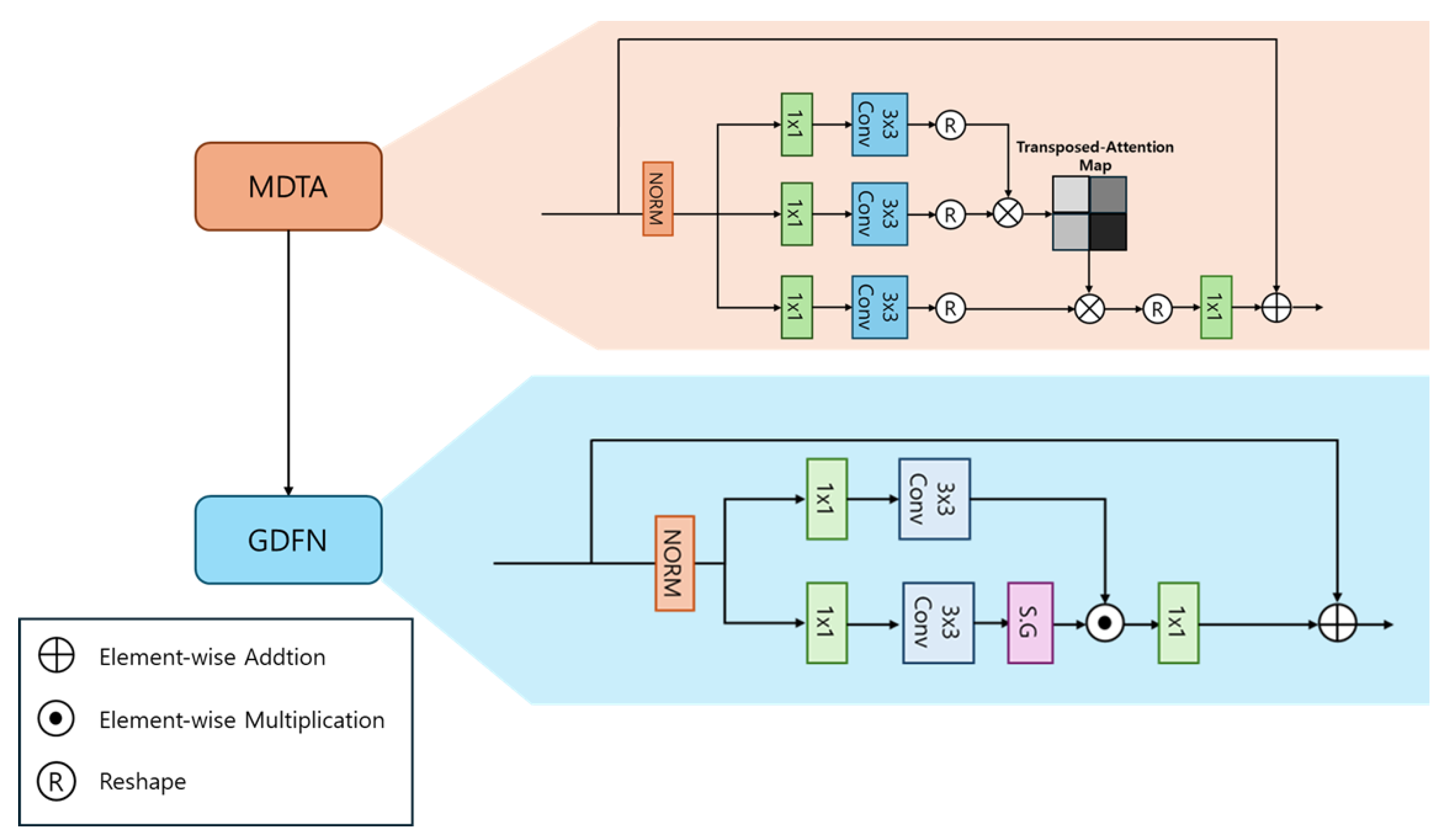
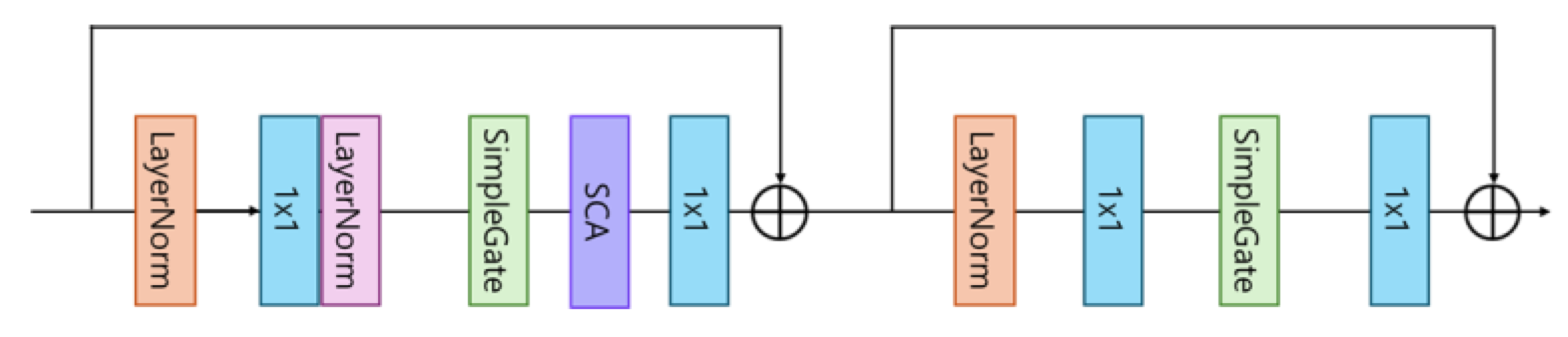
• Selective Component Integration: The proposed approach carefully integrates NAFNet’s lightweight CNN modules with Restormer’s efficient Transformer modules (MDTA, GDFN), combining the strengths of each component while maintaining manageable model complexity through explicit resource constraints (<5 M parameters, <25 G MACs).
• Balanced Performance–Efficiency Trade-off: In contrast to existing methods that either substantially increase computational cost to achieve performance gains or compromise performance for efficiency, the proposed approach demonstrates competitive performance (39.73 dB PSNR, 0.9588 SSIM on SIDD) with practical computational requirements suitable for deployment in resource-constrained environments.
• Simplified Integration: Our approach avoids the complex feature fusion mechanisms required by parallel architectures (HTCNet, HCformer) by using a unified encoder–decoder structure with strategic module placement, resulting in more stable training and easier implementation.

These characteristics position our model as a practical solution for real-world image denoising applications, providing a favorable balance between computational efficiency and denoising performance that is currently lacking in existing hybrid approaches.

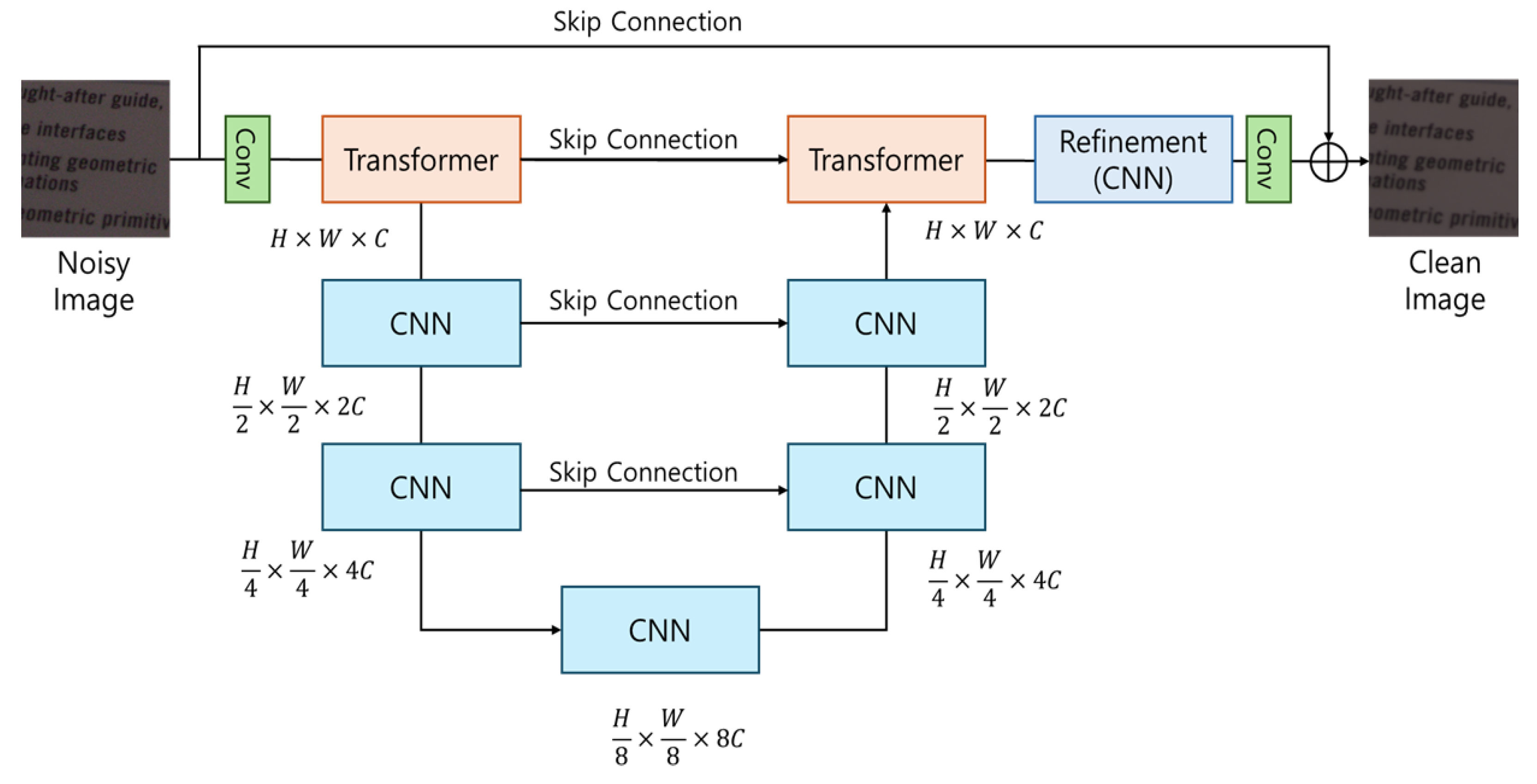
3. Methods

3.1. Architecture

In this paper, we propose a hybrid model combining Transformer and CNN to enhance image denoising performance while maintaining computational efficiency suitable for practical deployment. The fundamental structure of the model is based on a U-Net Encoder–Decoder architecture with an additional Refinement block to further improve the quality of the restored images. Its skip connections effectively preserve spatial details during resolution changes, and its symmetric structure provides a well-validated performance for image-to-image tasks.

The model uses skip connections to directly link the extracted features from each encoding stage to the corresponding decoding stage, thereby enhancing image reconstruction performance and minimizing information loss. The overall model can be defined as:

$$\mathbf{Y}=\mathrm{f}\_\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}({\mathbf{X}}_{\mathbf{0}})=\mathrm{R}(\mathrm{D}(\mathrm{E}({\mathbf{X}}_{\mathbf{0}}))+{\mathbf{X}}_{\mathbf{0}})$$

(1)

where ${\mathbf{X}}_{\mathbf{0}}\in R^{H \times W \times C}$ denotes the input noisy image and $\mathbf{Y}$ is the denoised output, E represents the encoder, D represents the decoder, and R represents the refinement. The addition of ${\mathbf{X}}_{\mathbf{0}}$ represents a skip connection that directly connects the input image to the final output, enabling the model to avoid gradient vanishing and preserving the original image structure.

The Encoder–Decoder consists of three levels. Given the input noisy image ${\mathbf{X}}_{\mathbf{0}}$, the encoder process is defined as:

$$\begin{gathered} {\mathbf{F}}_0=\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v}({\mathbf{X}}_{\mathbf{0}}), \\ {\mathbf{F}}_{\mathbf{1}}=\mathrm{T}\mathrm{B}({\mathbf{F}}_{\mathbf{1}}), \\ {\mathbf{F}}_{\mathbf{2}}=\mathrm{C}\mathrm{B}(\mathrm{D}\mathrm{S}({\mathbf{F}}_{\mathbf{1}})), \\ {\mathbf{F}}_{\mathbf{3}}=\mathrm{C}\mathrm{B}(\mathrm{D}\mathrm{S}({\mathbf{F}}_{\mathbf{2}})), \\ {\mathbf{F}}_{\mathbf{4}}=\mathrm{C}\mathrm{B}(\mathrm{D}\mathrm{S}({\mathbf{F}}_{\mathbf{3}})) \end{gathered}$$

(2)

where TB denotes the Transformer Block, CB denotes the CNN Block, and DS indicates the downsampling operation that reduces the spatial resolution by a factor of 2 while doubling the number of channels.

The decoder process with skip-connection is defined as:

$$\begin{gathered} {\mathbf{F}}_{\mathbf{3}}^{\mathbf{\prime }}=\mathrm{C}\mathrm{B}(\mathrm{U}\mathrm{S}({\mathbf{F}}_{\mathbf{4}})\oplus {\mathbf{F}}_{\mathbf{3}}), \\ {\mathbf{F}}_{\mathbf{2}}^{\mathbf{\prime }} = \mathrm{C}\mathrm{B}(\mathrm{U}\mathrm{S}({\mathbf{F}}_{\mathbf{3}}^{\mathbf{\prime }})\oplus {\mathbf{F}}_{\mathbf{2}}), \\ {\mathbf{F}}_{\mathbf{1}}^{\mathbf{\prime }}=\mathrm{T}\mathrm{B}(\mathrm{U}\mathrm{S}({\mathbf{F}}_{\mathbf{2}}^{\mathbf{\prime }})\oplus {\mathbf{F}}_{\mathbf{1}}) \end{gathered}$$

(3)

where US denotes upsampling, and ⊕ denotes element-wise addition for skip connections.

Transformer blocks are applied at the first level of both the encoder and decoder to capture global image features. Subsequently, the CNN-based NAFBlock is utilized to gradually downsample and learn high-dimensional representations while extracting fine-grained details and contextual information. The final refinement stage is formulated as:

$$\begin{gathered} \mathbf{R}=\mathrm{C}\mathrm{B}({\mathbf{F}}_{\mathbf{1}}^{\mathbf{\prime }}), \\ \mathbf{Y}=\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v}(\mathbf{R}\oplus {\mathbf{X}}_{\mathbf{0}}) \end{gathered}$$

(4)

This structure enables the preservation of the input image’s original structure while leveraging the Transformer module for global context extraction and the CNN module for detailed feature extraction, thereby improving image restoration performance. The placement of Transformer blocks exclusively at the first level is driven by both computational constraints and representational advantages. From a computational perspective, self-attention’s O (N²) complexity becomes practical at the first level, enabling global reasoning. At this level, the Transformer’s ability to capture long-range dependencies enables the model to integrate contextual information across the entire image, ensuring spatial consistency and coherent structural reconstruction—critical for handling spatially variant real-world noise patterns that require global coordination. In contrast, CNN blocks efficiently handle high-resolution processing at encoder and decoder stages, where their inductive bias for local feature extraction is well-suited for capturing fine-grained texture details, edge information, and local noise patterns without the prohibitive computational cost of attention mechanisms. The synergy between these components—CNN for local detail preservation and Transformer for global coherence—enables effective restoration of both high-frequency details and overall image structure. The proposed model is illustrated in Figure 3.

3.2. Transformer Block

The Transformer module applied in this study is based on Restormer, which addresses the limitations of traditional self-attention modules by incorporating two key algorithms: MDTA (Multi-Dconv Head Transposed Attention) and GDFN (Gated-Dconv Feed-Forward Network).

MDTA (Multi-Dconv Head Transposed Attention) represents a novel attention mechanism that fundamentally differs from traditional self-attention by performing attention computation in the channel dimension rather than the spatial dimension. This approach significantly reduces computational complexity from O ((HW)²) to O (C²) while effectively capturing global contextual information. Given the input feature $\mathbf{X}\in {\mathbf{R}}^{H \times W \times C}$, the MDTA process consists of the following sequential steps:

First, the module generates query(Q), key(K), and value(V) representation through a combination of pointwise and depth-wise convolutions:

$$\begin{gathered} \mathbf{Q}=\mathrm{W}\_\widehat{\mathrm{d}}(q)(\mathrm{W}\_\widehat{\mathrm{p}}(q)(\mathrm{L}\mathrm{N}(\mathbf{X})), \\ \mathbf{K}=\mathrm{W}\_\widehat{\mathrm{d}}(k)(\mathrm{W}\_\widehat{\mathrm{p}}(k)(\mathrm{L}\mathrm{N}(\mathbf{X})), \\ \mathbf{V}=\mathrm{W}\_\widehat{\mathrm{d}}(v)(\mathrm{W}\_\widehat{\mathrm{p}}(v)(\mathrm{L}\mathrm{N}(\mathbf{X})), \end{gathered}$$

(5)

where $\mathrm{W}\_\widehat{\mathrm{p}}(·)$ denotes 1 × 1 pointwise convolution for cross-channel aggregation, $\mathrm{W}\_\widehat{\mathrm{d}}(·)$ denotes 3 × 3 depth-wise convolution for encoding spatial context, and LN is layer normalization.

Then, the query, key, and value tensors are reshaped to facilitate channel-wise attention computation:

$$\begin{gathered} \widehat{\mathbf{Q}}=\mathrm{R}\mathrm{e}\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e}(\mathbf{Q},(HW,C)) \\ \widehat{\mathbf{K}}=\mathrm{R}\mathrm{e}\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e}(\mathbf{K},(HW,C)) \\ \widehat{\mathbf{V}}=\mathrm{R}\mathrm{e}\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e}(\mathbf{V},(HW,C)) \end{gathered}$$

(6)

The attention process is defined as:

$$\mathbf{A}=\mathrm{S}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}(\widehat{\mathit{K}}·\widehat{\mathit{Q}}/\alpha )\in {\mathbf{R}}^{C\times C}$$

(7)

where α is a learnable scaling parameter to control the magnitude of the dot product. Unlike traditional self-attention that computes attention maps of size HW × HW, MDTA calculates a transposed attention map of size C × C. The learnable scaling parameter α is initialized to 1.0 and allows the model to adaptively control the magnitude of attention weights during training, preventing gradient explosion issues that can occur with high-dimensional dot products.

The final output is obtained by applying the attention map to the value tensor and adding a residual connection:

$$\widehat{\mathbf{X}}= \widehat{\mathbf{V}} · \mathbf{A}+\mathbf{X}$$

(8)

The key mechanism of MDTA is a transposed attention mechanism, where attention is computed across feature channels rather than spatial locations. This enables the model to capture global dependencies while maintaining linear computational complexity with respect to spatial resolution. The integration of depth-wise convolutions before attention computation enriches local spatial context, allowing MDTA to effectively combine both local and global context extracting capabilities.

GDFN (Gated-Dconv Feed-Forward Network) represents an enhanced feed-forward network that incorporates a gating mechanism to perform controlled feature transformation. Unlike conventional feed-forward networks, GDFN selectively suppresses less informative features while allowing useful information to propagate through the network hierarchy. Given the input feature $\mathbf{X}\in R^{H \times W \times C}$, the GDFN process is formulated as follows.

First, the GDFN expands the input channels by a factor of r through 1 × 1 convolution, creating dual pathways for parallel processing:

$$\begin{gathered} {\mathbf{X}}_{\mathbf{1}}=\mathrm{W}\_\mathrm{p}1(\mathrm{L}\mathrm{N}(\mathbf{X}))\in R^{H\times W\times rC} \\ {\mathbf{X}}_{\mathbf{2}}=\mathrm{W}\_\mathrm{p}1(\mathrm{L}\mathrm{N}(\mathbf{X}))\in R^{H\times W\times rC} \end{gathered}$$

(9)

where W_p1 denotes separate 1 × 1 convolution for channel expansion, and LN denotes layer normalization.

After point-wise convolution, both pathways process 3 × 3 depth-wise convolution to encode spatially neighboring pixel information:

$$\begin{gathered} {\mathbf{X}}_{\mathbf{1}}^{\mathbf{\prime }}=\mathrm{W}\_\mathrm{d}({\mathbf{X}}_{\mathbf{1}})\in R^{H\times W\times rC}, \\ {\mathbf{X}}_{\mathbf{2}}^{\mathbf{\prime }}=\mathrm{W}\_\mathrm{d}({\mathbf{X}}_{\mathbf{2}})\in R^{H\times W\times rC} \end{gathered}$$

(10)

where W_d denotes 3 × 3 depth-wise convolution for spatial context aggregation.

The gating mechanism is implemented through the element-wise product of two parallel transformations, where one pathway is activated with GeLU non-linearity:

$${\mathbf{X}}_{\mathbf{g}\mathbf{a}\mathbf{t}\mathbf{e}\mathbf{d}}=\mathrm{G}\mathrm{e}\mathrm{L}\mathrm{U}({\mathbf{X}}_{\mathbf{1}}^{\mathbf{\prime }})\odot {\mathbf{X}}_{\mathbf{2}}^{\mathbf{\prime }}$$

(11)

where ⊙ denotes element-wise multiplication. In the original Restormer, the GeLU (Gaussian Error Linear Unit) activation function is used:

$$\mathrm{GeLU} (x) = 0.5x(1 + \tan \mathrm{h}(\sqrt{2/\pi }(x+0.044715{\times }^3)\left)\right)$$

(12)

However, in this study, we replaced GeLU with the Simple Gate mechanism proposed in NAFNet to ensure computational stability and consistency across the model. The final output is obtained by reducing the expanded channels back to the original dimension:

$$\widehat{\mathbf{X}}=\mathrm{W}\_\mathrm{p}2({\mathbf{X}}_{\mathbf{g}\mathbf{a}\mathbf{t}\mathbf{e}\mathbf{d}})+\mathbf{X}$$

(13)

where W_p2 denotes 1 × 1 convolution for channel reduction, and the residual connection preserves the original input information.

The key mechanism of GDFN is its controlled feature transformation capability. The gating mechanism enables the network to adaptively control information flow by suppressing irrelevant features while amplifying useful ones. The integration of depth-wise convolutions enriches the local spatial context, and the GeLU activation provides smooth non-linearity that enhances gradient flow during training. This design optimizes computational efficiency.

The transformer block, MDTA and GDFN are illustrated in Figure 4 and Figure 5. Leveraging these advantages, we incorporate Transformer modules into the proposed model, allowing effective global feature extraction.

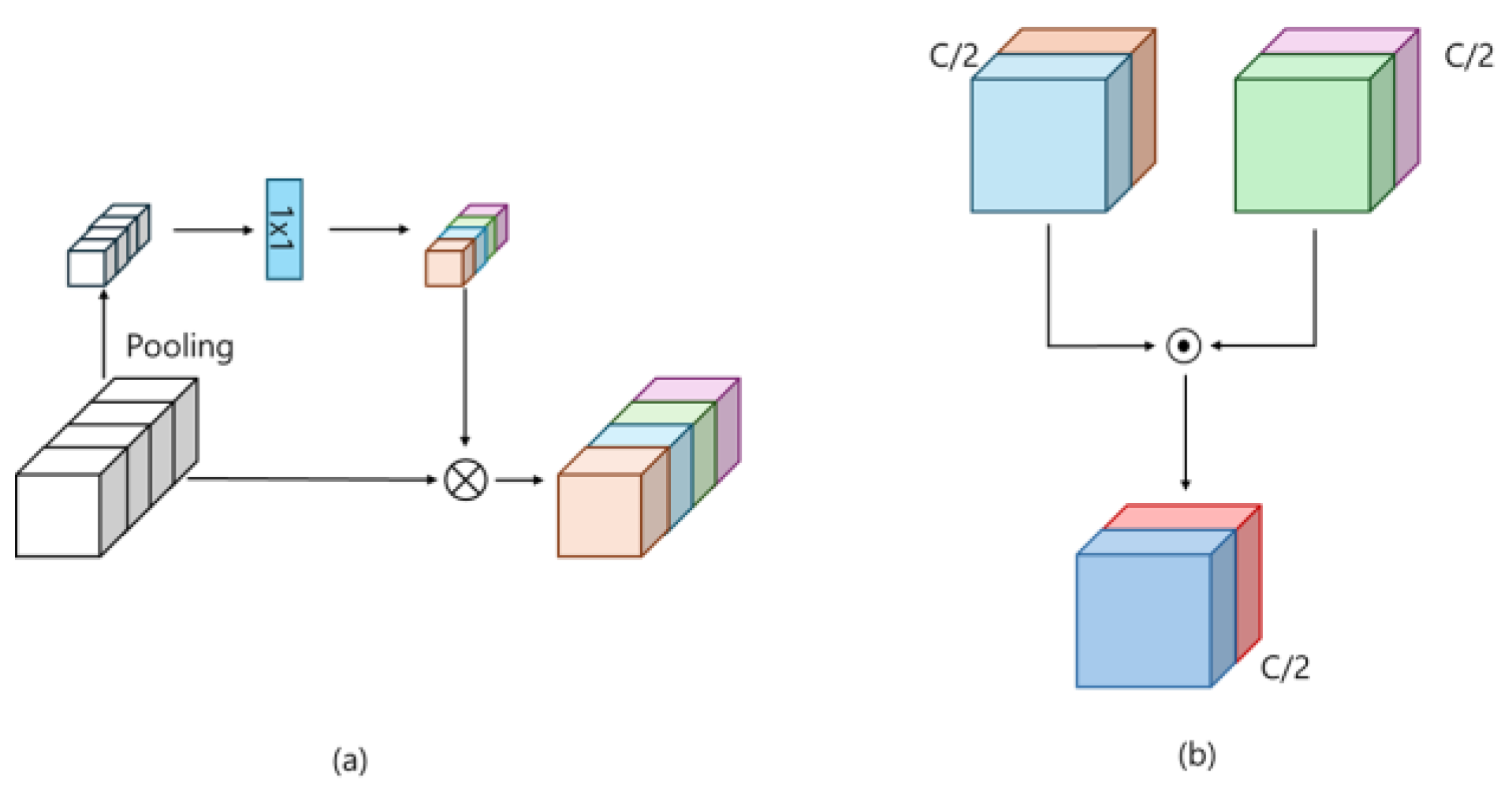
3.3. CNN Block

NAFBlock was selected for its high computational efficiency by eliminating nonlinear activation functions while maintaining competitive performance. Its architecture, comprising Simple Gate and Simplified Channel Attention mechanisms, complements the computationally intensive Transformer block, enabling the hybrid model to achieve a balance between performance and efficiency. Unlike conventional CNN models that rely on nonlinear activation functions, NAFBlock removes nonlinearity and employs purely linear transformations to reduce computational complexity. Given the input feature $\mathbf{X}\in R^{H \times W \times C}$, the NAFBlock process is formulated as follows.

The NAFBlock first applies layer normalization to stabilize the training process and mitigate instability caused by learning rate fluctuations:

$${\mathbf{X}}_{\mathbf{n}\mathbf{o}\mathbf{r}\mathbf{m}}=\mathrm{L}\mathrm{N}(\mathbf{X})= \gamma \odot ((\mathbf{X}-\mu )/\sigma )+\beta$$

(14)

where μ and σ are the mean and standard deviation computed across the channel dimension, and γ and β are learnable scale and shift parameters, respectively.

After normalization and convolution, the features are split and processed through the simple gate. The Simple Gate module is defined as:

$$\begin{gathered} {\mathbf{X}}_{\mathbf{1}},{\mathbf{X}}_{\mathbf{2}}=\mathrm{S}\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{t}({\mathbf{X}}_{\mathbf{d}\mathbf{w}},dim=channel), \\ {\mathit{X}}_{\mathit{g}\mathit{a}\mathit{t}\mathit{e}\mathit{d}}={\mathbf{X}}_{\mathbf{1}}\odot {\mathbf{X}}_{\mathbf{2}} \end{gathered}$$

(15)

where ⊙ denotes element-wise multiplication.

The channel attention mechanism reduces the complexity of self-attention while capturing global information. The SCA module is defined as:

$$\begin{gathered} {\mathbf{X}}_{\mathbf{c}\mathbf{a}}=\mathrm{S}\mathrm{C}\mathrm{A}({\mathbf{X}}_{\mathbf{n}\mathbf{o}\mathbf{r}\mathbf{m}})=\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v}1(\mathrm{G}\mathrm{A}\mathrm{P}({\mathbf{X}}_{\mathbf{n}\mathbf{o}\mathbf{r}\mathbf{m}}))\odot {\mathbf{X}}_{\mathbf{n}\mathbf{o}\mathbf{r}\mathbf{m}}, \\ \mathrm{G}\mathrm{A}\mathrm{P}(\mathbf{X})=\frac{1}{H\times W}\sum \sum \mathbf{X}(i,j,) \end{gathered}$$

(16)

where GAP denotes Global Average Pooling, Conv1 denotes 1 × 1 convolution, and ⊙ denotes element-wise multiplication. SCA maintains the activation-free design principle of NAFNet, where the attention weights are generated purely through linear transformations. Global Average Pooling generates channel-wise attention weights that emphasize important feature channels while suppressing less relevant ones.

Depth-wise convolution is employed to collect local features efficiently, replacing the fixed-sized local window approach used in self-attention:

$${\mathbf{X}}_{\mathbf{d}\mathbf{w}}=\mathrm{D}\mathrm{W}\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v}3({\mathbf{X}}_{\mathbf{c}\mathbf{a}})$$

(17)

where DWConv3 denotes 3 × 3 depth-wise convolution that processes each channel independently, significantly reducing computational complexity compared to standard convolution.

We incorporate NAFBlock’s lightweight and computationally efficient module to facilitate fast and effective extraction of fine-grained image features in the proposed hybrid model. The activation-free design combined with the simple gate mechanism enables the model to achieve competitive performance while maintaining computational efficiency, making it an ideal choice for the CNN components in our hybrid architecture. Figure 6 shows the structure of NAFBlock and Figure 7 shows the detailed architecture of the Simplified Channel Attention (SCA) and Simple Gate mechanisms.

4. Experiments

4.1. Training Settings

For robust training and performance validation, our model was trained and evaluated using the following training settings.

We validated the model performance using two real-world noise datasets: SIDD and DnD. The SIDD dataset provides three subsets: Small (160 image pairs), Medium (320 pairs), and Full (30,000 pairs for official benchmarking). Following standard practice, we use the Medium subset (320 pairs) for training and the validation set (1280 patches extracted from 40 scenes) for evaluation during training. Final performance is reported on the SIDD benchmark validation set to ensure fair comparison with published results. The DnD dataset consists of 50 pairs of noisy and clean images captured with consumer-grade cameras of different sensor sizes. Although DnD does not provide separate training data, it serves as an independent test set for cross-dataset generalization evaluation.

We selected SIDD and DnD datasets for training and evaluation for several reasons. First, both datasets are widely adopted in the image denoising research, enabling fair comparison with state-of-the-art methods and ensuring reproducible research outcomes. Second, these datasets contain real noise captured from real camera sensors, providing real-world scenarios that better reflect practical deployment conditions. Both datasets consist of high-resolution images with varying resolutions, over 3000 × 4000 pixels. However, for benchmarking purposes that require standardized processing, these high-resolution images are processed at 512 × 512 size. Specifically, images are divided into 512 × 512 patches for evaluation, and the final image is reconstructed by ensembling the patch-wise results. This approach reflects real-world deployment scenarios where high-resolution images are processed in patch units due to memory constraints, while simultaneously enabling fair performance comparison. This aligns with our primary focus on developing a real-world denoising model that can be effectively deployed in real-world environments. Finally, SIDD provides sufficient training data with diverse lighting conditions and scene types, and DnD offers high-resolution real-world test cases for robust cross-dataset validation and generalization assessment. All training and evaluation procedures were conducted using sRGB format data, and all experiments utilized 256 × 256 and 512 × 512 image patches.

The network architecture is organized into a hierarchical structure with specific block distributions across different levels: {4, 2, 6} in the encoder, 12 in the bottleneck, {4, 2, 2} in the decoder, and 4 in the refinement stage. This configuration is derived from the baseline architectures of NAFNet and Restormer, adapted to balance computational complexity and denoising performance. Following NAFNet’s principle of computational efficiency and Restormer’s multi-scale processing approach, we configured the encoder with progressively increasing blocks to extract hierarchical features, a deep bottleneck for intensive feature transformation at reduced resolution where computational cost is minimal, and an asymmetric decoder that leverages skip connections to reduce reconstruction overhead. This distribution maintains computational budget while achieving competitive denoising performance. To evaluate the trade-off between computational efficiency and performance, we implemented two variants: a baseline with base channel width of 32 and an enhanced version with width of 48. Both variants maintain identical block structure. The channel expansion factor γ = 2.66 in GDFN follows Restormer’s original configuration, maintaining consistency with the Transformer block design. Single attention head (h = 1) in MDTA was selected for computational efficiency.

We train models with AdamW optimizer (β1 = 0.9, β2 = 0.999, weight decay 0.0001) and Charbonnier Loss (ε = 1 × 10⁻³) for 300 K iterations with the initial learning rate 0.0002 gradually reduced to 0.000001 with cosine annealing strategy. The Charbonnier loss is defined as:

L_Charbonnier = √ (||y−ŷ||² + ε²)

(18)

where y is the ground truth, ŷ is the predicted output, and ε = 1 × 10⁻³ is a small constant for numerical stability. The model was implemented using the PyTorch 2.5.1 framework, and the training was conducted on NVIDIA RTX 4060 GPU.

4.2. Results

4.2.1. Model Complexity Comparison

To evaluate the computational efficiency and parameter requirements of our proposed approach, we conducted a comprehensive complexity analysis comparing our method with existing state-of-the-art denoising models and existing Transformer–CNN hybrid models. We implemented two variants of our model: Ours_32 with base channel width of 32 for resource-constrained environments and Ours_48 with base channel width of 48 for enhanced performance. All computational complexity measurements (MACs) were calculated based on 256 × 256 image patches, which is the standard input size used during training and evaluation.

As shown in

Table 2. Comparison of MACs and parameters across different denoising networks.

Network	MACS (G)	Parameter (M)
DnCNN-17	36.57	0.67
RIDNet	6.61	0.10
Restormer_32	64.46	11.74
Restormer_48	141.24	26.13
NAFNet_32	16.11	17.1
NAFNet_64	63.36	67.89
TECDNet (T/C)	21.90	20.87
Xformer	65.42	25.2
Ours_32	20.44	7.18
Ours_48	44.49	16.02

, our models demonstrate a well-balanced trade-off between computational cost and model capacity. Ours_32 requires 20.44 G MACs with 7.18 M parameters, positioning it between NAFNet_32 (16.11 G MACs, 17.1 M parameters) and Restormer_32 (64.46 G MACs, 11.74 M parameters). Notably, while our Ours_32 model has slightly higher MACs than NAFNet_32 (approximately 27% more), it achieves this with only 42% of NAFNet_32’s parameters, demonstrating superior parameter efficiency. Compared to TECDNet (21.90 G MACs, 20.87 M parameters), another CNN–Transformer hybrid model, Ours_32 requires nearly identical computational cost while achieving approximately 66% parameter reduction.

Ours_48 requires 44.49 G MACs with 16.02 M parameters. When compared to Restormer_48 (141.24 G MACs, 26.13 M parameters), Ours_48 reduces computational cost by 68% and parameters by 39%, demonstrating the effectiveness of our efficient hybrid CNN–Transformer architecture.

4.2.2. Quantitative Comparison

Table 3. SIDD Benchmark quantitative comparison.

Network	PSNR	SSIM
DnCNN-17	23.66	0.583
RIDNet	38.71	0.951
Restormer	40.03	0.959
NAFNet_32	39.96	0.960
NAFNet_64	40.30	0.961
TECDNet (T/C)	39.77	0.970
Xformer	39.98	0.957
Ours_32	39.98	0.958
Ours_48	40.05	0.961

shows the quantitative comparison results on the SIDD benchmark dataset. Our proposed models achieve competitive performance, with Ours_32 obtaining 39.98 dB PSNR and 0.958 SSIM, and Ours_48 achieving 40.05 dB PSNR and 0.961 SSIM on the SIDD dataset, demonstrating effective noise removal capabilities on real-world smartphone images. It is worth noting that the reported Restormer results are based on a width = 48 configuration, making direct comparison with our Ours_48 variant particularly relevant.

Compared with similar width configurations, our Ours_32 achieves slightly higher PSNR (39.98 dB) than NAFNet_32 (39.96 dB) while maintaining comparable SSIM (0.957 vs. 0.960). Both of our models outperform TECDNet (39.77 dB PSNR, 0.970 SSIM), with Ours_48 achieving 40.05 dB PSNR and Ours_32 achieving 39.98 dB PSNR, demonstrating improvements of 0.28 dB and 0.21 dB, respectively. Furthermore, when comparing models with the same width = 48, Ours_48 slightly outperforms Restormer (40.03 dB PSNR, 0.959 SSIM) in PSNR while achieving superior SSIM, indicating better structural preservation. Notably, this performance is achieved with significantly lower computational cost, as our Ours_48 requires only 44.49 G MACs compared to Restormer’s 141.24 G MACs (68% reduction), demonstrating the efficiency advantage of our hybrid architecture.

Table 4. DnD Benchmark quantitative comparison.

Network	PSNR	SSIM
DnCNN-17	32.43	0.790
RIDNet	39.23	0.953
Restormer	40.03	0.956
TECDNet (T/C)	39.92	0.956
Xformer	40.19	0.957
Ours_32	39.73	0.959
Ours_48	39.91	0.961

presents the performance comparison on the DnD benchmark dataset. Similarly, the Restormer results on DnD are also based on width = 48, allowing for fair comparison with our Ours_48 variant. Our models achieve strong results with Ours_32 obtaining 39.73 dB PSNR and 0.959 SSIM, and Ours_48 achieving 39.91 dB PSNR and 0.961 SSIM, demonstrating robust generalization across different datasets and imaging conditions. This indicates that our model, trained exclusively on SIDD (smartphone images), maintains competitive performance on DnD (DSLR camera images) despite the domain shift. While there is a slight PSNR decrease compared to SIDD results (approximately 0.25 dB for Ours_32 and 0.14 dB for Ours_48), the consistently high SSIM scores (0.959–0.961) validate its practical applicability in real-world deployment scenarios where imaging conditions vary significantly. Notably, our models achieve strong SSIM performance on the DnD dataset, with Ours_32 obtaining 0.959 and Ours_48 achieving 0.961, both surpassing Restormer’s 0.956 SSIM. While Restormer achieves higher PSNR compared to our Ours_48, both of our models demonstrate superior SSIM performance, indicating better structural preservation and perceptual quality. This consistent SSIM advantage across both model variants confirms that our hybrid architecture excels at preserving structural information and producing visually satisfying results that closely match the original image structure.

The consistently high SSIM scores across both datasets (0.957–0.961) demonstrate that our hybrid CNN–Transformer architecture effectively preserves the structural integrity of images during the denoising process. While PSNR measures pixel-level differences, SSIM evaluates structural similarity, including luminance, contrast, and structural information. High SSIM values indicate that our method successfully maintains important perceptual qualities such as edge sharpness, texture details, and overall image coherence, resulting in visually superior denoised images that retain the natural appearance of the original scenes. Across both benchmarks, our models demonstrate a well-balanced trade-off between PSNR and SSIM metrics.

The quantitative results are shown in Figure 8 and Figure 9. Each figure shows the restoration results on SIDD and DnD datasets, respectively.

5. Discussion

5.1. Balancing Efficiency and Performance

Our results validate that our CNN–Transformer hybrid architecture can leverage the strengths of each module while mitigating their respective weaknesses. We implemented two variants with different channel widths to evaluate the trade-off between computational efficiency and performance. The proposed models achieve competitive or superior noise removal performance compared to state-of-the-art methods while maintaining computational efficiency.

Our baseline model provides an excellent balance for resource-constrained environments. While achieving slightly lower PSNR (39.98 dB on SIDD, 39.73 dB on DnD) compared to some state-of-the-art methods, it provides a compelling trade-off by maintaining competitive performance (within 0.3 dB of top-performing models) while requiring 20.44 G MACs with 7.18 M parameters. This makes it significantly more efficient than pure Transformer approaches such as Restormer (64.46 G MACs, 11.74 M parameters for width = 32 configuration), representing a 68% reduction in computational cost.

Our enhanced model demonstrates that our hybrid architecture can scale effectively to achieve high performance. It achieves 40.05 dB PSNR on SIDD and 39.91 dB on DnD, while requiring only 44.49 G MACs with 16.02 M parameters compared to Restormer’s 141.24 G MACs and 26.13 M parameters (both at width = 48). This represents a 68% reduction in computational cost and 39% reduction in parameters while achieving comparable or better performance, demonstrating the superior efficiency of our hybrid architecture.

The balance between performance and computational efficiency achieved by our hybrid model has significant practical implications. With 20.44 G MACs, this model is much more efficient than pure Transformer-based approaches such as Restormer (64.46 G MACs), making it suitable for deployment in resource-constrained environments such as mobile devices.

Furthermore, the model’s generalization capability demonstrated in cross-dataset evaluation shows that it can perform reliably in real-world applications where noise characteristics may differ from training data. This robustness is important for practical deployment in diverse and unpredictable real-world scenarios.

5.2. Limitations and Challenges

There are several limitations and challenges in our research:

• High-Resolution Image Processing: The current model is optimized for 256 × 256 resolution, and memory usage and computation time increase dramatically when processing high-resolution images above 4 K.
• Real-Time Processing and Hardware Integration Constraints: Although more efficient than existing Transformer-based methods, the model still exhibits high computational complexity for integration into actual image sensors or embedded systems, which requires further optimization.
• Performance Improvement Limitations: The baseline model shows slightly lower PSNR performance compared to some SOTA models, while the enhanced version achieves competitive or superior performance. Additional model architecture and computational optimizations may be needed for handling complex noise patterns beyond the scope of standard benchmarks.

Future work should include systematic exploration of optimal architectural configurations through comprehensive ablation studies and multiple training runs with statistical validation to establish robust performance. Additionally, comprehensive perceptual quality assessment through user studies would validate the practical significance of our superior SSIM performance. Furthermore, incorporating learned perceptual metrics such as LPIPS could provide more comprehensive evaluation of visual quality.

6. Conclusions

This paper proposed a CNN–Transformer hybrid network for image denoising that strategically combines the computational efficiency of CNNs with the global context modeling capabilities of Transformers. We implemented two model variants with different channel widths to demonstrate the scalability and flexibility of our architecture for different deployment scenarios.

Our models were comprehensively evaluated on real-world denoising datasets, including SIDD and DnD. The experimental results demonstrate that our CNN–Transformer hybrid architecture achieves strong performance, obtaining 40.05 dB PSNR and 0.961 SSIM on SIDD, and 39.91 dB PSNR and 0.961 SSIM on DnD. Notably, both model variants consistently achieve superior SSIM performance (0.957–0.961) compared to state-of-the-art methods, including Restormer (0.956–0.959), indicating excellent preservation of structural integrity and perceptual quality.

The proposed approach successfully balances computational efficiency with denoising performance, demonstrating superior generalization capabilities across different datasets and imaging conditions. The consistent SSIM performance across both SIDD (smartphone) and DnD (DSLR) datasets validates the robustness of our architecture for diverse real-world scenarios.

Based on this research, future work will focus on developing practically deployable models that overcome current limitations and are optimized for integration into image sensors. The primary goal is to create AI models capable of processing high-resolution images with enhanced generalization performance across diverse real-world scenarios.