Analysis of Discretization Errors in the Signal Model of the Integrate-And-Dump Filter in Satellite Navigation Receivers

Abstract

The integrate-and-dump filter is a core component of satellite navigation receivers, enabling the tracking of navigation satellite signals and significantly influencing receiver performance. Currently, satellite navigation receivers, particularly onboard unmanned aerial vehicles (UAVs), are vulnerable to spoofing. Whether counterfeit signals can successfully hijack a receiver depends critically on how these signals alter the integrate-and-dump filter output. Existing research on satellite navigation spoofing often uses an output signal model for the integrate-and-dump filter derived from continuous-time integration. However, this model deviates from practical implementation because most modern navigation receivers are built on digital circuits that approximate continuous-time integration through discrete-time accumulation. Consequently, the discrete-time nature of actual hardware introduces errors that are not captured by the conventional continuous-time model. In this study, a mathematical model for the output signal of an integrate-and-dump filter was implemented via discrete-time accumulation. The accuracy of the proposed model was verified through simulations, and a comparative analysis with the traditional continuous-time integration model was conducted to highlight the impact of discretization errors.

1. Introduction

Satellite navigation has been widely utilized in both civilian and military sectors, making its security a significant area of research. There are two primary types of attacks that target satellite navigation receivers: suppression jamming and generative spoofing [1,2,3]. The former achieves its malicious objective by transmitting high-power interfering signals within the satellite navigation signal frequency band, thereby disrupting the normal operation of satellite navigation receivers. In contrast, the latter exploits the publicly available parameters of civil satellite navigation signals to generate counterfeit signals. This induces the receiver to switch from stably tracking authentic satellite signals to locking onto attacker-generated fake signals, ultimately leading the satellite navigation user to obtain erroneous positioning information [3,4,5,6]. Notably, this spoofing attack method is more concealed and exhibits higher destructiveness.

In terms of technical complexity, generative spoofing is considerably more challenging to implement than suppression jamming. During the normal operation of a navigation receiver, its internal tracking loop maintains a stable lock on real satellite signals [7,8,9,10,11]. According to existing research, to compel the receiver to switch from tracking authentic signals to tracking fake signals, two critical prerequisites must be met: first, the generated counterfeit signals must be fully consistent with the real satellite signals; second, the power of the fake signals must be continuously increased to enable the receiver’s tracking loop to smoothly transition and lock onto the counterfeit signals [12,13]. In particular, as the distance and relative velocity between the satellite navigation receiver and navigation satellites vary constantly, the key signal parameters of real satellite navigation signals, such as the Doppler shift and ranging code phase, undergo real-time changes. Consequently, the generative spoofer must dynamically adjust these parameters to generate fake signals that remain consistent with the real satellite signals at all times, which significantly increases technical difficulty [14,15,16,17].

In recent years, numerous scholars have investigated the mechanism underlying the covert control of receivers via generative spoofing signals and conducted theoretical and dynamic analyses of the impact exerted by counterfeit satellite navigation signals on the receiver’s signal-tracking loop [18,19,20,21]. The integrate-and-dump filter is a pivotal component of the tracking loop, and its core function is to implement coherent integration and periodic reset between the received satellite navigation signals and locally generated signals, thereby providing an input to the phase detector within the tracking loop. Therefore, the integrate-and-dump filter is a key component in investigating the operational principles of navigation spoofing signals acting on satellite navigation receivers [22,23,24,25,26,27].

The output signal model of the integrate-and-dump filter derived from continuous-time integration has been widely adopted in navigation spoofing technology studies. However, in the current prevalent digital circuit-based satellite navigation receivers, the integrate-and-dump filter implemented via digital circuits accomplishes computations through discrete-time accumulation rather than ideal continuous-time integration. This discrepancy may introduce uncertainties regarding the validity and applicability of research findings in the field of navigation spoofing technology. Therefore, this study was conducted from the perspective of discretization errors with the following contributions:

• The output signal model of the integrate-and-dump filter is derived using the discrete-time accumulation computation method. To investigate navigation spoofing techniques, a more precise integrate-and-dump filter output signal model was provided.
• From a qualitative perspective, it is demonstrated that the discretization error in the traditional integrate-and-dump filter output signal model derived via the continuous-time integration approach is negligible only under the ideal condition where the receiver tracks the input satellite signal without any error. In practical scenarios, however, the discretization error inevitably exists.
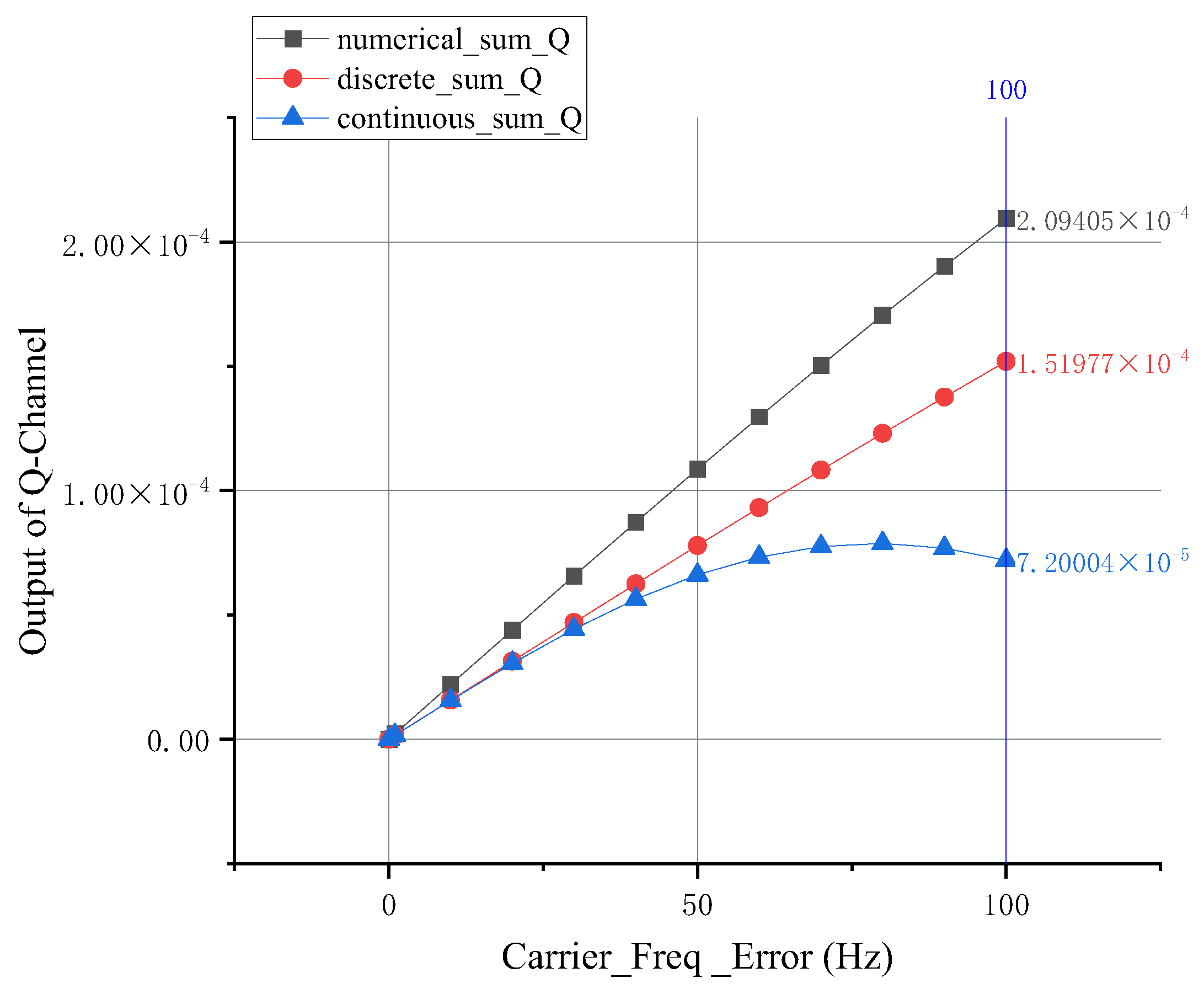
• Quantitative simulations reveal that when only ranging code phase error and initial carrier phase error are present, the results from the traditional integrate-and-dump filter output signal model, derived from continuous-time integration, align closely with the computational outcomes of the discrete-time accumulation-based model proposed in this paper, as well as with reference values obtained through numerical calculations. This consistency suggests that under these conditions, the discretization error is negligible. However, when carrier frequency error is introduced, the accuracy of the proposed model significantly exceeds that of the traditional model, indicating that the discretization error becomes pronounced and increases markedly with the magnitude of the frequency error.

2. Input Signal Model and Tracking Loop of Satellite Navigation Receivers

2.1. Input Signal Model of Satellite Navigation Receivers

The signal-modeling method discussed in this study is not limited to a specific navigation satellite system or a particular frequency band of a navigation satellite system. For the convenience of analysis and experimentation, this study selected the L1 frequency band of the GPS navigation system as the object of analysis. The signal transmitted from the navigation satellite propagates through space and is received by the receiver antenna. This signal is defined as the input signal to be processed by the satellite navigation receiver and is modeled as follows:

$$\mathrm{s}\left(t\right)=\sqrt{2P}\times D\left(t-\tau \left(t\right)\right)\times C\left(t-\tau \left(t\right)\right)\times cos\left(2\pi f_{L1}t+\varphi \left(t\right)\right)$$

(1)

where the following variables are defined as

$P$ denotes the signal power, which is related to the signal amplitude $A$ as $P=A^2/2$;

$D\left(t\right)$ represents binary navigation message data;

$\tau \left(t\right)$ denotes the range-code phase.

This is because, after the navigation satellite signal is transmitted from the satellite antenna and received by the receiver antenna, the time delay during signal transmission introduces this ranging code phase. Because the distance between the navigation satellite and receiver constantly changes and is affected by variations in the signal propagation environment (e.g., changes in the Earth’s ionosphere), the ranging code phase is a time-varying parameter.

$C\left(t\right)$ represents binary ranging code. Each GPS satellite generates a periodically repeating ranging code in the L1 frequency band using the same method, but with different initial parameters. This ranging code is also known as the C/A code.

$\varphi \left(t\right)$ denotes initial carrier phase. $f_{L1}$ is the carrier frequency of the GPS L1 frequency band. The GPS navigation system specifies that the carrier frequency of the L1 frequency band is 1575.42 MHz. This was caused by the time delay when the navigation satellite signal was transmitted from the satellite to the receiver antenna. There are two main factors affecting the carrier phase: the time-varying Doppler shift caused by the distance and relative velocity between the navigation satellite and receiver and the influence of changes in the Earth’s ionosphere. The Earth’s ionosphere affects GPS signals at different carrier frequencies in a frequency-dependent manner, with higher carrier frequencies experiencing a smaller effect. For the GPS L1 band, the pseudorange error induced by typical ionospheric variability is generally within 10 m. During periods of intense solar activity, however, ionospheric variations can cause equivalent pseudorange errors reaching tens of metres. Nevertheless, the pseudorange errors caused by the ionosphere can be partially mitigated through correction models and parameters provided in the navigation message.

2.2. The Integrate-And-Dump Filter in Satellite Navigation Receivers

The primary objective of signal tracking in satellite navigation receivers is to dynamically adjust the generation parameters of local replica signals, including carrier frequency, carrier phase, and ranging code phase, to maintain precise synchronization with incoming navigation satellite signals. This synchronization is fundamental for enabling two critical downstream processes: pseudorange measurement and navigation message demodulation. Ultimately, the position coordinates of the receiver were computed based on the pseudoranges and navigation message.

Operational initialization of a satellite navigation receiver involves two primary phases: signal acquisition and tracking. Signal acquisition, which is typically completed within minutes, provides initial estimates of the visible satellites and coarse signal parameters. Subsequently, the receiver operates predominantly in the tracking mode for extended periods. Consequently, when a receiver enters the influence range of a generative spoofing interference source, the impact of such spoofing signals primarily manifests in the tracking loops of the receiver. Thus, existing research has predominantly focused on analyzing the effects of generative spoofing interference on these critical tracking mechanisms.

Within the tracking loop of the receiver, the incoming navigation satellite signal undergoes coherent integration in an integrate-and-dump filter with locally generated carrier and ranging code signals. A widely adopted model for the output signal of this integrate-and-dump filter in the literature is as follows:

$$I=\sqrt{{\displaystyle \frac{P}{2}}}\times R\left({\epsilon }_{\tau }\right)\times D\left(t\right)\times sinc\left(\pi {\epsilon }_{f}T\right)\times cos\left({\epsilon }_{\varphi }\right)+n_I$$

(2)

$$Q=\sqrt{{\displaystyle \frac{P}{2}}\times }R\left({\epsilon }_{\tau }\right)\times D\left(t\right)\times sinc\left(\pi {\epsilon }_{f}T\right)\times sin\left({\epsilon }_{\varphi }\right)+n_Q$$

(3)

$$sinc\left(\pi {\epsilon }_{f}T\right)={\displaystyle \frac{sin\left(\pi {\epsilon }_{f}T\right)}{\pi {\epsilon }_{f}T}}$$

(4)

where the following variables are defined as

${\epsilon }_{\tau }$ is the carrier frequency deviation between the local carrier and incoming navigation signal;

${\epsilon }_f$ is the ranging code phase deviation between the local ranging code and the incoming navigation signal;

${\epsilon }_{\varphi }$ is the carrier phase deviation between the local carrier and incoming navigation signal.

The aforementioned model was derived using the continuous-time integration approach. Section 3 provides a detailed analysis of the derivation process for this signal model. Given that contemporary satellite navigation receivers are predominantly implemented using digital circuits, coherent integration in an integrate-and-dump filter is practically accomplished through discrete-time accumulation. Consequently, a discretization error exists between the output signal model of the integrate-and-dump filter described above and the actual computational results.

Considering that generative spoofing interference signals closely resemble genuine satellite navigation signals in their parameters, if the discretization error in the aforementioned formulation is significant, the model cannot be directly applied to analyze the impact of generative spoofing signals on navigation receivers without accounting for the effects of this discretization error. In Section 4, we derive the output signal model of the integrate-and-dump filter based on the discrete-time accumulation method, compare it with the formula derived from the continuous-time integration approach, and validate the accuracy of the proposed discrete-time accumulation-based model through numerical simulation experiments in Section 5.

3. Output Signal Modeling of the Integrate-And-Dump Filter via Continuous-Time Integration

In satellite navigation receivers implemented with digital circuits, the incoming navigation signal undergoes a series of processing stages at the radio frequency (RF) front-end, including RF reception, down-conversion, filtering, and analog-to-digital conversion, resulting in an intermediate frequency (IF) signal.

$$s_{IF}\left(t\right)=\sqrt{2P}\times D\left(t-\tau \left(t\right)\right)\times C\left(t-\tau \left(t\right)\right)\times cos\left(2\pi f_{IF}t+\varphi \left(t\right)\right)$$

(5)

A comparison with the signal model presented earlier revealed that the distinction between the two models lies in the carrier frequency, which shifts from the original GPS L1 frequency to an intermediate frequency after sampling.

In a satellite navigation receiver, the locally generated ranging code and carrier are utilized to construct replica signals of the incoming satellite signal comprising in-phase (I) and quadrature (Q) components. These local replicas can be mathematically modeled as follows:

$${LR}_I\left(t\right)=C\left(t-\hat{\tau }\left(t\right)\right)\times cos\left(2\pi {\hat{f}}_{IF}t+\hat{\varphi }\left(t\right)\right)$$

(6)

$${LR}_Q\left(t\right)=C\left(t-\hat{\tau }\left(t\right)\right)\times sin\left(2\pi {\hat{f}}_{IF}t+\hat{\varphi }\left(t\right)\right)$$

(7)

where

$\hat{\tau }\left(t\right)$ is the ranging code phase estimated by the receiver, which is an estimate containing the errors in $\tau \left(t\right)$. The receiver uses $\hat{\tau }\left(t\right)$ as a parameter to generate the local ranging code. The function of the ranging code tracking loop is to calculate the difference between $\hat{\tau }\left(t\right)$ and $\tau \left(t\right)$, and adjust $\hat{\tau }\left(t\right)$ until $\hat{\tau }\left(t\right)$ is completely consistent with $\tau \left(t\right)$.

$\hat{\varphi }\left(t\right)$ is the estimated ranging code phase of the receiver, which is an estimate that contains the errors of $\varphi \left(t\right)$. The receiver uses $\hat{\varphi }\left(t\right)$ as a parameter to generate the local carrier. The function of the carrier-tracking loop is to calculate the difference between $\hat{\varphi }\left(t\right)$ and $\varphi \left(t\right)$ and adjust $\hat{\varphi }\left(t\right)$ until $\hat{\varphi }\left(t\right)$ is completely consistent with $\varphi \left(t\right)$.

Based on the tracking loop algorithm of satellite navigation receivers, the locally generated signals were correlated with the input signals, and the results were processed using an integrate-and-dump filter to yield the in-phase (I) and quadrature (Q) components of the signal.

$$I={\displaystyle \frac{1}{T}}{\int }_{t_0}^{t_0+T}{s}_{IF}\left(t\right)\times {LR}_I\left(t\right) dt$$

(8)

$$Q={\displaystyle \frac{1}{T}}{\int }_{t_0}^{t_0+T}{s}_{IF}\left(t\right)\times {LR}_Q\left(t\right) dt$$

(9)

where $t_0$ represents the starting moment for the integration calculation and $T$ denotes the period length over which the integration is performed. The signal models are derived in the following subsections based on the continuous-time integration approach. The in-phase (I) branch signal model is developed in Section 3.1, followed by the quadrature (Q) branch signal model in Section 3.2.

This paper assumes that the integration $T$ is constant and two corresponding assumptions regarding the RF front-end filter and the ADC must be made. First, it must be assumed that the RF front-end filter exhibits a constant group delay. Second, it must be assumed that the ADC’s sampling clock is free from jitter, meaning it maintains a perfectly constant sampling period, and that this sampling period maintains an integer multiple relationship with the integration time $T$.

3.1. Modeling the Output Signal of the In-Phase Channel Integrate-And-Dump Filter via Continuous-Time Integration

The integrand within the integration formula of the in-phase (I) branch integrate-and-dump filter is first analyzed.

$$s_{IF}\left(t\right)\times {LR}_I\left(t\right)=\left[\sqrt{2P}\times D\left(t-\tau \left(t\right)\right)\times C\left(t-\tau \left(t\right)\right)\times cos\left(2\pi f_{IF}t+\varphi \left(t\right)\right)\right]\times \left[C\left(t-\hat{\tau }\left(t\right)\right)\times cos\left(2\pi {\hat{f}}_{IF}t+\hat{\varphi }\left(t\right)\right)\right]$$

(10)

Given that the GPS navigation message (D) has a bit rate of 50 Hz, corresponding to a bit duration of 20 ms, whereas the correlation integration period T is typically 1 ms, which is significantly shorter than the navigation message bit period, considering that the value of D is either +1 or −1, Equation (10) can be simplified to Equation (11).

$$s_{IF}\left(t\right)\times {LR}_I\left(t\right)=\sqrt{2P}\times \left[C\left(t-\tau \left(t\right)\right)\times C\left(t-\hat{\tau }\left(t\right)\right)\right]\times \left[cos\left(2\pi f_{IF}\left(t\right)t+\varphi \left(t\right)\right)\times cos\left(2\pi {\hat{f}}_{IF}\left(t\right)t+\hat{\varphi }\left(t\right)\right)\right]$$

(11)

The value of the first bracket $\left[C\left(t-\tau \left(t\right)\right)\times C\left(t-\hat{\tau }\left(t\right)\right)\right]$, determined by the autocorrelation properties of the GPS L1 C/A ranging code, is expressed in Equation (12) where $R\left({\epsilon }_{\tau }\right)$ is GPS C/A code autocorrelation function and $T_c$ denotes the duration of one chip of the ranging code. For the GPS L1 C/A code, the period of the C/A code is 1 ms, and each period consists of 1023 chips.

$$R\left({\epsilon }_{\tau }\right)=\left\{\begin{array}{c}\begin{array}{cc}1-\left|{\epsilon }_{\tau }\right|/T_c& \left|{\epsilon }_{\tau }\right|\le T_c\end{array}\\ \begin{array}{cc}0& \left|{\epsilon }_{\tau }\right|>T_c\end{array}\end{array}\right.{\epsilon }_{\tau }=\tau \left(t\right)-\hat{\tau }\left(t\right) T_c=1 ms/1023$$

(12)

The expression in the second bracket can be transformed using trigonometric product-to-sum identities, yielding Equation (13).

$$\begin{array}{l}\left[cos\left(2\pi f_{IF}\left(t\right)t+\varphi \left(t\right)\right)\times cos\left(2\pi {\hat{f}}_{IF}\left(t\right)t+\hat{\varphi }\left(t\right)\right)\right]\\ ={\displaystyle \frac{1}{2}}\left[cos\left(2\pi \left(f_{IF}\left(t\right)+{\hat{f}}_{IF}\left(t\right)\right)t+\left(\varphi \left(t\right)+\hat{\varphi }\left(t\right)\right)\right)+cos\left(2\pi \left(f_{IF}\left(t\right)-{\hat{f}}_{IF}\left(t\right)\right)t+\varphi \left(t\right)-\hat{\varphi }\left(t\right)\right)\right]\end{array}$$

(13)

Because of the low-pass filtering characteristic of the integrate-and-dump filter, the first term in the above equation represents a high-frequency signal and is thus filtered out. Consequently, Equation (10) can be simplified as shown in Equation (14).

$$\begin{array}{l}{s}_{IF}\left(t\right)\times {LR}_I\left(t\right)=\sqrt{2P}\times R\left({\epsilon }_{\tau }\right)\times {\displaystyle \frac{1}{2}}cos\left(2\pi {\epsilon }_{f}t+{\epsilon }_{\varphi }\right)\\ {\epsilon }_f=f_{IF}\left(t\right)-{\hat{f}}_{IF}\left(t\right) {\epsilon }_{\varphi }=\varphi \left(t\right)-\hat{\varphi }\left(t\right)\end{array}$$

(14)

Substituting the simplified integrand, as given in Equation (14), into Equation (8) yields a simplified output signal expression for the in-phase (I) branch integrate-and-dump filter, as expressed in Equation (15).

$$\begin{array}{c}I={\displaystyle \frac{1}{T}}{{\displaystyle \int }}_{t_0}^{t_0+T}{s}_{IF}\left(t\right)\times {LR}_I\left(t\right)dt=\sqrt{2P}R\left({\epsilon }_{\tau }\right){\displaystyle \frac{1}{2T}}{{\displaystyle \int }}_{t_0}^{t_0+T}cos\left(2\pi {\epsilon }_{f}t+{\epsilon }_{\varphi }\right)dt\\ =\sqrt{2P}R\left({\epsilon }_{\tau }\right){\displaystyle \frac{1}{2T}}{\displaystyle \frac{1}{2\pi {\epsilon }_f}}sin\left(2\pi {\epsilon }_{f}t+{\epsilon }_{\varphi }\right){|}_{t_0}^{t_0+T}\end{array}$$

(15)

Let $2\pi {\epsilon }_f=\mathrm{\Delta }\omega$ to convert the frequency error into an angular frequency error, and we obtain:

$$\begin{array}{c}\sqrt{2P}R\left({\epsilon }_{\tau }\right){\displaystyle \frac{1}{2T}}{\displaystyle \frac{1}{2\pi {\epsilon }_f}}sin\left(2\pi {\epsilon }_{f}t+{\epsilon }_{\varphi }\right){|}_{t_0}^{t_0+T}=\sqrt{2P}R\left({\epsilon }_{\tau }\right){\displaystyle \frac{1}{2T\mathrm{\Delta }\omega }}sin\left(\mathrm{\Delta }\omega t+{\epsilon }_{\varphi }\right){|}_{t_0}^{t_0+T}\\ =\sqrt{2P}R\left({\epsilon }_{\tau }\right){\displaystyle \frac{1}{2T\mathrm{\Delta }\omega }}\left[sin\left(\mathrm{\Delta }\omega (t_0+T)+{\epsilon }_{\varphi }\right)-sin\left(\mathrm{\Delta }\omega t_0+{\epsilon }_{\varphi }\right)\right]\end{array}$$

(16)

Based on trigonometric product-to-sum identities, Equation (16) can be transformed into Equation (17).

$$\begin{array}{ll}\sqrt{2P}R\left({\epsilon }_{\tau }\right){\displaystyle \frac{1}{2T\mathrm{\Delta }\omega }}& \left[sin\left(\mathrm{\Delta }\omega (t_0+T)+{\epsilon }_{\varphi }\right)-sin\left(\mathrm{\Delta }\omega t_0+{\epsilon }_{\varphi }\right)\right]=\\ & =\sqrt{2P}R\left({\epsilon }_{\tau }\right){\displaystyle \frac{1}{2T\mathrm{\Delta }\omega }}2sin\left({\displaystyle \frac{\mathrm{\Delta }\omega T}{2}}\right)cos\left(\mathrm{\Delta }\omega t_0+\mathrm{\Delta }\omega {\displaystyle \frac{T}{2}}+{\epsilon }_{\varphi }\right)\\ & =\sqrt{{\displaystyle \frac{P}{2}}}R\left({\epsilon }_{\tau }\right)sinc\left(\mathrm{\Delta }\omega T\right)cos\left(\mathrm{\Delta }\omega \left(t_0+T/2\right)+{\epsilon }_{\varphi }\right)\end{array}$$

(17)

The derivation result expressed in Equation (17) represents the output signal model of the in-phase (I) channel integrate-and-dump filter under the continuous-time integration approach, which is the model currently employed in theoretical investigations of navigation spoofing.

3.2. Modeling the Output Signal of the Quadrature-Phase Channel Integrate-And-Dump Filter via Continuous-Time Integration

Following the analytical approach established in Section 3.1, for the in-phase (I) branch, the quadrature (Q) branch integrate-and-dump filter output is derived by applying the same continuous-time integration methodology to its integral expression, as follows. The integral term for the Q branch was analyzed in a manner analogous to the preceding subsection, focusing on its distinct phase relationship relative to the local carrier replica.

$$\begin{array}{c}{s}_{IF}\left(t\right)\times {LR}_Q\left(t\right)=\left[\sqrt{2P}\times D\left(t-\tau \left(t\right)\right)\times C\left(t-\tau \left(t\right)\right)\times cos\left(2\pi f_{IF}t+\varphi \left(t\right)\right)\right]\\ \times \left[C\left(t-\hat{\tau }\left(t\right)\right)\times sin\left(2\pi {\hat{f}}_{IF}t+\hat{\varphi }\left(t\right)\right)\right]\end{array}$$

(18)

Based on the same rationale that the navigation message $D\left(t-\tau \left(t\right)\right)$ assumes a value of either +1 or −1 and that $D\left(t-\tau \left(t\right)\right)$ is 1, Equation (18) can be simplified as Equation (19).

$$s_{IF}\left(t\right)\times {LR}_Q\left(t\right)=\sqrt{2P}\times \left[C\left(t-\tau \left(t\right)\right)\times C\left(t-\hat{\tau }\left(t\right)\right)\right]\times \left[cos\left(2\pi f_{IF}\left(t\right)t+\varphi \left(t\right)\right)\times sin\left(2\pi {\hat{f}}_{IF}\left(t\right)t+\hat{\varphi }\left(t\right)\right)\right]$$

(19)

The expression within the second bracket in Equation (19) can be transformed into Equation (20) using trigonometric product-to-sum identities:

$$\begin{array}{l}\left[cos\left(2\pi f_{IF}\left(t\right)t+\varphi \left(t\right)\right)\times sin\left(2\pi {\hat{f}}_{IF}\left(t\right)t+\hat{\varphi }\left(t\right)\right)\right]\\ ={\displaystyle \frac{1}{2}}\left[sin\left(2\pi \left(f_{IF}\left(t\right)+{\hat{f}}_{IF}\left(t\right)\right)t+\left(\varphi \left(t\right)+\hat{\varphi }\left(t\right)\right)\right)-sin\left(2\pi \left(f_{IF}\left(t\right)-{\hat{f}}_{IF}\left(t\right)\right)t+\varphi \left(t\right)-\hat{\varphi }\left(t\right)\right)\right]\end{array}$$

(20)

Because of the low-pass filtering characteristic of the integrate-and-dump filter, the first term in Equation (20), which constitutes a high-frequency component, is attenuated by the filter. Consequently, Equation (20) can be simplified to yield Equation (21).

$$\begin{array}{l}\left[cos\left(2\pi f_{IF}\left(t\right)t+\varphi \left(t\right)\right)\times sin\left(2\pi {\hat{f}}_{IF}\left(t\right)t+\hat{\varphi }\left(t\right)\right)\right]\\ =-{\displaystyle \frac{1}{2}}sin\left[2\pi \left(f_{IF}\left(t\right)-{\hat{f}}_{IF}\left(t\right)\right)t+\left(\varphi \left(t\right)-\hat{\varphi }\left(t\right)\right)\right]\\ =-{\displaystyle \frac{1}{2}}sin\left(2\pi {\epsilon }_{f}t+{\epsilon }_{\varphi }\right)\end{array}$$

(21)

Substituting the simplified integrand, as given in Equation (20), into Equation (9) yields a simplified output signal expression for the quadrature (Q) branch integrate-and-dump filter, as shown in Equation (22).

$$Q={\displaystyle \frac{1}{T}}{\int }_{t_0}^{t_0+T}{s}_{IF}\left(t\right)\times {LR}_Q\left(t\right) dt=\sqrt{2P}R\left({\epsilon }_{\tau }\right){\displaystyle \frac{1}{2T}}{\displaystyle \frac{1}{2\pi {\epsilon }_f}}cos\left(2\pi {\epsilon }_{f}t+{\epsilon }_{\varphi }\right){|}_{t_0}^{t_0+T}$$

(22)

Let $2\pi {\epsilon }_f=\mathrm{\Delta }\omega$ to convert the frequency error into an angular frequency error, and we obtain:

$$\begin{array}{c}\sqrt{2P}R\left({\epsilon }_{\tau }\right){\displaystyle \frac{1}{2T}}{\displaystyle \frac{1}{2\pi {\epsilon }_f}}cos\left(2\pi {\epsilon }_{f}t+{\epsilon }_{\varphi }\right){|}_{t_0}^{t_0+T}=\sqrt{2P}R\left({\epsilon }_{\tau }\right){\displaystyle \frac{1}{2T\mathrm{\Delta }\omega }}cos\left(\mathrm{\Delta }\omega t+{\epsilon }_{\varphi }\right){|}_{t_0}^{t_0+T}\\ =\sqrt{2P}R\left({\epsilon }_{\tau }\right){\displaystyle \frac{1}{2T\mathrm{\Delta }\omega }}\left[cos\left(\mathrm{\Delta }\omega (t_0+T)+{\epsilon }_{\varphi }\right)-cos\left(\mathrm{\Delta }\omega t_0+{\epsilon }_{\varphi }\right)\right]\end{array}$$

(23)

Based on trigonometric product-to-sum identities, Equation (23) can be further simplified to obtain Equation (24).

$$\begin{array}{l}\sqrt{2P}R\left({\epsilon }_{\tau }\right){\displaystyle \frac{1}{2T\mathrm{\Delta }\omega }}\left[cos\left(\mathrm{\Delta }\omega \left(t_0+T\right)+{\epsilon }_{\varphi }\right)-cos\left(\mathrm{\Delta }\omega t_0+{\epsilon }_{\varphi }\right)\right]\\ =-\sqrt{{\displaystyle \frac{P}{2}}}R\left({\epsilon }_{\tau }\right)sinc\left(\mathrm{\Delta }\omega T\right)sin\left(\mathrm{\Delta }\omega \left(t_0+T/2\right)+{\epsilon }_{\varphi }\right)\end{array}$$

(24)

Based on the above derivation process, the mathematical expressions of the signal models for the in-phase (I) and quadrature (Q) channels obtained under continuous-time integration conditions represent the signal model widely adopted in current navigation spoofing studies. Under the assumption that the navigation message data is −1, the sign term in Equation (24) can be eliminated, resulting in the expression given in Equation (26).

$$I={\displaystyle \frac{1}{T}}{\int }_{t_0}^{t_0+T}{s}_{IF}\left(t\right)\times {LR}_I\left(t\right) dt=\sqrt{{\displaystyle \frac{P}{2}}}R\left({\epsilon }_{\tau }\right)sinc\left(2\pi {\epsilon }_{f}T\right)cos\left(2\pi {\epsilon }_f\left(t_0+{\displaystyle \frac{T}{2}}\right)+{\epsilon }_{\varphi }\right)$$

(25)

$$Q={\displaystyle \frac{1}{T}}{\int }_{t_0}^{t_0+T}{s}_{IF}\left(t\right)\times {LR}_Q\left(t\right) dt=\sqrt{{\displaystyle \frac{P}{2}}}R\left({\epsilon }_{\tau }\right)sinc\left(2\pi {\epsilon }_{f}T\right)sin\left(2\pi {\epsilon }_f\left(t_0+{\displaystyle \frac{T}{2}}\right)+{\epsilon }_{\varphi }\right)$$

(26)

According to Equations (25) and (26), under ideal steady-state conditions, where the carrier phase error ${\epsilon }_{\varphi }$, carrier frequency error ${\epsilon }_f$, and code phase error ${\epsilon }_{\tau }$ are all zero, indicating perfect alignment between the locally replicated ranging code/carrier and the input navigation satellite signal, the in-phase (I) channel output assumes a nonzero value, while the quadrature (Q) channel output equals zero. This result demonstrates that the carrier and code-tracking loops achieve stable and error-free locking. Consequently, the entire signal energy was captured by the in-phase (I) channel, whereas the quadrature (Q) channel did not acquire any energy.

4. Output Signal Modeling of the Integrate-And-Dump Filter via Discrete-Time Summation

This section describes the output signal models for the in-phase (I) and quadrature (Q) channel integrate-and-dump filters under the discrete-time accumulation algorithm. These models were subsequently compared with those derived in Section 3 to analyze the potential discretization errors.

The discretization error is defined in Section 4.1. Section 4.2 and Section 4.3 present the derivations of the discrete-time output signal models for the I- and Q-channels, respectively. Finally, Section 4.4 provides a comparative and qualitative analysis of the signal models obtained using the two computational approaches under steady-state tracking loop conditions.

4.1. Discretization of the Integrate-And-Dump Filter Output Signal Model and Definition of Discretization Error

Using the continuous-time integration approach, the integral expression resulting from the correlation of the input signal with the locally generated carrier and ranging code was derived. This expression corresponds to the widely adopted post-integration signal model for the in-phase (I) and quadrature (Q) channels found in the literature, as expressed by Equations (25) and (26).

Under the current paradigm, in which the majority of receivers are implemented using digital circuits rather than analog circuits, continuous-time integration is theoretically realized through discrete-time accumulation. Let $T_s$ denote the discretization step size of the integrator, and let the output signal of the in-phase (I) channel integrate-and-dump filter be discretized accordingly. The continuous-time integral form of the I-channel integrate-and-dump filter output signal is

$$I={\displaystyle \frac{1}{T}}{\int }_{t_0}^{t_0+T}{s}_{IF}\left(t\right)\times {LR}_I\left(t\right) dt=\sqrt{2P}R\left({\epsilon }_{\tau }\right){\displaystyle \frac{1}{2T}}{\int }_{t_0}^{t_0+T}cos\left(2\pi {\epsilon }_{f}t+{\epsilon }_{\varphi }\right) dt$$

(27)

The discretization process involves a continuous integral in the expression. Given the complexity constraints of hardware implementation, satellite navigation receivers typically employ the first-order Runge-Kutta method to approximate the integral, which corresponds to the following discrete-time accumulation computation scheme, and it is assumed that T is divisible by T_s.

$${\int }_{t_0}^{t_0+T}cos\left(2\pi {\epsilon }_{f}t+{\epsilon }_{\varphi }\right) dt={\sum }_{k=0}^{N}cos\left(2\pi {\epsilon }_f\left(T_{s}k+t_0\right)+{\epsilon }_{\varphi }\right)T_s, T_s\times N=T$$

(28)

Consequently, the discretized models for the output signals of the in-phase (I) and quadrature (Q) channel integrate-and-dump filters can be derived, as shown in Equations (29) and (30), respectively:

$$I={\displaystyle \frac{\sqrt{2P}R\left({\epsilon }_{\tau }\right)}{2T}}{\sum }_{k=0}^{N}cos\left(2\pi {\epsilon }_f(T_{s}k+t_0)+{\epsilon }_{\varphi }\right)T_s$$

(29)

$$Q={\displaystyle \frac{\sqrt{2P}R\left({\epsilon }_{\tau }\right)}{2T}}{\sum }_{k=0}^{N}sin\left(2\pi {\epsilon }_f(T_{s}k+t_0)+{\epsilon }_{\varphi }\right)T_s$$

(30)

The discretization error of the in-phase (I) channel integrate-and-dump filter signal model is defined as ${\epsilon }_I$, and that of the quadrature (Q) channel integrate-and-dump filter signal model is defined as ${\epsilon }_Q$. This section analyzes the following discretization error definitions.

$${\epsilon }_I=\sqrt{{\displaystyle \frac{P}{2}}}R\left({\epsilon }_{\tau }\right)sinc\left(2\pi {\epsilon }_{f}T\right)cos\left(2\pi {\epsilon }_f\left(t_0+T/2\right)+{\epsilon }_{\varphi }\right)-{\displaystyle \frac{\sqrt{2P}R\left({\epsilon }_{\tau }\right)}{2T}}{\sum }_{k=0}^{N}cos\left(2\pi {\epsilon }_f(T_{s}k+t_0)+{\epsilon }_{\varphi }\right)T_s$$

(31)

$${\epsilon }_Q=\sqrt{{\displaystyle \frac{P}{2}}}R\left({\epsilon }_{\tau }\right)sinc\left(2\pi {\epsilon }_f{T}_I\right)sin\left(2\pi {\epsilon }_f\left(t_0+T/2\right)+{\epsilon }_{\varphi }\right)-{\displaystyle \frac{\sqrt{2P}R\left({\epsilon }_{\tau }\right)}{2T}}{\sum }_{k=0}^{N}sin\left(2\pi {\epsilon }_f(T_{s}k+t_0)+{\epsilon }_{\varphi }\right)T_s$$

(32)

To facilitate subsequent analytical derivation, the initial integration time was assumed to be zero (i.e., $t_0=0$). Under this assumption, discretization errors can be simplified.

$${\epsilon }_I={\displaystyle \frac{\sqrt{2P}R\left({\epsilon }_{\tau }\right)}{2}}\left[sinc\left(2\pi {\epsilon }_{f}T\right)cos\left(\pi {\epsilon }_{f}T+{\epsilon }_{\varphi }\right)-{\displaystyle \frac{T_s}{T}}{\sum }_{k=0}^{N-1}cos\left(2\pi {\epsilon }_f{T}_{s}k+{\epsilon }_{\varphi }\right)\right]$$

(33)

$${\epsilon }_Q={\displaystyle \frac{\sqrt{2P}R\left({\epsilon }_{\tau }\right)}{2}}\left[sinc\left(2\pi {\epsilon }_{f}T\right)sin\left(\pi {\epsilon }_{f}T+{\epsilon }_{\varphi }\right)-{\displaystyle \frac{T_s}{T}}{\sum }_{k=0}^{N-1}sin\left(2\pi {\epsilon }_f{T}_{s}k+{\epsilon }_{\varphi }\right)\right]$$

(34)

4.2. Modeling the Output Signal of the In-Phase Channel Integrate-And-Dump Filter via Discrete-Time Summation

To derive the output signal model of the in-phase (I) channel integrate-and-dump filter using the discrete-time accumulation approach, the key step involves deriving the discrete cosine function summation term in the aforementioned expression. This is accomplished by first expanding the term using the cosine angle sum identity of the trigonometric functions, as follows:

$${\sum }_{k=0}^{N-1}cos\left(2\pi {\epsilon }_f{T}_{s}k+{\epsilon }_{\varphi }\right)=cos\left({\epsilon }_{\varphi }\right){\sum }_{k=0}^{N-1}cos\left(2\pi {\epsilon }_f{T}_{s}k\right)-sin\left({\epsilon }_{\varphi }\right){\sum }_{k=0}^{N-1}sin\left(2\pi {\epsilon }_f{T}_{s}k\right)$$

(35)

In the expanded expression, the first term involves the summation of the cosine series, whereas the second term comprises the summation of the sine series. To obtain an analytical solution for the discretization error, it is essential to derive closed-form expressions for both cosine and sine series summations. The sine series summation formula is derived as follows:

$$\sum _{k=0}^{n-1}sin\left(\theta \times k\right)={\displaystyle \frac{1}{sin\left(\frac{\theta }{2}\right)}}\left[sin\left(\theta \right)sin\left({\displaystyle \frac{\theta }{2}}\right)+\cdots +sin\left(\left(n-1\right)\theta \right)sin\left({\displaystyle \frac{\theta }{2}}\right)\right]$$

(36)

Based on the product-to-sum identities of the trigonometric functions, the result for each individual term can be derived, and partial cancellation occurs when the adjacent terms are summed.

$$sin\left(\left(n-1\right)\theta \right)sin\left({\displaystyle \frac{\theta }{2}}\right)=\left(-{\displaystyle \frac{1}{2}}\right)\left[cos\left({\displaystyle \frac{2n-1}{2}}\theta \right)-cos\left({\displaystyle \frac{2n-3}{2}}\theta \right)\right]$$

(37)

By substituting Equation (37) into Equation (36) and performing the summation, the following result is obtained.

$$\sum _{k=0}^{n-1}sin\left(\theta \times k\right)={\displaystyle \frac{sin\left(\frac{n\theta }{2}\right)sin\left[\frac{\left(n-1\right)\theta }{2}\right]}{sin\left(\frac{\theta }{2}\right)}}$$

(38)

With the derivation of the discrete sine series summation formula, the derivation of the discrete cosine series summation formula is as follows:

$$\sum _{k=0}^{n-1}cos\left(\theta \times k\right)={\displaystyle \frac{1}{sin\left(\frac{\theta }{2}\right)}}\left[sin\left({\displaystyle \frac{\theta }{2}}\right)+sin\left({\displaystyle \frac{\theta }{2}}\right)cos\left(\theta \right)+\cdots +sin\left({\displaystyle \frac{\theta }{2}}\right)cos\left(\left(n-1\right)\theta \right)\right]$$

(39)

Based on the product-to-sum identities of the trigonometric functions, the result for each individual term can be derived, and partial cancellation occurs when the adjacent terms are summed.

$$sin\left({\displaystyle \frac{\theta }{2}}\right)cos\left(\left(n-1\right)\theta \right)=\left({\displaystyle \frac{1}{2}}\right)\left[sin\left({\displaystyle \frac{2n-1}{2}}\theta \right)-sin\left({\displaystyle \frac{2n-3}{2}}\theta \right)\right]$$

(40)

By substituting Equation (40) into Equation (39) and performing the summation, the following result is obtained.

$$\sum _{k=0}^{n-1}cos\left(\theta \times k\right)={\displaystyle \frac{cos\left(\frac{\left(n-1\right)\theta }{2}\right)sin\left(\frac{n\theta }{2}\right)}{sin\left(\frac{\theta }{2}\right)}}$$

(41)

According to Equations (38) and (41), the summation of the cosine and sine series in Equation (35) can be obtained.

$${\sum }_{k=0}^{N-1}cos\left(2\pi {\epsilon }_f{T}_{s}k\right)={\displaystyle \frac{cos\left[\left(N-1\right)\pi {\epsilon }_f{T}_s\right]}{sin\left(\pi {\epsilon }_f{T}_s\right)}}sin\left(N\pi {\epsilon }_f{T}_s\right)$$

(42)

$${\sum }_{k=0}^{N-1}sin\left(2\pi {\epsilon }_f{T}_{s}k\right)={\displaystyle \frac{sin\left[\left(N-1\right)\pi {\epsilon }_f{T}_s\right]}{sin\left(\pi {\epsilon }_f{T}_s\right)}}sin\left(N\pi {\epsilon }_f{T}_s\right)$$

(43)

$${\sum }_{k=0}^{N-1}cos\left(2\pi {\epsilon }_f{T}_{s}k+{\epsilon }_{\varphi }\right)={\displaystyle \frac{sin\left[N\pi {\epsilon }_f{T}_s\right]}{sin\left(\pi {\epsilon }_f{T}_s\right)}}cos\left({\epsilon }_{\varphi }+\left(N-1\right)\pi {\epsilon }_f{T}_s\right)$$

(44)

Substituting Equation (44) into Equation (33) yields an analytical expression for the discretization error of the I-channel integrate-and-dump filter.

$${\epsilon }_I={\displaystyle \frac{\sqrt{2P}R\left({\epsilon }_{\tau }\right)}{2}}\left[sinc\left(2\pi {\epsilon }_{f}T\right)cos\left(\pi {\epsilon }_{f}T+{\epsilon }_{\varphi }\right)-{\displaystyle \frac{T_s}{T}}{\displaystyle \frac{sin\left(N\pi {\epsilon }_f{T}_s\right)}{sin\left(\pi {\epsilon }_f{T}_s\right)}}cos\left({\epsilon }_{\varphi }+\left(N-1\right)\pi {\epsilon }_f{T}_s\right)\right]$$

(45)

4.3. Modeling the Output Signal of the Quadrature-Phase Channel Integrate-And-Dump Filter via Discrete-Time Summation

The analytical expression for the discretization error of the Q-path integrate-and-dump filter output signal was derived by following the method described in Section 4.2.

$${\epsilon }_Q={\displaystyle \frac{\sqrt{2P}R\left({\epsilon }_{\tau }\right)}{2}}\left[sinc\left(2\pi {\epsilon }_{f}T\right)sin\left(\pi {\epsilon }_{f}T+{\epsilon }_{\varphi }\right)-{\displaystyle \frac{T_s}{T}}{\sum }_{k=0}^{N-1}sin\left(2\pi {\epsilon }_f{T}_{s}k+{\epsilon }_{\varphi }\right)\right]$$

(46)

The key to deriving Equation (46) lies in the derivation of its discrete sine series summation term, which is first expanded using the trigonometric sine addition formula as follows:

$${\sum }_{k=0}^{N-1}sin\left(2\pi {\epsilon }_f{T}_{s}k+{\epsilon }_{\varphi }\right)=cos\left({\epsilon }_{\varphi }\right){\sum }_{k=0}^{N-1}sin\left(2\pi {\epsilon }_f{T}_{s}k\right)+sin\left({\epsilon }_{\varphi }\right){\sum }_{k=0}^{N-1}cos\left(2\pi {\epsilon }_f{T}_{s}k\right)$$

(47)

Substituting Equations (42) and (43) into Equation (47) yields an analytical expression for the discrete sine-series summation term.

$${\sum }_{k=0}^{N-1}sin\left(2\pi {\epsilon }_f{T}_{s}k+{\epsilon }_{\varphi }\right)={\displaystyle \frac{sin\left(N\pi {\epsilon }_f{T}_s\right)}{sin\left(\pi {\epsilon }_f{T}_s\right)}}sin\left({\epsilon }_{\varphi }+\left(N-1\right)\pi {\epsilon }_f{T}_s\right)$$

(48)

Substituting Equation (48) into Equation (34) yields an analytical expression for the discretization error of the Q-channel integrate-and-dump filter.

$${\epsilon }_Q={\displaystyle \frac{\sqrt{2P}R\left({\epsilon }_{\tau }\right)}{2}}\left[sinc\left(2\pi {\epsilon }_{f}T\right)sin\left(\pi {\epsilon }_{f}T+{\epsilon }_{\varphi }\right)-{\displaystyle \frac{T_s}{T}}{\displaystyle \frac{sin\left(N\pi {\epsilon }_f{T}_s\right)}{sin\left(\pi {\epsilon }_f{T}_s\right)}}sin\left({\epsilon }_{\varphi }+\left(N-1\right)\pi {\epsilon }_f{T}_s\right)\right]$$

(49)

4.4. Qualitative Analysis of Discretization Error in Integrate-And-Dump Filters Under Steady-State Conditions

Analytical Expressions of Discretization Errors for I- and Q-Path Integrate-and-Dump Filters Derived in Section 4.2 and Section 4.3, as Equations (45) and (49), respectively, and shown in Figure 1.

Based on the derived analytical expressions for the discretization errors, a qualitative analysis of the discretization error under steady-state conditions is presented below:

The steady state is defined as the operational condition wherein, after the receiver enters stable operation, the locally generated ranging codes and carriers align completely with those received from the satellite signals, indicating that the ranging code phase error, carrier phase error, and carrier frequency error approach zero.

$$\underset{t\to \infty }{\lim }{\epsilon }_{\tau }\left(t\right)=0, \underset{t\to \infty }{\lim }{\epsilon }_f\left(t\right)=0, \underset{t\to \infty }{\lim }{\epsilon }_{\varphi }\left(t\right)=0$$

(50)

Under the steady-state assumption shown in Equation (50), the following equations are obtained:

$$\underset{{\epsilon }_{\tau }\left(t\right)\to 0}{\mathit{lim}}R\left({\epsilon }_{\tau }\right)=1$$

(51)

$$\underset{{\epsilon }_f\left(t\right)\to 0,{\epsilon }_{\varphi }\to 0}{\mathit{lim}}cos\left(\pi {\epsilon }_{f}T+{\epsilon }_{\varphi }\right)=1 \underset{{\epsilon }_f\left(t\right)\to 0,{\epsilon }_{\varphi }\to 0}{\mathit{lim}}sin\left(\pi {\epsilon }_{f}T+{\epsilon }_{\varphi }\right)=0$$

(52)

$$\underset{{\epsilon }_f\left(t\right)\to 0}{\mathit{lim}}{\displaystyle \frac{sin\left(N\pi {\epsilon }_f{T}_s\right)}{sin\left(\pi {\epsilon }_f{T}_s\right)}}={\displaystyle \frac{N\pi {\epsilon }_f{T}_s}{\pi {\epsilon }_f{T}_s}}=N \underset{{\epsilon }_f\left(t\right)\to 0}{\mathit{lim}}sinc\left(2\pi {\epsilon }_f{T}_I\right)=1$$

(53)

$$\underset{{\epsilon }_f\left(t\right)\to 0,{\epsilon }_{\varphi }\to 0}{\mathit{lim}}cos\left({\epsilon }_{\varphi }+\left(N-1\right)\pi {\epsilon }_{f}T\right)=1 \underset{{\epsilon }_f\left(t\right)\to 0,{\epsilon }_{\varphi }\to 0}{\mathit{lim}}sin\left({\epsilon }_{\varphi }+\left(N-1\right)\pi {\epsilon }_{f}T\right)=0$$

(54)

Substituting Equations (51)–(54) into Equations (45) and (49) yields the analytical expression for the discretization error of the Q-channel integrate-and-dump filter.

$$\begin{array}{ll}{\epsilon }_I={\displaystyle \frac{\sqrt{2P}R\left({\epsilon }_{\tau }\right)}{2}}& \left[sinc\left(2\pi {\epsilon }_{f}T\right)cos\left(\pi {\epsilon }_{f}T+{\epsilon }_{\varphi }\right)-{\displaystyle \frac{T_s}{T}}{\displaystyle \frac{sin\left(N\pi {\epsilon }_f{T}_s\right)}{sin\left(\pi {\epsilon }_f{T}_s\right)}}cos\left({\epsilon }_{\varphi }+\left(N-1\right)\pi {\epsilon }_f{T}_s\right)\right]\\ & ={\displaystyle \frac{\sqrt{2P}}{2}}\left[1-{\displaystyle \frac{{NT}_s}{T}}\right]=0\end{array}$$

(55)

$$\begin{array}{ll}{\epsilon }_Q={\displaystyle \frac{\sqrt{2P}R\left({\epsilon }_{\tau }\right)}{2}}& \left[sinc\left(2\pi {\epsilon }_{f}T\right)sin\left(\pi {\epsilon }_{f}T+{\epsilon }_{\varphi }\right)-{\displaystyle \frac{T_s}{T}}{\displaystyle \frac{sin\left(N\pi {\epsilon }_f{T}_s\right)}{sin\left(\pi {\epsilon }_f{T}_s\right)}}sin\left({\epsilon }_{\varphi }+\left(N-1\right)\pi {\epsilon }_f{T}_s\right)\right]\\ & ={\displaystyle \frac{\sqrt{2P}R\left({\epsilon }_{\tau }\right)}{2}}\left[0-{\displaystyle \frac{{NT}_s}{T}}*0\right]=0\end{array}$$

(56)

Based on an analysis of the calculated results under the aforementioned steady-state conditions, the following three qualitative conclusions can be drawn:

Qualitative Conclusion 1: Under idealized conditions, where the receiver can stably and perfectly replicate both the carrier and ranging codes locally without any errors, the discretization error of the integrate-and-dump filter would theoretically be absent. However, such perfect and stable local replication is practically unattainable; consequently, a discretization error inevitably exists.

Qualitative Conclusion 2: If the receiver can stably and perfectly replicate the carrier and ranging code locally without any errors, then the result obtained by continuous integration is identical to that obtained by discrete accumulation. This demonstrates that the output signal model of the integrate-and-dump filter derived in this study under the discrete-time accumulation method is correct under this steady-state boundary condition. The validity of the model under other error conditions is experimentally verified in Section 5.

Qualitative Conclusion 3: Analysis of the integrate-and-dump filter output signal model derived using continuous-time integration in existing navigation spoofing technology research exhibits certain qualitative limitations. However, it must also be considered that if the discretization error is sufficiently small, employing the model derived from continuous-time integration for the analysis remains feasible. A quantitative analysis of the discretization error is presented in Section 5 (Experiments).

5. Experiments

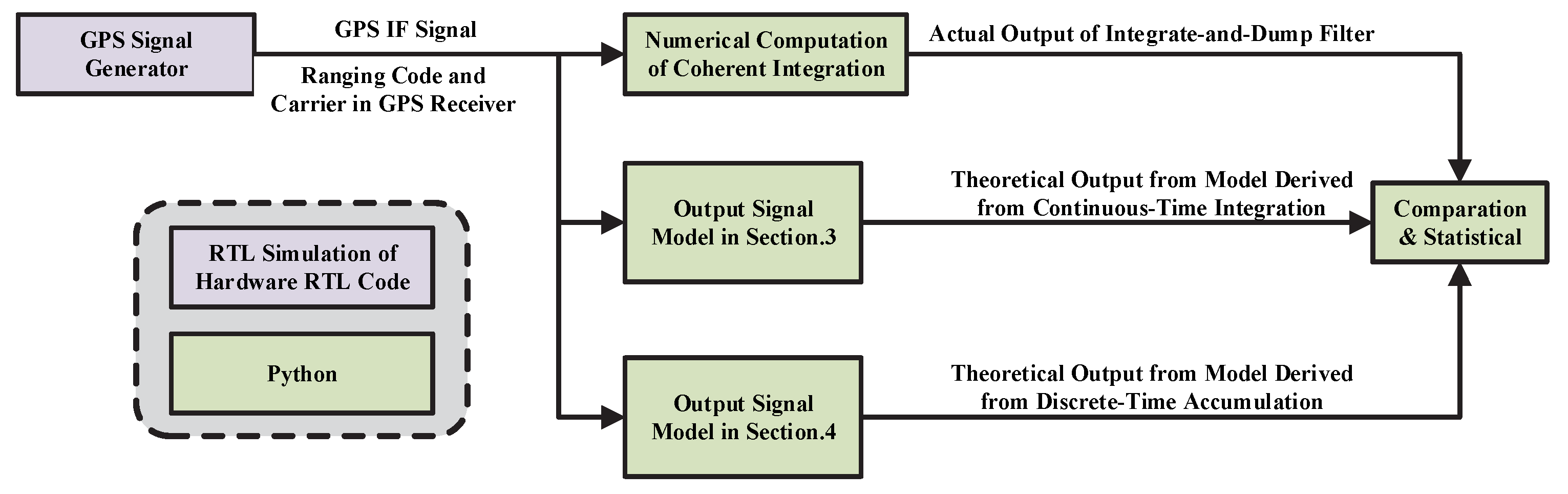
5.1. Experimental Objectives and Design

The objective of this experiment was to validate the accuracy of the integrate-and-dump filter output signal model derived using the discrete-time accumulation method. Validating this model simultaneously confirms the accuracy of the discretization error defined in this study.

The model’s validity was confirmed by generating GPS IF digital signals using a GPS signal generator. Following this, the operation of the integrate-and-dump filter within the GPS receiver was simulated through numerical computations. The results from these computations were then compared with the outcomes of the models derived in Section 3 and Section 4 to assess the impact of discretization errors on accuracy.

5.2. Experimental Environment and Setup

The experiment designed in this study was divided into four steps, as illustrated in Figure 1.

Step-1: GPS and Receiver Signal Generation

This step generates the GPS IF signal as the receiver input along with the locally replicated C/A Code and carrier signals in the GPS receiver. Using the hardware RTL code of a GPS signal generator, a simulation was performed to generate IF signals in the L1 band for a specific GPS satellite and C/A code and carrier signals in the GPS receiver.

Step-2: Determine the output of the integrate-and-dump filter

The GPS IF signals and locally replicated signals in the GPS receiver generated in Step 1 are processed to obtain the actual output value of the integrate-and-dump filter. The numerical computation of the coherent integration algorithm, based on the computational principle of the integrate-and-dump filter in satellite navigation receivers, produces the output of the integrate-and-dump filter.

Step-3: Theoretical output calculation via output signal model

Based on the signals generated in Step 1, the theoretical output value of the integrate-and-dump filter was calculated using the closed-form analytical solutions presented in Section 3 and Section 4.

Step 4: Model Validation and Discretization Error Analysis

By utilizing the actual output value of the integrate-and-dump filter obtained through the numerical methods in Step 2, a comparison is drawn with the theoretical output values calculated using the two output signal models in Step 3. This comparison serves a dual purpose: first, to assess the accuracy of the signal model derived from discrete-time accumulation in Section 3 and second, to quantitatively analyze the discretization error of the traditional integrate-and-dump filter output signal model in Section 2 under various conditions.

The experimental setup, as illustrated in the Figure 2, comprised five main components. One is the RTL simulation environment constructed from the GPS signal generator RTL code, whereas the remaining four are numerical computation environments implemented in Python 3.10.

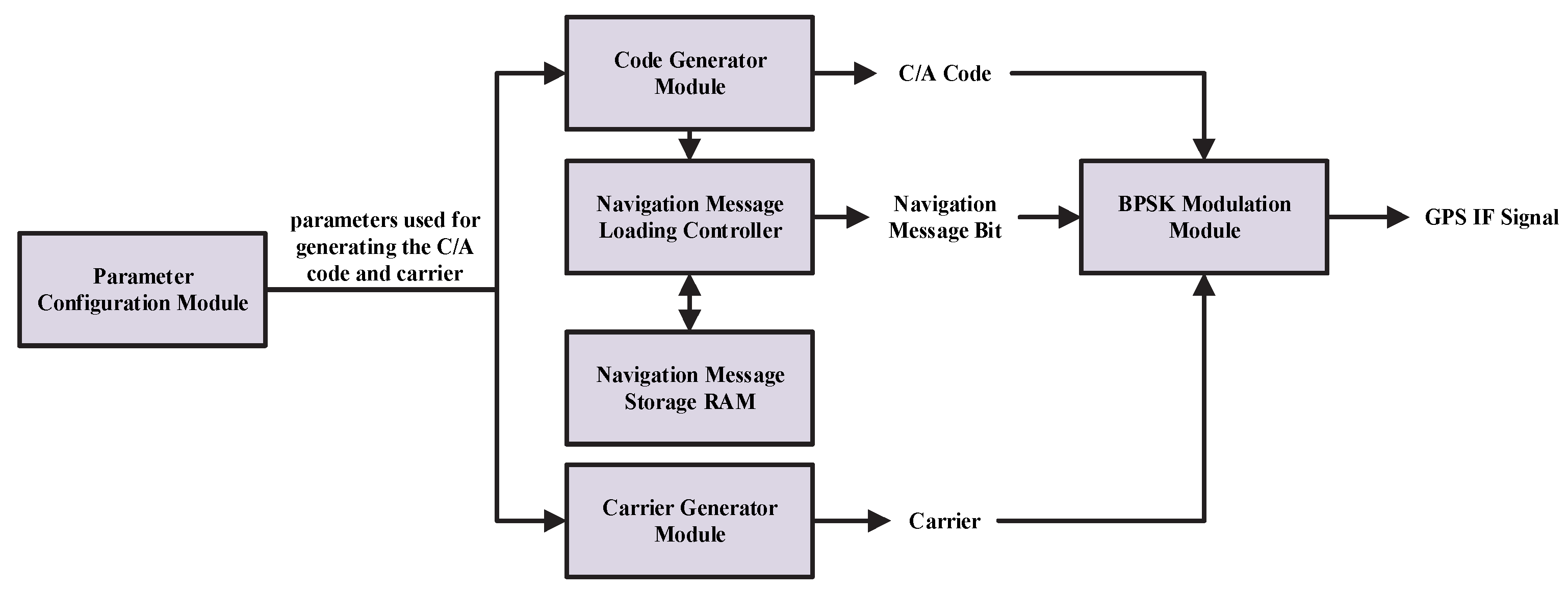
5.3. Intermediate Frequency Signal Generation Based on a GPS Satellite Signal Generator

The GPS satellite signal generator was employed to generate GPS IF signals along with the locally replicated C/A Code and carrier signals within the GPS receiver, which consisted of six modules, as illustrated in the Figure 3. The parameter configuration module was employed to set the parameters for both the ranging code phase, carrier initial phase and carrier frequency.

The parameter to be configured for the ranging code generator module is ranging code phase. Based on the configuration information, this module generates the ranging code for the navigation satellite and outputs it to the BPSK (Binary Phase-Shift Keying) modulation module. The parameters to be set for the carrier generation module include carrier initial phase and carrier frequency. According to the configuration, it produces an IF carrier signal and delivers it to the BPSK modulation module.

While generating the ranging code, the ranging code generator module produces corresponding time information based on the characteristics of the ranging code. This time, information is sent to the navigation message-loading controller. The navigation message loading controller, leveraging the correspondence between this time and the navigation message, generates a read address signal and outputs it to the navigation message storage random-access memory (RAM). Subsequently, the navigation message corresponding to the current time, which is read from RAM, is output to the BPSK modulation module. Finally, the BPSK modulation module performs BPSK modulation on the input ranging code, carrier signal, and navigation message to generate an IF signal of a specific GPS satellite.

Ensuring the accuracy of IF signals generated by a GPS signal generator involves two crucial steps: verifying the precision of the generated ranging codes and confirming the correctness of the generated carrier signals.

To verify the accuracy of the generated ranging codes, a comparison was conducted with the first 10 bits of the ranging code for a GPS satellite, as outlined in the GPS Interface Control Document (ICD) and illustrated in Figure 4. For example, when generating signals for a satellite with SV ID = 1, the output waveform is stored in VCD format. This VCD file is then transformed into a visual representation using the open-source waveform analysis tool, gtkwave. The generated C/A code is subsequently compared with the first 10 bits of the C/A code specified for SV ID = 1 in the GPS ICD, IS-GPS-200N (2022 edition), to confirm its accuracy.

As Shown in Figure 5, the Octal Value (1440) and Binary Representation (11_0010_0000) of the first 10 Bits of the Ranging Code for GPS SV ID = 1. The simulation results for the ranging code are shown in Figure 6. The first row shows the generated ranging code, the second row shows the chip count value of the ranging code, the third row illustrates the chip boundary marker signal, and the fourth row indicates the millisecond boundary marker signal. As observed, a logic ‘1’ pulse in the millisecond marker signal denotes the start of a new ranging code period. Based on the chip count value in the second row and the chip boundary marker in the third row, the first 10 bits of the generated ranging code were identified as 11_0010_0000. This result is consistent with the findings shown in Figure 4, confirming the correctness of the ranging code simulation.

To validate that the generated carrier met expectations, sine and cosine waves were plotted together to demonstrate their 90-degree phase difference, as shown in Figure 7. Additionally, the periods of both waves can be observed in the plot, thereby confirming that the carrier frequency aligns with the expected value. The generated sine and cosine carrier waves were plotted using Python 3.10, with a sampling interval of 20 ns (corresponding to a sampling rate of 50 MHz). One complete cycle of either the sine or cosine wave comprised ten sample points, equivalent to a duration of 200 ns, which corresponds to a carrier frequency of 5 MHz. The observed 90-degree phase difference between the two waveforms confirmed the accuracy of the generated carrier.

Given that the chip duration of the navigation message is 20 ms, which is 20 times longer than the C/A code period, throughout the simulation, the navigation message bit was set to one. A segment of the waveform was extracted and analyzed to verify the accuracy of the BPSK-modulated waveform. According to the definition of BPSK, the waveform should comprise C/A code, navigation message bit, and carrier signal. Visual inspection of the waveform confirmed that these components were properly integrated, thereby validating the accuracy of the BPSK modulation.

The spectral characteristics of the BPSK signals in the in-phase (I) and quadrature (Q) channels are illustrated in the Figure 8. The observed spectrum exhibits a main lobe centered at the carrier frequency with symmetrical side lobes, which is consistent with the theoretical spectrum of the BPSK signal. The absence of anomalous spectral components and adherence to the expected shape further demonstrates that the generated BPSK signal meets the theoretical specifications.

5.4. Validation Results of the Derived Integrate-And-Dump Filter Output Signal Model

(1)

Parameter Settings of the Integrator-and-Dump Filter

The experimental parameters to be set include sampling interval (Ts), integration time (T), and number of samples (N). In this paper, integration time (T) is set to 1 ms, because for GPS L1 C/A code receivers, integration time (T) is generally set to 1 ms to match the 1 ms period of the C/A code; setting the integration period to 1 ms allows complete coverage of one code period, achieving full despreading and coherent integration, and avoiding energy loss caused by code phase truncation. Sampling interval (Ts) is set to 200 ns, because the modulation scheme of the GPS L1 s error feedback control core ignal uses BPSK to modulate the 1.023 MHz C/A code, and the double-sideband bandwidth of a BPSK modulated signal is twice the C/A code rate, i.e., 2.046 MHz. According to the Nyquist sampling theorem, the sampling frequency is set to 5 MHz, i.e., sampling interval (Ts) is set to 200 ns. Number of samples (N) is obtained by dividing integration time (T) by sampling interval (Ts), i.e., number of samples (N) is 5000.

(2)

Verification Method

This subsection compares the Integrate-and-Dump Filter Output calculated using three methods. The first method directly computes the Integrate-and-Dump Filter Output based on Equations (29) and (30) using a numerical calculation approach. The results for the I-channel and Q-channel are denoted as numerical_sum_I and numerical_sum_Q, respectively.

The second method calculates the Integrate-and-Dump Filter Output using the signal model derived from the continuous integration method based on Equations (25) and (26) in Section 3. The calculation results for the I-channel and Q-channel are denoted as continuous_sum_I and continuous_sum_Q, respectively.

The third method calculates the Integrate-and-Dump Filter Output using the signal model obtained through the discrete accumulation method proposed in this paper, based on Equations (45) and (49) in Section 4. The calculation results for the I-channel and Q-channel are denoted as discrete_sum_I and discrete_sum_Q, respectively.

When the computational result of the model is closer to the result obtained directly by numerical computation, it indicates higher accuracy of the model. Through theoretical analysis, this paper considers that the deviation between the result calculated using the formula derived in Section 3 and the result obtained directly by numerical computation will be larger; this deviation is precisely the manifestation of the discretization error of the conventional model in Section 3.

(3)

Experimental Results Under Different Ranging Code Phase Error Conditions

The experiment initially focused on the ranging code phase error to validate the correctness of the analytical model for the integrate-and-dump filter output signal, which was derived using the discrete-time accumulation approach for varying conditions of the ranging code phase error. A comparison of the computational results for the integrate-and-dump filters in the I and Q channels is presented in

Table 1. The parameters used for generating the C/A code and carrier.

Parameters Used for Generating the C/A Code		Parameters Used for Generating Carrier
SV ID	No. 1	frequency of carrier	5.0 Mhz
initial code count	0 chip	initial phase of carrier	0 rad
initial phase of the initial code chip	0 chip	amplitude of carrier	1.0 V

and

Table 2. Comparison of I-channel Integrate-and-Dump Filter Output Signals Under Different Ranging Code Phase Errors.

CA_Code_Error/Chip	Numerical_Sum_I	Discrete_Sum_I	Continuous_Sum_I
0	4.999999997158 × 10−4	5.000000000000 × 10−4	5.000000000000 × 10−4
0.125	4.376312525976 × 10−4	4.375000000000 × 10−4	4.375000000000 × 10−4
0.25	3.751753314078 × 10−4	3.750000000000 × 10−4	3.750000000000 × 10−4
0.375	3.127238640510 × 10−4	3.125000000000 × 10−4	3.125000000000 × 10−4
0.5	2.500419028446 × 10−4	2.500000000000 × 10−4	2.500000000000 × 10−4
0.625	1.871505947997 × 10−4	1.875000000000 × 10−4	1.875000000000 × 10−4
0.75	1.244553337907 × 10−4	1.250000000000 × 10−4	1.250000000000 × 10−4
0.875	6.206546844291 × 10−5	6.250000000000 × 10−5	6.250000000000 × 10−5
1	−5.136220313802 × 10−8	0.000000000000	0.000000000000

.

As evidenced by the simulation results presented in Table 1 and Table 2, when only the ranging code phase error is present, the outputs from both integrate-and-dump filter signal models closely align with the numerical simulation results. Furthermore, the results obtained from the two signal models were identical. This observation is consistent with the analytical expressions of the models, which indicates that the discretization error is absent under the condition of a solitary ranging code phase error.

(4)

Experimental Results Under Different Initial Carrier Phase Error Conditions

An experiment was conducted to investigate the impact of the initial carrier phase error, with the aim of validating the accuracy of the analytical model for the integrate-and-dump filter output signal derived under the discrete-time accumulation approach in this study, under varying conditions of this error. The initial carrier phase error was incremented from 0 to 360° in steps of 10°. The computational results for the integrate-and-dump filters in the I and Q channels under these conditions are compared in

Table 3. Comparison of Q-hannel Integrate-and-Dump Filter Output Signals Under Different Ranging Code Phase Errors.

CA_Code_Error/Chip	Numerical_Sum_Q	Discrete_Sum_Q	Continuous_Sum_Q
0	−1.163311852706 × 10−16	0.000000000000	0.000000000000
0.125	2.292335467488 × 10−8	0.000000000000	0.000000000000
0.25	9.480574595260 × 10−8	0.000000000000	0.000000000000
0.375	−1.517970746122 × 10−7	0.000000000000	0.000000000000
0.5	−3.117096183879 × 10−7	0.000000000000	0.000000000000
0.625	−3.030659114376 × 10−7	0.000000000000	0.000000000000
0.75	−1.378690759851 × 10−8	0.000000000000	0.000000000000
0.875	1.432603077285 × 10−7	0.000000000000	0.000000000000
1	−1.163311852706 × 10−16	0.000000000000	0.000000000000

and

Table 4. Comparison of Calculated Output Signals from the I-Channel Integrate-and-Dump Filter Under Different Carrier Initial Phase Errors.

Carrier _Initial_Phase_Error/°	Numerical_Sum_I	Discrete_Sum_I	Continuous_Sum_I
0	5.00000000 × 10−4	5.00000000 × 10−4	5.00000000 × 10−4
60	2.50000000 × 10−4	2.50000000 × 10−4	2.50000000 × 10−4
120	−2.50000000 × 10−4	−2.50000000 × 10−4	−2.50000000 × 10−4
180	−5.00000000 × 10−4	−5.00000000 × 10−4	−5.00000000 × 10−4
240	−2.50000000 × 10−4	−2.50000000 × 10−4	−2.50000000 × 10−4
360	5.00000000 × 10−4	5.00000000 × 10−4	5.00000000 × 10−4

, respectively.

The complete experimental results are presented in Figure 9 and Figure 10, while Table 3 and Table 4 list a portion of these results for clarity. As shown in Table 3 and Table 4 and Figure 9 and Figure 10, the simulation results reveal that when only the initial carrier phase error is present, the outcomes from the two integrate-and-dump filter output signal models closely align with the numerical simulation results. Furthermore, the outputs of the two signal models were identical, indicating that there was no discretization error when only the initial carrier phase error was present.

(5)

Experimental Results Under Different Carrier Frequencies

An experiment was conducted to investigate the impact of the carrier frequency error to validate the accuracy of the analytical model for the integrate-and-dump filter output signal derived under the discrete-time accumulation approach in this study under varying carrier frequency error conditions. The carrier frequency error was increased from 0 Hz to 100 Hz in steps of 10 Hz. The computational results for the integrate-and-dump filters in the I and Q channels are compared in

Table 5. Comparison of Calculated Output Signals from the Q-Channel Integrate-and-Dump Filter Under Different Carrier Initial Phase Errors.

Carrier_Initial_Phase_Error/°	Numerical_Sum_Q	Discrete_Sum_Q	Continuous_Sum_Q
0	−1.16331185 × 10−16	0.00000000	0.00000000
60	4.33012702 × 10−4	4.33012702 × 10−4	4.33012702 × 10−4
120	4.33012702 × 10−4	4.33012702 × 10−4	4.33012702 × 10−4
180	5.58719301 × 10−16	6.12323400 × 10−20	6.12323400 × 10−20
240	−4.33012702 × 10−4	−4.33012702 × 10−4	−4.33012702 × 10−4
300	−4.33012702 × 10−4	−4.33012702 × 10−4	−4.33012702 × 10−4
360	2.34492444 × 10−16	−1.22464680 × 10−19	−1.22464680 × 10−19

, respectively.

As shown in Figure 11 and Figure 12, the simulation results indicate that when only the carrier frequency error is present, the integrate-and-dump filter output signal model derived using the discrete-time accumulation approach in this study aligns more closely with the numerical simulation results. Notably, when the carrier frequency error surpassed 20 Hz, the discrepancy between the results calculated using the traditional model derived from continuous-time integration and the numerical results began to widen. This increasing divergence highlights the significant impact of the discretization error under these conditions.

To compare the accuracy of the two signal output models more clearly, the following error formula is defined to quantitatively describe the deviation between the theoretically predicted values and measured values.

$$Error={\displaystyle \frac{measured values-theoretical predicted}{measured values}}\times 100\%$$

(57)

For instance, to evaluate the accuracy of the two integrate-and-dump output signal models for the I-channel, the precision of the conventional I-channel integrate-and-dump output signal model is calculated using Equation (58), whereas that of the model derived in this study is computed using Equation (59).

$$Error\_I\_continuous={\displaystyle \frac{continuous\_sum\_ I-numerical\_sum\_ I}{numerical\_sum\_ I}}\times 100\%$$

(58)

$$Error\_I\_discrete={\displaystyle \frac{discrete\_sum\_ I-numerical\_sum\_ I}{numerical\_sum\_ I}}\times 100\%$$

(59)

Similarly, the errors for the Q-channel are defined as shown in Equations (60) and (61):

$$Error\_Q\_continuous={\displaystyle \frac{continuous\_sum\_Q-numerical\_sum\_ Q}{numerical\_sum\_ Q}}\times 100\%$$

(60)

$$Error\_Q\_discrete={\displaystyle \frac{discrete\_sum\_ Q-numerical\_sum\_ Q}{numerical\_sum\_ Q}}\times 100\%$$

(61)

According to the computational results of the error definitions above, the results are shown in Figure 13 and Figure 14. It can be seen that the signal model derived by the discrete accumulation method in this paper exhibits better agreement with the results obtained directly by numerical computation. When the carrier frequency error is 100 Hz, the deviations from the direct numerical computation results are 5.1% (I channel) and −27.42% (Q channel), whereas the deviations of the conventional signal model reach −50.20% (I channel) and 65.62% (Q channel).

Compared with results obtained directly through numerical computation, the model derived from continuous integration exhibits a relative error exceeding 50% when the carrier frequency error exceeds 100 Hz, and this relative error continues to increase with growing carrier frequency error. This indicates that the signal model derived from continuous integration shows significant discretization error in the presence of large carrier frequency errors.

Comparing with previous experimental results, it can be seen that when only ranging code phase error or carrier initial phase error exists, the outputs of the integrate-and-dump sampler signal model derived from continuous-time integration and from discrete summation are essentially consistent and also very close to the direct numerical integration results. That is, when only ranging code phase error or carrier initial phase error exists, the discretization error is negligible. However, from the experimental results in this section, it is observed that when carrier frequency error exists, the discretization error of the integrate-and-dump sampler output signal model derived from continuous-time integration exhibits a significant nonlinear increase with increasing carrier frequency error, which we believe may be caused by the following reasons:

When ${\epsilon }_f$ increases, $sinc\left(2\pi {\epsilon }_{f}T\right)$ exhibits oscillatory variation with amplitude decay, whereas $sin\left(N\pi {\epsilon }_f{T}_s\right)/sin\left(\pi {\epsilon }_f{T}_s\right)$ merely oscillates without amplitude decay. This difference leads to a marked increase in the discretization error of the integrate-and-dump filter output model derived from continuous-time integration.

5.5. Discussion of Results

The following quantitative conclusions can be drawn from the experimental results in Section 5.4:

Quantitative Conclusion 1: When only the ranging code phase error and initial carrier phase error are considered, the results obtained using the traditional integrate-and-dump output signal model, which is based on continuous-time integration, are essentially consistent with those derived from the discrete-time accumulation-based model proposed in this paper. Both models were closely aligned with the numerical computation results.

Quantitative Conclusion 2: When only a carrier frequency error is present, the integrate-and-dump output signal model derived in this study aligns more closely with numerical computation results. Notably, when the carrier frequency error surpasses 20 Hz, the discrepancy between the traditional model, which relies on continuous-time integration, and the numerical results becomes significantly larger. For the I-channel results, at a carrier frequency error of 100 Hz, the proposed model exhibits an error of 5.1%, whereas the traditional model’s deviation reaches 50%, highlighting the substantial impact of the discretization error. In the Q-channel, the error of the traditional model increases sharply with the carrier frequency error, reaching 65% at 100 Hz, while the error of the proposed model remains relatively stable at approximately 28%. The error in the Q-channel is considerably larger than that in the I-channel, which is likely because of the distinct error characteristics between the two. This discrepancy is a valuable topic for future research.

Quantitative Conclusion 3: The three sets of experimental results demonstrate that the impact of the discretization error is negligible when only the ranging code error and initial carrier phase error are present. However, when a carrier frequency error is introduced, the influence of the discretization error becomes evident, particularly when the carrier frequency error exceeds 20 Hz, at which point its effect is significantly pronounced. Because carrier-frequency errors are almost unavoidable in practical scenarios, it is crucial to consider the impact of discretization errors in studies focused on navigation spoofing and related issues. Therefore, using the integrate-and-dump output signal model derived in this study based on discrete-time accumulationprovides more accurate analytical conclusions in the investigation of navigation spoofing techniques.

The theoretical and simulation results presented in this paper are based on the following assumptions, which do not always hold true in practical receiver implementations. The impact of these assumptions on the discretization error of the integrator-and-dump filter will be explored in further research. These assumptions primarily include:

First, this paper makes relatively ideal assumptions regarding the characteristics of the RF front-end filter and the ADC. Specifically, it is assumed that the RF front-end filter exhibits a constant group delay, and that the ADC’s sampling clock is free from jitter and that its sampling period maintains an integer multiple relationship with the integration time T of the integrator-and-dump filter. The influence of these assumptions on the derived signal model will be further analyzed in subsequent research.

Secondly, Many modern GNSS receivers use NCO-synchronized accumulators, introducing a fractional-phase offset between sampling and carrier phase. The fractional-phase offset between sampling and carrier phase introduced by NCO-synchronized accumulators essentially superimposes a small, non-integer-cycle phase perturbation onto the carrier phase at each sampling point. The summation term in Equation (44) changes from $cos\left(2\pi {\epsilon }_f{T}_{s}k+{\epsilon }_{\varphi }\right)$ to $cos\left(2\pi {\epsilon }_f{T}_{s}k+{\epsilon }_{\varphi }+\mathrm{\Delta }{\varphi }_k\right)$, and the summation term in Equation (48) changes from $sin\left(2\pi {\epsilon }_f{T}_{s}k+{\epsilon }_{\varphi }\right)$ to $sin\left(2\pi {\epsilon }_f{T}_{s}k+{\epsilon }_{\varphi }+\mathrm{\Delta }{\varphi }_k\right)$, where $\mathrm{\Delta }{\varphi }_k$ is the small, non-integer-cycle phase perturbation. Therefore, the summation terms in Equations (44) and (48) change from ideal in-phase accumulation to accumulation with phase perturbation, where the added phase perturbation alters the law of linear phase accumulation. If $\mathrm{\Delta }{\varphi }_k$ is a constant $\mathrm{\Delta }\varphi$ or varies extremely slowly, Equations (44) and (48) can still be simplified to yield analytical closed-form solutions; however, the initial phase changes from $2\pi {\epsilon }_f{T}_{s}k+{\epsilon }_{\varphi }$ to $2\pi {\epsilon }_f{T}_{s}k+{\epsilon }_{\varphi }+\mathrm{\Delta }{\varphi }_k$. If $\mathrm{\Delta }{\varphi }_k$ is a varying perturbation, the linear relationship of the phase is disrupted, and the summation can no longer be simplified using an ideal geometric series, thus precluding an analytical closed-form expression.

Thirdly, Front-end filtering and sampling jitter cause the autocorrelation function $R\left({\epsilon }_{\tau }\right)$ to deviate from the ideal triangle, such as rounding of the peak and reduction of the slope. If the peak becomes rounded, the correlation peak of the C/A code decreases. If the slope becomes shallower, non-correlated energy is mixed into the integration process, such as interference from adjacent code chips. In Equation (12), $R\left({\epsilon }_{\tau }\right)$ is the amplitude scaling factor, deviation of the autocorrelation function from the ideal triangle destroys the linear phase–amplitude correspondence of the accumulation terms, and preventing derivation of the closed analytical model obtained in Section 4 via discrete accumulation.

6. Conclusions

In the current research on satellite navigation spoofing, the output signal model of the integrate-and-dump filter is a fundamental assumption. However, the model widely adopted in existing studies is derived based on continuous-time integration, whereas practical satellite navigation receivers implemented with digital circuits approximate continuous-time integration by using discrete-time accumulation. This implementation gap introduces discretization errors into the commonly used integrate-and-dump filter output signal model. Consequently, the influence of such discretization errors should be considered in studies of navigation spoofing techniques.

This study theoretically deduces the mathematical model of the integrate-and-dump filter output signal implemented via discrete-time accumulation and verifies its correctness through simulations by comparing it with the traditional signal model derived from continuous-time integration. The simulation results demonstrate that when only the ranging code phase error or carrier initial phase error is present, the existing model based on continuous integration exhibits no discretization error. However, when a carrier frequency error exists, particularly when it exceeds 20 Hz, the discretization error in the continuous-integration-based model becomes significant. In contrast, the model derived in this study based on discrete-time accumulation showed results that were nearly identical to those of the numerical simulations, thereby validating the correctness and necessity of the proposed output signal model.

This paper presents a theoretical analysis of the discretization error of the integrate-and-dump filter; further studies can be conducted as follows.

One of the commonly used methods for a receiver to detect whether it has received a spoofed GPS signal is to examine the output of the integrator-and-dump filter. When abnormal changes in amplitude, phase, or other characteristics of the integrator-and-dump output signal are detected, it can be judged that the influence of a spoofing signal is present. In the design of detection thresholds, the influence of discretization error should be taken into account to improve detection accuracy. The integrator-and-dump signal output model derived from discrete accumulation in this paper can provide a reference for the design of detection thresholds.

Classical GNSS receiver tracking loops consist of ranging code tracking loops and carrier tracking loops, together forming the GNSS receiver tracking loop. The integrate-and-dump (I&D) sampler is an essential component of the GNSS receiver tracking loop, performing coherent integration of the baseband signal and providing high-precision input signals for the loop phase/frequency discriminators. The relationship among the I&D sampler, code loop, and carrier loop can be summarized as follows: the I&D sampler serves as the signal preprocessing core of the tracking loop, while the code loop and carrier loop constitute the error feedback control core. The discretization error model derived in this work can serve as an input error source and be incorporated into classical GNSS tracking loop models to further derive the impact of the I&D sampler discretization error on the overall tracking loop accuracy, which will be one of the future research directions.