Spatiotemporal Pattern Selection in a Modified Leslie–Gower Predator–Prey System with Fear Effect and Self-Diffusion

Abstract

Indirect fear effects profoundly influence predator–prey dynamics by reducing prey reproduction. Whereas previous studies have investigated fear effects or self-diffusion separately in Leslie–Gower models, the novelty of this work lies in their simultaneous incorporation into a modified Leslie–Gower predator–prey system with Allee effect, leading to previously unreported bifurcations and spatiotemporal pattern selection. The temporal system exhibits up to six equilibria and undergoes a codimension-2 Bogdanov–Takens bifurcation. In the spatial extension, Turing instability is triggered when the predator diffusion coefficient exceeds a critical threshold. Using weak nonlinear multiple-scale analysis, amplitude equations are derived, and their stability analysis classifies stationary patterns into spots, stripes, and spot–stripe mixtures depending on the distance from the Turing onset. Numerical simulations confirm that low, moderate, and high predator diffusivity, respectively, favour spotted, mixed, and striped prey distributions. These results emphasise the critical role of fear-mediated indirect interactions and diffusion in driving spatial heterogeneity and ecosystem stability.

1. Introduction

Predator–prey interactions lie at the heart of theoretical ecology. The pioneering works of Lotka [1] and Volterra [2] introduced ordinary differential equations to describe population cycles, inspiring a century of mathematical developments ranging from limit cycles and homoclinic orbits to Hopf, homoclinic, and higher-codimension bifurcations [3,4,5,6]. Among various formulations, the modified Leslie–Gower model, in which predator carrying capacity depends on prey abundance, has proven particularly successful for systems with alternative prey or environmental protection [7,8,9,10,11,12,13,14].

In recent years, two biologically crucial mechanisms have attracted increasing attention. First, empirical evidence has repeatedly shown that the perceived risk of predation (“fear effect”) can dramatically reduce prey reproduction and alter population dynamics even in the absence of direct killing [15,16,17,18]. Theoretical studies confirm that fear can stabilise or destabilise coexistence, induce Hopf bifurcations, and even drive prey to extinction while predators survive on alternative resources [18,19,20,21,22,23,24,25,26]. Second, spatial self-diffusion is now recognised as a primary driver of Turing pattern formation in predator–prey systems [27,28,29].

Despite substantial independent progress on both fronts, their simultaneous incorporation into a Leslie–Gower framework remains largely unexplored. Existing studies either include fear without diffusion [22,24,25,26], or incorporate diffusion without fear [27,28,30], or combine them with alternative functional responses (e.g., Holling type-II or Beddington–DeAngelis) but omit the Allee effect or lack in-depth codimension-2 bifurcations and pattern-selection analysis [31]. For instance, the model presented in [32] incorporates fear, Allee, and cross-diffusion, revealing codimension-1 bifurcations (saddle-node and Hopf) and general Turing patterns, but does not explore self-diffusion-driven transitions or weakly nonlinear classifications of specific pattern sequences.

Based on the previous discussion, we seek to explore the combined impact of incorporating both fear effect and self-diffusion into a modified Leslie–Gower predator–prey model. To our knowledge, this aspect has not been previously examined. Our focus is on understanding how these factors influence the system’s dynamic behavior, which is expressed in the following form:

$$\left\{\begin{array}{c}{\displaystyle \frac{dx}{dt}}={\displaystyle \frac{rx}{1+ey}}\left(1-{\displaystyle \frac{x}{k}}\right)(x-M)-{\displaystyle \frac{\alpha xy}{x+m}}+D_1\Delta x,\hfill \\ {\displaystyle \frac{dy}{dt}}=sy\left(1-{\displaystyle \frac{\beta y}{x+m}}\right)+D_2\Delta y,\hfill \end{array}\right.$$

(1)

where e represents the fear level, while r and s denote the birth rates of the prey and predator populations, respectively. M is the Allee threshold, and $D_1$ and $D_2$ are the diffusion coefficients for the prey and predator populations, respectively. The term $\Delta$ refers to the two-dimensional Laplace operator on $\Omega \subset {\mathbb{R}}^2$. In this context, we will describe the pattern formation mechanism for the system (1) with the initial conditions $x(u,v,0)>0$ and $y(u,v,0)>0$ and zero-flow boundary conditions (i.e., individuals cannot enter or exit through the boundary).

$${\left.{\displaystyle \frac{\partial x}{\partial n}}\right|}_{(u,v)}={\left.{\displaystyle \frac{\partial y}{\partial n}}\right|}_{(u,v)}=0,(u,v)\in \partial \Omega .$$

(2)

Our system assumes homogeneous environmental parameters (e.g., resource availability, and habitat quality) across the spatial domain, excluding spatial heterogeneity (e.g., resource gradients, and refuges) that could alter pattern formation and species coexistence.

The present work closes this gap by introducing a fear term $1/(1+ey)$ and self-diffusion into a modified Leslie–Gower predator–prey model with Allee effect in the prey. To the best of our knowledge, this specific combination has not been previously investigated. Our analysis reveals three qualitatively new phenomena that arise only from the interplay between fear and diffusion:

(i)

Fear shifts the location of the codimension-2 Bogdanov–Takens cusp in the temporal system, generating enhanced multistability with up to six equilibria (Section 3).

(ii)

Fear raises the critical predator diffusion coefficient required for Turing instability and modulates the wavelength of emergent patterns (Section 4).

(iii)

The coupled system exhibits a clear predator-diffusivity-driven pattern sequence: spots to spot–stripe mixtures to pure stripes—a transition not observed in fear-free counterparts (Section 5 and Section 6).

These results demonstrate that indirect non-consumptive effects can profoundly reshape both temporal bifurcation structure and spatial self-organization, with direct implications for understanding patchy distributions observed in savannas, grasslands, and marine ecosystems.

We find that the diffusion coefficient significantly influences pattern emergence and transition: in the absence of diffusion, the model is spatially homogeneous; small diffusion induces spot patterns, while large diffusion leads to stripe patterns—likely associated with prey avoiding predators and predators chasing prey.

In order to simplify the system (1), we transform

$$x=k\overline{x},y={\displaystyle \frac{r{k}^2\overline{y}}{\alpha }},t={\displaystyle \frac{\overline{t}}{rk}}.$$

(3)

We still use $x,y$ to denote $\overline{x},\overline{y}$, and system (1) becomes

$$\left\{\begin{array}{c}{\displaystyle \frac{dx}{dt}}={\displaystyle \frac{x(1-x)(x-a)}{1+fy}}-{\displaystyle \frac{xy}{x+b}}+d_1\Delta x,\hfill \\ {\displaystyle \frac{dy}{dt}}=cy\left(1-{\displaystyle \frac{dy}{x+b}}\right)+d_2\Delta y,\hfill \end{array}\right.$$

(4)

where $a={\displaystyle \frac{M}{k}},b={\displaystyle \frac{m}{k}},f={\displaystyle \frac{er{k}^2}{\alpha }},c={\displaystyle \frac{s}{rk}},d={\displaystyle \frac{r\beta k}{\alpha }},d_1={\displaystyle \frac{D_1}{rk}},d_2={\displaystyle \frac{D_2}{rk}}$ are positive constants, and their biology interpretation is given in

Table 1. The biology interpretation of the parameters in system (1).

Parameters	Biology Interpretation
r	Birth rates of the prey
s	Birth rates of the predator
k	Environment carrying capacity of the prey
M	Strength of Allee effect on the prey
m	Environmental protection on both species
$\alpha$	The consumption rate of the prey
$\beta$	Competition coefficient
$D_1$	Diffusion rate of the prey
$D_2$	Diffusion rate of the predator

.

The remainder of the paper is organised as follows. Section 2 presents the model and basic properties of the non-spatial (temporal) system. Section 3 analyses equilibria, local stability, and the Bogdanov–Takens bifurcation of codimension-2 (lengthy algebraic expressions are moved to Appendix A). Building on these temporal insights, Section 4 transitions to the spatial domain by deriving conditions for Turing instability in the reaction–diffusion system. Section 5 performs weakly nonlinear analysis to obtain amplitude equations and determines pattern selection and stability regions. We provide extensive numerical simulations confirming the analytical predictions. We conclude in Section 6 with ecological implications and directions for future research.

2. Equilibria and Their Properties of the Temporal System

The temporal model corresponds to the spatial model (4) and is

$$\left\{\begin{array}{c}\dot{x}={\displaystyle \frac{x(1-x)(x-a)}{1+fy}}-{\displaystyle \frac{xy}{x+b}},\hfill \\ \dot{y}=cy\left(1-{\displaystyle \frac{dy}{x+b}}\right).\hfill \end{array}\right.$$

(5)

The existence of equilibrium points is easily obtained by considering the prey nullcline and predator nullcline of system (5), which are given by

$${\displaystyle \frac{x(1-x)(x-a)}{1+fy}}-{\displaystyle \frac{xy}{x+b}}=0,cy\left(1-{\displaystyle \frac{dy}{x+b}}\right)=0.$$

After a simple calculation, the following conclusions can be reached.

Theorem 1. 

(1) 

System (5) has four boundary equilibria, $E_1\left(0,0\right)$, $E_2\left(1,0\right)$, $E_3\left(a,0\right)$, and $E_4\left(0,{\displaystyle \frac{b}{d}}\right);$ $E_1$ and $E_2$ are always saddles, $E_4$ is always a stable node, and $E_3$ is always an unstable node.

(2) 

When $\mathcal{D}>0,$ system (5) has two positive equilibria $E_5\left(x_5,{\displaystyle \frac{1}{d}}\left(x_5+b\right)\right),E_6\left(x_6,{\displaystyle \frac{1}{d}}\left(x_6+b\right)\right),$ where $x_5={\displaystyle \frac{d+ad-\frac{f}{d}-\sqrt{\mathcal{D}}}{2d}},x_6={\displaystyle \frac{d+ad-\frac{f}{d}+\sqrt{\mathcal{D}}}{2d}},\mathcal{D}={\left({\displaystyle \frac{f}{d}}-ad-d\right)}^2-4d\left({\displaystyle \frac{bf}{d}}+ad+1\right)$. $E_5$ is always a saddle, $E_6$ can be a source, a sink, or a center relying on the parametric values (see Figure 1).

In the phase space of system (5), there are always four boundary equilibria: the origin $E_1(0,0)$ (saddle, extinction attractor), $E_2(1,0)$ (saddle, prey-only attractor), $E_3(a,0)$ (unstable node, Allee-induced prey extinction), and $E_4(0,b/d)$ (stable node, predator-only attractor). When $\mathcal{D}>0$, two interior equilibria $E_5$ (saddle) and $E_6$ (possible stable node, focus, or center) emerge, leading to up to two attractors. No limit cycles or homoclinic loops are present; transitions occur via saddle-node bifurcations. Biologically, the fear and Allee effects create multistability, allowing the ecosystem to converge to extinction or coexistence depending on initial conditions and fear level f, emphasizing vulnerability to perturbations like increased perceived risk causing regime shifts in prey–predator dynamics.

The Jacobian of system (5) is shown by

$$\begin{array}{cc}& J=\left(\begin{array}{cc}{\displaystyle \frac{1}{1+fy}}\left[-3x^2+2(a+1)x-a\right]-{\displaystyle \frac{by}{{(x+b)}^2}}\hfill & x(x-1)(x-a){\displaystyle \frac{f}{{(1+fy)}^2}}-{\displaystyle \frac{x}{x+b}}\\ {\displaystyle \frac{cd{y}^2}{{(x+b)}^2}}\hfill & -c\end{array}\right)\hfill \\ \end{array},$$

(6)

and we obtain

$$\begin{gathered} trJ={\displaystyle \frac{1}{1+fy}}[(1-x)(x-a)-x(x-a)+x(1-x)]-{\displaystyle \frac{by}{{(x+b)}^2}}-c, \\ detJ={\displaystyle \frac{-c}{1+fy}}[(1-x)(x-a)-x(x-a)+x(1-x)]+{\displaystyle \frac{bcy}{{(x+b)}^2}}-{\displaystyle \frac{cx(x-1)(x-a)}{d{(1+fy)}^2}}+{\displaystyle \frac{cx}{d(x+b)}.} \end{gathered}$$

So, we can obtain the stability of each equilibrium, which is stated in Theorem 2.

Theorem 2. 

If $\mathcal{D}=0$, system (5) has a unique positive equilibrium $E_7(x_7,y_7)=({\displaystyle \frac{1+a-\frac{f}{d^2}}{2}},$${\displaystyle \frac{1+a+2b-\frac{f}{d^2}}{2d}})$, then

(1) 

if $a_{10}+b_{01}\ne 0$, $E_7$ is a saddle-node;

(2) 

if $a_{10}+b_{01}=0$ and $e_2\ne 0$, $E_7$ is a cusp of codimension-2 (see Figure 2).

Proof. 

Let $x-x_7\to x$ and $y-y_7\to y$ to change the equilibrium point $E_7$ to $(0,0)$. Then the Taylor expansion of system (5) near $(0,0)$ can be reformulated as

$$\left\{\begin{array}{c}\dot{x}=a_{10}x+a_{01}y+a_{20}{x}^2+a_{11}xy+a_{02}{y}^2+o\left({|x,y|}^2\right),\hfill \\ \dot{y}=b_{10}x+b_{01}y+b_{20}{x}^2+b_{11}xy+b_{02}{y}^2+o\left({|x,y|}^2\right),\hfill \end{array}\right.$$

(7)

where

$$\begin{array}{cc}\hfill & a_{10}={\displaystyle \frac{-a+2(a+1)x_7-3x_7^2}{1+f{y}_7}}-{\displaystyle \frac{b{y}_7}{{(x_7+b)}^2}},a_{01}=-{\displaystyle \frac{x_7}{x_7+b}}-{\displaystyle \frac{f{x}_7(1-x_7)(x_7-a)}{{(1+f{y}_7)}^2}},\hfill \\ \hfill & a_{20}={\displaystyle \frac{1+a-3x_7}{1+f{y}_7}}+{\displaystyle \frac{b{y}_7}{{(x_7+b)}^3}},a_{11}=-{\displaystyle \frac{b}{{(x_7+b)}^2}}-{\displaystyle \frac{f\left(-a+2(a+1)x_7-3x_7^2\right)}{{(1+f{y}_7)}^2}},\hfill \\ \hfill & a_{02}={\displaystyle \frac{f^2{x}_7(1-x_7)(x_7-a)}{{(1+f{y}_7)}^3}},b_{10}={\displaystyle \frac{c}{d}},b_{01}=-c,b_{20}=-{\displaystyle \frac{cd{y}_7^2}{{(x_7+b)}^3}},b_{11}={\displaystyle \frac{2cd{y}_7}{{(x_7+b)}^2}},\hfill \\ \hfill & b_{02}=-{\displaystyle \frac{cd}{x_7+b}}.\hfill \end{array}$$

Case 1: $a_{10}+b_{01}\ne 0.$ Let

$$\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{cc}d& {\displaystyle \frac{d{a}_{10}}{c}}\\ 1& 1\end{array}\right)\left(\begin{array}{c}u\\ v\end{array}\right),$$

and system (7) becomes

$$\left\{\begin{array}{c}\dot{u}=c_{20}{u}^2+c_{11}uv+c_{02}{v}^2+{o\left(\right|u,v|}^2),\hfill \\ \dot{v}=(-c+a_{10})v+d_{20}{u}^2+d_{11}uv+d_{02}{v}^2+{o\left(\right|u,v|}^2),\hfill \end{array}\right.$$

(8)

where $c_{20}=-{\displaystyle \frac{x_{7}cd}{(1-x_7)(x_7-a)}},$ since $c_{20}\ne 0,E_7(x_7,y_7)$ is saddle-node.

Case 2: $a_{10}+b_{01}=0.$ Let

$$\left(\begin{array}{c}u\hfill \\ v\hfill \end{array}\right)=\left(\begin{array}{cc}0& 1\\ 1& -d\end{array}\right)\left(\begin{array}{c}x\hfill \\ y\hfill \end{array}\right),$$

(9)

and system (7) becomes

$$\left\{\begin{array}{c}\dot{u}=v+b_{20}{v}^2+{o\left(\right|u,v|}^2),\hfill \\ \dot{v}=e_1{u}^2+e_{2}uv+e_3{v}^2+{o\left(\right|u,v|}^2),\hfill \end{array}\right.$$

(10)

where

$$\begin{array}{c}\hfill e_1=-{\displaystyle \frac{d{x}_7}{(1-x_7)(x_7-a)}},e_2={\displaystyle \frac{b}{a+b^2+ab+b+\frac{4}{d}}}-{\displaystyle \frac{a}{{(x_7-a)}^2}}-{\displaystyle \frac{1}{{(x_7-1)}^2}}<0.\end{array}$$

(11)

If $e_2\ne 0$, $E_7(x_7,y_7)$ is a cusp of codimension-2.   □

When $\mathcal{D}=0$, the unique interior equilibrium $E_7$ is a saddle-node if $a_{10}+b_{01}\ne 0$ (bistable with extinction attractor) or a codimension-2 cusp if $a_{10}+b_{01}=0$ and $e_2\ne 0$ (tipping point for multiple attractors). No homoclinic loops; supercritical Hopf bifurcation may introduce a stable limit cycle as a periodic attractor near the cusp. Biologically, moderate fear stabilizes coexistence by damping cycles, but high fear triggers Hopf bifurcation, eliminating oscillations and leading to prey extinction while predators persist, mirroring “silent” prey declines in ecosystems with intense perceived predation.

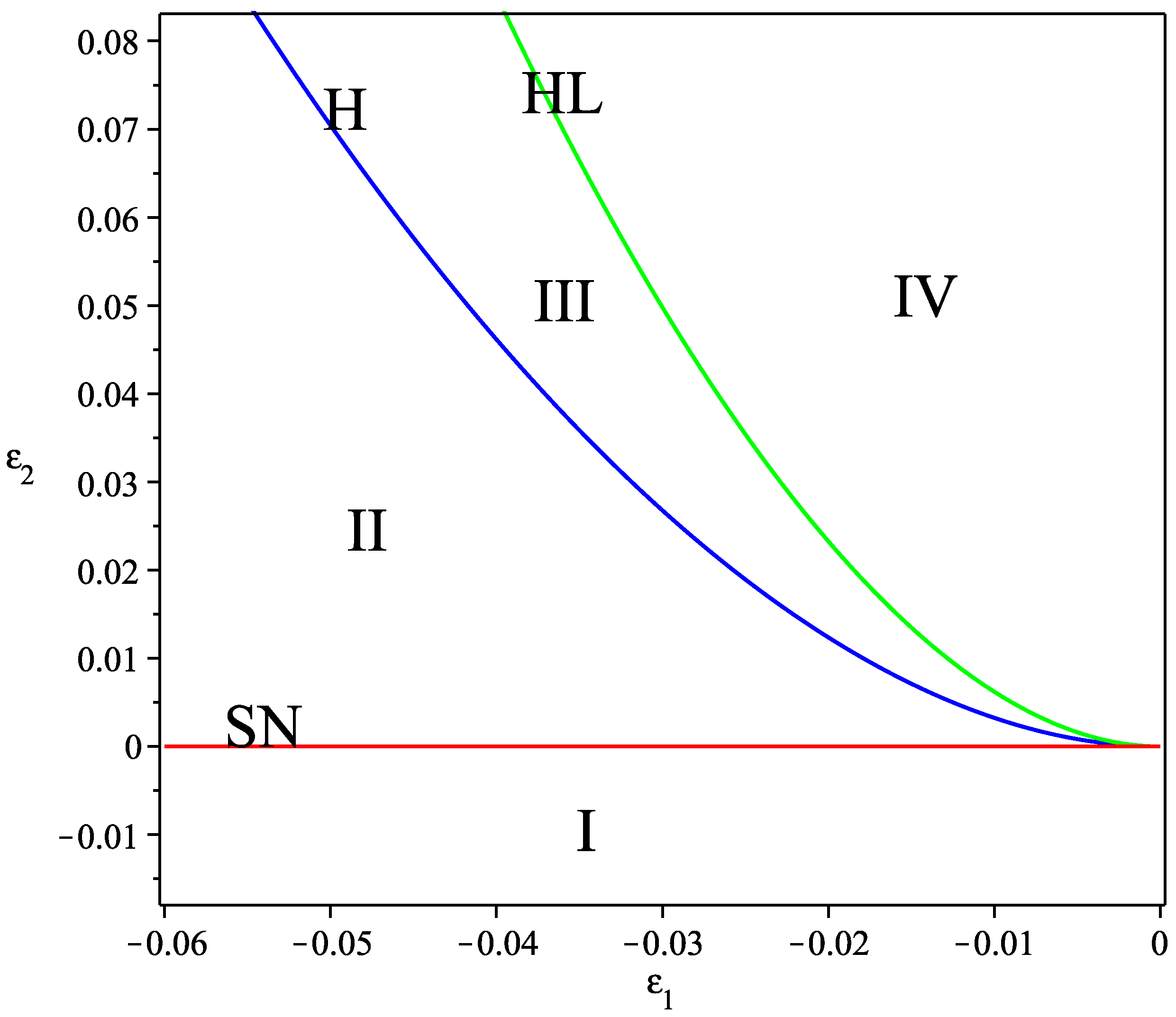
3. Bogdanov–Takens Bifurcation Analysis of the Temporal System

In this section, we perform a Bogdanov–Takens (BT) bifurcation analysis of the temporal system. This codimension-2 bifurcation occurs when an equilibrium has a double zero eigenvalue (i.e., both the determinant and the trace of the Jacobian vanish) and corresponds to the interaction of saddle-node, Hopf, and homoclinic bifurcations in the parameter plane.

Theorem 3. 

When c and d are selected as two bifurcation parameters, system (5) undergoes a Bogdanov–Takens bifurcation of codimension-2 in a small neighborhood of $E_7$ as $(c,d)$ changes nearby $(c_{BT},d_{BT})$, where $det{J}_{E_7}{|}_{(c,d)=(c_{BT},d_{BT})}=0$ and $tr{J}_{E_7}{|}_{(c,d)=(c_{BT},d_{BT})}=0$ (see Figure 3 and Figure 4).

Proof. 

Disturbing the parameters c and d by $c=c_{BT}+{\epsilon }_1$ and $d=d_{BT}+{\epsilon }_2$, where $({\epsilon }_1,{\epsilon }_2)$ is small enough [33], and system (5) takes the form as follows:

$$\left\{\begin{array}{c}{\displaystyle \frac{dx}{dt}}={\displaystyle \frac{x\left(1-x\right)(x-a)}{1+fy}}-{\displaystyle \frac{xy}{x+b}},\hfill \\ {\displaystyle \frac{dy}{dt}}=(c_{BT}+{\epsilon }_1)y\left(1-{\displaystyle \frac{(d_{BT}+{\epsilon }_2)y}{x+b}}\right).\hfill \end{array}\right.$$

(12)

The Taylor expansion of the system (12) at $E_7(x_7,y_7)$ is

$$\left\{\begin{array}{cc}\hfill {\displaystyle \frac{dx}{dt}}=& p_{10}x+p_{01}y+p_{20}{x}^2+p_{11}xy+O\left({\left|x,y,{\epsilon }_1,{\epsilon }_2\right|}^3\right),\hfill \\ \hfill {\displaystyle \frac{dy}{dt}}=& q_{00}+q_{10}x+q_{01}y+q_{11}xy+q_{02}{y}^2+O\left({\left|x,y,{\epsilon }_1,{\epsilon }_2\right|}^3\right),\hfill \end{array}\right.$$

(13)

where

$$\begin{array}{c}{p}_{10}={\displaystyle \frac{-a+2(a+1)x_7-3x_7^2}{1+f{y}_7}}-{\displaystyle \frac{b{y}_7}{{(x_7+b)}^2}},p_{01}=-{\displaystyle \frac{x_7}{x_7+b}}-{\displaystyle \frac{f{x}_7(1-x_7)(x_7-a)}{{(1+f{y}_7)}^2}},\hfill \\ p_{20}={\displaystyle \frac{1+a-3x_7}{1+f{y}_7}}+{\displaystyle \frac{b{y}_7}{{(x_7+b)}^3}},p_{11}=-{\displaystyle \frac{b}{{(x_7+b)}^2}}-{\displaystyle \frac{f\left(-a+2(a+1)x_7-3x_7^2\right)}{{(1+f{y}_7)}^2}},\hfill \\ p_{02}={\displaystyle \frac{f^2{x}_7(1-x_7)(x_7-a)}{{(1+f{y}_7)}^3}},q_{00}=-{\displaystyle \frac{{\epsilon }_2{y}_7(c_{BT}+{\epsilon }_1)}{d_{BT}}},q_{10}={\displaystyle \frac{(c_{BT}+{\epsilon }_1)(d_{BT}+{\epsilon }_2)}{d_{BT}^2}},\hfill \\ q_{01}=(c_{BT}+{\epsilon }_1)(1-{\displaystyle \frac{2(d_{BT}+{\epsilon }_2)}{d_{BT}}}),q_{11}={\displaystyle \frac{2(c_{BT}+{\epsilon }_1)(d_{BT}+{\epsilon }_2)}{d_{BT}(x_7+b)}},q_{02}=-{\displaystyle \frac{(c_{BT}+{\epsilon }_1)(d_{BT}+{\epsilon }_2)}{x_7+b}}.\hfill \end{array}$$

After a series of $C^{\infty }$ transformations (see Appendix A), system (13) becomes

$$\left\{\begin{array}{c}\dot{u_5}=v_5,\hfill \\ \dot{v_5}={\mu }_1+{\mu }_2{v}_5+u_5^2+u_5{v}_5+O\left({\left|u_5,v_5,{\epsilon }_1,{\epsilon }_2\right|}^3\right).\hfill \end{array}\right.$$

(14)

When the matrix ${\left|{\displaystyle \frac{\partial ({\mu }_1,{\mu }_2)}{\partial ({\epsilon }_1,{\epsilon }_2)}}\right|}_{{\epsilon }_1={\epsilon }_2=0}$ is nonsingular, the parameter transformations are homeomorphisms in a small neighborhood of $(0,0)$, and ${\mu }_1,{\mu }_2$ are independent parameters.

Through Perko [34], we learn systems (5) and (12) undergo Bogdanov–Takens bifurcation when $\epsilon =({\epsilon }_1,{\epsilon }_2)$ is in a small neighborhood of the origin. The local representations of the unfolding bifurcation curves are given below (“+” for ${\theta }_{20}>0$, “−” for ${\theta }_{20}<0$):

(1)

The saddle-node bifurcation curve SN $=\left\{\left({\epsilon }_1,{\epsilon }_2\right):{\mu }_1\left({\epsilon }_1,{\epsilon }_2\right)=0,{\mu }_2\left({\epsilon }_1,{\epsilon }_2\right)\ne 0\right\}$;

(2)

The Hopf bifurcation curve H $=\{\left({\epsilon }_1,{\epsilon }_2\right):{\mu }_2\left({\epsilon }_1,{\epsilon }_2\right)=\pm \sqrt{-{\mu }_1\left({\epsilon }_1,{\epsilon }_2\right)},{\mu }_1\left({\epsilon }_1,{\epsilon }_2\right)<0\}$;

(3)

The homoclinic bifurcation curve

$\mathrm{HL}=\left\{\left({\epsilon }_1,{\epsilon }_2\right):{\mu }_2\left({\epsilon }_1,{\epsilon }_2\right)=\pm {\displaystyle \frac{5}{7}}\sqrt{-{\mu }_1\left({\epsilon }_1,{\epsilon }_2\right)},{\mu }_1\left({\epsilon }_1,{\epsilon }_2\right)<0\right\}.$□

Near the codimension-2 Bogdanov–Takens point with parameters $(c,d)$ close to $(c_{BT},d_{BT})$, the phase space features saddle-node, Hopf, and homoclinic bifurcations: up to two attractors (stable node and limit cycle) or a large homoclinic loop as a single attractor enclosing an unstable saddle. Bifurcation curves divide the plane into regions with distinct attractor counts and types. Biologically, the system is at a “tipping edge” where slight fear-induced changes in reproduction or mortality can destroy stable states and cycles, causing abrupt shifts from persistence to large oscillations or extinction, akin to sudden collapses in fearful wildlife populations.

4. Dynamics of the Spatiotemporal System

Building upon the temporal equilibrium $E_6$, we first derive the conditions under which diffusion destabilizes this uniform state, leading to Turing instability. After a simple calculation, we can obtain

$$J_{E_6}=\left(\begin{array}{cc}{J}_{11}& J_{12}\\ J_{21}& J_{22}\end{array}\right),$$

(15)

where

$$J_{11}={\displaystyle \frac{1}{1+f{y}_6}}[(1-x_6)(x_6-a)-x_6(x_6-a)+x_6(1-x_6)]-{\displaystyle \frac{b{y}_6}{{(x_6+b)}^2}},$$

(16)

$$J_{12}=-{\displaystyle \frac{x_6}{x_6+b}}-{\displaystyle \frac{f{x}_6(1-x_6)(x_6-a)}{{(1+f{y}_6)}^2}},J_{21}={\displaystyle \frac{c}{d}},J_{22}=-c.$$

(17)

So, we obtain $\det J_{E_6}>0.$ Letting

$$tr J_{E_6}=0,$$

we obtain

$$c=c_H={\displaystyle \frac{1}{1+f{y}_6}}[(1-x_6)(x_6-a)-x_6(x_6-a)+x_6(1-x_6)]-{\displaystyle \frac{b{y}_6}{{(x_6+b)}^2}}.$$

(18)

When $\mathcal{D}>0$, system (5) undergoes a Hopf bifurcation at $c=c_H$. For $c>c_H$ (slightly), the equilibrium $E_6$ is stable in the absence of spatial diffusion (see Figure 5) but becomes unstable once self-diffusion (or cross-diffusion) is introduced. In this subsection, we show that this loss of stability is triggered by diffusion-driven (Turing) instability in the reaction–diffusion system (4).

Theorem 4. 

If $c>c_H$, $J_{11}{d}_2+J_{22}{d}_1>0$ and $Det\left[J\right(k\left)\right]<0$, Turing instability occurs when $d_2=d_2^{+}$ or $d_2=d_2^{-}$. The critical wave count for Turing instability is provided by $k^2=\sqrt{{\displaystyle \frac{det{J}_{E_6}}{d_1{d}_2}}}$.

Proof. 

We will carry out the linearization of system (4) at $E_6$ to obtain the following linear system as follows:

$$\dot{\mathbf{w}}=J_{E_6}\mathbf{w}+D\Delta \mathbf{w},$$

(19)

where

$$J_{E_6}=\left(\begin{array}{cc}{J}_{11}& J_{12}\\ J_{21}& J_{22}\end{array}\right),\mathbf{w}=\left(\begin{array}{c}u-u_6\hfill \\ v-v_6\hfill \end{array}\right),D=\left(\begin{array}{cc}{d}_1& 0\\ 0& d_2\end{array}\right).$$

(20)

Following the standard approach, we assume that (19) has a solution of the form

$$\mathbf{w}=\left(\begin{array}{c}A\\ B\end{array}\right)e^{\lambda t+i\mathbf{k}·\mathbf{r}},$$

(21)

where $\lambda$ is the growth rate of the perturbation in time t; i is the imaginary unit, $i^2=-1$; $r={(x,y)}^T$ is a spatial vector in two dimensions, and $\mathbf{k}$ is a wave vector in the plane. Replacing (21) by (19), we obtain the following relation

$$\lambda \left(\begin{array}{c}A\hfill \\ B\hfill \end{array}\right)=\left(\begin{array}{cc}{J}_{11}-d_1{k}^2& J_{12}\\ J_{21}& J_{22}-d_2{k}^2\end{array}\right)\left(\begin{array}{c}A\hfill \\ B\hfill \end{array}\right).$$

(22)

We can obtain the characteristic equation at the wave number $k=\left|\mathbf{k}\right|:$

$${\lambda }^2-Tr\left[J\left(k\right)\right]\lambda +Det\left[J\left(k\right)\right]=0,$$

(23)

where

$$\begin{gathered} J\left(k\right)=J_{E_6}-k^2\left(\begin{array}{cc}{d}_1& 0\\ 0& d_2\end{array}\right),Tr\left[J\left(k\right)\right]=tr{J}_{E_6}-k^2\left(d_1+d_2\right), \\ Det\left[J\left(k\right)\right]=d_1{d}_2{k}^4-k^2\left(J_{11}{d}_2+J_{22}{d}_1\right)+det{J}_{E_6}. \end{gathered}$$

Let $J_{11}{d}_2+J_{22}{d}_1>0,$ and we find that $Det\left[J\right(k\left)\right]$ is a quadratic polynomial in $k^2.$ It has the minimum value at some $k_{min}^2$ in which

$$k_{min}^2={\displaystyle \frac{J_{11}{d}_2+J_{22}{d}_1}{2d_1{d}_2}}.$$

(24)

Substituting $k^2=k_{min}^2$ for $Det\left[J\right(k\left)\right]$, we can obtain

$$Det\left[J\left(k\right)\right]=det{J}_{E_6}-{\displaystyle \frac{{\left(J_{11}{d}_2+J_{22}{d}_1\right)}^2}{4d_1{d}_2}}.$$

(25)

If $\det J_{E_6}<{\displaystyle \frac{{\left(J_{11}{d}_2+J_{22}{d}_1\right)}^2}{4d_1{d}_2}}$, $Det\left[J\right(k\left)\right]<0$.

The conditions for the criticality of a Turing instability (Turing bifurcation) are $Re\left(\lambda \right(k\left)\right)=0$ and $Im\left(\lambda \right(k\left)\right)=0$, which requires the satisfaction of the transversality condition and $Det\left[J\left(k_{min}\right)\right]=0$, i.e., $Det\left[J\left(k\right)\right]=det{J}_{E_6}-{\displaystyle \frac{{\left(J_{11}{d}_2+J_{22}{d}_1\right)}^2}{4d_1{d}_2}}=0$. The number of critical waves $k^2=k_{min}^2$ is then given (with Equation (25)) by

$$k_{min}^2={\displaystyle \frac{J_{11}{d}_2+J_{22}{d}_1}{2d_1{d}_2}}=\sqrt{{\displaystyle \frac{det{J}_{E_6}}{d_1{d}_2}}}.$$

(26)

Considering the following marginal stability condition $Det\left[J\left(k_{min}\right)\right]=0$, we can obtain

$$J_{11}^2{d}_2^2+2d_1\left(J_{11}{J}_{22}-2det{J}_{E_6}\right)d_2+J_{22}^2{d}_1^2=0.$$

(27)

A short calculation shows that

$$\begin{array}{cc}& d_2^{+}={\displaystyle \frac{d_1\left(2det{J}_{E_6}-J_{11}{J}_{22}\right)+2d_1\sqrt{det{J}_{E_6}\left(det{J}_{E_6}-J_{11}{J}_{22}\right)}}{J_{11}^2}}>0,\hfill \\ & d_2^{-}={\displaystyle \frac{d_1\left(2det{J}_{E_6}-J_{11}{J}_{22}\right)-2d_1\sqrt{det{J}_{E_6}\left(det{J}_{E_6}-J_{11}{J}_{22}\right)}}{J_{11}^2}}>0.\hfill \end{array}$$

(28)

So, $\mathrm{Det}\left[J\left(k_{min}\right)\right]<0$ if $d_2>d_2^{+}$ or $d_2<d_2^{-}$, and $k_{min}^2=\sqrt{{\displaystyle \frac{det{J}_{E_6}}{d_1{d}_2^{+}}}}$ or $k_{min}^2=\sqrt{{\displaystyle \frac{det{J}_{E_6}}{d_1{d}_2^{-}}}}$ is the threshold number of waves of Turing instability.   □

For $c>c_H$, $J_{11}{d}_2+J_{22}{d}_1>0$, and $det\left[J\right(k\left)\right]<0$ at critical $d_2=d_2^{\pm }$, the homogeneous equilibrium $E_6$ (stable node without diffusion) becomes an unstable focus in spatial modes k, shifting the phase space to infinite heterogeneous attractors (stationary patterns). The Turing bifurcation diagram is given by Figure 6. No explicit cycles or homoclinic loops at onset; potential for quasi-periodic or chaotic spatiotemporal attractors. Biologically, predator diffusivity exceeding prey’s destabilizes uniform distributions, fostering spatial heterogeneity as predators exploit local prey clusters, explaining patchy patterns in ecosystems like savannas where fear amplifies diffusion-driven instability.

5. Amplitude Equations

To determine the type and stability of stationary Turing patterns near the onset, we perform a standard multiple-scale weak nonlinear analysis around the critical Turing threshold $d_2=d_2^c$. Three pairs of active modes with critical wavenumber $k_c$ and 120° phase relationship are excited simultaneously. After lengthy but standard calculations (details are given in Appendix B), the dynamics on the finite-dimensional center manifold are governed by the following three coupled real-amplitude equations:

$$\left\{\begin{array}{c}{\tau }_0{\displaystyle \frac{\partial {\rho }_1}{\partial t}}=\mu {\rho }_1+\left|h\right|{\rho }_2{\rho }_3-g_1{\rho }_1^3-g_2\left({\left|{\rho }_2\right|}^2+{\left|{\rho }_3\right|}^2\right){\rho }_1,\hfill \\ {\tau }_0{\displaystyle \frac{\partial {\rho }_2}{\partial t}}=\mu {\rho }_2+\left|h\right|{\rho }_1{\rho }_3-g_1{\rho }_2^3-g_2\left({\left|{\rho }_1\right|}^2+{\left|{\rho }_3\right|}^2\right){\rho }_2,\hfill \\ {\tau }_0{\displaystyle \frac{\partial {\rho }_3}{\partial t}}=\mu {\rho }_3+\left|h\right|{\rho }_2{\rho }_1-g_1{\rho }_3^3-g_2\left({\left|{\rho }_1\right|}^2+{\left|{\rho }_2\right|}^2\right){\rho }_3.\hfill \end{array}\right.$$

(29)

where $\mu \propto (d_2-d_2^c)>0$ is the normalized distance from the Turing bifurcation point, and the coefficients ${\tau }_0>0$, h, $g_1$, $g_2$ are functions of the original biological parameters (explicit expressions in Appendix B). Stability and bifurcation analysis of Equation (29) on the equilateral triangular lattice yields the following pattern selection result:

Theorem 5. 

In a sufficiently small supercritical neighborhood of the Turing onset, the following statements hold, as follows:

(i) 

Steady state: ${\rho }_1={\rho }_2={\rho }_3=0$; it is stable as $\mu <{\mu }_2=0$ and is unstable when $\mu >{\mu }_2=0$.

(ii) 

Stripe pattern: ${\rho }_1=\sqrt{{\displaystyle \frac{\mu }{g_1}}}\ne 0,{\rho }_2={\rho }_3=0$; it is stable when $\mu >{\mu }_3$ and is unstable when $\mu <{\mu }_3$.

(iii) 

Spot pattern:

$${\rho }_1={\rho }_2={\rho }_3={\displaystyle \frac{\left|h\right|\pm \sqrt{h^2+4\left(g_1+2g_2\right)\mu }}{2\left(g_1+2g_2\right)}}.$$

(30)

Its existence condition is $\mu >{\mu }_1$. The solution ${\rho }^{+}$ is stable as $\mu <{\mu }_4$, while ${\rho }^{-}$ is always unstable, where

$${\rho }^{+}={\displaystyle \frac{\left|h\right|+\sqrt{h^2+4\left(g_1+2g_2\right)\mu }}{2\left(g_1+2g_2\right)}},{\rho }^{-}={\displaystyle \frac{\left|h\right|-\sqrt{h^2+4\left(g_1+2g_2\right)\mu }}{2\left(g_1+2g_2\right)}}.$$

(31)

(iv) 

Mixed structural state: ${\rho }_1={\displaystyle \frac{\left|h\right|}{g_2-g_1}},{\rho }_2={\rho }_3=\sqrt{{\displaystyle \frac{\mu -g_1{\rho }_1^2}{g_1+g_2}}}$. It exists when $\mu >{\mu }_3$ and is always unstable as $g_2>g_1.$ The explicit thresholds are

$${\mu }_1=-{\displaystyle \frac{h^2}{4(g_1+2g_2)}},{\mu }_2=0,{\mu }_3={\displaystyle \frac{h^2{g}_1}{{(g_2-g_1)}^2}},{\mu }_4={\displaystyle \frac{(2g_1+g_2)h^2}{{(g_2-g_1)}^2}}.$$

(32)

The bifurcation diagram of Turing patterns is given in Figure 7. These analytical predictions are fully confirmed by direct numerical simulations of the original system (4) in Figure 8, Figure 9 and Figure 10.

We perform two-dimensional simulations of the system (2) using MATLAB R2020b. To study the dynamic behavior of the system, we study the system on a 200 × 200 discrete grid with Neumann boundary conditions, a spatial step of 1, and a time step of 0.01.

We set $a=0.1,b=0.112,c=0.32,d=4.9449,$ and $f=0.01,d_1=1,$ and select the diffusion rate $d_2$ as the bifurcation parameter. The patterns with corresponding $d_2$ are given in

Table 2. Patterns for different parameters $d_2$.

${\mathit{d}}_2$	$\mathit{\mu }$	Pattern
5.5	$\mu <{\mu }_3$	Spot
7	${\mu }_3<\mu <{\mu }_4$	Mixed (Spot and Stripe)
16	$\mu >{\mu }_4$	Stripe

.

We denote the number of the prey and the predator at the point $(i,j)$ at time t as $x(i,j,t)$ and $y(i,j,t),i=1,2,\dots ,200,j=1,2,\dots ,200,$ respectively. Then, we have

$$\left\{\begin{array}{c}x(i,j,t+dt)=x(i,j,t)+\left\{f\right(x(i,j,t),y(i,j,t))+\hfill \\ d_1\left[x(i+1,j,t)+x(i-1,j,t)+x(i,j+1,t)+x(i,j-1,t)-4x(i,j,t)\right]\}dt,\hfill \\ y(i,j,t+dt)=y(i,j,t)+\left\{g\right(x(i,j,t),y(i,j,t))+\hfill \\ d_2\left[y(i+1,j,t)+y(i-1,j,t)+y(i,j+1,t)+y(i,j-1,t)-4y(i,j,t)\right]\}dt,\hfill \end{array}\right.$$

(33)

where $dt=0.01$.

The physical domain size is $\Omega =[0,L]\times [0,L]$, where $L=200$.

The initial distributions are

$$x(i,j,0)=x_6+{\displaystyle \frac{2\chi (i,j)-1}{10}},y(i,j,0)=y_6+{\displaystyle \frac{2\chi (i,j)-1}{10}},$$

where $\chi (i,j)$ is a random variable uniformly distributed over the interval $(0,1)$.

The Neumann boundary conditions are satisfied by setting

$$x(L+1,j,t)=x(1,j,t),x(i,L+1,t)=x(i,1,t),$$

$$y(L+1,j,t)=y(1,j,t),y(i,L+1,t)=y(i,1,t).$$

If the diffusion rate $d_2=5.5$, system (4) exhibits spot pattern (Figure 8). The total simulation time is 2400, which means we iterate Equation (33) 240,000 times, and we take samples and depict the snapshots every 800 time units.

If the diffusion rate $d_2=7$, system (4) exhibits mixed pattern (Figure 9). The total simulation time is 1200, and we depict the snapshots every 400 time units.

If the diffusion rate $d_2=16$, system (4) exhibits stripe pattern (Figure 10). The total simulation time is 600, and we depict the snapshots every 200 time units.

The numerical results indicate that a small diffusion rate of the predator leads to spot pattern, which means that the prey will gather in some separate regions. A relatively big diffusion rate will make the strip pattern, which means the prey will distribute averagely in the space. This phenomenon can be explained as the prey tend to hide from the predator in different ways according to the diffusion rate of the predator. If the predators move slowly, the prey will gather at the place where there are fewer predators. If the predators move fast, the prey will distribute averagely because no place is safer.

Near the Turing threshold (small supercritical $\mu >0$), stationary attractors include hexagonal spots (${\rho }_1={\rho }_2={\rho }_3>0$ stable for ${\mu }_1<\mu <{\mu }_4$), stripes (${\rho }_1>0,{\rho }_2={\rho }_3=0$ stable for $\mu >{\mu }_3$), and mixed states (metastable). These are spatial fixed points without temporal cycles or homoclinic loops; selection depends on $\mu$ thresholds. Biologically, varying predator mobility elicits prey anti-predator strategies: spots (isolated refugia, e.g., savanna herds) at low diffusivity and stripes (linear corridors, e.g., marine systems) at high diffusivity; fear modulates pattern scale, highlighting indirect effects in structuring natural communities.

6. Conclusions

In this study, we have investigated the temporal and spatiotemporal dynamics of a modified Leslie–Gower predator–prey model that simultaneously incorporates fear effects and self-diffusion—a combination not previously explored in the literature. Our analysis revealed that the temporal system exhibits a codimension-2 Bogdanov–Takens bifurcation, leading to multistability with up to six equilibria and transitions among stable nodes, limit cycles, homoclinic loops, and extinction states. Extending the model to the spatiotemporal domain, we derived explicit Turing instability conditions and, using weakly nonlinear multiple-scale analysis, obtained amplitude equations that classify stationary patterns into spots, stripes, and mixed states across different parameter regimes, with predator diffusivity emerging as the key driver of pattern selection. Extensive numerical simulations confirmed these analytical predictions, demonstrating clear sequential transitions from spots to mixed states to stripes as predator diffusivity increases.

The novelty of this work lies in integrating fear-induced reproductive suppression with self-diffusion within the Leslie–Gower framework, thereby uncovering qualitative behaviours absent in prior studies. Unlike fear-only models [25,26], where excessive fear typically drives uniform prey extinction, or diffusion-only models [3,27,28,29,30,35,36,37,38] that produce standard Turing patterns, our coupled model shows that fear significantly shifts the cusp position, alters bifurcation curves, modulates the Turing threshold, and changes pattern wavelength and selection regions. These interactions generate enhanced multistability and previously undocumented pattern-selection mechanisms compared with earlier bifurcation and pattern-formation studies in similar systems [7,9,10].

Biologically, our findings highlight the critical and often overlooked role of indirect fear effects in ecosystem resilience and spatial organization. Moderate fear stabilizes coexistence by damping population oscillations, whereas strong fear combined with high predator mobility spontaneously generates persistent spatial heterogeneity. The resulting spot and stripe patterns correspond to distinct anti-predator spatial strategies: clustered refugia under low-to-moderate predator mobility (common in African savannas) versus linear escape corridors under high mobility (typical of marine and open grassland systems). Ignoring fear therefore substantially underestimates ecosystem vulnerability to regime shifts and extinction risk.

Future research could incorporate stochastic environmental noise, seasonally varying fear intensity, or multiple prey refuges to further bridge theoretical predictions with empirical ecological data and inform conservation strategies.