Optimization Techniques for Improving Economic Profitability Through Supply Chain Processes: A Systematic Literature Review

Abstract

In today’s dynamic and global business landscape, economic profitability is essential for creating and sustaining competitive advantage. Nevertheless, a critical gap persists in the literature regarding the application of advanced optimization techniques that systematically link operational improvements in the supply chain with strategic financial indicators. Accordingly, this study aims to identify and synthesize the optimization techniques applied to supply chain processes and their impact on economic profitability. To achieve this objective, the PRISMA methodology was employed. A systematic literature review covering the last ten years (2015–2025) was conducted using the Web of Science database. After applying inclusion and exclusion criteria, 35 studies were selected, revealing a growing methodological diversity. Nature-Inspired Algorithms (NIAs) and hybrid approaches (such as MILP combined with Simulation) demonstrate greater capacity to address complex and multi-objective scenarios. Notably, hybrid techniques have been successfully applied to the maximization of Economic Value Added (EVA), a key strategic value indicator. Despite the sophistication of these optimization techniques, the predominant objective remains total cost minimization, often sidelining the direct optimization of strategic indicators such as EVA or the Cash Conversion Cycle (CCC). Additionally, a key research gap was identified in the development of adaptive and resilient models that integrate technologies such as Digital Twins, Blockchain, and Artificial Intelligence to dynamically manage physical and financial disruptions in supply chains. The study concludes by emphasizing the need for a theoretical shift toward models that go beyond cost minimization and focus on real value metrics, as well as the exploration of more accessible solutions for SMEs. This review contributes a reference framework for academics and practitioners to align the most suitable optimization techniques with strategic financial objectives in supply chain management.

1. Introduction

In today’s highly competitive and continuously evolving global landscape, business management must be oriented toward value creation to meet the expectations of diverse stakeholders. Enhancing processes through technological strategies and supply chain improvement is essential, provided that the objectives are clearly defined and aligned with the pursuit of value generation [1]. Therefore, placing particular emphasis on economic value is essential for the continuity and success of any organization. This performance is crucial, as it provides the essential resources needed to execute the necessary investments that sustain operations, achieve strategic objectives, and, fundamentally, maintain a competitive advantage in a dynamic business environment.

Despite the centrality of economic profitability, organizations face the challenge of aligning their objectives due to the tension between short-term financial pressures and long-term sustainability imperatives. This conflict demands a strategic approach that balances these priorities [2]. Consequently, performance measurement must transcend strictly financial indicators and adopt a holistic vision that incorporates both financial and non-financial elements (social, environmental, or operational). This holistic approach not only enables informed decision making but also promotes the necessary balance between various organizational areas and objectives, thereby consolidating long-term competitiveness [3].

The management of profitability in general has evolved significantly from the traditional vision. Prior to the work of Rafuse [4], efforts to improve performance through working capital management primarily focused on isolated tactics, such as delaying payments to creditors. However, this approach proved counterproductive for the economic system, as it merely transferred financial limitations to suppliers and other supply chain actors, thereby compromising the viability of the ecosystem as a whole. To overcome this limited view, Rafuse proposed a systemic financial approach based on the use of efficient supply chain techniques. This new paradigm demands the integral participation of all actors with whom the focal firm maintains relationships, thus acknowledging economic interdependence.

Following Rafuse’s systemic proposal [4], corporate finance research has begun to focus on integrating the supply chain as a key mechanism for improving financial performance. Within this framework, various studies have validated the importance of interorganizational collaboration. On one hand, Padachi [5] demonstrated that effective collaboration between firms can reduce financial risks and significantly increase corporate liquidity. However, the literature has also identified a structural problem, recognizing a persistent dilemma between the need to achieve financial improvements (such as liquidity, profit, and growth) and the difficulty of establishing solid interorganizational connections and relationships within supply chains [6].

With the structural problem identified, the need for the integration of financial and operational areas has been emphasized [7]. This integration is vital because the disconnect between material and financial flows across the supply chain can be a major source of conflict. For example, the physical resource may exist at the supplier, but the focal firm lacks the necessary liquidity to acquire it. Conversely, a lack of coordination can lead the firm to accumulate excess inventory, which generates idle resources and, consequently, limits its financial capacity and power. This conflict of flows demonstrates that efficiency in one area, without due integration with the other, ultimately subtracts value from the chain as a whole [7].

The inadequate integration of supply chain links amplifies risks, creating a snowball effect where the financial disruptions of one actor propagate and escalate throughout the entire network [8]. This lack of cohesion is not exclusive to external relationships of a focal firm; the literature suggests a critical need for better internal integration between the firm’s own operational and financial areas [9]. This lack of integration in core functions exacerbates problems of liquidity and efficiency, making financial management a critical and cross-cutting issue for the entirety of the organization [10].

In the face of liquidity problems and the propagation of risks, the literature has demonstrated that integrating various trading partners in the supply chain significantly improves cash flow management and, consequently, the economic profitability of its members [10]. This finding, combined with the adoption of the systemic perspective in corporate finance, has generated the need to develop dynamic models [11]. These models seek to incorporate the interdependence between the chain links and the connections between the various variables of the working capital cycle, in order to optimize the use of financial resources and mitigate problems arising from the lack of coordination.

Despite the growing recognition of the importance of integration and collaboration in supply chains for improving economic profitability, the literature still shows a critical gap in the exploration of advanced tools and technologies that allow for a holistic and predictive view of financial dynamics throughout these chains [12]. Although the so-called Industry 4.0 has offered diverse technologies (real-time data capture and processing) that demonstrate the capacity to enhance corporate financial performance [13,14], a significant limitation persists: it has not been determined which specific elements or variables of economic profitability should be optimized using these technologies.

The discussion regarding the measurement of supply chain success in financial terms is an area of debate. Chopra and Meindl [15] seminally argued that success should be measured by the impact on key indicators such as ROE (deváty) and ROA (Return On Assets); however, they did not clearly establish the superiority of one metric over the other. Other authors have deepened this perspective by arguing that the primary goal of the supply chain is precisely to generate profit for shareholders, which underscores the importance of fully considering the flows of materials, information, and money. In this sense, supply chain improvement is considered a highly effective way to achieve this objective [16].

In the search for optimal economic profitability, some studies have addressed the criticality of the supply chain. It has been demonstrated that the implementation of Lean practices, the integration of flows (material and financial), and strategic partnerships with suppliers contribute significantly to cost reduction, quality improvement, and increased profit, achieving initial logistical and financial optimizations [17,18]. Even the application of multi-criteria analysis has facilitated the search for this optimum, although this approach has been restricted by considering a limited set of variables, such as cash flow, debt levels, inventory, and existing obligations [19]. While there is a growing use of optimization techniques in finance, their application has been concentrated in strategic areas like investment portfolio selection or risk control. A crucial gap persists, however: the scarcity of models that apply these optimization techniques to daily management financial problems, such as operational costs, revenue, expenses, working capital, or accounts receivable [20].

Finally, with regard to supply chain optimization, the field has progressed from linear and integer programming (mid-20th century) to simulation, heuristics, and metaheuristics (1980s–2010s), and more recently toward artificial intelligence, machine learning, graph neural networks (GNNs), and hybrid reinforcement learning (2020–2025) [21]. Current research priorities include hybrid simulation–optimization approaches, interpretability, sustainability, and resilience—further underscoring the need to integrate diverse components that increasingly align financial and operational domains [13].

The systemic interconnection between supply chain management and economic profitability has been explored in the literature. It is recognized that the optimization of material, information, and money flows is fundamental for long-term sustainability and competitiveness. However, despite widespread recognition of the critical role financial optimization plays within the supply chain, there remains a lack of systematic literature reviews aimed at identifying the key value drivers and the most suitable optimization techniques capable of integrating supply chain optimization with economic performance.

Therefore, this research aims to address this limitation by providing a detailed exploration of the supply chain’s impact on financial performance. The central objective is to identify and synthesize the optimization techniques and their impact on economic profitability through supply chain processes, in order to contribute to the understanding and application of advanced financial management strategies.

To concretize this objective and guide the development of the present work, the following research questions are formulated:

• Which optimization techniques have been applied to improve economic profitability through supply chain processes?
• Which Value Drivers are being addressed through the application of optimization techniques?
• In which Supply Chain processes are the proposed optimization techniques being applied?

2. Background

For the development of the conceptual foundations of this review, three interconnected conceptual pillars are established. The first provides a conceptual understanding of the supply chain; the second describes economic profitability within the domain of corporate finance; and the last point reviews the fundamentals for the generation and classification of optimization methods.

2.1. Supply Chain

For the purposes of this review, the supply chain is conceptualized as a network operating under the logic of a complex adaptive system. Within this network, each agent, understood as a node with visibility both backward (suppliers) and forward (customers), operates under a constant tension between the search for local control and systemic emergence. In this context, each agent seeks to exert influence over its operational section, subject to inherent limitations, in order to maximize its individual performance [22].

Given the above, the representation of a supply chain will depend on the focal node or the firm under analysis, which is situated at the center of the network and is subject to various interconnected flows. Traditionally, the literature recognizes three primary flows: material, information, and financial flow. However, some authors expand this classification to include energy or service flows [15,23] (see Figure 1).

Based on the above, a supply chain can be viewed as a network of different flows, firms, and organizational areas that interact with each other. Given this, it is necessary to develop processes to adequately coordinate these flows. Since these activities are complex, they require appropriate planning, control, and execution that allow the flows to move from suppliers to final customers and vice versa. These activities constitute the main processes of Supply Chain Management (SCM) and determine how value is created and delivered throughout the chain [24].

Supply chain management is typically structured through a sequence of high-level processes that ensure the flow of value. This framework begins at a strategic level with Plan (which includes forecasting and network and operations planning); continues with Source (supplier selection, sourcing, and management); is followed by Make (the transformation of inputs into finished products); moves toward Delivery (transportation, warehousing, and order management); and concludes with Return (which includes service, reverse logistics, and product disposition) [15,25].

Likewise, the execution of each main stage is supported by fundamental support processes, such as information systems, inventory management, performance measurement, and risk management [24,25]. These processes are crucial, as they coordinate the sequence of activities and mediate the inherent operational frictions within the chain, such as balancing cost, speed of response, and system resilience.

In summary, the supply chain is defined as a complex adaptive system that requires robust and active management to coordinate its flows and processes. The success of this coordination is ultimately measured by its capacity to generate value for stakeholders and ensure the long-term financial sustainability of the focal firm. Consequently, the next conceptual point will focus on defining and analyzing economic profitability from the perspective of corporate finance.

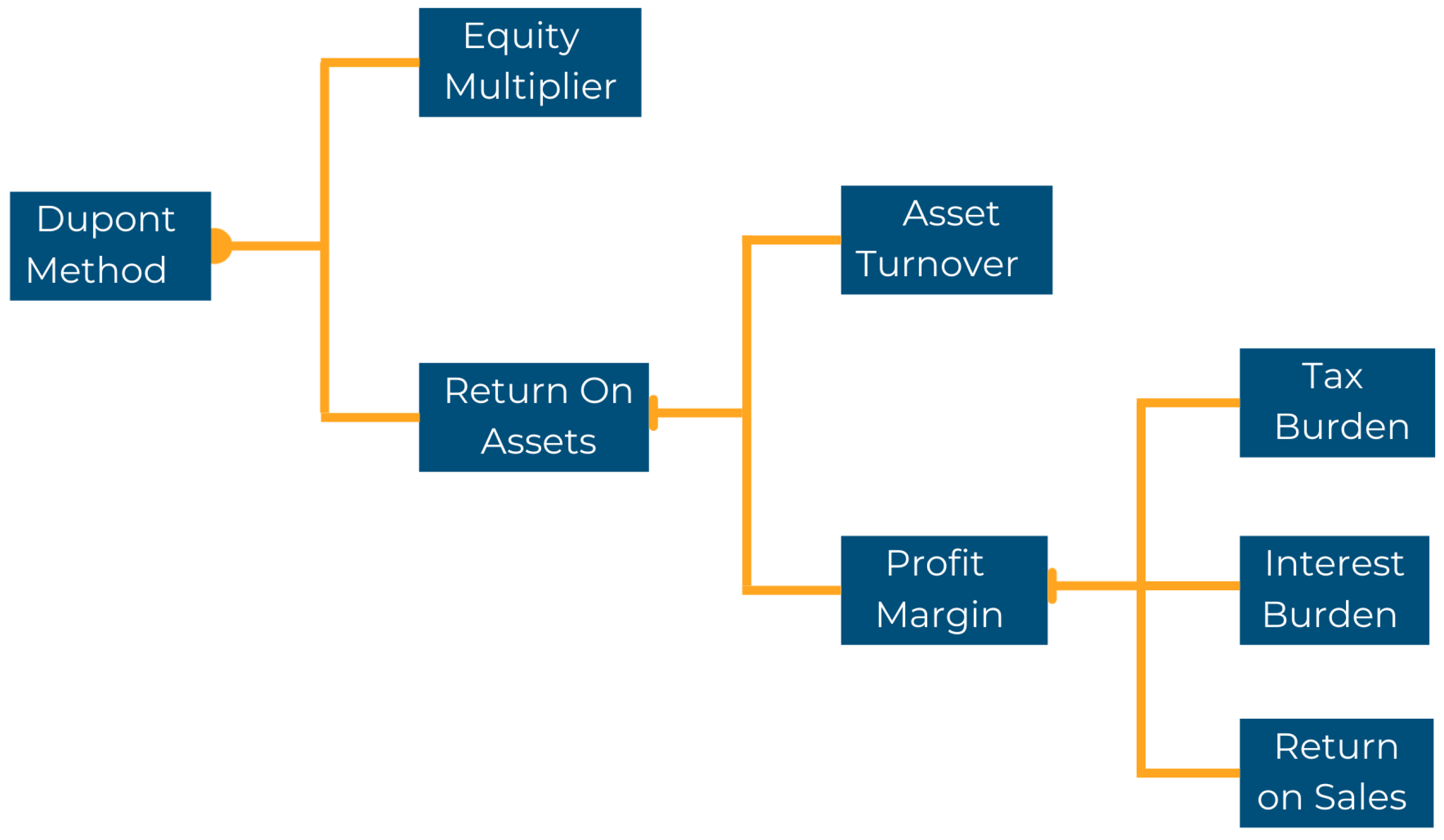
2.2. Economic Profitability

The theoretical foundation of economic profitability lies in the paradigm of classical economics, where market adjustments lead to the maximization of economic benefits [26], sustained by various principles such as the law of supply and demand. These principles have laid the groundwork for Corporate Finance, whose study focuses on how organizations obtain and manage their resources to generate value. Along these lines, the primary objective of finance is the maximization of shareholder wealth [27], which demands a rigorous understanding of capital structuring alternatives and the ability to primarily invest in profitable projects [28].

To quantify the objective of wealth maximization, it is crucial to identify the appropriate metrics for evaluating the organization’s financial performance and their respective application methods. The central concept used for this purpose is profitability. Specialized literature establishes that profitability is classified into two main types, as defined by Lizcano [29]: Financial profitability and Economic profitability. The definitions of these two key aspects are detailed below.

• Financial profitability: It is a measure, referred to a specific period of time, of the company’s own funds (equity).
• Economic profitability: It is a measure referred to a specific period of time, independent of its financing.

To calculate financial profitability, one of the most common measures is the Return On Equity (ROE), which is calculated as follows [27]:

$$\mathrm{ROE}={\displaystyle \frac{\mathrm{Net}\mathrm{Income}}{\mathrm{Net}\mathrm{Equity}}}$$

(1)

On the other hand, several metrics have been proposed for economic profitability. One of these is the Return On Assets (ROA), which is expressed by the following formula [30]:

$$\mathrm{ROA}={\displaystyle \frac{\mathrm{Net}\mathrm{Income}}{\mathrm{Average}\mathrm{Assets}}}$$

(2)

Also, we can consider the total capital invested, thus calculating the company’s economic profitability using the following indicator [27]:

$$\mathrm{Economic}\mathrm{Profitability}={\displaystyle \frac{\mathrm{Profit}}{\mathrm{Invested}\mathrm{capital}}}$$

(3)

where:

$$\mathrm{Invested}\mathrm{capital}=\mathrm{Own}\mathrm{capital} + \mathrm{Long-term}\mathrm{debt}$$

In line with the need for precise metrics, the DuPont Analysis metric, developed by F. Donaldson Brown, emerges. This tool stands as one of the most prominent and long-standing profitability indicators [31]. This method allows for the evaluation of both economic profitability and financial profitability and is based on the detailed decomposition of the ROE. By integrating the ROA (Return on Assets) with other operating and leverage indicators, this metric provides a disaggregated and in-depth view of the economic-financial results, serving as an essential reference for the organization’s strategic analysis (see Figure 2).

$$\mathrm{Return}\mathrm{on}\mathrm{Equity}=\mathrm{Net}\mathrm{Profit}\mathrm{Margin}\times \mathrm{Asset}\mathrm{Turnover}\times \mathrm{Equity}\mathrm{Multiplier}$$

(4)

Although the integration of financial and economic profitability through the DuPont metric represented a crucial advance in financial management, this indicator presents a significant limitation: the exclusion of the cost of capital, thereby omitting an essential element for measuring the real creation of value [27].

To rectify this omission, the literature has suggested the use of Economic Value Added (EVA), a metric that promises to be superior to ROA or DuPont itself [27]. EVA is defined as the surplus amount resulting from subtracting operating costs and expenses from sales and, simultaneously, considering the financial cost for the use of capital and tax rates [33].

The integration of the cost of capital into its formula ensures a more robust measure of the creation or destruction of economic value within a corporate entity [33,34].

For all these reasons, EVA is considered the main metric of value creation, and, for its analysis, the following formula is used:

$$\mathrm{EVA}=\mathrm{NOPAT}-(\mathrm{WACC}\times \mathrm{Capital}\mathrm{Invested})$$

(5)

where

Net Operating Profit After Tax (NOPAT): This shows a company’s performance from its core operations, once expenses and taxes have been deducted. NOPAT helps measure the company’s profitability after tax and without considering debt; it does not include the tax savings that many companies gain due to existing debt. NOPAT is calculated as follows:

$$\mathrm{NOPAT}=\mathrm{Operating}\mathrm{Income}\times (1-\mathrm{Tax}\mathrm{Rate})$$

(6)

where

• Operating Income = Revenue − Cost of Good Sold − Operating Expenses − Depreciation − Amortization
• Tax Rate = The relevant income or profit tax rate in the country.

The Weighted Average Cost of Capital (WACC): Weighted Average Cost of Capital (WACC) is a metric that helps evaluate a company’s financing costs by averaging the after-tax cost of its sources of capital, which include both equity and funds obtained through debt. WACC is determined with the following formula:

$$\mathrm{WACC}=\left({\displaystyle \frac{E}{V}}\times Re\right)+\left({\displaystyle \frac{D}{V}}\times Rd\times (1-Tc)\right)$$

(7)

where

• E = Market value of the firm’s equity.
• D = Market value of the firm’s debt.
• V = E + D.
• Re = Cost of equity.
• Rd = Cost of debt.
• Tc = Corporate tax rate.

Invested Capital: It is the investment made in a company by both shareholders and creditors. Given that a company can be financed through the issuance of shares or bonds, two parties are involved in this situation: the shareholders who acquire the shares and the creditors who acquire the bonds. Invested Capital can be calculated using the following formula:

$$\mathrm{Invested}\mathrm{Capital}=\left(\begin{array}{c}\mathrm{TD}\\ \&\\ \mathrm{Leases}\end{array}\right)+\left(\begin{array}{c}\mathrm{TE}\\ \&\\ \mathrm{EE}\end{array}\right)+\left(\begin{array}{c}\text{Non-Operating}\mathrm{Cash}\\ \&\\ \mathrm{Investments}\end{array}\right)$$

(8)

where

• TD & Leases = Total Debt + Leases.
• TE & EE = Total Equity & Equity Equivalents = Common stock + Retained Earnings.
• Non-Operating Cash & Investments = Cash from Financing + Cash from Investing.

Therefore, the EVA metric supports business management by offering a clear tool to identify the corporate aspects that drive the creation of economic value. The analysis of EVA is articulated around three major categories of managerial decisions: Operating Decisions (O), Investment Decisions (I), and Financing Decisions (F). The decomposition of EVA into these categories, as illustrated in Figure 3, in turn allows for the identification of up to 15 third-level Value Drivers that directly influence the creation or destruction of economic value. These drivers can be further disaggregated, depending on corporate characteristics, facilitating a detailed view for improving financial performance through strategic value management.

The evaluation of economic-financial performance is based on the management and measurement of crucial variables. Although the literature has proposed robust metrics like EVA to measure profitability, decision making remains complex due to the interdependence of aspects such as revenue, costs, expenses, interest rates, and the cost of capital. The optimal integration of these variables within a complex organizational context presents a critical challenge that requires the application of advanced tools for decision making.

2.3. Optimization Techniques

The foundation of mathematical modeling resides in the capacity to represent complex real-world systems through abstractions that preserve the essential structural relationships necessary to achieve analytical feasibility [37]. In this sense, a mathematical model is a simplified representation of reality designed to capture and focus only on the most vital characteristics of the problem [38]. This process of abstraction, which is essential for the application of optimization techniques, fundamentally requires three stages [39]:

• Conceptualization and problem definition;
• Mathematical formulation and representation;
• Solution and interpretation.

While the theoretical foundations of mathematical optimization originated in the calculus of variations developed by Euler and Lagrange in the 18th century, modern optimization theory emerged in the mid-20th century. This paradigm shift was catalyzed by the development of Linear Programming (LP) by Dantzig in 1947 [40]. The Simplex Method, conceived by Dantzig, was established as the first efficient algorithm for solving Linear Programming problems, transforming optimization into a practical and viable tool for managerial and operational decision making [41].

On the other hand, the theoretical basis of dynamic optimization was established by Bellman and Dreyfus (1962) in their seminal work on Dynamic Programming [42]. Through the Principle of Optimality, they demonstrated how complex sequential decision problems can be rigorously decomposed into more manageable subproblems. This decomposition approach became a methodological pillar of the field, giving rise to and sustaining a significant portion of the optimization models applied in various areas, including operations and financial management [43].

As a complement to Linear Programming, the work of Kuhn and Tucker was fundamental to optimization theory by developing the Karush–Kuhn–Tucker (KKT) conditions [44]. These conditions provide the necessary optimality criterion for solving non-linear programming problems that incorporate constraints. The relevance of the KKT conditions lies in the fact that they allow for the rigorous application of optimization to a broader class of problems, where functional relationships are not strictly linear.

Based on these foundations, the key elements necessary for the formulation of any mathematical optimization model can be identified. These essential elements vary depending on the type of optimization to be modeled (linear, non-linear, or dynamic) and are crucial for solving complex problems.

In mathematical optimization models, decision variables represent the possibilities and constitute the core of the model. The rigorous selection and definition of these variables are crucial, as they directly impact the realism, analytical validity, and quality of the solution obtained. Given their relevance, decision variables can be categorized as follows:

• Continuous Variables: This type of variable is suitable for representing quantities that can take any real value within a specific range, such as production quantities, inventory levels, or financial flows [45].
• Integer Variables: These variables are used in optimization problems where the decision variables must be whole numbers. This is common in scenarios such as programming, routing, and assignment, where fractional solutions are not feasible or do not make sense, such as the number of trucks or planes assigned to routes [46,47,48].
• Binary Variables: These variables naturally represent decisions that are binary in nature, such as whether an element should be included in a set or if a particular process should be activated. This simplifies the modeling of problems where decisions are inherently discrete, such as facility location, product assortment, and security games [49,50]. They allow for the representation of constraints and logical relationships within optimization models, which can be crucial for accurately capturing the problem structure [50].
• Stochastic Variables: In stochastic programming, decision variables can be classified as first-stage variables (here-and-now) or second-stage variables (wait-and-see), reflecting the timing of decisions in relation to the resolution of uncertainty [51].

The Objective Functions are the central component of any optimization model, tasked with translating abstract goals into a quantifiable mathematical expression that is sought to be maximized or minimized [46]. However, optimization problems can involve one or more combinations of these traditional quantitative measures, such as minimizing costs while simultaneously maximizing customer service [52].

To manage the complexity of these multi-objective scenarios, Pareto optimality theory is the fundamental framework [53]. The concept establishes that a solution is Pareto-optimal (or non-dominated) if it is not possible to improve the value of one objective without necessarily sacrificing or worsening the value of at least one other. This principle compels decision-makers to carefully analyze the trade-offs between conflicting goals. To simplify the solution process, scalarization methods are employed to convert the multi-objective formulation into a single-objective one. Among the most common methods are:

• The weighted sum approach, which assigns a predefined weight to each objective [54].

• The epsilon-constraint method $ϵ-constraintmethod$, which optimizes a main objective while restricting the values of the others [55].

• Goal programming, which seeks to minimize the deviation with respect to a predefined target value [45].

Constraints, within an optimization model, are the limits and rules that define the set of feasible solutions for a given problem. These limitations can be physical, technological, financial, regulatory, or of other nature. There are two main types of constraints. Equality constraints refer to exact relationships that must be satisfied [48], and inequality constraints impose limits or thresholds, such as productive or budgetary caps that cannot be exceeded [45]. A third type, logical constraints, represents conditional relationships between variables, often implemented using binary variables [37].

Mathematical modeling provides the fundamental framework for representing complex real-world systems through abstractions that capture their essential relationships, a process that culminates in the solution and interpretation of a problem. For solving these problems, different techniques, called optimization techniques, have been developed, which can be classified as classical, heuristics, and metaheuristics based on their currency, use of computational resources, and algorithm application [56], or based on their application to particular problems [57].

Given the diversity of ways to classify optimization techniques, the present work is based primarily on the classification proposed by Mandal [58], who divides optimization techniques into three major categories according to the nature of the proposed problem. Mandal proposes two initial broad classifications: Classical Optimization Approaches, which can be used if the problem exhibits certain mathematical properties, and Nature-Inspired Algorithms (NIAs).

Classical Optimization Approaches are used if the proposed problem possesses specific mathematical properties that guarantee optimal solutions. This category includes fundamental techniques such as Linear Programming (LP), Mixed-Integer Linear Programming (MILP), and Quadratic Programming.

The second major classification proposed by Mandal [58] is Nature-Inspired Algorithms (NIAs), which are specifically designed to address optimization problems of a highly complex nature that lack the necessary mathematical properties for classical approaches. A key subdivision is distinguished within this category: Evolutionary Algorithms, which include techniques based on evolution and natural selection, such as the Genetic Algorithm, the Non-dominated Sorting Genetic Algorithm II (NSGA-II), and the Strength Pareto Evolutionary Algorithm 2 (SPEA2). Additionally, there are Swarm Intelligence-Based Algorithms, which model the collective behavior of groups (swarms), with prominent examples such as Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO), and the Artificial Bee Colony Algorithm (ABC). Finally, this classification groups Other Metaheuristics that do not fit into the previous categories, such as the Artificial Neural Network, the Flower Pollination Algorithm (FPA), and the Simulated Annealing Algorithm (SA).

Furthermore, by mixing any of the techniques implicit in these two classifications, a third classification is derived, which is a Mixed Hybrid classification. This yields the classification of optimization techniques according to Figure 4.

In summary, the conceptual pillars of this research supply chain, economic profitability, and optimization techniques demonstrate an evolution toward a systemic and integrated vision for addressing the complexity of contemporary organizations. Therefore, this literature review has been carried out using a rigorous methodology to identify the main advances and areas of opportunity in the convergence of these fields.

3. Methodology

To answer the research questions posed, the PRISMA (Preferred Reporting Items for Systematic Reviews and Meta-Analyses) methodology is developed [62]. This framework aims to provide a clear and transparent structure for the identification, selection, evaluation, and synthesis of relevant literature. This method seeks to ensure a systematic and reproducible review process, minimizing bias and offering a comprehensive overview of the current state of knowledge on the topics of interest. The details of the methodology developed are presented in Figure 5.

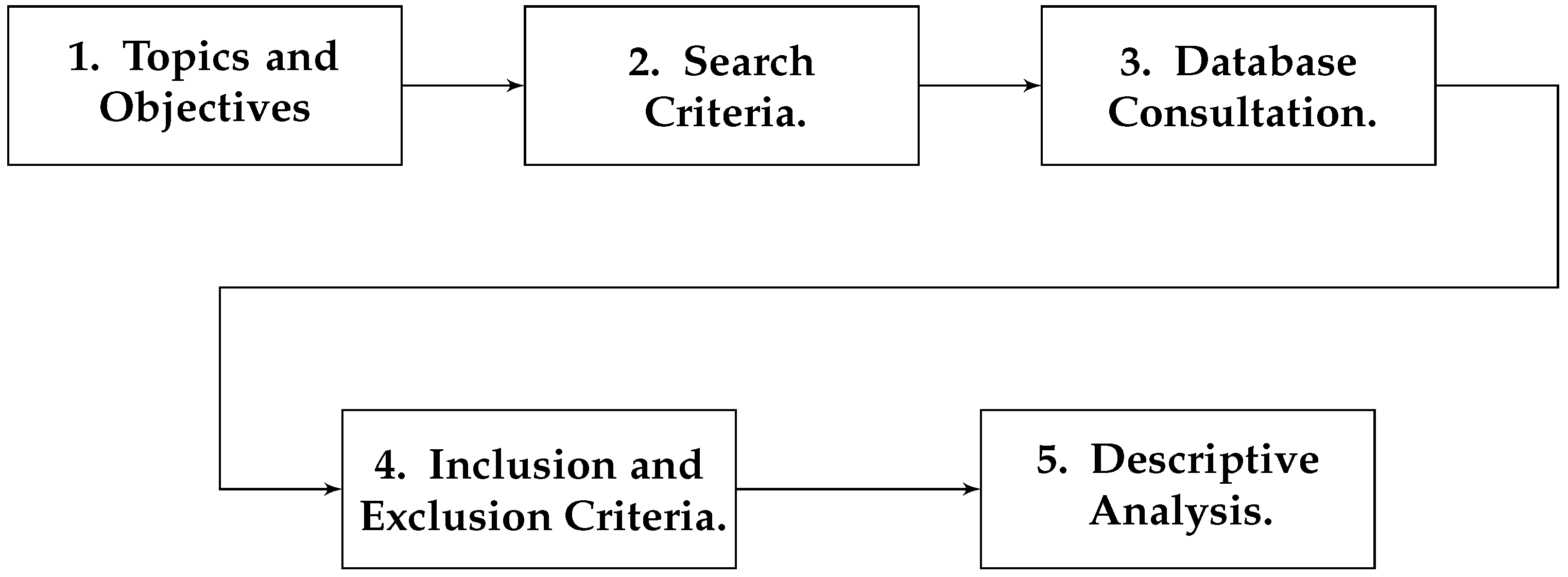
3.1. Topics and Objectives

In the introduction of the present work, the topic to be developed is established, which is framed within optimization techniques applied to supply chains to improve economic profitability. Given these general themes, the specific objectives of this work are the following:

• To identify and classify the optimization techniques applied to supply chains to improve economic profitability.
• To determine the Value Drivers addressed through the application of the identified optimization techniques.
• To identify the Supply Chain processes in which the classified optimization techniques are applied.

3.2. Search Criteria

For the elaboration of this literature review, keywords related to the topic of interest and the research objectives were used, which can be grouped into three main categories:

Considering the keywords derived from the Conceptual Foundations, they were searched for in English, following the IEEE-thesaurus [63], thus obtaining the key words shown in

Table 1. Key Words.

Base Word	Thesaurus
Supply Chain	Supply Chain, logistics, supply network, value chain.
Economic Profitability	Financial performance, cost reduction, cost optimization, revenue generation, profitability, working capital, liquidity, financial risk, cash flow, return on investment, ROI.
Optimization Technique	Mathematical model, optimization, optimisation, algorithm, simulation, predictive model, data analytic, machine learning, deep learning, artificial intelligence, stochastic model, control theory, game theory, network model, forecasting model, statistical model computational method, quantitative method.

.

With the selected key words, the search equation was established, to which the most common synonyms used for the chosen key words were added. Furthermore, for a more refined review, the Boolean operators OR and AND are used between each of the search rules [64].

Regarding the search period, a range from 2015 to 2025 was determined, in order to cover the last 10 years, thus aiming to include the most current works.

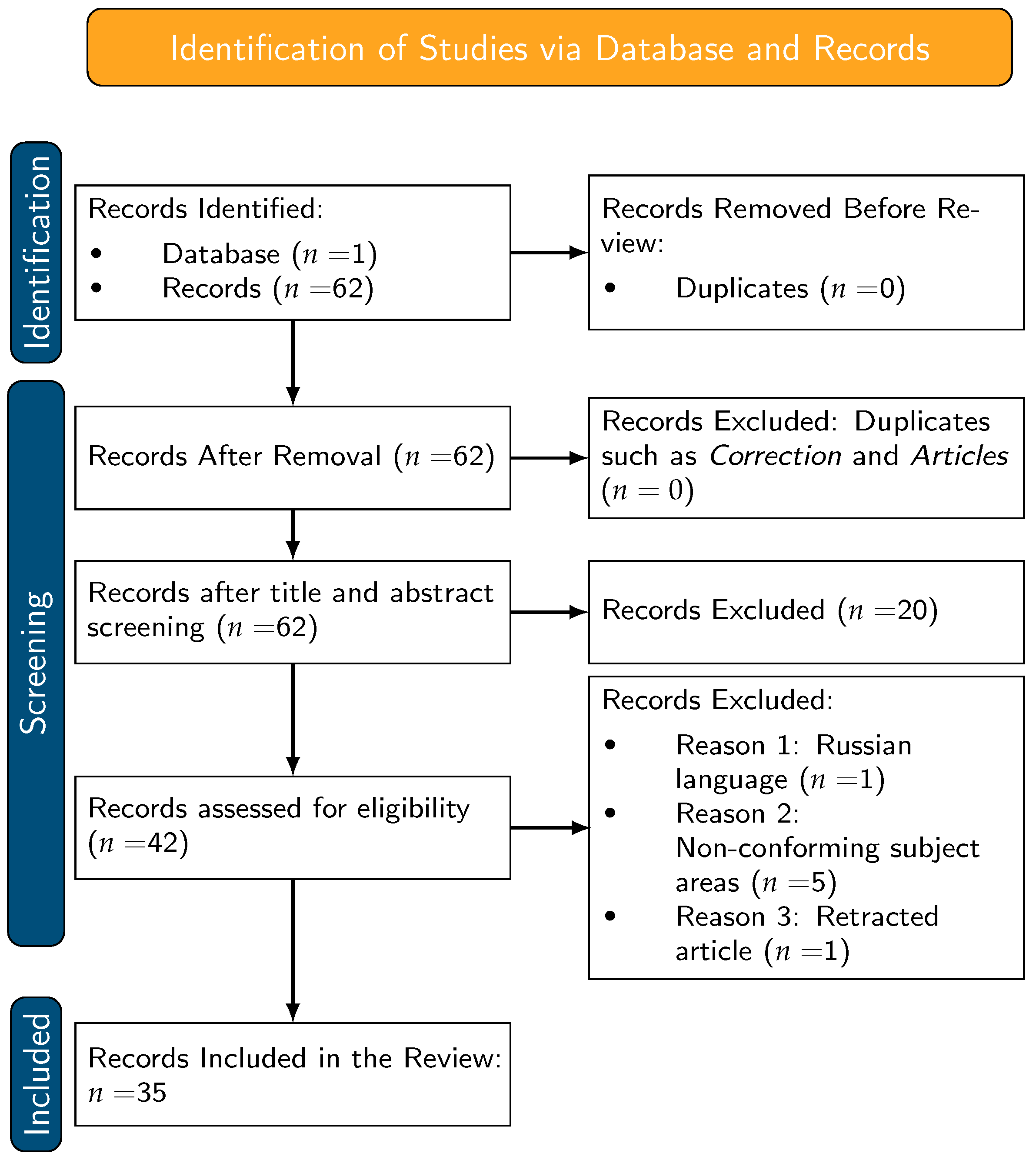
3.3. Database Consultation

The database consulted for the present research was Web of Science, as it is one of the most important search engines within the international academic community [65]. Furthermore, this database has powerful and user-friendly consultation and analysis tools that are very helpful for conducting bibliometric reviews.

With the selected keywords, the following search equation was obtained and applied in the Web of Science database:

• Key words: “supply chain*” OR “logistics” OR “supply network*” OR “value chain*” (Author Keywords) AND “supply chain*” OR “logistics” OR “supply network*” OR “value chain*” (Author Keywords) AND “financial impact” OR “financial performance” OR “economic performance” OR “cost reduction” OR “cost optimization” OR “revenue generation” OR “profitability” OR “working capital” OR “liquidity” OR “financial risk*” OR “cash flow” OR “return on investment” OR “ROI” (Author Keywords) AND “mathematical model*” OR “optimization” OR “optimisation” OR “algorithm*” OR “simulation” OR “predictive model*” OR “data analytic*” OR “machine learning” OR “deep learning” OR “artificial intelligence” OR “stochastic model*” OR “control theory” OR “game theory” OR “network model*” OR “forecasting model*” OR “statistical model*” OR “computational method*” OR “quantitative method*” (Author Keywords) and 2025 or 2024 or 2023 or 2022 or 2021 or 2020 or 2019 or 2018 or 2017 or 2016 or 2015 (Publication Years).

The objective of the presented equation is to narrow down the topic of interest as much as possible. The database was last searched on 1 August 2025.

3.4. Inclusion and Exclusion Criteria

The search equation yielded a total of 62 records. The inclusion and exclusion criteria, detailed in Figure 6, are then applied to these results.

During the execution of the PRISMA model, records with the status of Correction and Article were excluded, though none were found in this specific category. Additionally, upon reviewing the abstracts and titles, all documents that did not align with the research objectives were excluded. Records whose abstracts indicated they were a literature review were also discarded; this category specifically included the works [66,67,68,69]. Likewise, works whose title or abstract did not explicitly indicate the proposal and development of a mathematical or optimization model were excluded. This category included the works [70,71,72,73,74,75,76,77,78].

Finally, during the title and abstract screening phase, works focused on supply chains other than industrial transformation were excluded from the review. This category includes the works [79,80,81,82,83,84,85].

In the same screening stage, during a third phase, one article was excluded for being written in Russian [86] and another for being a retracted article. Finally, six additional articles were removed for belonging to non-conforming subject areas, such as biology [87], energy [88,89], and transport [90,91].

In this way, the 35 works that form the basis of the present review were obtained.

The inclusion and exclusion criteria were developed by the authors. Initially, the titles and abstracts of the 62 records retrieved from the search were independently screened. The results were compared, and a consensus list of 42 papers was obtained through discussion. Subsequently, the same two authors independently assessed the full text of the 42 potentially eligible reports against the inclusion criteria. Disagreements at this stage were again resolved through discussion to determine the final 35 studies for inclusion.

Once the studies were selected, a 14-column spreadsheet was developed to systematically extract data from the 35 final papers. These columns specified: #, title, authors, abstract, problem addressed, proposed solution, objective function, optimization technique, classification of technique, decision type, number of citations, supply chain process, process key, and monitoring indicator.

The authors extracted the relevant data from all 35 papers; furthermore, they independently validated the accuracy of the information by comparing it with the original sources. Any discrepancies were resolved via consensus.

To evaluate the methodological quality of the 35 included studies, a critical appraisal was performed. Supported by the developed worksheet, the authors jointly verified that the selected papers met several criteria. First, they confirmed that the studies had at least one objective function focused on improving financial performance, in accordance with the value drivers specified in Figure 3. It was also verified that the studies were developed within one or more typical supply chain processes. Finally, it was verified that the objective function(s) specified in the papers were resolved by a clearly specified optimization technique.

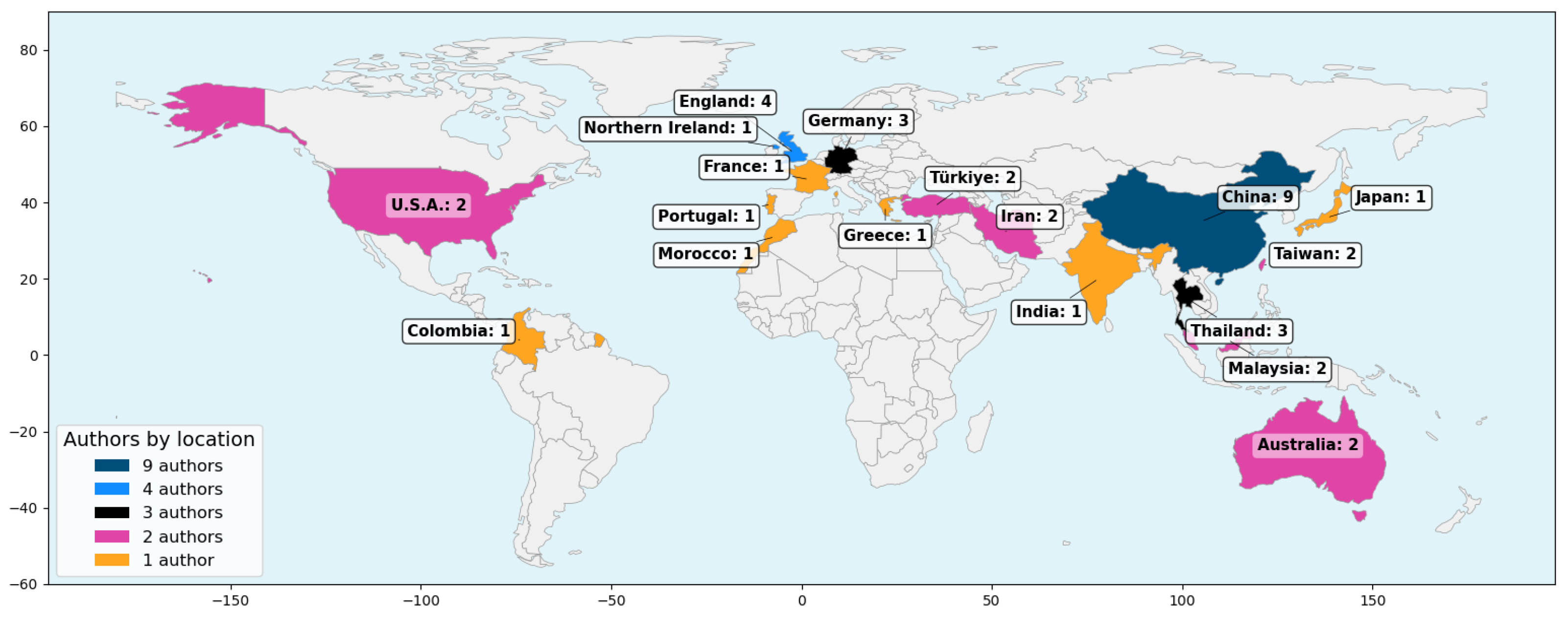
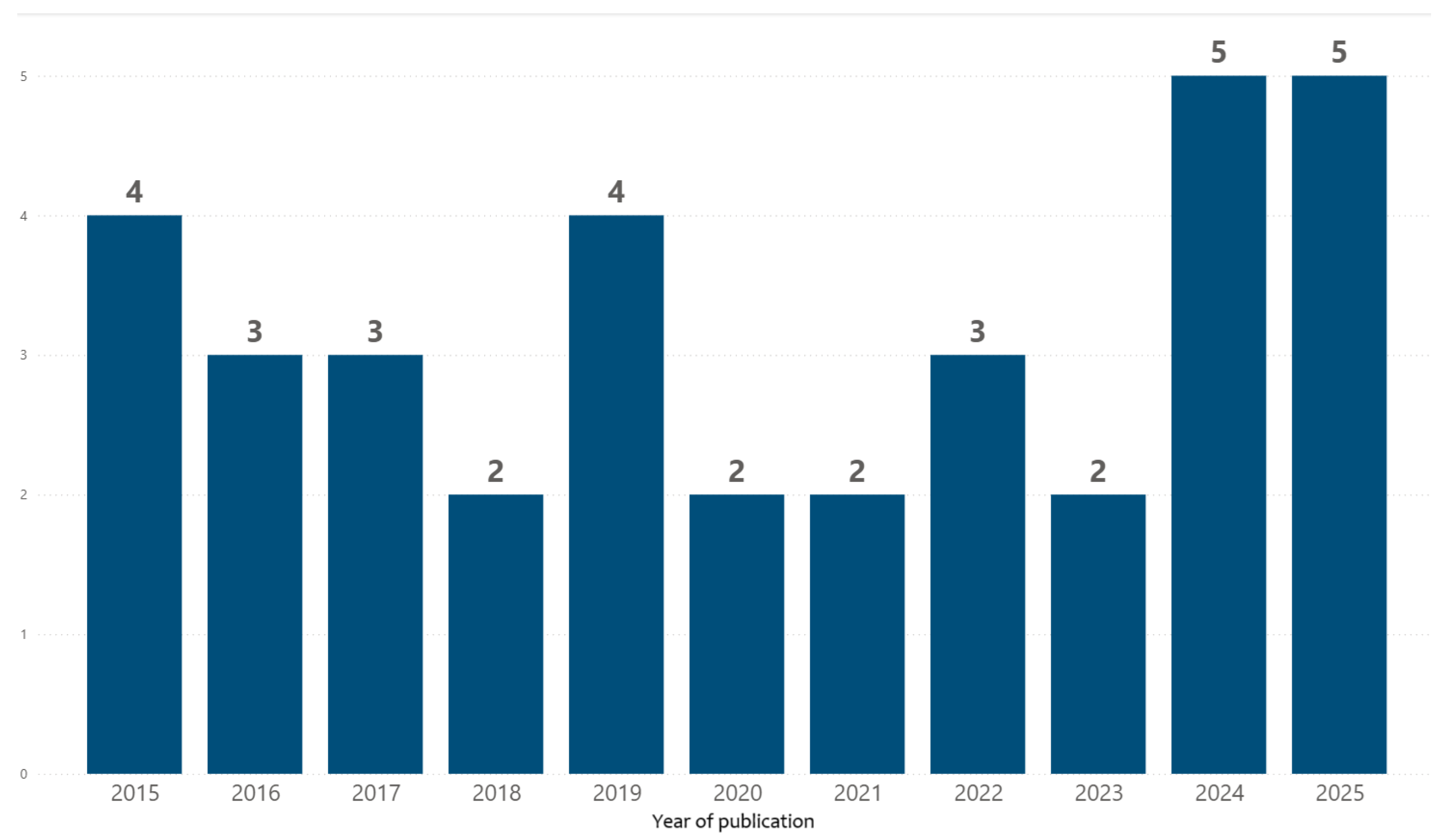
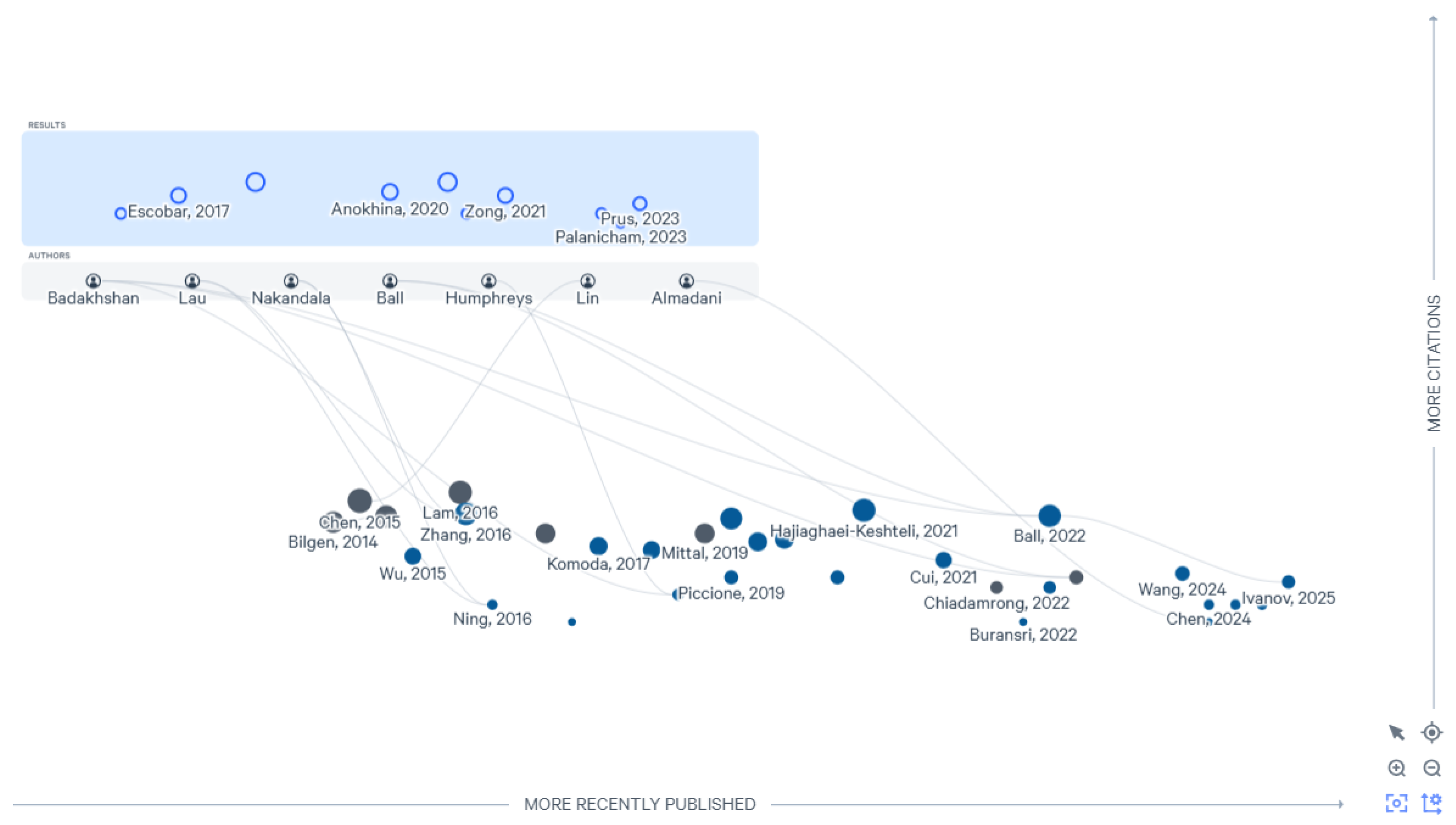
3.5. Descriptive Analysis

The 35 analyzed works were written by a total of 41 authors of diverse nationalities. As shown in Figure 7, the authors come from 20 countries, with China having the largest number of collaborators with 9.

China was followed by England with four authors. Subsequently, Germany and Thailand each had three authors, while Australia, Iran, Malaysia, Taiwan, the United States of America, and Turkey each had two authors. Finally, one author was found in each of the following countries: Colombia, France, India, Japan, Morocco, the Netherlands, Northern Ireland, Portugal, and Switzerland.

Regarding the works published per year (see Figure 8), an increase in publications is observed during the last two years (2024–2025). This trend is particularly notable given that 2025 is still an incomplete year, which suggests that the topic is gaining particular relevance in recent years.

As observed in Figure 9, which relates the year of publication to the number of citations, the research topic has gained substantial relevance in recent years, even considering the recent publication of some works. This is evident with the most recent articles (located on the right side of the visualization) that directly build upon earlier, highly cited, and influential works (located at the top), thus confirming that the research is both cumulative and dynamic.

Finally, in the descriptive part of the selected works, a co-occurrence analysis of keywords is performed. As illustrated in Figure 10, the works form three main clusters, distinguished by color. The first of these, a blue-gray cluster (center), represents the core theme of the selected works, focusing on optimization models related to inventories, decisions, and systems. This central relationship extends to the exploration of aspects such as multi-objective optimization and system dynamics.

The second significant concentration is the purple cluster (left side), which largely focuses on the supply chain and cost optimization, as well as some financial aspects such as risk, general finance, and working capital. This cluster is connected to aspects like machine learning and simulation. The blue cluster (upper right side) highlights the use of tools such as simulation, hybrid models, and specific aspects of the supply chain such as production planning.

The application of mathematical models for optimization is a central practice in this field. The presence of the purple cluster, which connects the terms supply chain with cost optimization and working capital management, suggests that mathematical models are applied to enhance financial performance. The network visualizes that the models are not an end in themselves but rather a methodological tool to address practical optimization problems in the supply chain, with direct implications for financial performance.

There are also indications regarding the financial challenges that are addressed, although not clearly evident through the works’ key words. Regarding the cost optimization cluster, it is noted that it is a key concept within the supply chain cluster, signaling that the reduction and control of costs are a primary and central objective in a large portion of the works. Similarly, the term financial risk appears as a node that connects with supply chain, indicating that the mitigation of financial risks is another relevant challenge.

4. Findings

This section presents the findings derived from the analysis and synthesis of the 35 selected works, organized according to the research questions formulated. The obtained results are detailed below:

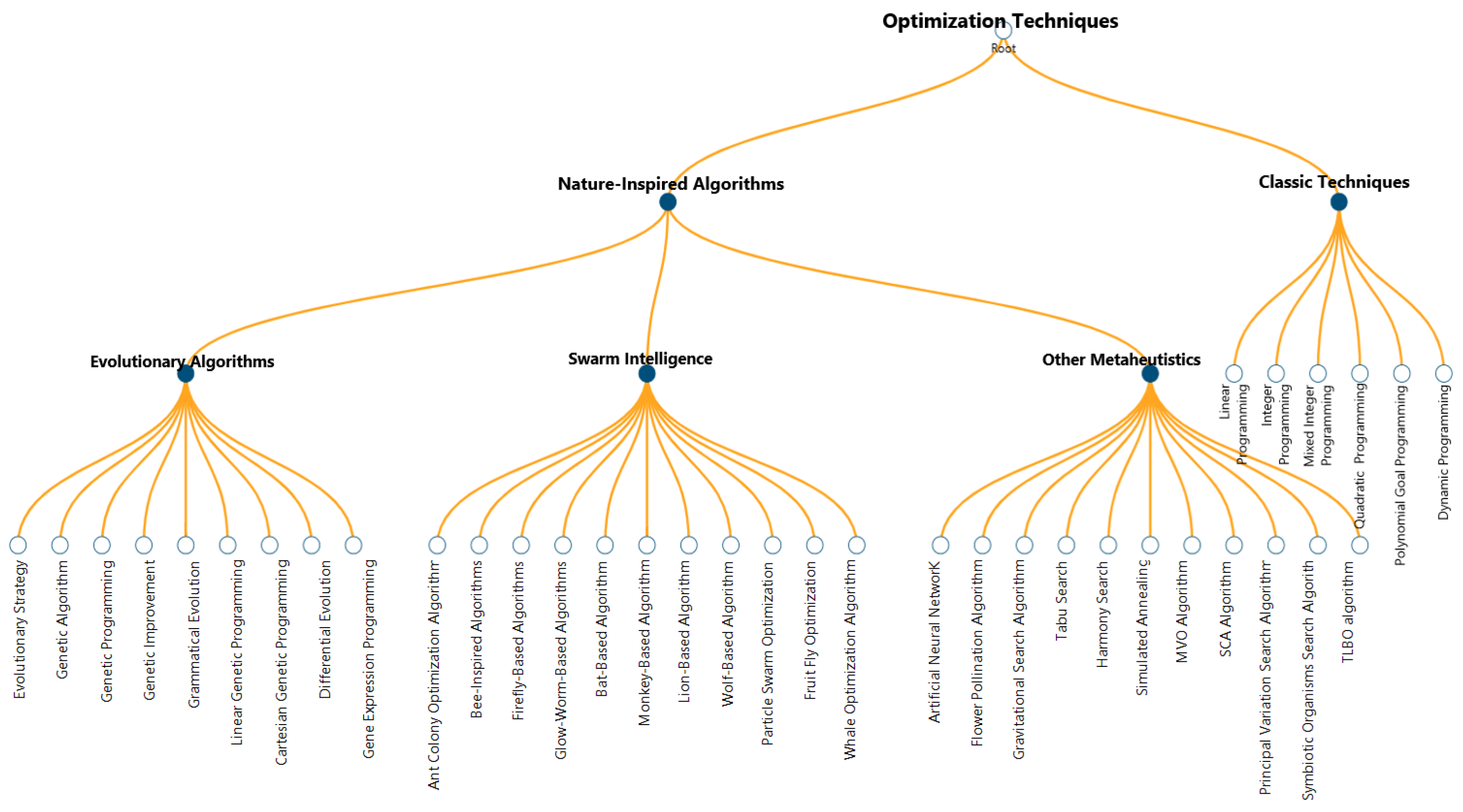
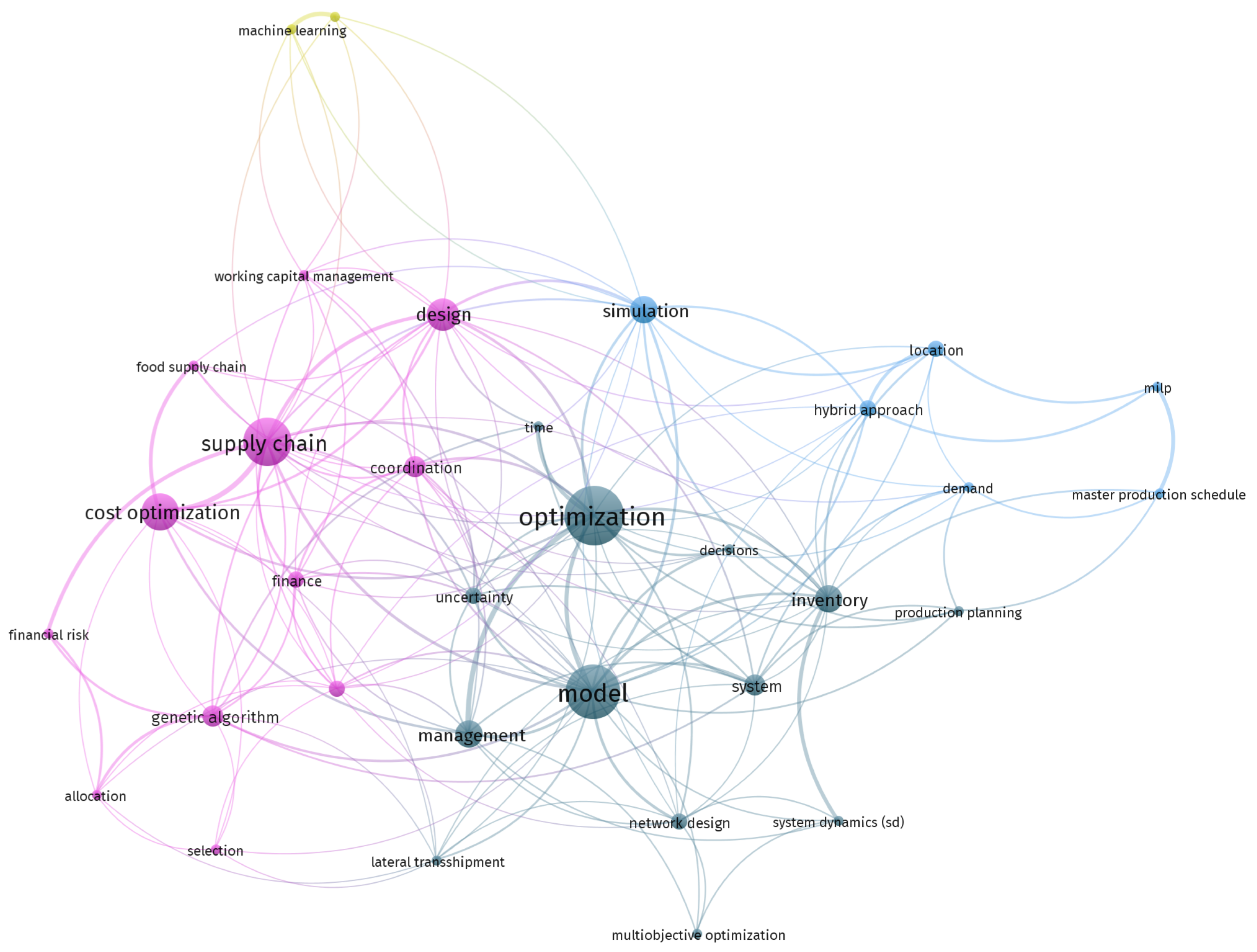
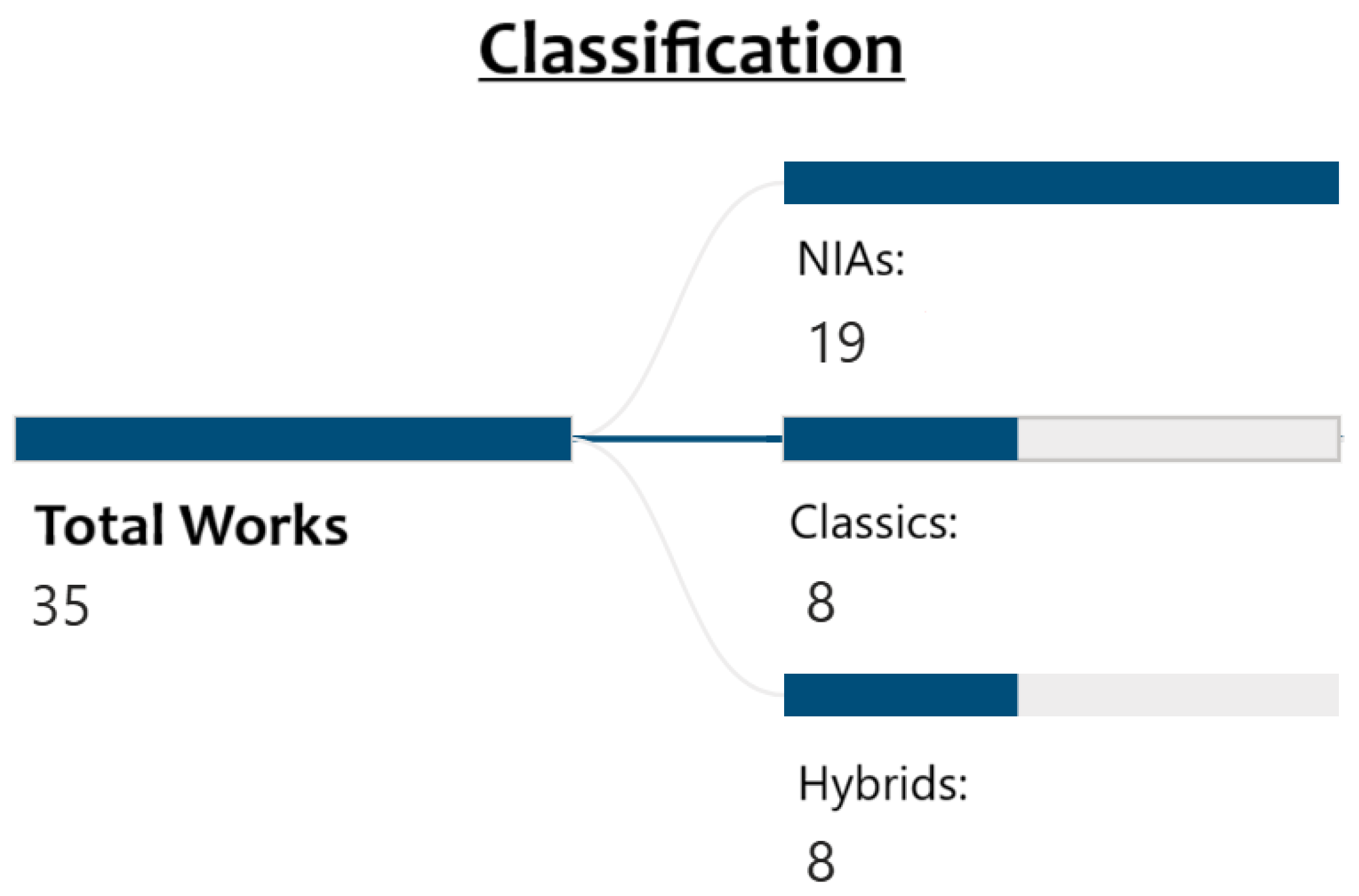
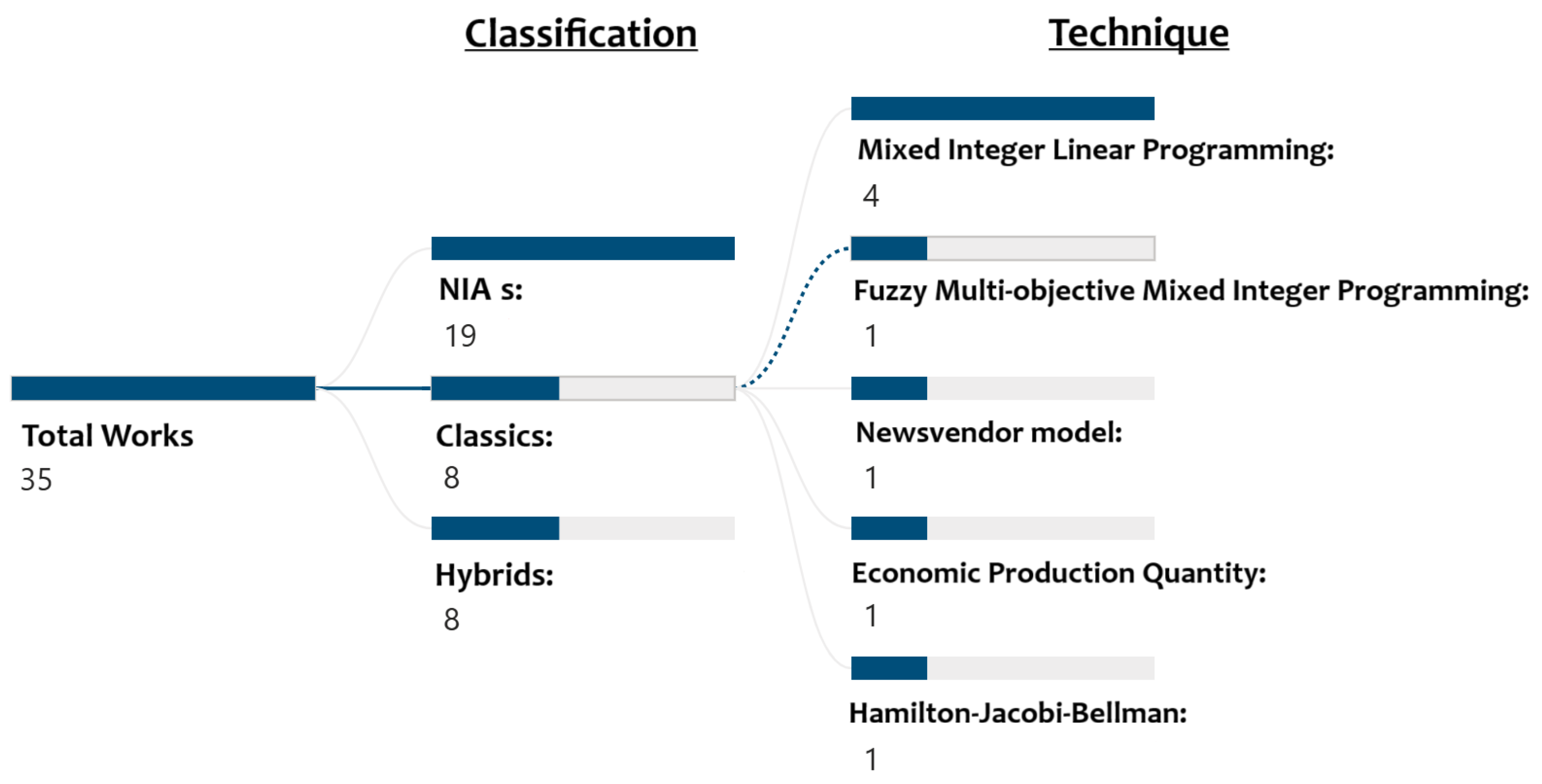
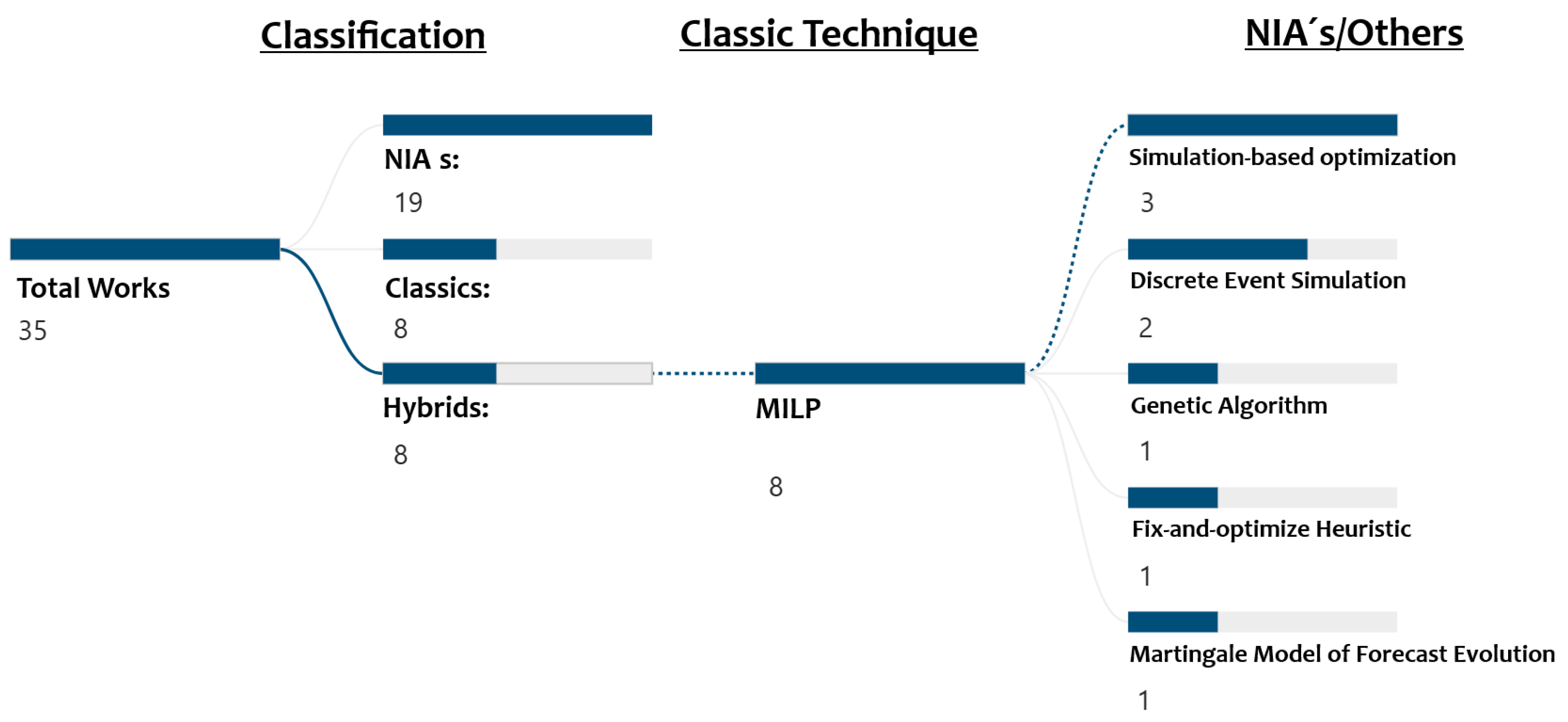
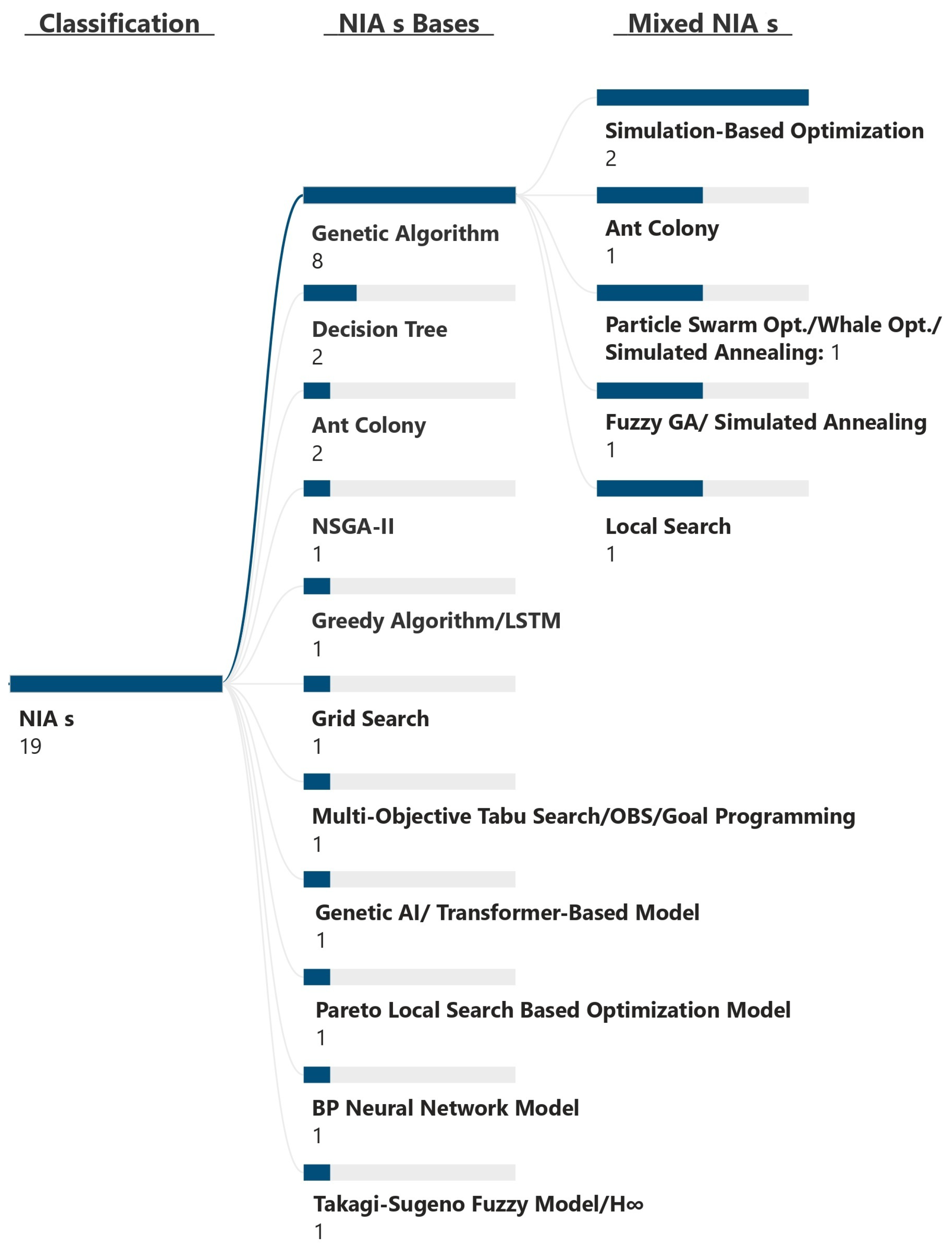
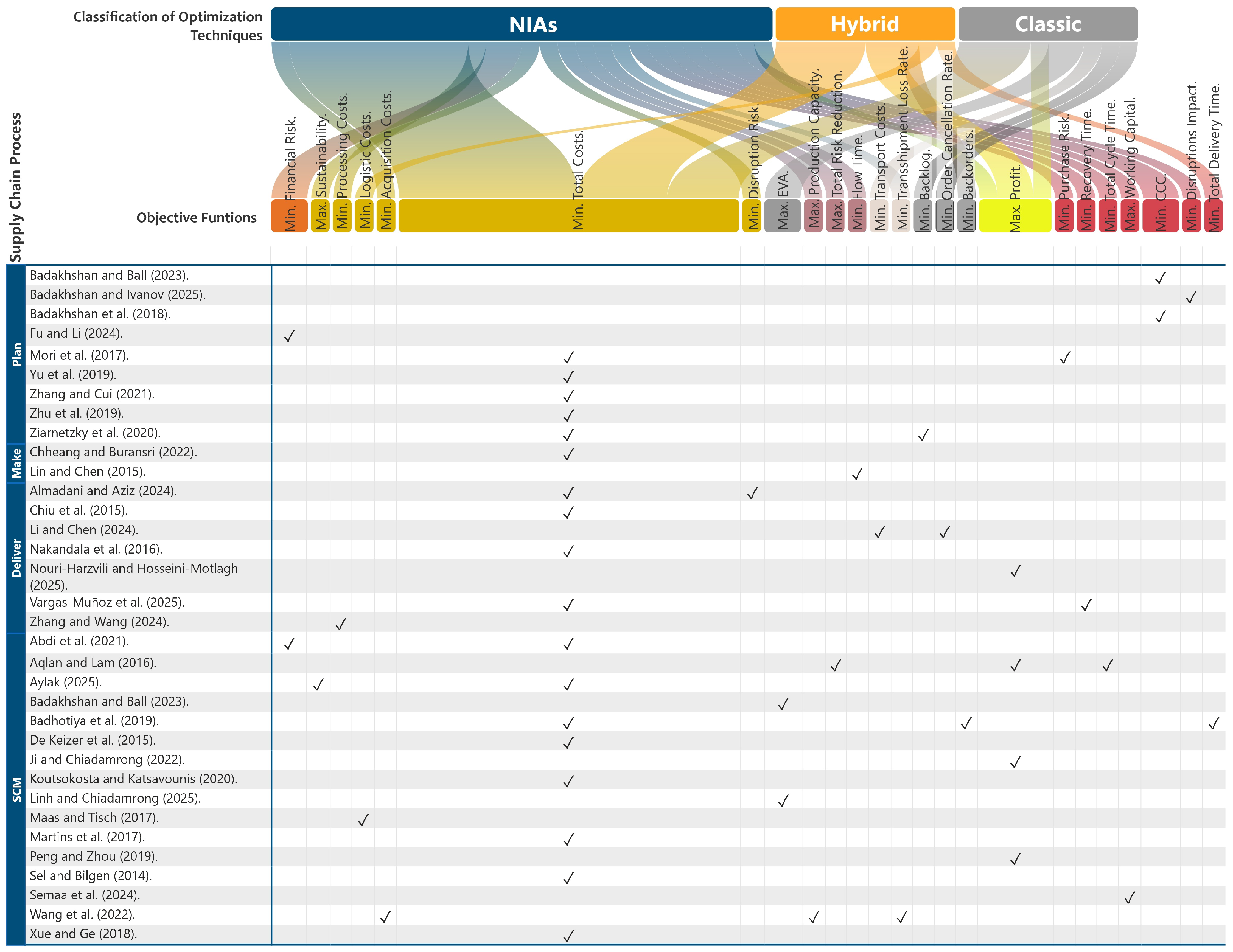
4.1. Optimization Techniques

In response to the first research question, the main optimization techniques applied in the literature to improve economic profitability through supply chain processes were identified. For the organization and analysis of these findings, the classification proposed by Mandal [58] was used, which was complemented in Figure 4. Based on this structure, the studies were classified into three categories: Classical, Nature-Inspired Algorithms (NIAs), and, given its prevalence, a Hybrid classification that integrates both approaches. The distribution of the 35 analyzed publications into these three categories is summarized according to Figure 11.

Within the Classical Methods classification (see Figure 12), Mixed-Integer Linear Programming (MILP) constitutes the most used technique in the reviewed works. The literature reveals a strong focus on cost minimization and logistics efficiency. For example, Maas C. & Tisch A. [92] propose a model based on mixed-integer programming to minimize logistics costs in a trucking company, while Chheang H. & Buransri N. [93] propose the use of MILP to address the stochastic lot-sizing optimization problem. Their proposal seeks to simultaneously determine the optimal replenishment periods and orders for multiple items with shared resources and thereby balance inventory and setup costs to produce the exact quantity of products needed, resulting in zero excess inventory at the end of each period.

For their part, Zhu et al. [94] seek to optimize the seed supply chain, a highly complex sector. The authors propose an optimization model that considers multiple constraints and preferences in agricultural practices, based on mixed-integer linear programming. The proposed solution, based on industrial case studies, demonstrated a reduction of up to 16% in total costs and 9% in land use, mitigating significant risks during the planning phase. Finally, regarding mixed-integer linear programming methods, the work of Koutsokosta, A. & Katsavounis, S. [95] is found, whose proposal is a dynamic mixed-integer linear programming model that seeks cost minimization in a three-echelon, multi-site, and multi-product supply chain, thereby assisting with strategic and tactical decision making.

Distinct from the Mixed-Integer Linear Programming models is the proposal by Badhotiya G., Soni G. & Mittal M. [96]. Their work addresses a problem of integrated production and distribution planning in a two-echelon supply chain. To solve it, they propose a multi-objective fuzzy mixed-integer programming model, which considers the minimization of three objectives: total cost, delivery time, and the level of backorders. Additionally, classical methods have been used for the optimization of inventory costs in multinational companies through the use of the economic production quantity model (EPQ), thereby obtaining optimal operational policies that generate significant savings in inventory costs [97]. The Hamilton–Jacobi–Bellman Method proved useful for establishing discount prices in electronic markets. Using this method, a reduction in stockouts and an improvement in company reputation were achieved. Optimization within the adaptable framework leads to a reduction of 18% and 24% in inventory shortages and an increase of 3.5% in prestige [98]. Finally, the newsvendor model and game theory are used to optimize the deployment of working capital and maximize the overall profit in a supply chain [99].

Within the Hybrid category (see Figure 13), the combination of Mixed-Integer Linear Programming (MILP) with Simulation-Based Optimization (SBO) stands out, proving to be particularly useful for enhancing financial performance under complex conditions.

The integration of these approaches allows for modeling uncertainty and the impact of capital. For example, Badakhshan et al. [100] used a hybrid SBO with MILP model to integrate financial and physical flows in supply chain planning, achieving a 6% increase in Economic Value Added (EVA). Reinforcing this focus on economic value creation, Linh et al. [101] proposed a hybrid approach of (MILP and SBO) that managed to identify the impact of the capital charge on investments, rather than just short-term operating profits. This study evidenced that focusing solely on operating profits is insufficient to maximize the creation of economic value in the Cocoa supply chain.

This hybrid combination also proves effective in operational management. Ji et al. [102] applied the integration of MILP and SBO to feasibly plan production and distribution, ensuring desired customer service levels. The result was a maximization of profits through precise and correct inventory management.

The hybrid approach that integrates MILP and DES (Discrete Event Simulation) is another effective combination used in the literature to address logistical problems that lead to economic-financial improvements [1].

This methodological integration has allowed for the optimization of costs while meeting quality requirements. For example, De Keizer et al. [103] used an iterative method that combines DES and MILP to solve network design problems in perishable product supply chains. The model uses feedback from the simulation to refine the solutions obtained by the MILP, successfully optimizing costs and, simultaneously, ensuring compliance with strict quality requirements.

Similarly, Martins S. et al. [104] applied a hybrid MILP and DES approach for the redesign of the distribution network of pharmaceutical wholesalers. This approach proved suitable for optimizing both strategic and tactical decisions, resulting in a decrease in inventory and annual savings of approximately 3% by optimizing the current supply chain design.

Furthermore, a combination of MILP with the Fix and Optimize Heuristic is a suitable tool for production and distribution planning in the beverage industry, achieving an optimal assignment of production volumes and thus the minimization of total cost [105].

The effectiveness of hybrid approaches extends to the integration of analytical models with forecasting and deep learning methods for advanced planning. By analyzing the performance of production planning models for semiconductor fabrication plants under stochastic demand, decisions regarding safety stock inventory and production planning are integrated, thereby achieving a minimization of work-in-process and backlog costs. This is done through the generation of a hybrid model that integrates MILP and the Martingale Forecast Evolution Model [106].

Furthermore, the literature also presents the integration of more advanced optimization techniques. The integration of MILP with Genetic Algorithms that incorporates deep learning has successfully reduced transportation costs by utilizing a customer segmentation system and optimizing product assignment with an improved genetic algorithm. The results of this combination show a significant improvement in user classification accuracy, a reduction in order cancellation rates, and an increase in profits [107].

In the classification of Nature-Inspired Algorithms (NIAs), which comprises 19 of the reviewed publications (see Figure 14), the Genetic Algorithm (GA) is presented as the most recurrent technique, used both individually and in hybrid approaches with other metaheuristics.

The use of Genetic Algorithms (GAs) has been shown to work in addressing problems of financial flow desynchronization in a supply chain, which negatively impacts working capital. To this end, strategies for customer payment incentives and extending payment to suppliers are proposed, with the application of a metaheuristic based on the genetic algorithm to optimize financial performance [108]. For their part, Xue Y. & Ge L. [109] use the GA to reduce the total cost of quality and thus improve customer satisfaction, thereby simplifying decision making. The Non-dominated Sorting Genetic Algorithm II (NSGA-II) has proven useful for cost optimization and the minimization of disruption risks in the supply chain of the automotive industry [110].

Complementing the hybrid works, the study by Nakandala D. et al. [111] addresses a problem of cost optimization and demand satisfaction in inventory management for wholesalers. The authors propose the use of a stochastic search technique called the Hybrid Genetic Algorithm (HGA), which developed a mixture of random and greedy solutions and implemented a local search method, thus obtaining more effective solutions.

The mix of GA with Whale Optimization Algorithms, Particle Swarm Optimization, and Simulated Annealing proved useful for the network design of a closed-loop supply chain (CLSC) under conditions of uncertainty, with the objective of minimizing total cost and financial risk. The blending of these algorithms allows for addressing complex problems by generating different comparable solutions [112]. In the distribution of perishable products, the comparative use of GA, Fuzzy Genetic Algorithm, and Simulated Annealing have been compared to address problems of cost and quality, with the Fuzzy Genetic Algorithm showing better performance in the results obtained [113].

Delving further into this classification, the work by Lin J.T. & Chien-Ming C. [114] addresses the problem of production scheduling in a hybrid flow shop in semiconductor manufacturing, with the objective of achieving the minimum feasible flow time. For this problem, they used the simulation optimization approach. The technique utilized includes a simulation model to evaluate performance, an optimization strategy that applies a GA (Genetic Algorithm), and an acceleration technique through optimal computation budget allocation. With this, the effectiveness of this approach for practical applications is demonstrated.

Reducing the costs of dynamic supply chain scheduling while simultaneously improving customer satisfaction, through an adaptive Ant Colony Optimization (ACO) algorithm that adjusts pheromone rules to achieve efficient scheduling, is suitable in an experimental context [115]. For their part, Fu, H. & Li, H. [116] address a financial risk problem in the supply chain to control risks and improve companies’ ability to withstand financial crises. They do this through a supply chain risk management model based on the backpropagation (BP) neural network, using it to categorize risk types, extract their financial characteristics, and perform a dynamic measurement to effectively mitigate supply chain financial risk.

Problems of financial and inventory management in supply chains facing physical and financial disruptions have been addressed using DES and digital twins as techniques to manage inventory and working capital [117]. Furthermore, the strengthening of digital twins through blockchain technologies also helps achieve the stated objective. The second work, for its part, goes further, proposing an integrated solution that combines DES, digital twins, machine learning techniques, and blockchain technology for a more reactive working capital management [118].

Other varieties of algorithmic and simulation techniques have been used for various objectives. The Ant Colony Optimization (ACO) algorithm is employed for inventory optimization [119]. Simulation models have been integrated to evaluate logistics performance in the Colombian citrus supply chain [120] by minimizing total cost and recovery time and to optimize server supply chains under risk and uncertainty [121]. In the latter, simulation has been used to maximize profit, reduce total risk, and minimize total cycle time. Similarly, solutions are proposed that incorporate artificial intelligence and deep learning to automate processes and improve performance with a focus on sustainability [122] and supply chain optimization strategy [123]. The use of fuzzy models to create robust financing strategies and mitigate the impact of uncertainties on working capital [124] is also an objective addressed within the NIAs.

The combination of advanced methodologies proves to be an effective solution for addressing the interconnected financial challenges in the supply chain. A notable example is the study that addresses Working Capital management in multi-echelon supply chains. For this objective, a Simulation-Based Optimization (SBO) model that integrates System Dynamics and the Genetic Algorithm was proposed [125]. Through this complex blend, it was demonstrated that the application of the optimal values obtained by the model led to a significant and shared decrease in the Cash Conversion Cycle (CCC) for all participating entities in the chain.

4.2. Value Drivers

The second research question fundamentally aims to identify how optimization techniques are applied to directly improve Economic Profitability. For this analysis, the present section uses the decomposition of EVA into its three major Management Decisions (Operating, Investment, and Financing) as a reference framework, as illustrated in Figure 3. Based on this framework, the synthesis of the 35 reviewed works reveals clear patterns regarding the prioritized financial objectives and the concentration of optimization decisions, which will be detailed in the following sections.

Figure 15 synthesizes the classification of optimization techniques, the specific objective functions, and the underlying value drivers identified in the 35 reviewed works. This figure is organized by the Optimization Techniques Classification (Top Row), which groups the studies into NIAs, Hybrid, and Classical, allowing for the analysis of methodological relationships.

The core of the figure links each technique with the Objective Function addressed in the study. Each of these objective functions is associated with a Value Driver that impacts Economic Value Added creation. The value drivers identified in the reviewed literature cover the following categories: Cost of Capital, Cost of Goods Sold, EVA, Fixed Assets, Operating Costs, Revenue, NOPAT, and Working Capital. Each driver is distinguished by a specific color and its corresponding name, which facilitates the visual analysis of the relationships between technique and financial objective.

It is notable that different types of techniques (NIAs, Hybrid, Classical) show a tendency to focus on certain groups of objective functions and, therefore, on a Value Driver. NIAs and hybrid techniques seem to cover a broader and more complex spectrum of objectives, including those related to sustainability and supply chain resilience, whereas classical techniques may be more focused on cost minimization and profit maximization.

The analysis of Classical Techniques reveals that the minimization of total cost is the predominant objective function in this category [93,94,95,96,97].

It is observed that the minimization of total cost is applied to diverse components of the supply chain. For example, the focus is directed at the reduction of total cost in supply networks serving multiple construction projects [95], or the minimization of a composite total cost that includes processing, transportation, and penalties for shortage and overproduction [94]. Other studies focus on the minimization of the expected total cost [93] and the optimization of the total cost of production, inventory, and delivery [97].

Although the main focus is cost, classical techniques also extend to multi-objective formulations and the maximization of profitability. In the multi-objective sphere, they have proven useful in minimizing total cost along with total delivery time and backorders [96]. In addition to logistics costs [92], classical techniques are applied directly in the maximization of Profit or utility [98,99].

Hybrid models also show a significant focus on total cost minimization [103,104,105,106], which they share with classical methods. However, their main methodological advantage is their capacity to address more robust and complex financial objectives, for example, the maximization of Economic Value Added, considered one of the most solid indicators for measuring corporate economic profitability [100,101]. Likewise, hybrid techniques are suitable for the maximization of Profit or utility [102].

Finally, regarding hybrid methods, the financial aspects addressed by hybrid techniques extend to the protection and growth of revenue and customer service. This is achieved by seeking the minimization of backlog [106], an aspect that affects sales, and by seeking the minimization of the order cancellation rate simultaneously with transportation cost [107].

In the NIA’s classification, the minimization of Total Costs is consolidated as the principal Operational Value Driver in the analyzed works. This is addressed as a multi-phase problem that integrates aspects from logistics [120] and inventory costs [119] as well as the trade-off with disruption risk [110] or the maintenance of fresh food quality [113].

Given the complex, uncertain, and multi-objective nature of these challenges, the dominant optimization technique is the Genetic Algorithm in its Cloud variants [109,111], as well as advanced techniques like Pareto Local Search [126] for the dual cost-risk problem. Even in the field of automation, advanced agentic artificial intelligence models based on transformer models are used to achieve a significant total cost reduction [122]. The potential of NIAs has even allowed for the modeling of financial risk to deal with it more robustly [124].

In other works, the minimization of Total Costs proves insufficient, making it necessary to simultaneously seek to optimize risk, lead time, supplier satisfaction, and logistics efficiency [115,121].

The Adaptive Ant Colony Optimization Algorithm is used to achieve the minimization of the total cost of dynamic scheduling, considering key variables such as transportation costs and supplier satisfaction [115]. Meanwhile, the use of algorithms like the Whale Optimization Algorithm supports the minimization of total cost in closed-loop networks [112].

On the other hand, the management of uncertainty drives the adoption of Hybrid Simulation Optimization Approaches, which are essential for modeling complex and stochastic systems such as high-end server manufacturing or the scheduling of hybrid flow shops in semiconductors [114], where Discrete Event Simulation is combined with algorithms like the Genetic Algorithm. Finally, the incursion of Advanced artificial intelligence is evident with the use of Deep Learning algorithms to define supply chain optimization strategies that rely on large volumes of data [123], thereby seeking the minimization of acquisition cost, the loss rate, and the maximization of production capacity.

There is a group of models whose focus is explicitly directed at financial topics. Primary objectives include the minimization of the Cash Conversion Cycle, which is successfully addressed using simulation models [125]. Likewise, the optimization of the income statement and payments [108] are addressed objectives, achieving the maximization of working capital through the use of Genetic Algorithms.

The literature also reveals the application of advanced modeling and control technologies for economic-financial purposes. Neural Networks are used for the active control of financial and operational risk [116]. Furthermore, the integration of technologies like digital twins and blockchain is a promising approach for achieving superior working capital management and mitigating the impact of supply chain disruptions [117,118].

4.3. Supply Chain Processes

Regarding the supply chain processes considered in the 35 works, the framework presented in the background of this study is taken as a reference, recalling that the supply chain processes can be divided into 5: Plan, Source, Make, Deliver, and Return. Furthermore, the analysis and addressing of two or more of these processes is called Supply Chain Management (SCM). Based on this, Figure 16 is developed, which shows which supply chain processes the analyzed works are focusing on.

Within the analyzed works, the Plan process focuses on two crucial aspects of management: the strategic-financial and the tactical-operational.

Planning is primarily directed at the management and optimization of Working Capital in the face of financial disruptions. This is a fundamental aspect at the strategic level, both for the supply chain and for financial planning. Recent literature addresses this through the integration of advanced technologies such as digital twins to mitigate disruptions [116,117,118,124,125].

Furthermore, at the supply chain’s strategic level, the Plan process emphasizes the need for effective planning. For example, the analysis of the seed supply chain underscores the urgency of transitioning from experience-based approaches to solutions based on mathematical programming for regional production optimization [94].

In the field of production planning and inventory management, particularly in semiconductor production, the objective is to optimize profits while ensuring customer service amid uncertain demand [106]. A recurrent objective is to determine the optimal inventory and production policy (how much, when, and where to hold stock) to minimize overall supply chain costs [119,126].

For the Make process, establishing the optimal production scheduling seeks to optimize production quantities through capacitated lot-sizing [93]. The semiconductor manufacturing process, which includes wafer fabrication, probing, and assembly, is also analyzed, highlighting an assembly scheduling problem aimed at minimizing flow time [114].

The Delivery process concentrates a high proportion of the works, which reflects the direct impact of logistics on costs and customer satisfaction.

Within the analyzed works, there is a focus on the optimization of logistical operations to reduce costs and improve service. For example, dynamic scheduling based on an adaptive Ant Colony Optimization (ACO) algorithm is used to optimize these operations [115]. The complexities of multi-modal transport, a critical aspect of distribution, are also addressed through a dual-objective mathematical model to optimize the automotive supply chain [110].

The literature highlights the importance of logistical operations by developing a hybrid genetic algorithm that addresses transshipment between multiple suppliers and wholesalers with variable lead times [111]. A significant line of research analyzes the transport of multiple fresh food or citrus products from various origins to retailers or warehouses [113,120]. To this logistical complexity is added the need to monitor the quality of deliveries [97].

In a digital environment, optimization extends to transport and order fulfillment efficiency in global e-commerce [107]. Finally, the literature addresses how decisions in the Delivery process intersect with the revenue strategy, analyzing the impact of discount offers in e-marketplaces [98].

The Supply Chain Management category encompasses works with an integrated vision, addressing the optimization of multiple processes with the objective of improving efficiency, overall resilience, and, primarily, the financial performance of the chain.

A prominent line of research focuses on the integration of operational and financial flows for Economic Value Added creation. The integral flow of the supply chain is analyzed, from the sourcing of raw materials (such as cocoa pods) to distribution to retailers, to maximize EVA [100,101]. In the same area, the importance of managing financial flows alongside operational ones is emphasized, including planning and sourcing strategies to improve working capital [108] and the analysis of payment periods and commercial credit between suppliers and retailers [99].

The comprehensive optimization of operational processes (Planning, Sourcing, Operations, and Logistics) seeks to optimize material flows, product quantities, and inventory levels within the network [95]. Models cover the entirety or large sections of the chain, from flower cutting (Make) to retail points (Delivery) to optimize the complete supply network [103]. In the ordering and transport processes within the supply chain, the need for specific studies on these processes is emphasized to improve efficiency and decision making [123].

In network design and logistics, both closed-loop supply network design [112] and the integration of sourcing and operations to improve inventory levels are analyzed [121]. In pharmaceutical wholesalers, network redesign affects acquisition, supplier review, and picking and shipping activities [104].

For its part, in production and distribution, the integration of diverse processes to achieve high-quality, low-cost operations in logistical service is highlighted [109], as well as approaches for direct delivery [92]. The integration between production and distribution includes the allocation of volumes on production lines and delivery to distribution centers in industries such as soft drinks [102,105]. Regarding multi-objective works, production planning and logistics/distribution (such as backorder and transport capacity) are incorporated for the minimization of total cost and delivery time [96].

The studies emphasize the automation of decision making to improve logistics efficiency and inventory management, as demonstrated by the Sustai-SCM framework, which integrates sourcing, operations, and logistics [122]. Finally, a summary of the optimization techniques utilized for given objective functions is provided in Appendix A Figure A1.

5. Research Gaps

In accordance with the present literature review, it can be noted that the convergence of the topics of interest is a dynamic and growing field of study that has significant research gaps. The main ones are listed below:

• Lack of exploration of classical optimization techniques in economic performance: Overall, there is a significant opportunity to systematically apply and compare classical optimization techniques to complex problems that address economic performance and supply chain processes.
• Fragmentation and Limited Application of NIAs: Within the NIA category, there is a high fragmentation of techniques. The Genetic Algorithm is the most common, either individually or in combination, while the benefits of advanced artificial intelligence and optimization methods have yet to be explored for improving economic performance in supply chain contexts.
• Lack of Accessible and Interpretable Approaches in Resource-Constrained Contexts: Despite the growing sophistication of nature-inspired algorithms (NIAs), current research predominantly emphasizes complex techniques (such as genetic algorithms) without adequately addressing the operational constraints of small and medium-sized enterprises. These firms often lack the computational resources and technical expertise required to implement such methods, and instead demand solutions that are both cost-effective and interpretable. This gap suggests a need for future studies to explore rule-based heuristics (IF-THEN systems) and approximation methods tailored to financially constrained supply chain environments.
• Insufficient Focus on Strategic Financial Metrics: The predominant objective in the 35 works, regardless of the technique classification, is the Minimization of Total Costs or cost variants, neglecting more robust and strategic financial metrics such as EVA, the Cash Conversion Cycle, or Cash Flow.
• Lack of Models for Disruption and Resilience Scenarios: Although financial and disruption risk is mentioned, few models address it dynamically or adaptively. Thus, a gap exists in the design and development of predictive models that integrate digital twins, blockchain, and simulation to manage physical and financial disruptions in quasi real time.
• Imbalance in the Addressing of Supply Chain Processes: Regarding the relationship between supply chain processes, it is observed that the Plan, Make, Deliver, and SCM processes concentrate the majority of the works. And, although the SCM classification encompasses two or more supply chain processes, the Source and Return processes are underexplored—yet they are key processes in corporate financial metrics.
• Technological Maturity of Optimization Techniques: Finally, a formal assessment of the technological maturity of the identified optimization techniques would enable a distinction between mature applications and research frontiers. Such an evaluation could assist researchers in identifying emerging areas and help practitioners assess implementation risks and expected returns. Future studies may address this gap by combining literature reviews with commercial software analyses or industry surveys, aiming to map the maturity status of various optimization techniques applied to enhancing economic profitability within the supply chain.

6. Theorical and Practical Implications

This systematic review yields significant implications for both managerial practice and academic research at the intersection of optimization and corporate finance within the supply chain domain.

6.1. Practical Implications

For corporate decision-makers, this study offers a comprehensive overview of the available tools and their alignment with strategic objectives. Moreover, it provides a framework for linking strategic outcomes with operational activities, thereby facilitating more coherent and goal-oriented supply chain financial management.

• Linking Decision Levels with Optimization Techniques: This review clarifies which families of optimization methods are most suitable for distinct decision-making levels (see Appendix A). Managers can observe that for strategic decisions aimed at maximizing robust metrics such as Economic Value Added (EVA), hybrid techniques—such as Mixed-Integer Linear Programming (MILP) combined with simulation—are particularly appropriate, as prior studies have already addressed these approaches. In contrast, for tactical or operational decisions focused on cost minimization, classical techniques remain both fundamental and effective
• Enhancing Economic Performance Beyond Cost Reduction: This study highlights the inherent complexity involved in aligning key strategic elements—such as value drivers—with supply chain processes. While cost reduction remains a commonly used metric to establish this connection, the review identifies additional supply chain activities and optimization techniques that can be leveraged to support the creation of economic value through operational processes.
• Consideration of Accessible Methods: This study reveals that current research predominantly focuses on advanced algorithms such as Genetic Algorithms and Deep Learning. This emphasis carries important implications for small and medium-sized enterprises, as it highlights the lack of lightweight methods (simple heuristics or IF-THEN rules) within high-impact literature. Such a gap not only suggests a promising direction for future research but also provides guidance for preparation and investment strategies among firms operating with limited resources.
• Focus on Investment in Technologies: This study identifies that certain rising technologies such as artificial intelligence, digital twins, and blockchain serve not only operational efficiency purposes but also represent valuable tools for managing financial resilience. This insight provides executives with a compelling rationale to invest in these technologies not merely as IT expenditures but as strategic assets for protecting working capital, fostering economic value creation, and mitigating financial risk.

6.2. Theorical Implications

• Moving Beyond Cost Minimization: This study identifies a theoretical need to transcend the prevailing cost-centric paradigm, signaling the maturation of the research field. The vast majority of the reviewed literature focuses on Total Cost Minimization or its variants essentially tactical metrics. In contrast, this work advocates for a shift in academic focus toward models that optimize strategic financial indicators capable of generating real economic value, such as Economic Value Added and the Cash Conversion Cycle.
• Integrating Operational and Financial Resilience: The study identifies a scarcity of models capable of dynamically managing disruptions. This implies that future theoretical frameworks should not only pursue operational robustness but also incorporate financial resilience that extends beyond cost and expenditure metrics. Such resilience should be enabled by key emerging technologies (such as digital twins, blockchain, artificial intelligence, and others) within the context of supply chain management.
• Contribution to the Economic Value Debate: This study expands the theoretical discourse on how logistics processes can be designed not only for operational efficiency but also for measurable economic value creation. Furthermore, it advocates for the exploration of rule-based heuristics, hybrid methods, and classical approaches capable of linking strategic indicators, such as Economic Value Added, with operational activities across the supply chain.

7. Conclusions

The results of this systematic review show that financial optimization in supply chains is a dynamic field with a growing methodological diversity. Classical techniques such as mixed-integer linear programming remain fundamental for structured problems, while NIAs (Nature-Inspired Algorithms) and hybrid approaches have demonstrated a greater capacity to address complex, uncertain, and multi-objective scenarios. This methodological evolution reflects a trend toward more adaptive models capable of simultaneously integrating logistical and financial decisions.

Likewise, a shift in focus from tactical to strategic is imperative. The primacy of Total Cost Minimization as the central objective demonstrates that the majority of studies do not address strategic financial metrics that truly reflect corporate value creation. There is a critical need to develop and validate models that directly optimize Economic Value Added (EVA), the Cash Conversion Cycle, and Cash Flow. In addition to this, the imbalance in process coverage must be remedied by focusing research on Source and Return, processes that are fundamental for working capital management but have been consistently underexplored.

Finally, the most relevant gap for the future is the design of resilient and adaptive models. The scarcity of models capable of addressing disruption and financial risk dynamically and predictively is a key limitation to the applicability of the works. Future research must focus on the integration of emerging technologies such as digital twins, blockchain, artificial intelligence, and Advanced Simulation with optimization techniques. This will enable the creation of models capable of managing physical and financial interruptions in quasi-real time, driving robust financial resilience and truly proactive decision making.

8. Limitations

• This study is constrained by its reliance on a single database. The literature search was conducted exclusively within the Web of Science database, which, while ensuring high-quality sources, systematically excluded potentially relevant studies indexed in other major repositories such as Scopus, IEEE Xplore, ProQuest, or EBSCO.
• Although the final 35 studies met the established inclusion criteria—namely, the presence of a financial objective function, the analysis of a supply chain process, and the application of an optimization technique—this review did not assess potential bias or the internal methodological quality of those studies. In other words, it is assumed that all 35 articles possess comparable methodological rigor, yet no formal evaluation was conducted to confirm this assumption.
• The classification of optimization techniques into Classical, Nature-Inspired Algorithms, and Hybrid approaches provides a clear structure grounded in the origin and nature of the methods. However, this framework may overlook other relevant classificatory dimensions. For instance, a secondary categorization based on the type of problem addressed (deterministic vs. stochastic) or the structure of the objective function (single-objective vs. multi-objective) could yield additional insights into the specific applicability scenarios of each technique family. The present review does not systematically explore these secondary dimensions within its primary classification framework, which may limit the reader’s ability to directly match specific problem types with the most suitable algorithm classes based on such structural characteristics.
• Another limitation of this study is the exclusion of non-English publications as well as studies focused on specific domains such as energy and transportation. It is possible that the excluded articles may contain relevant models or approaches that could enrich the findings and broaden the scope of analysis.