EAPO: A Multi-Strategy-Enhanced Artificial Protozoa Optimizer and Its Application to 3D UAV Path Planning
Abstract
1. Introduction
2. Modeling of UAV Path Planning
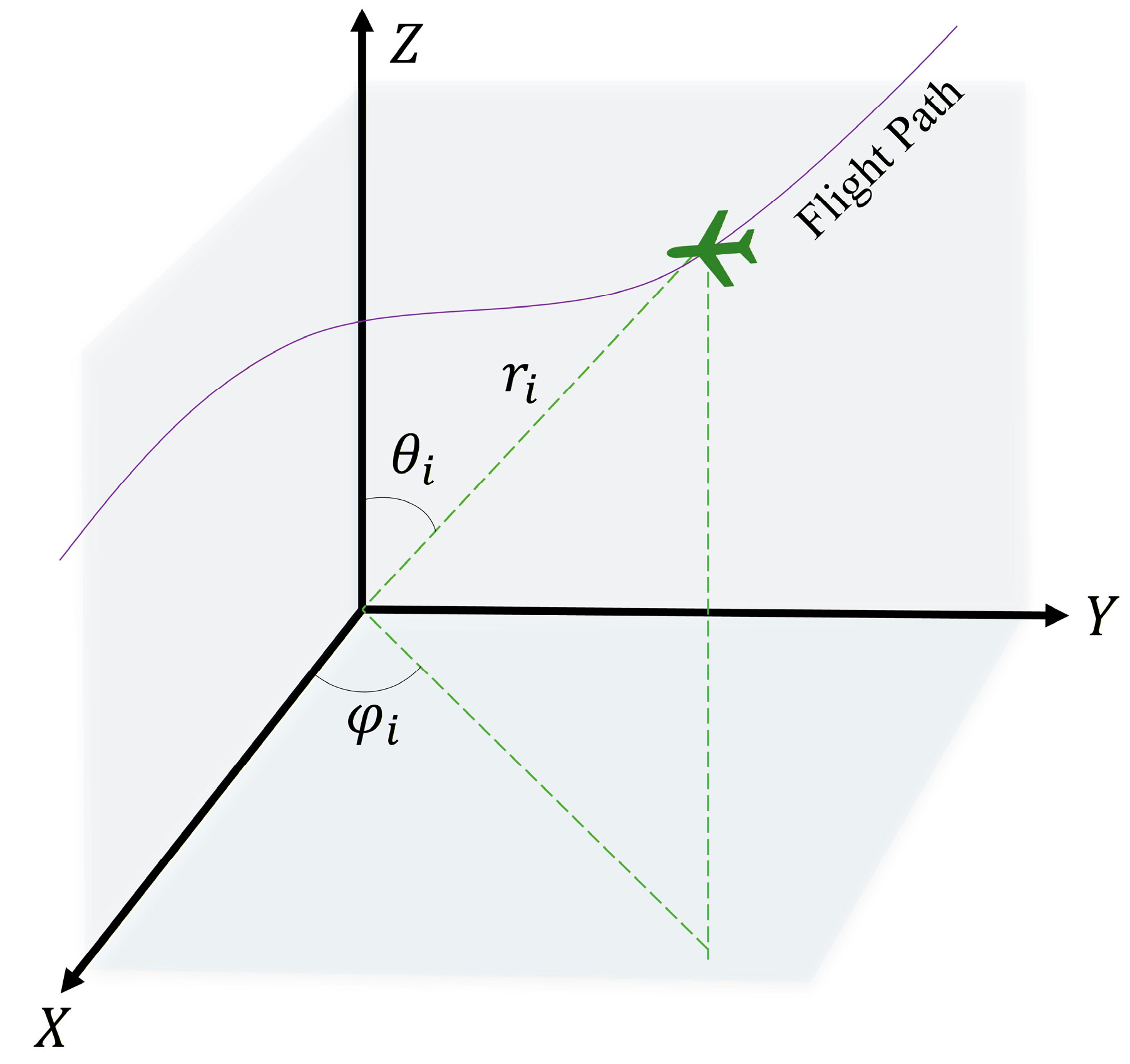
2.1. Decision Variables
2.2. Objective Function
2.2.1. Weighted Cost Function
2.2.2. Penalty Term
2.3. Cost Function Components
2.3.1. Flight Path Cost
2.3.2. Altitude Cost
2.3.3. Threat Cost
2.3.4. Angular Constraint Cost
2.3.5. Trajectory Segment Constraint Cost
2.3.6. No-Fly Zone Constraint Cost
3. Artificial Protozoa Optimizer (APO)
3.1. Foraging
3.1.1. Autotrophic Mode
3.1.2. Heterotrophic Mode
3.2. Dormancy
3.3. Reproduction
4. Enhanced Artificial Protozoan Optimization Algorithm (EAPO)
4.1. Latin Hypercube Sampling
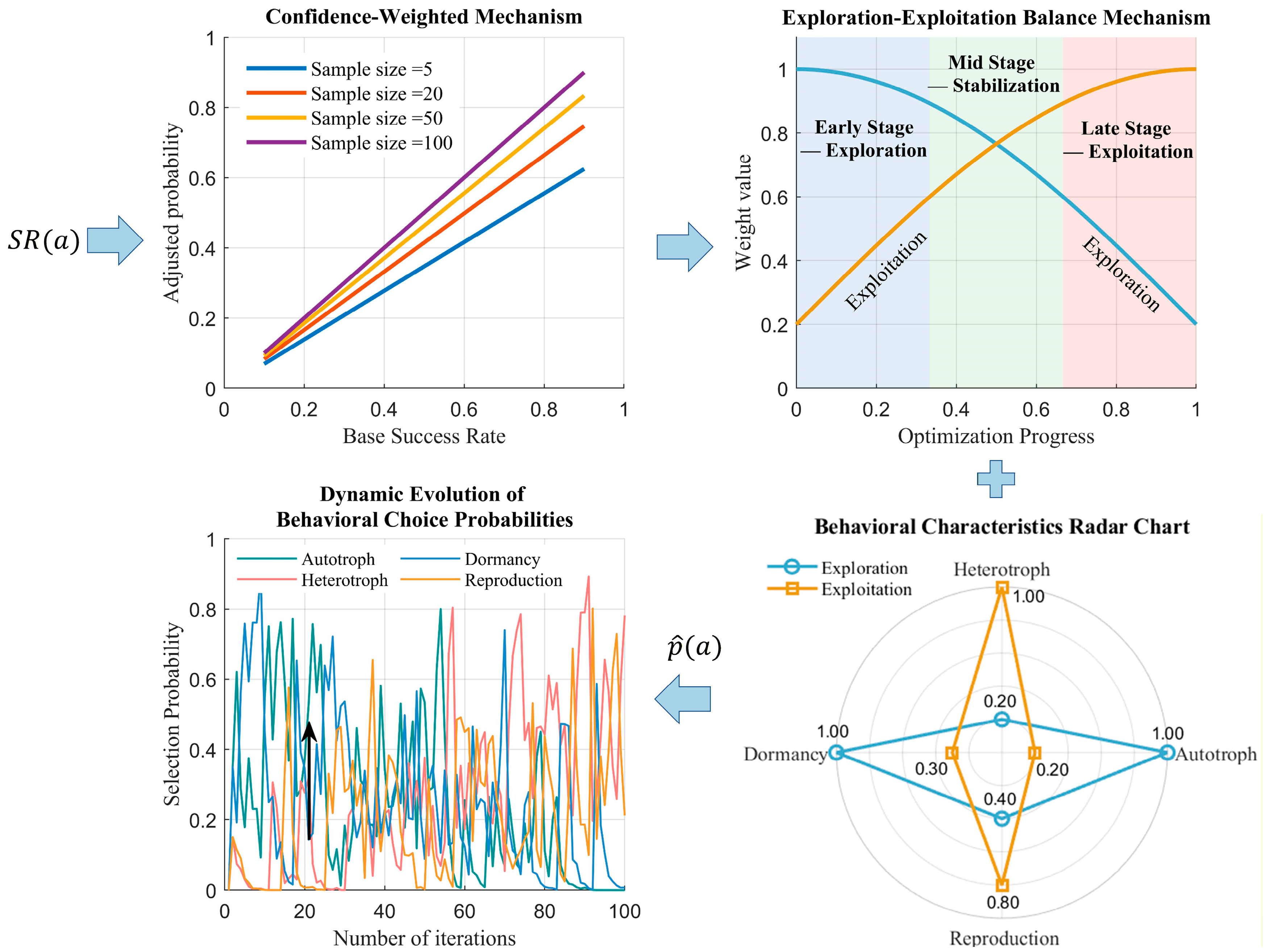
4.2. Behavioral Adaptive Selection Strategy Based on Historical Success
4.2.1. Historical Feedback Mechanism
4.2.2. Sample Confidence Mechanism
4.2.3. Adaptive Mechanism for Exploration/Exploitation Phases
4.2.4. Calculation of Combined Action Probability
4.2.5. Behavior Selection Mechanism
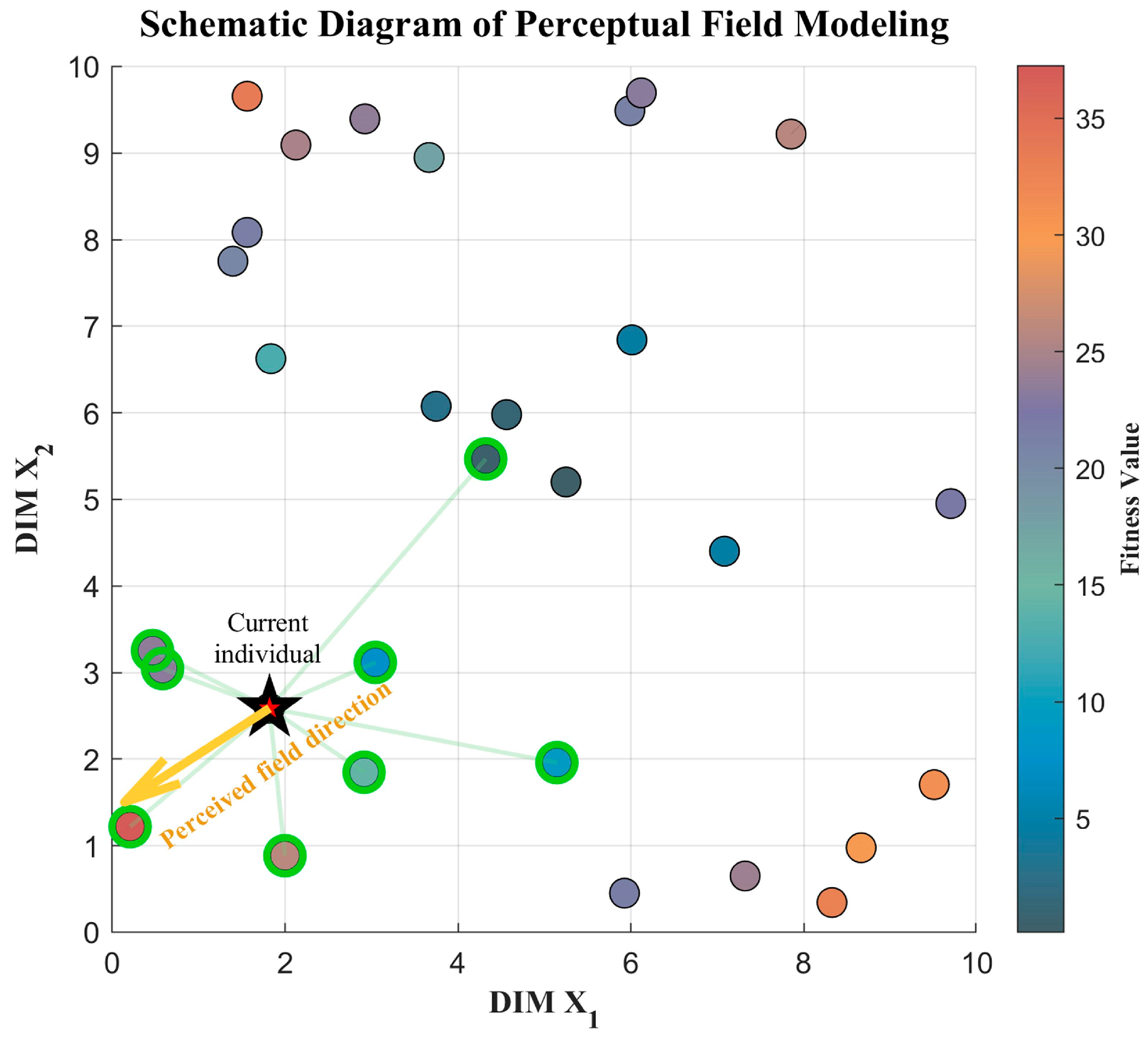
4.3. Environmental Structure Modeling Strategy Based on Sensory Field
4.4. Adaptive Hibernation Reconstruction Strategy
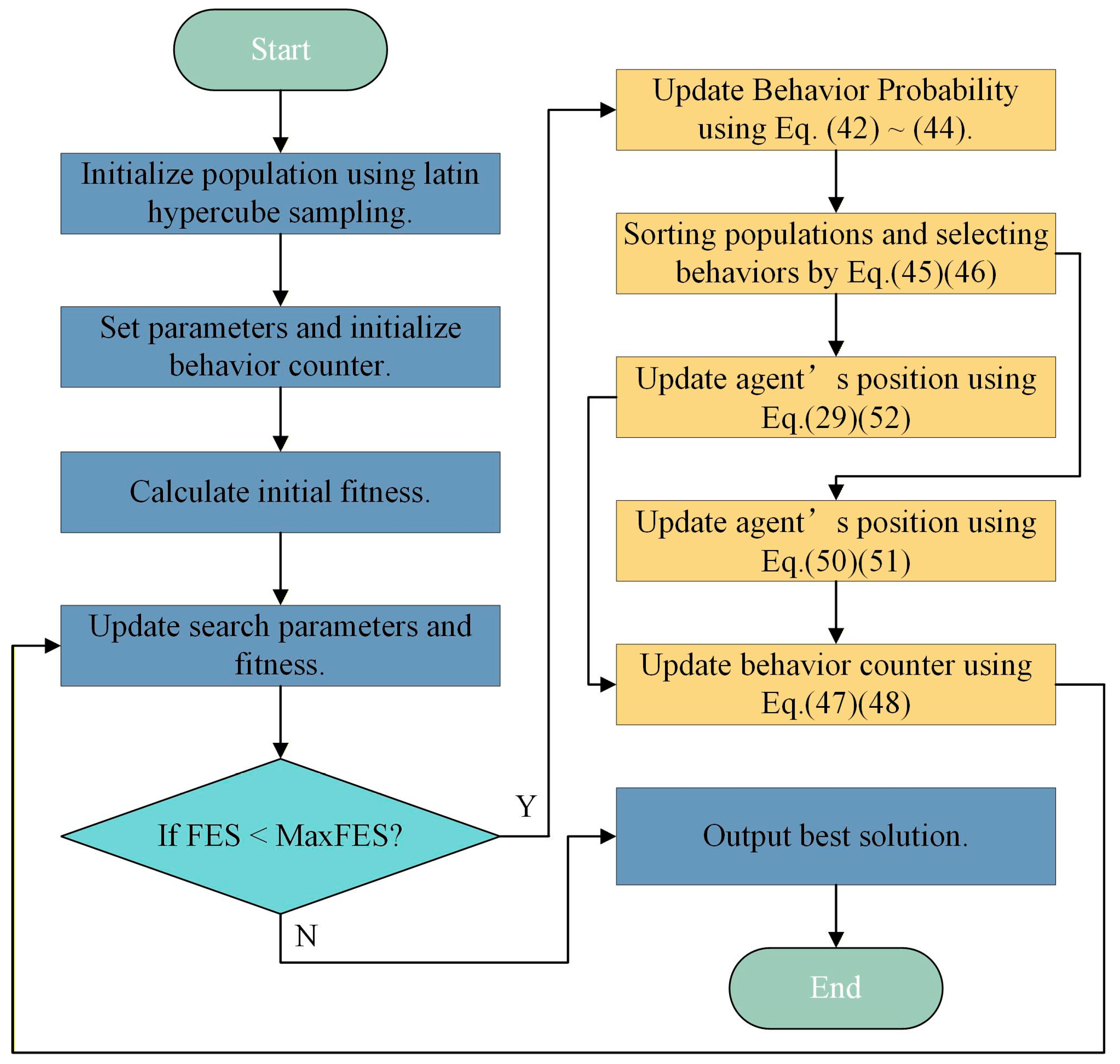
4.5. EAPO Algorithm Pseudocode and Flowchart
| Algorithm 1 Pseudocode for EAPO |
| Input: |
| Output: |
| Set Parameters: , , , |
| 1: Initialize population using Latin hypercube sampling and elite strategy. 2: Initialize behavior counter , . |
| do |
| using Equations (38) and (39). |
| = 1 to 4 do |
| then |
| using Equations (34), (36), (37) and (42). |
| 8: else |
| using Equation (43). |
| 10: end if |
| 11: end for |
| individuals. |
| do |
| then |
| ) using Equation (46). |
| then |
| using Equation (52). |
| 18: else |
| using Equation (29). |
| 20: end if |
| 21: else |
| , f using Equations (19), (49) and (52). |
| ) using Equation (45). |
| then |
| using Equation (50). |
| 26: else |
| using Equation (51). |
| 28: end if |
| if better solution found. |
| 30: end for |
| using Equations (47) and (48). |
| 32: end while |
| . |
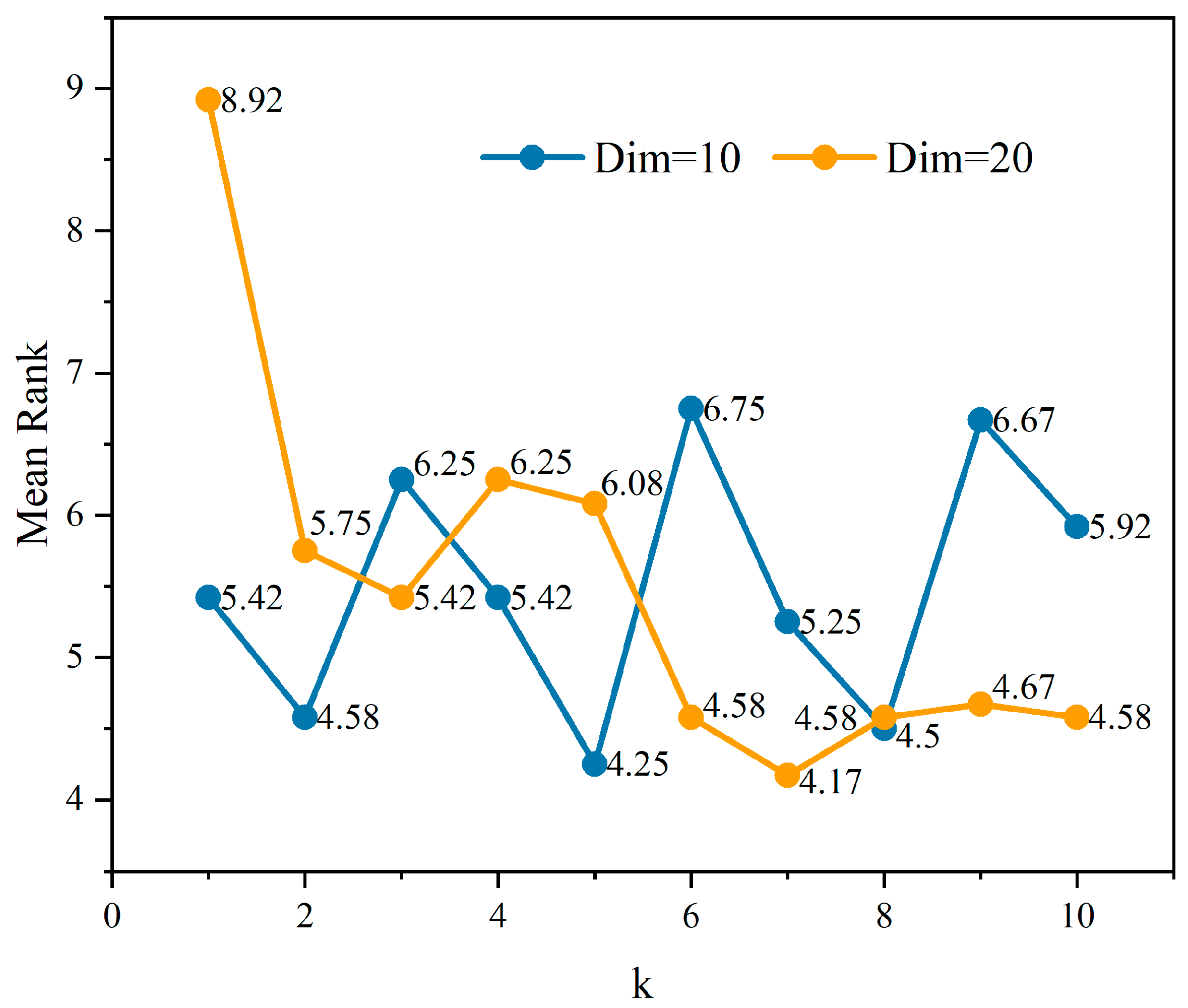
5. Parameter Sensitivity Analysis of EAPO
6. Algorithm Performance Testing and Analysis
6.1. Experimental Configuration
6.2. Ablation Experiment
6.3. Exploration and Exploitation Capability Analysis
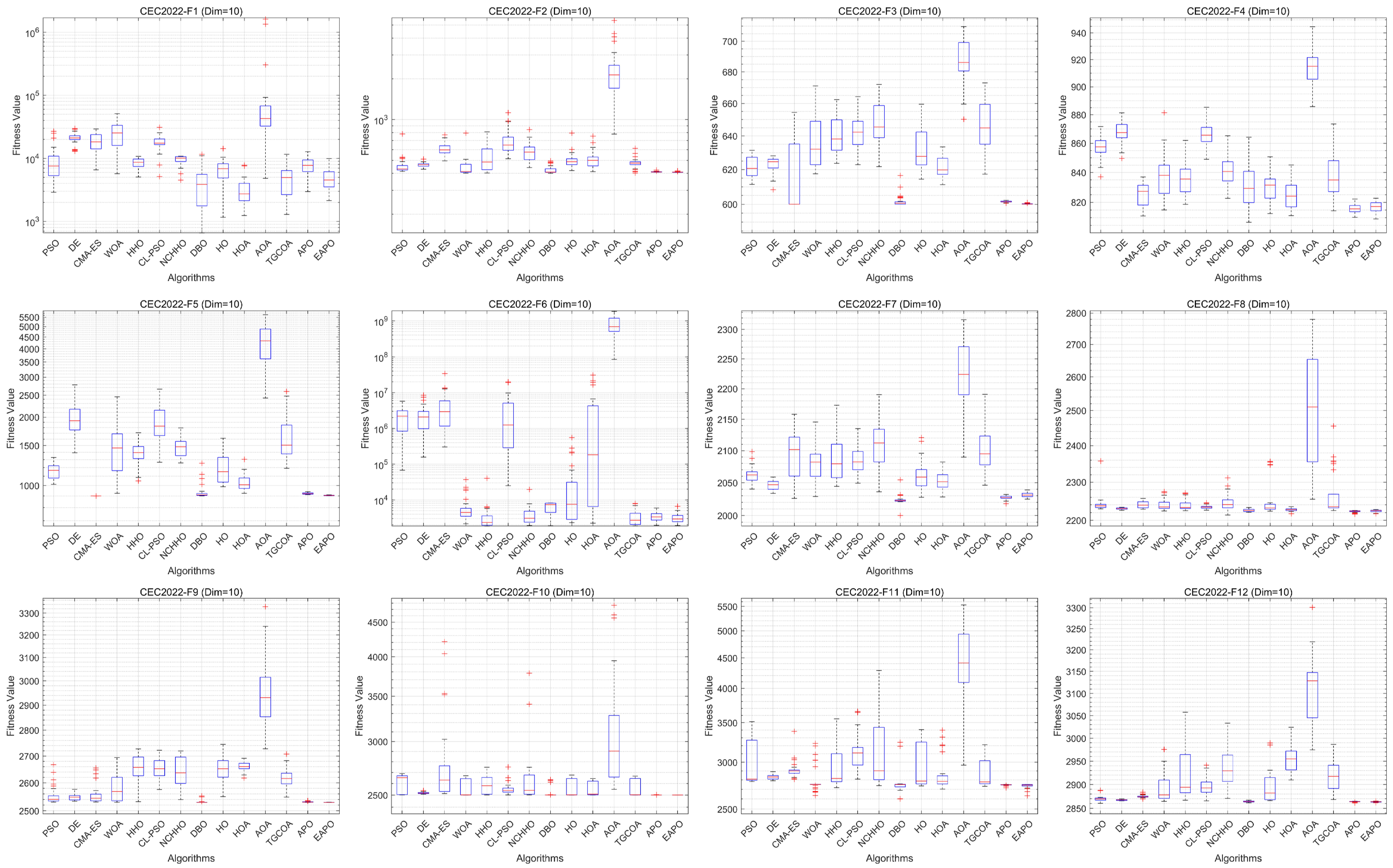
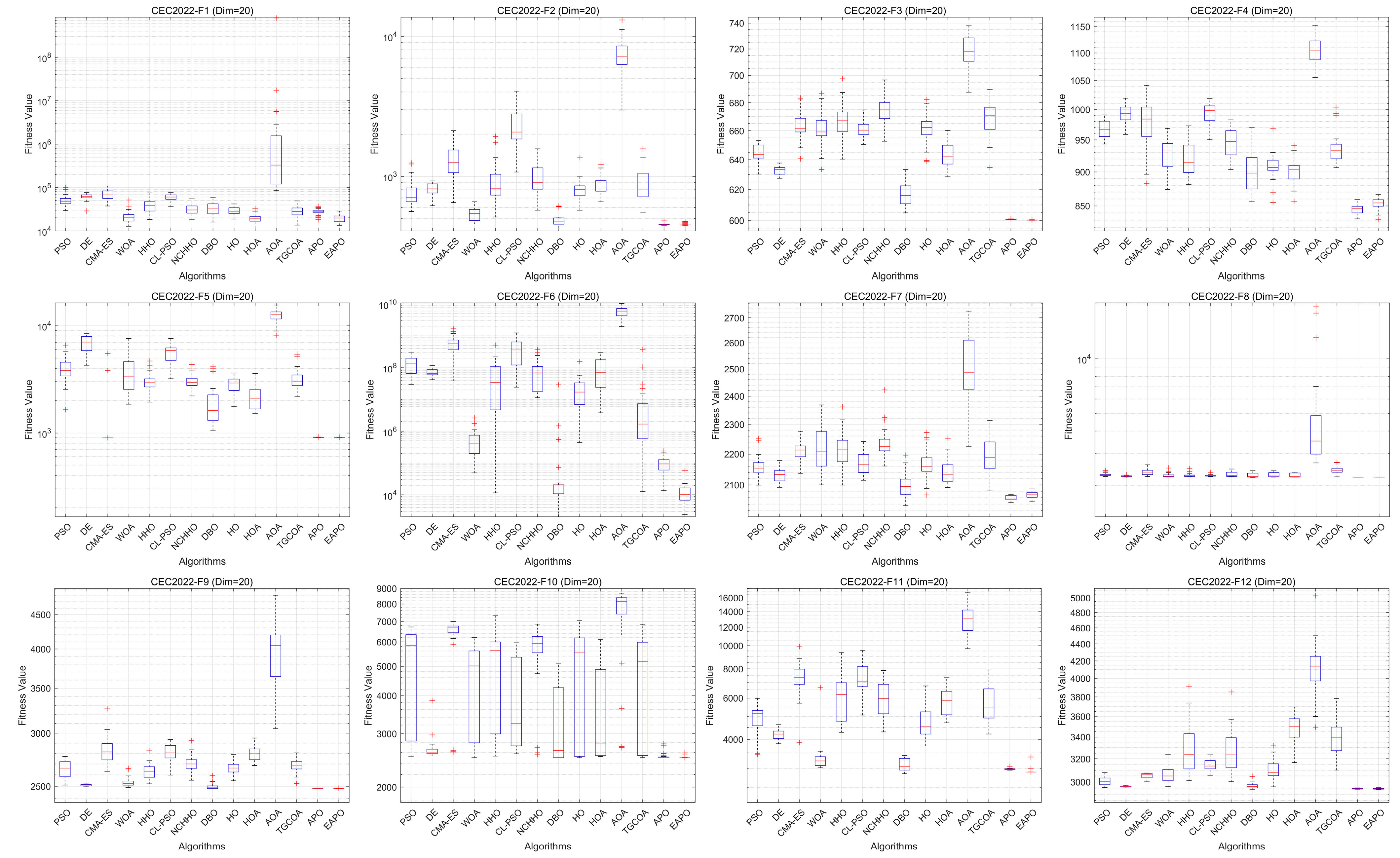
6.4. Testing on the CEC2022 Benchmark Suite
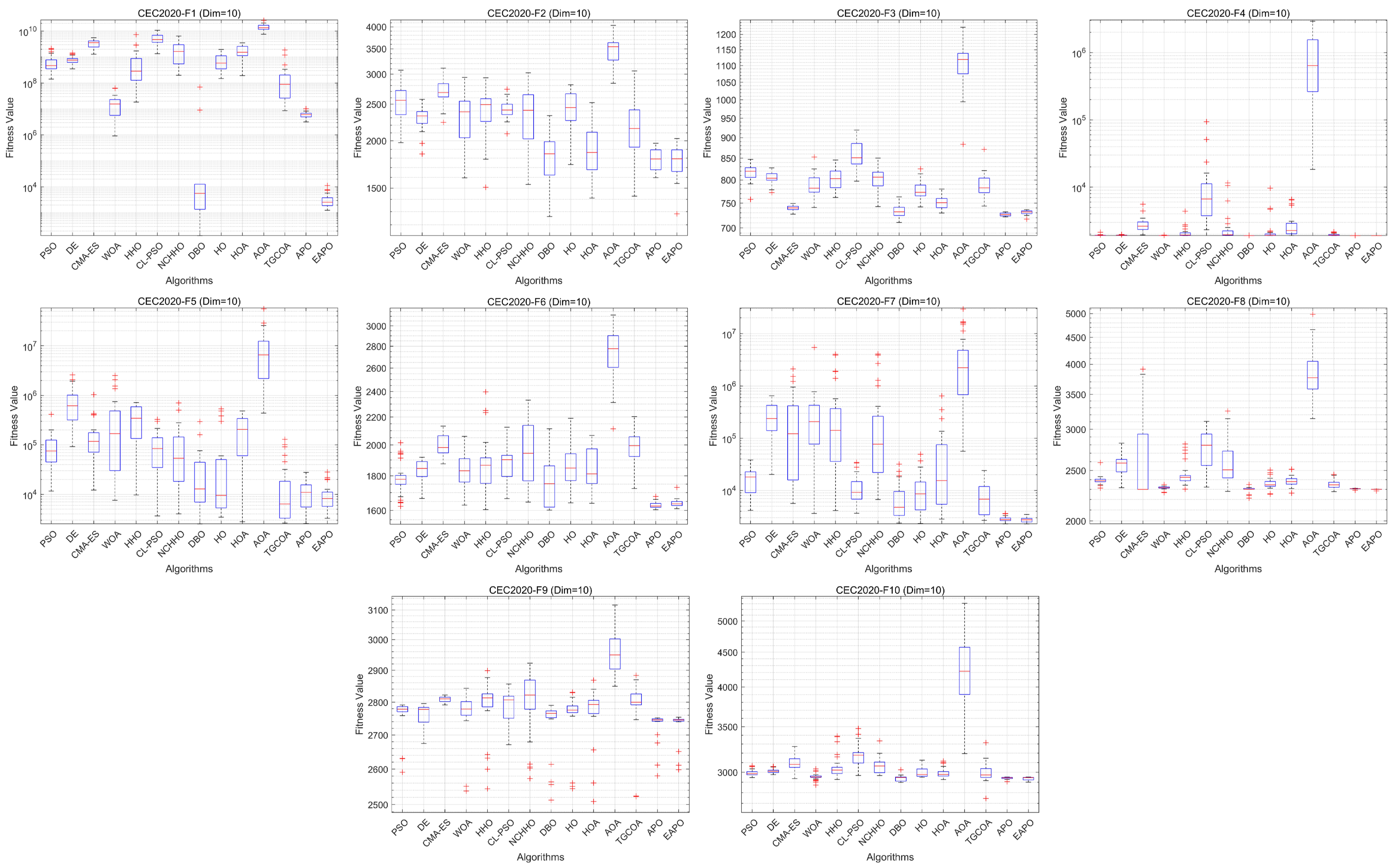
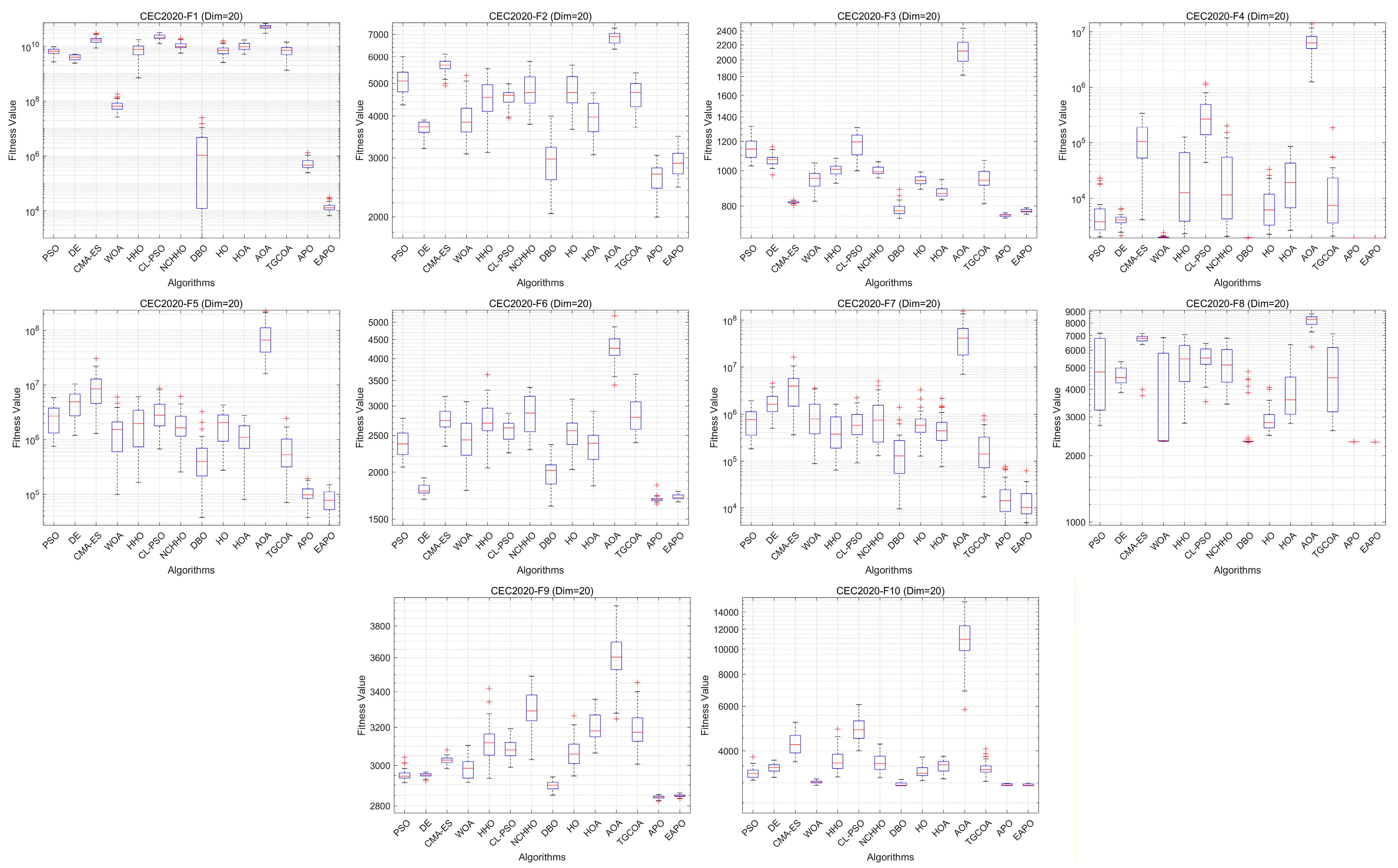
6.5. Testing on the CEC2020 Benchmark Suite
6.6. Testing and Analysis of Engineering Optimization Problems
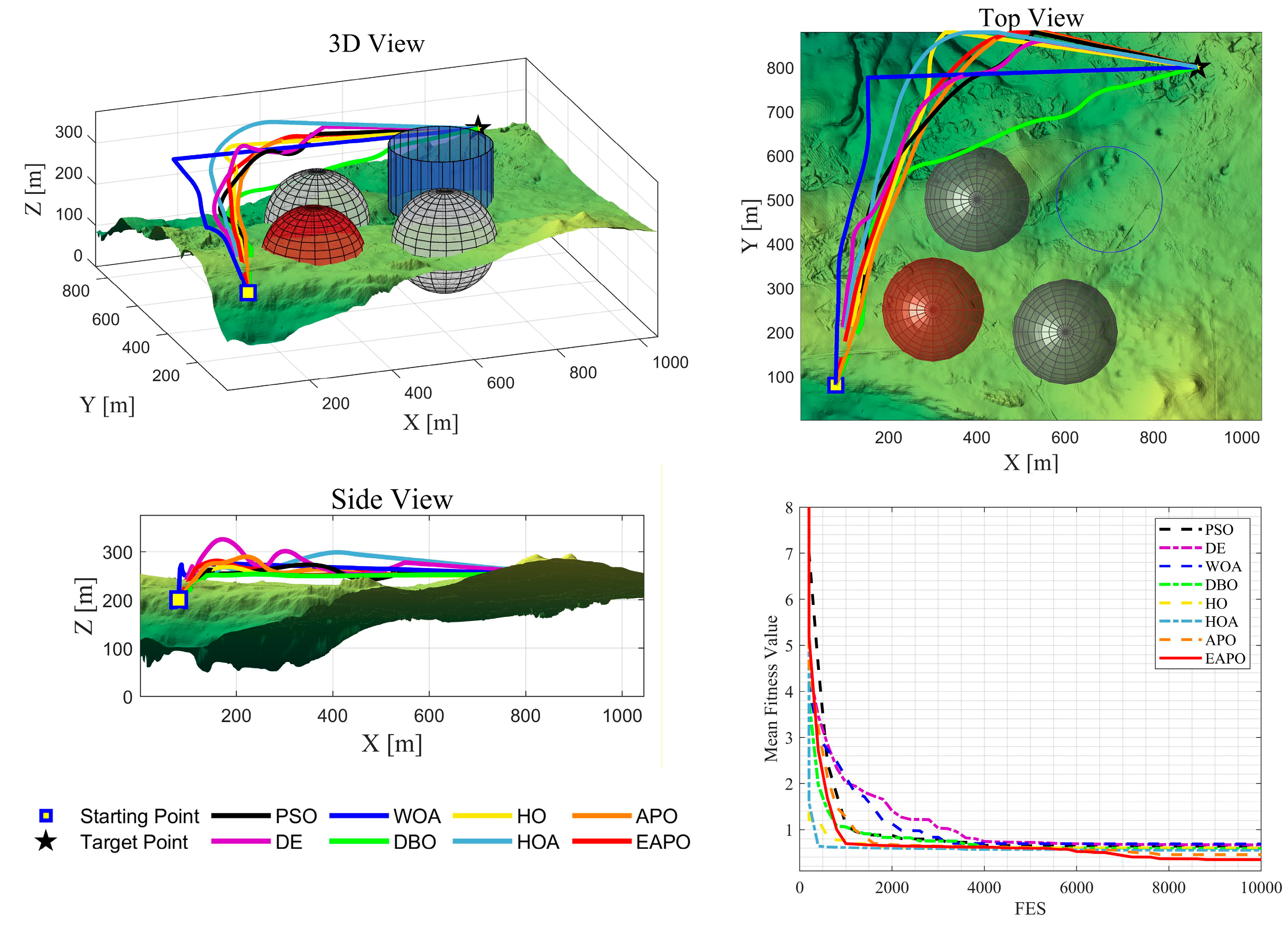
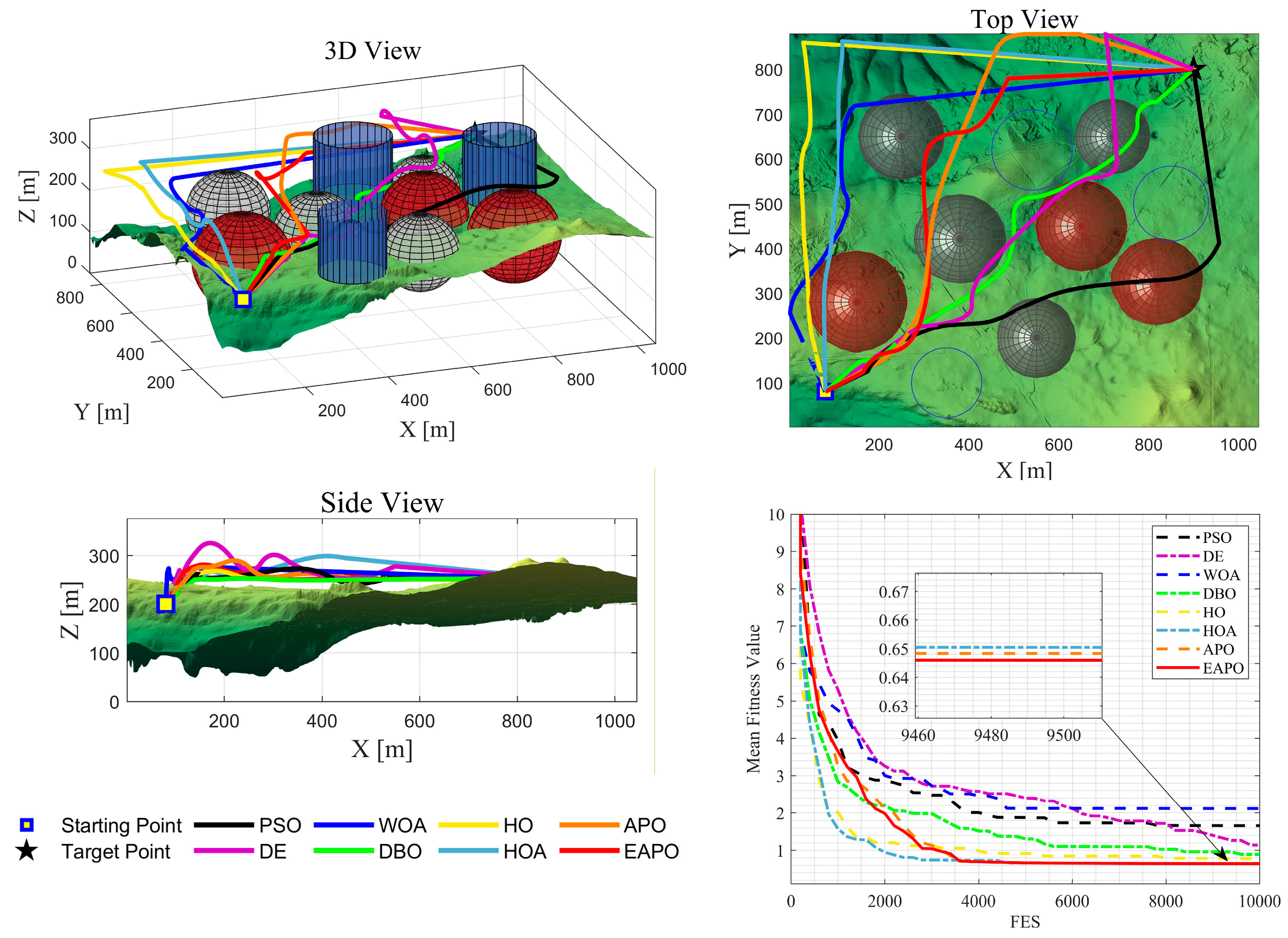
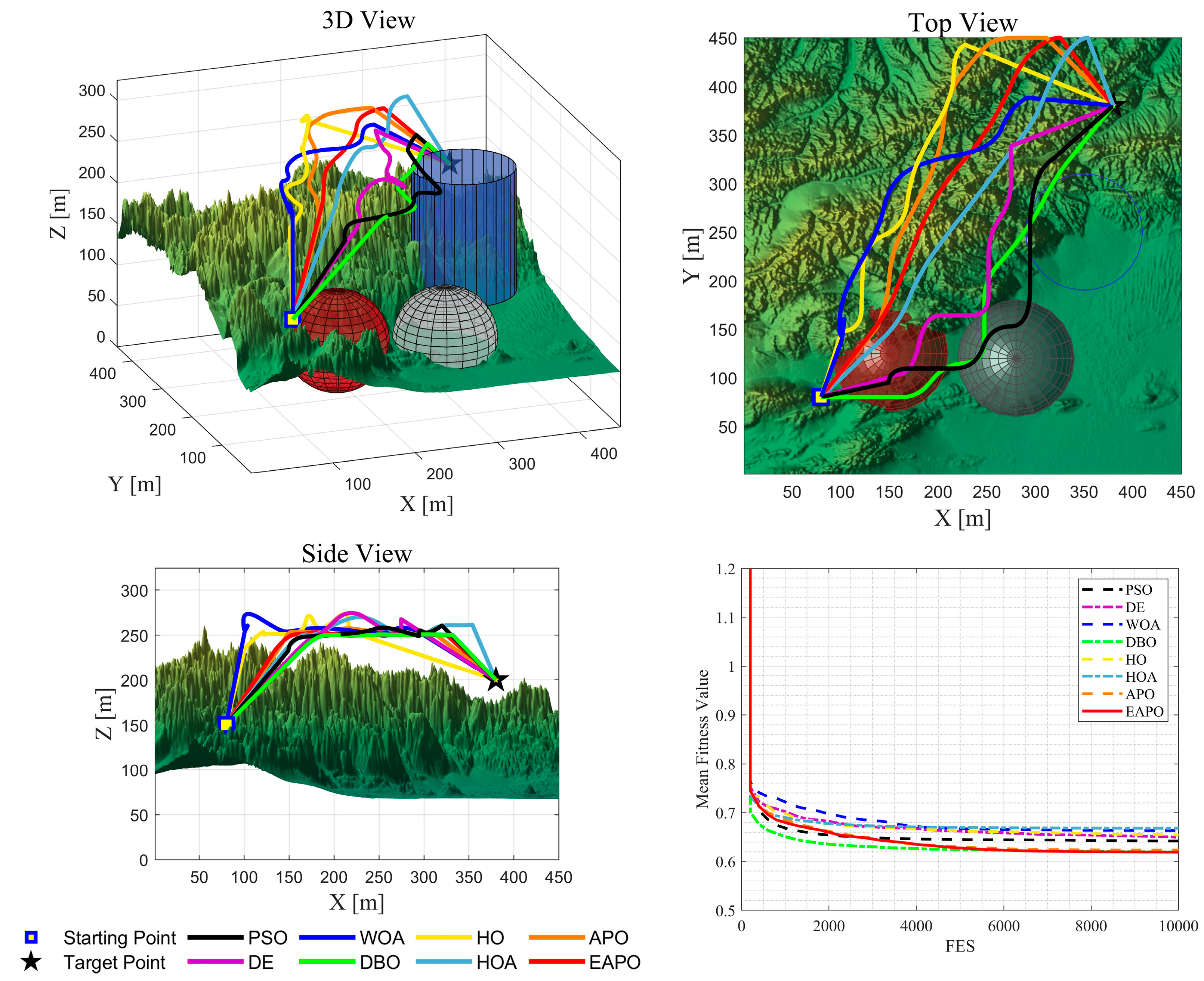
7. UAV Path Planning Simulation Experiment
7.1. Experimental Configuration for UAV Path Planning
7.2. Path Quality Evaluation Metrics
7.2.1. Path Length
7.2.2. Path Smoothness
7.2.3. Altitude Variation
7.2.4. Climb and Descent Angles
7.2.5. Threat Distance
7.2.6. Energy Consumption
7.3. Analysis of Experimental Results
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1
- Latin hypercube sampling initialization: The additional complexity introduced by occurs only during the initialization phase and is therefore negligible.
- Behavioral probability update based on historical success: . Negligible relative to the main loop.
- Environmental structure modeling based on perceptual fields: . Due to , the actual impact is relatively limited.
- Adaptive hibernation strategy: . With , the additional overhead is minimal.
Appendix A.2
| Type | No. | Functions | |
|---|---|---|---|
| Unimodal Functions | 1 | Shifted and full Rotated Zakharov Function | 300 |
| Basic Functions | 2 | Shifted and full Rotated Rosenbrock’s Function | 400 |
| 3 | Shifted and full Rotated Expanded Schaffer’s f6 Function | 600 | |
| 4 | Shifted and full Rotated Non-Continuous Rastrigin’s Function | 800 | |
| 5 | Shifted and full Rotated Levy Function | 900 | |
| Hybrid Functions | 6 | Hybrid Function 1 (N = 3) | 1800 |
| 7 | Hybrid Function 2 (N = 3) | 2000 | |
| 8 | Hybrid Function 3 (N = 3) | 2200 | |
| Composition Functions | 9 | Composition Function 1 (N = 3) | 2300 |
| 10 | Composition Function 2 (N = 4) | 2400 | |
| 11 | Composition Function 3 (N = 5) | 2600 | |
| 12 | Composition Function 4 (N = 6) | 2700 | |
| Type | No. | Functions | |
|---|---|---|---|
| Unimodal Functions | 1 | Shifted and Rotated Bent Cigar Function | 100 |
| Basic Functions | 2 | Shifted and Rotated Schwefel’s Function | 1100 |
| 3 | Shifted and Rotated Rastrigin’s Function | 700 | |
| 4 | Shifted and Rotated Lunacek bi-Rastrigin Function | 1900 | |
| Hybrid Functions | 5 | Hybrid Function 1 (N = 3) | 1700 |
| 6 | Hybrid Function 2 (N = 3) | 1600 | |
| 7 | Hybrid Function 3 (N = 3) | 2100 | |
| Composition Functions | 8 | Composition Function 1 (N = 3) | 2200 |
| 9 | Composition Function 2 (N = 4) | 2400 | |
| 10 | Composition Function 3 (N = 5) | 2500 | |
| No. | Name | ||||
|---|---|---|---|---|---|
| Industrial Chemical Processes | |||||
| RW01 | Heat Exchanger Network Design 2 | 11 | 0 | 9 | 7.049 × 103 |
| RW02 | Blending-Pooling-Separation problem | 38 | 0 | 32 | 1.864 × 100 |
| RW03 | Propane, Isobutane, n-Butane Non-sharp Separation | 48 | 0 | 38 | 2.116 × 100 |
| Process Synthesis and Design Problems | |||||
| RW04 | Process synthesis problem 2 | 7 | 9 | 0 | 2.925 × 100 |
| RW05 | Multi-product batch plant | 10 | 10 | 0 | 5.364 × 104 |
| Mechanical Engineering Problems | |||||
| RW06 | Optimal Design of Industrial refrigeration System | 14 | 15 | 0 | 3.221 × 10−2 |
| RW07 | Pressure vessel design | 4 | 4 | 0 | 5.885 × 103 |
| RW08 | Step-cone pulley problem | 5 | 8 | 3 | 1.607 × 101 |
| Livestock Feed Ration Optimization | |||||
| RW09 | Beef Cattle (case 1) | 59 | 14 | 1 | 4.551 × 103 |
| RW10 | Beef Cattle (case 2) | 59 | 14 | 1 | 3.349 × 103 |
Appendix B
| Function | Item Name | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | ||
| F1 | Best | 3.640 × 103 | 2.979 × 103 | 2.246 × 103 | 2.452 × 103 | 1.899 × 103 | 2.187 × 103 | 2.588 × 103 | 1.003 × 103 | 2.973 × 103 |
| Mean | 5.365 × 103 | 5.419 × 103 | 4.344 × 103 | 4.599 × 103 | 5.576 × 103 | 4.738 × 103 | 5.743 × 103 | 5.379 × 103 | 5.271 × 103 | |
| Std | 1.611 × 103 | 1.624 × 103 | 1.367 × 103 | 1.736 × 103 | 2.252 × 103 | 1.927 × 103 | 1.744 × 103 | 2.384 × 103 | 1.828 × 103 | |
| Rank | 2 | 3 | 1 | 8 | 7 | 5 | 9 | 6 | 4 | |
| F2 | Best | 4.070 × 102 | 4.069 × 102 | 4.071 × 102 | 4.068 × 102 | 4.071 × 102 | 4.072 × 102 | 4.071 × 102 | 4.070 × 102 | 4.070 × 102 |
| Mean | 4.085 × 102 | 4.083 × 102 | 4.083 × 102 | 4.084 × 102 | 4.094 × 102 | 4.113 × 102 | 4.090 × 102 | 4.087 × 102 | 4.109 × 102 | |
| Std | 1.453 × 100 | 1.248 × 100 | 9.623 × 10−1 | 1.151 × 100 | 2.393 × 100 | 1.018 × 101 | 1.272 × 100 | 1.125 × 100 | 7.269 × 100 | |
| Rank | 8 | 2 | 4 | 3 | 6 | 1 | 7 | 5 | 9 | |
| F3 | Best | 6.000 × 102 | 6.000 × 102 | 6.000 × 102 | 6.000 × 102 | 6.000 × 102 | 6.000 × 102 | 6.000 × 102 | 6.000 × 102 | 6.000 × 102 |
| Mean | 6.002 × 102 | 6.002 × 102 | 6.002 × 102 | 6.001 × 102 | 6.002 × 102 | 6.002 × 102 | 6.003 × 102 | 6.004 × 102 | 6.005 × 102 | |
| Std | 1.751 × 10−1 | 1.833 × 10−1 | 2.374 × 10−1 | 1.000 × 10−1 | 1.840 × 10−1 | 2.197 × 10−1 | 3.171 × 10−1 | 3.620 × 10−1 | 4.053 × 10−1 | |
| Rank | 2 | 1 | 7 | 5 | 3 | 4 | 6 | 9 | 8 | |
| F4 | Best | 8.088 × 102 | 8.116 × 102 | 8.110 × 102 | 8.083 × 102 | 8.112 × 102 | 8.108 × 102 | 8.116 × 102 | 8.137 × 102 | 8.076 × 102 |
| Mean | 8.160 × 102 | 8.174 × 102 | 8.181 × 102 | 8.154 × 102 | 8.160 × 102 | 8.166 × 102 | 8.175 × 102 | 8.179 × 102 | 8.171 × 102 | |
| Std | 4.376 × 100 | 3.710 × 100 | 3.838 × 100 | 4.165 × 100 | 2.917 × 100 | 3.642 × 100 | 3.905 × 100 | 2.496 × 100 | 3.622 × 100 | |
| Rank | 4 | 1 | 9 | 7 | 2 | 3 | 5 | 8 | 6 | |
| F5 | Best | 9.010 × 102 | 9.009 × 102 | 9.011 × 102 | 9.003 × 102 | 9.005 × 102 | 9.008 × 102 | 9.018 × 102 | 9.009 × 102 | 9.020 × 102 |
| Mean | 9.056 × 102 | 9.042 × 102 | 9.042 × 102 | 9.036 × 102 | 9.041 × 102 | 9.046 × 102 | 9.054 × 102 | 9.057 × 102 | 9.069 × 102 | |
| Std | 3.460 × 100 | 2.349 × 100 | 3.087 × 100 | 2.705 × 100 | 2.268 × 100 | 2.661 × 100 | 3.416 × 100 | 3.560 × 100 | 3.977 × 100 | |
| Rank | 3 | 2 | 1 | 4 | 5 | 7 | 6 | 8 | 9 | |
| F6 | Best | 2.177 × 103 | 1.998 × 103 | 1.942 × 103 | 1.963 × 103 | 2.032 × 103 | 2.192 × 103 | 2.066 × 103 | 2.353 × 103 | 2.018 × 103 |
| Mean | 3.054 × 103 | 2.717 × 103 | 2.796 × 103 | 3.019 × 103 | 3.412 × 103 | 3.139 × 103 | 3.173 × 103 | 3.383 × 103 | 3.343 × 103 | |
| Std | 8.711 × 102 | 6.923 × 102 | 6.287 × 102 | 8.537 × 102 | 1.334 × 103 | 9.945 × 102 | 7.738 × 102 | 7.866 × 102 | 9.896 × 102 | |
| Rank | 6 | 3 | 2 | 1 | 7 | 4 | 5 | 9 | 8 | |
| F7 | Best | 2.025 × 103 | 2.023 × 103 | 2.025 × 103 | 2.015 × 103 | 2.017 × 103 | 2.025 × 103 | 2.025 × 103 | 2.023 × 103 | 2.026 × 103 |
| Mean | 2.030 × 103 | 2.031 × 103 | 2.031 × 103 | 2.029 × 103 | 2.032 × 103 | 2.032 × 103 | 2.031 × 103 | 2.032 × 103 | 2.031 × 103 | |
| Std | 3.768 × 100 | 4.223 × 100 | 3.444 × 100 | 4.787 × 100 | 4.728 × 100 | 4.068 × 100 | 2.963 × 100 | 3.152 × 100 | 3.339 × 100 | |
| Rank | 6 | 2 | 3 | 4 | 8 | 1 | 5 | 9 | 7 | |
| F8 | Best | 2.224 × 103 | 2.213 × 103 | 2.215 × 103 | 2.217 × 103 | 2.215 × 103 | 2.217 × 103 | 2.215 × 103 | 2.217 × 103 | 2.221 × 103 |
| Mean | 2.226 × 103 | 2.224 × 103 | 2.225 × 103 | 2.223 × 103 | 2.224 × 103 | 2.224 × 103 | 2.224 × 103 | 2.224 × 103 | 2.225 × 103 | |
| Std | 1.022 × 100 | 3.216 × 100 | 2.679 × 100 | 2.950 × 100 | 2.519 × 100 | 2.673 × 100 | 2.730 × 100 | 2.670 × 100 | 1.655 × 100 | |
| Rank | 2 | 1 | 6 | 7 | 5 | 9 | 4 | 3 | 8 | |
| F9 | Best | 2.529 × 103 | 2.529 × 103 | 2.529 × 103 | 2.529 × 103 | 2.529 × 103 | 2.529 × 103 | 2.529 × 103 | 2.529 × 103 | 2.529 × 103 |
| Mean | 2.530 × 103 | 2.530 × 103 | 2.530 × 103 | 2.530 × 103 | 2.530 × 103 | 2.530 × 103 | 2.530 × 103 | 2.531 × 103 | 2.530 × 103 | |
| Std | 3.514 × 10−1 | 1.227 × 100 | 1.063 × 100 | 6.917 × 10−1 | 4.754 × 10−1 | 1.342 × 100 | 1.370 × 100 | 2.200 × 100 | 4.480 × 10−1 | |
| Rank | 2 | 4 | 3 | 6 | 1 | 5 | 7 | 8 | 9 | |
| F10 | Best | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 |
| Mean | 2.502 × 103 | 2.501 × 103 | 2.501 × 103 | 2.501 × 103 | 2.500 × 103 | 2.506 × 103 | 2.500 × 103 | 2.500 × 103 | 2.501 × 103 | |
| Std | 4.413 × 100 | 6.506 × 10−1 | 1.578 × 100 | 4.345 × 100 | 7.847 × 10−2 | 2.566 × 101 | 5.978 × 10−2 | 1.105 × 10−1 | 1.522 × 100 | |
| Rank | 8 | 3 | 9 | 4 | 5 | 7 | 2 | 6 | 1 | |
| F11 | Best | 2.716 × 103 | 2.696 × 103 | 2.660 × 103 | 2.683 × 103 | 2.647 × 103 | 2.722 × 103 | 2.666 × 103 | 2.655 × 103 | 2.675 × 103 |
| Mean | 2.738 × 103 | 2.739 × 103 | 2.739 × 103 | 2.730 × 103 | 2.727 × 103 | 2.739 × 103 | 2.734 × 103 | 2.735 × 103 | 2.736 × 103 | |
| Std | 1.215 × 101 | 1.457 × 101 | 2.229 × 101 | 2.270 × 101 | 3.000 × 101 | 9.953 × 100 | 1.942 × 101 | 2.292 × 101 | 2.045 × 101 | |
| Rank | 4 | 3 | 9 | 5 | 1 | 7 | 2 | 6 | 8 | |
| F12 | Best | 2.860 × 103 | 2.862 × 103 | 2.860 × 103 | 2.862 × 103 | 2.860 × 103 | 2.862 × 103 | 2.859 × 103 | 2.862 × 103 | 2.862 × 103 |
| Mean | 2.864 × 103 | 2.864 × 103 | 2.864 × 103 | 2.863 × 103 | 2.864 × 103 | 2.864 × 103 | 2.863 × 103 | 2.864 × 103 | 2.863 × 103 | |
| Std | 1.027 × 100 | 9.228 × 10−1 | 1.201 × 100 | 7.583 × 10−1 | 1.329 × 100 | 6.742 × 10−1 | 1.362 × 100 | 6.663 × 10−1 | 5.828 × 10−1 | |
| Rank | 4 | 1 | 6 | 8 | 7 | 9 | 2 | 5 | 3 | |
| Mean Rank | 4.25 | 2.17 | 5 | 5.17 | 4.75 | 5.17 | 5 | 6.83 | 6.67 | |
| Function | Item Name | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | ||
| F1 | Best | 1.454 × 104 | 1.155 × 104 | 1.258 × 104 | 1.440 × 104 | 1.574 × 104 | 1.179 × 104 | 1.535 × 104 | 1.626 × 104 | 1.531 × 104 |
| Mean | 2.262 × 104 | 2.233 × 104 | 1.819 × 104 | 2.092 × 104 | 1.904 × 104 | 1.568 × 104 | 2.250 × 104 | 2.572 × 104 | 2.545 × 104 | |
| Std | 8.043 × 103 | 9.517 × 103 | 2.546 × 103 | 5.583 × 103 | 3.031 × 103 | 2.439 × 103 | 5.362 × 103 | 5.489 × 103 | 4.472 × 103 | |
| Rank | 6 | 5 | 2 | 4 | 3 | 1 | 7 | 9 | 8 | |
| F2 | Best | 4.449 × 102 | 4.491 × 102 | 4.491 × 102 | 4.453 × 102 | 4.491 × 102 | 4.423 × 102 | 4.491 × 102 | 4.491 × 102 | 4.491 × 102 |
| Mean | 4.517 × 102 | 4.555 × 102 | 4.508 × 102 | 4.537 × 102 | 4.516 × 102 | 4.497 × 102 | 4.540 × 102 | 4.527 × 102 | 4.518 × 102 | |
| Std | 6.395 × 100 | 1.024 × 101 | 2.767 × 100 | 8.569 × 100 | 7.301 × 100 | 4.496 × 100 | 7.587 × 100 | 7.812 × 100 | 7.323 × 100 | |
| Rank | 1 | 8 | 5 | 7 | 3 | 2 | 9 | 6 | 4 | |
| F3 | Best | 6.001 × 102 | 6.001 × 102 | 6.001 × 102 | 6.001 × 102 | 6.001 × 102 | 6.001 × 102 | 6.001 × 102 | 6.001 × 102 | 6.001 × 102 |
| Mean | 6.002 × 102 | 6.002 × 102 | 6.002 × 102 | 6.002 × 102 | 6.002 × 102 | 6.002 × 102 | 6.003 × 102 | 6.002 × 102 | 6.003 × 102 | |
| Std | 1.077 × 10−1 | 7.721 × 10−2 | 8.023 × 10−2 | 8.878 × 10−2 | 1.337 × 10−1 | 7.131 × 10−2 | 2.319 × 10−1 | 7.130 × 10−2 | 1.528 × 10−1 | |
| Rank | 7 | 3 | 4 | 2 | 6 | 1 | 8 | 5 | 9 | |
| F4 | Best | 8.392 × 102 | 8.460 × 102 | 8.542 × 102 | 8.469 × 102 | 8.451 × 102 | 8.463 × 102 | 8.457 × 102 | 8.468 × 102 | 8.462 × 102 |
| Mean | 8.528 × 102 | 8.556 × 102 | 8.573 × 102 | 8.545 × 102 | 8.573 × 102 | 8.546 × 102 | 8.569 × 102 | 8.532 × 102 | 8.550 × 102 | |
| Std | 8.538 × 100 | 6.799 × 100 | 2.475 × 100 | 8.171 × 100 | 6.573 × 100 | 6.112 × 100 | 5.521 × 100 | 5.115 × 100 | 7.660 × 100 | |
| Rank | 5 | 6 | 9 | 2 | 7 | 4 | 8 | 1 | 3 | |
| F5 | Best | 9.000 × 102 | 9.001 × 102 | 9.005 × 102 | 9.000 × 102 | 9.003 × 102 | 9.000 × 102 | 9.006 × 102 | 9.000 × 102 | 9.000 × 102 |
| Mean | 9.017 × 102 | 9.009 × 102 | 9.028 × 102 | 9.053 × 102 | 9.019 × 102 | 9.019 × 102 | 9.032 × 102 | 9.016 × 102 | 9.012 × 102 | |
| Std | 2.414 × 100 | 7.856 × 10−1 | 2.713 × 100 | 6.173 × 100 | 1.541 × 100 | 2.965 × 100 | 4.780 × 100 | 1.454 × 100 | 1.051 × 100 | |
| Rank | 4 | 1 | 9 | 7 | 6 | 3 | 8 | 5 | 2 | |
| F6 | Best | 5.252 × 103 | 3.185 × 103 | 3.493 × 103 | 2.360 × 103 | 5.564 × 103 | 3.745 × 103 | 6.716 × 103 | 3.330 × 103 | 4.982 × 103 |
| Mean | 9.018 × 103 | 7.781 × 103 | 1.126 × 104 | 8.838 × 103 | 1.319 × 104 | 9.031 × 103 | 2.244 × 104 | 2.035 × 104 | 1.823 × 104 | |
| Std | 3.432 × 103 | 4.294 × 103 | 7.965 × 103 | 5.657 × 103 | 5.972 × 103 | 3.573 × 103 | 2.047 × 104 | 1.327 × 104 | 1.009 × 104 | |
| Rank | 3 | 1 | 4 | 2 | 6 | 5 | 9 | 7 | 8 | |
| F7 | Best | 2.048 × 103 | 2.052 × 103 | 2.047 × 103 | 2.055 × 103 | 2.042 × 103 | 2.046 × 103 | 2.054 × 103 | 2.044 × 103 | 2.051 × 103 |
| Mean | 2.065 × 103 | 2.072 × 103 | 2.067 × 103 | 2.070 × 103 | 2.067 × 103 | 2.062 × 103 | 2.067 × 103 | 2.068 × 103 | 2.063 × 103 | |
| Std | 8.660 × 100 | 1.134 × 101 | 1.009 × 101 | 1.018 × 101 | 1.183 × 101 | 1.031 × 101 | 9.601 × 100 | 9.835 × 100 | 7.442 × 100 | |
| Rank | 3 | 9 | 6 | 8 | 5 | 1 | 4 | 7 | 2 | |
| F8 | Best | 2.228 × 103 | 2.227 × 103 | 2.227 × 103 | 2.229 × 103 | 2.227 × 103 | 2.228 × 103 | 2.227 × 103 | 2.227 × 103 | 2.228 × 103 |
| Mean | 2.230 × 103 | 2.230 × 103 | 2.230 × 103 | 2.230 × 103 | 2.230 × 103 | 2.230 × 103 | 2.229 × 103 | 2.230 × 103 | 2.230 × 103 | |
| Std | 1.030 × 100 | 1.176 × 100 | 1.721 × 100 | 8.783 × 10−1 | 2.234 × 100 | 1.214 × 100 | 1.600 × 100 | 1.729 × 100 | 1.498 × 100 | |
| Rank | 9 | 1 | 6 | 3 | 5 | 4 | 2 | 7 | 8 | |
| F9 | Best | 2.481 × 103 | 2.481 × 103 | 2.481 × 103 | 2.481 × 103 | 2.481 × 103 | 2.481 × 103 | 2.481 × 103 | 2.481 × 103 | 2.481 × 103 |
| Mean | 2.482 × 103 | 2.481 × 103 | 2.481 × 103 | 2.481 × 103 | 2.481 × 103 | 2.481 × 103 | 2.481 × 103 | 2.482 × 103 | 2.481 × 103 | |
| Std | 7.970 × 10−1 | 3.344 × 10−1 | 1.347 × 10−1 | 3.013 × 10−1 | 6.915 × 10−1 | 3.124 × 10−1 | 6.724 × 10−1 | 1.116 × 100 | 6.122 × 10−1 | |
| Rank | 9 | 5 | 1 | 3 | 8 | 2 | 4 | 6 | 7 | |
| F10 | Best | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.501 × 103 | 2.500 × 103 | 2.500 × 103 |
| Mean | 2.521 × 103 | 2.501 × 103 | 2.501 × 103 | 2.750 × 103 | 2.504 × 103 | 2.518 × 103 | 2.534 × 103 | 2.501 × 103 | 2.511 × 103 | |
| Std | 5.197 × 101 | 7.140 × 10−2 | 5.893 × 10−2 | 5.266 × 102 | 1.064 × 101 | 5.544 × 101 | 6.802 × 101 | 7.363 × 10−2 | 3.372 × 101 | |
| Rank | 6 | 1 | 5 | 4 | 7 | 2 | 9 | 3 | 8 | |
| F11 | Best | 2.901 × 103 | 2.901 × 103 | 2.902 × 103 | 2.901 × 103 | 2.738 × 103 | 2.901 × 103 | 2.901 × 103 | 2.902 × 103 | 2.901 × 103 |
| Mean | 2.902 × 103 | 2.902 × 103 | 2.942 × 103 | 2.902 × 103 | 2.886 × 103 | 2.938 × 103 | 2.902 × 103 | 2.942 × 103 | 2.973 × 103 | |
| Std | 3.703 × 10−1 | 2.481 × 10−1 | 1.246 × 102 | 7.237 × 10−1 | 5.203 × 101 | 1.134 × 102 | 4.294 × 10−1 | 1.248 × 102 | 1.516 × 102 | |
| Rank | 1 | 2 | 7 | 5 | 4 | 6 | 3 | 8 | 9 | |
| F12 | Best | 2.941 × 103 | 2.939 × 103 | 2.936 × 103 | 2.939 × 103 | 2.939 × 103 | 2.940 × 103 | 2.938 × 103 | 2.940 × 103 | 2.941 × 103 |
| Mean | 2.945 × 103 | 2.944 × 103 | 2.946 × 103 | 2.945 × 103 | 2.945 × 103 | 2.943 × 103 | 2.944 × 103 | 2.945 × 103 | 2.945 × 103 | |
| Std | 3.393 × 100 | 2.125 × 100 | 7.639 × 100 | 3.704 × 100 | 3.551 × 100 | 2.440 × 100 | 3.718 × 100 | 4.017 × 100 | 2.629 × 100 | |
| Rank | 3 | 4 | 7 | 8 | 9 | 1 | 2 | 5 | 6 | |
| Mean Rank | 4.75 | 3.83 | 5.42 | 4.58 | 5.75 | 2.67 | 6.08 | 5.75 | 6.17 | |
| Function | Item Name | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| F1 | Best | 3.128 × 103 | 2.559 × 103 | 3.674 × 103 | 2.096 × 103 | 4.632 × 103 | 3.356 × 103 | 3.700 × 103 | 3.433 × 103 | 3.954 × 103 | 2.599 × 103 |
| Mean | 5.458 × 103 | 3.985 × 103 | 5.114 × 103 | 4.894 × 103 | 6.058 × 103 | 6.273 × 103 | 5.865 × 103 | 5.272 × 103 | 6.151 × 103 | 4.610 × 103 | |
| Std | 1.946 × 103 | 1.025 × 103 | 1.541 × 103 | 1.696 × 103 | 1.177 × 103 | 2.071 × 103 | 1.248 × 103 | 1.002 × 103 | 1.779 × 103 | 1.707 × 103 | |
| Rank | 6 | 1 | 4 | 3 | 7 | 10 | 8 | 5 | 9 | 2 | |
| F2 | Best | 4.073 × 102 | 4.072 × 102 | 4.075 × 102 | 4.074 × 102 | 4.056 × 102 | 4.073 × 102 | 4.072 × 102 | 4.072 × 102 | 4.072 × 102 | 4.075 × 102 |
| Mean | 4.084 × 102 | 4.080 × 102 | 4.096 × 102 | 4.100 × 102 | 4.094 × 102 | 4.089 × 102 | 4.087 × 102 | 4.088 × 102 | 4.083 × 102 | 4.091 × 102 | |
| Std | 9.251 × 10−1 | 1.006 × 100 | 2.952 × 100 | 3.695 × 100 | 3.798 × 100 | 9.312 × 10−1 | 9.228 × 10−1 | 9.202 × 10−1 | 9.169 × 10−1 | 7.495 × 10−1 | |
| Rank | 4 | 1 | 7 | 10 | 5 | 8 | 3 | 6 | 2 | 9 | |
| F3 | Best | 6.002 × 102 | 6.001 × 102 | 6.001 × 102 | 6.001 × 102 | 6.000 × 102 | 6.000 × 102 | 6.001 × 102 | 6.000 × 102 | 6.000 × 102 | 6.000 × 102 |
| Mean | 6.005 × 102 | 6.004 × 102 | 6.004 × 102 | 6.003 × 102 | 6.003 × 102 | 6.003 × 102 | 6.003 × 102 | 6.004 × 102 | 6.003 × 102 | 6.001 × 102 | |
| Std | 2.410 × 10−1 | 3.504 × 10−1 | 2.801 × 10−1 | 1.990 × 10−1 | 1.952 × 10−1 | 2.656 × 10−1 | 3.714 × 10−1 | 3.445 × 10−1 | 2.673 × 10−1 | 1.850 × 10−1 | |
| Rank | 10 | 9 | 8 | 4 | 6 | 2 | 5 | 7 | 3 | 1 | |
| F4 | Best | 8.114 × 102 | 8.089 × 102 | 8.097 × 102 | 8.154 × 102 | 8.121 × 102 | 8.137 × 102 | 8.103 × 102 | 8.101 × 102 | 8.099 × 102 | 8.128 × 102 |
| Mean | 8.166 × 102 | 8.151 × 102 | 8.155 × 102 | 8.167 × 102 | 8.155 × 102 | 8.182 × 102 | 8.171 × 102 | 8.159 × 102 | 8.158 × 102 | 8.176 × 102 | |
| Std | 4.633 × 100 | 4.299 × 100 | 3.858 × 100 | 1.611 × 100 | 2.125 × 100 | 3.027 × 100 | 4.182 × 100 | 4.285 × 100 | 3.761 × 100 | 3.324 × 100 | |
| Rank | 4 | 1 | 5 | 7 | 3 | 10 | 8 | 2 | 6 | 9 | |
| F5 | Best | 9.008 × 102 | 9.009 × 102 | 9.025 × 102 | 9.009 × 102 | 9.011 × 102 | 9.009 × 102 | 9.018 × 102 | 9.011 × 102 | 9.010 × 102 | 9.014 × 102 |
| Mean | 9.065 × 102 | 9.057 × 102 | 9.056 × 102 | 9.052 × 102 | 9.036 × 102 | 9.036 × 102 | 9.033 × 102 | 9.047 × 102 | 9.024 × 102 | 9.059 × 102 | |
| Std | 4.760 × 100 | 4.671 × 100 | 2.922 × 100 | 2.764 × 100 | 2.367 × 100 | 2.145 × 100 | 1.223 × 100 | 3.220 × 100 | 9.747 × 10−1 | 4.160 × 100 | |
| Rank | 9 | 5 | 10 | 8 | 4 | 2 | 3 | 6 | 1 | 7 | |
| F6 | Best | 2.659 × 103 | 2.115 × 103 | 2.139 × 103 | 1.959 × 103 | 2.094 × 103 | 2.166 × 103 | 1.922 × 103 | 2.346 × 103 | 2.066 × 103 | 2.541 × 103 |
| Mean | 3.968 × 103 | 3.039 × 103 | 3.421 × 103 | 3.060 × 103 | 2.905 × 103 | 3.168 × 103 | 2.713 × 103 | 3.557 × 103 | 2.970 × 103 | 3.799 × 103 | |
| Std | 1.630 × 103 | 1.174 × 103 | 1.006 × 103 | 7.081 × 102 | 8.531 × 102 | 9.538 × 102 | 5.070 × 102 | 9.450 × 102 | 7.538 × 102 | 9.708 × 102 | |
| Rank | 9 | 2 | 7 | 6 | 3 | 5 | 1 | 8 | 4 | 10 | |
| F7 | Best | 2.025 × 103 | 2.027 × 103 | 2.025 × 103 | 2.026 × 103 | 2.026 × 103 | 2.027 × 103 | 2.024 × 103 | 2.027 × 103 | 2.029 × 103 | 2.022 × 103 |
| Mean | 2.031 × 103 | 2.031 × 103 | 2.029 × 103 | 2.032 × 103 | 2.030 × 103 | 2.033 × 103 | 2.031 × 103 | 2.030 × 103 | 2.032 × 103 | 2.031 × 103 | |
| Std | 3.198 × 100 | 2.697 × 100 | 3.383 × 100 | 3.674 × 100 | 3.378 × 100 | 3.968 × 100 | 4.169 × 100 | 2.515 × 100 | 2.828 × 100 | 4.330 × 100 | |
| Rank | 4 | 6 | 1 | 8 | 3 | 10 | 5 | 2 | 9 | 7 | |
| F8 | Best | 2.221 × 103 | 2.220 × 103 | 2.221 × 103 | 2.209 × 103 | 2.216 × 103 | 2.211 × 103 | 2.220 × 103 | 2.219 × 103 | 2.220 × 103 | 2.219 × 103 |
| Mean | 2.224 × 103 | 2.224 × 103 | 2.225 × 103 | 2.222 × 103 | 2.221 × 103 | 2.224 × 103 | 2.225 × 103 | 2.225 × 103 | 2.225 × 103 | 2.224 × 103 | |
| Std | 1.609 × 100 | 2.604 × 100 | 1.605 × 100 | 5.887 × 100 | 3.501 × 100 | 4.970 × 100 | 1.773 × 100 | 2.305 × 100 | 1.928 × 100 | 2.718 × 100 | |
| Rank | 2 | 5 | 6 | 3 | 1 | 9 | 7 | 4 | 10 | 8 | |
| F9 | Best | 2.529 × 103 | 2.529 × 103 | 2.529 × 103 | 2.529 × 103 | 2.529 × 103 | 2.529 × 103 | 2.529 × 103 | 2.529 × 103 | 2.529 × 103 | 2.529 × 103 |
| Mean | 2.530 × 103 | 2.531 × 103 | 2.530 × 103 | 2.530 × 103 | 2.530 × 103 | 2.530 × 103 | 2.530 × 103 | 2.530 × 103 | 2.530 × 103 | 2.531 × 103 | |
| Std | 8.413 × 10−1 | 2.076 × 100 | 4.889 × 10−1 | 2.068 × 100 | 7.222 × 10−1 | 1.814 × 100 | 1.379 × 100 | 8.030 × 10−1 | 3.129 × 10−1 | 3.065 × 100 | |
| Rank | 5 | 10 | 6 | 7 | 3 | 9 | 2 | 1 | 8 | 4 | |
| F10 | Best | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 |
| Mean | 2.500 × 103 | 2.500 × 103 | 2.501 × 103 | 2.500 × 103 | 2.501 × 103 | 2.501 × 103 | 2.501 × 103 | 2.500 × 103 | 2.501 × 103 | 2.500 × 103 | |
| Std | 1.133 × 10−1 | 2.319 × 10−2 | 1.465 × 10−1 | 6.388 × 10−2 | 7.403 × 10−1 | 7.931 × 10−2 | 1.817 × 10−1 | 6.871 × 10−2 | 2.892 × 10−1 | 5.213 × 10−2 | |
| Rank | 2 | 3 | 5 | 1 | 8 | 9 | 6 | 7 | 10 | 4 | |
| F11 | Best | 2.679 × 103 | 2.701 × 103 | 2.713 × 103 | 2.656 × 103 | 2.716 × 103 | 2.688 × 103 | 2.706 × 103 | 2.697 × 103 | 2.645 × 103 | 2.646 × 103 |
| Mean | 2.737 × 103 | 2.735 × 103 | 2.738 × 103 | 2.729 × 103 | 2.738 × 103 | 2.732 × 103 | 2.743 × 103 | 2.736 × 103 | 2.736 × 103 | 2.734 × 103 | |
| Std | 2.195 × 101 | 1.743 × 101 | 1.347 × 101 | 2.651 × 101 | 1.098 × 101 | 1.905 × 101 | 1.447 × 101 | 1.762 × 101 | 3.272 × 101 | 3.212 × 101 | |
| Rank | 8 | 4 | 6 | 1 | 2 | 3 | 10 | 5 | 9 | 7 | |
| F12 | Best | 2.862 × 103 | 2.863 × 1003 | 2.863 × 103 | 2.862 × 103 | 2.860 × 103 | 2.861 × 103 | 2.860 × 103 | 2.861 × 103 | 2.862 × 103 | 2.863 × 103 |
| Mean | 2.863 × 103 | 2.864 × 1003 | 2.864 × 103 | 2.864 × 103 | 2.863 × 103 | 2.863 × 103 | 2.863 × 103 | 2.863 × 103 | 2.864 × 103 | 2.863 × 103 | |
| Std | 6.712 × 10−1 | 5.493 × 10−1 | 6.343 × 10−1 | 1.183 × 100 | 1.210 × 100 | 1.279 × 100 | 1.166 × 100 | 9.406 × 10−1 | 6.436 × 10−1 | 3.016 × 10−1 | |
| Rank | 2 | 8 | 10 | 7 | 6 | 4 | 5 | 1 | 9 | 3 | |
| Mean Rank | 5.42 | 4.58 | 6.25 | 5.42 | 4.25 | 6.75 | 5.25 | 4.5 | 6.67 | 5.92 | |
| Function | Item Name | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| F1 | Best | 1.313 × 104 | 8.988 × 103 | 1.140 × 104 | 1.152 × 104 | 1.288 × 104 | 1.321 × 104 | 1.429 × 104 | 1.224 × 104 | 1.258 × 104 | 1.333 × 104 |
| Mean | 2.256 × 104 | 1.836 × 104 | 2.359 × 104 | 2.027 × 104 | 1.882 × 104 | 2.015 × 104 | 2.009 × 104 | 1.764 × 104 | 2.433 × 104 | 2.060 × 104 | |
| Std | 6.043 × 103 | 5.429 × 103 | 7.038 × 103 | 8.987 × 103 | 4.098 × 103 | 6.461 × 103 | 3.846 × 103 | 3.764 × 103 | 1.072 × 104 | 5.498 × 103 | |
| Rank | 9 | 2 | 10 | 3 | 4 | 5 | 6 | 1 | 8 | 7 | |
| F2 | Best | 4.491 × 102 | 4.492 × 102 | 4.491 × 102 | 4.491 × 102 | 4.491 × 102 | 4.491 × 102 | 4.491 × 102 | 4.491 × 102 | 4.491 × 102 | 4.491 × 102 |
| Mean | 4.541 × 102 | 4.541 × 102 | 4.564 × 102 | 4.557 × 102 | 4.530 × 102 | 4.541 × 102 | 4.521 × 102 | 4.567 × 102 | 4.552 × 102 | 4.527 × 102 | |
| Std | 8.072 × 100 | 8.240 × 100 | 1.212 × 101 | 1.020 × 101 | 7.360 × 100 | 1.052 × 101 | 7.448 × 100 | 1.082 × 101 | 9.286 × 100 | 8.937 × 100 | |
| Rank | 9 | 10 | 6 | 8 | 7 | 3 | 1 | 4 | 5 | 2 | |
| F3 | Best | 6.002 × 102 | 6.001 × 102 | 6.001 × 102 | 6.001 × 102 | 6.001 × 102 | 6.001 × 102 | 6.001 × 102 | 6.001 × 102 | 6.001 × 102 | 6.001 × 102 |
| Mean | 6.003 × 102 | 6.003 × 102 | 6.002 × 102 | 6.003 × 102 | 6.003 × 102 | 6.002 × 102 | 6.002 × 102 | 6.002 × 102 | 6.002 × 102 | 6.002 × 102 | |
| Std | 1.149 × 10−1 | 1.008 × 10−1 | 8.454 × 10−2 | 9.944 × 10−2 | 2.539 × 10−1 | 1.741 × 10−1 | 9.909 × 10−2 | 1.044 × 10−1 | 9.300 × 10−2 | 1.290 × 10−1 | |
| Rank | 10 | 8 | 5 | 9 | 4 | 1 | 3 | 6 | 7 | 2 | |
| F4 | Best | 8.465 × 102 | 8.453 × 102 | 8.453 × 102 | 8.512 × 102 | 8.365 × 102 | 8.273 × 102 | 8.423 × 102 | 8.460 × 102 | 8.501 × 1002 | 8.431 × 102 |
| Mean | 8.562 × 102 | 8.530 × 102 | 8.570 × 102 | 8.571 × 102 | 8.535 × 102 | 8.530 × 102 | 8.540 × 102 | 8.549 × 102 | 8.581 × 102 | 8.556 × 102 | |
| Std | 6.388 × 100 | 6.182 × 100 | 5.873 × 100 | 3.494 × 100 | 6.710 × 100 | 1.033 × 101 | 7.164 × 100 | 5.527 × 100 | 5.408 × 100 | 7.629 × 100 | |
| Rank | 7 | 2 | 6 | 8 | 3 | 5 | 1 | 4 | 10 | 9 | |
| F5 | Best | 9.000 × 102 | 9.001 × 102 | 9.000 × 102 | 9.001 × 102 | 9.001 × 102 | 9.002 × 102 | 9.001 × 102 | 9.011 × 102 | 9.001 × 102 | 9.004 × 102 |
| Mean | 9.049 × 102 | 9.031 × 102 | 9.029 × 102 | 9.019 × 102 | 9.027 × 102 | 9.017 × 102 | 9.016 × 102 | 9.043 × 102 | 9.013 × 102 | 9.017 × 102 | |
| Std | 7.111 × 100 | 5.835 × 100 | 3.551 × 100 | 2.130 × 100 | 2.247 × 100 | 1.689 × 100 | 1.169 × 100 | 4.876 × 100 | 1.452 × 100 | 1.007 × 100 | |
| Rank | 8 | 2 | 4 | 6 | 9 | 5 | 3 | 10 | 1 | 7 | |
| F6 | Best | 5.371 × 103 | 2.468 × 103 | 6.923 × 103 | 4.078 × 103 | 2.898 × 103 | 3.524 × 103 | 3.488 × 103 | 2.682 × 103 | 3.643 × 103 | 4.973 × 103 |
| Mean | 1.662 × 104 | 1.591 × 104 | 1.400 × 104 | 1.283 × 104 | 1.183 × 104 | 1.089 × 104 | 1.285 × 104 | 9.385 × 103 | 1.237 × 104 | 1.030 × 104 | |
| Std | 7.920 × 103 | 1.244 × 104 | 5.953 × 103 | 7.449 × 103 | 8.854 × 103 | 1.011 × 104 | 6.398 × 103 | 4.497 × 103 | 8.187 × 103 | 4.175 × 103 | |
| Rank | 10 | 8 | 9 | 5 | 3 | 2 | 7 | 1 | 6 | 4 | |
| F7 | Best | 2.053 × 103 | 2.053 × 103 | 2.044 × 103 | 2.059 × 103 | 2.052 × 103 | 2.054 × 103 | 2.060 × 103 | 2.052 × 103 | 2.035 × 103 | 2.043 × 103 |
| Mean | 2.069 × 103 | 2.062 × 103 | 2.063 × 103 | 2.070 × 103 | 2.068 × 103 | 2.063 × 103 | 2.069 × 103 | 2.066 × 103 | 2.065 × 103 | 2.061 × 103 | |
| Std | 7.043 × 100 | 7.263 × 100 | 1.284 × 101 | 6.545 × 100 | 1.464 × 101 | 6.634 × 100 | 5.752 × 100 | 1.156 × 101 | 1.550 × 101 | 9.566 × 100 | |
| Rank | 10 | 3 | 4 | 9 | 7 | 1 | 8 | 6 | 5 | 2 | |
| F8 | Best | 2.227 × 103 | 2.228 × 103 | 2.229 × 103 | 2.226 × 103 | 2.229 × 103 | 2.226 × 103 | 2.229 × 103 | 2.228 × 103 | 2.227 × 103 | 2.226 × 103 |
| Mean | 2.230 × 103 | 2.230 × 103 | 2.230 × 103 | 2.229 × 103 | 2.230 × 103 | 2.229 × 103 | 2.230 × 103 | 2.230 × 103 | 2.229 × 103 | 2.229 × 103 | |
| Std | 1.474 × 100 | 1.182 × 100 | 8.012 × 10−1 | 1.305 × 100 | 1.093 × 100 | 1.409 × 100 | 7.423 × 10−1 | 1.018 × 100 | 1.504 × 100 | 2.361 × 100 | |
| Rank | 9 | 7 | 5 | 1 | 8 | 3 | 6 | 10 | 4 | 2 | |
| F9 | Best | 2.481 × 103 | 2.481 × 103 | 2.481 × 103 | 2.481 × 103 | 2.481 × 103 | 2.481 × 103 | 2.481 × 103 | 2.481 × 103 | 2.481 × 103 | 2.481 × 103 |
| Mean | 2.482 × 103 | 2.481 × 103 | 2.481 × 103 | 2.482 × 103 | 2.482 × 103 | 2.481 × 103 | 2.482 × 103 | 2.481 × 103 | 2.481 × 103 | 2.482 × 103 | |
| Std | 5.243 × 10−1 | 3.630 × 10−1 | 4.709 × 10−1 | 5.124 × 10−1 | 6.593 × 10−1 | 5.065 × 10−1 | 1.153 × 100 | 6.032 × 10−1 | 3.866 × 10−1 | 9.217 × 10−1 | |
| Rank | 9 | 4 | 5 | 10 | 8 | 7 | 1 | 3 | 2 | 6 | |
| F10 | Best | 2.501 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 |
| Mean | 2.516 × 103 | 2.512 × 103 | 2.543 × 103 | 2.518 × 103 | 2.508 × 103 | 2.537 × 103 | 2.623 × 103 | 2.513 × 103 | 2.501 × 103 | 2.510 × 103 | |
| Std | 3.072 × 101 | 3.539 × 101 | 1.040 × 102 | 3.559 × 101 | 1.564 × 101 | 9.630 × 101 | 3.824 × 102 | 2.740 × 101 | 7.912 × 10−2 | 2.270 × 101 | |
| Rank | 10 | 5 | 2 | 8 | 6 | 9 | 4 | 1 | 3 | 7 | |
| F11 | Best | 2.905 × 103 | 2.902 × 103 | 2.902 × 103 | 2.902 × 103 | 2.902 × 103 | 2.902 × 103 | 2.901 × 103 | 2.901 × 103 | 2.901 × 103 | 2.901 × 103 |
| Mean | 2.988 × 103 | 3.021 × 103 | 2.902 × 103 | 2.926 × 103 | 2.902 × 103 | 2.941 × 103 | 2.943 × 103 | 2.941 × 103 | 2.955 × 103 | 2.952 × 103 | |
| Std | 1.700 × 102 | 1.912 × 102 | 4.893 × 10−1 | 7.579 × 101 | 5.263 × 10−1 | 1.239 × 102 | 1.311 × 102 | 1.227 × 102 | 1.232 × 102 | 1.167 × 102 | |
| Rank | 10 | 9 | 6 | 3 | 7 | 4 | 2 | 8 | 1 | 5 | |
| F12 | Best | 2.937 × 103 | 2.941 × 103 | 2.938 × 103 | 2.940 × 103 | 2.940 × 103 | 2.941 × 103 | 2.939 × 103 | 2.940 × 103 | 2.935 × 103 | 2.939 × 103 |
| Mean | 2.944 × 103 | 2.946 × 103 | 2.944 × 103 | 2.945 × 103 | 2.945 × 103 | 2.946 × 103 | 2.946 × 103 | 2.943 × 103 | 2.944 × 103 | 2.943 × 103 | |
| Std | 3.589 × 100 | 2.610 × 100 | 3.001 × 100 | 3.427 × 100 | 4.687 × 100 | 3.069 × 100 | 4.654 × 100 | 2.995 × 100 | 5.198 × 100 | 2.867 × 100 | |
| Rank | 6 | 9 | 3 | 5 | 7 | 10 | 8 | 1 | 4 | 2 | |
| Mean Rank | 8.92 | 5.75 | 5.42 | 6.25 | 6.08 | 4.58 | 4.17 | 4.58 | 4.67 | 4.58 | |
References
- Jones, M.; Djahel, S.; Welsh, K. Path-planning for unmanned aerial vehicles with environment complexity considerations: A survey. ACM Comput. Surv. 2023, 55, 234. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, X.X.; Zheng, M.Y.; Zhan, Z.H. Evolutionary computation for unmanned aerial vehicle path planning: A survey. Artif. Intell. Rev. 2024, 57, 267. [Google Scholar] [CrossRef]
- Kumar, P.; Pal, K.; Govil, M.C. Comprehensive review of path planning techniques for unmanned aerial vehicles (uavs). ACM Comput. Surv. 2025, 58, 73. [Google Scholar] [CrossRef]
- Wayahdi, M.R.; Ginting, S.H.N.; Syahputra, D. Greedy, A-Star, and Dijkstra’s algorithms in finding shortest path. Int. J. Adv. Data Inf. Syst. 2021, 2, 45–52. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- LaValle, S. Rapidly-Exploring Random Trees: A New Tool for Path Planning; Iowa State University: Ames, IA, USA, 1998. [Google Scholar]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. Int. J. Robot. Res. 1986, 5, 90–98. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: New York, NY, USA; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Storn, R. Differrential Evolution: A Simple and Efficient Adaptive Scheme for Global Optimization Over Continuous Spaces; International Computer Science Institute: Berkeley, CA, USA, 1995. [Google Scholar]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Zhao, J.; Deng, C.; Yu, H.; Fei, H.; Li, D. Path planning of unmanned vehicles based on adaptive particle swarm optimization algorithm. Comput. Commun. 2024, 216, 112–129. [Google Scholar] [CrossRef]
- Freitas, E.J.; Cohen, M.W.; Neto, A.A.; Guimarães, F.G.; Pimenta, L.C. DE3D-NURBS: A differential evolution-based 3D path-planner integrating kinematic constraints and obstacle avoidance. Knowl. Based Syst. 2024, 300, 112084. [Google Scholar] [CrossRef]
- Li, Y.; Gao, A.; Li, H.; Li, L. An improved whale optimization algorithm for UAV swarm trajectory planning. Adv. Contin. Discret. Models 2024, 2024, 40. [Google Scholar] [CrossRef]
- You, G.; Hu, Y.; Lian, C.; Yang, Z. Mixed-strategy Harris Hawk optimization algorithm for UAV path planning and engineering applications. Appl. Sci. 2024, 14, 10581. [Google Scholar] [CrossRef]
- Wang, R.B.; Wang, W.F.; Geng, F.D.; Pan, J.S.; Chu, S.C.; Xu, L. UAV path planning in mountain areas based on a hybrid parallel compact arithmetic optimization algorithm. Neural Comput. Appl. 2025, 37, 22353–22368. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, Y.; Sun, Y. An improved dung beetle optimizer for UAV 3D path planning. J. Supercomput. 2024, 80, 26537–26567. [Google Scholar] [CrossRef]
- Wang, X.; Snášel, V.; Mirjalili, S.; Pan, J.S.; Kong, L.; Shehadeh, H.A. Artificial Protozoa Optimizer (APO): A novel bio-inspired metaheuristic algorithm for engineering optimization. Knowl.-Based Syst. 2024, 295, 111737. [Google Scholar] [CrossRef]
- Elamy, M.I.; Abd Elaziz, M.; Al-Betar, M.A.; Fathy, A.; Elmahdy, M. Enhanced random vector functional link based on artificial protozoa optimizer to predict wear characteristics of Cu-ZrO2 nanocomposites. Results Eng. 2024, 24, 103007. [Google Scholar] [CrossRef]
- Liao, J.; Melethil Sethumadhavan, S.; Ke, R.; Gao, Z.M.; Zhao, J. A leaded sine–cosine artificial protozoa optimizer algorithm for solving multi-objective optimization problems. Clust. Comput. 2025, 28, 304. [Google Scholar] [CrossRef]
- Wang, X.; Snášel, V.; Mirjalili, S.; Pan, J.S. MAAPO: An innovative membrane algorithm based on artificial protozoa optimizer for multilevel threshold image segmentation. Artif. Intell. Rev. 2025, 58, 324. [Google Scholar] [CrossRef]
- Bo, H.; Wu, J.; Hu, G. MSAPO: A Multi-Strategy Fusion Artificial Protozoa Optimizer for Solving Real-World Problems. Mathematics 2025, 13, 2888. [Google Scholar] [CrossRef]
- Tang, X.; Jia, C.; He, Z. UAV Path Planning: A Dual-Population Cooperative Honey Badger Algorithm for Staged Fusion of Multiple Differential Evolutionary Strategies. Biomimetics 2025, 10, 168. [Google Scholar] [CrossRef]
- Chai, X.; Zheng, Z.; Xiao, J.; Yan, L.; Qu, B.; Wen, P.; Wang, H.; Zhou, Y.; Sun, H. Multi-strategy fusion differential evolution algorithm for UAV path planning in complex environment. Aerosp. Sci. Technol. 2022, 121, 107287. [Google Scholar] [CrossRef]
- Yu, X.; Jiang, N.; Wang, X.; Li, M. A hybrid algorithm based on grey wolf optimizer and differential evolution for UAV path planning. Expert Syst. Appl. 2023, 215, 119327. [Google Scholar] [CrossRef]
- Tang, X.; Lian, J.J.; Ma, L.; Wu, X.; Zhong, R.; Zhang, Y.; Chen, H. IECO: An improved educational competition optimizer for state-of-the-art engineering optimization. J. Big Data 2025, 12, 200. [Google Scholar] [CrossRef]
- McKay, M.D. Latin hypercube sampling as a tool in uncertainty analysis of computer models. In Proceedings of the 24th Conference on Winter Simulation, Arlington, VA, USA, 13–16 December 1992; pp. 557–564. [Google Scholar] [CrossRef]
- Stein, M. Large sample properties of simulations using Latin hypercube sampling. Technometrics 1987, 29, 143–151. [Google Scholar] [CrossRef]
- Nesterov, Y.; Vial, J.P. Confidence level solutions for stochastic programming. Automatica 2008, 44, 1559–1568. [Google Scholar] [CrossRef]
- Hansen, N.; Müller, S.D.; Koumoutsakos, P. Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation (CMA-ES). Evol. Comput. 2003, 11, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Amiri, M.H.; Mehrabi Hashjin, N.; Montazeri, M.; Mirjalili, S.; Khodadadi, N. Hippopotamus optimization algorithm: A novel nature-inspired optimization algorithm. Sci. Rep. 2024, 14, 5032. [Google Scholar] [CrossRef]
- Oladejo, S.O.; Ekwe, S.O.; Mirjalili, S. The Hiking Optimization Algorithm: A novel human-based metaheuristic approach. Knowl. Based Syst. 2024, 296, 111880. [Google Scholar] [CrossRef]
- Gámez, M.G.M.; Vázquez, H.P. A Novel Swarm Optimization Algorithm Based on Hive Construction by Tetragonula carbonaria Builder Bees. Mathematics 2025, 13, 2721. [Google Scholar] [CrossRef]
- Dehkordi, A.A.; Sadiq, A.S.; Mirjalili, S.; Ghafoor, K.Z. Nonlinear-based chaotic harris hawks optimizer: Algorithm and internet of vehicles application. Appl. Soft Comput. 2021, 109, 107574. [Google Scholar] [CrossRef]
- Shahzad, W.; Khan, F.A.; Siddiqui, A.B. Clustering in mobile ad hoc networks using comprehensive learning particle swarm optimization (CLPSO). In Proceedings of the International Conference on Future Generation Communication and Networking, Jeju Island, Republic of Korea, 10–12 December 2009; Springer: Berlin/Heidelberg, Germany; pp. 342–349. [Google Scholar] [CrossRef]
- Ch Cheng, S.; Shi, Y.; Qin, Q.; Zhang, Q.; Bai, R. Population diversity maintenance in brain storm optimization algorithm. J. Artif. Intell. Soft Comput. Res. 2014, 4, 83–97. [Google Scholar] [CrossRef]
- Morales-Castañeda, B.; Zaldivar, D.; Cuevas, E.; Fausto, F.; Rodríguez, A. A better balance in metaheuristic algorithms: Does it exist? Swarm Evol. Comput. 2020, 54, 100671. [Google Scholar] [CrossRef]
- Garg, V.; Deep, K.; Bansal, S. Improved teaching learning algorithm with Laplacian operator for solving nonlinear engineering optimization problems. Eng. Appl. Artif. Intell. 2023, 124, 106549. [Google Scholar] [CrossRef]
- Shen, B.; Khishe, M.; Mirjalili, S. Evolving Marine Predators Algorithm by dynamic foraging strategy for real-world engineering optimization problems. Eng. Appl. Artif. Intell. 2023, 123, 106207. [Google Scholar] [CrossRef]
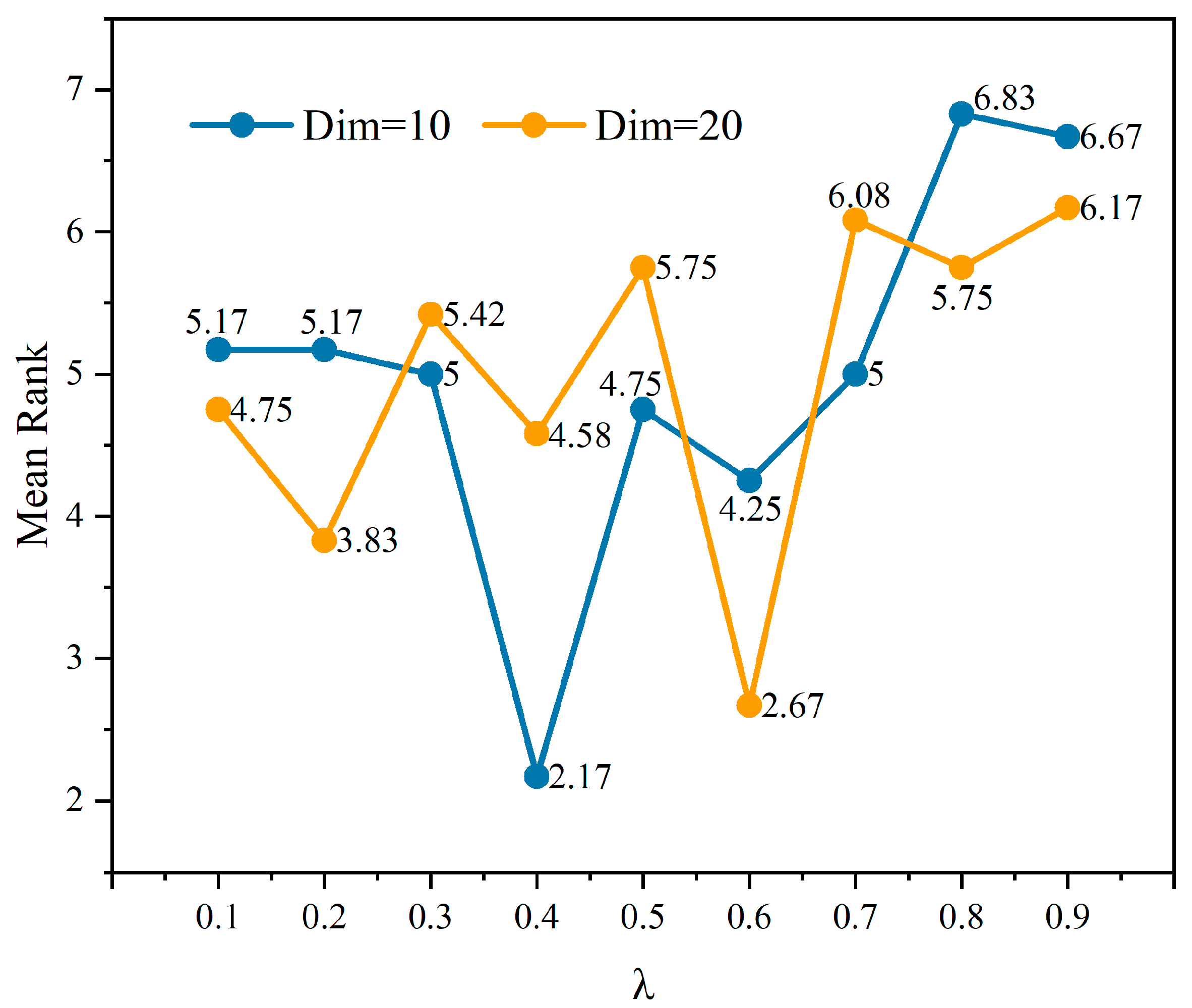
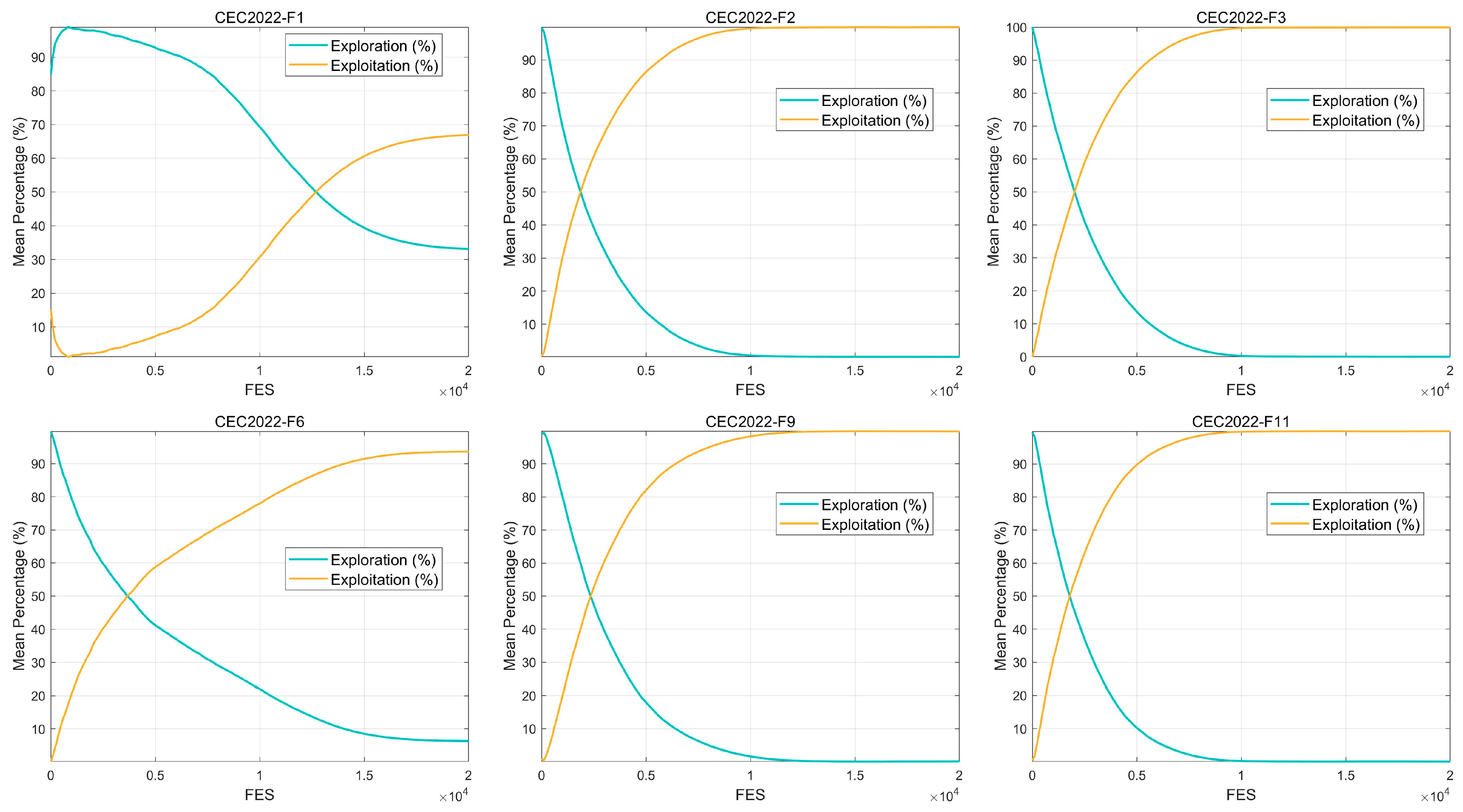
| Algorithms | Parameters Setting |
|---|---|
| PSO | |
| DE | |
| CMA-ES | |
| WOA | |
| HHO | |
| CL-PSO | |
| NCHHO | |
| DBO | |
| HO | Parameter free |
| HOA | |
| AOA | |
| TGCOA | |
| APO | |
| EAPO |
| Function | Item Name | APO | APO_L | APO_H | APO_S | APO_D | EAPO |
|---|---|---|---|---|---|---|---|
| F1 | Best | 3.441 × 103 | 3.829 × 103 | 1.729 × 103 | 2.098 × 103 | 2.094 × 103 | 2.464 × 103 |
| Mean | 7.274 × 103 | 7.249 × 103 | 6.752 × 103 | 7.078 × 103 | 6.201 × 103 | 5.198 × 103 | |
| Std | 1.671 × 103 | 2.228 × 103 | 2.236 × 103 | 2.347 × 103 | 2.271 × 103 | 1.903 × 103 | |
| Rank | 6 | 5 | 3 | 4 | 2 | 1 | |
| F2 | Best | 4.080 × 102 | 4.078 × 102 | 4.076 × 102 | 4.076 × 102 | 4.073 × 102 | 4.071 × 102 |
| Mean | 4.107 × 102 | 4.102 × 102 | 4.126 × 102 | 4.098 × 102 | 4.088 × 102 | 4.086 × 102 | |
| Std | 2.409 × 100 | 2.082 × 100 | 6.368 × 100 | 1.962 × 100 | 1.059 × 100 | 8.597 × 10−1 | |
| Rank | 6 | 4 | 5 | 3 | 2 | 1 | |
| F3 | Best | 6.009 × 102 | 6.008 × 102 | 6.004 × 102 | 6.009 × 102 | 6.008 × 102 | 6.000 × 102 |
| Mean | 6.016 × 102 | 6.016 × 102 | 6.010 × 102 | 6.019 × 102 | 6.012 × 102 | 6.002 × 102 | |
| Std | 3.579 × 10−1 | 3.740 × 10−1 | 2.703 × 10−1 | 4.945 × 10−1 | 2.811 × 10−1 | 2.659 × 10−1 | |
| Rank | 4 | 5 | 2 | 6 | 3 | 1 | |
| F4 | Best | 8.080 × 102 | 8.102 × 102 | 8.111 × 102 | 8.119 × 102 | 8.064 × 102 | 8.072 × 102 |
| Mean | 8.172 × 102 | 8.154 × 102 | 8.170 × 102 | 8.169 × 102 | 8.140 × 102 | 8.165 × 102 | |
| Std | 3.619 × 100 | 2.937 × 100 | 3.260 × 100 | 3.122 × 100 | 3.801 × 100 | 3.506 × 100 | |
| Rank | 6 | 2 | 5 | 4 | 1 | 3 | |
| F5 | Best | 9.053 × 102 | 9.136 × 102 | 9.080 × 102 | 9.086 × 102 | 9.029 × 102 | 9.004 × 102 |
| Mean | 9.217 × 102 | 9.215 × 102 | 9.165 × 102 | 9.163 × 102 | 9.104 × 102 | 9.048 × 102 | |
| Std | 7.598 × 100 | 7.471 × 100 | 5.562 × 100 | 5.999 × 100 | 4.161 × 100 | 2.820 × 100 | |
| Rank | 6 | 5 | 4 | 3 | 2 | 1 | |
| F6 | Best | 2.449 × 103 | 2.437 × 103 | 1.909 × 103 | 1.993 × 103 | 2.058 × 103 | 1.904 × 103 |
| Mean | 4.302 × 103 | 4.389 × 103 | 3.669 × 103 | 4.199 × 103 | 4.352 × 103 | 3.513 × 103 | |
| Std | 1.703 × 103 | 1.600 × 103 | 1.661 × 103 | 1.383 × 103 | 1.458 × 103 | 1.162 × 103 | |
| Rank | 3 | 6 | 2 | 4 | 5 | 1 | |
| F7 | Best | 2.021 × 103 | 2.012 × 103 | 2.018 × 103 | 2.016 × 103 | 2.017 × 103 | 2.021 × 103 |
| Mean | 2.029 × 103 | 2.027 × 103 | 2.028 × 103 | 2.030 × 103 | 2.027 × 103 | 2.031 × 103 | |
| Std | 3.696 × 100 | 4.167 × 100 | 3.824 × 100 | 4.671 × 100 | 3.720 × 100 | 4.225 × 100 | |
| Rank | 4 | 2 | 3 | 5 | 1 | 6 | |
| F8 | Best | 2.213 × 103 | 2.214 × 103 | 2.217 × 103 | 2.221 × 103 | 2.216 × 103 | 2.218 × 103 |
| Mean | 2.222 × 103 | 2.223 × 103 | 2.223 × 103 | 2.225 × 103 | 2.223 × 103 | 2.225 × 103 | |
| Std | 3.209 × 100 | 2.653 × 100 | 1.995 × 100 | 1.213 × 100 | 2.361 × 100 | 2.015 × 100 | |
| Rank | 1 | 3 | 4 | 6 | 2 | 5 | |
| F9 | Best | 2.530 × 103 | 2.529 × 103 | 2.530 × 103 | 2.529 × 103 | 2.529 × 103 | 2.529 × 103 |
| Mean | 2.534 × 103 | 2.532 × 103 | 2.532 × 103 | 2.531 × 103 | 2.531 × 103 | 2.530 × 103 | |
| Std | 6.907 × 100 | 1.757 × 100 | 2.232 × 100 | 1.541 × 100 | 1.534 × 100 | 1.471 × 100 | |
| Rank | 6 | 5 | 4 | 3 | 2 | 1 | |
| F10 | Best | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 |
| Mean | 2.501 × 103 | 2.501 × 103 | 2.501 × 103 | 2.505 × 103 | 2.501 × 103 | 2.501 × 103 | |
| Std | 1.421 × 100 | 8.305 × 10−1 | 2.753 × 100 | 2.113 × 101 | 2.036 × 100 | 4.090 × 10−1 | |
| Rank | 5 | 4 | 3 | 6 | 2 | 1 | |
| F11 | Best | 2.716 × 103 | 2.741 × 103 | 2.738 × 103 | 2.733 × 103 | 2.720 × 103 | 2.665 × 103 |
| Mean | 2.747 × 103 | 2.747 × 103 | 2.749 × 103 | 2.746 × 103 | 2.744 × 103 | 2.735 × 103 | |
| Std | 7.346 × 100 | 2.849 × 100 | 2.994 × 100 | 4.653 × 100 | 7.199 × 100 | 1.858 × 101 | |
| Rank | 5 | 4 | 6 | 3 | 2 | 1 | |
| F12 | Best | 2.862 × 103 | 2.861 × 103 | 2.863 × 103 | 2.861 × 103 | 2.861 × 103 | 2.861 × 103 |
| Mean | 2.864 × 103 | 2.864 × 103 | 2.864 × 103 | 2.864 × 103 | 2.864 × 103 | 2.863 × 103 | |
| Std | 7.076 × 10−1 | 7.757 × 10−1 | 7.868 × 10−1 | 8.428 × 10−1 | 7.667 × 10−1 | 9.569 × 10−1 | |
| Rank | 2 | 4 | 5 | 6 | 3 | 1 | |
| Mean Rank | 4.5 | 4.08 | 4.08 | 4.17 | 2.25 | 1.92 | |
| Final Ranking | 6 | 3 | 3 | 5 | 2 | 1 | |
| Function | Item Name | PSO | DE | CMA-ES | WOA | HHO | CL-PSO | NC-HHO | DBO | HO | HOA | AOA | TG-COA | APO | EAPO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Best | 4.192 × 103 | 7.024 × 103 | 2.971 × 103 | 7.056 × 103 | 4.694 × 103 | 5.551 × 103 | 5.076 × 103 | 5.348 × 102 | 1.659 × 103 | 9.697 × 102 | 1.727 × 104 | 1.563 × 103 | 2.769 × 103 | 2.739 × 103 |
| Mean | 7.337 × 103 | 2.080 × 104 | 1.848 × 104 | 2.583 × 104 | 8.749 × 103 | 1.744 × 104 | 9.386 × 103 | 3.226 × 103 | 6.559 × 103 | 3.516 × 103 | 1.207 × 105 | 5.136 × 103 | 7.999 × 103 | 5.136 × 103 | |
| Std | 2.401 × 103 | 5.527 × 103 | 1.054 × 104 | 1.341 × 104 | 1.474 × 103 | 4.335 × 103 | 1.471 × 103 | 1.997 × 103 | 2.535 × 103 | 1.272 × 103 | 3.379 × 105 | 2.226 × 103 | 2.156 × 103 | 1.987 × 103 | |
| p | 1.709 × 10−3 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.127 × 10−5 | 1.734 × 10−6 | 3.515 × 10−6 | 2.831 × 10−4 | 2.067 × 10−2 | 1.197 × 10−0 | 1.734 × 10−6 | 7.655 × 10−1 | 6.320 × 10−5 | ~ | |
| Rank | 6 | 12 | 10 | 13 | 8 | 11 | 9 | 1 | 5 | 2 | 14 | 3 | 7 | 4 | |
| F2 | Best | 4.138 × 102 | 4.295 × 102 | 4.950 × 102 | 4.016 × 102 | 4.028 × 102 | 5.135 × 102 | 4.418 × 102 | 4.006 × 102 | 4.197 × 102 | 4.122 × 102 | 7.812 × 102 | 4.019 × 102 | 4.081 × 102 | 4.069 × 102 |
| Mean | 4.563 × 102 | 4.623 × 102 | 6.021 × 102 | 4.451 × 102 | 5.171 × 102 | 6.894 × 102 | 5.789 × 102 | 4.278 × 102 | 4.997 × 102 | 5.099 × 102 | 2.298 × 103 | 4.770 × 102 | 4.107 × 102 | 4.090 × 102 | |
| Std | 7.060 × 101 | 1.703 × 101 | 6.205 × 101 | 7.397 × 101 | 1.065 × 102 | 1.498 × 102 | 9.076 × 101 | 3.058 × 101 | 6.966 × 101 | 7.573 × 101 | 1.029 × 103 | 4.194 × 101 | 2.991 × 100 | 2.243 × 100 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 4.390 × 10−3 | 4.286 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.245 × 10−2 | 1.734 × 10−6 | 1.921 × 10−6 | 1.734 × 10−6 | 2.127 × 10−6 | 5.287 × 10−4 | ~ | |
| Rank | 5 | 6 | 12 | 4 | 8 | 13 | 11 | 3 | 9 | 10 | 14 | 7 | 2 | 1 | |
| F3 | Best | 6.114 × 102 | 6.084 × 102 | 6.000 × 102 | 6.175 × 102 | 6.237 × 102 | 6.229 × 102 | 6.217 × 102 | 6.000 × 102 | 6.144 × 102 | 6.112 × 102 | 6.502 × 102 | 6.173 × 102 | 6.005 × 102 | 6.000 × 102 |
| Mean | 6.215 × 102 | 6.229 × 102 | 6.156 × 102 | 6.365 × 102 | 6.405 × 102 | 6.427 × 102 | 6.475 × 102 | 6.018 × 102 | 6.318 × 102 | 6.214 × 102 | 6.865 × 102 | 6.463 × 102 | 6.015 × 102 | 6.002 × 102 | |
| Std | 5.720 × 100 | 4.489 × 100 | 1.923 × 101 | 1.509 × 101 | 1.167 × 101 | 9.533 × 100 | 1.266 × 101 | 3.465 × 100 | 1.244 × 101 | 6.113 × 100 | 1.405 × 101 | 1.439 × 101 | 4.004 × 10−1 | 2.276 × 10−1 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 4.492 × 10−2 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 2.415 × 10−3 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | ~ | |
| Rank | 5 | 7 | 4 | 9 | 10 | 11 | 13 | 2 | 8 | 6 | 14 | 12 | 3 | 1 | |
| F4 | Best | 8.371 × 102 | 8.496 × 102 | 8.111 × 102 | 8.150 × 102 | 8.187 × 102 | 8.490 × 102 | 8.227 × 102 | 8.070 × 102 | 8.127 × 102 | 8.113 × 102 | 8.858 × 102 | 8.145 × 102 | 8.102 × 102 | 8.091 × 102 |
| Mean | 8.576 × 102 | 8.678 × 102 | 8.255 × 102 | 8.382 × 102 | 8.361 × 102 | 8.660 × 102 | 8.408 × 102 | 8.316 × 102 | 8.303 × 102 | 8.253 × 102 | 9.148 × 102 | 8.387 × 102 | 8.159 × 102 | 8.168 × 102 | |
| Std | 7.439 × 100 | 7.699 × 100 | 7.242 × 100 | 1.449 × 101 | 1.060 × 101 | 7.449 × 100 | 1.031 × 101 | 1.623 × 101 | 8.938 × 100 | 8.850 × 100 | 1.365 × 101 | 1.474 × 101 | 3.133 × 100 | 3.471 × 100 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 5.792 × 10−5 | 2.353 × 10−6 | 1.921 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.742 × 10−4 | 6.984 × 10−6 | 1.036 × 10−3 | 1.734 × 10−6 | 1.734 × 10−6 | 5.577 × 10−1 | ~ | |
| Rank | 11 | 13 | 4 | 7 | 8 | 12 | 10 | 5 | 6 | 3 | 14 | 9 | 1 | 2 | |
| F5 | Best | 1.012 × 103 | 1.394 × 103 | 9.000 × 102 | 9.242 × 102 | 1.047 × 103 | 1.266 × 103 | 1.258 × 103 | 9.005 × 102 | 9.882 × 102 | 9.241 × 102 | 2.429 × 103 | 1.191 × 103 | 9.116 × 102 | 9.017 × 102 |
| Mean | 1.155 × 103 | 1.971 × 103 | 9.000 × 102 | 1.473 × 103 | 1.385 × 103 | 1.901 × 103 | 1.469 × 103 | 9.384 × 102 | 1.193 × 103 | 1.031 × 103 | 4.235 × 103 | 1.665 × 103 | 9.222 × 102 | 9.046 × 102 | |
| Std | 8.676 × 101 | 3.356 × 102 | 2.404 × 10−5 | 3.646 × 102 | 1.716 × 102 | 3.669 × 102 | 1.507 × 102 | 7.870 × 101 | 1.752 × 102 | 8.543 × 101 | 8.750 × 102 | 3.818 × 102 | 7.559 × 100 | 2.573 × 100 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 2.105 × 10−3 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | ~ | |
| Rank | 6 | 13 | 1 | 9 | 8 | 12 | 10 | 3 | 7 | 5 | 14 | 11 | 4 | 2 | |
| F6 | Best | 6.735 × 104 | 1.566 × 105 | 3.017 × 105 | 2.142 × 103 | 1.845 × 103 | 2.490 × 104 | 1.908 × 103 | 1.882 × 103 | 2.299 × 103 | 2.227 × 103 | 8.483 × 107 | 1.869 × 103 | 1.936 × 103 | 1.905 × 103 |
| Mean | 2.179 × 106 | 2.489 × 106 | 5.242 × 106 | 7.117 × 103 | 4.163 × 103 | 3.550 × 106 | 4.117 × 103 | 6.077 × 103 | 5.559 × 104 | 4.015 × 106 | 8.333 × 108 | 3.458 × 103 | 3.590 × 103 | 3.172 × 103 | |
| Std | 1.478 × 106 | 2.093 × 106 | 6.734 × 106 | 7.599 × 103 | 6.861 × 103 | 5.157 × 106 | 3.370 × 103 | 2.322 × 103 | 1.168 × 105 | 7.733 × 106 | 4.633 × 108 | 1.868 × 103 | 1.268 × 103 | 1.018 × 103 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 4.196 × 10−4 | 2.989 × 10−1 | 1.734 × 10−6 | 2.536 × 10−1 | 2.843 × 10−5 | 8.944 × 10−4 | 9.316 × 10−6 | 1.734 × 10−6 | 9.426 × 10−1 | 2.989 × 10−1 | ~ | |
| Rank | 12 | 11 | 13 | 6 | 1 | 10 | 5 | 8 | 7 | 9 | 14 | 2 | 4 | 3 | |
| F7 | Best | 2.040 × 103 | 2.034 × 103 | 2.026 × 103 | 2.029 × 103 | 2.044 × 103 | 2.049 × 103 | 2.036 × 103 | 2.000 × 103 | 2.028 × 103 | 2.028 × 103 | 2.090 × 103 | 2.046 × 103 | 2.018 × 103 | 2.025 × 103 |
| Mean | 2.062 × 103 | 2.046 × 103 | 2.092 × 103 | 2.083 × 103 | 2.088 × 103 | 2.086 × 103 | 2.108 × 103 | 2.024 × 103 | 2.062 × 103 | 2.053 × 103 | 2.221 × 103 | 2.100 × 103 | 2.027 × 103 | 2.031 × 103 | |
| Std | 1.298 × 101 | 6.873 × 100 | 4.101 × 101 | 3.178 × 101 | 3.695 × 101 | 1.948 × 101 | 3.482 × 101 | 7.764 × 100 | 2.357 × 101 | 1.326 × 101 | 5.565 × 101 | 3.455 × 101 | 2.997 × 100 | 3.136 × 100 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 6.339 × 10−6 | 1.921 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 5.792 × 10−5 | 2.603 × 10−6 | 1.921 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 5.307 × 10−5 | ~ | |
| Rank | 7 | 4 | 9 | 8 | 10 | 11 | 13 | 1 | 6 | 5 | 14 | 12 | 2 | 3 | |
| F8 | Best | 2.230 × 103 | 2.226 × 103 | 2.229 × 103 | 2.224 × 103 | 2.225 × 103 | 2.226 × 103 | 2.214 × 103 | 2.221 × 103 | 2.224 × 103 | 2.217 × 103 | 2.255 × 103 | 2.225 × 103 | 2.216 × 103 | 2.217 × 103 |
| Mean | 2.242 × 103 | 2.230 × 103 | 2.241 × 103 | 2.239 × 103 | 2.240 × 103 | 2.234 × 103 | 2.247 × 103 | 2.226 × 103 | 2.252 × 103 | 2.227 × 103 | 2.503 × 103 | 2.263 × 103 | 2.223 × 103 | 2.224 × 103 | |
| Std | 2.247 × 101 | 2.250 × 100 | 8.718 × 100 | 1.329 × 101 | 1.490 × 101 | 4.525 × 100 | 2.094 × 101 | 3.771 × 100 | 4.589 × 101 | 3.649 × 100 | 1.720 × 102 | 5.795 × 101 | 2.460 × 100 | 3.264 × 100 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 2.879 × 10−6 | 1.734 × 10−6 | 1.921 × 10−6 | 2.603 × 10−6 | 8.730 × 10−3 | 2.603 × 10−6 | 5.287 × 10−4 | 1.734 × 10−6 | 1.921 × 10−6 | 1.306 × 10−1 | ~ | |
| Rank | 10 | 5 | 12 | 9 | 8 | 6 | 13 | 3 | 7 | 4 | 14 | 11 | 1 | 2 | |
| F9 | Best | 2.531 × 103 | 2.534 × 103 | 2.531 × 103 | 2.530 × 103 | 2.532 × 103 | 2.576 × 103 | 2.540 × 103 | 2.529 × 103 | 2.550 × 103 | 2.618 × 103 | 2.727 × 103 | 2.548 × 103 | 2.529 × 103 | 2.529 × 103 |
| Mean | 2.555 × 103 | 2.547 × 103 | 2.557 × 103 | 2.586 × 103 | 2.655 × 103 | 2.653 × 103 | 2.639 × 103 | 2.533 × 103 | 2.650 × 103 | 2.660 × 103 | 2.953 × 103 | 2.617 × 103 | 2.531 × 103 | 2.530 × 103 | |
| Std | 3.365 × 101 | 1.006 × 101 | 3.500 × 101 | 5.412 × 101 | 5.141 × 101 | 3.709 × 101 | 5.798 × 101 | 7.776 × 100 | 5.002 × 101 | 1.667 × 101 | 1.421 × 102 | 3.440 × 101 | 1.629 × 100 | 2.956 × 10−1 | |
| p | 1.921 × 10−6 | 1.734 × 10−6 | 2.127 × 10−6 | 2.879 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 9.918 × 10−1 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | ~ | |
| Rank | 4 | 5 | 6 | 7 | 11 | 12 | 9 | 2 | 10 | 13 | 14 | 8 | 3 | 1 | |
| F10 | Best | 2.502 × 103 | 2.510 × 103 | 2.513 × 103 | 2.500 × 103 | 2.501 × 103 | 2.516 × 103 | 2.501 × 103 | 2.500 × 103 | 2.501 × 103 | 2.501 × 103 | 2.540 × 103 | 2.501 × 103 | 2.500 × 103 | 2.500 × 103 |
| Mean | 2.576 × 103 | 2.520 × 103 | 2.771 × 103 | 2.563 × 103 | 2.609 × 103 | 2.550 × 103 | 2.627 × 103 | 2.544 × 103 | 2.580 × 103 | 2.570 × 103 | 3.192 × 103 | 2.564 × 103 | 2.501 × 103 | 2.500 × 103 | |
| Std | 8.326 × 101 | 6.368 × 10 | 3.486 × 102 | 1.625 × 102 | 3.051 × 102 | 4.279 × 101 | 1.398 × 102 | 6.332 × 101 | 7.441 × 101 | 6.330 × 101 | 6.623 × 102 | 1.163 × 102 | 2.448 × 10 | 9.281 × 10−2 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 2.127 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 2.353 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 8.221 × 10−2 | ~ | |
| Rank | 10 | 7 | 13 | 4 | 6 | 11 | 12 | 3 | 9 | 8 | 14 | 5 | 2 | 1 | |
| F11 | Best | 2.783 × 103 | 2.791 × 103 | 2.806 × 103 | 2.635 × 103 | 2.717 × 103 | 2.809 × 103 | 2.738 × 103 | 2.600 × 103 | 2.736 × 103 | 2.702 × 103 | 2.966 × 103 | 2.732 × 103 | 2.716 × 103 | 2.633 × 103 |
| Mean | 2.991 × 103 | 2.832 × 103 | 2.915 × 103 | 2.804 × 103 | 2.947 × 103 | 3.108 × 103 | 3.132 × 103 | 2.752 × 103 | 2.941 × 103 | 2.857 × 103 | 4.402 × 103 | 2.865 × 103 | 2.746 × 103 | 2.736 × 103 | |
| Std | 8.339 × 102 | 2.604 × 102 | 1.327 × 103 | 4.846 × 102 | 1.422 × 103 | 9.098 × 102 | 1.250 × 103 | 8.121 × 102 | 7.938 × 102 | 7.909 × 102 | 2.010 × 103 | 9.381 × 102 | 2.256 × 101 | 7.474 × 101 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 3.160 × 10−2 | 4.729 × 10−6 | 1.734 × 10−6 | 2.127 × 10−6 | 4.284 × 10−1 | 3.515 × 10−6 | 2.597 × 10−5 | 1.734 × 10−6 | 4.729 × 10−6 | 3.501 × 10−2 | ~ | |
| Rank | 10 | 9 | 12 | 4 | 8 | 13 | 11 | 3 | 7 | 5 | 14 | 6 | 2 | 1 | |
| F12 | Best | 2.860 × 103 | 2.866 × 103 | 2.870 × 103 | 2.864 × 103 | 2.867 × 103 | 2.866 × 103 | 2.871 × 103 | 2.861 × 103 | 2.866 × 103 | 2.910 × 103 | 2.975 × 103 | 2.868 × 103 | 2.861 × 103 | 2.862 × 103 |
| Mean | 2.870 × 103 | 2.867 × 103 | 2.875 × 103 | 2.893 × 103 | 2.923 × 103 | 2.895 × 103 | 2.937 × 103 | 2.864 × 103 | 2.892 × 103 | 2.954 × 103 | 3.109 × 103 | 2.919 × 103 | 2.864 × 103 | 2.863 × 103 | |
| Std | 5.579 × 100 | 1.143 × 100 | 2.742 × 100 | 3.055 × 101 | 5.743 × 101 | 1.724 × 101 | 4.529 × 101 | 1.504 × 100 | 3.364 × 101 | 2.685 × 101 | 7.643 × 101 | 2.899 × 101 | 7.257 × 10−1 | 8.084 × 10−1 | |
| p | 4.286 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 4.277 × 10−2 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 8.590 × 10−2 | ~ | |
| Rank | 5 | 4 | 6 | 8 | 10 | 9 | 12 | 3 | 7 | 13 | 14 | 11 | 2 | 1 | |
| Mean Rank | 7.58 | 8 | 8.5 | 7.33 | 8 | 10.92 | 10.67 | 3.08 | 7.33 | 6.92 | 14 | 8.08 | 2.75 | 1.83 | |
| Final Ranking | 7 | 8 | 11 | 6 | 8 | 13 | 12 | 3 | 5 | 4 | 14 | 10 | 2 | 1 | |
| +/=/− | 12/0/0 | 12/0/0 | 11/0/1 | 12/0/0 | 11/1/0 | 12/0/0 | 11/1/0 | 8/1/3 | 12/0/0 | 11/1/0 | 12/0/0 | 10/0/0 | 7/3/2 | ~ | |
| Function | Item Name | PSO | DE | CMA-ES | WOA | HHO | CL-PSO | NC-HHO | DBO | HO | HOA | AOA | TG-COA | APO | EAPO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Best | 2.941 × 104 | 2.869 × 104 | 3.745 × 104 | 1.272 × 104 | 1.819 × 104 | 3.662 × 104 | 1.803 × 104 | 1.603 × 104 | 1.880 × 104 | 9.905 × 103 | 8.485 × 104 | 1.360 × 104 | 1.821 × 104 | 1.346 × 104 |
| Mean | 5.077 × 104 | 6.218 × 104 | 6.962 × 104 | 2.168 × 104 | 3.946 × 104 | 5.997 × 104 | 3.257 × 104 | 3.347 × 104 | 2.974 × 104 | 1.979 × 104 | 2.827 × 107 | 2.870 × 104 | 2.783 × 104 | 1.995 × 104 | |
| Std | 1.569 × 104 | 9.490 × 103 | 1.957 × 104 | 7.843 × 103 | 1.489 × 104 | 1.053 × 104 | 9.899 × 103 | 1.166 × 104 | 6.187 × 103 | 4.989 × 103 | 1.466 × 108 | 8.135 × 103 | 4.366 × 103 | 4.297 × 103 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 4.284 × 10−1 | 5.216 × 10−6 | 1.734 × 10−6 | 6.984 × 10−6 | 2.843 × 10−5 | 4.286 × 10−6 | 9.918 × 10−1 | 1.734 × 10−6 | 6.892 × 10−5 | 2.163 × 10−5 | ~ | |
| Rank | 10 | 12 | 13 | 3 | 9 | 11 | 8 | 7 | 6 | 2 | 14 | 5 | 4 | 1 | |
| F2 | Best | 5.611 × 102 | 6.176 × 102 | 6.497 × 102 | 4.564 × 102 | 5.133 × 102 | 1.072 × 103 | 5.733 × 102 | 4.067 × 102 | 5.727 × 102 | 6.573 × 102 | 2.978 × 103 | 5.545 × 102 | 4.461 × 102 | 4.449 × 102 |
| Mean | 7.674 × 102 | 8.061 × 102 | 1.293 × 103 | 5.366 × 102 | 9.269 × 102 | 2.268 × 103 | 9.636 × 102 | 4.897 × 102 | 7.982 × 102 | 8.664 × 102 | 7.456 × 103 | 8.880 × 102 | 4.523 × 102 | 4.536 × 102 | |
| Std | 1.813 × 102 | 8.522 × 101 | 3.483 × 102 | 5.630 × 101 | 3.234 × 102 | 6.481 × 102 | 2.338 × 102 | 5.268 × 101 | 1.436 × 102 | 1.393 × 102 | 2.185 × 103 | 2.478 × 102 | 6.009 × 100 | 9.448 × 100 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 2.225 × 10−4 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.254 × 10−1 | ~ | |
| Rank | 5 | 7 | 12 | 4 | 10 | 13 | 11 | 3 | 6 | 9 | 14 | 8 | 2 | 1 | |
| F3 | Best | 6.302 × 102 | 6.275 × 102 | 6.406 × 102 | 6.333 × 102 | 6.404 × 102 | 6.504 × 102 | 6.527 × 102 | 6.048 × 102 | 6.388 × 102 | 6.285 × 102 | 6.876 × 102 | 6.346 × 102 | 6.004 × 102 | 6.001 × 102 |
| Mean | 6.443 × 102 | 6.326 × 102 | 6.637 × 102 | 6.620 × 102 | 6.675 × 102 | 6.609 × 102 | 6.752 × 102 | 6.170 × 102 | 6.615 × 102 | 6.425 × 102 | 7.182 × 102 | 6.687 × 102 | 6.006 × 102 | 6.002 × 102 | |
| Std | 6.435 × 100 | 2.914 × 100 | 1.042 × 101 | 1.208 × 101 | 1.307 × 101 | 5.290 × 100 | 1.074 × 101 | 7.650 × 100 | 1.083 × 101 | 8.660 × 100 | 1.299 × 101 | 1.224 × 101 | 1.698 × 10−1 | 8.296 × 10−2 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.921 × 10−6 | ~ | |
| Rank | 6 | 4 | 10 | 8 | 11 | 7 | 13 | 3 | 9 | 5 | 14 | 12 | 2 | 1 | |
| F4 | Best | 9.437 × 102 | 9.590 × 102 | 8.830 × 102 | 8.739 × 102 | 8.810 × 102 | 9.504 × 102 | 9.041 × 102 | 8.560 × 102 | 8.549 × 102 | 8.563 × 102 | 1.055 × 103 | 9.066 × 102 | 8.317 × 102 | 8.308 × 102 |
| Mean | 9.677 × 102 | 9.936 × 102 | 9.794 × 102 | 9.246 × 102 | 9.183 × 102 | 9.920 × 102 | 9.465 × 102 | 9.025 × 102 | 9.084 × 102 | 9.011 × 102 | 1.104 × 103 | 9.365 × 102 | 8.446 × 102 | 8.535 × 102 | |
| Std | 1.357 × 101 | 1.428 × 101 | 3.826 × 101 | 2.562 × 101 | 2.699 × 101 | 1.841 × 101 | 2.163 × 101 | 3.196 × 101 | 1.910 × 101 | 1.864 × 101 | 2.109 × 101 | 2.360 × 101 | 7.077 × 100 | 8.997 × 100 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.965 × 10−3 | ~ | |
| Rank | 10 | 13 | 11 | 7 | 6 | 12 | 9 | 4 | 5 | 3 | 14 | 8 | 1 | 2 | |
| F5 | Best | 1.646 × 103 | 4.266 × 103 | 9.000 × 102 | 1.852 × 103 | 1.944 × 103 | 3.204 × 103 | 2.213 × 103 | 1.058 × 103 | 1.770 × 103 | 1.523 × 103 | 8.116 × 103 | 2.189 × 103 | 9.018 × 102 | 9.000 × 102 |
| Mean | 4.010 × 103 | 6.840 × 103 | 1.151 × 103 | 3.655 × 103 | 3.019 × 103 | 5.616 × 103 | 3.036 × 103 | 1.891 × 103 | 2.825 × 103 | 2.162 × 103 | 1.246 × 104 | 3.195 × 103 | 9.061 × 102 | 9.027 × 102 | |
| Std | 1.057 × 103 | 1.145 × 103 | 9.812 × 102 | 1.388 × 103 | 5.897 × 102 | 1.128 × 103 | 4.659 × 102 | 8.300 × 102 | 4.354 × 102 | 4.901 × 102 | 1.814 × 103 | 7.338 × 102 | 4.191 × 100 | 3.071 × 100 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 4.534 × 10−4 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.036 × 10−3 | ~ | |
| Rank | 11 | 13 | 1 | 10 | 8 | 12 | 7 | 4 | 6 | 5 | 14 | 9 | 3 | 2 | |
| F6 | Best | 2.999 × 107 | 4.160 × 107 | 3.832 × 107 | 4.905 × 104 | 1.155 × 104 | 2.440 × 107 | 1.134 × 107 | 2.032 × 103 | 4.433 × 105 | 3.783 × 106 | 1.939 × 109 | 1.280 × 104 | 1.360 × 104 | 2.375 × 103 |
| Mean | 1.454 × 108 | 7.068 × 107 | 5.967 × 108 | 5.363 × 105 | 7.310 × 107 | 4.382 × 108 | 8.449 × 107 | 1.148 × 106 | 2.585 × 107 | 1.047 × 108 | 5.571 × 109 | 2.017 × 107 | 9.664 × 104 | 1.271 × 104 | |
| Std | 8.499 × 107 | 1.878 × 107 | 3.849 × 108 | 5.391 × 105 | 1.052 × 108 | 3.395 × 108 | 8.887 × 107 | 5.279 × 106 | 2.989 × 107 | 9.671 × 107 | 2.202 × 109 | 6.931 × 107 | 5.277 × 104 | 1.017 × 104 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 6.424 × 10−3 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 2.353 × 10−6 | ~ | |
| Rank | 11 | 10 | 13 | 4 | 7 | 12 | 8 | 2 | 6 | 9 | 14 | 5 | 3 | 1 | |
| F7 | Best | 2.099 × 103 | 2.093 × 103 | 2.137 × 103 | 2.100 × 103 | 2.100 × 103 | 2.115 × 103 | 2.161 × 103 | 2.036 × 103 | 2.068 × 103 | 2.092 × 103 | 2.226 × 103 | 2.081 × 103 | 2.045 × 103 | 2.047 × 103 |
| Mean | 2.159 × 103 | 2.132 × 103 | 2.212 × 103 | 2.222 × 103 | 2.217 × 103 | 2.172 × 103 | 2.237 × 103 | 2.099 × 103 | 2.166 × 103 | 2.143 × 103 | 2.504 × 103 | 2.195 × 103 | 2.060 × 103 | 2.069 × 103 | |
| Std | 3.439 × 101 | 2.323 × 101 | 2.914 × 101 | 7.585 × 101 | 6.176 × 101 | 3.753 × 101 | 5.173 × 101 | 3.749 × 101 | 4.657 × 101 | 3.770 × 101 | 1.179 × 102 | 6.184 × 101 | 7.695 × 100 | 1.086 × 101 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 2.412 × 10−4 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 3.609 × 10−3 | ~ | |
| Rank | 7 | 4 | 12 | 10 | 11 | 8 | 13 | 3 | 6 | 5 | 14 | 9 | 1 | 2 | |
| F8 | Best | 2.250 × 103 | 2.234 × 103 | 2.247 × 103 | 2.236 × 103 | 2.242 × 103 | 2.243 × 103 | 2.240 × 103 | 2.222 × 103 | 2.230 × 103 | 2.230 × 103 | 2.672 × 103 | 2.239 × 103 | 2.225 × 103 | 2.227 × 103 |
| Mean | 2.302 × 103 | 2.259 × 103 | 2.384 × 103 | 2.282 × 103 | 2.282 × 103 | 2.273 × 103 | 2.310 × 103 | 2.277 × 103 | 2.298 × 103 | 2.281 × 103 | 5.128 × 103 | 2.451 × 103 | 2.227 × 103 | 2.230 × 103 | |
| Std | 4.045 × 101 | 1.349 × 101 | 9.697 × 101 | 6.334 × 101 | 5.555 × 101 | 2.397 × 101 | 7.782 × 101 | 5.858 × 101 | 6.218 × 101 | 5.801 × 101 | 4.190 × 103 | 1.193 × 102 | 8.364 × 10−1 | 1.050 × 100 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 9.711 × 10−5 | 1.921 × 10−6 | 4.286 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 2.353 × 10−6 | ~ | |
| Rank | 11 | 5 | 12 | 6 | 7 | 8 | 10 | 3 | 9 | 4 | 14 | 13 | 1 | 2 | |
| F9 | Best | 2.511 × 103 | 2.496 × 103 | 2.633 × 103 | 2.491 × 103 | 2.522 × 103 | 2.598 × 103 | 2.554 × 103 | 2.481 × 103 | 2.549 × 103 | 2.685 × 103 | 3.048 × 103 | 2.524 × 103 | 2.481 × 103 | 2.481 × 103 |
| Mean | 2.648 × 103 | 2.510 × 103 | 2.830 × 103 | 2.538 × 103 | 2.633 × 103 | 2.803 × 103 | 2.703 × 103 | 2.498 × 103 | 2.664 × 103 | 2.802 × 103 | 3.937 × 103 | 2.685 × 103 | 2.482 × 103 | 2.481 × 103 | |
| Std | 7.640 × 101 | 8.349 × 100 | 1.224 × 102 | 4.245 × 101 | 6.514 × 101 | 9.317 × 101 | 7.475 × 101 | 2.427 × 101 | 5.318 × 101 | 7.774 × 101 | 4.471 × 102 | 6.228 × 101 | 9.008 × 10−1 | 6.883 × 10−1 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 2.613 × 10−4 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.742 × 10−4 | ~ | |
| Rank | 7 | 4 | 13 | 5 | 6 | 11 | 10 | 3 | 8 | 12 | 14 | 9 | 2 | 1 | |
| F10 | Best | 2.517 × 103 | 2.532 × 103 | 2.609 × 103 | 2.501 × 103 | 2.528 × 103 | 2.575 × 103 | 2.557 × 103 | 2.501 × 103 | 2.502 × 103 | 2.521 × 103 | 2.695 × 103 | 2.503 × 103 | 2.500 × 103 | 2.500 × 103 |
| Mean | 5.059 × 103 | 2.669 × 103 | 6.094 × 103 | 4.539 × 103 | 4.993 × 103 | 3.880 × 103 | 5.623 × 103 | 3.310 × 103 | 4.521 × 103 | 3.739 × 103 | 7.466 × 103 | 4.393 × 103 | 2.534 × 103 | 2.506 × 103 | |
| Std | 1.665 × 103 | 2.392 × 102 | 1.402 × 103 | 1.323 × 103 | 1.546 × 103 | 1.285 × 103 | 1.121 × 103 | 9.327 × 102 | 1.845 × 103 | 1.304 × 103 | 1.684 × 103 | 1.689 × 103 | 7.810 × 101 | 2.087 × 101 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 5.792 × 10−5 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 4.286 × 10−6 | 7.655 × 10−1 | ~ | |
| Rank | 10 | 4 | 13 | 6 | 11 | 7 | 12 | 3 | 9 | 5 | 14 | 8 | 2 | 1 | |
| F11 | Best | 3.456 × 103 | 3.833 × 103 | 3.879 × 103 | 3.025 × 103 | 4.285 × 103 | 5.079 × 103 | 4.299 × 103 | 2.850 × 103 | 3.749 × 103 | 4.701 × 103 | 9.720 × 103 | 4.213 × 103 | 2.953 × 103 | 2.901 × 103 |
| Mean | 4.862 × 103 | 4.227 × 103 | 7.302 × 103 | 3.359 × 103 | 6.230 × 103 | 7.301 × 103 | 6.055 × 103 | 3.109 × 103 | 4.770 × 103 | 5.855 × 103 | 1.299 × 104 | 5.697 × 103 | 2.987 × 103 | 2.921 × 103 | |
| Std | 7.499 × 102 | 2.275 × 102 | 1.107 × 103 | 6.378 × 102 | 1.359 × 103 | 1.090 × 103 | 1.069 × 103 | 1.829 × 102 | 7.110 × 102 | 7.680 × 102 | 1.746 × 103 | 9.836 × 102 | 1.975 × 101 | 8.469 × 101 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 5.216 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 3.112 × 10−5 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 3.405 × 10−5 | ~ | |
| Rank | 7 | 5 | 12 | 4 | 11 | 13 | 10 | 3 | 6 | 9 | 14 | 8 | 2 | 1 | |
| F12 | Best | 2.955 × 103 | 2.951 × 103 | 3.002 × 103 | 2.963 × 103 | 3.012 × 103 | 3.056 × 103 | 3.003 × 103 | 2.941 × 103 | 2.960 × 103 | 3.166 × 103 | 3.494 × 103 | 3.102 × 103 | 2.941 × 103 | 2.938 × 103 |
| Mean | 3.010 × 103 | 2.962 × 103 | 3.052 × 103 | 3.066 × 103 | 3.310 × 103 | 3.143 × 103 | 3.277 × 103 | 2.967 × 103 | 3.106 × 103 | 3.486 × 103 | 4.130 × 103 | 3.391 × 103 | 2.945 × 103 | 2.945 × 103 | |
| Std | 3.870 × 101 | 5.283 × 100 | 2.164 × 101 | 7.354 × 101 | 2.323 × 102 | 5.165 × 101 | 1.949 × 102 | 2.332 × 101 | 8.774 × 101 | 1.302 × 102 | 2.882 × 102 | 1.622 × 102 | 3.114 × 100 | 3.806 × 100 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 3.182 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 7.036 × 10−1 | ~ | |
| Rank | 5 | 3 | 6 | 7 | 11 | 9 | 10 | 4 | 8 | 13 | 14 | 12 | 1 | 2 | |
| Mean Rank | 8.33 | 7 | 10.67 | 6.17 | 9 | 10.25 | 10.08 | 3.5 | 7 | 6.75 | 14 | 8.83 | 2 | 1.41 | |
| Final Ranking | 8 | 6 | 13 | 4 | 10 | 12 | 11 | 3 | 6 | 5 | 14 | 9 | 2 | 1 | |
| +/=/− | 12/0/0 | 12/0/0 | 12/0/0 | 11/1/0 | 12/0/0 | 12/0/0 | 12/0/0 | 12/0/0 | 12/0/0 | 11/1/0 | 12/0/0 | 12/0/0 | 9/2/1 | ~ | |
| Function | Item Name | PSO | DE | CMA-ES | WOA | HHO | CL-PSO | NC-HHO | DBO | HO | HOA | AOA | TG-COA | APO | EAPO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Best | 1.419 × 108 | 3.522 × 108 | 1.292 × 109 | 9.222 × 105 | 1.848 × 107 | 1.349 × 109 | 1.990 × 108 | 1.326 × 102 | 1.493 × 108 | 1.932 × 108 | 7.592 × 109 | 8.608 × 106 | 3.190 × 106 | 1.259 × 103 |
| Mean | 7.644 × 108 | 8.076 × 108 | 3.401 × 109 | 1.768 × 107 | 8.225 × 108 | 5.160 × 109 | 2.096 × 109 | 4.980 × 106 | 7.235 × 108 | 1.805 × 109 | 1.433 × 1010 | 2.112 × 108 | 5.919 × 106 | 3.338 × 103 | |
| Std | 6.282 × 108 | 2.580 × 108 | 1.165 × 109 | 1.519 × 107 | 1.448 × 109 | 2.136 × 109 | 1.799 × 109 | 1.777 × 107 | 4.869 × 108 | 9.251 × 108 | 4.255 × 109 | 3.870 × 108 | 1.650 × 106 | 2.237 × 103 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 2.765 × 10−3 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | ~ | |
| Rank | 7 | 9 | 12 | 4 | 6 | 13 | 10 | 2 | 8 | 11 | 14 | 5 | 3 | 1 | |
| F2 | Best | 1.978 × 103 | 1.846 × 103 | 2.237 × 103 | 1.597 × 103 | 1.507 × 103 | 2.088 × 103 | 1.534 × 103 | 1.262 × 103 | 1.731 × 103 | 1.412 × 103 | 2.839 × 103 | 1.428 × 103 | 1.599 × 103 | 1.283 × 103 |
| Mean | 2.538 × 103 | 2.302 × 103 | 2.697 × 103 | 2.323 × 103 | 2.414 × 103 | 2.429 × 103 | 2.340 × 103 | 1.831 × 103 | 2.409 × 103 | 1.911 × 103 | 3.475 × 103 | 2.177 × 103 | 1.783 × 103 | 1.776 × 103 | |
| Std | 2.520 × 102 | 1.554 × 102 | 1.893 × 102 | 3.462 × 102 | 3.427 × 102 | 1.374 × 102 | 4.034 × 102 | 2.621 × 102 | 3.012 × 102 | 2.659 × 102 | 2.713 × 102 | 3.825 × 102 | 1.217 × 102 | 1.651 × 102 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 8.466 × 10−6 | 2.879 × 10−6 | 1.734 × 10−6 | 9.316 × 10−6 | 2.895 × 10−1 | 3.882 × 10−6 | 1.319 × 10−2 | 1.734 × 10−6 | 6.320 × 10−5 | 8.612 × 10−1 | ~ | |
| Rank | 12 | 6 | 13 | 7 | 9 | 10 | 8 | 3 | 11 | 4 | 14 | 5 | 2 | 1 | |
| F3 | Best | 7.579 × 102 | 7.724 × 102 | 7.273 × 102 | 7.410 × 102 | 7.618 × 102 | 7.974 × 102 | 7.428 × 102 | 7.107 × 102 | 7.422 × 102 | 7.296 × 102 | 8.835 × 102 | 7.439 × 102 | 7.219 × 102 | 7.173 × 102 |
| Mean | 8.168 × 102 | 8.050 × 102 | 7.398 × 102 | 7.876 × 102 | 8.010 × 102 | 8.579 × 102 | 8.015 × 102 | 7.336 × 102 | 7.769 × 102 | 7.515 × 102 | 1.109 × 103 | 7.878 × 102 | 7.266 × 102 | 7.310 × 102 | |
| Std | 1.877 × 101 | 1.293 × 101 | 4.855 × 100 | 2.381 × 101 | 2.470 × 101 | 3.465 × 101 | 2.349 × 101 | 1.259 × 101 | 1.868 × 101 | 1.313 × 101 | 6.833 × 101 | 2.543 × 101 | 3.182 × 100 | 4.386 × 100 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 4.286 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 4.528 × 10−1 | 1.734 × 10−6 | 4.286 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 6.156 × 10−4 | ~ | |
| Rank | 12 | 11 | 4 | 7 | 9 | 13 | 10 | 3 | 6 | 5 | 14 | 8 | 1 | 2 | |
| F4 | Best | 1.907 × 103 | 1.914 × 103 | 1.951 × 103 | 1.902 × 103 | 1.903 × 103 | 2.327 × 103 | 1.906 × 103 | 1.901 × 103 | 1.903 × 103 | 1.907 × 103 | 1.836 × 104 | 1.904 × 103 | 1.901 × 103 | 1.901 × 103 |
| Mean | 1.928 × 103 | 1.931 × 103 | 2.783 × 103 | 1.908 × 103 | 2.108 × 103 | 1.189 × 104 | 2.822 × 103 | 1.904 × 103 | 2.405 × 103 | 2.826 × 103 | 9.525 × 105 | 1.957 × 103 | 1.902 × 103 | 1.902 × 103 | |
| Std | 4.423 × 101 | 1.653 × 101 | 7.388 × 102 | 5.425 × 100 | 4.800 × 102 | 1.806 × 104 | 2.390 × 103 | 3.778 × 100 | 1.542 × 103 | 1.338 × 103 | 8.239 × 105 | 6.971 × 101 | 3.186 × 10−1 | 4.323 × 10−1 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.204 × 10−1 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 3.872 × 10−2 | ~ | |
| Rank | 5 | 8 | 12 | 4 | 9 | 13 | 10 | 3 | 7 | 11 | 14 | 6 | 1 | 2 | |
| F5 | Best | 1.163 × 104 | 9.216 × 104 | 1.218 × 104 | 7.560 × 103 | 9.704 × 103 | 3.651 × 103 | 4.026 × 103 | 2.520 × 103 | 3.445 × 103 | 2.786 × 103 | 4.384 × 105 | 2.626 × 103 | 2.560 × 103 | 3.282 × 103 |
| Mean | 9.556 × 104 | 7.830 × 105 | 1.708 × 105 | 4.179 × 105 | 3.588 × 105 | 9.797 × 104 | 1.144 × 105 | 4.429 × 104 | 7.965 × 104 | 2.032 × 105 | 1.006 × 107 | 2.060 × 104 | 1.145 × 104 | 9.740 × 103 | |
| Std | 7.971 × 104 | 6.335 × 105 | 1.949 × 105 | 6.434 × 105 | 2.483 × 105 | 8.431 × 104 | 1.515 × 105 | 7.554 × 104 | 1.520 × 105 | 1.529 × 105 | 1.159 × 107 | 3.270 × 104 | 6.384 × 103 | 5.862 × 103 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 2.127 × 10−6 | 3.515 × 10−6 | 1.734 × 10−6 | 3.882 × 10−6 | 1.127 × 10−5 | 5.667 × 10−3 | 2.849 × 10−2 | 3.515 × 10−6 | 1.734 × 10−6 | 8.290 × 10−1 | 2.452 × 10−1 | ~ | |
| Rank | 8 | 13 | 10 | 11 | 12 | 7 | 6 | 4 | 5 | 9 | 14 | 1 | 3 | 2 | |
| F6 | Best | 1.622 × 103 | 1.667 × 103 | 1.875 × 103 | 1.629 × 103 | 1.604 × 103 | 1.666 × 103 | 1.646 × 103 | 1.601 × 103 | 1.642 × 103 | 1.639 × 103 | 2.113 × 103 | 1.724 × 103 | 1.604 × 103 | 1.610 × 103 |
| Mean | 1.787 × 103 | 1.830 × 103 | 1.991 × 103 | 1.836 × 103 | 1.881 × 103 | 1.879 × 103 | 1.969 × 103 | 1.764 × 103 | 1.884 × 103 | 1.851 × 103 | 2.724 × 103 | 1.978 × 103 | 1.629 × 103 | 1.640 × 103 | |
| Std | 1.014 × 102 | 7.346 × 101 | 6.859 × 101 | 9.580 × 101 | 1.671 × 102 | 1.116 × 102 | 2.008 × 102 | 1.373 × 102 | 1.450 × 102 | 1.289 × 102 | 2.477 × 102 | 1.262 × 102 | 1.663 × 101 | 2.224 × 101 | |
| p | 1.921 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.921 × 10−6 | 1.921 × 10−6 | 1.734 × 10−6 | 1.921 × 10−6 | 2.831 × 10−4 | 1.921 × 10−6 | 1.921 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 2.703 × 10−2 | ~ | |
| Rank | 4 | 6 | 13 | 5 | 8 | 10 | 11 | 3 | 9 | 7 | 14 | 12 | 1 | 2 | |
| F7 | Best | 4.155 × 103 | 2.024 × 104 | 5.643 × 103 | 3.626 × 103 | 4.122 × 103 | 3.653 × 103 | 6.712 × 103 | 2.381 × 103 | 2.330 × 103 | 2.830 × 103 | 5.623 × 104 | 2.676 × 103 | 2.292 × 103 | 2.288 × 103 |
| Mean | 1.735 × 104 | 2.769 × 105 | 3.260 × 105 | 4.441 × 105 | 5.679 × 105 | 1.217 × 104 | 6.326 × 105 | 8.418 × 103 | 1.190 × 104 | 6.809 × 104 | 4.980 × 106 | 8.061 × 103 | 2.836 × 103 | 2.740 × 103 | |
| Std | 9.366 × 103 | 1.783 × 105 | 5.082 × 105 | 9.759 × 105 | 1.057 × 106 | 8.113 × 103 | 1.271 × 106 | 8.456 × 103 | 1.083 × 104 | 1.341 × 105 | 7.005 × 106 | 5.316 × 103 | 3.142 × 102 | 3.144 × 102 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.025 × 10−5 | 2.127 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.921 × 10−6 | 2.289 × 10−1 | ~ | |
| Rank | 7 | 13 | 9 | 12 | 11 | 6 | 10 | 3 | 5 | 8 | 14 | 4 | 2 | 1 | |
| F8 | Best | 2.314 × 103 | 2.317 × 103 | 2.300 × 103 | 2.268 × 103 | 2.302 × 103 | 2.323 × 103 | 2.280 × 103 | 2.213 × 103 | 2.252 × 103 | 2.261 × 103 | 3.146 × 103 | 2.277 × 103 | 2.291 × 103 | 2.285 × 103 |
| Mean | 2.394 × 103 | 2.569 × 103 | 2.619 × 103 | 2.317 × 103 | 2.459 × 103 | 2.763 × 103 | 2.583 × 103 | 2.301 × 103 | 2.361 × 103 | 2.385 × 103 | 3.876 × 103 | 2.356 × 103 | 2.306 × 103 | 2.300 × 103 | |
| Std | 4.532 × 101 | 1.115 × 1002 | 5.178 × 102 | 1.598 × 101 | 1.312 × 102 | 2.167 × 102 | 2.400 × 102 | 2.644 × 101 | 5.474 × 101 | 5.418 × 101 | 4.149 × 102 | 4.495 × 101 | 3.329 × 100 | 2.865 × 100 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 6.435 × 10−1 | 2.052 × 10−4 | 1.734 × 10−6 | 1.734 × 10−6 | 1.921 × 10−6 | 2.765 × 10−3 | 2.597 × 10−5 | 2.603 × 10−6 | 1.734 × 10−6 | 4.286 × 10−6 | 2.370 × 10−5 | ~ | |
| Rank | 9 | 12 | 5 | 4 | 10 | 13 | 11 | 2 | 7 | 8 | 14 | 6 | 3 | 1 | |
| F9 | Best | 2.591 × 103 | 2.675 × 103 | 2.791 × 103 | 2.538 × 103 | 2.544 × 103 | 2.671 × 103 | 2.573 × 103 | 2.512 × 103 | 2.544 × 103 | 2.508 × 103 | 2.849 × 103 | 2.522 × 103 | 2.581 × 103 | 2.598 × 103 |
| Mean | 2.763 × 103 | 2.763 × 103 | 2.809 × 103 | 2.768 × 103 | 2.791 × 103 | 2.788 × 103 | 2.803 × 103 | 2.740 × 103 | 2.760 × 103 | 2.775 × 103 | 2.958 × 103 | 2.781 × 103 | 2.733 × 103 | 2.733 × 103 | |
| Std | 5.035 × 101 | 3.334 × 101 | 8.519 × 100 | 6.581 × 101 | 8.131 × 101 | 5.123 × 101 | 9.564 × 101 | 7.332 × 101 | 7.312 × 101 | 7.508 × 101 | 6.457 × 101 | 9.228 × 101 | 4.037 × 101 | 3.922 × 101 | |
| p | 1.593 × 10−3 | 8.217 × 10−3 | 1.734 × 10−6 | 3.589 × 10−4 | 4.390 × 10−3 | 4.534 × 10−4 | 4.390 × 10−3 | 1.319 × 10−2 | 2.765 × 10−3 | 1.833 × 10−3 | 1.734 × 10−6 | 1.833 × 10−3 | 5.038 × 10−1 | ~ | |
| Rank | 5 | 4 | 13 | 7 | 10 | 9 | 12 | 3 | 6 | 8 | 14 | 11 | 2 | 1 | |
| F10 | Best | 2.946 × 103 | 2.976 × 103 | 2.936 × 103 | 2.872 × 103 | 2.927 × 103 | 2.967 × 103 | 2.966 × 103 | 2.898 × 103 | 2.949 × 103 | 2.926 × 103 | 3.195 × 103 | 2.746 × 103 | 2.906 × 103 | 2.901 × 103 |
| Mean | 2.994 × 103 | 3.011 × 103 | 3.091 × 103 | 2.953 × 103 | 3.054 × 103 | 3.177 × 103 | 3.066 × 103 | 2.938 × 103 | 2.994 × 103 | 2.992 × 103 | 4.211 × 103 | 2.994 × 103 | 2.941 × 103 | 2.935 × 103 | |
| Std | 2.928 × 101 | 1.993 × 101 | 7.328 × 101 | 3.128 × 101 | 1.210 × 102 | 1.160 × 102 | 8.135 × 101 | 2.818 × 101 | 4.673 × 101 | 4.779 × 101 | 5.076 × 102 | 9.466 × 101 | 9.829 × 100 | 1.621 × 101 | |
| p | 1.921 × 10−6 | 1.734 × 10−6 | 1.921 × 10−6 | 1.108 × 10−2 | 2.127 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 8.936 × 10−1 | 1.734 × 10−6 | 2.127 × 10−6 | 1.734 × 10−6 | 4.534 × 10−4 | 1.254 × 10−1 | ~ | |
| Rank | 8 | 10 | 12 | 4 | 9 | 13 | 11 | 3 | 7 | 6 | 14 | 5 | 2 | 1 | |
| Mean Rank | 7.5 | 9.3 | 10.2 | 6.5 | 9.4 | 10.6 | 10.1 | 2.9 | 6.7 | 8.4 | 14 | 6 | 2 | 1.4 | |
| Final Ranking | 7 | 9 | 12 | 5 | 10 | 13 | 11 | 3 | 6 | 8 | 14 | 4 | 2 | 1 | |
| +/=/− | 10/0/0 | 10/0/0 | 10/1/0 | 10/0/0 | 10/0/0 | 10/0/0 | 10/0/0 | 5/4/1 | 10/0/0 | 10/0/0 | 10/0/0 | 9/1/0 | 4/6/1 | ~ | |
| Function | Item Name | PSO | DE | CMA-ES | WOA | HHO | CL-PSO | NC-HHO | DBO | HO | HOA | AOA | TG-COA | APO | EAPO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Best | 2.632 × 109 | 2.397 × 109 | 8.724 × 109 | 2.643 × 107 | 7.027 × 108 | 1.255 × 1010 | 5.643 × 109 | 1.020 × 103 | 2.552 × 109 | 5.216 × 109 | 2.975 × 1010 | 1.317 × 109 | 2.450 × 105 | 6.582 × 103 |
| Mean | 6.571 × 109 | 3.968 × 109 | 1.744 × 1010 | 7.331 × 107 | 8.219 × 109 | 2.171 × 1010 | 1.091 × 1010 | 3.373 × 106 | 7.716 × 109 | 1.028 × 1010 | 5.106 × 1010 | 7.270 × 109 | 5.500 × 105 | 1.460 × 104 | |
| Std | 1.771 × 109 | 8.734 × 108 | 5.121 × 109 | 3.515 × 107 | 4.500 × 109 | 5.131 × 109 | 3.607 × 109 | 5.604 × 106 | 3.094 × 109 | 3.266 × 109 | 9.958 × 109 | 3.034 × 109 | 2.535 × 105 | 6.298 × 103 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 4.897 × 10−4 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | ~ | |
| Rank | 6 | 5 | 12 | 4 | 9 | 13 | 11 | 2 | 8 | 10 | 14 | 7 | 3 | 1 | |
| F2 | Best | 4.315 × 103 | 3.195 × 103 | 4.917 × 103 | 3.080 × 103 | 3.110 × 103 | 3.944 × 103 | 3.779 × 103 | 2.043 × 103 | 3.641 × 103 | 3.059 × 103 | 6.326 × 103 | 3.694 × 103 | 1.995 × 103 | 2.454 × 103 |
| Mean | 5.108 × 103 | 3.660 × 103 | 5.629 × 103 | 3.915 × 103 | 4.521 × 103 | 4.529 × 103 | 4.785 × 103 | 2.937 × 103 | 4.732 × 103 | 3.961 × 103 | 6.848 × 103 | 4.634 × 103 | 2.617 × 103 | 2.880 × 103 | |
| Std | 4.130 × 102 | 2.002 × 102 | 2.743 × 102 | 5.294 × 102 | 5.172 × 102 | 2.645 × 102 | 5.263 × 102 | 5.088 × 102 | 5.072 × 102 | 4.745 × 102 | 2.627 × 102 | 4.499 × 102 | 2.547 × 102 | 2.373 × 102 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.921 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 6.435 × 10−1 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.965 × 10−3 | ~ | |
| Rank | 12 | 4 | 13 | 5 | 7 | 8 | 11 | 3 | 10 | 6 | 14 | 9 | 1 | 2 | |
| F3 | Best | 1.030 × 103 | 9.732 × 102 | 8.036 × 102 | 8.245 × 102 | 9.237 × 102 | 9.984 × 102 | 9.553 × 102 | 7.403 × 102 | 8.901 × 102 | 8.331 × 102 | 1.817 × 103 | 8.114 × 102 | 7.426 × 102 | 7.592 × 102 |
| Mean | 1.154 × 103 | 1.067 × 103 | 8.185 × 102 | 9.458 × 102 | 1.001 × 103 | 1.172 × 103 | 9.995 × 102 | 7.853 × 102 | 9.408 × 102 | 8.743 × 102 | 2.112 × 103 | 9.554 × 102 | 7.548 × 102 | 7.768 × 102 | |
| Std | 7.951 × 101 | 4.047 × 101 | 5.706 × 100 | 5.474 × 101 | 3.539 × 101 | 9.090 × 101 | 2.549 × 101 | 3.405 × 101 | 2.765 × 101 | 2.982 × 101 | 1.571 × 102 | 5.832 × 101 | 6.289 × 100 | 7.849 × 100 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 3.933 × 10−1 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | ~ | |
| Rank | 12 | 11 | 4 | 7 | 10 | 13 | 9 | 3 | 6 | 5 | 14 | 8 | 1 | 2 | |
| F4 | Best | 2.000 × 103 | 2.115 × 103 | 4.075 × 103 | 1.916 × 103 | 2.272 × 103 | 4.361 × 104 | 2.049 × 103 | 1.904 × 103 | 2.225 × 103 | 2.614 × 103 | 1.259 × 106 | 2.071 × 103 | 1.903 × 103 | 1.904 × 103 |
| Mean | 6.563 × 103 | 4.053 × 103 | 1.306 × 105 | 1.982 × 103 | 3.421 × 104 | 3.881 × 105 | 3.771 × 104 | 1.916 × 103 | 8.683 × 103 | 2.810 × 104 | 6.543 × 106 | 1.934 × 104 | 1.904 × 103 | 1.906 × 103 | |
| Std | 6.587 × 103 | 9.507 × 102 | 9.504 × 104 | 9.119 × 101 | 3.859 × 104 | 3.382 × 105 | 5.154 × 104 | 1.224 × 101 | 7.711 × 103 | 2.500 × 104 | 3.256 × 106 | 3.479 × 104 | 6.551 × 10−1 | 7.098 × 10−1 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 4.449 × 10−5 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 2.603 × 10−6 | ~ | |
| Rank | 6 | 5 | 12 | 4 | 10 | 13 | 9 | 3 | 7 | 11 | 14 | 8 | 1 | 2 | |
| F5 | Best | 7.484 × 105 | 1.185 × 106 | 1.286 × 106 | 9.891 × 104 | 1.651 × 105 | 6.724 × 105 | 2.584 × 105 | 3.771 × 104 | 2.774 × 105 | 7.996 × 104 | 1.604 × 107 | 7.094 × 104 | 3.756 × 104 | 2.718 × 104 |
| Mean | 2.824 × 106 | 4.837 × 106 | 9.443 × 106 | 1.748 × 106 | 2.123 × 106 | 3.397 × 106 | 2.022 × 106 | 6.159 × 105 | 1.978 × 106 | 1.272 × 106 | 8.384 × 107 | 7.290 × 105 | 1.060 × 105 | 8.271 × 104 | |
| Std | 1.533 × 106 | 2.432 × 106 | 6.965 × 106 | 1.427 × 106 | 1.595 × 106 | 2.106 × 106 | 1.388 × 106 | 6.742 × 105 | 1.170 × 106 | 7.694 × 105 | 5.529 × 107 | 5.763 × 105 | 3.577 × 104 | 3.598 × 104 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 2.353 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 2.353 × 10−6 | 3.160 × 10−2 | ~ | |
| Rank | 10 | 12 | 13 | 6 | 8 | 11 | 7 | 3 | 9 | 5 | 14 | 4 | 2 | 1 | |
| F6 | Best | 2.061 × 103 | 1.689 × 103 | 2.339 × 103 | 1.789 × 103 | 2.052 × 103 | 2.249 × 103 | 2.292 × 103 | 1.623 × 103 | 2.032 × 103 | 1.840 × 103 | 3.405 × 103 | 2.392 × 103 | 1.645 × 103 | 1.666 × 103 |
| Mean | 2.394 × 103 | 1.800 × 103 | 2.761 × 103 | 2.482 × 103 | 2.721 × 103 | 2.588 × 103 | 2.866 × 103 | 1.983 × 103 | 2.540 × 103 | 2.367 × 103 | 4.277 × 103 | 2.853 × 103 | 1.696 × 103 | 1.719 × 103 | |
| Std | 1.949 × 102 | 6.006 × 101 | 1.895 × 102 | 3.223 × 102 | 3.749 × 102 | 1.656 × 102 | 3.243 × 102 | 1.785 × 102 | 2.824 × 102 | 2.680 × 102 | 3.995 × 102 | 3.218 × 102 | 3.377 × 101 | 2.865 × 101 | |
| p | 1.734 × 10−6 | 5.216 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 4.286 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.114 × 10−3 | ~ | |
| Rank | 6 | 3 | 11 | 7 | 10 | 9 | 12 | 4 | 8 | 5 | 14 | 13 | 1 | 2 | |
| F7 | Best | 1.815 × 105 | 4.964 × 105 | 3.600 × 105 | 8.786 × 104 | 6.482 × 104 | 9.171 × 104 | 1.301 × 105 | 9.613 × 103 | 1.271 × 105 | 7.606 × 104 | 6.979 × 106 | 1.716 × 104 | 4.283 × 103 | 4.901 × 103 |
| Mean | 8.156 × 105 | 1.835 × 106 | 4.209 × 106 | 1.141 × 106 | 5.698 × 105 | 7.369 × 105 | 1.203 × 106 | 2.384 × 105 | 7.795 × 105 | 5.922 × 105 | 4.887 × 107 | 2.358 × 105 | 2.246 × 104 | 1.569 × 104 | |
| Std | 4.977 × 105 | 9.568 × 105 | 3.407 × 106 | 1.001 × 106 | 4.257 × 105 | 5.173 × 105 | 1.243 × 106 | 2.979 × 105 | 6.737 × 105 | 4.792 × 105 | 3.804 × 107 | 2.343 × 105 | 2.143 × 104 | 1.281 × 104 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 2.353 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.921 × 10−6 | 3.286 × 10−1 | ~ | |
| Rank | 9 | 12 | 13 | 10 | 5 | 8 | 11 | 3 | 7 | 6 | 14 | 4 | 2 | 1 | |
| F8 | Best | 2.736 × 103 | 3.869 × 103 | 3.745 × 103 | 2.319 × 103 | 2.802 × 103 | 3.513 × 103 | 3.427 × 103 | 2.300 × 103 | 2.470 × 103 | 2.795 × 103 | 6.215 × 103 | 2.594 × 103 | 2.309 × 103 | 2.300 × 103 |
| Mean | 5.002 × 103 | 4.603 × 103 | 6.617 × 103 | 3.876 × 103 | 5.264 × 103 | 5.508 × 103 | 5.157 × 103 | 2.656 × 103 | 2.953 × 103 | 4.036 × 103 | 8.159 × 103 | 4.620 × 103 | 2.312 × 103 | 2.302 × 103 | |
| Std | 1.834 × 103 | 4.044 × 102 | 7.734 × 102 | 1.857 × 103 | 1.135 × 103 | 6.683 × 102 | 1.056 × 103 | 7.745 × 102 | 4.155 × 102 | 1.239 × 103 | 5.592 × 102 | 1.555 × 103 | 1.547 × 100 | 1.209 × 100 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 3.182 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | ~ | |
| Rank | 9 | 8 | 13 | 5 | 11 | 12 | 10 | 3 | 4 | 6 | 14 | 7 | 2 | 1 | |
| F9 | Best | 2.914 × 103 | 2.922 × 103 | 2.983 × 103 | 2.915 × 103 | 2.935 × 103 | 2.990 × 103 | 3.029 × 103 | 2.851 × 103 | 2.947 × 103 | 3.063 × 103 | 3.245 × 103 | 3.006 × 103 | 2.822 × 103 | 2.835 × 103 |
| Mean | 2.952 × 103 | 2.951 × 103 | 3.026 × 103 | 2.984 × 103 | 3.118 × 103 | 3.087 × 103 | 3.286 × 103 | 2.899 × 103 | 3.062 × 103 | 3.194 × 103 | 3.604 × 103 | 3.189 × 103 | 2.841 × 103 | 2.848 × 103 | |
| Std | 2.943 × 101 | 1.064 × 101 | 2.039 × 101 | 5.029 × 101 | 1.038 × 102 | 4.947 × 101 | 1.238 × 102 | 2.145 × 101 | 7.490 × 101 | 7.417 × 101 | 1.602 × 102 | 1.091 × 102 | 7.777 × 100 | 6.755 × 100 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 2.415 × 10−3 | ~ | |
| Rank | 4 | 5 | 7 | 6 | 10 | 9 | 13 | 3 | 8 | 12 | 14 | 11 | 1 | 2 | |
| F10 | Best | 3.073 × 103 | 3.153 × 103 | 3.629 × 103 | 2.928 × 103 | 3.163 × 103 | 4.006 × 103 | 3.141 × 103 | 2.914 × 103 | 3.065 × 103 | 3.114 × 103 | 5.833 × 103 | 3.046 × 103 | 2.914 × 103 | 2.914 × 103 |
| Mean | 3.293 × 103 | 3.438 × 103 | 4.287 × 103 | 3.025 × 103 | 3.696 × 103 | 4.902 × 103 | 3.624 × 103 | 2.961 × 103 | 3.326 × 103 | 3.514 × 103 | 1.067 × 104 | 3.429 × 103 | 2.947 × 103 | 2.945 × 103 | |
| Std | 1.705 × 102 | 1.438 × 102 | 4.686 × 102 | 4.541 × 101 | 3.981 × 102 | 5.709 × 102 | 3.066 × 102 | 5.800 × 101 | 1.956 × 102 | 1.919 × 102 | 2.319 × 103 | 2.425 × 102 | 3.088 × 101 | 3.088 × 101 | |
| p | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 4.286 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 4.405 × 10−1 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 1.734 × 10−6 | 9.426 × 10−1 | ~ | |
| Rank | 5 | 8 | 12 | 4 | 11 | 13 | 10 | 2 | 6 | 9 | 14 | 7 | 3 | 1 | |
| Mean Rank | 7.9 | 7.3 | 11 | 5.8 | 9.1 | 10.9 | 10.3 | 2.9 | 7.3 | 7.5 | 14 | 7.8 | 1.7 | 1.5 | |
| Final Ranking | 9 | 5 | 13 | 4 | 10 | 12 | 11 | 3 | 5 | 7 | 14 | 8 | 2 | 1 | |
| +/=/− | 10/0/0 | 10/0/0 | 10/0/0 | 10/0/0 | 10/0/0 | 10/0/0 | 10/0/0 | 7/3/0 | 10/0/0 | 10/0/0 | 10/0/0 | 9/1/0 | 4/2/4 | ~ | |
| Function | Item Name | PSO | DE | CMA-ES | WOA | HHO | CL-PSO | NC-HHO | DBO | HO | HOA | AOA | TG-COA | APO | EAPO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RW01 | Best | 5.199 × 1015 | 7.031 × 1013 | 9.257 × 1021 | 2.354 × 1013 | 4.887 × 1010 | 9.257 × 1021 | 7.779 × 1013 | 7.049 × 103 | 2.896 × 1014 | 2.176 × 1016 | 1.137 × 1017 | 1.131 × 1015 | 4.699 × 109 | 5.036 × 107 |
| Mean | 3.636 × 1016 | 2.487 × 1014 | 9.257 × 1021 | 4.408 × 1014 | 1.083 × 1015 | 9.270 × 1021 | 1.201 × 1015 | 3.834 × 1014 | 1.167 × 1016 | 5.948 × 1016 | 4.777 × 1017 | 2.309 × 1016 | 6.585 × 1010 | 3.224 × 109 | |
| Std | 2.852 × 1016 | 1.209 × 1014 | 7.466 × 1006 | 2.938 × 1014 | 3.288 × 1015 | 1.880 × 1019 | 1.419 × 1015 | 6.695 × 1014 | 1.280 × 1016 | 2.446 × 1016 | 1.726 × 1017 | 2.192 × 1016 | 4.587 × 1010 | 5.103 × 109 | |
| p | 3.020 × 10−11 | 3.020 × 10−11 | 1.212 × 10−12 | 3.020 × 10−11 | 3.020 × 10−11 | 2.982 × 10−11 | 3.020 × 10−11 | 6.607 × 10−01 | 3.020 × 10−11 | 3.020 × 10−11 | 3.020 × 10−11 | 3.020 × 10−11 | 8.993 × 10−11 | 3.020 × 10−11 | |
| Rank | 10 | 5 | 13 | 6 | 4 | 14 | 7 | 3 | 8 | 11 | 12 | 9 | 2 | 1 | |
| RW02 | Best | 2.514 × 100 | 2.644 × 100 | 7.883 × 100 | 2.828 × 100 | 3.243 × 100 | 5.102 × 102 | 3.243 × 100 | 1.102 × 100 | 3.035 × 100 | 9.474 × 100 | 1.243 × 102 | 9.245 × 100 | 1.920 × 100 | 1.405 × 100 |
| Mean | 8.391 × 100 | 3.177 × 100 | 1.027 × 101 | 5.049 × 100 | 7.466 × 101 | 2.541 × 104 | 1.662 × 101 | 2.373 × 100 | 5.819 × 100 | 2.168 × 101 | 2.192 × 102 | 2.653 × 101 | 2.579 × 100 | 1.926 × 100 | |
| Std | 5.649 × 100 | 2.961 × 10−1 | 4.875 × 100 | 4.556 × 100 | 6.273 × 101 | 2.576 × 104 | 1.006 × 101 | 9.085 × 10−1 | 4.238 × 100 | 7.489 × 100 | 4.877 × 101 | 1.101 × 101 | 2.510 × 10−1 | 2.706 × 10−1 | |
| p | 3.020 × 10−11 | 3.020 × 10−11 | 6.387 × 10−12 | 3.020 × 10−11 | 2.521 × 10−11 | 3.020 × 10−11 | 3.020 × 10−11 | 1.911 × 10−02 | 3.012 × 10−11 | 3.020 × 10−11 | 3.020 × 10−11 | 3.020 × 10−11 | 1.070 × 10−9 | 3.020 × 10−11 | |
| Rank | 7 | 4 | 8 | 5 | 12 | 14 | 9 | 2 | 6 | 10 | 13 | 11 | 3 | 1 | |
| RW03 | Best | 2.324 × 100 | 2.669 × 100 | 6.356 × 101 | 2.067 × 100 | 2.672 × 100 | 2.627 × 102 | 3.143 × 100 | 1.282 × 100 | 2.663 × 100 | 9.996 × 100 | 3.348 × 101 | 5.703 × 100 | 2.052 × 100 | 1.345 × 100 |
| Mean | 6.313 × 100 | 3.333 × 100 | 7.183 × 101 | 2.929 × 100 | 9.258 × 100 | 1.623 × 103 | 9.347 × 100 | 2.419 × 100 | 6.088 × 100 | 1.529 × 101 | 4.998 × 101 | 1.170 × 101 | 2.476 × 100 | 1.615 × 100 | |
| Std | 3.428 × 100 | 3.401 × 10−1 | 5.558 × 100 | 4.773 × 10−1 | 6.093 × 100 | 1.123 × 103 | 4.455 × 100 | 4.628 × 10−1 | 1.852 × 100 | 2.989 × 100 | 8.998 × 100 | 3.332 × 100 | 2.033 × 10−1 | 2.041 × 10−1 | |
| p | 3.020 × 10−11 | 3.020 × 10−11 | 2.932 × 10−11 | 3.685 × 10−11 | 3.020 × 10−11 | 3.020 × 10−11 | 3.020 × 10−11 | 6.518 × 10−9 | 3.020 × 10−11 | 3.020 × 10−11 | 3.020 × 10−11 | 3.020 × 10−11 | 4.077 × 10−11 | 3.020 × 10−11 | |
| Rank | 6 | 5 | 13 | 4 | 8 | 14 | 9 | 2 | 7 | 11 | 12 | 10 | 3 | 1 | |
| RW04 | Best | 3.907 × 100 | 3.010 × 100 | 1.117 × 101 | 2.951 × 100 | 4.762 × 100 | 8.280 × 100 | 2.926 × 100 | 2.925 × 100 | 2.925 × 100 | 2.928 × 100 | 1.412 × 109 | 4.618 × 100 | 2.925 × 100 | 2.926 × 100 |
| Mean | 6.534 × 100 | 6.412 × 100 | 1.615 × 101 | 5.419 × 100 | 7.964 × 100 | 1.178 × 101 | 3.782 × 100 | 4.040 × 100 | 3.327 × 100 | 3.903 × 100 | 2.492 × 1012 | 4.799 × 100 | 2.947 × 100 | 2.937 × 100 | |
| Std | 1.709 × 100 | 3.113 × 100 | 1.313 × 100 | 2.015 × 100 | 2.035 × 100 | 2.717 × 100 | 8.537 × 10−1 | 9.609 × 10−1 | 5.337 × 10−1 | 6.146 × 10−1 | 6.830 × 1012 | 2.023 × 10−1 | 3.861 × 10−2 | 1.323 × 10−2 | |
| p | 3.020 × 10−11 | 3.012 × 10−11 | 2.088 × 10−11 | 6.066 × 10−11 | 3.020 × 10−11 | 3.009 × 10−11 | 9.260 × 10−9 | 1.269 × 10−8 | 3.010 × 10−7 | 3.197 × 10−9 | 3.020 × 10−11 | 3.020 × 10−11 | 9.234 × 10−01 | 3.020 × 10−11 | |
| Rank | 10 | 9 | 13 | 8 | 11 | 12 | 4 | 5 | 3 | 6 | 14 | 7 | 2 | 1 | |
| RW05 | Best | 5.507 × 104 | 5.551 × 104 | 7.663 × 1011 | 6.260 × 104 | 6.504 × 104 | 7.663 × 1011 | 5.747 × 104 | 5.380 × 104 | 6.414 × 104 | 6.567 × 104 | 1.261 × 105 | 6.739 × 104 | 5.407 × 104 | 5.368 × 104 |
| Mean | 6.789 × 104 | 5.892 × 104 | 7.663 × 1011 | 8.824 × 104 | 9.873 × 104 | 7.663 × 1011 | 8.248 × 104 | 6.388 × 104 | 7.502 × 104 | 8.515 × 104 | 2.044 × 106 | 9.069 × 104 | 5.528 × 104 | 5.472 × 104 | |
| Std | 9.398 × 103 | 1.731 × 103 | 3.725 × 10−4 | 1.484 × 104 | 2.619 × 104 | 1.885 × 106 | 1.823 × 104 | 1.284 × 104 | 7.852 × 103 | 1.034 × 104 | 2.850 × 106 | 1.062 × 104 | 1.401 × 103 | 1.243 × 103 | |
| p | 2.154 × 10−10 | 4.200 × 10−10 | 1.212 × 10−12 | 3.020 × 10−11 | 3.020 × 10−11 | 2.232 × 10−11 | 3.690 × 10−11 | 1.385 × 10−6 | 3.020 × 10−11 | 3.020 × 10−11 | 3.020 × 10−11 | 3.020 × 10−11 | 2.709 × 10−2 | 2.154 × 10−10 | |
| Rank | 5 | 3 | 13 | 8 | 10 | 14 | 7 | 4 | 6 | 9 | 12 | 11 | 2 | 1 | |
| RW06 | Best | 5.833 × 10−2 | 4.474 × 10−1 | 5.925 × 103 | 7.620 × 10−2 | 1.371 × 100 | 1.619 × 103 | 1.753 × 100 | 4.424 × 10−2 | 5.685 × 100 | 2.090 × 100 | 6.628 × 106 | 6.435 × 103 | 5.173 × 10−2 | 3.663 × 10−2 |
| Mean | 1.220 × 105 | 4.346 × 100 | 6.748 × 104 | 1.513 × 105 | 1.617 × 106 | 6.079 × 105 | 5.300 × 104 | 8.748 × 104 | 1.195 × 106 | 1.180 × 103 | 5.973 × 107 | 1.159 × 106 | 3.062 × 104 | 1.872 × 104 | |
| Std | 4.733 × 105 | 4.329 × 100 | 1.950 × 105 | 2.419 × 105 | 3.726 × 106 | 5.654 × 105 | 1.470 × 105 | 9.512 × 104 | 1.740 × 106 | 2.240 × 103 | 4.988 × 107 | 1.328 × 106 | 6.899 × 104 | 5.713 × 104 | |
| p | 5.462 × 10−6 | 1.868 × 10−5 | 8.131 × 10−8 | 8.352 × 10−8 | 6.010 × 10−8 | 4.200 × 10−10 | 1.359 × 10−7 | 1.111 × 10−3 | 1.174 × 10−9 | 1.596 × 10−7 | 3.020 × 10−11 | 5.573 × 10−10 | 1.004 × 10−3 | 5.462 × 10−6 | |
| Rank | 4 | 2 | 10 | 8 | 9 | 12 | 7 | 5 | 11 | 6 | 14 | 13 | 3 | 1 | |
| RW07 | Best | 5.762 × 103 | 5.745 × 103 | 6.183 × 103 | 5.921 × 103 | 6.322 × 103 | 6.181 × 103 | 6.100 × 103 | 5.743 × 103 | 5.918 × 103 | 6.161 × 103 | 9.732 × 103 | 5.746 × 103 | 5.743 × 103 | 5.746 × 103 |
| Mean | 6.314 × 103 | 6.012 × 103 | 6.420 × 103 | 7.285 × 103 | 1.005 × 104 | 6.352 × 103 | 8.443 × 103 | 5.926 × 103 | 6.846 × 103 | 6.719 × 103 | 2.152 × 104 | 6.783 × 103 | 5.923 × 103 | 5.888 × 103 | |
| Std | 5.552 × 102 | 1.262 × 102 | 2.962 × 102 | 1.289 × 103 | 3.381 × 103 | 2.007 × 102 | 3.291 × 103 | 2.855 × 102 | 9.953 × 102 | 3.610 × 102 | 7.230 × 103 | 1.094 × 103 | 1.623 × 102 | 1.023 × 102 | |
| p | 2.126 × 10−4 | 2.891 × 10−3 | 1.174 × 10−9 | 2.439 × 10−9 | 3.690 × 10−11 | 8.101 × 10−10 | 5.494 × 10−11 | 1.180 × 10−1 | 5.462 × 10−9 | 9.919 × 10−11 | 3.020 × 10−11 | 1.385 × 10−6 | 7.845 × 10−1 | 2.126 × 10−4 | |
| Rank | 5 | 4 | 8 | 11 | 13 | 6 | 12 | 2 | 9 | 10 | 14 | 7 | 3 | 1 | |
| RW08 | Best | 1.821 × 101 | 1.611 × 101 | 1.010 × 1010 | 1.619 × 101 | 1.655 × 101 | 1.010 × 1010 | 1.652 × 101 | 1.604 × 101 | 1.633 × 101 | 1.640 × 101 | 9.152 × 102 | 1.606 × 101 | 1.606 × 101 | 1.605 × 101 |
| Mean | 2.145 × 101 | 1.675 × 101 | 1.010 × 1010 | 1.684 × 101 | 1.068 × 102 | 1.010 × 1010 | 3.900 × 101 | 1.711 × 101 | 1.791 × 101 | 1.998 × 101 | 2.447 × 109 | 3.502 × 101 | 1.636 × 101 | 1.616 × 101 | |
| Std | 4.588 × 100 | 3.519 × 10−1 | 1.185 × 102 | 2.642 × 10−1 | 3.133 × 102 | 2.899 × 101 | 2.668 × 101 | 1.994 × 100 | 1.967 × 100 | 9.937 × 100 | 2.196 × 109 | 2.943 × 101 | 2.289 × 10−1 | 1.642 × 10−1 | |
| p | 3.020 × 10−11 | 4.573 × 10−9 | 3.020 × 10−11 | 1.613 × 10−10 | 3.690 × 10−11 | 3.020 × 10−11 | 5.494 × 10−11 | 3.912 × 10−2 | 1.464 × 10−10 | 8.993 × 10−11 | 3.020 × 10−11 | 7.773 × 10−9 | 1.430 × 10−5 | 3.020 × 10−11 | |
| Rank | 10 | 4 | 14 | 5 | 11 | 13 | 9 | 3 | 6 | 7 | 12 | 8 | 2 | 1 | |
| RW09 | Best | 5.313 × 106 | 7.108 × 104 | 4.422 × 106 | 3.539 × 104 | 1.926 × 105 | 1.016 × 1010 | 4.538 × 104 | 4.525 × 103 | 4.291 × 104 | 1.653 × 106 | 2.757 × 1010 | 8.635 × 104 | 2.493 × 105 | 1.934 × 104 |
| Mean | 1.345 × 109 | 2.362 × 105 | 5.089 × 107 | 8.291 × 105 | 6.760 × 106 | 1.406 × 1010 | 6.792 × 105 | 1.555 × 105 | 4.936 × 105 | 3.040 × 106 | 3.375 × 1010 | 1.347 × 106 | 9.880 × 105 | 4.434 × 104 | |
| Std | 7.180 × 108 | 1.380 × 105 | 1.924 × 107 | 4.172 × 105 | 4.956 × 106 | 2.018 × 109 | 3.451 × 105 | 2.646 × 105 | 4.274 × 105 | 8.519 × 105 | 2.691 × 109 | 1.337 × 106 | 4.279 × 105 | 2.822 × 104 | |
| p | 3.020 × 10−11 | 9.919 × 10−11 | 3.020 × 10−11 | 2.154 × 10−10 | 3.020 × 10−11 | 3.020 × 10−11 | 1.206 × 10−10 | 1.171 × 10−2 | 1.547 × 10−9 | 3.020 × 10−11 | 3.020 × 10−11 | 4.077 × 10−11 | 3.020 × 10−11 | 3.020 × 10−11 | |
| Rank | 12 | 3 | 11 | 6 | 9 | 13 | 5 | 2 | 4 | 10 | 14 | 7 | 8 | 1 | |
| RW10 | Best | 4.840 × 108 | 4.882 × 103 | 1.972 × 107 | 7.763 × 103 | 3.392 × 106 | 2.433 × 109 | 5.272 × 103 | 4.082 × 103 | 5.220 × 103 | 3.250 × 105 | 2.894 × 1010 | 2.787 × 104 | 4.618 × 103 | 4.136 × 103 |
| Mean | 3.708 × 109 | 7.854 × 103 | 6.825 × 107 | 1.942 × 105 | 8.833 × 106 | 6.574 × 109 | 3.572 × 104 | 6.643 × 103 | 1.804 × 104 | 1.557 × 106 | 3.532 × 1010 | 4.819 × 106 | 6.430 × 103 | 4.878 × 103 | |
| Std | 2.608 × 109 | 3.580 × 103 | 1.791 × 107 | 4.086 × 105 | 4.771 × 106 | 1.722 × 109 | 2.817 × 104 | 3.235 × 103 | 6.969 × 103 | 8.407 × 105 | 3.637 × 109 | 8.760 × 106 | 2.331 × 103 | 3.970 × 102 | |
| p | 3.020 × 10−11 | 3.020 × 10−11 | 3.020 × 10−11 | 3.020 × 10−11 | 3.020 × 10−11 | 3.020 × 10−11 | 3.020 × 10−11 | 6.414 × 10−01 | 3.020 × 10−11 | 3.020 × 10−11 | 3.020 × 10−11 | 3.020 × 10−11 | 3.020 × 10−11 | 3.020 × 10−11 | |
| Rank | 12 | 4 | 11 | 7 | 10 | 13 | 6 | 2 | 5 | 8 | 14 | 9 | 3 | 1 | |
| Mean Rank | 8.1 | 4.3 | 11.4 | 6.8 | 9.7 | 12.5 | 7.5 | 3 | 6.5 | 8.8 | 13 | 9.2 | 3.1 | 1 | |
| Final Ranking | 8 | 4 | 12 | 6 | 11 | 13 | 7 | 2 | 5 | 9 | 14 | 10 | 3 | 1 | |
| +/=/− | 10/0/0 | 10/0/0 | 10/0/0 | 10/0/0 | 10/0/0 | 10/0/0 | 10/0/0 | 7/3/0 | 10/0/0 | 10/0/0 | 10/0/0 | 10/0/0 | 8/2/0 | ~ | |
| Constraint Parameter | Symbol | Numerical Value |
|---|---|---|
| Minimum flight speed | ||
| Maximum flight speed | ||
| Maximum turn angle | ||
| Maximum climb angle | ||
| Maximum descent angle | ||
| Minimum turn radius | ||
| Maximum climb rate | ||
| Maximum descent rate | ||
| Minimum flight segment length | ||
| Minimum flight altitude | ||
| Maximum flight altitude | ||
| Safety margin coefficient | ||
| Minimum terrain clearance | ||
| Maximum acceleration | ||
| Maximum deceleration |
| Map | Starting Point | Target Point | Threat | No-Fly Zone | ||||
|---|---|---|---|---|---|---|---|---|
| Radar | Artillery | |||||||
| Center | R | Center | R | Center | R | |||
| 1 | (80, 80, 200) | (900, 800, 250) | (400, 500, 190) (600, 200, 220) | 100 100 | (300, 250, 200) | 100 | (700, 500) | 100 |
| 2 | (80, 80, 200) | (900, 800, 250) | (380, 420, 200) (550, 200, 215) (720, 650, 185) (250, 650, 195) | 85 75 70 80 | (150, 280, 215) (650, 450, 205) (820, 320, 180) | 95 85 90 | (540, 620) (850, 500) (350, 100) | 75 70 65 |
| 3 | (80, 80, 150) | (380, 380, 200) | (150, 380, 90) | 50 | (150, 125, 100) | 50 | (350, 250) | 60 |
| 4 | (80, 80, 150) | (380, 380, 200) | (200, 200, 105) (150, 75, 110) (410, 150, 85) | 45 40 40 | (85, 160, 110) (310, 250, 120) | 50 45 | (325, 135) (400, 300) (200, 330) | 40 45 45 |
| Map | Item Name | PSO | DE | WOA | DBO | HO | HOA | APO | EAPO |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Best | 5.997 × 10−1 | 6.431 × 10−1 | 5.984 × 10−1 | 5.635 × 10−1 | 5.809 × 10−1 | 1.180 × 10−1 | 9.865 × 10−2 | 8.854 × 10−2 |
| Mean | 6.409 × 10−1 | 6.699 × 10−1 | 6.883 × 10−1 | 5.897 × 10−1 | 6.050 × 10−1 | 5.468 × 10−1 | 4.524 × 10−1 | 3.451 × 10−1 | |
| Std | 2.433 × 10−2 | 1.360 × 10−2 | 8.804 × 10−2 | 1.660 × 10−2 | 1.466 × 10−2 | 1.131 × 10−1 | 2.245 × 10−1 | 2.449 × 10−1 | |
| Rank | 6 | 8 | 7 | 4 | 5 | 2 | 3 | 1 | |
| 2 | Best | 6.323 × 10−1 | 6.716 × 10−1 | 5.949 × 10−1 | 5.850 × 10−1 | 6.213 × 10−1 | 6.206 × 10−1 | 6.249 × 10−1 | 6.325 × 10−1 |
| Mean | 1.662 × 100 | 1.140 × 100 | 2.118 × 100 | 8.932 × 10−1 | 7.848 × 10−1 | 6.498 × 10−1 | 6.483 × 10−1 | 6.453 × 10−1 | |
| Std | 1.538 × 100 | 7.829 × 10−1 | 2.905 × 100 | 6.840 × 10−1 | 7.260 × 10−1 | 1.754 × 10−2 | 1.003 × 10−2 | 9.010 × 10−3 | |
| Rank | 7 | 8 | 6 | 1 | 4 | 5 | 3 | 2 | |
| 3 | Best | 6.266 × 10−1 | 6.398 × 10−1 | 6.007 × 10−1 | 6.041 × 10−1 | 6.400 × 10−1 | 6.494 × 10−1 | 6.200 × 10−1 | 6.130 × 10−1 |
| Mean | 6.423 × 10−1 | 6.496 × 10−1 | 6.636 × 10−1 | 6.199 × 10−1 | 6.545 × 10−1 | 6.684 × 10−1 | 6.237 × 10−1 | 6.194 × 10−1 | |
| Std | 8.482 × 10−3 | 4.902 × 10−3 | 4.046 × 10−2 | 9.723 × 10−3 | 1.145 × 10−2 | 1.244 × 10−2 | 2.320 × 10−3 | 3.072 × 10−3 | |
| Rank | 4 | 5 | 6 | 2 | 7 | 8 | 3 | 1 | |
| 4 | Best | 6.237 × 10−1 | 6.466 × 10−1 | 6.282 × 10−1 | 6.250 × 10−1 | 6.481 × 10−1 | 6.567 × 10−1 | 6.238 × 10−1 | 6.174 × 10−1 |
| Mean | 6.428 × 10−1 | 6.594 × 10−1 | 7.119 × 10−1 | 6.343 × 10−1 | 6.774 × 10−1 | 6.823 × 10−1 | 6.318 × 10−1 | 6.291 × 10−1 | |
| Std | 1.119 × 10−2 | 6.859 × 10−3 | 5.142 × 10−2 | 4.532 × 10−3 | 2.043 × 10−2 | 1.394 × 10−2 | 4.231 × 10−3 | 5.481 × 10−3 | |
| Rank | 4 | 5 | 8 | 3 | 6 | 7 | 2 | 1 | |
| Mean Rank | 5.25 | 6.5 | 6.75 | 2.5 | 5.5 | 5.5 | 2.75 | 1.25 | |
| Final Ranking | 4 | 7 | 8 | 2 | 5 | 5 | 3 | 1 | |
| Item Name | APO | EAPO | Percentage Improvement |
|---|---|---|---|
| Path length | 1.419 × 103 | 1.422 × 103 | −0.21% |
| Path smoothness index | 1.926 × 10−1 | 2.201 × 10−1 | 14.28% |
| Flight altitude variation | 1.902 × 102 | 1.549 × 102 | 18.56% |
| Actual maximum climb angle | 29.66 | 28.28 | 4.65% |
| Actual maximum descent angle | −21.29 | −13.77 | 35.18% |
| Energy consumption | 1.722 × 103 | 1.680 × 103 | 2.44% |
| Threat distance | 6.330 × 101 | 6.599 × 101 | 4.25% |
| Computation time | 1.436 | 1.618 | −12.67% |
| Item Name | APO | EAPO | Percentage Improvement |
|---|---|---|---|
| Path length | 1.521 × 103 | 1.515 × 103 | 0.39% |
| Path smoothness index | 1.250 × 10−1 | 1.312 × 10−1 | 4.96% |
| Flight altitude variation | 3.774 × 102 | 3.579 × 102 | 5.17% |
| Actual maximum climb angle | 42.91 | 40.32 | 6.04% |
| Actual maximum descent angle | −34.20 | −34.93 | −2.13% |
| Energy consumption | 2.059 × 103 | 2.028 × 103 | 15.06% |
| Threat distance | 4.604 × 100 | 5.040 × 100 | 9.47% |
| Computation time | 2.108 | 2.365 | −12.19% |
| Item Name | APO | EAPO | Percentage Improvement |
|---|---|---|---|
| Path length | 6.227 × 102 | 6.189 × 102 | 0.61% |
| Path smoothness index | 1.560 × 10−1 | 1.638 × 10−1 | 5.00% |
| Flight altitude variation | 1.965 × 102 | 1.838 × 102 | 6.46% |
| Actual maximum climb angle | 44.43 | 44.55 | −0.27% |
| Actual maximum descent angle | −37.83 | −37.32 | 1.35% |
| Energy consumption | 9.336 × 102 | 9.137 × 102 | 2.13% |
| Threat distance | 3.542 × 101 | 3.517 × 101 | 0.71% |
| Computation time | 1.443 | 1.605 | −11.22% |
| Item Name | APO | EAPO | Percentage Improvement |
|---|---|---|---|
| Path length | 6.385 × 102 | 6.412 × 102 | −0.42% |
| Path smoothness index | 1.814 × 10−2 | 1.797 × 10−2 | 0.94% |
| Flight altitude variation | 2.139 × 102 | 2.074 × 102 | 3.04% |
| Actual maximum climb angle | 43.80 | 44.08 | −0.64% |
| Actual maximum descent angle | −39.11 | −38.10 | 2.58% |
| Energy consumption | 9.716 × 102 | 9.660 × 102 | 0.58% |
| Threat distance | 2.808 × 101 | 2.812 × 101 | 0.14% |
| Computation time | 1.845 | 2.044 | −10.78% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Tang, X.; Jia, C.; Qu, P. EAPO: A Multi-Strategy-Enhanced Artificial Protozoa Optimizer and Its Application to 3D UAV Path Planning. Mathematics 2026, 14, 153. https://doi.org/10.3390/math14010153
Tang X, Jia C, Qu P. EAPO: A Multi-Strategy-Enhanced Artificial Protozoa Optimizer and Its Application to 3D UAV Path Planning. Mathematics. 2026; 14(1):153. https://doi.org/10.3390/math14010153
Chicago/Turabian StyleTang, Xiaojie, Chengfen Jia, and Pengju Qu. 2026. "EAPO: A Multi-Strategy-Enhanced Artificial Protozoa Optimizer and Its Application to 3D UAV Path Planning" Mathematics 14, no. 1: 153. https://doi.org/10.3390/math14010153
APA StyleTang, X., Jia, C., & Qu, P. (2026). EAPO: A Multi-Strategy-Enhanced Artificial Protozoa Optimizer and Its Application to 3D UAV Path Planning. Mathematics, 14(1), 153. https://doi.org/10.3390/math14010153






