Bifurcation Geometry, Global Stability, and Nonlinear Nematicon Dynamics of the Generalized Hunter–Saxton Model
Abstract
1. Introduction
2. Mathematical Analysis
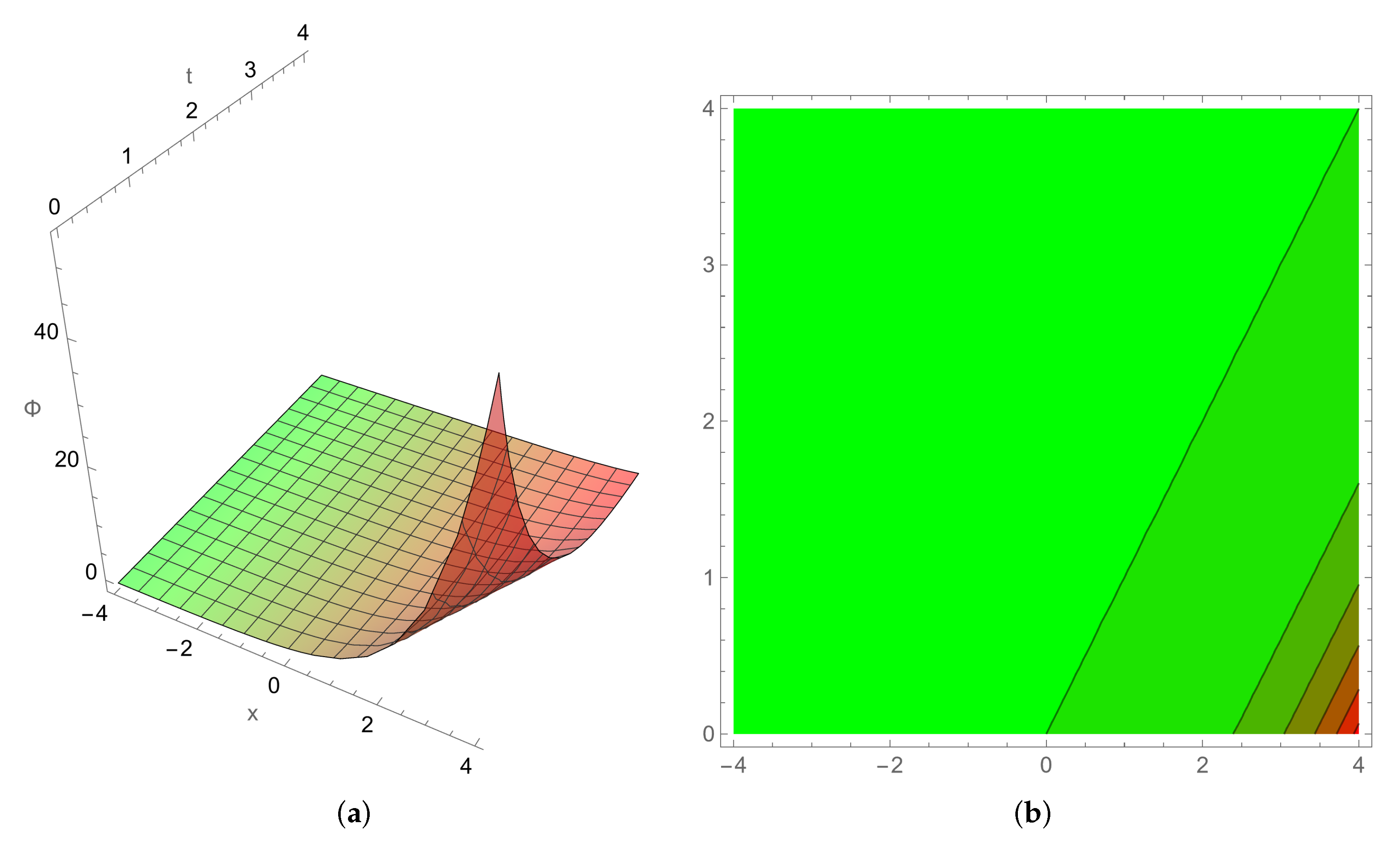
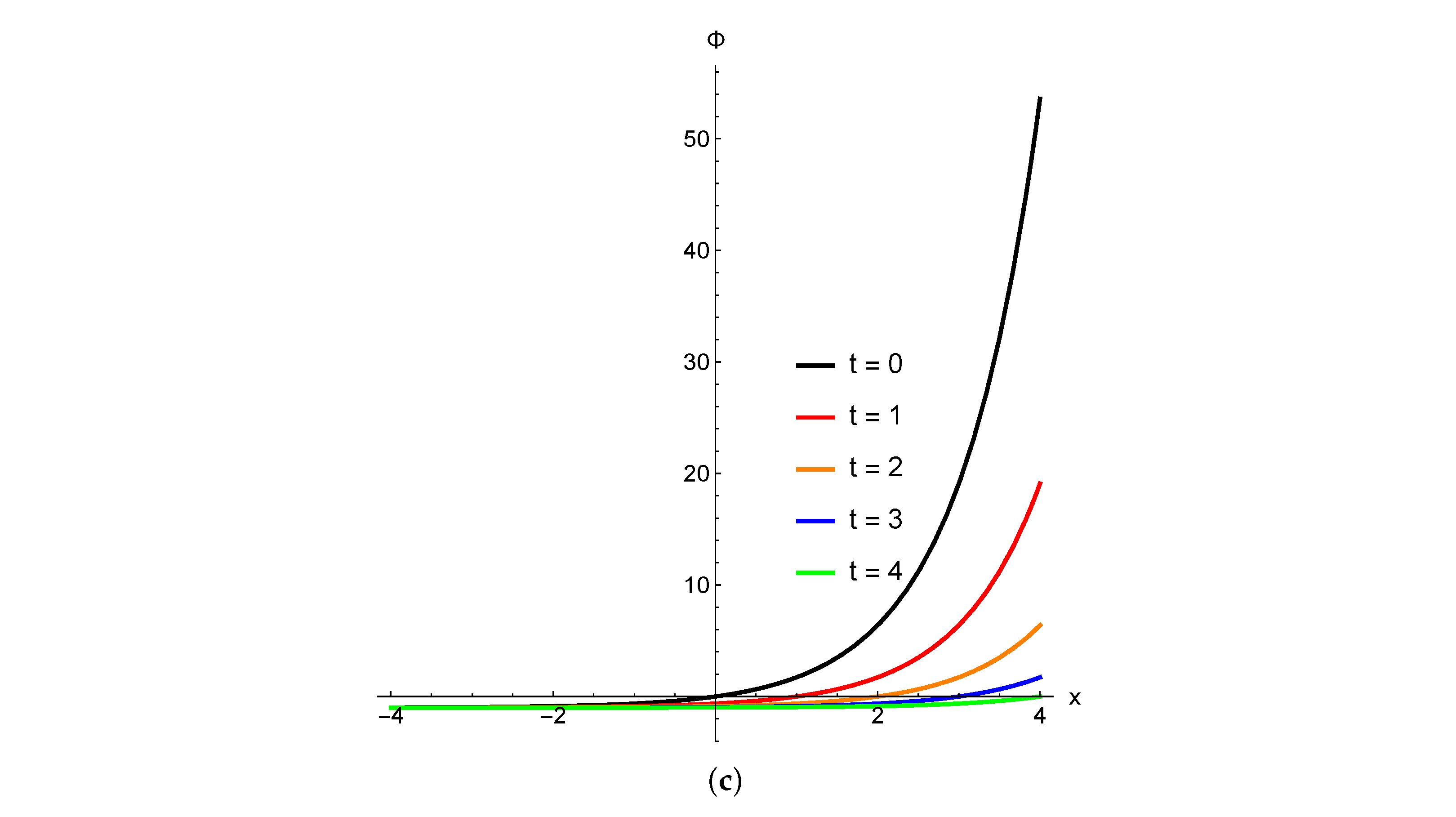
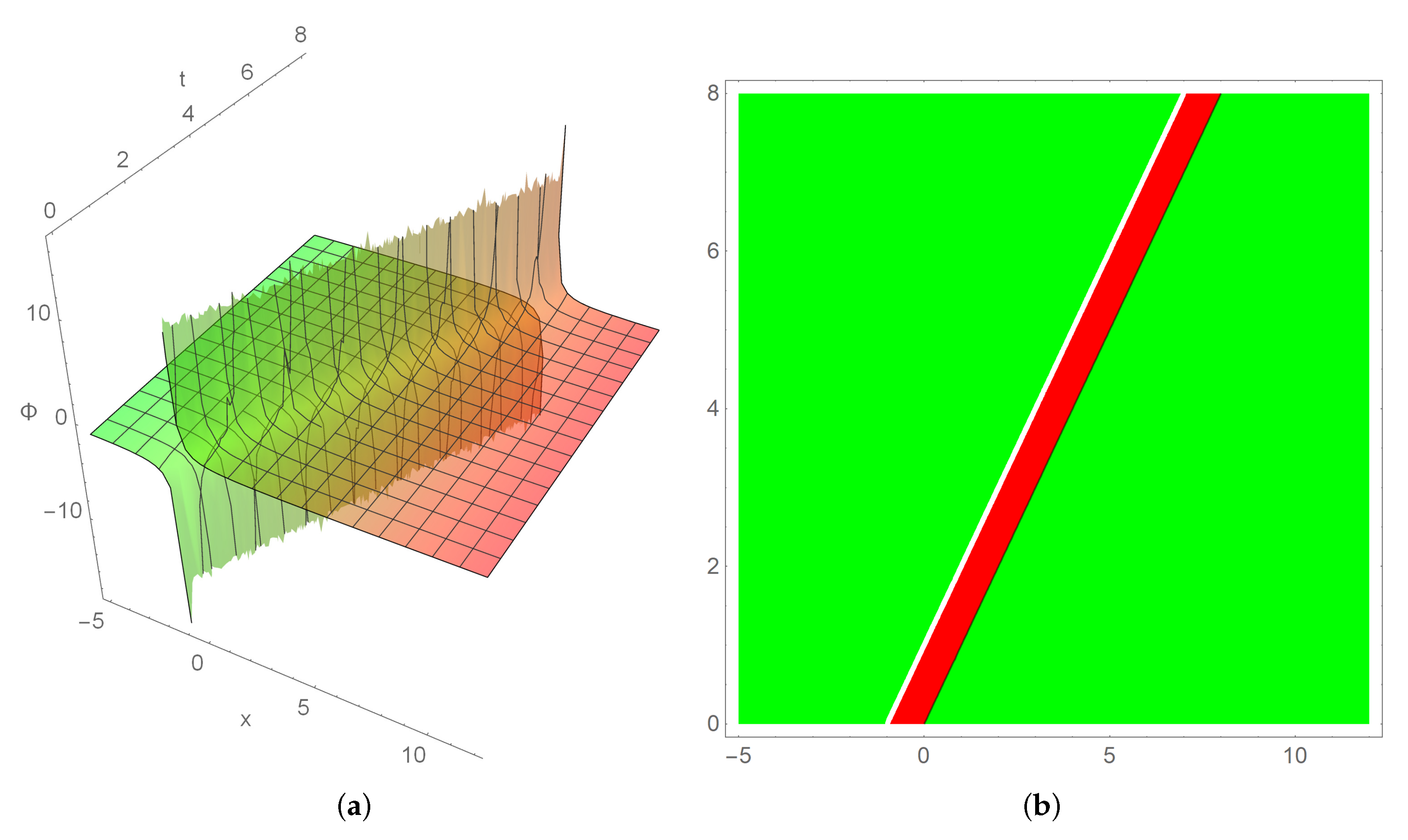
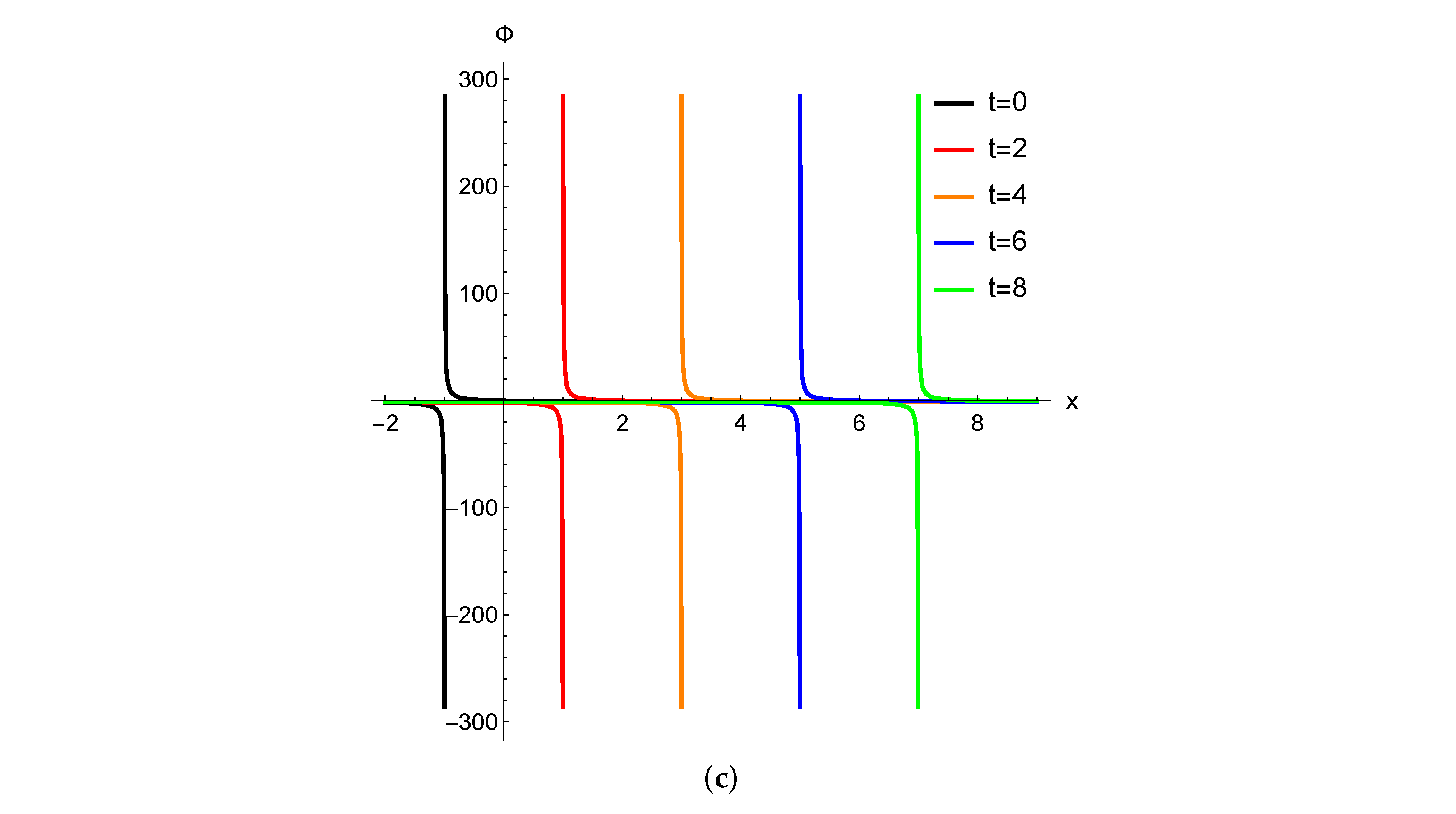
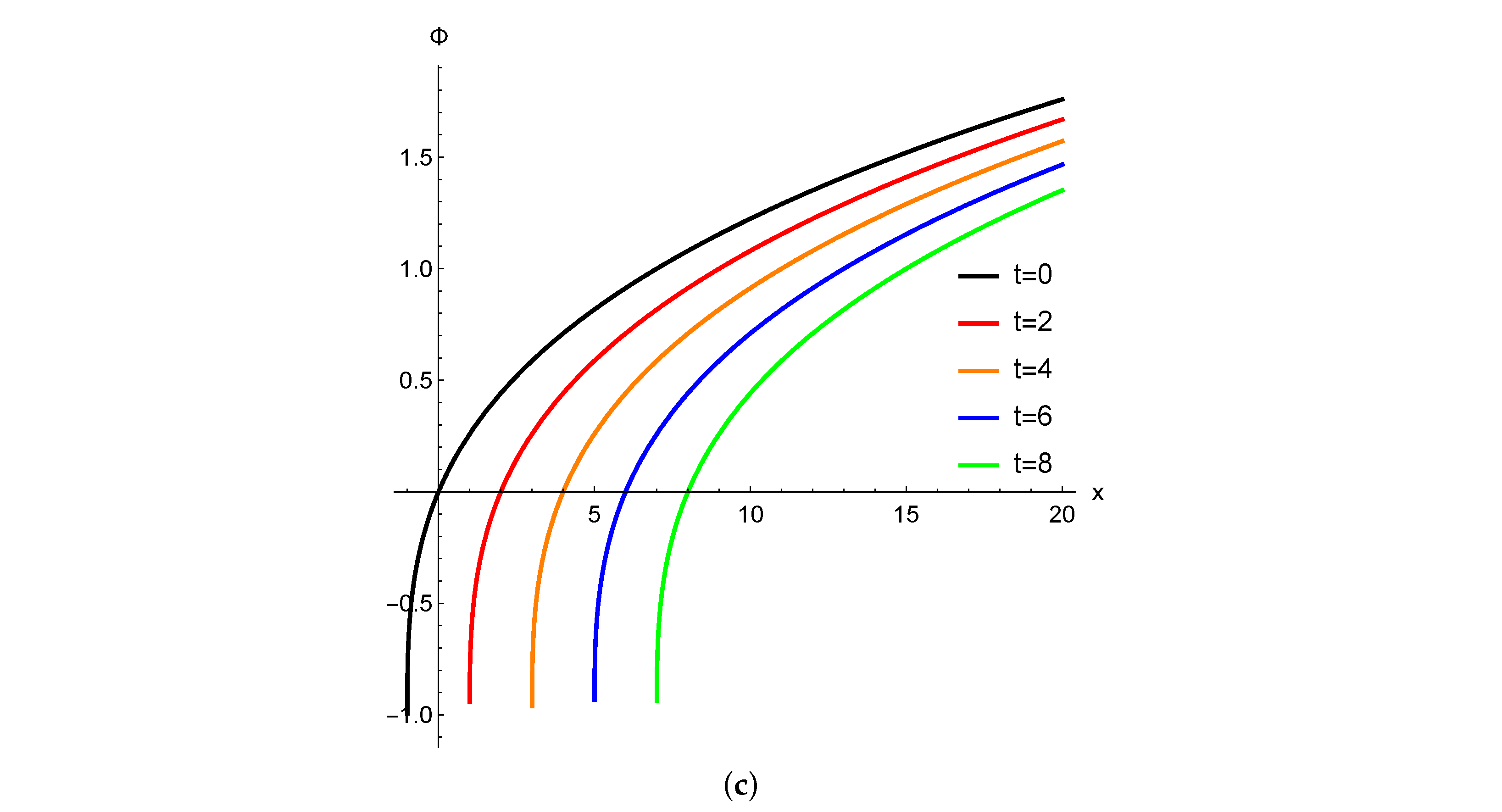
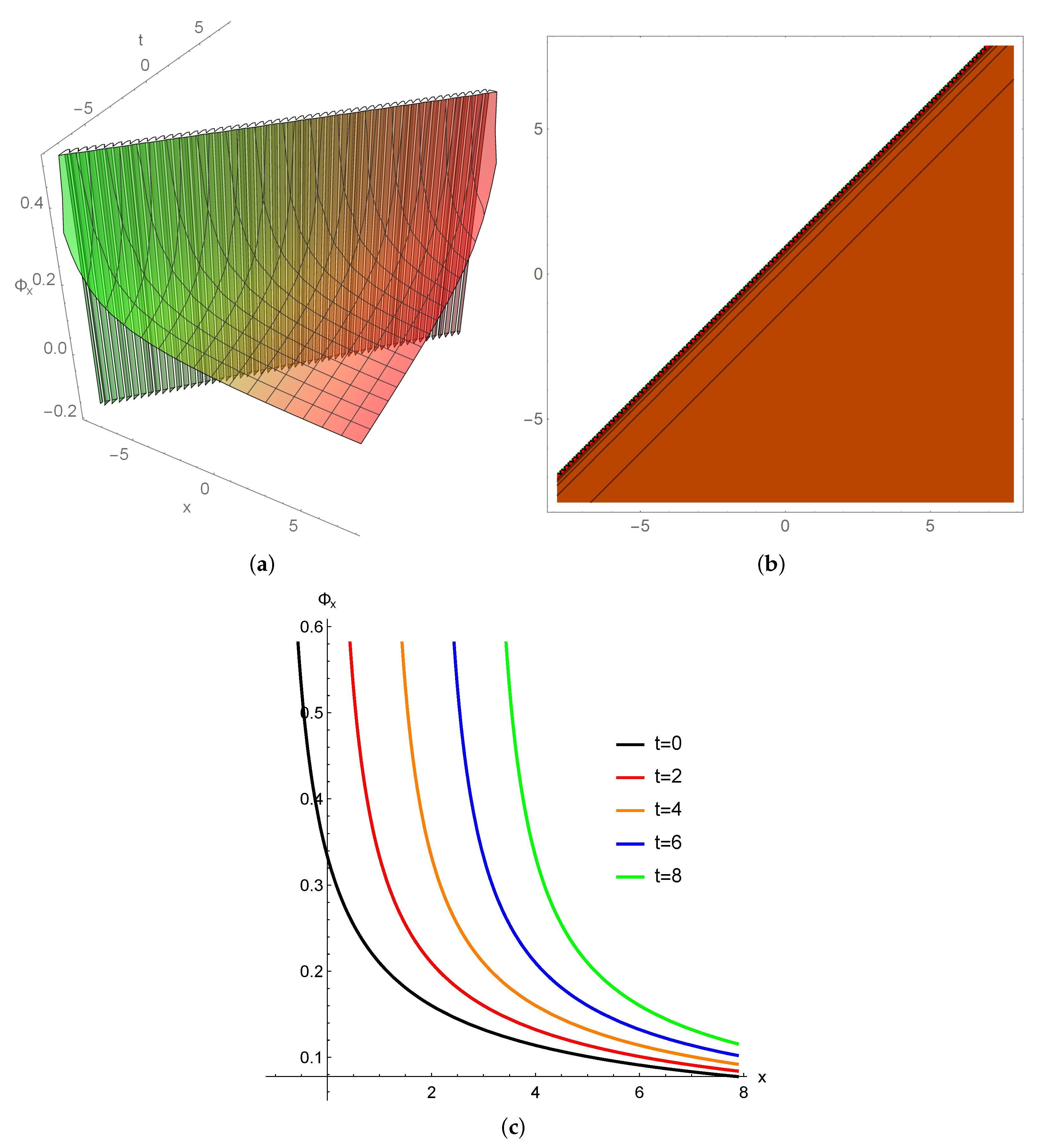
3. Illustrations
4. Dynamical Analysis
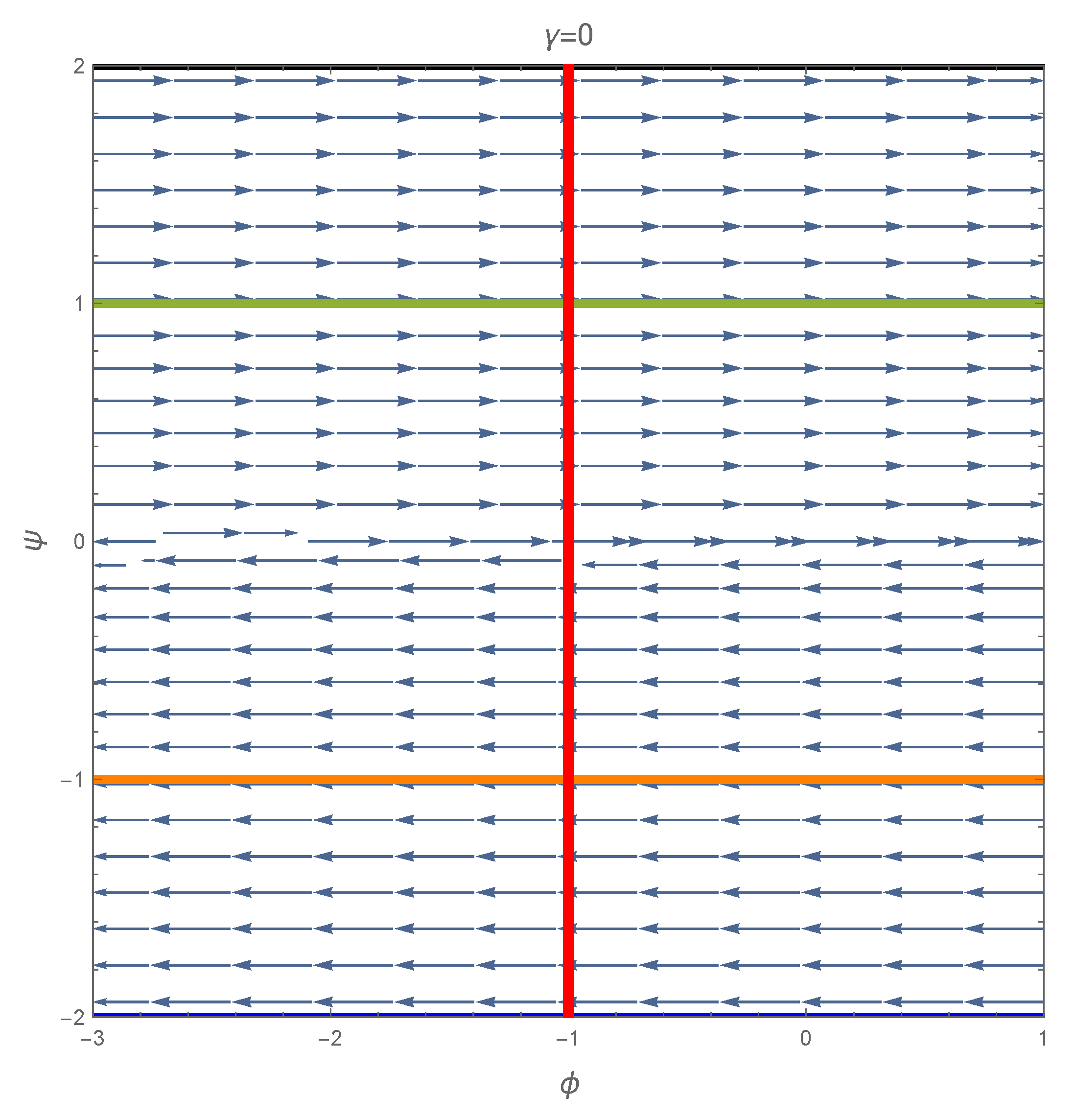
4.1. The Phase Plane Method
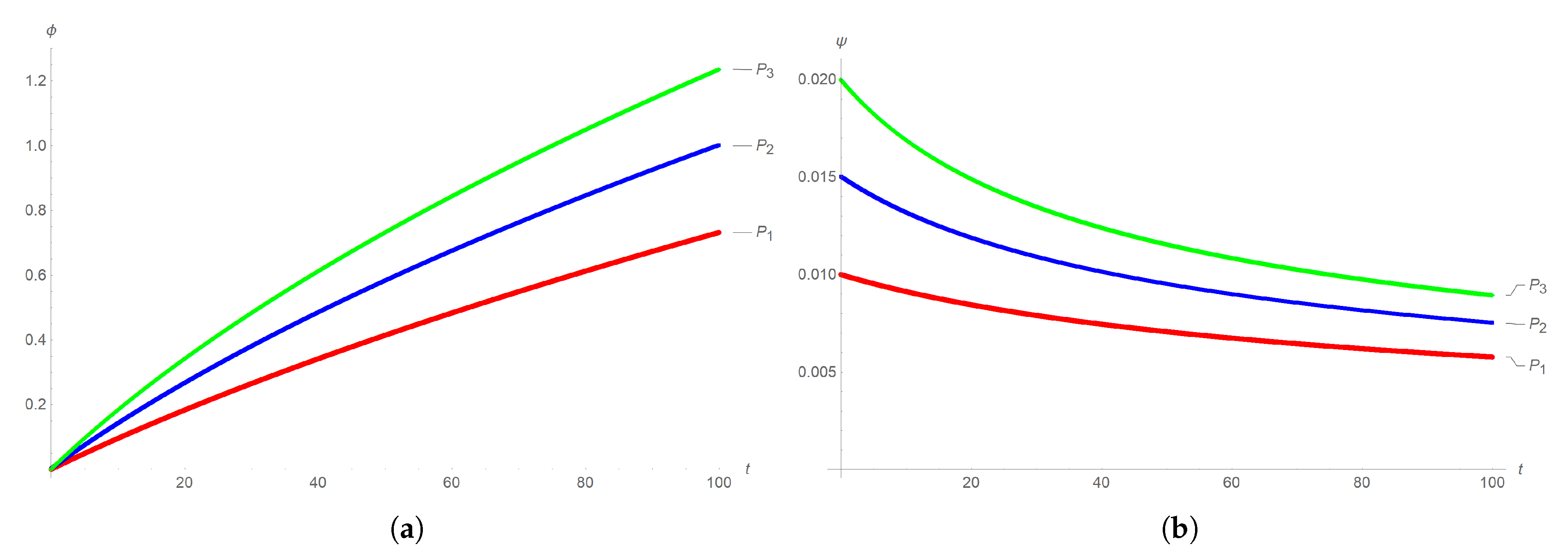
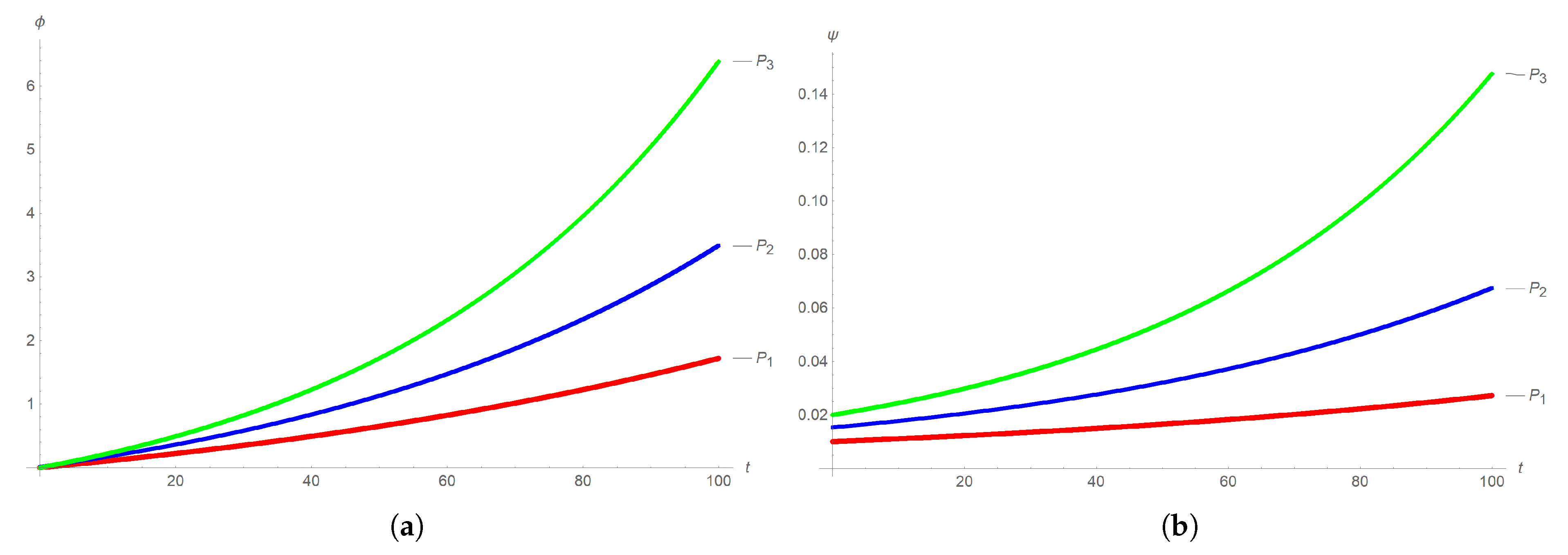
4.2. Sensitivity Dynamics
4.3. Bifurcation Dynamics
4.4. Chaotic Dynamics
5. Conclusions and Future Work
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hunter, J.K.; Saxton, R. Dynamics of director fields. SIAM J. Appl. Math. 1991, 51, 1498–1521. [Google Scholar] [CrossRef]
- Hunter, J.K.; Zheng, Y. On a completely integrable nonlinear hyperbolic variational equation. Physical D 1994, 79, 361–386. [Google Scholar] [CrossRef]
- Lenells, J. The Hunter–Saxton equation: A geometric approach. SIAM J. Math. Anal. 2008, 40, 266–277. [Google Scholar] [CrossRef]
- Bressan, A.; Constantin, A. Global solutions of the Hunter–Saxton equation. SIAM J. Math. Anal. 2005, 37, 996–1026. [Google Scholar] [CrossRef]
- Cotter, C.J.; Deasy, J.; Pryer, T. The r-Hunter–Saxton equation: Smooth and singular solutions and their approximation. Nonlinearity 2020, 33, 7016–7039. [Google Scholar] [CrossRef]
- Grunert, K.; Holden, H. Uniqueness of conservative solutions for the Hunter–Saxton equation. Res. Math. Sci. 2022, 9, 19. [Google Scholar] [CrossRef]
- Kakuli, M.C.; Sinkala, W.; Masemola, P. Conservation laws and symmetry reductions of the Hunter–Saxton equation via the double reduction method. Math. Comput. Appl. 2023, 28, 92. [Google Scholar] [CrossRef]
- Thube, N.H.; Lodhi, R.K. Numerical solution of Hunter–Saxton type equation via exponential cubic B-spline collocation method. Bound. Value Probl. 2025, 2025, 156. [Google Scholar] [CrossRef]
- Nirmala, A.; Kumbinarasaiah, S. Numerical solution of nonlinear Hunter–Saxton, Benjamin–Bona–Mahony, and Klein–Gordon equations using Hosoya polynomial method. Results Control Optim. 2024, 14, 100388. [Google Scholar] [CrossRef]
- Zhang, C.; Qiu, C.; Zhou, X.; He, X. Cell-average based neural network method for Hunter–Saxton equations. Adv. Appl. Math. Mech. 2024, 16, 833–859. [Google Scholar] [CrossRef]
- Christiansen, T.; Grunert, K.; Nordli, A.; Solem, S. A convergent numerical algorithm for α-dissipative solutions of the Hunter–Saxton equation. J. Sci. Comput. 2024, 99, 14. [Google Scholar] [CrossRef]
- Tod, K.P. Einstein–Weyl spaces and third-order differential equations. J. Math. Phys. 2000, 41, 5572–5581. [Google Scholar] [CrossRef]
- Dryuma, V. Applications of Riemannian and Einstein–Weyl geometry in the theory of second-order ordinary differential equations. Theor. Math. Phys. 2001, 128, 845–855. [Google Scholar] [CrossRef]
- Morozov, O.I. Integrability structures of the generalized Hunter–Saxton equation. Anal. Math. Phys. 2021, 11, 50. [Google Scholar] [CrossRef]
- Ahmad, I.; Ilyas, H.; Kutlu, K.; Anam, V.; Hussain, S.I.; Guirao, J.L.G. Numerical computing approach for solving Hunter–Saxton equation through sinc collocation method. Heliyon 2021, 7, e07600. [Google Scholar] [CrossRef]
- Assanto, G.; Peccianti, M.; Conti, C. Nematicons: Optical spatial solitons in nematic liquid crystals. Opt. Photonics News 2003, 14, 44–48. [Google Scholar] [CrossRef]
- Az-Zo’bi, E.A.; Hussain, E.; Iqbal, M.; Alomari, M.; Shah, A.; Yaro, D.; Aljawi, S.; Alsubaie, A.S.; Tashtoush, M.A. Chaotic and soliton dynamics of the nonlinear coupled Konno–Oono system in a magnetic field. AIP Adv. 2025, 15, 095101. [Google Scholar] [CrossRef]
- Hassaballa, A.A.; Gumma, E.A.E.; Adam, A.M.A.; Hamed, O.M.A.; Satty, A.; Salih, M.; Abdalla, F.A.; Mohammed, Z.M.S. Exact analytical solutions of the STFKS equation using Tanh–Coth and HSI methods. Front. Appl. Math. Stat. 2025, 11, 1568757. [Google Scholar] [CrossRef]
- Altawallbeh, Z.; Az-Zo’bi, E.; Alleddawi, A.O.; Senol, M.; Akinyemi, L. Novel liquid crystal model and its nematicons. Opt. Quantum Electron. 2022, 54, 795. [Google Scholar] [CrossRef]
- Al Zubi, M.A.; Afef, K.; Az-Zo’bi, E.A. Assorted spatial optical dynamics of a generalized fractional quadruple nematic liquid crystal system. Symmetry 2024, 16, 778. [Google Scholar] [CrossRef]
- Qiao, C.; Long, X.; Yang, L.; Zhu, Y.; Cai, W. Dynamical substitute for the Earth–Moon system via Hamiltonian analysis. Astrophys. J. 2025, 991, 46. [Google Scholar] [CrossRef]
- Zill, D.G.; Cullen, M.R. Differential Equations with Boundary-Value Problems, 7th ed.; Brooks/Cole Cengage Learning: Belmont, CA, USA, 2009. [Google Scholar]
- Coddington, E.A.; Levinson, N. Theory of Ordinary Differential Equations; Krieger: Malabar, FL, USA, 1984. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Az-Zo’bi, E.A. Bifurcation Geometry, Global Stability, and Nonlinear Nematicon Dynamics of the Generalized Hunter–Saxton Model. Mathematics 2026, 14, 142. https://doi.org/10.3390/math14010142
Az-Zo’bi EA. Bifurcation Geometry, Global Stability, and Nonlinear Nematicon Dynamics of the Generalized Hunter–Saxton Model. Mathematics. 2026; 14(1):142. https://doi.org/10.3390/math14010142
Chicago/Turabian StyleAz-Zo’bi, Emad A. 2026. "Bifurcation Geometry, Global Stability, and Nonlinear Nematicon Dynamics of the Generalized Hunter–Saxton Model" Mathematics 14, no. 1: 142. https://doi.org/10.3390/math14010142
APA StyleAz-Zo’bi, E. A. (2026). Bifurcation Geometry, Global Stability, and Nonlinear Nematicon Dynamics of the Generalized Hunter–Saxton Model. Mathematics, 14(1), 142. https://doi.org/10.3390/math14010142





