Task-Oriented Local Feature Rectification Network for Few-Shot Image Classification

Abstract

Few-shot image classification aims to classify unlabeled samples when only a small number of labeled samples are available for each class. Recently, local feature-based few-shot learning methods have made significant progress. However, existing methods often treat all local descriptors equally, without considering the importance of each local descriptor in different tasks. Therefore, the few-shot learning model is easily disturbed by class-irrelevant features, which results in a decrease in accuracy. To address this issue, we propose a task-oriented local feature rectification network (TLFRNet) with two feature rectification modules (support rectification module and query rectification module). The former module uses the relationship between each local descriptor and prototypes within the support set to rectify the support features. The latter module uses a CNN to rectify the similarity tensors between the query and support local features and then models the importance of the query local features. Through these two modules, our model can effectively reduce the intra-class variation of class-relevant features, thus obtaining more accurate image-to-class similarity for classification. Extensive experiments on five datasets show that TLFRNet achieves more superior classification performance than the related methods.

1. Introduction

Deep learning is a crucial approach in implementing artificial intelligence, and it has surpassed human-level performance in various computer vision applications such as object detection [1], semantic segmentation [2], and image classification [3]. However, traditional deep learning heavily relies on extensive data for training, and the collection and labeling of such large training datasets consume significant time, money, and manpower. Moreover, in many scenarios with scarce data, such as rare disease diagnosis, recognition of endangered species, and industrial defect detection, obtaining a substantial amount of labeled data is challenging or even impossible. In such cases, persisting with traditional deep learning would inevitably lead to severe overfitting issues, resulting in a significant decline in model performance. In contrast, humans can quickly discern unfamiliar categories with just a few examples. Inspired by this powerful learning ability under extremely limited data conditions, many few-shot learning methods [4] have been proposed. The objective is to mimic the strong generalization capability of humans in learning useful information from very limited data.

Among the existing methods, metric learning-based few-shot learning [5] has received extensive research attention in recent years due to its simplicity and effectiveness. It consists of two main modules: the feature extraction module and the similarity measurement module. The general idea is to extract features using a feature extraction network, compare the similarities based on these features, and classify the sample by choosing the class with the highest similarity. A common approach is to obtain global features for all images as image-level representations, then average all features of each class as prototypes [6]. During prediction, the similarity between the query image and prototype of each class is calculated to determine the classification results. In general, image data contain a lot of local information. Directly using the global feature to model the image may lose valuable detailed information. Therefore, many state-of-the-art methods [7,8,9,10] have tried to construct a few-shot classifier by using the rich local features. However, existing methods often treat all local descriptors equally, without considering the importance of each local descriptor in different tasks. In fact, many parts of an image are irrelevant to the task and may not reflect the essential characteristics of the class. These areas may not contribute to classification and can even be harmful. Therefore, treating all local features equally in similarity computation may lead to inaccurate results that interfere with the classification outcome.

In order to address the aforementioned issues, we propose a task-oriented local feature rectification model, shown in Figure 1, that can adaptively rectify the local features based on the domain knowledge included in the specific task. The intuition behind our method is to rectify the local features by utilizing the feature weights. For example, when dealing with fine-grained classification tasks, the significant intra-class variations in images and local features often result in the failure of metric learning-based classifiers to obtain accurate image-to-class distances. Our model, by modeling the task-dependent feature weights to reduce the intra-class variation of class-relevant features, can effectively address this issue and obtain more accurate image-to-class similarity for classification. Our proposed few-shot learning network comprises four modules: the feature extraction module, support rectification module (SRM), query rectification module (QRM), and similarity calculation module. Firstly, the feature extraction module obtains local features for all images. The SRM utilizes similarity vectors between support features and prototypes to characterize the importance of support features for specific tasks. This enables task-dependent rectification to these features. The QRM models the importance of each local feature in the query image for the current task by utilizing the similarity tensor between the query image and all categories. In order to obtain a more accurate similarity tensor, we rectify the initial tensor by using a similarity rectification network (SRN). Finally, the similarity computation module calculates the similarity between the query image and each class for classification.

Our main contributions are summarized as follows:

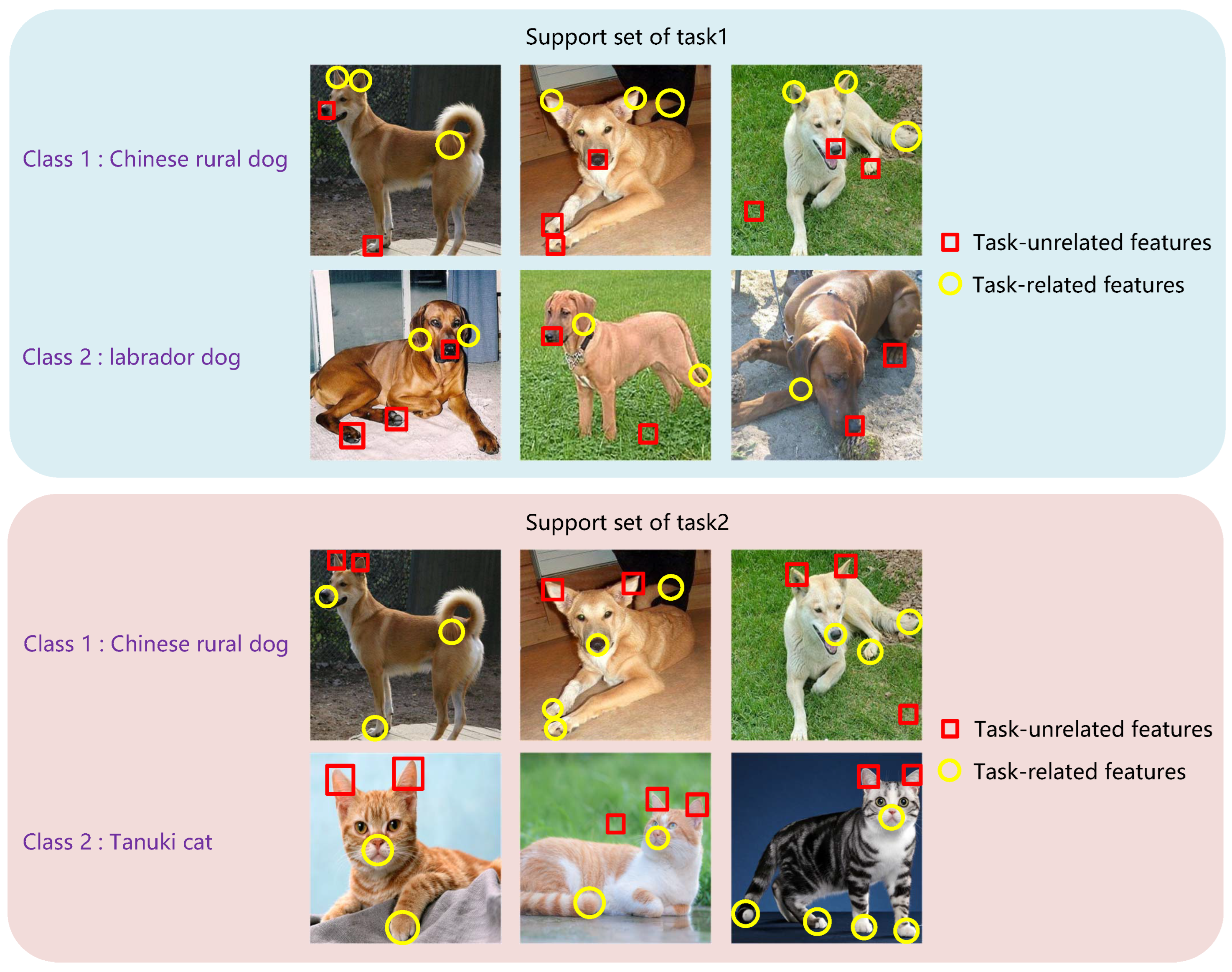
• We separately design the SRM and the QRM to rectify the local features in a task-oriented form. Thus, the model can focus on the features closely related to the corresponding category while suppressing the influence of irrelevant features.
• We use a similarity rectification network to rectify the similarity tensors in order to obtain more accurate feature similarities for the computation of query local feature weight.
• We conduct extensive experiments on multiple datasets, and demonstrate that our method can effectively rectify the local features, resulting in a significant improvement over related methods.

2. Related Work

To address the few-shot learning problem, many excellent methods have been proposed from different perspectives. These methods can be mainly categorized into three types: data augmentation, meta-learning, and metric learning.

2.1. Data Augmentation-Based Methods

Data augmentation refers to the expansion of data by augmenting existing samples, thereby transforming a few-shot learning task into a conventional classification task. This can be achieved by applying various transformations to the training data, such as rotation, cropping, and flipping [11], to increase the diversity of the training samples. Additionally, synthetic samples can be generated to augment the training set, enhancing the model’s generalization performance. Representative methods include delta-encoder [12] and generative adversarial nets [13].

2.2. Meta-Learning-Based Methods

Meta-learning, also known as learning to learn, is a concept that involves acquiring knowledge or experience from a large number of previous tasks, such as neural network initialization parameters, network structures, etc. The key idea is to utilize this knowledge effectively on new tasks to achieve rapid learning, rather than starting from scratch each time. Meta-Learner LSTM [14] utilized an LSTM-based network as a meta-learner, learning an optimization algorithm that could be applied to train other machine learning models. MAML [15] is another popular meta-learning method that aims to find a model initialization that allows the model to achieve good performance on new tasks with only a few gradient update steps from this initialization. Meta-SGD [16] not only learns the initialization parameters but also learns the update direction and learning rate of the meta-learner, enabling more efficient adaptation to new tasks. MetaDiff [17] uses the gradient descent algorithm as a diffusion model, which effectively reduces the memory burden and the risk of gradient vanishing in the inner-loop optimization.

2.3. Metric Learning-Based Methods

Methods based on metric learning have attracted much attention due to their simplicity and effectiveness, making them a popular approach in the field of few-shot learning. The core idea to address the few-shot problem is “learning to compare”, ensuring that the similarity of samples within the same class is greater than the similarity of samples from different classes [18]. The existing methods can be further categorized into image-level feature-based methods [6,19] and local feature-based methods [7,10,20,21]. The first category involves obtaining the global features of query images and all images in the support set through the global average pooling layer of the feature extraction network, i.e., mapping each image into a compact feature vector. The similarity between the query image and each class is then calculated using a similarity calculation module for classification. For example, Matching Net [22] incorporates episodic training mechanisms into few-shot learning, enhancing network learning capabilities through a combination of attention and memory. Prototype networks [6] assumes that each class has a prototype, and the feature vectors are centered around this prototype. Therefore, the average of the feature vectors of each class in the support set is taken as the prototype of the class. The Euclidean distance between the query image and each class prototype is then computed for classification. Relation networks [23] use neural networks to measure similarities, avoiding the need for manually selecting a metric.

Due to the scarcity of samples in few-shot tasks, just using image-level global features may lead to the loss of a considerable amount of discriminative information and cannot effectively model the distribution of each category. In contrast, rich local features possess greater discriminative and representational power. Recent research focusing on local features has made significant progress. For instance, the DN4 [7] network extracts local features from query and support set images. And then, it aggregates the similarities between all local descriptors of the query image and their nearest descriptors to obtain the similarity with each class. DeepEMD [8] solves a linear programming problem to obtain optimal structural distances between local features of different images. In developing LMPNet [9], the authors argued that a single prototype may not sufficiently reflect the feature distribution of a class and utilized the channel squeezing and spatial attention mechanisms to adaptively learn multiple prototypes for each support class. By integrating semantic information into the implicit feature transformation process, SIFT [24] enables the model to better understand the intrinsic meaning of samples and reduces the problem of excessive feature representation deviation.

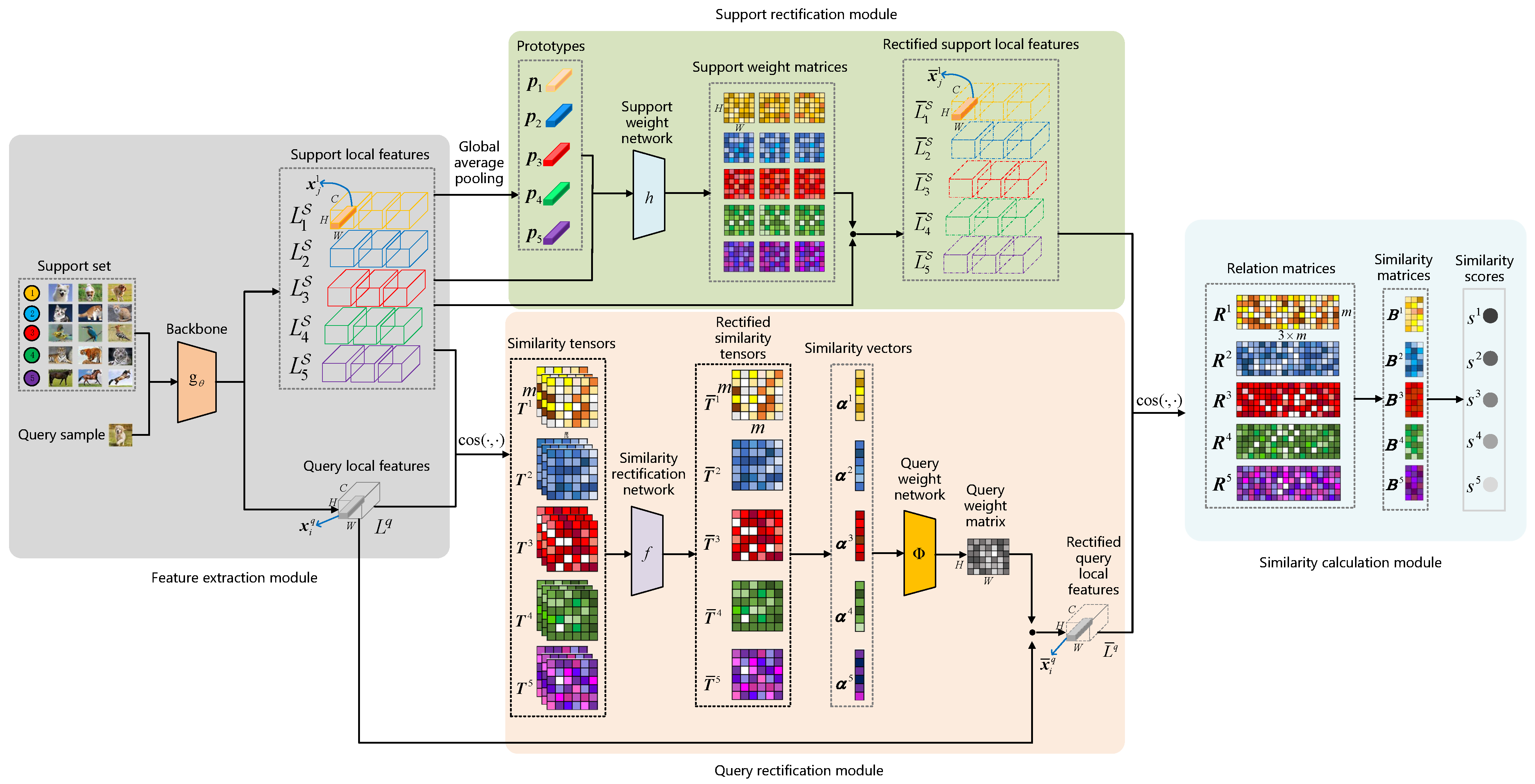
3. Task-Oriented Local Feature Rectification Network

3.1. Problem Description

In the standard definition of a few-shot learning task, given a support set $\mathcal{S}=\left\{(X_1^{\mathcal{S}},Y_1^{\mathcal{S}}),\cdots ,(X_{NK}^{\mathcal{S}},Y_{NK}^{\mathcal{S}})\right\}$, there are N classes, each with K labeled images. Here, $X_i^{\mathcal{S}}$ represents the i-th image of the support set $\mathcal{S}$, and $Y_i^{\mathcal{S}}\in \left\{1,\cdots ,N\right\}$ is its label. Given a query set $\mathcal{Q}=\left\{X_1^{\mathit{q}},\dots ,X_{NM}^{\mathit{q}}\right\}$, where $X_j^q$ represents the j-th image in the query set $\mathcal{Q}$, our objective is to classify each image in the query set $\mathcal{Q}$ with the assistance of a support set $\mathcal{S}$. This constitutes the definition of an N-way K-shot task in the context of few-shot learning. Due to the limited number of samples in the support set, traditional deep learning methods, which treat the support set as the training set and the query set as the test set, are prone to overfitting. Therefore, in few-shot learning tasks, a widely adopted episode-based training mechanism is often employed to simulate the few-shot learning scenario. To achieve this goal, we can utilize an auxiliary dataset $\mathcal{A}$ to learn transferable knowledge. $\mathcal{A}$ contains a large number of classes, each with numerous labeled images. The label space of $\mathcal{A}$ does not overlap the label space of $\mathcal{S}$. We can construct numerous N-way K-shot auxiliary tasks from $\mathcal{A}$ to help the model acquire cross-task generalization ability. Such a task is also referred to as an episode [22].

3.2. The Proposed TLFRNet Framework

The overall framework of TLFRNet is illustrated in Figure 1. It mainly consists of four components: the feature extraction module, the support rectification module, the query rectification module, and the similarity calculation module. Following convention, the feature extraction module is composed of a common CNN, which extracts rich local features from both support and query images. Subsequently, the two rectification modules characterize the importance of the learned local features and adaptively rectify them to obtain the final local features. Finally, the similarity calculation module computes the similarity between the query image and each class.

3.3. Feature Extraction Module

In the feature extraction module, we use a convolutional neural network to extract the local features from images. It is worth noting that this network only comprises convolutional layers and does not include fully connected layers. Given an image X, the feature extraction network $g_{\theta }$ maps it to $g_{\theta }\left(X\right)$, with $\theta$ representing the parameters of the neural network, and the corresponding output is a tensor of size $H\times W\times C$, where H and W denote height and width, while C represents the number of channels. Assuming $H\times W=m$, from another perspective $g_{\theta }\left(X\right)$ can be regarded as a collection of m vectors. In many papers [7,25], it has been introduced that these m vectors are local descriptors. Each local descriptor, denoted as ${\mathit{x}}_i$, encapsulates local feature information from a small region of the image. For an N-way K-shot task, we use the feature extraction network $g_{\theta }$ to map the K images of the n-th class in the support set denoted as ${\mathcal{S}}_n$ to a collection of $Km$ local descriptors, denoted as $L_n^{\mathcal{S}}$:

$$L_n^{\mathcal{S}}=g_{\theta }\left({\mathcal{S}}_n\right)=\left\{{\mathit{x}}_1^n,{\mathit{x}}_2^n,\cdots ,{\mathit{x}}_{Km}^n\right\}$$

(1)

where ${\mathit{x}}_j^n\in {\mathbb{R}}^C$ represents the j-th local descriptor of class n. In the same way, a query image $X^q$ can be mapped to a set of m local descriptors through the feature extraction network $g_{\theta }$, denoted as $L^q$:

$$L^q=g_{\theta }\left(X^q\right)=\left\{{\mathit{x}}_1^q,{\mathit{x}}_2^q,\cdots ,{\mathit{x}}_m^q\right\}$$

(2)

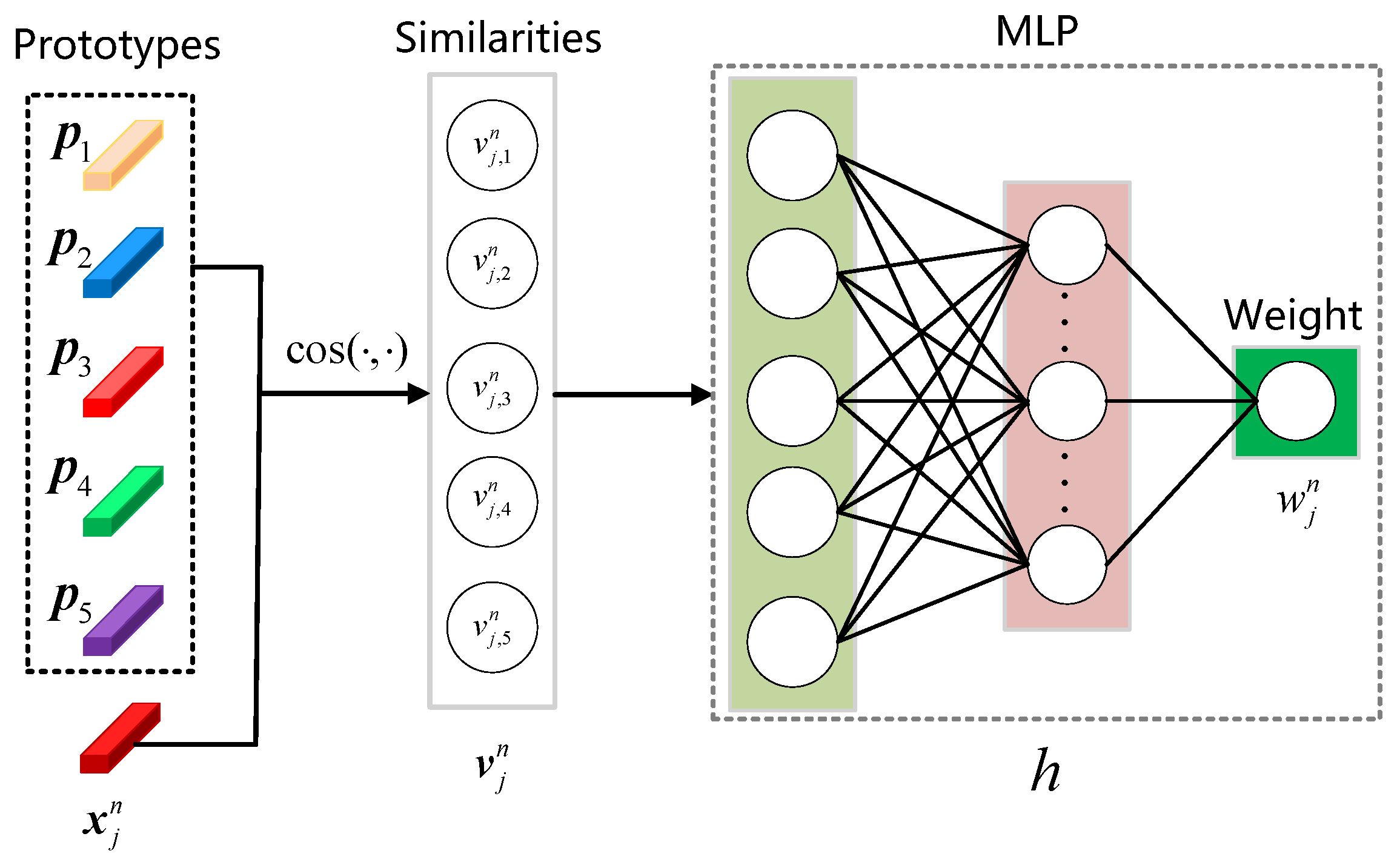
3.4. Support Rectification Module

In many previous works [7,8], all local descriptors were treated as equally important. In fact, not all local descriptors in the support set are equally valuable. As shown in Figure 2, distinctive and task-related local descriptors, such as a dog’s ears in task 1 and a dog’s nose in task 2, are crucial. These types of local descriptors contribute significantly to the classification task. On the other hand, local descriptors unrelated to the category, such as background or regions like a dog’s nose in task 1 and a dog’s ears in task 2, are less important. These descriptors often act as interference in the classification process. To address this problem, our SRM adaptively generates support weight matrices within the support set based on the neural network, emphasizing discriminative local descriptors closely related to the category, and suppressing the influence of class-unrelated local descriptors. In our perspective, the discriminative quality of a support descriptor relies on a comprehensive evaluation of its connection with all the classes. This connection can be quantified by the feature-to-class similarity. We employ the mean of local descriptors as the prototype of each class, denoted as ${\mathit{p}}_n$ for the n-th class. The computation is as follows:

$${\mathit{p}}_n={\displaystyle \frac{1}{Km}}\sum _{j=1}^{Km}{\mathit{x}}_j^n$$

(3)

Therefore, we obtain the set of N prototypes: $\left\{{\mathit{p}}_1,{\mathit{p}}_2,\cdots ,{\mathit{p}}_N\right\}$. Each prototype encapsulates unique information about that class. We model the class relevance of a local descriptor from the perspective of similarity with each class prototype. For a local descriptor ${\mathit{x}}_j^n$ from the support set of the n-th class, we calculate its cosine similarity with each prototype, resulting in a similarity vector ${\mathit{v}}_j^n\in {\mathbb{R}}^N$:

$${\mathit{v}}_j^n={\left[cos({\mathit{x}}_j^n,{\mathit{p}}_1),cos({\mathit{x}}_j^n,{\mathit{p}}_2),\cdots ,cos({\mathit{x}}_j^n,{\mathit{p}}_N)\right]}^T$$

(4)

where $cos(·,·)$ represents the cosine similarity function. Subsequently, the similarity vector ${\mathit{v}}_j^n$ is input into a fully connected neural network (support weight network) to obtain the weight values $w_j^n=h\left({\mathit{v}}_j^n\right)$ for the local descriptor, as illustrated in Figure 3. Therefore, we can obtain the support weight matrices for each class in the support set $\mathcal{S}$. Then, for the n-th class, we multiply each of its local descriptors by its corresponding weight values to obtain the rectified support local descriptors ${\overline{L}}_n^{\mathcal{S}}$:

$${\overline{L}}_n^{\mathcal{S}}=\left\{{\overline{\mathit{x}}}_1^n,{\overline{\mathit{x}}}_2^n,\cdots ,{\overline{\mathit{x}}}_{Km}^n\right\}=\left\{w_1^n{\mathit{x}}_1^n,w_2^n{\mathit{x}}_2^n,\cdots ,w_{Km}^n{\mathit{x}}_{Km}^n\right\}$$

(5)

where ${\overline{\mathit{x}}}_j^n$ represents the j-th rectified local descriptor for the n-th class. In this way, we can enhance important features that are highly relevant to specific classes, while diminishing interfering features that are unrelated to those classes.

3.5. Query Rectification Module

The SRM, by modeling the class relevance of each local descriptor within the support set based on similarity, achieves the rectification of each support set local descriptor. However, relying solely on the SRM is insufficient, as query images also contain many class-unrelated regions that may introduce interference to the classification. In order to consider this issue, we design a QRM for the rectification of query image features, as shown in Figure 1. Specifically, we calculate the cosine similarity between query local descriptors and support local descriptors. For the K images in the n-th class of the support set, we can construct a similarity tensor ${\mathit{T}}^n\in {\mathbb{R}}^{K\times m\times m}$, where the element at the k-th channel, i-th row, and j-th column is represented as $T_{k,i,j}^n$. The computation is as follows:

$$T_{k,i,j}^n=cos({\mathit{x}}_i^q,{\mathit{x}}_j^{n,k})$$

(6)

This represents the cosine similarity between the i-th local descriptor in the query image and the j-th local descriptor in the k-th support image of the n-th class, where $i\in \left\{1,\cdots ,m\right\}$, $j\in \left\{1,\cdots ,m\right\}$, and ${\mathit{x}}_j^{n,c}$ denotes the j-th local descriptor of the k-th image in the n-th class of the support set. Obviously, ${\mathit{T}}^n$ encapsulates the relationships between query local descriptors and support local descriptors of the n-th class.

In general, the initial similarity tensor is inaccurate. As we know, the local features of images are highly correlated in adjacent regions. Similarly, the similarity matrix of local features also possesses this property. Therefore, we can leverage the ability of convolutional neural networks to integrate the local neighboring information and rectify the similarity matrix. First, each of these N similarity tensors undergoes cross-channel pooling, reducing their channel number to 1. Then, a $3\times 3$ convolutional kernel $\mathrm{\Theta }$ is applied to correct them, resulting in N rectified similarity tensors. Among them, the rectified similarity tensor between the query image and the n-th class is denoted as ${\overline{\mathit{T}}}^n$:

$${\overline{\mathit{T}}}^n=f\left({\mathit{T}}^{\mathit{n}}\right)=ReLU(maxpool({\mathit{T}}^{\mathit{n}})\ast \mathrm{\Theta })$$

(7)

Next, the top k maximum values in each row of ${\overline{\mathit{T}}}^n$ are identified to form a matrix ${\mathit{M}}^n\in {\mathbb{R}}^{m\times k}$. The sum of each row in matrix ${\mathit{M}}^n$ is calculated to obtain a similarity vector ${\mathit{\alpha }}^n\in {\mathbb{R}}^m$, where the i-th value ${\alpha }_i^n$ represents the similarity between the i-th local descriptor ${\mathit{x}}_i^q$ in the query image and the n-th class. This process is repeated for all N similarity tensors, resulting in N similarity vectors $\left\{{\mathit{\alpha }}^1,{\mathit{\alpha }}^2,\cdots ,{\mathit{\alpha }}^N\right\}$.

In QRM, the weight of the i-th local descriptor ${\mathit{x}}_i^q$ in the query image is comprehensively considered based on its similarity with all the N classes. These similarities are concatenated into a vector ${\mathit{a}}_i=\left[{\alpha }_i^1,{\alpha }_i^2,\cdots ,{\alpha }_i^N\right]$ with a length of N. Subsequently, this vector ${\mathit{a}}_i$ is input into a fully connected neural network to obtain the weight $w_i^q=\mathrm{\Phi }\left({\mathit{a}}_i\right)$ for ${\mathit{x}}_i^q$. Thus, a query weight matrix ${\mathit{W}}^q\in {\mathbb{R}}^{H\times W}$ composed of weights for all query local descriptors is obtained.

Finally, each local descriptor in the query image is multiplied by its corresponding weight, resulting in the rectified query local descriptors ${\overline{L}}^q$:

$${\overline{L}}^q=\left\{{\overline{\mathit{x}}}_1^q,{\overline{\mathit{x}}}_2^q,\cdots ,{\overline{\mathit{x}}}_m^q\right\}=\left\{w_1^q{\mathit{x}}_1^q,w_2^q{\mathit{x}}_2^q,\cdots ,w_m^q{\mathit{x}}_m^q\right\}$$

(8)

where ${\overline{\mathit{x}}}_i^q\in {\mathbb{R}}^C$ represents the i-th rectified local descriptor.

3.6. Similarity Calculation Module

After the collaborative action of SRM and QRM, all image local features are adaptively rectified by the neural network. The next stage involves similarity computation and classification based on these features. The rectified support local descriptors ${\overline{L}}_n^{\mathcal{S}}$ and the rectified query local descriptors ${\overline{L}}_n^q$ are both input into the similarity calculation module. This module employs the widely used KNN (K-Nearest Neighbors) method to compute the similarity between the query image and each class. In simple terms, for any local descriptor in the query image, we find the k nearest local descriptors in each class. Then, the sum of similarities between all local descriptors in the query image and their respective k nearest local descriptors is calculated, providing the similarity result for each class. Specifically, for the n-th class, we need to construct a relationship matrix ${\mathit{R}}^n\in {\mathbb{R}}^{m\times Km}$. The element at the i-th row and j-th column is computed according to the following formula:

$${\mathit{R}}_{i,j}^n=cos({\overline{\mathit{x}}}_i^q,{\overline{\mathit{x}}}_j^n)$$

(9)

This represents the similarity between the i-th local descriptor of the query image and the j-th local descriptor of the n-th class. Subsequently, for the relation matrix ${\mathit{R}}^n\in {\mathbb{R}}^{m\times Km}$, we find the top k maximum values for each row, forming a matrix ${\mathit{B}}^n\in {\mathbb{R}}^{m\times k}$. Finally, the summation of all elements within matrix ${\mathit{B}}^n$ yields the ultimate similarity score $s^n$ between the query image and the n-th class. During classification, the query image is assigned to the class with the highest similarity score. At this point, we use the softmax function to calculate the probability that the query image $X^q$ belongs to class c:

$$P\left(y=c|X^q\right)={\displaystyle \frac{exp\left(s^c\right)}{{\sum }_{n=1}^{N}exp\left(s^n\right)}}$$

(10)

The cross-entropy loss for this query image is

$$L\left(X^q\right)=-logP\left(y=y^q|X^q\right)$$

(11)

where $y^q\in \left\{1,\cdots ,N\right\}$ is the label of the query image $X^q$.

4. Performance Evaluation

4.1. Experimental Settings

Datasets: We selected five widely used few-shot learning datasets to assess the performance of our method. These datasets were miniImageNet [22], tieredImagenet, CUB-200 [26], Stanford Dogs [27], and Stanford Cars [28]. The dataset partitioning method in the experiment was consistent with DN4 [7] and SANet [25].

Network architecture: For the sake of fairness, we adopted two popular network architectures, Conv-64F and ResNet12 [29], which are commonly used in the few-shot learning literature [7,9,17,30,31].

Implementation details: All our experiments were conducted using the PyTorch 2.0.1 framework on an NVIDIA RTX 4090 GPU. We performed common 5-way 1-shot and 5-way 5-shot tasks on the aforementioned five datasets. The implementation details are the same as for DN4 [7]. We set the hyperparameter k of KNN to 3 in our experiments.

Competing methods: We compared our TLFRNet with a range of metric learning-based methods: Matching Net [22], Prototypical Net [6], Relation Net [23], GNN [32], CovaMNet [33], and LMPNet [9]. Given the close relevance of our method to feature alignment, we also compared it with recent works related to feature alignment: SAML [34], ATL-Net [35], MATANet [36], DLDA [37], DeepEMD [8], SAPENet [38], MADN4 [21], DMN4 [10], and SANet [25]. Additionally, we compared our method with two classic meta-learning-based approaches: Meta-Learner LSTM [14] and MAML [15].

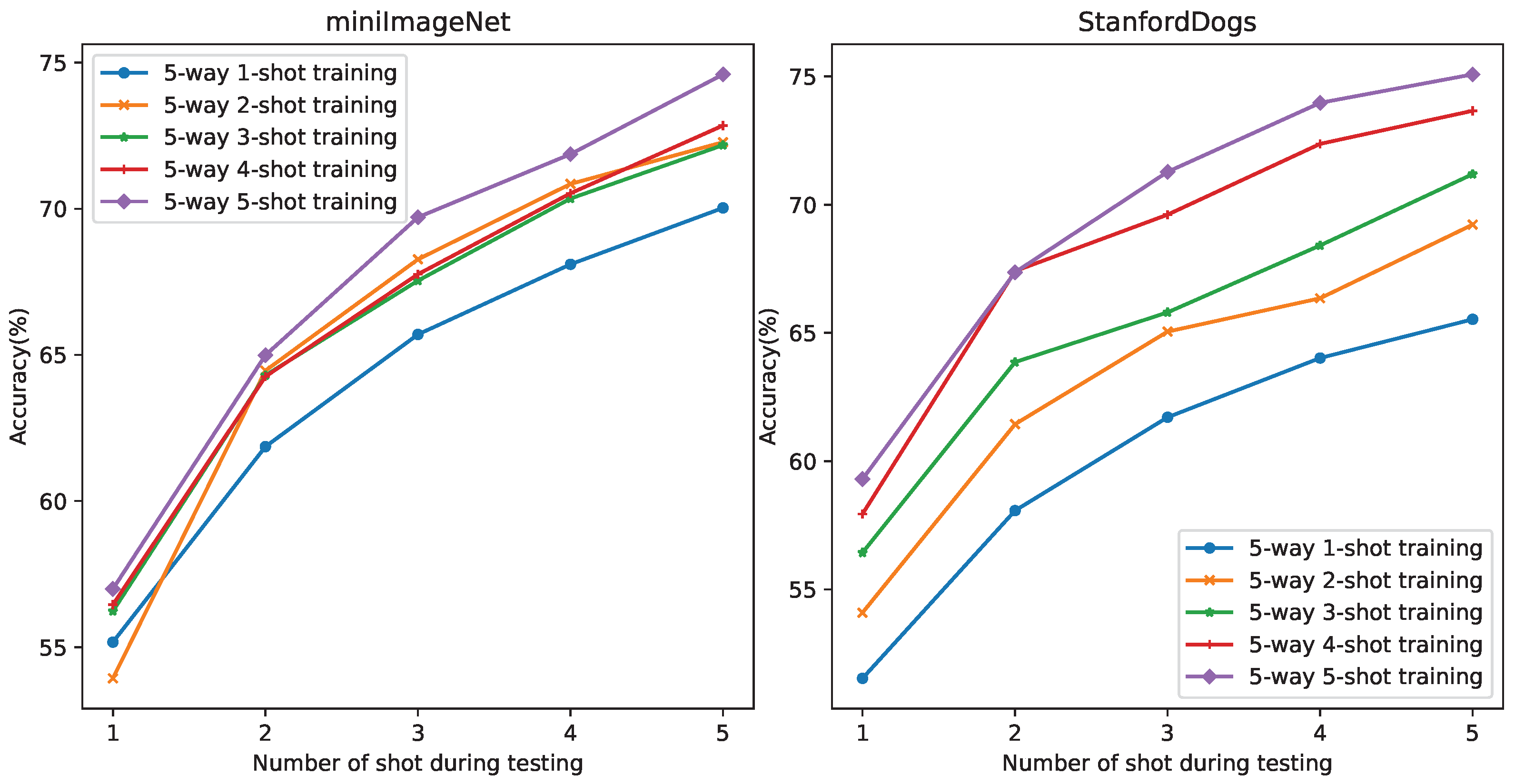
4.2. Experimental Results on miniImageNet and tieredImagenet

On the miniImageNet dataset and the tieredImagenet dataset, we used Conv-64F as the feature extraction network for conducting 5-way 1-shot and 5-way 5-shot experiments, comparing the results with other methods as shown in

Table 1. Classification accuracy (%) on the miniImageNet and tieredImagenet datasets. * denotes the results from the original work, and the results with † are the experimental results in DMN4 [10].

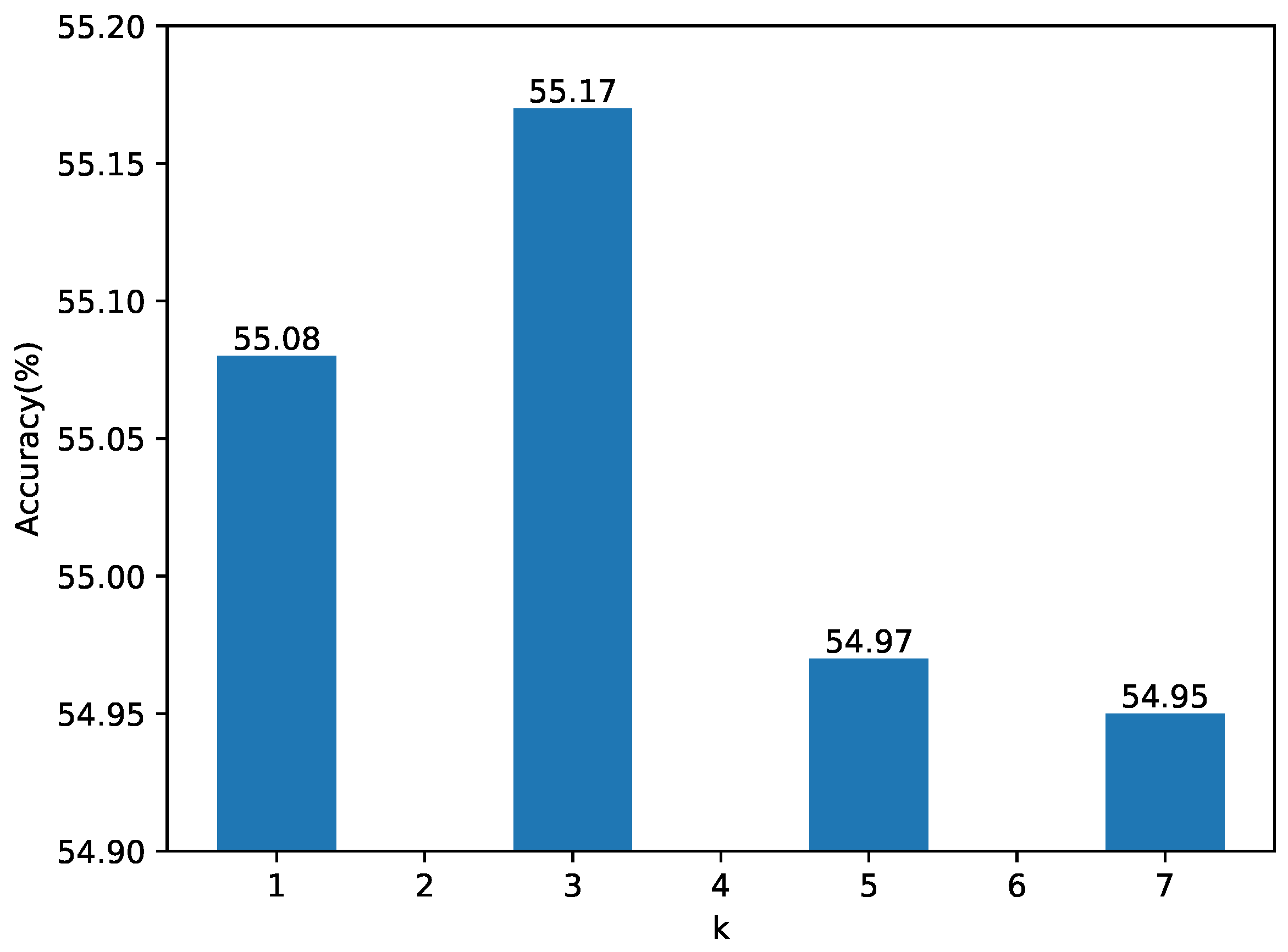
Model	miniImageNet		tieredImagenet
	5-Way 1-Shot	5-Way 5-Shot	5-Way 1-Shot	5-Way 5-Shot
MAML † [15]	48.70 ± 1.84	63.11 ± 0.92	51.67 ± 1.81	70.30 ± 0.08
Meta-Learner LSTM * [14]	43.44 ± 0.77	60.60 ± 0.71	—	—
Matching Net * [22]	43.56 ± 0.84	55.31 ± 0.73	—	—
Prototypical Net * [6]	49.42 ± 0.78	68.20 ± 0.66	48.58 ± 0.00	69.57 ± 0.00
Relation Net * [23]	50.44 ± 0.82	65.32 ± 0.70	54.48 ± 0.00	71.31 ± 0.00
GNN * [32]	50.33 ± 0.36	66.41 ± 0.63	—	—
CovaMNet * [33]	51.19 ± 0.76	67.65 ± 0.63	54.98 ± 0.90	71.51 ± 0.75
SAML * [34]	52.22 ± 0.00	66.49 ± 0.00	—	—
DN4 * [7]	51.24 ± 0.74	71.02 ± 0.64	56.86 ± 0.00	72.16 ± 0.00
LMPNet * [9]	49.87 ± 0.20	68.81 ± 0.16	47.50 ± 0.11	72.65 ± 0.20
ATL-Net * [35]	54.30 ± 0.76	73.22 ± 0.63	—	—
DeepEMD † [8]	52.15 ± 0.28	65.52 ± 0.72	50.89 ± 0.00	66.129 ± 0.00
MATANet * [36]	53.63 ± 0.83	72.67 ± 0.76	—	—
DLDA * [37]	53.20 ± 0.82	71.76 ± 0.47	—	—
MADN4 * [21]	53.20 ± 0.52	71.66 ± 0.47	—	—
SANet * [25]	52.59 ± 0.79	71.46 ± 0.65	57.01 ± 0.62	73.04 ± 0.58
DMN4 * [10]	55.77 ± 0.84	74.22 ± 0.64	56.99 ± 0.90	74.13 ± 0.73
LDCA (k = 1) * [40]	53.03 ± 0.63	74.02 ± 0.49	—	—
TALDS-Net * [39]	56.78 ± 0.37	74.63 ± 0.13	57.54 ± 0.71	75.79 ± 0.43
TLFRNet (ours)	55.17 ± 0.63	74.60 ± 0.48	58.26 ± 0.43	74.61 ± 0.41

. It is evident that the series of methods utilizing local descriptors outperform those relying on global features. The methods related to feature alignment, SAML [34], ATL-Net [35], MATANet [36], DLDA [37], SANet [25], and DMN4 [10] exhibit better performance compared to the methods that do not utilize feature alignment: CovaMNet [33], DN4 [7], and LMPNet [9]. On the miniImageNet dataset, our method achieves accuracy improvements of 3.93% and 3.58% over DN4 [7] in 5-way 1-shot and 5-way 5-shot, respectively. Compared to most recent relevant methods, our approach outperforms SAML [34], ATL-Net [35], MATANet [36], DLDA [37], and SANet [25] by 2.95%/8.11%, 0.87%/1.38%, 1.54%/1.93%, 1.97%/2.84%, and 2.58%/3.14% in 1-shot/5-shot, respectively. The performance of our method is very close to that of TALDS-Net [39].

4.3. Experiments on Three Fine-Grained Datasets

Fine-grained few-shot classification is a highly challenging task, characterized by a limited number of samples for each class and facing the issue of significant intra-class variation coupled with small inter-class differences. To validate the effectiveness of our model in fine-grained few-shot classification tasks, we conducted 5-way 1-shot and 5-way 5-shot experiments using Conv-64F as the feature extraction network on three fine-grained datasets. The results are presented in

Table 2. Classification accuracy (%) on three fine-grained datasets. * denotes the original results, and results marked with † are from the experiments reported in works [7,41,42].

Model	Stanford Dogs		Stanford Cars		CUB-200
	1-Shot	5-Shot	1-Shot	5-Shot	1-Shot	5-Shot
Matching Nets † [22]	35.80 ± 0.99	47.50 ± 1.03	34.80 ± 0.98	44.70 ± 1.03	45.30 ± 1.03	59.50 ± 1.01
DN4 * [7]	45.41 ± 0.76	63.51 ± 0.62	59.84 ± 0.80	88.65 ± 0.44	46.84 ± 0.81	74.92 ± 0.64
CovaMNet * [33]	49.10 ± 0.76	63.04 ± 0.65	56.65 ± 0.86	71.33 ± 0.62	60.58 ± 0.69	74.24 ± 0.68
Relation Net † [23]	44.75 ± 0.70	58.36 ± 0.66	56.02 ± 0.74	66.93 ± 0.63	59.82 ± 0.77	71.83 ± 0.61
GNN † [32]	46.98 ± 0.98	62.27 ± 0.95	55.85 ± 0.97	71.25 ± 0.89	51.83 ± 0.98	63.69 ± 0.94
DeepEMD † [8]	46.73 ± 0.49	65.74 ± 0.63	61.63 ± 0.27	72.95 ± 0.38	64.08 ± 0.50	80.55 ± 0.71
DLDA * [37]	49.08 ± 0.83	70.16 ± 0.67	60.04 ± 0.83	89.62 ± 0.42	54.53 ± 0.85	75.85 ± 0.68
LMPNet * [9]	51.17 ± 0.22	64.06 ± 0.18	62.52 ± 0.12	78.44 ± 0.16	53.50 ± 0.24	66.60 ± 0.19
SAPENet * [38]	—	—	—	—	70.38 ± 0.23	84.47 ± 0.14
SANet * [25]	50.97 ± 0.91	64.70 ± 0.90	63.11 ± 0.87	78.90 ± 0.67	64.28 ± 0.89	76.94 ± 0.71
MADN4 * [21]	50.42 ± 0.27	70.75 ± 0.47	62.89 ± 0.50	89.25 ± 0.34	57.11 ± 0.70	77.83 ± 0.40
FAFD-LDWR * [43]	55.72 ± 0.72	72.76 ± 0.48	56.95 ± 0.66	81.91 ± 0.34	65.45 ± 0.67	79.63 ± 0.33
TLFRNet (ours)	51.53 ± 0.65	75.08 ± 0.49	61.90 ± 0.65	88.99 ± 0.34	71.46 ± 0.66	85.89 ± 0.42

. It can be observed that our approach outperforms all other methods on CUB-200, and achieves results comparable to MADN4 on Stanford Cars. This suggests that our method can accurately generate weights for local descriptors, emphasizing discriminative features closely related to the categories while suppressing the influence of irrelevant features when dealing with fine-grained few-shot classification.

4.4. Comparison with Other Feature Extraction Networks

To further validate the effectiveness of our model under different feature extraction networks, we also selected ResNet12, a widely used feature extraction network in the field of few-shot learning, for 5-way 1-shot and 5-way 5-shot experiments on miniImageNet. The results are shown in

Table 3. Classification accuracy (%) on miniImageNet using ResNet12 as the feature extraction network.* denotes the results from the original work.

Model	Embedding	5-Way 1-Shot	5-Way 5-Shot
DN4 * [7]	ResNet12	54.37 ± 0.36	74.44 ± 0.29
SNAIL * [44]	ResNet12	55.71 ± 0.99	68.88 ± 0.92
Dynamic-Net * [45]	ResNet12	55.45 ± 0.89	70.13 ± 0.68
SANet * [25]	ResNet12	54.75 ± 0.83	73.80 ± 0.62
MATANet * [36]	ResNet12	60.13 ± 0.81	75.42 ± 0.72
TLFRNet (ours)	ResNet12	60.75 ± 0.65	75.83 ± 0.48

. It can be observed that using the deeper ResNet12 as the feature extraction network outperforms the use of Conv-64F. Our method achieves an accuracy improvement of 6.00% and 2.03% in 5-way 1-shot and 5-way 5-shot experiments, respectively, compared to SANet. The accuracy is comparable to MATANet.

4.5. Ablation Experiments

To verify the effectiveness of the designed SRM, QRM, and SRN, we conducted ablation experiments on the miniImageNet, Stanford Dogs, Stanford Cars, and CUB-200 datasets. Specifically, we sequentially removed the QRM, SRM, and the SRN in QRM from TLFRNet. The accuracies of these models are shown in

Table 4. The results of the ablation experiments on four datasets.

Model	miniImageNet		Stanford Dogs		Stanford Cars		CUB-200
	1-Shot	5-Shot	1-Shot	5-Shot	1-Shot	5-Shot	1-Shot	5-Shot
TLFRNet with SRM w/o QRM	54.24	73.56	50.59	70.08	60.44	86.35	70.34	84.73
TLFRNet with QRM w/o SRM	54.37	73.74	49.95	72.51	59.88	86.34	71.02	81.56
TLFRNet w/o SRN	52.78	73.42	51.01	73.36	61.34	86.05	69.52	84.26
TLFRNet	55.17	74.60	51.53	75.08	61.90	88.99	71.46	85.89

. It is evident that removing any module results in a varying degree of accuracy degradation. Therefore, the SRM, QRM, and SRN within TLFRNet all contribute to enhancing the model’s performance.

In general, for the convenience of few-shot learning experiments, we usually assume that the number of shots used during training is consistent with the number of shots used during testing. However, in many real-world scenarios, it is challenging to ensure the same number of shots for training and testing. To investigate the performance variation of our model when the number of shots is inconsistent between training and testing, we conducted numerous experiments on the miniImageNet and Stanford Dogs datasets. The results are shown in Figure 4. It is evident that regardless of the number of shots used during training, the model’s accuracy increases as the number of shots during testing increases.

To investigate the performance of our model with respect to the hyperparameter k in KNN, we conducted a 5-way 1-shot experiment on the miniImageNet dataset by varying the value of k. The results are shown in Figure 5. The model performs best when k = 3. This indicates that the hyperparameter k indeed has an impact on model performance. In practical applications, it is necessary to select an appropriate parameter value based on the specific task.

4.6. Computational Complexity

Compared with existing local feature-based methods, the main computational cost of our TLFRNet comes from the computation of the support weight matrices in the SRM, the query weight matrices in the QRM, and the relation matrix in the similarity calculation module. In the SRM, we need to calculate the similarities between the support features and prototypes for the construction of support weights, which has a computational complexity of $\mathcal{O}\left(N^{2}Km\right)$. In the QRM, we need to calculate the similarities between the query features and support features for the construction of query weight, which has a computational complexity of $\mathcal{O}\left(NK{m}^2\right)$. The computational process of TLFRNet in the similarity calculation module is similar to the classification process of DN4 [7], which has a computational complexity of $\mathcal{O}\left(NK{m}^2\right)$. As a result, our model requires additional computational overhead of $\mathcal{O}(N^{2}Km+NK{m}^2)$. However, this computation cost is lower than other local feature-based methods. For example, DeepEMD [8] needs to solve a linear programming problem which has cubic time complexity with respect to the number of local features. LMPNet [9] uses a multi-prototype strategy, which also significantly increases the computation cost.

5. Conclusions

This paper proposes a task-oriented local feature rectification network with two feature rectification modules (SRM and QRM) for few-shot image classification. By utilizing neural networks to model the relationship between local feature similarities for specific task, adaptive weights are generated for each local descriptor of support set and query images. Additionally, a convolutional neural network is introduced to rectify the similarity tensor. Extensive experiments on five datasets demonstrate that our proposed method effectively rectifies local features, outperforming baseline methods significantly. However, our method focuses solely on local features while ignoring global features. In future work, we will explore the fusion of local and global features, as well as incorporating uncertainty [46] in the data and model caused by the scarcity of data to further enhance the accuracy of few-shot learning.