Volatility Spillover Between China’s Carbon Market and Traditional Manufacturing
Abstract
:1. Introduction
2. Model Construction
2.1. MSV Model
2.2. GC-MSV Model
2.3. DC-MSV Model
2.4. DGC-t-MSV Model
2.5. Model Estimation Method
3. Empirical Results Analysis
3.1. Data and Preprocessing
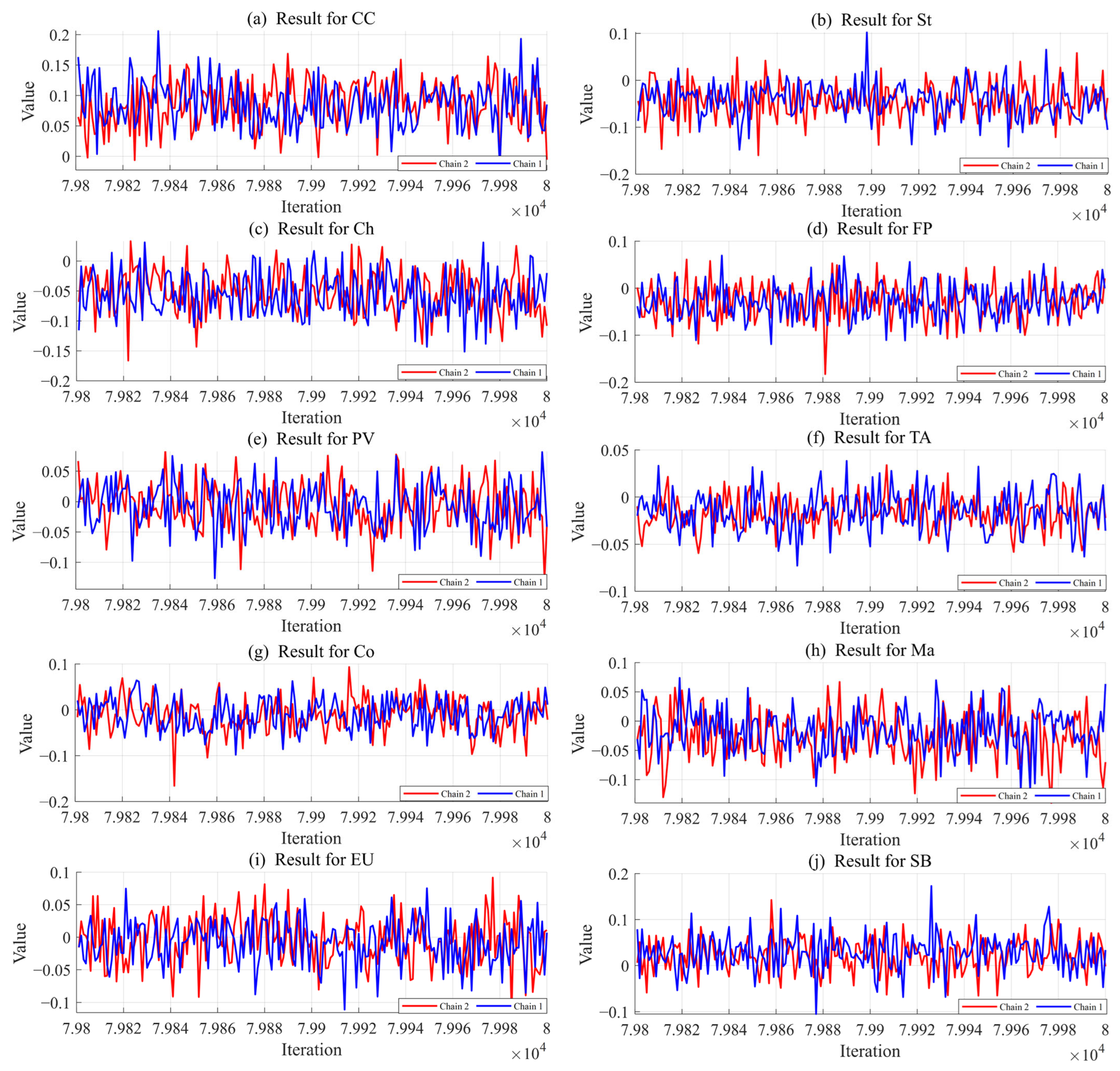
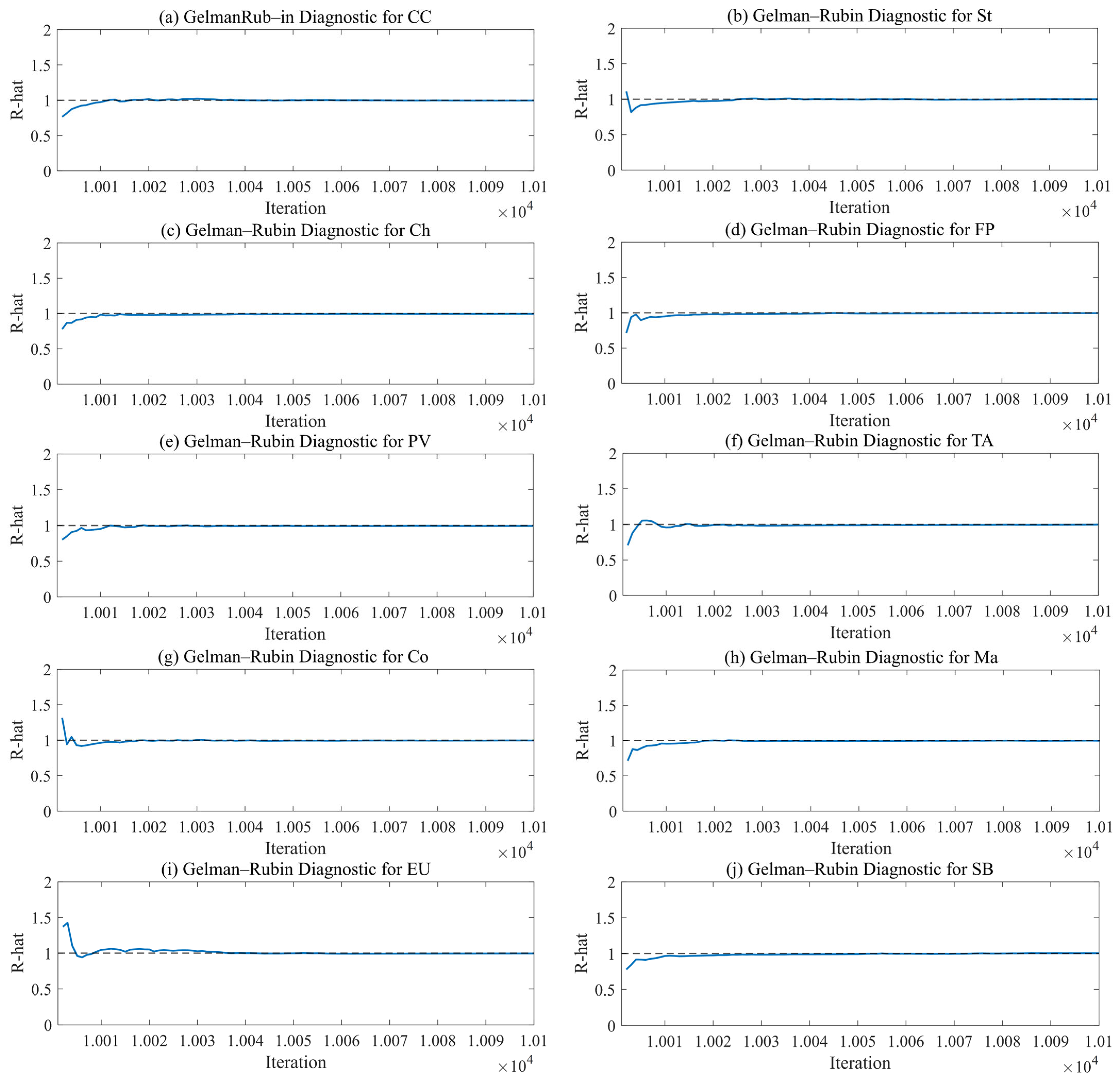
3.2. Convergence Analysis of the DGC-t-MSV Model
3.3. Analysis of Mean Spillover Effect
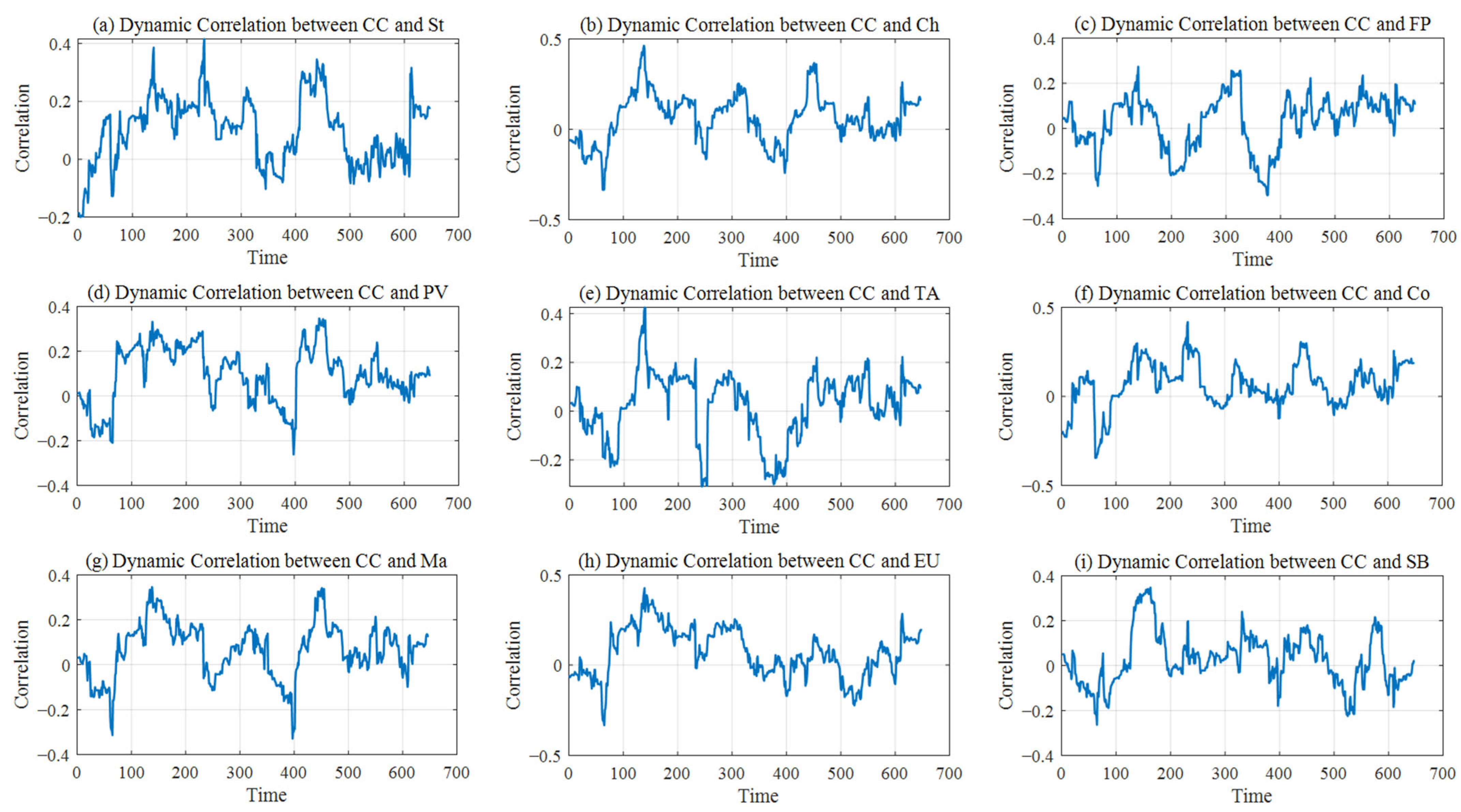
3.4. Analysis of the Volatility Spillover Effect
3.5. Analysis of Model Convergence
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gong, X.; Shi, R.; Xu, J.; Lin, B. Analyzing spillover effects between carbon and fossil energy markets from a time-varying perspective. Appl. Energy 2021, 285, 116384. [Google Scholar] [CrossRef]
- Su, C.W.; Pang, L.D.; Qin, M.; Lobonț, O.R.; Umar, M. The spillover effects among fossil fuel, renewables and carbon markets: Evidence under the dual dilemma of climate change and energy crises. Energy 2023, 274, 127304. [Google Scholar] [CrossRef]
- Xu, C.; Chen, Z.; Zhu, W.; Zhi, J.; Yu, Y.; Shi, C. Time-frequency Spillover and Early Warning of Climate Risk in International Energy Markets and Carbon Markets: From the Perspective of Complex Network and Machine Learning. Energy 2025, 318, 134857. [Google Scholar] [CrossRef]
- Entezaminia, A.; Gharbi, A.; Ouhimmou, M. A joint production and carbon trading policy for unreliable manufacturing systems under cap-and-trade regulation. J. Clean. Prod. 2021, 293, 125973. [Google Scholar] [CrossRef]
- Xi, B.; Jia, W. Research on the impact of carbon trading on enterprises’ green technology innovation. Energy Policy 2025, 197, 114436. [Google Scholar] [CrossRef]
- Li, J.; Wan, Q.; Zhang, J.; Zhang, L.; Ou, Z. Application research on deep learning algorithms supporting cross-border low-carbon IoT systems in manufacturing—Taking Guangdong, China, as an example. Int. J. Low-Carbon Technol. 2025, 20, 315–322. [Google Scholar] [CrossRef]
- Löschel, A.; Lutz, B.J.; Managi, S. The impacts of the EU ETS on efficiency and economic performance–An empirical analyses for German manufacturing firms. Resour. Energy Econ. 2019, 56, 71–95. [Google Scholar] [CrossRef]
- Zhang, W.; Li, J.; Li, G.; Guo, S. Emission reduction effect and carbon market efficiency of carbon emissions trading policy in China. Energy 2020, 196, 117117. [Google Scholar] [CrossRef]
- Cui, J.; Wang, C.; Zhang, J.; Zheng, Y. The effectiveness of China’s regional carbon market pilots in reducing firm emissions. Proc. Natls. Acad. Sci. USA 2021, 118, e2109912118. [Google Scholar] [CrossRef]
- An, Y.; Zhou, D.; Yu, J.; Shi, X.; Wang, Q. Carbon emission reduction characteristics for China’s manufacturing firms: Implications for formulating carbon policies. J. Environ. Manag. 2021, 284, 112055. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, Y.J. Does China’s carbon emissions trading scheme affect the market power of high-carbon enterprises? Energy Econ. 2022, 108, 105906. [Google Scholar] [CrossRef]
- Tang, M.; Cheng, S.; Guo, W.; Ma, W.; Hu, F. Effects of carbon emission trading on companies’ market value: Evidence from listed companies in China. Atmosphere 2022, 13, 240. [Google Scholar] [CrossRef]
- Sun, Y.; Huang, Z.; Chi, F.; Zhang, W. Exploring a low-carbon transition quality assessment framework for Chinese energy-intensive industries: From carbon reduction perspective. Environ. Dev. Sustain. 2024, 2024, 1–32. [Google Scholar] [CrossRef]
- Zhang, J.; Zhuang, Y. Cross-Market Infection Research on Stock Herding Behavior Based on DGC-MSV Models and Bayesian Network. Complexity 2021, 2021, 6645151. [Google Scholar] [CrossRef]
- Wang, J.; Zeng, R.; Wang, L. Volatility Spillover Between the Carbon Market and Traditional Energy Market Using the DGC-t-MSV Model. Mathematics 2024, 12, 3789. [Google Scholar] [CrossRef]
- Li, J.; Umar, M.; Huo, J. The spillover effect between Chinese crude oil futures market and Chinese green energy stock market. Energy Econ. 2023, 119, 106568. [Google Scholar] [CrossRef]
- Liang, Y.; Jin, X.; Taghvaee, V. Sustainable development spillover effects among selected Asian countries: Analysis of integrated sustainability perspective. Socio-Econ. Plan. Sci. 2024, 91, 101781. [Google Scholar] [CrossRef]
- Yu, J.; Meyer, R. Multivariate stochastic volatility models: Bayesian estimation and model comparison. Econom. Rev. 2006, 25, 361–384. [Google Scholar] [CrossRef]
- Chen, T.; Zheng, X.; Wang, L. Systemic risk among Chinese petrochemical firms based on dynamic tail risk spillover networks. North Am. J. Econ. Financ. 2025, 77, 102404. [Google Scholar] [CrossRef]
- Wan, Y.; Sheng, N.; Wei, X.; Su, H. Study on the spatial spillover effect and path mechanism of green finance development on China’s energy structure transformation. J. Clean. Prod. 2023, 415, 137820. [Google Scholar] [CrossRef]
- Chen, W.; Wang, G.; Yang, L.; Huang, C.; Xu, N.; Gu, T.; Zeng, J. Spillover effects of urbanization on carbon emissions: A global view from 2000 to 2019. Environ. Impact Assess. Rev. 2023, 102, 107182. [Google Scholar] [CrossRef]
- Radmehr, R.; Shayanmehr, S.; Baba, E.A.; Samour, A.; Adebayo, T.S. Spatial spillover effects of green technology innovation and renewable energy on ecological sustainability: New evidence and analysis. Sustain. Dev. 2024, 32, 1743–1761. [Google Scholar] [CrossRef]
- Ren, X.; Li, J.; He, F.; Lucey, B. Impact of climate policy uncertainty on traditional energy and green markets: Evidence from time-varying granger tests. Renew. Sustain. Energy Rev. 2023, 173, 113058. [Google Scholar] [CrossRef]
- Hung, Y.S.; Lee, C.; Chen, P.F. China’s monetary policy and global stock markets: A new cointegration approach with smoothing structural changes. Econ. Anal. Policy 2022, 76, 643–666. [Google Scholar] [CrossRef]
- Wu, R.; Tan, Z.; Lin, B. Does carbon emission trading scheme really improve the CO2 emission efficiency? Evidence from China’s iron and steel industry. Energy 2023, 277, 127743. [Google Scholar] [CrossRef]
- Li, Z.Z.; Li, Y.; Huang, C.Y.; Dumitrescu Peculea, A. Volatility spillover across Chinese carbon markets: Evidence from quantile connectedness method. Energy Econ. 2023, 119, 106542. [Google Scholar] [CrossRef]
- Klarić, K.; Pirc Barčić, A.; Basarac Sertić, M. Assessing the role of forest certification and macroeconomic indicators on croatian wood exports to the EU: A panel data approach. Forests 2023, 14, 1908. [Google Scholar] [CrossRef]


| Mean | Median | SD | Var | Kurtosis | Skewness | Range | Min | Max | |
|---|---|---|---|---|---|---|---|---|---|
| CC | 0.0865 | 0.0000 | 1.6747 | 2.8045 | 7.1808 | 0.0083 | 19.5193 | −10.2982 | 9.2211 |
| St | −0.0448 | −0.0424 | 1.4348 | 2.0586 | 6.0546 | −0.1973 | 17.3347 | −8.7336 | 8.6011 |
| Ch | −0.0557 | −0.0863 | 1.4809 | 2.1931 | 4.6343 | −0.1152 | 17.1045 | −8.5116 | 8.5929 |
| FP | −0.0273 | −0.0043 | 1.5388 | 2.3679 | 3.8515 | −0.3767 | 16.2768 | −8.3624 | 7.9145 |
| PV | −0.0058 | −0.0730 | 1.7661 | 3.1190 | 1.6289 | 0.1343 | 15.8171 | −7.1895 | 8.6275 |
| TA | −0.0311 | 0.0221 | 1.3841 | 1.9157 | 7.0716 | −0.5836 | 18.0303 | −9.9153 | 8.1149 |
| Co | −0.0081 | −0.0617 | 1.5984 | 2.5550 | 3.3010 | 0.1492 | 17.1366 | −9.0112 | 8.1254 |
| Ma | −0.0217 | 0.0110 | 1.6011 | 2.5635 | 4.9326 | −0.0080 | 18.8491 | −9.0264 | 9.8227 |
| EU | −0.0069 | −0.0211 | 1.2925 | 1.6705 | 3.2216 | −0.2563 | 13.7645 | −7.2778 | 6.4867 |
| SB | 0.0212 | −0.0359 | 1.7747 | 3.1497 | 2.9940 | 0.2874 | 15.8020 | −7.6599 | 8.1421 |
| Series | ADF Statistic | ADF p-Value | ARCH LM Stat | ARCH LM p-Value |
|---|---|---|---|---|
| CC | −35.1293 | 0 | 110.9146 | 0 |
| St | −25.0754 | 0 | 133.676 | 0 |
| Ch | −23.8302 | 0 | 176.9961 | 0 |
| FP | −16.8489 | 0 | 102.5928 | 0 |
| PV | −25.0161 | 0 | 78.6356 | 0 |
| TA | −25.3569 | 0 | 129.9223 | 0 |
| Co | −17.5676 | 0 | 139.5696 | 0 |
| Ma | −25.4978 | 0 | 205.1657 | 0 |
| EV | −26.7173 | 0 | 56.2428 | 0 |
| SB | −27.9325 | 0 | 50.5449 | 0 |
| Dbar | Dhat | pD | DIC | |
|---|---|---|---|---|
| DC-MSV | 7.91 | −52.67 | 60.58 | 68.49 |
| DCGC-MSV | 9.45 | −36.67 | 46.12 | 55.57 |
| DGC-t-MSV | 8.32 | −4.72 | 13.04 | 21.35 |
| Node | Mean | SD | 50% | 97.5% | Max | Min | Range |
|---|---|---|---|---|---|---|---|
| CCSt | 0.0980 | 0.1032 | 0.1115 | 0.2777 | 0.3529 | −0.1445 | 0.4974 |
| CCCh | 0.0633 | 0.1162 | 0.0763 | 0.3068 | 0.3732 | −0.2008 | 0.5741 |
| CCFP | 0.0295 | 0.1089 | 0.0654 | 0.2118 | 0.2552 | −0.2362 | 0.4914 |
| CCPV | 0.0990 | 0.1106 | 0.0998 | 0.2797 | 0.3792 | −0.1749 | 0.5541 |
| CCTA | 0.0268 | 0.1219 | 0.0571 | 0.2059 | 0.3382 | −0.2836 | 0.6219 |
| CCCo | 0.0632 | 0.1058 | 0.0545 | 0.2919 | 0.3645 | −0.2383 | 0.6028 |
| CCMa | 0.0679 | 0.1049 | 0.0793 | 0.2728 | 0.3604 | −0.1947 | 0.5550 |
| CCEU | 0.0734 | 0.1226 | 0.0659 | 0.3184 | 0.3905 | −0.1830 | 0.5735 |
| CCSB | 0.0262 | 0.1041 | 0.0168 | 0.2991 | 0.3249 | −0.2274 | 0.5523 |
| Node | Mean | SD | 2.50% | 50.00% | 97.50% | Naive SE | Time-Series SE |
|---|---|---|---|---|---|---|---|
| μCC | 6.8092 | 4.0883 | 1.1842 | 8.8931 | 11.7794 | 0.0334 | 0.2738 |
| μSt | −0.2051 | 0.1726 | −0.6548 | −0.1517 | −0.0155 | 0.0014 | 0.0222 |
| μCh | −0.0491 | 0.4360 | −0.7586 | −0.0873 | 0.8134 | 0.0036 | 0.0318 |
| μFP | −0.6146 | 0.1885 | −1.0180 | −0.6041 | −0.2780 | 0.0015 | 0.0214 |
| μPV | −0.7841 | 0.3106 | −1.2214 | −0.8866 | −0.1673 | 0.0025 | 0.0448 |
| μTA | −0.2096 | 0.1306 | −0.4870 | −0.2045 | 0.0243 | 0.0097 | 0.0123 |
| μCo | −0.5890 | 0.1453 | −0.8840 | −0.5869 | −0.3238 | 0.0012 | 0.0124 |
| μMa | −1.2957 | 0.9289 | −2.8296 | −1.1359 | −0.3552 | 0.0076 | 0.0644 |
| μEU | 0.9456 | 0.4433 | 0.4448 | 0.8820 | 2.0301 | 0.0036 | 0.0958 |
| μSB | −0.8389 | 0.1077 | −1.0310 | −0.8456 | −0.6014 | 0.0009 | 0.0097 |
| Node | Mean | SD | 2.50% | 50.00% | 97.50% | Naive SE | Time-Series SE |
|---|---|---|---|---|---|---|---|
| CCSt | −1.3316 | 1.4160 | −4.7391 | −1.1994 | 0.0997 | 0.0116 | 0.3589 |
| StCC | 0.8171 | 5.6030 | 0.7033 | 0.8148 | 0.9366 | 0.0004 | 0.0181 |
| CCCh | −0.2040 | 1.7400 | −3.7857 | 0.0085 | 2.9408 | 0.0142 | 0.4040 |
| ChCC | 0.9107 | 0.0521 | 0.8467 | 0.9126 | 0.9758 | 0.0004 | 0.0018 |
| CCFP | 4.2693 | 3.5040 | −0.5651 | 4.0530 | 10.0388 | 0.0286 | 0.8674 |
| FPCC | 0.8326 | 0.0584 | 0.7084 | 0.8483 | 0.9282 | 0.0005 | 0.0160 |
| CCPV | −3.0193 | 6.6522 | −12.4294 | −4.2722 | 9.9695 | 0.0543 | 1.2401 |
| PVCC | 0.9371 | 0.0241 | 0.8884 | 0.9452 | 0.9629 | 0.0002 | 0.0059 |
| CCTA | 3.0110 | 2.0600 | 0.5326 | 2.5189 | 7.9183 | 0.0168 | 0.5601 |
| TACC | 0.7838 | 0.0531 | 0.6800 | 0.7782 | 0.8914 | 0.0004 | 0.0132 |
| CCCo | 4.1737 | 1.7740 | −4.1737 | 0.3966 | 1.5352 | 0.0145 | 0.2709 |
| CoCC | 0.8561 | 0.0621 | 0.7182 | 0.8665 | 0.9476 | 0.0005 | 0.0124 |
| CCMa | 1.4275 | 0.9146 | 0.2468 | 1.5104 | 2.7243 | 0.0075 | 0.1004 |
| MaCC | 0.9280 | 0.0737 | 0.8252 | 0.9747 | 0.9936 | 0.0006 | 0.0024 |
| CCEU | −1.321 | 0.7263 | −2.4643 | −1.1618 | −0.4983 | 0.0059 | 0.0779 |
| EUCC | 0.9222 | 0.0736 | 0.8188 | 0.9647 | 0.9880 | 0.0006 | 0.0011 |
| CCSB | −0.5027 | 6.875 | −12.1574 | 2.6903 | 7.6510 | 0.0561 | 0.6781 |
| SBCC | 0.4949 | 0.0115 | 0.2467 | 0.5309 | 0.7275 | 0.0013 | 0.0261 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Sheng, D.; Wang, L. Volatility Spillover Between China’s Carbon Market and Traditional Manufacturing. Mathematics 2025, 13, 1514. https://doi.org/10.3390/math13091514
Wang J, Sheng D, Wang L. Volatility Spillover Between China’s Carbon Market and Traditional Manufacturing. Mathematics. 2025; 13(9):1514. https://doi.org/10.3390/math13091514
Chicago/Turabian StyleWang, Jining, Dian Sheng, and Lei Wang. 2025. "Volatility Spillover Between China’s Carbon Market and Traditional Manufacturing" Mathematics 13, no. 9: 1514. https://doi.org/10.3390/math13091514
APA StyleWang, J., Sheng, D., & Wang, L. (2025). Volatility Spillover Between China’s Carbon Market and Traditional Manufacturing. Mathematics, 13(9), 1514. https://doi.org/10.3390/math13091514







