Efficient Numerical Quadrature for Highly Oscillatory Integrals with Bessel Function Kernels
Abstract
1. Introduction
2. Numerical Methods for the Integrals in (1) and (2)
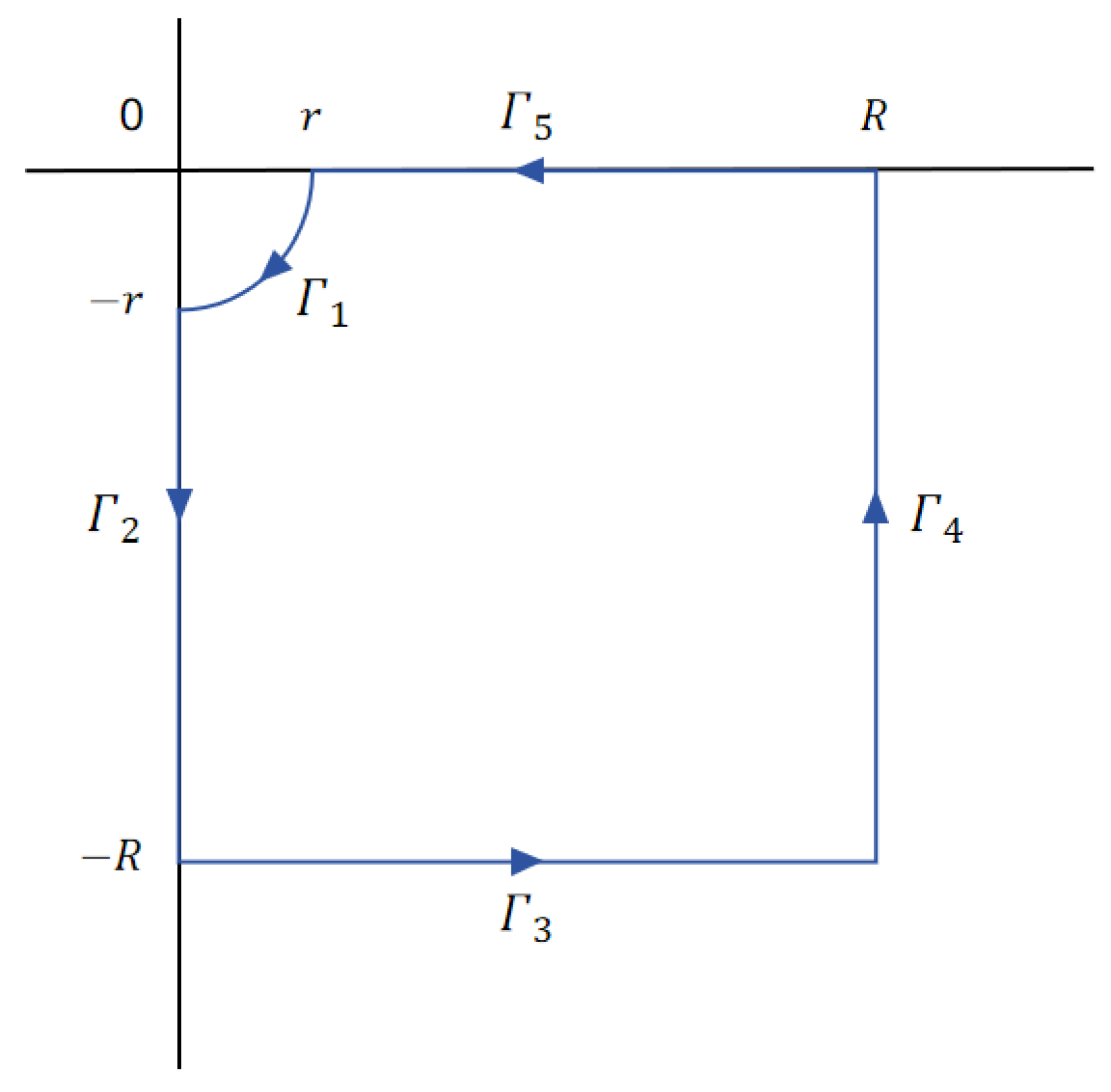
2.1. Complex Integration Method for the Integral
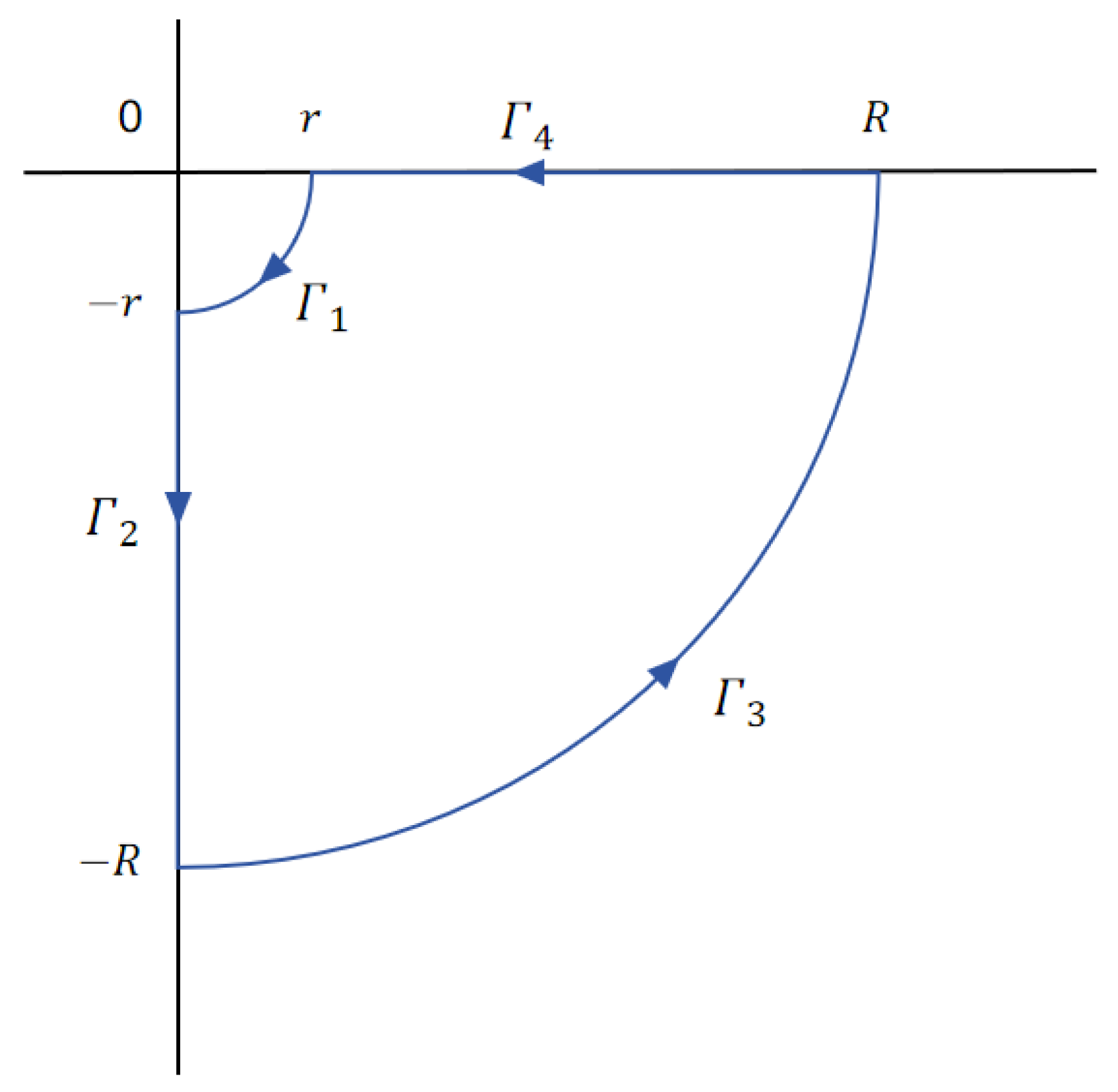
2.2. Complex Integration Method for the Integral
3. Error Analysis of the Numerical Method for the Integral (1) and (2)
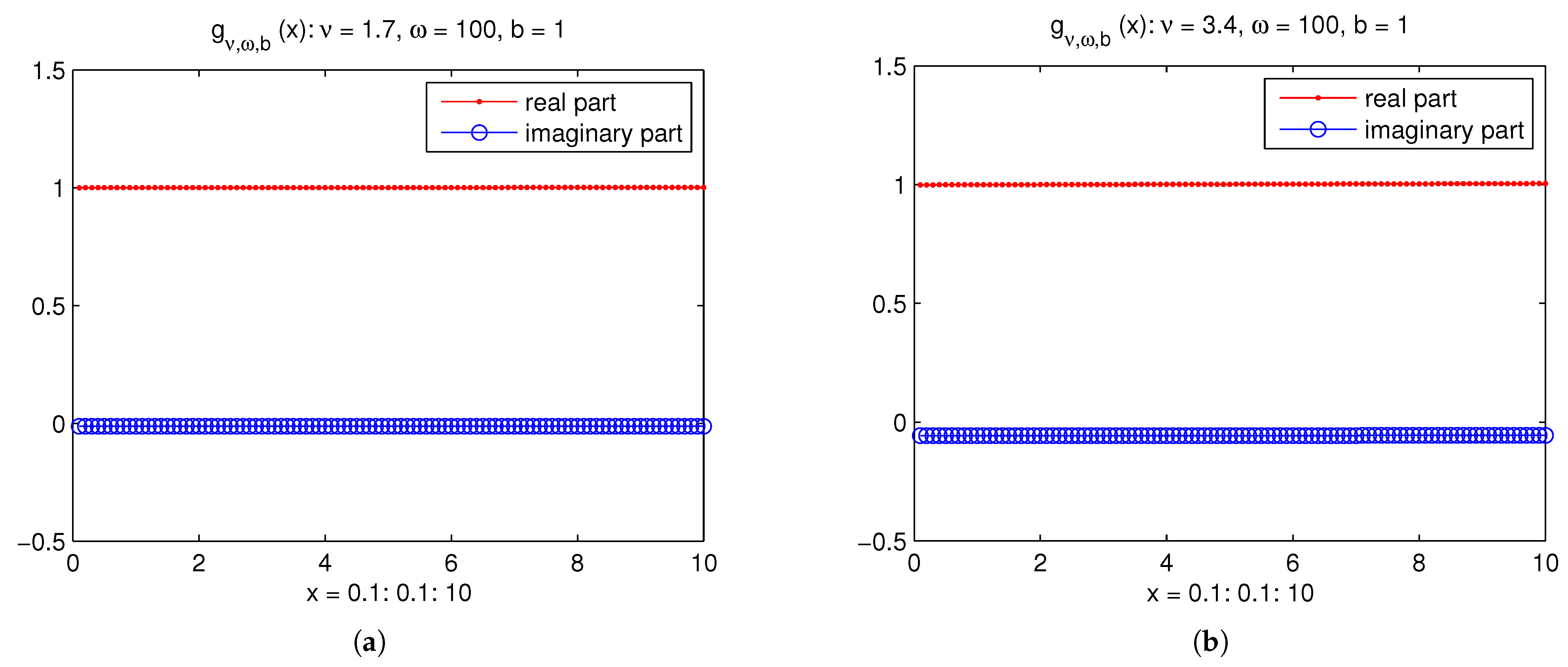
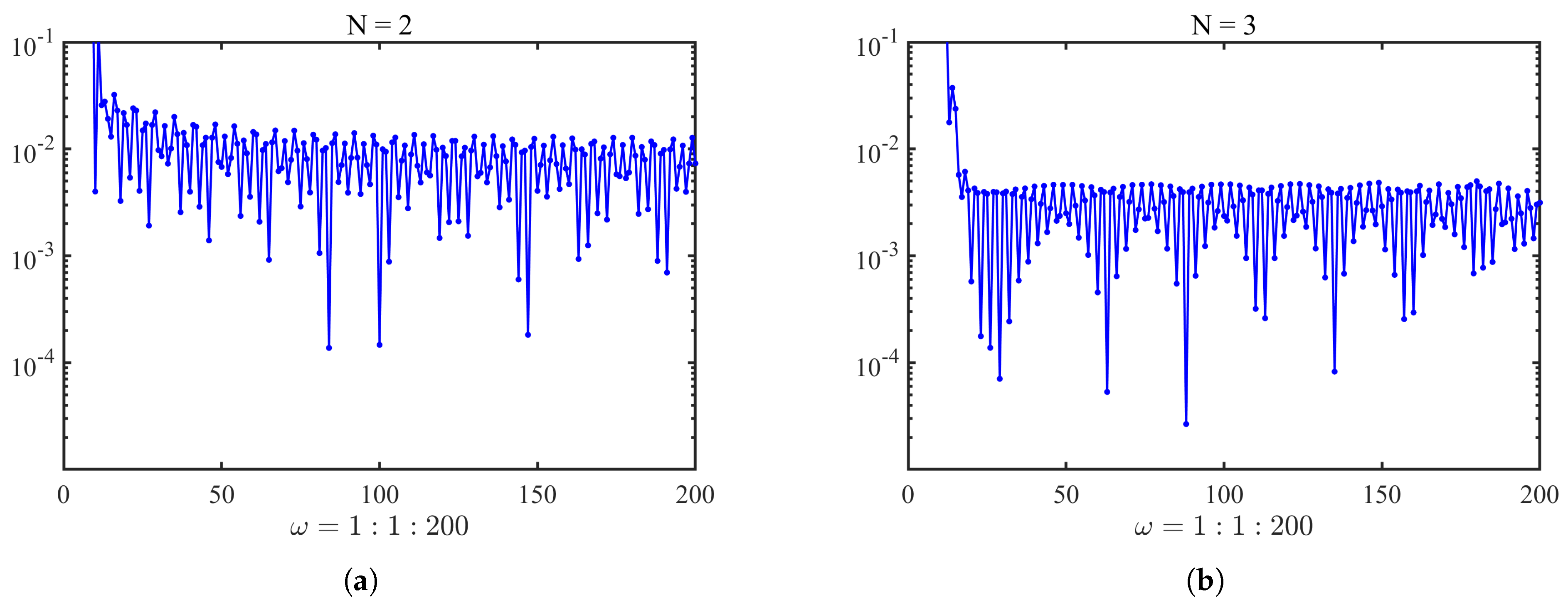
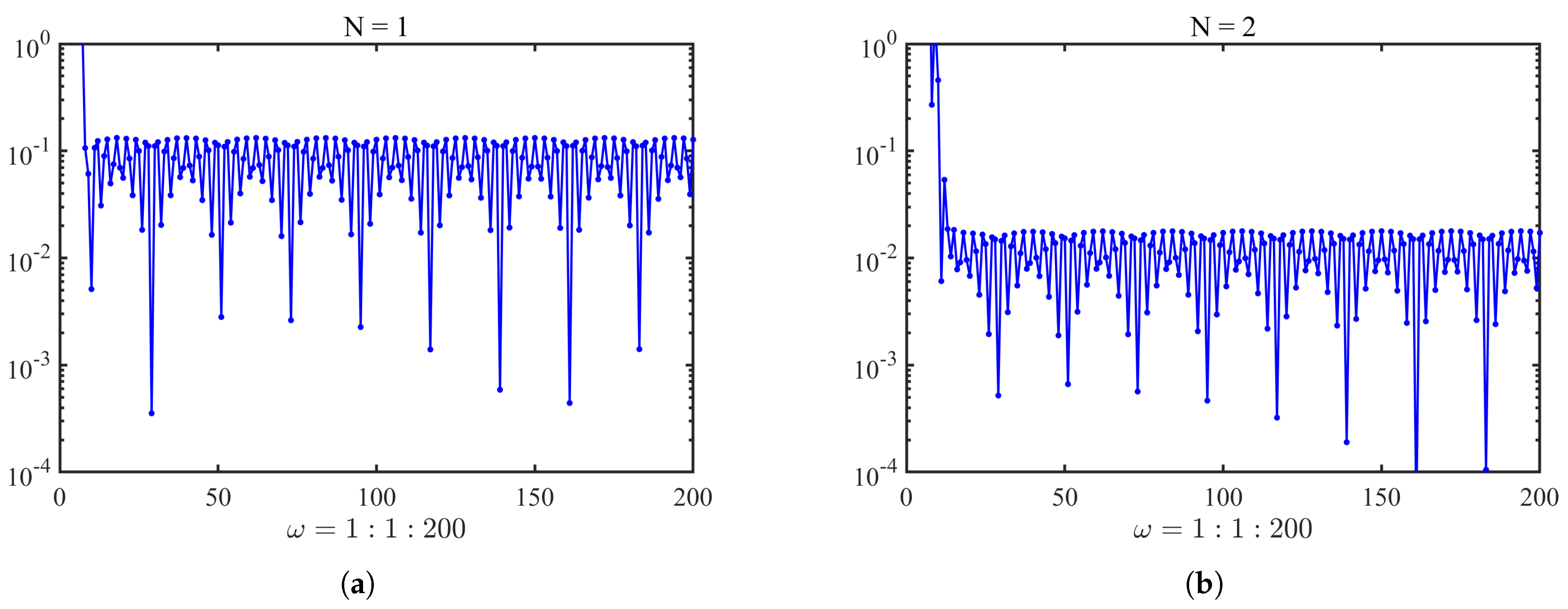
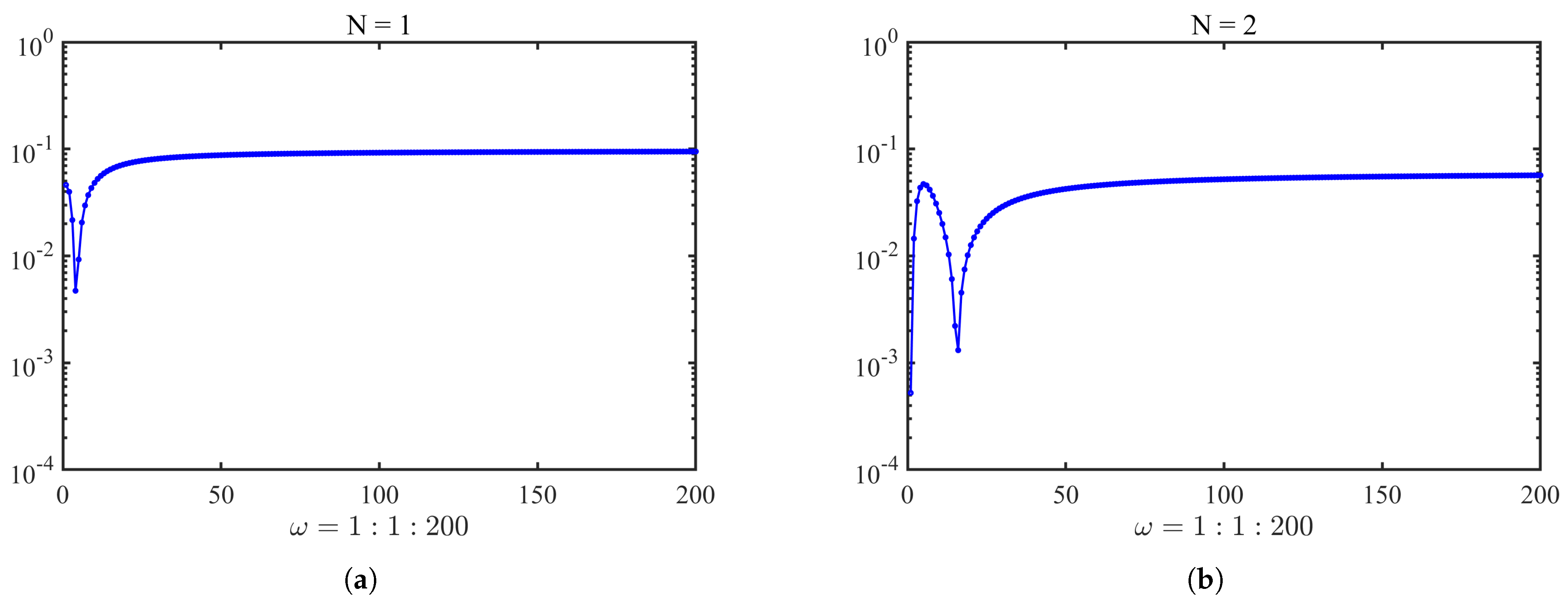
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. (Eds.) NIST Handbook of Mathematical Functions; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Bao, G.; Sun, W. A fast algorithm for the electromagnetic scattering from a large cavity. SIAM J. Sci. Comput. 2005, 27, 553–574. [Google Scholar] [CrossRef]
- Duncan, D.B. Stability and convergence of collocation schemes for retarded potential integral equations. SIAM J. Numer. Anal. 2005, 42, 1167–1188. [Google Scholar]
- Bisseling, R.; Kosloff, R. The fast Hankel transform as a tool in the solution of the time dependent Schrödinger equation. J. Comput. Phys. 1985, 59, 136–151. [Google Scholar] [CrossRef]
- Erdélyi, A. Asymptotic representations of Fourier integrals and the method of stationary phase. J. Soc. Indust. Appl. Math. 1955, 3, 17–27. [Google Scholar] [CrossRef]
- Iserles, A.; Nørsett, S.P. Efficient quadrature of highly oscillatory integrals using derivatives. Proc. R. Soc. A 2005, 461, 1383–1399. [Google Scholar] [CrossRef]
- Iserles, A.; Nørsett, S.P. Quadrature methods for multivariate highly oscillatory integrals using derivatives. Math. Comput. 2006, 75, 1233–1258. [Google Scholar] [CrossRef]
- Wang, H.; Xiang, S. Asymptotic expansion and Filon-type methods for a Volterra integral equation with a highly oscillatory kernel. IMA J. Numer. Anal. 2010, 31, 469–490. [Google Scholar] [CrossRef]
- Levin, D. Procedures for computing one-and-two dimensional integrals of functions with rapid irregular oscillations. Math. Comput. 1982, 38, 531–538. [Google Scholar] [CrossRef]
- Levin, D. Fast integration of rapidly oscillatory functions. J. Comput. Appl. Math. 1996, 67, 95–101. [Google Scholar] [CrossRef]
- Levin, D. Analysis of a collocation method for integrating rapidly oscillatory functions. J. Comput. Appl. Math. 1997, 78, 131–138. [Google Scholar] [CrossRef]
- Olver, S. Moment-free numerical integration of highly oscillatory functions. IMA J. Numer. Anal. 2006, 26, 213–227. [Google Scholar] [CrossRef]
- Chen, R.; An, C. On evaluation of Bessel transform with oscillatory and algebraic singular integrands. J. Comput. Appl. Math. 2014, 264, 71–81. [Google Scholar] [CrossRef]
- Domínguez, V.; Graham, I.G.; Smyshlyaev, V.P. Stability and error estimates for Filon-Clenshaw-Curtis rules for highly-oscillatory integrals. IMA J. Num. Anal. 2011, 31, 1253–1280. [Google Scholar] [CrossRef]
- Filon, L.N.G. On a quadrature formula for trigonometric integrals. Proc. R. Soc. Edinb. 1928, 49, 38–47. [Google Scholar] [CrossRef]
- He, G.; Xiang, S. An improved algorithm for the evaluation of Cauchy principal value integrals of oscillatory functions and its application. J. Comput. Appl. Math. 2015, 280, 1–13. [Google Scholar] [CrossRef]
- Kang, H.; Ling, C. Computation of integrals with oscillatory singular factors of algebraic and logarithmic type. J. Comput. Appl. Math. 2015, 285, 72–85. [Google Scholar] [CrossRef]
- Piessens, R.; Branders, M. On the computation of Fourier transforms of singular functions. J. Comput. Appl. Math. 1992, 43, 159–169. [Google Scholar] [CrossRef]
- Piessens, R.; Branders, M. Modified Clenshaw-Curtis method for the computation of Bessel functions. BIT Numer. Math. 1983, 23, 370–381. [Google Scholar] [CrossRef]
- Xiang, S.; He, G.; Cho, Y. On error bounds of Filon-Clenshaw-Curtis quadrature for highly oscillatory integrals. Adv. Comput. Math. 2015, 41, 573–597. [Google Scholar] [CrossRef]
- Xiang, S.; Wang, H. Fast integration of highly oscillatory integrals with exotic oscillators. Math. Comput. 2010, 79, 829–844. [Google Scholar] [CrossRef]
- Xiang, S.; Cho, Y.J.; Wang, H.; Brunner, H. Clenshaw-Curtis-Filon-type methods for highly oscillatory Bessel transforms and applications. IMA J. Num. Anal. 2011, 31, 1281–1314. [Google Scholar] [CrossRef]
- Xu, Z.; Xiang, S. Numerical evaluation of a class of highly oscillatory integrals involving Airy functions. Appl. Math. Comput. 2014, 246, 54–63. [Google Scholar] [CrossRef]
- Xu, Z.; Xiang, S. On the evaluation of highly oscillatory finite Hankel transform using special functions. Numer. Algorithms 2016, 72, 37–56. [Google Scholar] [CrossRef]
- He, G.; Xiang, S.; Zhu, E. Efficient computation of highly oscillatory integrals with weak singularities by Gauss-type method. Int. J. Comput. Math. 2016, 93, 83–107. [Google Scholar] [CrossRef]
- Huybrechs, D.; Vandewalle, S. On the evaluation of highly oscillatory integrals by analytic continuation. SIAM J. Numer. Anal. 2006, 44, 1026–1048. [Google Scholar] [CrossRef]
- Kang, H.; Xiang, S. On the calculation of highly oscillatory integrals with an algebraic singularity. Appl. Math. Comput. 2010, 217, 3890–3897. [Google Scholar] [CrossRef]
- Kang, H.; Shao, X. Fast computation of singular oscillatory Fourier Transforms. Abstr. Appl. Anal. 2014, 2014, 984834. [Google Scholar] [CrossRef]
- Milovanović, G.V. Numerical calculation of integrals involving oscillatory and singular kernels and some applications of quadratures. Comput. Math. Appl. 1998, 36, 19–39. [Google Scholar] [CrossRef]
- Wang, H.; Xiang, S. On the evaluation of Cauchy principal value integrals of oscillatory functions. J. Comput. Appl. Math. 2010, 234, 95–100. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, L.; Huybrechs, D. Asymptotic expansions and fast computation of oscillatory Hilbert transforms. Numer. Math. 2013, 123, 709–743. [Google Scholar] [CrossRef]
- Wong, R. Quadrature formulas for oscillatory integral transforms. Numer. Math. 1982, 39, 351–360. [Google Scholar] [CrossRef]
- Xu, Z.; Milovanović, G.V.; Xiang, S. Efficient computation of highly oscillatory integrals with Hankel kernel. Appl. Math. Comput. 2015, 261, 312–322. [Google Scholar] [CrossRef]
- Feng, W.; Salgado, A.J.; Wang, C.; Wise, S.M. Preconditioned steepest descent methods for some nonlinear elliptic equations involving p-Laplacian terms. J. Comput. Phys. 2016, 334, 45–67. [Google Scholar] [CrossRef]
- Feng, W.; Wang, C.; Wise, S.M.; Zhang, Z. A second-order energy stable backward differentiation formula method for the epitaxial thin film equation with slope selection. Numer. Methods Partial Differ. Equ. 2018, 34, 1975–2007. [Google Scholar] [CrossRef]
- Cheng, K.; Wang, C.; Wise, S.M. An Energy Stable BDF2 Fourier Pseudo-Spectral Numerical Scheme for the Square Phase Field Crystal Equation. arXiv 2019, arXiv:1906.12255. [Google Scholar]
- Hasegawa, T.; Sugiura, H. Uniform approximation to finite Hilbert transform of oscillatory functions and its algorithm. J. Comput. Appl. Math. 2019, 358, 327–342. [Google Scholar] [CrossRef]
- Chen, R. Fast integration for Cauchy principal value integrals of oscillatory kind. Acta Appl. Math. 2013, 123, 21–30. [Google Scholar] [CrossRef]
- Xu, Z.; Xiang, S.; He, G. Efficient evaluation of oscillatory Bessel Hilbert transforms. J. Comput. Appl. Math. 2014, 258, 57–66. [Google Scholar] [CrossRef]
- Chen, R. Numerical approximations to integrals with a highly oscillatory Bessel kernel. Appl. Numer. Math. 2012, 62, 636–648. [Google Scholar] [CrossRef]
- Chen, R. Numerical approximations for highly oscillatory Bessel transforms and applications. J. Math. Anal. Appl. 2015, 421, 1635–1650. [Google Scholar] [CrossRef]
- Xu, Z.; Milovanović, G.V. Efficient method for the computation of oscillatory Bessel transform and Bessel Hilbert transform. J. Comput. Appl. Math. 2016, 308, 117–137. [Google Scholar] [CrossRef]
- Zaman, S.; Siraj-ul-Islam; Khan, M.M.; Ahmad, I. New algorithms for approximation of Bessel transforms with high frequency parameter. J. Comput. Appl. Math. 2022, 399, 113705. [Google Scholar] [CrossRef]
- Kang, H.; Wang, R.; Zhang, M.; Xiang, C. Efficient computation of oscillatory Bessel transforms with a singularity of Cauchy type. J. Comput. Appl. Math. 2023, 429, 115220. [Google Scholar] [CrossRef]
- Ansari, K.J.; Özger, F. Pointwise and weighted estimates for Bernstein-Kantorovich type operators including beta function. Indian J. Pure Appl. Math. 2024, 1–13. [Google Scholar] [CrossRef]
- Savaş, E.; Mursaleen, M. Bézier Type Kantorovich q-Baskakov Operators via Wavelets and Some Approximation Properties. Bull. Iran. Math. Soc. 2023, 49, 68. [Google Scholar] [CrossRef]
- Alamer, A.; Nasiruzzaman, M. Approximation by Stancu variant of λ-Bernstein shifted knots operators associated by Bézier basis function. J. King Saud Univ. Sci. 2024, 36, 103333. [Google Scholar] [CrossRef]
- Fokas, A.S. Complex variables: Introduction and applications. Math. Gaz. 2003, 83, 530–534. [Google Scholar]
- Henkici, P. Applied and Computational Complex Analysis; Wiley-Interscience: New York, NY, USA, 1974; Volume I. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 8th ed.; Academic Press: Cambridge, MA, USA; Elsevier Inc.: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Kress, R. Numerical Analysis; Springer: New York, NY, USA, 1998. [Google Scholar]




| Method | Range | Derivative | Computational Complexity |
|---|---|---|---|
| Method in [41] | Integer | Medium (polynomial evaluation) | |
| Method in [42] | Medium (polynomial evaluation) | ||
| Our Method | Any real | Low (explicit formula) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, G.; Liu, Y. Efficient Numerical Quadrature for Highly Oscillatory Integrals with Bessel Function Kernels. Mathematics 2025, 13, 1508. https://doi.org/10.3390/math13091508
He G, Liu Y. Efficient Numerical Quadrature for Highly Oscillatory Integrals with Bessel Function Kernels. Mathematics. 2025; 13(9):1508. https://doi.org/10.3390/math13091508
Chicago/Turabian StyleHe, Guo, and Yuying Liu. 2025. "Efficient Numerical Quadrature for Highly Oscillatory Integrals with Bessel Function Kernels" Mathematics 13, no. 9: 1508. https://doi.org/10.3390/math13091508
APA StyleHe, G., & Liu, Y. (2025). Efficient Numerical Quadrature for Highly Oscillatory Integrals with Bessel Function Kernels. Mathematics, 13(9), 1508. https://doi.org/10.3390/math13091508





