Abstract
Using the eight-dimensional framework of the integral formalism of one-dimensional quasicrystals, the analytical expressions for the displacement fields and stress functions of line defects, which are dislocations and line forces, in one-dimensional hexagonal quasicrystals of Laue class 10 are derived. The self-energy of a straight dislocation, the self-energy of a line force, the Peach–Koehler force between two straight dislocations, and the Cherepanov force between two straight line forces in one-dimensional hexagonal quasicrystals of Laue class 10 are calculated. In addition, the two-dimensional Green tensor of one-dimensional hexagonal quasicrystals of Laue class 10 is given within the framework of the integral formalism.
Keywords:
line defects; dislocations; line forces; anisotropic elasticity; integral formalism; Stroh formalism; quasicrystals MSC:
52C23; 74Bxx; 74E10; 35Qxx
1. Introduction
Quasicrystals represent an interesting class of novel materials discovered by Shechtman et al. [1]. Quasicrystals are aperiodic crystals and possess long-range orientational order but no translational symmetry in quasiperiodic directions. Quasicrystals have unusual physical properties such as high hardness, low conductivity, resistivity that decreases with temperature, very low conductivity, small specific heat, low friction coefficients, and wear and oxidation resistance [2,3,4]. The basis of the continuum theory of solid quasicrystals consists of two elementary excitations, namely the phonons and the phasons [5,6]. In the atomistic picture, phonons are related to the translation of atoms, and phasons lead to local rearrangements of atoms in a cell. The generalized elasticity theory of quasicrystals including phonon and phason fields was developed by Ding et al. [7].
Dislocations are important line defects in quasicrystals that cause plasticity and influence the physical properties of quasicrystals (see, e.g., [6,8,9,10,11,12,13,14]). Dislocations have been observed in quasicrystals in many experimental studies (see, e.g., [15,16,17,18,19,20,21]). To understand the effects of dislocations on the physical properties of quasicrystals and to simulate the electron micrographs of dislocations in quasicrystals, the elastic fields of dislocations in quasicrystals are necessary. Therefore, the determination of the elastic fields of dislocations in quasicrystals is an important task in theory and experiment. For quasicrystals, the basic key equations of dislocations were given by Ding et al. [22,23] and Lazar and Agiasofitou [24]. The general expressions for the displacement fields induced by straight dislocations in quasicrystals in terms of the elastic Green tensor were given by Ding et al. [22,23]. Ding et al. [25] extended the Stroh formalism [26,27] and the integral formalism [28,29] for the displacement field of a dislocation in quasicrystals (see also [14,30]). Ding et al. [25] derived the integral formalism from the Stroh formalism for quasicrystals using the eigenvectors and eigenvalues of the Stroh formalism. Using the extended Stroh formalism, Li and Liu [31] studied a dislocation in an icosahedral quasicrystal and Radi and Mariano [32] investigated the steady-state propagation of dislocations in quasicrystals. Wang and Schiavone [33] have given the detailed structure of the extended Stroh formalism for quasicrystals. In the Stroh formalism, the fields of line defects are given as complex form solutions of an eigenvalue problem and in the integral formalism, the fields of line defects are given as real-form solutions of a matrix partial differential equation of the first order (see [34]).
Lazar [35] recently derived the extended integral formalism of line defects (straight dislocations and line forces) for the displacement fields and stress functions for quasicrystals in a straightforward manner without an unnecessary detour via the Stroh formalism. Lazar [35] extended the six-dimensional framework of the integral formalism for line defects in anisotropic elasticity towards a -dimensional integral formalism for line defects in quasicrystals ( for one-, two-, three-dimensional quasicrystals). For generalized plane strain in quasicrystals, the appropriate two-dimensional matrix partial differential equation of the first order and its solution of the integral formalism have been given in [35]. For line defects in quasicrystals, the solution gives the -dimensional vector of the n-dimensional displacement vector and the n-dimensional stress function vector of a straight dislocation with Burgers vector and a line force with strength . The integral formalism provides suitable expressions for both analytical and numerical modelling of line defects in quasicrystals.
Explicit analytical solutions require analytical expressions for the integrals in the integral formalism. In the general case, only numerical solutions are possible using numerical integration. For quasicrystals with high symmetry and symmetrical orientation of the defect line, the complexity is reduced and analytical solutions become possible because the integrals in the integral formalism can be computed analytically. In the case of lower symmetry of quasicrystals and of the orientation of the line defect, numerical treatment is required in the integral formalism. The successful derivation of analytic solutions is of particular value because it confirms and manifests the theoretical prediction. The form of the analytic solutions shows their functional dependence on all relevant parameters. Analytic solutions are always useful as benchmark solutions with which to verify numerical results, and they are useful for degenerate cases (special orientations or ratios of elastic constants) where the numerics may diverge [36].
The most suitable type of quasicrystals for testing the integral formalism are one-dimensional hexagonal quasicrystals of Laue class 10. The Laue class 10 is the Laue class with the highest symmetry for one-dimensional quasicrystals. A one-dimensional quasicrystal is defined as a three-dimensional body which is periodic in the -plane and quasiperiodic in the -direction. One-dimensional quasicrystals are quasicrystals with crystallographic symmetries, namely 31 point groups and 10 Laue classes [13,30,37].
In this work, analytical solutions of line defects in one-dimensional quasicrystals are derived for the first time using the integral formalism. In particular, the closed-form expressions for the displacement fields and the stress functions of line defects in one-dimensional hexagonal quasicrystals of Laue class 10, where the defect line is parallel to the aperiodic direction, are the aim of this work. Within the framework of the integral formalism, the self-energies of a straight dislocation and a line force, the Peach–Koehler force between two straight dislocations, and the Cherepanov force between two line forces in one-dimensional hexagonal quasicrystals of Laue class 10 are calculated. In addition, the two-dimensional Green tensor of one-dimensional hexagonal quasicrystals of Laue class 10 is derived within the framework of the integral formalism.
2. Generalized Elasticity of One-Dimensional Quasicrystals
We consider one-dimensional quasicrystals which are periodic in the -plane and quasiperiodic in the -direction. A one-dimensional quasicrystal can be obtained by projecting a four-dimensional periodic structure onto the three-dimensional physical space. The four-dimensional hyperspace can be decomposed into the direct sum of two orthogonal subspaces:
where is the three-dimensional physical or parallel space of the phonon fields and is the one-dimensional perpendicular space of the phason field with quasiperiodicity in the -direction. Throughout the text, phonon fields will be denoted and phason fields . Note that all quantities (phonon and phason fields) depend on the so-called material space coordinates . Indices in the parallel space are denoted by small Latin letters with .
In the theory of generalized elasticity of one-dimensional quasicrystals, the (elastic) phonon and phason distortion tensors, and , are defined as the gradients of the phonon displacement vector and the phason displacement field , respectively,
where denotes the partial differentiation with respect to . Therefore, the phason displacement vector has only one component . The constitutive relations for a one-dimensional quasicrystal are given by
where and are the phonon and phason stress tensors, respectively. Note that the phonon stress tensor is symmetric, , whereas (see [24,38]). is the tensor of the elastic moduli of phonons, is the tensor of the elastic moduli of phasons, and is the tensor of the elastic moduli of the phonon–phason coupling. The constitutive tensors possess the following symmetries [7,24]:
Using the hyperspace notation of quasicrystals given by Lazar and Agiasofitou [24], the phonon and phason fields can be unified in the corresponding extended fields in the hyperspace. The components of the extended fields will be denoted by capital letters, e.g., . In the hyperspace notation, we have the extended displacement vector :
the extended elastic distortion tensor :
the extended stress tensor :
and the tensor of the extended elastic moduli :
The tensor retains the major symmetry:
In matrix form, Equation (10) can be written as
Using the hyperspace notation, Equations (2) and (3) reduce to
and the constitutive relations (4) and (5) become
which is the extended Hooke law for quasicrystals.
In the absence of external forces, the extended stress tensor (9) can be written in terms of an extended stress function tensor :
with
where and are the phonon and phason stress function tensors, respectively. Here, denotes the three-dimensional Levi–Civita tensor. Substituting Equation (15) into the left hand side of the extended Hooke law (14), we obtain
which is nothing but the extended Hooke law (14) written in terms of and .
3. Integral Formalism for One-Dimensional Quasicrystals
The integral formalism for one-dimensional quasicrystals is based on the framework of generalized plane strain of one-dimensional quasicrystals. In generalized plane strain, all fields are independent of the variable . The extended displacement fields depend only on and , and , but with index in the hyperspace , .
We consider a Cartesian coordinate system in the parallel space. Using a unit vector in the -direction and a unit vector in the -direction (, ) and the notation
which is a matrix in the hyperspace, it follows from the major symmetry (11) of the extended constitutive tensor that
The extended constitutive relation (14) reads for generalized plane strain:
with . For a one-dimensional quasicrystal, the characteristic blocks of the constitutive tensor entering the extended constitutive relations (20) and (21) are given by
Due to the major symmetry of , and are symmetric.
For generalized plane strain, the extended stress tensor can be written in terms of an extended stress function vector , and Equation (15) reduces to
Substituting Equations (13), (25) and (26) into the extended Hooke law (20) and (21), we obtain
Equations (27) and (28), which have the meaning of the extended Hooke law (14) written in terms of and for generalized plane strain, are the two components of Equation (17) for generalized plane strain with .
After rearrangement of Equations (27) and (28), we obtain the following matrix partial differential equation of the first order
This is the matrix differential equation for generalized plane strain of one-dimensional quasicrystals. We have introduced the 8-vector of the extended displacement vector and the extended stress function vector for generalized plane strain:
and the real matrix is defined by its blocks
Here, is the identity matrix. The matrix is the fundamental elasticity matrix for one-dimensional quasicrystals depending on the elastic constants of quasicrystals.
Now, we choose two orthogonal unit vectors and , which are orthogonal to such that forms a right-handed Cartesian basis in . This basis is rotated around by an angle against another fixed basis in , such that
as shown in Figure 1. It yields and . Only the independent variable is transformed, but not the dependent variables and . Using the rotation given in Equation (32) and polar coordinates , the matrix partial differential Equation (29) becomes
Here, the matrix is defined by contraction of the elastic constants with orthogonal unit vectors and according to Equation (18). As mentioned above, the vectors and are turned against the , coordinate system by an angle (see Figure 1), so that depends on the angle
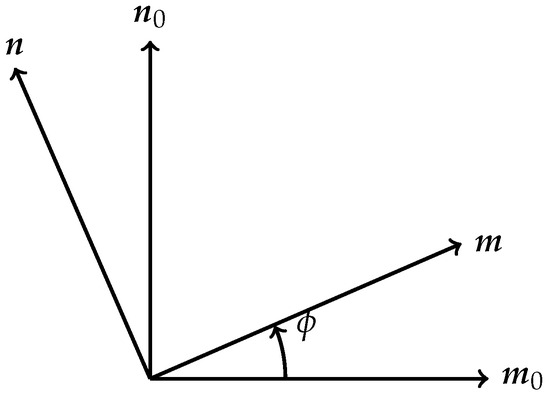
Figure 1.
The unit vectors and are to be turned anticlockwise from and by an angle .
4. Line Defects in One-Dimensional Quasicrystals
Here, we consider a line defect in a one-dimensional quasicrystal, namely a straight dislocation with extended Burgers vector and a line force with extended strength in a one-dimensional quasicrystal located at the origin of the coordinate system. The defect line runs along the axis , which is parallel to the quasiperiodic direction. The fields of the straight dislocation and line force are the extended displacement vector and the extended stress function vector . In the hyperspace notation, the extended Burgers vector of a straight dislocation in a one-dimensional quasicrystal is given by
where is the phonon component and is the phason component of the extended Burgers vector, , and the extended body force vector of a line force in a one-dimensional quasicrystal reads
where is the phonon component and is the phason component of the extended strength .
For one-dimensional quasicrystals, the solution of Equation (33) for a straight dislocation with extended Burgers vector and a line force with extended strength reads (see [35])
Equation (37) is the 8-vector of the solution of the extended displacement vector and the extended stress function vector for a straight dislocation with extended Burgers vector and a line force with extended strength in a one-dimensional quasicrystal. Using
and , the solution (37) can be written in compact form as (see also [35,39])
The matrices , and , which are tensors of rank two in the hyperspace, are the blocks of the matrix , Equation (38), with the block structure (34)
and
where , , and (the transpose of ) are matrices resulting from the four blocks in (see Equations (34) and (38)).
Equation (39) can be decomposed into its four pieces, which are four vectors in the four-dimensional hyperspace (see [35]):
- The extended displacement vector of a straight dislocation with extended Burgers vector :
- The extended displacement vector of a line force with extended strength :
- The extended stress function vector of a straight dislocation with extended Burgers vector :
- The extended stress function vector of a line force with extended strength :
Using the extended stress function vector of a straight dislocation (47) for and , the elastic self-energy of a straight dislocation per unit length reads [35]
where and R are the inner and outer cutoff radii. Using the extended displacement vector of a line force (48) for and , the elastic self-energy of a line force per unit length reads [35]
The Peach–Koehler force per unit length between a straight dislocation with Burgers vector at position in the stress field produced by another dislocation with Burgers vector located at the position is given by (see [35])
In polar coordinates, the two non-vanishing components of the Peach–Koehler force (51) read
The radial component (52) is connected with the matrix , and the tangential component (53) is connected with the matrices and . Note that the -dependence in Equation (53) is due to the -dependence of and .
The Cherepanov force per unit length between a line force with strength at position in the elastic distortion field produced by another line force with strength located the the position is given by (see [35])
In polar coordinates, the two non-vanishing components of the Cherepanov force (54) read
The radial component (55) is connected with the matrix , and the tangential component (56) is connected with the matrices and . The -dependence in Equation (56) is due to the -dependence of and .
5. Line Defects in One-Dimensional Hexagonal Quasicrystals of Laue Class 10
We consider one-dimensional hexagonal quasicrystals of Laue class 10 characterized by the following elastic constants (see [37]), namely five elastic moduli of phonons:
three elastic moduli of phonon–phason coupling:
and two elastic moduli of phasons:
The conditions of positive definiteness for the elastic constants of one-dimensional hexagonal quasicrystals of Laue class 10 to ensure a positive elastic energy density read [40,41]
A one-dimensional hexagonal quasicrystal of Laue class 10 is a transversely isotropic medium, concerning generalized elasticity of quasicrystals, namely, a one-dimensional hexagonal quasicrystal of Laue class 10 is isotropic in the basal -plane (see [38]). Laue class 10 consists of the following point groups [13]: , , , . Therefore, the Laue class 10 is the Laue class with the highest symmetry for one-dimensional quasicrystals. In order to keep equations as simple as possible, we may use instead of in the formulas. For one-dimensional hexagonal quasicrystals of Laue class 10, Equations (22)–(24) reduce to
Therefore, for generalized plane strain, only three elastic moduli of phonons , , , ; one elastic modulus of phonon–phason coupling ; and one elastic modulus of phasons are relevant.
The four blocks of the matrix read
and
where
The angular behaviour of the matrices , , and is obtained by the transformations (see also [42,43])
where
is a rotation matrix in the -plane.
Carrying out the integrations, we obtain
where
and
For , the matrices (75), (78), and (79) reduce to
and
These three matrices (80)–(82) obey the relations
as in anisotropic elasticity (see [44,45]).
Now, substituting Equations (75), (79)–(82) into Equation (45), the extended displacement vector of a straight dislocation with extended Burgers vector reads in matrix form:
and the four components of Equation (86) read explicitly:
Equations (87)–(90) are the displacement components of a straight dislocation with extended Burgers vector in a one-dimensional hexagonal quasicrystal of Laue class 10. Equations (87) and (88) are the displacement components of an edge dislocation with Burgers vector or . Equations (89) and (90) are the displacement components of a screw dislocation with Burgers vector components and . It can be seen that all four components of the Burgers vector are uncoupled. The displacement components of a straight dislocation in a one-dimensional hexagonal quasicrystal of Laue class 10 (87)–(90) obtained in the framework of the integral formalism are in agreement with the expressions given by Li and Fan [46], directly solving the field equations for the phonon and phason displacement fields (see also [47]). The only difference is an irrelevant constant displacement in Equation (88), leading to instead of in [46]. The phonon displacement fields (87)–(89) take the same form as in hexagonal crystals.
Substituting Equations (75), (79), (80), and (82) into Equation (46), the extended displacement vector of a line force with extended strength reads in matrix form:
and the four components of Equation (91) read explicitly:
Equations (92)–(95) are the displacement components of a line force with strength components , , and . In Equations (94) and (95), it can be seen that the phonon and phason components and are coupled due to the elastic constant of the phonon–phason coupling .
Substituting Equations (78), (79), (81), and (82) into Equation (47), the extended stress function vector of a straight dislocation with extended Burgers vector reads in matrix form:
and the four components of Equation (96) read explicitly:
Equations (97)–(100) are the stress function components of a straight dislocation with extended Burgers vector in a one-dimensional hexagonal quasicrystal of Laue class 10. Equations (97) and (98) are the stress function components of an edge dislocation with Burgers vector or . Equations (99) and (100) are the stress function components of a screw dislocation with Burgers vector components and . In Equations (99) and (100), it can be seen that the phonon and phason components and are coupled due to the elastic constant of the phonon–phason coupling . It is interesting to note the similarity between the displacements of a line force (92)–(95) and the stress functions of a dislocation (97)–(100).
Substituting Equations (78)–(80) and (82) into Equation (48), the extended stress function vector of a line force with extended strength reads in matrix form:
and the four components of Equation (101) read explicitly:
Equations (102)–(105) are the stress functions of a line force with strength components , , and . It can be seen that all four components of the strength components , , , and are uncoupled. The phonon stress functions (102)–(104) take the same form as in hexagonal crystals. It is interesting to note the similarity between the displacements of a dislocation (87)–(90) and the stress functions of a line force (102)–(105).
Substituting Equation (81) into Equation (49), the self-energy per unit length of a straight dislocation in a one-dimensional hexagonal quasicrystal of Laue class 10 is given by
Substituting Equation (80) into Equation (50), the self-energy per unit length of a line force in a one-dimensional hexagonal quasicrystal of Laue class 10 is given by
Using Equations (81) and (82), the non-vanishing components of the Peach–Koehler force per unit length between two straight dislocations, Equations (52) and (53), read for a one-dimensional hexagonal quasicrystal of Laue class 10:
Equation (108) contains phonon, phason and phonon–phason-coupling contributions, whereas Equation (109) contains only phonon contributions. If we consider only two parallel screw dislocations, Equations (108) and (109) reduce to the Peach–Kohler force given in [38,46]. In the isotropic limit (see below), the Peach–Koehler force, given in Equations (108) and (109), reduces to the Peach–Koehler force between straight dislocations in isotropic elasticity given in [48,49,50,51].
Using Equations (80) and (82), the non-vanishing components of the Cherepanov force per unit length of between two line forces, Equations (55) and (56), read for a one-dimensional hexagonal quasicrystal of Laue class 10
Equation (110) contains phonon, phason and phonon–phason-coupling contributions, whereas Equation (111) contains only phonon contributions. In the isotropic limit (see below), the Cherepanov force, given in Equations (110) and (111), reduces to the Cherepanov force between straight line forces in isotropic elasticity given in [52].
6. Green Tensor in the Integral Formalism
Within the framework of the integral formalism, the displacement field of a line force, Equations (92)–(95), gives the two-dimensional Green tensor for quasicrystals in the hyperspace, namely
with
Therefore, the non-vanishing components of the two-dimensional Green tensor for one-dimensional hexagonal quasicrystals of Laue class 10 read
Note that the three-dimensional Green tensor of one-dimensional hexagonal quasicrystals of Laue class 10 has been recently given by Lazar et al. [40].
7. Isotropic Limit
Now, we obtain the isotropic limit of the phonon displacement fields and stress functions of a straight dislocation and a straight line force:
, , and .
To verify the isotropic limit of Equations (87)–(89), we need , , where denotes the Poisson ratio; we obtain for the three components of the displacement vector of a straight dislocation in an isotropic medium
which are in agreement with deWit [53] and Mura [54].
To verify the isotropic limit of Equations (92)–(94), we need , , and , where denotes the shear modulus, and we obtain for the three components of the displacement vector of a line force in an isotropic medium
which are in agreement with Lazar and Agiasofitou [52].
To verify the isotropic limit of Equations (97)–(99), we need , , , and we obtain for the three stress functions of a straight dislocation in an isotropic medium
which are in agreement with Ni and Nemat-Nasser [55].
To verify the isotropic limit of Equations (102)–(104), we need , , and we obtain for the three stress functions of a line force in an isotropic medium
Note that the components (129) and (130) are in agreement with Ni and Nemat-Nasser [55]. It is obvious that the component given in Ni and Nemat-Nasser [55] has a mistaken pre-factor.
8. Conclusions
Using the eight-dimensional integral formalism for one-dimensional quasicrystals, we have derived exact analytical solutions of the displacement fields and the stress functions of line defects, namely straight dislocations and line forces, parallel to the aperiodic direction in a one-dimensional hexagonal quasicrystal of Laue class 10. Moreover, we have calculated the self-energies of a straight dislocation and a line force, the Peach–Koehler force between two straight dislocations, and the Cherepanov force between two straight line forces. It has been shown that in the limit to isotropic elasticity, well-known results for the displacement fields and the stress functions of straight dislocations and line forces are recovered. The two-dimensional Green tensor of one-dimensional hexagonal quasicrystals of Laue class 10 has been derived within the framework of the integral formalism.
Funding
This research was funded by the Deutsche Forschungsgemeinschaft, grant number LA1974/5-1.
Data Availability Statement
The original contributions presented in this study are included in the article.
Acknowledgments
Markus Lazar gratefully acknowledges the grant from the Deutsche Forschungsgemeinschaft (Grant number LA1974/5-1). The author wishes to thank Eleni Agiasofitou for their many useful and stimulating discussions on the fascinating subject of quasicrystals.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J.-W. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 1984, 53, 1951–1953. [Google Scholar] [CrossRef]
- Maciá-Barber, E. Quasicrystals: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Maciá Barber, E. Chemical bonding and physical properties in quasicrystals and their related approximant phases: Known facts and current perspectives. Appl. Sci. 2019, 9, 2132. [Google Scholar] [CrossRef]
- Maciá, E. The role of aperiodic order in science and technology. Rep. Prog. Phys. 2006, 69, 397–441. [Google Scholar] [CrossRef]
- Bak, P. Symmetry, stability, and elastic properties of icosahedral incommensurate crystals. Phys. Rev. B 1985, 32, 5764–5772. [Google Scholar] [CrossRef]
- Levine, D.; Lubensky, T.C.; Ostlund, S.; Ramaswamy, S.; Steinhardt, P.J.; Toner, J. Elasticity and dislocations in pentagonal and icosahedral quasicrystals. Phys. Rev. Lett. 1985, 54, 1520–1523. [Google Scholar] [CrossRef]
- Ding, D.-H.; Wang, W.; Hu, C.; Yang, R. Generalized elasticity theory of quasicrystals. Phys. Rev. B 1993, 48, 7003–7010. [Google Scholar] [CrossRef]
- Socolar, J.E.S.; Lubensky, T.C.; Steinhardt, P.J. Phonons, phasons, and dislocations in quasicrystals. Phys. Rev. B 1986, 34, 3345–3360. [Google Scholar] [CrossRef] [PubMed]
- Lubensky, T.C.; Ramaswamy, S.; Toner, J. Dislocation motion in quasicrystals and implications for macroscopic properties. Phys. Rev. B 1986, 33, 7715–7719. [Google Scholar] [CrossRef]
- Edagawa, K. Dislocations in quasicrystals. Mater. Sci. Eng. A 2001, 309–310, 528–538. [Google Scholar] [CrossRef]
- Edagawa, K.; Takeuchi, S. Elasticity, dislocation and their motion in quasicrystals. In Dislocations in Solids; Nabarro, F.R.N., Hirth, J.P., Eds.; Elsevier B.V.: Amsterdam, The Netherlands, 2007; Volume 13, pp. 365–417. [Google Scholar]
- Kleman, M. Phasons and the plastic deformation of quasicrystals. Eur. Phys. J. B 2003, 31, 315–325. [Google Scholar] [CrossRef]
- Fan, T.Y. Mathematical Theory of Elasticity of Quasicrystals and Its Applications; Science Press and Springer Science+Business Media Singapore: Beijing, China, 2011. [Google Scholar]
- Wang, R.; Hu, C. Dislocations in Quasicrystals. In Intermetallic Compounds—Principles and Practice: Progress; Westbrook, J.H., Fleischer, R.L., Eds.; John Wiley & Sons, Ltd.: Chichester, UK, 2002; Volume 3, pp. 379–402. [Google Scholar]
- Zhang, Z.; Urban, K. Transmission electron microscope observations of dislocations and stacking faults in a decagonal Al-Cu-Co alloy. Philos. Mag. Lett. 1989, 60, 97–102. [Google Scholar] [CrossRef]
- Wollgarten, M.; Zhang, Z.; Urban, K. Diffraction contrast of quasicrystalline dislocations in the transmission electron microscope. Philos. Mag. Lett. 1992, 65, 1–6. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhuang, Y. A transmission electron microscopy study of dislocations in Al70Ni10Co20 and Al75Ni10Fe15 decagonal quasicrystals. Philos. Mag. Lett. 1992, 65, 203–209. [Google Scholar] [CrossRef]
- Wollgarten, M.; Beyss, M.; Urban, K.; Liebertz, H.; Köster, K. Direct evidence for plastic deformation of quasicrystals by means of a dislocation mechanism. Phys. Rev. Lett. 1993, 71, 549–552. [Google Scholar] [CrossRef]
- Urban, K.; Wollgarten, M.; Gratias, D.M.; Zhang, Z. Electron microscopy of dislocations in quasicrystals. Phase Transit. 1993, 44, 187–194. [Google Scholar] [CrossRef]
- Wollgarten, M.; Bartsch, M.; Messerschmidt, U.; Feuerbacher, M.; Rosenfeld, R.; Beyss, M.; Urban, K. In-situ observation of dislocation motion in icosahedral Al-Pd-Mn single quasicrystals. Philos. Mag. Lett. 1995, 71, 99–105. [Google Scholar] [CrossRef]
- Feuerbacher, M. Dislocations in icosahedral quasicrystals. Chem. Soc. Rev. 2012, 41, 6745–6759. [Google Scholar] [CrossRef] [PubMed]
- Ding, D.; Yang, W.; Hu, C.; Wang, R. Linear elasticity theory of quasicrystals and defects in quasicrystals. In Materials Science Forum; Trans Tech Publications, Ltd.: Baech, Switzerland, 1994; Volumes 150–151, pp. 345–354. [Google Scholar]
- Ding, D.-H.; Wang, R.; Yang, W.; Hu, C. General expressions for the elastic displacement fields induced by dislocations in quasicrystals. J. Phys. Condens. Matter 1995, 7, 5423–5436. [Google Scholar] [CrossRef]
- Lazar, M.; Agiasofitou, E. Fundamentals in generalized elasticity and dislocation theory of quasicrystals: Green tensor, dislocation key-formulas and dislocation loops. Philos. Mag. 2014, 94, 4080–4101. [Google Scholar] [CrossRef]
- Ding, D.-H.; Wang, R.; Yang, W.; Hu, C.; Qin, Y. Elasticity theory of straight dislocations in quasicrystals. Philos. Mag. Lett. 1995, 72, 353–359. [Google Scholar] [CrossRef]
- Stroh, A.N. Dislocations and cracks in anisotropic elasticity. Philos. Mag. 1958, 3, 625–646. [Google Scholar] [CrossRef]
- Stroh, A.N. Steady state problems in anisotropic elasticity. J. Math. Phys. 1962, 41, 77–103. [Google Scholar] [CrossRef]
- Barnett, D.M.; Lothe, J. Synthesis of the sextic and the integral formalism for dislocations, Green’s function and structure waves in anisotropic elastic solids. Phys. Norv. 1973, 7, 13–19. [Google Scholar]
- Asaro, R.J.; Hirth, J.P.; Barnett, D.M.; Lothe, J. A further synthesis of sextic and integral theories for dislocations and line forces in anisotropic media. Phys. Stat. Sol. (b) 1973, 60, 261–271. [Google Scholar] [CrossRef]
- Hu, C.; Wang, R.; Ding, D.-H. Symmetry groups, physical property tensors, elasticity and dislocations in quasicrystals. Rep. Prog. Phys. 2000, 63, 1–39. [Google Scholar] [CrossRef]
- Li, L.H.; Liu, G.T. Stroh formalism for icosahedral quasicrystal and its application. Phys. Lett. A 2012, 376, 987–990. [Google Scholar] [CrossRef]
- Radi, E.; Mariano, P.M. Steady-state propagation of dislocations in quasi-crystals. Proc. R. Soc. A 2011, 467, 3490–3508. [Google Scholar] [CrossRef]
- Wang, X.; Schiavone, P. Dislocations, imperfect interfaces and interface cracks in anisotropic elasticity for quasicrystals. Math. Mech. Complex Syst. 2013, 1, 1–17. [Google Scholar] [CrossRef]
- Ting, T.C.T. Anisotropic Elasticity; Oxford Science Publishers: Oxford, UK, 1996. [Google Scholar]
- Lazar, M. Line defects in quasicrystals. Crystals 2025, 15, 275. [Google Scholar] [CrossRef]
- Wu, M.S.; Kirchner, H.O.K. Line defects in the (110)-plane of a cubic crystal—An outstanding problem solved by the integral formalism. Proc. R. Soc. Lond. A 2003, 459, 2033–2047. [Google Scholar] [CrossRef]
- Wang, R.; Yang, W.; Hu, C.; Ding, D.-H. Point and space groups and elastic behaviours of one-dimensional quasicrystals. J. Phys. Condens. Matter 1997, 9, 2411–2422. [Google Scholar] [CrossRef]
- Lazar, M.; Agiasofitou, E. Eshelbian mechanics of novel materials: Quasicrystals. J. Micromech. Mol. Phys. 2016, 1, 1640008. [Google Scholar] [CrossRef]
- Lazar, M.; Kirchner, H.O.K. Generalized plane strain embedded in three-dimensional anisotropic elasticity. Philos. Mag. 2021, 101, 2584–2598. [Google Scholar] [CrossRef]
- Lazar, M.; Michelitsch, T.; Agiasofitou, E. Three-dimensional Green tensor of one-dimensional hexagonal quasicrystals. Crystals 2024, 14, 1034. [Google Scholar] [CrossRef]
- Agiasofitou, E.; Lazar, M. On elastic stability and positive definiteness for one-dimensional quasicrystals. Crystals 2025, 15, 219. [Google Scholar] [CrossRef]
- Ting, T.C.T. Some identities and the structure of Ni in the Stroh formalism of anisotropic elasticity. Q. J. Mech. Appl. Math. 1988, 46, 109–120. [Google Scholar]
- Kirchner, H.O.K.; Bluemel, K.H. Elastic quasi-isotropy normal to the basal plane in the hexagonal system. Phys. Stat. Sol. (b) 1976, 75, 527–532. [Google Scholar] [CrossRef]
- Bacon, D.J.; Barnett, D.M.; Scattergood, R.O. Anisotropic continuum theory of defects. Prog. Mater. Sci. 1980, 23, 51–262. [Google Scholar] [CrossRef]
- Hirth, J.P.; Lothe, J. Theory of Dislocations, 2nd ed.; John Wiley: New York, NY, USA, 1982. [Google Scholar]
- Li, X.F.; Fan, T.Y. A straight dislocation in one-dimensional hexagonal quasicrystals. Phys. Stat. Sol. (b) 1999, 212, 19–26. [Google Scholar] [CrossRef]
- Fan, T.Y.; Li, X.F.; Sun, Y.F. A moving screw dislocation in a one-dimensional hexagonal quasicrystal. Acta Phys. Sin. 1999, 8, 288–295. [Google Scholar]
- Lardner, R.W. Mathematical Theory of Dislocations and Fracture; University of Toronto Press: Toronto, ON, Canada, 1974. [Google Scholar]
- Weertman, J.; Weertman, J.R. Elementary Dislocation Theory; Oxford University Press: Oxford, UK; New York, NY, USA, 1992. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity; Pergamon Press Ltd.: New York, NY, USA, 1970. [Google Scholar]
- Agiasofitou, E.; Lazar, M. Micromechanics of dislocations in solids: J-, M-, and L-integrals and their fundamental relations. Int. J. Eng. Sci. 2017, 114, 16–40. [Google Scholar] [CrossRef]
- Lazar, M.; Agiasofitou, E. J-, M- and L-integrals of line charges and line forces. Acta Mech. 2023, 234, 3131–3159. [Google Scholar] [CrossRef]
- DeWit, R. Theory of disclinations IV. J. Res. Natl. Bur. Stand. 1973, 77A, 607–658. [Google Scholar] [CrossRef]
- Mura, T. Micromechanics of Defects in Solids, 2nd ed.; Martinus Nijhoff: Dordrecht, The Netherlands, 1987. [Google Scholar]
- Ni, L.; Nemat-Nasser, S. A general duality in elasticity. Mech. Mater. 1996, 24, 87–123. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).