Finite-Time Stability of a Class of Nonstationary Nonlinear Fractional Order Time Delay Systems: New Gronwall–Bellman Inequality Approach
Abstract
1. Introduction
- There have been very few research papers on nonlinear nonstationary two-term fractional-order systems with time delays in the state. In particular, we focus on the case of nonautonomous (FOTDS) with state time delays.
- By implementing the new type of Gronwall-Bellman inequality, we derive sufficient conditions for FTS, resulting in new criteria for nonstationary nonlinear fractional-order time delay systems. This includes two cases: (a) with a fractional derivative , and a fractional integral of order , and (b) with two fractional derivatives , where .
- The formulated FTS conditions can be easily validated through three numerical examples.
2. Preliminaries and Problem Statement
2.1. Preliminaries
2.2. Problem Statement
3. Main Results
Robust FTS of Nonstationary Nonlinear Fractional Integro-Differential Time Delay System
4. Numerical Simulations
4.1. Numerical Method
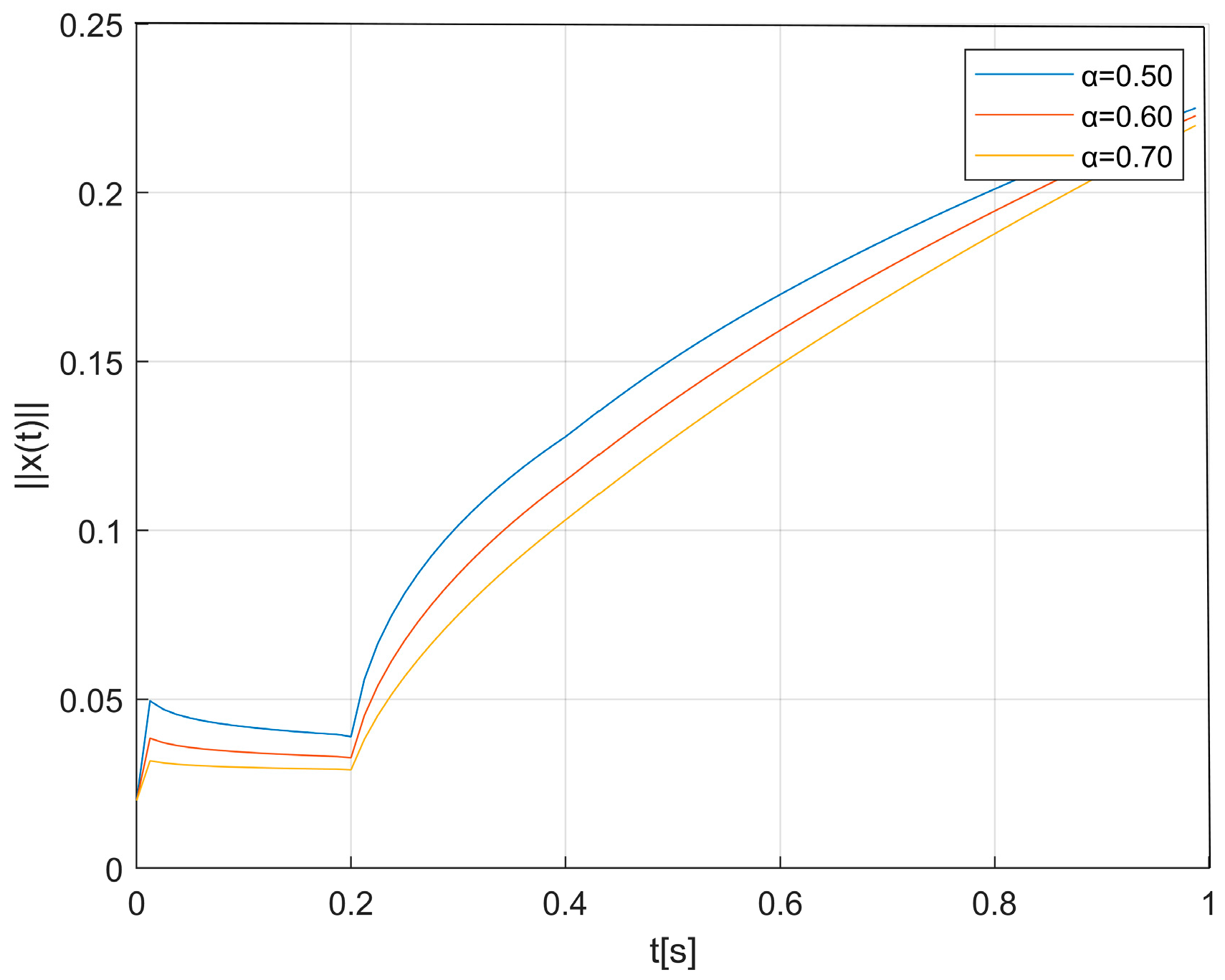
4.2. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zavarei, M.; Jamshidi, M. Time-Delay Systems: Analysis, Optimization and Applications; North-Holland: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Gu, K.; Kharitonov, V.L.; Chen, J. Stability of Time-Delay Systems; Birkhauser: Boston, MA, USA, 2003. [Google Scholar]
- Lee, J.; Haddad, W.M. On finite-time stability and stabilization of nonlinear hybrid dynamical systems. AIMS Math. 2021, 6, 5535–5562. [Google Scholar] [CrossRef]
- Liu, P.L. A delay decomposition approach to robust stability analysis of uncertain systems with time-varying delay. ISA Trans. 2012, 51, 694–701. [Google Scholar] [CrossRef]
- Kolmanovskii, V.; Myshkis, A. Introduction to the Theory and Applications of Functional Differential Equations; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999. [Google Scholar]
- Caponetto, R. Fractional Order Systems: Modeling and Control Applications; World Scientific: Singapore, 2010; Volume 72. [Google Scholar] [CrossRef]
- Petráš, I. Stability of Fractional-Order Systems. In Fractional-Order Nonlinear Systems; Luo, A., Ibragimov, N., Eds.; Nonlinear Physical Science; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Bonnet, C.; Partington, J.R. Analysis of fractional delay systems of retarded and neutral type. Automatica 2002, 38, 1133–1138. [Google Scholar] [CrossRef]
- Deng, W.H.; Li, C.P.; Lu, J.H. Stability analysis of linear fractional differential system with multiple time delays. Nonlinear Dyn. 2007, 48, 409–416. [Google Scholar] [CrossRef]
- Sadati, S.J.; Baleanu, D.; Ranjbar, A.; Ghaderi, R.; Abdeljawad, T. Mittag-Leffler Stability Theorem for Fractional Nonlinear Systems with Delay. In Abstract and Applied Analysis; Hindawi Publishing Corporation: London, UK, 2010; p. 7, Art. ID 108651. [Google Scholar] [CrossRef]
- Lazarević, M.P. Non-Lyapunov Stability and Stabilization of Fractional Order Systems Including Time-Varying Delays, Recent Researches in System Science. In Proceedings of the 15th WSEAS International Conference on Systems, Part of 15th WSEAS CSCC Multiconference, Corfu, Greece, 14–16 July 2011; pp. 196–201. [Google Scholar]
- Naifar, O.; Nagy, A.M.; Makhlouf, A.B.; Kharrat, M.; Hammami, M.A. Finite-time stability of linear fractional-order time-delay systems. Int. J. Robust. Nonlin. 2019, 29, 180–187. [Google Scholar] [CrossRef]
- Lazarević, M. Stability and stabilization of fractional order time delay systems. Sci. Tech. Rev. 2011, 61, 31–45. [Google Scholar]
- Lazarević, M. Finite Time Stability Analysis of PDα Fractional Control of Robotic Time-Delay Systems. Mech. Res. Commun. 2006, 33, 269–279. [Google Scholar] [CrossRef]
- Lazarević, M.; Spasić, A. Finite-Time Stability Analysis of Fractional Order Time Delay Systems: Gronwall’s Approach. Math. Comput. Model. 2009, 49, 475–481. [Google Scholar] [CrossRef]
- Chen, L.; Pan, W.; Wu, R.; He, Y. New result on finite-time stability of fractional order nonlinear delayed systems. J. Comput. Nonlinear Dynam. 2015, 10, 64504. [Google Scholar] [CrossRef]
- Ma, Y.; Wu, B.W.; Wang, Y.E. Finite-time stability and finite-time boundedness of fractional order linear systems. Neurocomputing 2016, 173, 2076–2082. [Google Scholar] [CrossRef]
- Phat, V.N.; Thanh, N.T. New criteria for finite-time stability of nonlinear fractional-order delay systems: A Gronwall inequality approach. Appl. Math. Lett. 2018, 83, 169–175. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D.; Zeng, S.D. Finite-time stability of discrete fractional delay systems: Gronwall inequality and stability criterion. Commun. Nonlinear Sci. Numer. Simul. 2018, 57, 299–308. [Google Scholar] [CrossRef]
- Arthi, G.; Brindha, N.; Baleanu, D. Finite-time stability results for fractional damped dynamical systems with time delays. Nonlinear Anal. Model. Control. 2022, 27, 221–233. [Google Scholar] [CrossRef]
- Panda, S.K.; Vijayakumar, V. Results on finite time stability of various fractional order systems. Chaos Solit. 2023, 174, 113906. [Google Scholar] [CrossRef]
- Du, F.; Lu, J.G. Finite-time stability of neutral fractional order time delay systems with Lipschitz nonlinearities. Appl. Math. Comput. 2020, 375, 125079. [Google Scholar] [CrossRef]
- Zitane, H.; Torres, D.F.M. Finite time stability of tempered fractional systems with time delays. Chaos Solit. 2023, 177, 114265. [Google Scholar] [CrossRef]
- Makhlouf, B. A novel finite time stability analysis of nonlinear fractional-order time delay systems: A fixed point approach. Asian J. Control 2021, 6, 3580–3587. [Google Scholar] [CrossRef]
- Makhlouf, B.A.; Mchiri, L.; Rhaima, M. Stability Analysis of Finite Time for a Class of Nonlinear Time-Delay Fractional-Order Systems. Fractal Fract. 2024, 8, 4. [Google Scholar] [CrossRef]
- Du, F.; Lu, J.G. New criterion for finite-time stability of fractional delay systems. Appl. Math. Lett. 2020, 104, 106248. [Google Scholar] [CrossRef]
- Du, F.; Lu, J.G. New Criteria on Finite-Time Stability of Fractional-Order Hopfield Neural Networks with Time Delays. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3858–3866. [Google Scholar] [CrossRef]
- Lazarević, P.M.; Pišl, S.; Radojević, D. New results on finite-time stability of nonlinear fractional-order multi-time delay systems: Delayed Gronwall inequality approach. Filomat 2024, 38, 5209–5221. [Google Scholar] [CrossRef]
- Wu, Q. A new type of the Gronwall-Bellman inequality and its application to fractional stochastic differential equations. Cogent Math. 2017, 4, 1279781. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999; Available online: https://www.sciencedirect.com/bookseries/mathematics-in-science-and-engineering/vol/198/suppl/C (accessed on 15 February 2025).
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Gao, Y.J.; Ding, Y. A generalized Gronwall inequality and its application to a fractional differential equation. J. Math. Anal. Appl. 2007, 328, 1075–1081. [Google Scholar] [CrossRef]
- Sheng, J.; Jiang, W. Existence and uniqueness of the solution of fractional damped dynamical systems. Adv. Differ. Equ. 2017, 2017, 16. [Google Scholar] [CrossRef]
- Liang, C.; Wei, W.; Wang, J. Stability of delay differential equations via delayed matrix sine and cosine of polynomial degrees. Adv. Differ. Equ. 2017, 2017, 131. [Google Scholar] [CrossRef]
- Bhalekar, S.; Daftardar-Gejji, V. A predictor-corrector scheme for solving nonlinear delay differential equations of fractional order. J. Fract. Calc. Appl. 2011, 1, 1–9. [Google Scholar]
- Wang, F.; Chen, D.D.; Xinguang, Z.; Yonghong, W. Finite time stability of a class of nonlinear fractional-order system with the discrete time delay. Int. J. Syst. Sci. 2016, 48, 984–993. [Google Scholar] [CrossRef]
| 0.5 | 0.556 | 2.281 | 7.997 | 26.395 |
| 0.7 | 0.165 | 0.452 | 1.039 | 2.222 |
| 0.9 | 0.082 | 0.192 | 0.385 | 0.721 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lazarević, M.P.; Pišl, S.; Radojević, D. Finite-Time Stability of a Class of Nonstationary Nonlinear Fractional Order Time Delay Systems: New Gronwall–Bellman Inequality Approach. Mathematics 2025, 13, 1490. https://doi.org/10.3390/math13091490
Lazarević MP, Pišl S, Radojević D. Finite-Time Stability of a Class of Nonstationary Nonlinear Fractional Order Time Delay Systems: New Gronwall–Bellman Inequality Approach. Mathematics. 2025; 13(9):1490. https://doi.org/10.3390/math13091490
Chicago/Turabian StyleLazarević, Mihailo P., Stjepko Pišl, and Darko Radojević. 2025. "Finite-Time Stability of a Class of Nonstationary Nonlinear Fractional Order Time Delay Systems: New Gronwall–Bellman Inequality Approach" Mathematics 13, no. 9: 1490. https://doi.org/10.3390/math13091490
APA StyleLazarević, M. P., Pišl, S., & Radojević, D. (2025). Finite-Time Stability of a Class of Nonstationary Nonlinear Fractional Order Time Delay Systems: New Gronwall–Bellman Inequality Approach. Mathematics, 13(9), 1490. https://doi.org/10.3390/math13091490






