Finite-Time Stability of a Class of Nonstationary Nonlinear Fractional Order Time Delay Systems: New Gronwall–Bellman Inequality Approach

Abstract

This paper aims to analyze finite-time stability (FTS) for a class of nonstationary nonlinear two-term fractional-order time-delay systems with $\alpha ,\beta \in \left(0,2\right)$. Using a new type of generalized Gronwall–Bellman inequality, we derive new FTS stability criteria for these systems in terms of the Mittag–Leffler function. We demonstrate that our theoretical results are less conservative than those presented in the existing literature. Finally, we provide three numerical examples using a modified Adams–Bashforth–Moulton algorithm to illustrate the applicability of the proposed stability conditions.

1. Introduction

Time delay frequently occurs in various engineering systems, potentially leading to bifurcation, chaos, and instability [1]. The control design and stability issues of time-delay systems (TDS) have been extensively studied due to the impact of delay phenomena on system dynamics, which can result in poor performance or even instability. Specifically, a system may be stable in the Lyapunov sense yet remain ineffective if it exhibits undesirable transient performance. This suggests that it may be beneficial to examine the stability of these systems within certain predefined subsets of state space that are defined a priori in a given case. While the concept of Lyapunov stability, which pertains to infinite-time behavior, has been thoroughly investigated, this work focuses on system stability in the non-Lyapunov sense—finite-time stability (FTS). FTS is relevant because it confines the system’s trajectory to a predefined time-varying domain over a finite time interval for a bounded initial condition [2]. As a crucial aspect of studying the transient behavior of control systems, FTS can enhance anti-interference and robustness over a time interval, as well as improve control precision [3]. Moreover, the stability of time-delay systems may be jeopardized by uncertainties and nonlinear perturbations; thus, it is essential to explore the FTS analysis of time-delay systems with uncertain parameters and nonlinear perturbations [4].

On the other hand, the stability properties of neutral-type systems with delays have been studied extensively over the last few decades due to their effectiveness in describing a wide range of physical phenomena [5]. These systems represent a more general class than those of the delayed type. A key characteristic of neutral time-delay systems is the presence of a term with the highest order of derivative, which involves at least one time delay. Additionally, fractional-order dynamical systems have garnered significant attention from researchers and engineers in recent years [6,7], particularly concerning various types of stability. Stability analysis methods are typically divided into time-domain and frequency-domain approaches. Fractional-order time-delay systems (FOTDS) refer to dynamical systems that include both fractional-order derivatives and time delays, and they can be classified into two categories: retarded type and neutral type. Consequently, the stability analysis of FOTDS has emerged as a challenging issue [8,9,10,11].

In [12,13], the solution to the time-delay system (TDS) has been directly examined to check the stability of time-delay fractional-order systems. Here, we focus on fractional-time systems (FTS), specifically investigating the FTS analysis of fractional-order time-delay systems (FOTDS) of the retarded type, as initially presented in [14,15] using the generalized Gronwall inequality (GGI). Gronwall-type inequalities, also known as Gronwall–Bellman (GB) inequalities, are essential tools for analyzing the behavior of solutions to differential equations of both integer and fractional order, and they serve to verify the boundedness property of the system in question [16,17,18,19,20,21]. The stability of neutral fractional order time delay systems with Lipschitz nonlinearities in finite time has been investigated by F. Du et al. in [22]. The analysis of FTS for tempered fractional systems with time delays and variable coefficients has been established in [23]. Furthermore, using the Banach fixed-point method, FTS for FOTDS has been studied in [24,25]. Recently, the authors in [26,27] introduced and applied a fractional Gronwall inequality with time delay (FGIT) for the class of FOTDS. Also, in [28] we studied for the first time, the FTS of nonautonomous FOTDS with time delay in both state and control, characterized by a fractional derivative of order $0<\alpha <1$ and a two-term $0<\beta <\alpha <1$ fractional order system via FGIT. Moreover, the author in [29] introduced and applied a new type of Gronwall–Bellman inequality for a class of fractional differential equations.

In this contribution, motivated by the previous works, we aim to study, for the first time, FTS for a class of nonstationary, nonlinear FOTDS characterized by a fractional derivative of order $0<\alpha <1,$ and a corresponding fractional integral of order $0<\beta <1$, where $\beta =1-\alpha$, using a new type of Gronwall–Bellman inequality [29]. Additionally, we examine two-term FOTDS defined for parameters $0<\beta <1<\alpha <2$ where $\beta =\alpha -1$. It can be observed that the class of FOTDS considered here differs from that in [28], as it incorporates both the fractional integral of order $0<\beta <1$ as well as the fractional derivative order $\alpha \in \left(0,2\right)$.

To our knowledge, the problem of determining the conditions for FTS in nonstationary nonlinear fractional-order systems with time delays in the state, using this new type of Gronwall–Bellman inequality, has not yet been addressed.

The core contributions and novelties of this work are as follows:

• There have been very few research papers on nonlinear nonstationary two-term fractional-order systems with time delays in the state. In particular, we focus on the case of nonautonomous (FOTDS) with state time delays.
• By implementing the new type of Gronwall-Bellman inequality, we derive sufficient conditions for FTS, resulting in new criteria for nonstationary nonlinear fractional-order time delay systems. This includes two cases: (a) with a fractional derivative $0<\alpha <1$, and a fractional integral of order $0<\beta <1, \beta =1-\alpha$, and (b) with two fractional derivatives $0<\beta <1<\alpha <2$, where $\beta =\alpha -1$.
• The formulated FTS conditions can be easily validated through three numerical examples.

The rest of this paper is structured as follows. Section 2 provides basic definitions, notations, and lemmas related to fractional calculus. In Section 3, we establish new criteria for FTS for a nonstationary nonlinear fractional integro-differential time delay system with a fractional derivative $\alpha$, and fractional integral order $\beta$:$\alpha ,\beta \in \left(0,1\right)$ as well as for a nonstationary nonlinear time delay system with two-term fractional derivatives $\beta \in \left(0,1\right)$ and $\alpha \in \left(1,2\right)$. Section 4 presents three numerical examples to illustrate the application and verify the effectiveness of our theoretical results. Finally, Section 5 concludes with remarks summarizing our findings.

2. Preliminaries and Problem Statement

2.1. Preliminaries

This section presents basic notations, essential definitions, and concepts related to the Riemann–Liouville fractional integral and the Caputo fractional derivative. Throughout this paper, the norm $‖\left(\cdot \right)‖$ denotes any vector norm., i.e., ${‖\left(\cdot \right)‖}_1,$ ${‖\left(\cdot \right)‖}_2,$ or ${‖\left(\cdot \right)‖}_{\infty },$ or the corresponding matrix norm induced by the equivalent vector norm, i.e., $1-,$ $2-,$ or $\infty -$ norm, respectively.

Definition 1.

The Riemann–Liouville (RL) fractional integral of order $\alpha$ for an integrable function $h\left(t\right):\left[t_0,\infty \right)\to R$ is defined as follows [30]:

$$\begin{array}{l}{}_{t_0}{}^{\mathrm{RL}}\mathrm{D}_t^{-\alpha }f\left(t\right)\equiv {}_{t_0}\mathrm{I}_t^{\alpha }h\left(t\right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\displaystyle \underset{t_0}{\overset{t}{\int }}{\left(t-s\right)}^{\alpha -1}h\left(s\right)\mathrm{d}s},t\ge t_0,\\ \alpha \in C,t>0,\mathrm{Re}\left(\alpha \right)>0.\end{array}$$

(1)

where $\mathsf{\Gamma }\left(\cdot \right)$ is the Gamma function, $\mathsf{\Gamma }\left(\xi \right)={\displaystyle \underset{0}{\overset{\infty }{\int }}{s}^{\xi -1}{e}^{-s}}ds$.

Definition 2

([30]). The left Caputo fractional derivative of order $\alpha$, ($n-1\le \alpha <n\in {\mathbb{Z}}^{+}$) of the function $h\left(t\right)$ is as follows:

$${}^{c}D_{t_0,t}^{\alpha }h\left(t\right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(n-\alpha \right)}}{\displaystyle \underset{t_0}{\overset{t}{\int }}{\left(t-\tau \right)}^{n-\alpha -1}{h}^{\left(n\right)}\left(\tau \right)d\tau ,}$$

(2)

where $h^{(n)}(\tau )=d^{n}h(\tau )/d{\tau }^n$.

Definition 3

([31]). The Mittag–Leffler function with one parameter is given as follows:

$$E_{\alpha }\left(h\right)={\displaystyle \sum _{k=0}^{\infty }{h}^k}/\mathsf{\Gamma }\left(k\alpha +1\right), \left(\alpha =1, E_1\left(h\right)=e^h\right), \alpha >0, h\in C.$$

(3)

Lemma 1

([31]). Let $h\left(t\right)\in A{C}^n\left[a,b\right]$ and $n-1<\alpha <n, t>0$, then

$${}_{0}I_t^{\alpha }\left({}^{c}D_0^{\alpha }h\left(t\right)\right)=h\left(t\right)-{\displaystyle \sum _{k=0}^{n-1}\frac{t^k}{k!}}{h}^{\left(k\right)}\left(0\right).$$

(4)

Then for $1<\alpha <2$, it yields the following:

$${}_{0}I_t^{\alpha }\left({}^{c}D_0^{\alpha }h\left(t\right)\right)=h\left(t\right)-h\left(0\right)-t{h}^{\prime }\left(0\right),t>0.$$

(5)

Lemma 2.

Let $\alpha >\beta >0,n-1<\beta <n$ and $h\left(t\right)\in A{C}^n\left[a,b\right]$. Then,

$${}_{0}I_t^{\alpha }\left({}^{c}D_0^{\beta }h\left(t\right)\right)={}_{0}I_t^{\alpha -\beta }h\left(t\right)-{\displaystyle \sum _{k=0}^{n-1}\frac{t^{k+\alpha -\beta }}{\mathsf{\Gamma }\left(\alpha -\beta +k+1\right)}{h}^{\left(k\right)}\left(0\right)}.$$

(6)

Remark 1.

Assume that $1<\beta <\alpha <2$, then we get the following:

$${}_{0}I_t^{\alpha }\left({}^{c}D_0^{\beta }h\left(t\right)\right)={}_{0}I_t^{\alpha -\beta }h\left(t\right)-{\displaystyle \frac{h\left(0\right)\cdot t^{\alpha -\beta }}{\mathsf{\Gamma }\left(\alpha -\beta +1\right)}}-{\displaystyle \frac{h^{(1)}\left(0\right)\cdot t^{\alpha -\beta +1}}{\mathsf{\Gamma }\left(\alpha -\beta +2\right)}},t\ge 0.$$

(7)

Lemma 3

([32], Generalized Gronwall Inequality). Suppose $\alpha >0$, $z(t),v(t)$ are nonnegative and local integrable on $0\le t<T, T\le +\infty$ and $g(t)$ is a nonnegative, nondecreasing continuous function defined on $0\le t<T, g(t)\le M=const$, $\alpha >0$ with the following:

$$z(t)\le v(t)+g(t){\displaystyle \underset{0}{\overset{t}{\int }}{\left(t-s\right)}^{\alpha -1}z(s)ds},$$

(8)

on this interval. Then,

$$z(t)\le v(t)+{\displaystyle \underset{0}{\overset{t}{\int }}\left[{\displaystyle \sum _{n=1}^{\infty }\frac{{\left(g(t)\mathsf{\Gamma }\left(\alpha \right)\right)}^n}{\mathsf{\Gamma }\left(n\alpha \right)}{\left(t-s\right)}^{n\alpha -1}}a(s)\right]ds, } 0\le t<T.$$

(9)

Corollary 1.

Under the hypothesis of Lemma 3, let $v(t)$ be a nondecreasing function on $\left[0,T\right)$. Then it holds as follows:

$$z\left(t\right)\le v(t)E_{\alpha }\left(g(t)\mathsf{\Gamma }\left(\alpha \right)t^{\alpha }\right),$$

(10)

where $E_{\alpha }$ is the Mittag–Leffler function.

Lemma 4

(an extended form of the GGI, [33]). Suppose non-integer orders $\alpha >0, \beta >0,$ and $v\left(t\right)$ is nonnegative function locally integrable on $\left[0,T\right)$, $g_1\left(t\right)$, and $g_2\left(t\right)$ are nonnega-tive, nondecreasing, continuous functions defined on $\left[0,T\right)$, $g_1\left(t\right)\le N_1$, $g_2\left(t\right)\le N_2$, $(N_1,N_2=const)$. Suppose $z\left(t\right)$ is nonnegative and locally integrable on $\left[0,T\right)$, with the following:

$$z\left(t\right)\le v\left(t\right)+g_1\left(t\right){\displaystyle \underset{0}{\overset{t}{\int }}{\left(t-s\right)}^{\alpha -1}z\left(s\right)}ds+g_2\left(t\right){\displaystyle \underset{0}{\overset{t}{\int }}{\left(t-s\right)}^{\beta -1}z\left(s\right)}ds,t\in \left[0,T\right).$$

(11)

It follows:

$$z\left(t\right)\le v\left(t\right)+{\displaystyle \underset{0}{\overset{t}{\int }}{\displaystyle \sum _{n=1}^{\infty }{\left[g\left(t\right)\right]}^n}\cdot {\displaystyle \sum _{k=0}^n\frac{C_n^k{\left[\mathsf{\Gamma }\left(\alpha \right)\right]}^{n-k}{\left[\mathsf{\Gamma }\left(\beta \right)\right]}^k}{\mathsf{\Gamma }\left(\left(n-k\right)\alpha +k\beta \right)}}{\left(t-s\right)}^{\left(n-k\right)\alpha +k\beta -1}v\left(s\right)}ds,t\in \left[0,T\right)$$

(12)

where $g\left(t\right)=g_1\left(t\right)+g_2\left(t\right)$ and $C_n^k=n\left(n-1\right)\left(n-2\right)\dots \left(n-k+1\right)/k!$.

Corollary 2.

Under the hypothesis of Lemma 4, let $v\left(t\right)$ be a nondecreasing function on $\left[0,T\right)$. Then,

$$z\left(t\right)\le v\left(t\right)E_{\varpi }\left[g\left(t\right)\left(\mathsf{\Gamma }\left(\alpha \right)t^{\alpha }+\mathsf{\Gamma }\left(\beta \right)t^{\beta }\right)\right],\varpi =min\left(\alpha ,\beta \right).$$

(13)

Lemma 5

(Theorem 2.1 in [29], p. 3). Let 0 < α < 1 and consider the time interval $I=\left[0,T\right)$, where $T\le \infty$. Suppose a(t) is a nonnegative function, which is locally integrable on I and b(t) and g(t) are nonnegative, nondecreasing continuous functions defined on I, with both bounded by a positive constant, M. If $z\left(t\right)$ is nonnegative, and locally integrable on I and satisfies the following:

$$z\left(t\right)\le a\left(t\right)+b\left(t\right){\displaystyle \underset{0}{\overset{t}{\int }}z\left(s\right)}ds+g\left(t\right){\displaystyle \underset{0}{\overset{t}{\int }}{\left(t-s\right)}^{\alpha -1}z\left(s\right)}ds,$$

(14)

Then,

$$z\left(t\right)\le a\left(t\right)+{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{i=0}^n\left(\begin{array}{c}n\\ i\end{array}\right)}}{b}^{n-i}\left(t\right)g^i\left(t\right){\displaystyle \frac{{\left[\mathsf{\Gamma }\left(\alpha \right)\right]}^i}{\mathsf{\Gamma }\left(i\alpha +n-i\right)}}{\displaystyle \underset{0}{\overset{t}{\int }}{\left(t-s\right)}^{\left\{i\alpha -\left(i+1-n\right)\right\}}a\left(s\right)}ds.$$

(15)

Corollary 3

([29]). Suppose the conditions in Lemma 5 are satisfied and a(t) is nondecreasing on $0\le t<T$. Then,

$$z\left(t\right)\le a(t)E_{\mathsf{\alpha }}\left(g(t)\mathsf{\Gamma }\left(\mathsf{\alpha }\right)t^{\mathsf{\alpha }}\right)\exp \left({\displaystyle \frac{1}{\mathsf{\alpha }}}b\left(t\right)t\right).$$

(16)

Remark 2.

If b(t) ≡ 0, Lemma 5, and Corollary 3 become Corollary 1.

2.2. Problem Statement

Case 1.

The analysis focuses on a nonstationary, nonlinear fractional time delay system characterized by a fractional derivative of order $0<\alpha <1,$ and a corresponding fractional integral of order $0<\beta <1$ where $\beta =1-\alpha$. The system with state time delays is represented by the following equation:

$${}^c\mathrm{D}_t^{\alpha }\mathit{x}\left(t\right)=A_0\left(t\right)\mathit{x}\left(t\right)+A_1\left(t\right)x\left(t-{\gamma }_x\right)+A_2\left(t\right){\mathrm{I}}_t^{\beta }\mathit{x}\left(t\right)+B_{0}u\left(t\right)+g\left(t,x\left(t\right),x\left(t-{\gamma }_g\right)\right),$$

(17)

with the associated continuous function of the initial state, as follows:

$$\mathit{x}\left(t\right)={\psi }_x\left(t\right),t\in \left[-\gamma ,0\right],$$

(18)

where ${\gamma }_x,{\gamma }_g$ are the time state delays, and without loss of generality it is assumed that ${\gamma }_x={\gamma }_g=\gamma$; $x\left(t\right)\in R^n$ is the state vector and $u\left(t\right)\in {ℝ}^m$ is the control input; $A_0\left(t\right),A_1\left(t\right),A_2\left(t\right)$, are time-varying matrices and $B_0$ denotes constant matrix with appropriate dimensions; ${\psi }_x\left(t\right)\in C\left(\left[-\gamma ,0\right],R^n\right)$ is the initial function of $x\left(t\right)$ with the norm ${‖{\psi }_x‖}_C={\sup }_{-\gamma \le s\le 0}‖{\psi }_x\left(s\right)‖$. Here, the following assumption for the nonlinear term $g\left(.\right)$ is introduced. The nonlinear term $g\left(t,x\left(t\right),x\left(t-{\gamma }_x\right)\right)$ satisfies the condition, i.e., there is a continuous function $M\left(t\right)$ on $\left[0,+\infty \right]$ such that

$$‖g\left(t,x\left(t\right),x\left(t-{\gamma }_x\right)\right)‖\le M\left(t\right)\left(‖x\left(t\right)‖+‖x\left(t-{\gamma }_x\right)‖\right).$$

(19)

Also, matrices $A_0\left(t\right),A_1\left(t\right),A_2\left(t\right)$ contain time-varying structural uncertainties $\Delta A_i\left(t\right), i=0,1,2$ satisfying the following:

$$A_0\left(t\right)=A_0+\Delta A_0\left(t\right), A_1\left(t\right)=A_1+\Delta A_1\left(t\right), A_2\left(t\right)=A_2+\Delta A_2\left(t\right),$$

(20)

where $A_0,A_1,A_2$ are known constant matrices. The norm ${‖x\left(t\right)‖}_{\infty }$ will be used here as well:

$${\sup }_{t\in \left[0,T\right]}‖A_i\left(t\right)‖=a_i, i=0,1,2 {\sup }_{t\in \left[0,T\right]}‖\Delta A_i\left(t\right)‖=\Delta a_i, i=0,1,2$$

$${\sup }_{t\in \left[0,T\right]}\left(‖A_0\left(t\right)‖+‖A_1\left(t\right)‖\right)<\infty ,{\sup }_{t\in \left[0,T\right]}\left(M\left(t\right)\right)=m.$$

(21)

Definition 4

([15,34]). The nonlinear fractional-order delay system with state time delay given by nonhomogeneous state Equation (17) satisfying initial condition (18) is finite-time stable w.r.t. $\left\{\delta ,\epsilon ,t_0,{\chi }_u,J,‖\left(\cdot \right)‖\right\},$ $0<\delta <\epsilon ,$ if and only if:

$${‖{\psi }_x‖}_C<\delta , ‖\mathit{u}\left(t\right)‖<{\chi }_u \Rightarrow ‖\mathit{x}\left(t\right)‖<\epsilon ,\forall t\in J.$$

(22)

Definition 5

([15,34]). The nonlinear fractional-order time delay system with state delay given by homogeneous state Equation (17), $u\left(t\right)\equiv 0,$ satisfying initial condition (18) is finite-time stable w.r.t. $\left\{\delta ,\epsilon ,t_0,J,‖\left(\cdot \right)‖\right\},$ $0<\delta <\epsilon ,$ if and only if:

$${‖{\psi }_x‖}_C<\delta \Rightarrow ‖\mathit{x}\left(t\right)‖<\epsilon ,\forall t\in J.$$

(23)

Case 2.

This case examines a nonstationary, nonlinear two-term fractional-order time delay system defined for parameters $0<\beta <1<\alpha <2$ where $\beta =\alpha -1$. The considered system with state time delays is given by the following equation:

$${}^c\mathrm{D}_t^{\alpha }\mathit{x}\left(t\right)=A_0\left(t\right)\mathit{x}\left(t\right)+A_1\left(t\right)\mathit{x}\left(t-\gamma \right)+A_2{}^c\mathrm{D}_t^{\beta }\mathit{x}\left(t\right)+B_0\mathit{u}\left(t\right)+g\left(t,x\left(t\right),x\left(t-\gamma \right)\right),$$

(24)

with the associated continuous function of the initial state as well as the initial value of the first derivative of $\dot{x}\left(t\right)$:

$$\mathit{x}\left(t\right)={\psi }_x\left(t\right),t\in \left[-\gamma ,0\right],\dot{x}\left(0\right)={x^{\prime }}_0.$$

(25)

Definition 6

([15,34]). The nonlinear fractional-order two-term $0<\beta <1<\alpha <2, \beta =\alpha -1$ delay system with state time delays given by nonhomogeneous state Equation (24) satisfying initial conditions (25) is finite-time stable w.r.t. $\left\{\delta ,\epsilon ,t_0,{\chi }_u,J,‖\left(\cdot \right)‖\right\},$ $0<\delta <\epsilon ,$ if and only if:

$$\left.\rho <\delta ,‖\mathit{u}\left(t\right)‖<{\chi }_u\right\}\Rightarrow ‖\mathit{x}\left(t\right)‖<\epsilon ,\forall t\in J.$$

(26)

where $\rho =\max \left\{{‖\psi ‖}_C,‖{x^{\prime }}_0‖\right\}$ and ${\chi }_u$ is positive constant.

Definition 7

([15,34]). The nonlinear fractional-order two-term $0<\beta <1<\alpha <2, \beta =\alpha -1$ delay system with state delays given by homogeneous state Equation (24), $u\left(t\right)\equiv 0,$ satisfying initial conditions (25) is finite-time stable w.r.t. $\left\{\delta ,\epsilon ,t_0,J,‖\left(\cdot \right)‖\right\},$$0<\delta <\epsilon ,$ if and only if:

$$\rho <\delta \Rightarrow ‖\mathit{x}\left(t\right)‖<\epsilon ,\forall t\in J,$$

(27)

where $\rho =\max \left\{{‖\psi ‖}_C,‖{x^{\prime }}_0‖\right\}$.

3. Main Results

Robust FTS of Nonstationary Nonlinear Fractional Integro-Differential Time Delay System

Theorem 1.

The nonstationary nonlinear fractional integro-differential time delay system (17) satisfying initial condition (18) is finite-time stable w.r.t. $\left\{\delta ,\epsilon ,t_0,{\chi }_u,J,‖\left(\cdot \right)‖\right\},$ $\delta <\epsilon ,$ if the following condition holds:

$$\left(1+{\displaystyle \frac{b_0{{\mathsf{\chi }}^{\ast }}_u{\left|t\right|}^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}}\right)E_{\alpha }\left(a_{\Sigma }{t}^{\alpha }\right)\exp \left({\displaystyle \frac{1}{\alpha }}{a}_{2}t\right)\le \mathsf{\epsilon }/\mathsf{\delta },$$

(28)

where ${\chi }_u^{\ast }={\chi }_u/\delta$, $‖A_i‖=a_i, i=0,1,2,$ $‖B_0‖=b_0,$ $a_{\Sigma }=a_0+a_1+\Delta a_0+\Delta a_1+2\cdot m$.

Proof of Theorem 1.

The fractional order satisfies $0<\alpha <1, \beta =1-\alpha$ and the solution can be obtained in the form of the equivalent Volterra integral equation, where $t_0=0,$

$$\begin{array}{l}\mathit{x}\left(t\right)={\psi }_x\left(0\right)+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha +\beta \right)}}{\displaystyle \underset{0}{\overset{t}{\int }}{\left(t-s\right)}^{\alpha +\beta -1}{A}_2\left(s\right)x\left(s\right)ds+}\\ +{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\displaystyle \underset{0}{\overset{t}{\int }}{\left(t-s\right)}^{\alpha -1}\left[\begin{array}{l}{A}_0\left(s\right)\mathit{x}\left(s\right)+A_1\left(s\right)\mathit{x}\left(s-\gamma \right)+\\ +B_0\left(s\right)u\left(s\right)+g\left(s,x\left(s\right),\mathit{x}\left(s-\gamma \right)\right)\end{array}\right]}ds,\end{array}$$

(29)

or, taking into account that $\beta =1-\alpha$, we have the following:

$$\begin{array}{l}\mathit{x}\left(t\right)={\psi }_x\left(0\right)+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(1\right)}}{\displaystyle \underset{0}{\overset{t}{\int }}{A}_2\left(s\right)x\left(s\right)ds+}.\\ +{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\displaystyle \underset{0}{\overset{t}{\int }}{\left(t-s\right)}^{\alpha -1}\left[\begin{array}{l}{A}_0\left(s\right)\mathit{x}\left(s\right)+A_1\left(s\right)\mathit{x}\left(s-\gamma \right)\\ +B_0\left(s\right)u\left(s\right)+g\left(s,x\left(s\right),\mathit{x}\left(s-\gamma \right)\right)\end{array}\right]}ds.\end{array}$$

(30)

Applying the norm $‖\left(.\right)‖$ and previous assumptions to the earlier expression, we find the following:

$$\begin{array}{l}‖\mathit{x}\left(t\right)‖\le ‖{\psi }_x\left(0\right)‖+{\displaystyle \underset{0}{\overset{t}{\int }}‖A_2\left(s\right)‖‖x\left(s\right)‖ds+}\\ +{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\displaystyle \underset{0}{\overset{t}{\int }}{\left|t-s\right|}^{\alpha -1}\left[\begin{array}{l}‖A_0\left(s\right)‖‖\mathit{x}\left(s\right)‖+‖A_1\left(s\right)‖‖\mathit{x}\left(s-\gamma \right)‖+‖B_0‖‖u\left(s\right)‖\\ +M\left(s\right)\left(‖x\left(s\right)‖+‖x\left(s-\gamma \right)‖\right)\end{array}\right]}ds.\end{array}$$

(31)

On the other hand, there are the following equations:

$$\begin{array}{l}‖A_0\left(t\right)\mathit{x}\left(t\right)+A_1\left(t\right)\mathit{x}\left(t-\gamma \right)+B_0\mathit{u}\left(t\right)+g\left(t,x\left(t\right),x\left(t-\gamma \right)\right)‖\le \\ \le ‖A_0\left(t\right)‖‖\mathit{x}\left(t\right)‖+‖A_1\left(t\right)‖‖\mathit{x}\left(t-\gamma \right)‖+‖B_0‖‖u\left(t\right)‖+M\left(t\right)\left(‖x\left(t\right)‖+‖x\left(t-\gamma \right)‖\right)\\ \le \left(a_0+\Delta a_0+m\right)‖\mathit{x}\left(t\right)‖+\left(a_1+\Delta a_1+m\right)‖\mathit{x}\left(t-\gamma \right)‖+b_0‖u\left(t\right)‖\\ =a_{om}‖\mathit{x}\left(t\right)‖+a_{1m}‖\mathit{x}\left(t-\gamma \right)‖+b_0‖u\left(t\right)‖.\end{array}$$

(32)

Combining the previous two expressions, taking into account $‖\mathit{u}\left(t\right)‖<{\chi }_u,$ $\forall t\in J$, we obtain the following:

$$\begin{array}{l}‖\mathit{x}\left(t\right)‖\le {‖{\psi }_x‖}_C+a_2{\displaystyle \underset{0}{\overset{t}{\int }}‖x\left(s\right)‖ds+}\\ +{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\displaystyle \underset{0}{\overset{t}{\int }}{\left|t-s\right|}^{\alpha -1}\left[a_{0m}‖\mathit{x}\left(s\right)‖+a_{1m}‖\mathit{x}\left(s-\gamma \right)‖\right]}ds+{\displaystyle \frac{b_0{\chi }_u{\left|t\right|}^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}}.\end{array}$$

(33)

Also, the next nondecreasing function is introduced $z\left(t\right)=\underset{\theta \in \left[-{\gamma }_m,t\right]}{\sup }‖x\left(\theta \right)‖,\forall t\in \left[0,T\right]$, where for $\forall t^{•}\in \left[0,t\right],$ the following conditions satisfy:

$$‖x\left(t^{*}\right)‖\le \underset{t^{*}\in \left[t-{\gamma }_{xm},t\right]}{\sup }\left\{‖\mathit{x}\left(t^{*}\right)‖\right\}\le z\left(t^{*}\right), ‖x\left(t^{*}-{\gamma }_{x\ast }\left(t^{*}\right)\right)‖\le z\left(t^{*}\right).$$

(34)

Applying the previous inequalities, the expression (33) takes the following form:

$$‖\mathit{x}\left(t\right)‖\le {‖{\psi }_x‖}_C+a_2{\displaystyle \underset{0}{\overset{t}{\int }}z\left(s\right)ds}+{\displaystyle \frac{a_{\Sigma }}{\mathsf{\Gamma }\left(\alpha \right)}}{\displaystyle \underset{0}{\overset{t}{\int }}{\left|t-s\right|}^{\alpha -1}z\left(s\right)}ds+{\displaystyle \frac{b_0{\chi }_u{\left|t\right|}^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}},$$

(35)

where $a_{\Sigma }=\left(a_{0m}+a_{1m}\right)$. For $\forall \theta \in \left[0,t\right]$ we have the following:

$$‖\mathit{x}\left(\theta \right)‖\le {‖{\psi }_x‖}_C+{\displaystyle \frac{b_0{\chi }_u{\left|t\right|}^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}}+a_2{\displaystyle \underset{0}{\overset{\theta }{\int }}z\left(\theta -s\right)ds}+{\displaystyle \frac{a_{\Sigma }}{\mathsf{\Gamma }\left(\alpha \right)}}{\displaystyle \underset{0}{\overset{\theta }{\int }}{\left|s\right|}^{\alpha -1}z\left(\theta -s\right)}ds.$$

(36)

Since the function ${\displaystyle {\int }_0^t{\left|s\right|}^{\alpha -1}z\left(t-s\right)}ds$ is increasing with respect to $t\ge 0$ because of the increase in the nonnegative function $z\left(t\right)$, we get the following:

$${\displaystyle {\int }_0^{\theta }{\left|s\right|}^{\alpha -1}z\left(\theta -s\right)}ds\le {\displaystyle {\int }_0^t{\left|s\right|}^{\alpha -1}z\left(t-s\right)}ds,$$

(37)

so, one obtains

$$‖\mathit{x}\left(\theta \right)‖\le {‖{\psi }_x‖}_C+{\displaystyle \frac{b_0{\chi }_u{\left|t\right|}^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}}+a_2{\displaystyle \underset{0}{\overset{t}{\int }}z\left(s\right)ds}+{\displaystyle \frac{a_{\Sigma }}{\mathsf{\Gamma }\left(\alpha \right)}}{\displaystyle \underset{0}{\overset{t}{\int }}{\left|t-s\right|}^{\alpha -1}z\left(s\right)}ds, \forall \theta \in \left[0,t\right].$$

(38)

Moreover, based on the property of the function $z\left(t\right)$, we have the following:

$$\begin{array}{l}z\left(t\right)=\underset{\theta \in \left[-{\gamma }_{xm},t\right]}{\sup }‖x\left(\theta \right)‖\le \max \left\{\underset{\theta \in \left[-{\gamma }_{xm},0\right]}{\sup }‖x\left(\theta \right)‖,\underset{\theta \in \left[0,t\right]}{\sup }‖x\left(\theta \right)‖\right\}\le \\ \le \max \left\{{‖{\psi }_x‖}_C,{‖{\psi }_x‖}_C+{\displaystyle \frac{b_0{\chi }_u{\left|t\right|}^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}}+a_2{\displaystyle \underset{0}{\overset{t}{\int }}z\left(s\right)ds}+{\displaystyle \frac{a_{\Sigma }}{\mathsf{\Gamma }\left(\alpha \right)}}{\displaystyle \underset{0}{\overset{t}{\int }}{\left|t-s\right|}^{\alpha -1}z\left(s\right)}ds\right\}\\ ={‖{\psi }_x‖}_C+{\displaystyle \frac{b_0{\chi }_u{\left|t\right|}^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}}+a_2{\displaystyle \underset{0}{\overset{t}{\int }}z\left(s\right)ds}+{\displaystyle \frac{a_{\Sigma }}{\mathsf{\Gamma }\left(\alpha \right)}}{\displaystyle \underset{0}{\overset{t}{\int }}{\left|t-s\right|}^{\alpha -1}z\left(s\right)}ds.\end{array}$$

(39)

Now, one can observe that ${‖{\psi }_x‖}_C+b_0{\chi }_u{\left|t\right|}^{\alpha }/\mathsf{\Gamma }\left(\alpha +1\right)$ is a nondecreasing function on $J_0=\left[0,T\right]$ and applying Corollary 3. we get the following:

$$‖x\left(t\right)‖\le z\left(t\right)\le \left({‖{\mathrm{\psi }}_x‖}_C+{\displaystyle \frac{b_0{\mathsf{\chi }}_u{\left|t\right|}^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}}\right)E_{\alpha }\left(a_{\Sigma }{t}^{\alpha }\right)\exp \left({\displaystyle \frac{1}{\alpha }}{a}_{2}t\right).$$

(40)

Finally, under (22) and the basic condition of Theorem 1, one deduces that $‖\mathit{x}\left(t\right)‖<\epsilon ,\forall t\in J$, which proves the FTS of the nonhomogeneous system (17). □

Remark 3.

In the case $A_2\left(t\right)\equiv 0$, we can get the next stability criterion from (28) as follows:

$$\left(1+{\displaystyle \frac{b_0{{\mathsf{\chi }}^{\ast }}_u{\left|t\right|}^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}}\right)E_{\alpha }\left(a_{\Sigma }{t}^{\alpha }\right)\le \mathsf{\epsilon }/\mathsf{\delta }.$$

(41)

In the homogeneous case, we obtain from Theorem 1, the following result.

Corollary 4.

The homogeneous system (17), $g\left(t,x\left(t\right),x\left(t-\gamma \right)\right)=0,u\left(t\right)\equiv 0$, is finite-time stable w.r.t. $\left\{\delta ,\epsilon ,t_0,J,‖\left(\cdot \right)‖\right\},$ $0<\delta <\epsilon ,$ if the following condition holds:

$$E_{\alpha }\left({\tilde{a}}_{\Sigma }{t}^{\alpha }\right)\exp \left({\displaystyle \frac{1}{\alpha }}{a}_{2}t\right)\le \mathsf{\epsilon }/\mathsf{\delta },$$

(42)

where ${\tilde{a}}_{\Sigma }=a_0+a_1+\Delta a_0+\Delta a_1$.

Corollary 5.

The homogeneous system (17), $g\left(t,x\left(t\right),x\left(t-\gamma \right)\right)=0,u\left(t\right)\equiv 0$, $A_2\equiv 0$ is finite-time stable w.r.t. $\left\{\delta ,\epsilon ,t_0,J,‖\left(\cdot \right)‖\right\},$ $0<\delta <\epsilon ,$ if it satisfies the following:

$$E_{\alpha }\left({\tilde{a}}_{\Sigma }{t}^{\alpha }\right)\le \mathsf{\epsilon }/\mathsf{\delta }.$$

(43)

Remark 3.

Previous condition (43) was obtained and proved in [18] (Remark 2), for the Caputo fractional order time-delay system.

$$\begin{array}{l}{}^c\mathrm{D}_t^{\alpha }\mathit{x}\left(t\right)=A\mathit{x}\left(t\right)+Bx\left(t-\gamma \right), t\ge 0\\ x\left(\theta \right)={\psi }_x\left(\theta \right), \in \left[-\gamma ,0\right]\end{array}$$

(44)

which is firstly considered in [14] and it is a special case of a given system (17) where $A_2=0, B_0=0, g(.)=0$,$A_0\left(t\right)=A, A_1\left(t\right)=B.$

Theorem 2.

The nonstationary nonlinear two-term fractional order time-varying delay system (24) satisfying initial conditions (25) is finite-time stable w.r.t. $\left\{\delta ,\epsilon ,t_0,{\chi }_u,J,‖\left(\cdot \right)‖\right\},$ $\delta <\epsilon ,$ if the following condition holds:

$$\left[\left(1+\left(1+a_2\right)\left|t\right|\right)+{\displaystyle \frac{b_0{\mathsf{\chi }}_u^{\ast }{\left|t\right|}^{\mathsf{\alpha }}}{\mathsf{\Gamma }\left(\mathsf{\alpha }+1\right)}}\right]E_{\mathsf{\alpha }}\left(a_{\Sigma }{t}^{\mathsf{\alpha }}\right)\exp \left({\displaystyle \frac{1}{\mathsf{\alpha }}}{a}_{2}t\right)\le \mathsf{\epsilon }/\mathsf{\delta },$$

(45)

where ${\chi }_u^{\ast }={\chi }_u/\delta$.

Proof of Theorem 2.

The fractional order satisfies $0<\beta <1<\alpha <2, \beta =\alpha -1$ and if an integral of fractional order ${}_0{}^{}I_t^{\alpha }, t_0=0$ is applied on both sides, one has the following:

$${}_{0}I_t^{\alpha }\left({}^c\mathrm{D}_t^{\alpha }\mathit{x}\left(t\right)-A_2{\left(t\right)}^c{\mathrm{D}}_t^{\beta }\mathit{x}\left(t\right)\right)={}_{0}I_t^{\alpha }\left(\begin{array}{l}{A}_0\left(t\right)\mathit{x}\left(t\right)+A_1\left(t\right)\mathit{x}\left(t-\gamma \right)\\ +B_0\mathit{u}\left(t\right)+g\left(t,x\left(t\right),x\left(t-\gamma \right)\right)\end{array}\right).$$

(46)

Following the properties of the fractional derivatives $0<\beta <1<\alpha <2, \beta =\alpha -1$ and taking into account Lemmas 1 and 2 solution can be obtained in the form of the equivalent Volterra integral equation:

$$\begin{array}{l}x\left(t\right)={\psi }_x\left(0\right)+t\dot{x}\left(0\right)-{\psi }_x\left(0\right){\displaystyle \frac{A_2\left(t\right)\cdot t^{\alpha -\beta }}{\mathsf{\Gamma }\left(\alpha -\beta +1\right)}}+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha -\beta \right)}}{\displaystyle \underset{0}{\overset{t}{\int }}{\left(t-s\right)}^{\alpha -\beta -1}{A}_2\left(s\right)x\left(s\right)ds}+\\ +{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\displaystyle \underset{0}{\overset{t}{\int }}{\left(t-s\right)}^{\alpha -1}\left(\begin{array}{l}{A}_0\left(s\right)\mathit{x}\left(s\right)+A_1\left(s\right)\mathit{x}\left(s-\gamma \right)\\ +B_0\mathit{u}\left(s\right)+g\left(s,x\left(s\right),x\left(s-\gamma \right)\right)\end{array}\right)}ds,\end{array}$$

(47)

or taking into account $\beta =\alpha -1$,

$$\begin{array}{l}x\left(t\right)={\psi }_x\left(0\right)+t\dot{x}\left(0\right)-{\psi }_x\left(0\right){\displaystyle \frac{A_2\left(t\right)\cdot t}{\mathsf{\Gamma }\left(2\right)}}+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(1\right)}}{\displaystyle \underset{0}{\overset{t}{\int }}{A}_2\left(s\right)x\left(s\right)ds}+\\ +{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\displaystyle \underset{0}{\overset{t}{\int }}{\left(t-s\right)}^{\alpha -1}\left(\begin{array}{l}{A}_0\left(s\right)\mathit{x}\left(s\right)+A_1\left(s\right)\mathit{x}\left(s-\gamma \right)+\\ +B_0\mathit{u}\left(s\right)+g\left(s,x\left(s\right),x\left(s-\gamma \right)\right)\end{array}\right)}ds.\end{array}$$

(48)

By employing the norm $‖\left(\cdot \right)‖$ on both sides of the previous expression, one gets

$$\begin{gathered} ‖x\left(t\right)‖\le ‖{\psi }_x\left(0\right)‖+\left|t\right|‖\dot{x}\left(0\right)‖+‖A_2\left(t\right)‖‖{\psi }_x\left(0\right)‖{\displaystyle \frac{\left|t\right|}{\mathsf{\Gamma }\left(2\right)}}+{\displaystyle \underset{0}{\overset{t}{\int }}‖A_2\left(t\right)‖‖x\left(s\right)‖ds}+ \\ +{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\displaystyle \underset{0}{\overset{t}{\int }}{\left|\left(t-s\right)\right|}^{\alpha -1}‖\left(A_0\left(s\right)\mathit{x}\left(s\right)+A_1\left(s\right)\mathit{x}\left(s-\gamma \right)+B_0\mathit{u}\left(s\right)+g\left(s,x\left(s\right),x\left(s-\gamma \right)\right)\right)‖}ds. \end{gathered}$$

(49)

Consequently, we have

$$\begin{array}{l}‖x\left(t\right)‖\le {‖{\psi }_x‖}_C\left[1+{\displaystyle \frac{a_2\left|t\right|}{\mathsf{\Gamma }\left(2\right)}}\right]+‖{x^{\prime }}_0‖\left|t\right|+a_2{\displaystyle \underset{0}{\overset{t}{\int }}‖x\left(s\right)‖ds}+\\ +{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\displaystyle \underset{0}{\overset{t}{\int }}{\left|\left(t-s\right)\right|}^{\alpha -1}‖\begin{array}{l}\left(A_0\left(s\right)\mathit{x}\left(s\right)+A_1\left(s\right)\mathit{x}\left(s-\gamma \right)+B_0\mathit{u}\left(s\right)\right)\\ +g\left(s,x\left(s\right),x\left(s-\gamma \right)\right)\end{array}‖}ds.\end{array}$$

(50)

Previous expression (50) based on (21) can be rewritten as follows:

$$\begin{array}{l}‖x\left(t\right)‖\le {‖{\psi }_x‖}_C\left[1+{\displaystyle \frac{a_2\left|t\right|}{\mathsf{\Gamma }\left(2\right)}}\right]+‖{x^{\prime }}_0‖\left|t\right|+a_2{\displaystyle \underset{0}{\overset{t}{\int }}‖x\left(s\right)‖ds}+\\ +{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\displaystyle \underset{0}{\overset{t}{\int }}{\left|\left(t-s\right)\right|}^{\alpha -1}\left[\begin{array}{l}{a}_0‖x\left(s\right)‖+a_1‖x\left(s-\gamma \right)‖+b_0‖u\left(s\right)‖+\\ +M\left(s\right)\left(‖x\left(s\right)‖+‖x\left(s-\gamma \right)‖\right)\end{array}\right]}ds,\end{array}$$

(51)

or taking into account (32), we get

$$\begin{array}{l}‖x\left(t\right)‖\le {‖{\psi }_x‖}_C\left[1+{\displaystyle \frac{a_2\left|t\right|}{\mathsf{\Gamma }\left(2\right)}}\right]+‖{x^{\prime }}_0‖\left|t\right|+{\displaystyle \frac{b_0{\chi }_u{\left|t\right|}^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}}+a_2{\displaystyle \underset{0}{\overset{t}{\int }}‖x\left(s\right)‖ds}+\\ +{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\displaystyle \underset{0}{\overset{t}{\int }}{\left|\left(t-s\right)\right|}^{\alpha -1}\left[a_{0m}‖\mathit{x}\left(s\right)‖+a_{1m}‖\mathit{x}\left(s-\gamma \right)‖\right]}ds.\end{array}$$

(52)

Introducing nondecreasing function $\omega \left(t\right)={‖{\psi }_x‖}_C\left[1+{\displaystyle \frac{a_2\left|t\right|}{\mathsf{\Gamma }\left(2\right)}}\right]+‖{x^{\prime }}_0‖\left|t\right|+{\displaystyle \frac{b_0{\chi }_u{\left|t\right|}^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}}$, it yields

$$‖x\left(t\right)‖\le \omega \left(t\right)+a_2{\displaystyle \underset{0}{\overset{t}{\int }}‖x\left(s\right)‖ds} +{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\displaystyle \underset{0}{\overset{t}{\int }}{\left|\left(t-s\right)\right|}^{\alpha -1}\left[a_{0m}‖x\left(s\right)‖+a_{1m}‖x\left(s-\gamma \right)‖\right]}ds.$$

(53)

Also, the next nondecreasing function is introduced $z\left(t\right)=\underset{\theta \in \left[-{\gamma }_m,t\right]}{\sup }‖x\left(\theta \right)‖,\forall t\in \left[0,T\right]$, where for $\forall t^{•}\in \left[0,t\right],$ the following conditions satisfy

$$‖x\left(t^{*}\right)‖\le \underset{t^{*}\in \left[t-{\gamma }_{xm},t\right]}{\sup }\left\{‖\mathit{x}\left(t^{*}\right)‖\right\}\le z\left(t^{*}\right), ‖x\left(t^{*}-{\gamma }_{x\ast }\left(t^{*}\right)\right)‖\le z\left(t^{*}\right).$$

(54)

Applying the previous inequalities, the expression (53) takes the following form:

$$‖x\left(t\right)‖\le \omega \left(t\right)+a_2{\displaystyle \underset{0}{\overset{t}{\int }}z\left(s\right)ds}+{\displaystyle \frac{a_{\Sigma }}{\mathsf{\Gamma }\left(\alpha \right)}}{\displaystyle \underset{0}{\overset{t}{\int }}{\left|\left(t-s\right)\right|}^{\alpha -1}z\left(s\right)}ds,$$

(55)

where $a_{\Sigma }=\left(a_{0m}+a_{1m}\right)$. For $\forall \theta \in \left[0,t\right]$ and taking into account (37) we have

$$‖\mathit{x}\left(\theta \right)‖\le \omega \left(t\right)+a_2{\displaystyle \underset{0}{\overset{\theta }{\int }}z\left(\theta -s^{\ast }\right)d{s}^{\ast }}+{\displaystyle \frac{a_{\Sigma }}{\mathsf{\Gamma }\left(\alpha \right)}}{\displaystyle \underset{0}{\overset{\theta }{\int }}{\left|s^{\ast }\right|}^{\alpha -1}z\left(\theta -s^{\ast }\right)}d{s}^{\ast }, \forall \theta \in \left[0,t\right],$$

(56)

or

$$‖\mathit{x}\left(\theta \right)‖\le \omega \left(t\right)+a_2{\displaystyle \underset{0}{\overset{t}{\int }}z\left(s\right)ds}+{\displaystyle \frac{a_{\Sigma }}{\mathsf{\Gamma }\left(\alpha \right)}}{\displaystyle \underset{0}{\overset{t}{\int }}{\left|t-s\right|}^{\alpha -1}z\left(s\right)}ds, \forall \theta \in \left[0,t\right].$$

(57)

Moreover, based on the property of the function $z\left(t\right)$, we conclude that:

$$\begin{array}{l}z\left(t\right)=\underset{\theta \in \left[-{\gamma }_{xm},t\right]}{\sup }‖x\left(\theta \right)‖\le \max \left\{\underset{\theta \in \left[-{\gamma }_{xm},0\right]}{\sup }‖x\left(\theta \right)‖,\underset{\theta \in \left[0,t\right]}{\sup }‖x\left(\theta \right)‖,\right\}\le \\ \le \max \left\{{‖{\psi }_x‖}_C,\omega \left(t\right)+a_2{\displaystyle \underset{0}{\overset{t}{\int }}z\left(s\right)ds}+{\displaystyle \frac{a_{\Sigma }}{\mathsf{\Gamma }\left(\alpha \right)}}{\displaystyle \underset{0}{\overset{t}{\int }}{\left|t-s\right|}^{\alpha -1}z\left(s\right)}ds,\right\}\\ =\omega \left(t\right)+a_2{\displaystyle \underset{0}{\overset{t}{\int }}z\left(s\right)ds}+{\displaystyle \frac{a_{\Sigma }}{\mathsf{\Gamma }\left(\alpha \right)}}{\displaystyle \underset{0}{\overset{t}{\int }}{\left|t-s\right|}^{\alpha -1}z\left(s\right)}ds.\end{array}$$

(58)

Now, if we take $\rho =\max \left\{{‖\psi ‖}_C,‖{x^{\prime }}_0‖\right\}$ we can obtain the following:

$$\begin{array}{l}‖x\left(t\right)‖\le z\left(t\right)\le \rho \left[\left[1+{\displaystyle \frac{a_2\left|t\right|}{\mathsf{\Gamma }\left(2\right)}}\right]+\left|t\right|\right]+{\displaystyle \frac{b_0{\chi }_u{\left|t\right|}^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}}+a_2{\displaystyle \underset{0}{\overset{t}{\int }}z\left(s\right)ds}+{\displaystyle \frac{a_{\Sigma }}{\mathsf{\Gamma }\left(\alpha \right)}}{\displaystyle \underset{0}{\overset{t}{\int }}{\left|t-s\right|}^{\alpha -1}z\left(s\right)}ds\\ \le \varpi \left(t\right)+a_2{\displaystyle \underset{0}{\overset{t}{\int }}z\left(s\right)ds}+{\displaystyle \frac{a_{\Sigma }}{\mathsf{\Gamma }\left(\alpha \right)}}{\displaystyle \underset{0}{\overset{t}{\int }}{\left|t-s\right|}^{\alpha -1}z\left(s\right)}ds.\end{array}$$

(59)

Observing that $\varpi \left(t\right)$ is a nondecreasing function on $J_0=\left[0,T\right]$ and applying Corollary 3, we get the following:

$$‖x\left(t\right)‖\le \left[\rho \left(1+\left|t\right|+{\displaystyle \frac{a_2\left|t\right|}{\mathsf{\Gamma }\left(2\right)}}\right)+{\displaystyle \frac{b_0{\mathsf{\chi }}_u{\left|t\right|}^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}}\right]E_{\alpha }\left(a_{\Sigma }{t}^{\alpha }\right)\exp \left({\displaystyle \frac{1}{\alpha }}{a}_{2}t\right).$$

(60)

Finally, using the basic condition of Theorem 2, and $\rho <\delta$ (27), we can obtain the required FTS condition: $‖\mathit{x}\left(t\right)‖<\epsilon ,\forall t\in J.$ □

Corollary 6.

The nonlinear fractional order time-delay system (24), $A_2\left(t\right)\equiv 0$ is finite-time stable w.r.t. $\left\{\delta ,\epsilon ,t_0,J,‖\left(\cdot \right)‖\right\},$ $0<\delta <\epsilon ,$ if it satisfies the following condition:

$$\left[\left(1+\left|t\right|\right)+{\displaystyle \frac{b_0{\mathsf{\chi }}_u^{\ast }{\left|t\right|}^{\mathsf{\alpha }}}{\mathsf{\Gamma }\left(\mathsf{\alpha }+1\right)}}\right]E_{\mathsf{\alpha }}\left(a_{\Sigma }{t}^{\mathsf{\alpha }}\right)\le \mathsf{\epsilon }/\mathsf{\delta }.$$

(61)

Corollary 7.

The homogeneous system nonlinear fractional order time-delay system (24), $A_2\left(t\right)\equiv 0$, $u\left(t\right)\equiv 0$ is finite-time stable w.r.t. $\left\{\delta ,\epsilon ,t_0,J,‖\left(\cdot \right)‖\right\},$ $0<\delta <\epsilon ,$ if it satisfies the following condition:

$$\left[1+\left|t\right|\right]E_{\mathsf{\alpha }}\left(a_{\Sigma }{t}^{\mathsf{\alpha }}\right)\le \mathsf{\epsilon }/\mathsf{\delta }.$$

(62)

4. Numerical Simulations

4.1. Numerical Method

Here, based on the Adams–Bashforth–Moulton (ABM) algorithm presented in [35], modified ABM algorithm is introduced to solve (17). Consider the following integro-differential nonlinear fractional-order time delay system.

$${}^c\mathrm{D}_t^{\alpha }\nu \left(t\right)=A_0\nu \left(t\right)+A_1\nu \left(t-\gamma \right)+A_2{\mathrm{I}}_t^{\beta }\nu \left(t\right)+B_{0}u\left(t\right)+g\left(t,\nu \left(t\right),\nu \left(t-\gamma \right)\right),$$

(63)

with the associated continuous function of the initial state:

$$\nu \left(t\right)={\psi }_{\nu }\left(t\right),t\in \left[-\gamma ,0\right],$$

(64)

with a uniform grid $\left\{t_n=nh, n=-k,-k+1,\dots ,0,1,\dots N\right\}$ where are $k$ and $N$ are integers such that $T=Nh$ and $\gamma =kh$. Let

$${\nu }_h\left(t_j\right)={\psi }_{\nu }\left(t_j\right), \mathrm{j}=-\mathrm{k},-\mathrm{k}+1,\dots 0,$$

(65)

as well as

$${\nu }_h\left(t_j-\gamma \right)={\nu }_h\left(jh-kh\right)={\nu }_h\left(t_{j-k}\right), \mathrm{j}=0,1,\dots ,\mathrm{N}.$$

(66)

Suppose that we have previously calculated approximations ${\nu }_h\left(t_j\right)\approx \nu \left(t_j\right), j=-k,-k+1,\dots 0,1,2,\dots ,n$, we wish to calculate ${\nu }_h\left(t_{j+1}\right)$ and taking into account that $\beta =\alpha -1$, using the following:

$$\begin{array}{l}\nu \left(t_{n+1}\right)={\psi }_{\nu }\left(0\right)+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(1\right)}}{\displaystyle \underset{0}{\overset{t_{n+1}}{\int }}{A}_2\nu \left(s\right)ds+}\\ +{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\displaystyle \underset{0}{\overset{t_{n+1}}{\int }}{\left(t_{n+1}-s\right)}^{\alpha -1}\left[\begin{array}{l}{A}_0\nu \left(s\right)+A_1\nu \left(s-\gamma \right)+\\ +B_{0}u\left(s\right)+g\left(s,\nu \left(s\right),\nu \left(s-\gamma \right)\right)\end{array}\right]}ds.\end{array}$$

(67)

Next, we use approximations ${\nu }_h\left(t_j\right)$ for $\nu \left(t_j\right)$ as well as for the integral in (67), which is determined applying the product trapezoidal quadrature formula. Thus, the corrector formula is given as follows:

$$\begin{array}{l}{\nu }_h\left(t_{n+1}\right)={\psi }_{\nu }\left(0\right)+{\displaystyle \frac{h}{2}}{A}_2{v}_h^p\left(t_{n+1}\right)+h{\displaystyle \sum _{j=0}^n{\tilde{a}}_{j,n+1}}{A}_2{v}_h\left(t_j\right)+\\ +{\displaystyle \frac{h^{\alpha }}{\mathsf{\Gamma }\left(\alpha +2\right)}}\left[\begin{array}{l}{A}_0{\nu }_h^p\left(t_{n+1}\right)+{\displaystyle \sum _{j=0}^n{a}_{j,n+1}{A}_0{\nu }_h\left(t_j\right)+A_1{\nu }_h\left(t_{n+1-k}\right)+}\\ +{\displaystyle \sum _{j=0}^n{a}_{j,n+1}{A}_1{\nu }_h\left(t_{j-k}\right)+B_{0}u\left(t_{n+1}\right)+{\displaystyle \sum _{j=0}^n{a}_{j,n+1}{B}_{0}u\left(t_j\right)}}\\ +g\left(t_{n+1},{\nu }_h^p\left(t_{n+1}\right),{\nu }_h\left(t_{n+1-k}\right)\right)+\\ +{\displaystyle \sum _{j=0}^n{a}_{j,n+1}g\left(t_{n+1},{\nu }_h\left(t_j\right),{\nu }_h\left(t_{j-k}\right)\right)}\end{array}\right],\\ \end{array}$$

(68)

where

$$a_{j,n+1}=\left\{\begin{array}{c}{n}^{\alpha +1}-\left(n-\alpha \right){\left(n+1\right)}^{\alpha } if j=0\\ {\left(n-j+2\right)}^{\alpha +1}+{\left(n-j\right)}^{\alpha +1}-2{\left(n-j+1\right)}^{\alpha +1} if 1\le j\le n\\ 1 if j=n+1\end{array}\right.$$

(69)

$${\tilde{a}}_{j,n+1}=\left\{\begin{array}{c}1/2, j=0\\ 1, 1\le j\le n.\end{array}\right.$$

(70)

One may observe that the unknown term ${\nu }_h\left(t_{n+1}\right)$ appears on both sides of (68), and due to its nonlinearity of $g\left(.\right)$, it cannot be obtained explicitly. Therefore, it is necessary to use approximation of ${\nu }_h\left(t_{n+1}\right)$ on the right-hand side of (68), known as the predictor term ${\nu }_h^p\left(t_{n+1}\right)$. Next, the product rectangle rule is employed to calculate it.

$$\begin{array}{l}{\nu }_h^p\left(t_{n+1}\right)={\psi }_{\nu }\left(0\right)+h{\displaystyle \sum _{j=0}^n{A}_2{v}_h\left(t_j\right)}+\\ +{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}\left[{\displaystyle \sum _{j=0}^n{b}_{j,n+1}\left(\begin{array}{l}{A}_0{\nu }_h\left(t_j\right)A_1{\nu }_h\left(t_{j-k}\right)+\\ +B_{0}u\left(t_j\right)+g\left(t_j,{\nu }_h\left(t_j\right),{\nu }_h\left(t_{j-k}\right)\right)\end{array}\right)}\right],\\ \end{array}$$

(71)

where

$$b_{j,n+1}={\displaystyle \frac{h^{\alpha }}{\alpha }}\left[{\left(n-j+1\right)}^{\alpha }-{\left(n-j\right)}^{\alpha }\right].$$

(72)

4.2. Numerical Examples

Here, we provide three examples to illustrate the applicability of our theoretical results stated in the previous section.

Example 1.

Let us consider the following nonlinear fractional-order system with a constant time delay $\gamma$, ref. [36]:

$${}^c\mathrm{D}_t^{\alpha }\mathit{x}\left(t\right)=A_0\left(t\right)\mathit{x}\left(t\right)+A_1\left(t\right)\mathit{x}\left(t-\gamma \right)+g\left(t,x\left(t\right),x\left(t-\gamma \right)\right),$$

(73)

where

$$A_0=\left[\begin{array}{cc}-0.8& 0\\ 0& -0.5\end{array}\right], A_1=\left[\begin{array}{cc}0.1& 0\\ 0& 0.3\end{array}\right],$$

(74)

With the associated continuous function of the initial state: ${\psi }_x\left(t\right)={\left[0.01, 0.02\right]}^T,t\in \left[-\gamma ,0\right]$, and  $g\left(t,x\left(t\right),x\left(t-\gamma \right)\right)={\left(\begin{array}{cc}-x_1\left(t\right)x_2\left(t-\gamma \right)& -x_2\left(t\right)x_1\left(t-\gamma \right)\end{array}\right)}^T$, $\gamma =0.2$ it can be easily verified that assumption (19) is satisfied for $M=1$. Additionally, we can derive the following results taking into account $‖A_0‖=0.8$, $‖A_1‖=0.3$, $\delta =0.02$ and $\epsilon =1$. First, we consider the case $\alpha =0.7<1$ and, based on inequality (16) in Theorem 3.1 in [36], we can estimate the time of the FTS of the system (73) as $T_e\approx 0.1672 \mathrm{s}$. Using Corollary 4 (41) and $u\left(t\right)=0$, we can further calculate the estimated time of the FTS of the system (73) as $T_e\approx 0.7066 \mathrm{s}$. In the case of $\alpha =1.8$, using inequality (45) in Theorem 3.2 in [36], we can estimate the time of the FTS of the system $T_e\approx 1.5283 \mathrm{s}$ as well. Furthermore, by checking the condition in (62) (Corollary 7), we can obtain another estimate for the time of the FTS of the system (73) as $T_e\approx 1.842 \mathrm{s}$. Since a larger estimated time $T_e$ for the FTS was obtained for two values of $\alpha \in \left(0,2\right)$, it can be concluded that the obtained results are less conservative compared to those from the paper [36].

Example 2.

Let us consider the following nonlinear fractional-order system $0<\alpha <1,$ $0<\beta <1,$$\beta =1-\alpha$with a constant time delay, $\gamma$:

$${}^c\mathrm{D}_t^{\alpha }\mathit{x}\left(t\right)=A_0\left(t\right)\mathit{x}\left(t\right)+A_1\left(t\right)x\left(t-\gamma \right)+A_2\left(t\right)I_t^{\beta }\mathit{x}\left(t\right)+B_{0}u\left(t\right)+g\left(t,x\left(t\right),x\left(t-\gamma \right)\right),$$

(75)

where

$$A_0=\left[\begin{array}{cc}-0.8& 0\\ 0& -0.5\end{array}\right], A_1=\left[\begin{array}{cc}0.1& 0\\ 0& 0.3\end{array}\right] A_2=\left[\begin{array}{cc}0.3& -0.2\\ 0.4& 0.1\end{array}\right], B_0=\left[\begin{array}{l}0\\ 0.5\end{array}\right],$$

(76)

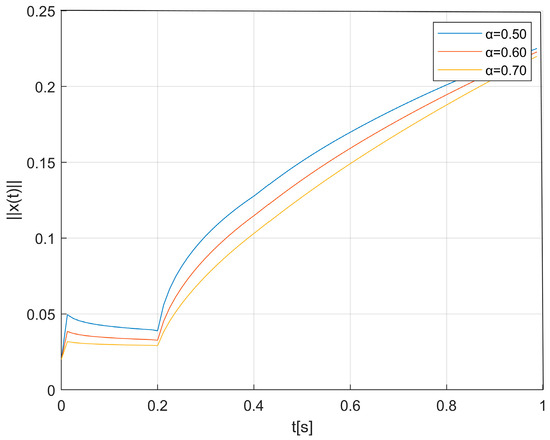
with the associated continuous function of the initial state: ${\psi }_x\left(t\right)={\left[0.01, 0.02\right]}^T,t\in \left[-\gamma ,0\right]$, and $g\left(t,x\left(t\right),x\left(t-\gamma \right)\right)={\left(\begin{array}{cc}-x_1\left(t\right)x_2\left(t-\gamma \right)& -x_2\left(t\right)x_1\left(t-\gamma \right)\end{array}\right)}^T$, $\gamma =0.2$,$\alpha =0.8, \beta =0.2$. For control$u\left(t\right)=0.5\sin t$, it follows that${\chi }_u=0.5$. It is easily verified that assumption (19) is satisfied for $M=1$. Additionally, one can get,$‖A_2‖=0.5, ‖B_0‖=0.5$, $\delta =0.021$ and $\epsilon =1$. Based on the FTS criterion (28) in Theorem 1, it can be calculated that the estimated time of FTS for the system (75) is $T_e\approx 0.37 \mathrm{s}$. For different parameters, the numerical simulations of the system (75) are carried out in Figure 1. From the numerical simulations, it can be seen that the influence on the estimated bounds of finite-time stability with varying order, (

Table 1. $\epsilon$ for $\delta =0.02$ in Example 2.

$\mathit{\alpha }$	$\mathit{T}=0.1$	$\mathit{T}=0.2$	$\mathit{T}=0.3$	$\mathit{T}=0.4$
0.5	0.556	2.281	7.997	26.395
0.7	0.165	0.452	1.039	2.222
0.9	0.082	0.192	0.385	0.721

).

Example 3.

Here, we consider the two-term fractional damped system [20]:

$$\begin{array}{l}{}^c\mathrm{D}_t^{\alpha }\mathit{x}\left(t\right)-A^c{\mathrm{D}}_t^{\beta }\mathit{x}\left(t\right)=B\mathit{x}\left(t\right)+C\mathit{x}\left(t-\gamma \right)+D_0\mathit{u}\left(t\right)\\ x\left(t\right)=0, x^{\prime }\left(t\right)=0, -\gamma \le t\le 0.\end{array}$$

(77)

where $t_0=0, \alpha =1.25, \beta =\alpha -1=0.25, \gamma =0.1$ as well as

$$A=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right], B=\left[\begin{array}{cc}1& 0\\ 0& 0.5\end{array}\right],C=\left[\begin{array}{cc}0.2& 0\\ 0& 0.5\end{array}\right], D=\left[\begin{array}{l}0\\ 1\end{array}\right].$$

(78)

The task is to check the FTS stability of system (77) w.r.t $\left\{\delta =0.05, \epsilon =2, {\chi }_u=1\right\}$,$\varpi =min\left(\alpha ,\alpha -\beta \right)=1$. Also, we have $a=‖A‖=1, d=‖D‖=1,{\sigma }_{\max }\left(B\right)=1, {\sigma }_{\max }\left(C\right)=0.5,$ ${\sigma }_{\max \Sigma }={\sigma }_{\max }\left(B\right)+{\sigma }_{\max }\left(C\right)=1.5$, $u\left(t\right)=\sin t$. Applying these values to the condition given in Theorem 1 [20], we can obtain the estimated time $T_e\approx 0.587 \mathrm{s}$ of FTS. On the other hand, by checking the condition in (45), one can obtain the estimated time of the FTS of system (78) for the case $\beta =\alpha -1$ as $T_e\approx 0.63 \mathrm{s}$. Similar to Example 1, larger $T_e$ of FTS was obtained, demonstrating the lower conservatism of our stability criterion compared to that from [20].

5. Conclusions

In this contribution, we focus on researching a new and robust FTS for a class of nonstationary nonlinear two-term fractional order time-delay systems with $\alpha ,\beta \in \left(0,2\right)$. We derive a novel FTS analysis by applying a new type of generalized Gronwall–Bellman inequality. Our findings include new sufficient conditions expressed in terms of inequalities that ensure the FTS of both systems. Additionally, we provide three numerical examples to validate the theoretical results and estimate the time of the FTS. Furthermore, our theoretical results demonstrate less conservativeness compared to those in the existing literature. In future work, we plan to extend the application of our FTS methodology to more complex fractional-order time-delay systems.