Accelerated Numerical Simulations of a Reaction-Diffusion- Advection Model Using Julia-CUDA
Abstract
1. Introduction
2. Related Works
3. Mathematical and Numerical Background
3.1. Numerical Framework
- (1)
- , , and : These terms represent the standard parabolic stability constraints for the diffusion components of the endothelial cell, protease, and inhibitor equations, respectively. Considering a heat equation discretized with central differences, the von Neumann stability analysis yields the condition . These constraints become more restrictive as the diffusion coefficients increase or as the spatial mesh is refined.
- (2)
- : This term addresses the stability requirement for the reaction term in the ECM equation. Since , the local exponential decay rate is . Taking into account an ODE of the form , the forward Euler method requires for stability. Setting and applying a safety factor, we obtain .
3.2. Algorithm and Complexity Analysis
4. Parallel Approach
- Domain discretization and initialization of state variables;
- Construction of discrete operators and system matrices;
- Evaluation of the TAF profile;
- Assembly and evaluation of nonlinear terms;
- Time integration and solution update.
| Algorithm 1 Numerical solution of the tumor angiogenesis system |
|
Ensure: Numerical solution
|
- Domain discretization. The spatial discretization of the domain requires the generation of a uniform grid with M points. In our parallel implementation, this is achieved through the Equation (6). This discretization is implemented using CUDA arrays to ensure all subsequent computations remain on the GPU:The state variables are initialized according to the conditions specified in Equation (5). The parallel initialization is performed through specialized CUDA kernels that handle the piecewise definition of the initial conditions. This initialization is implemented using thread blocks configured to maximize memory coalescing:where is chosen to optimize GPU occupancy while maintaining efficient memory access patterns.
- Discrete operator construction. The central difference operators and defined in Equation (6) are implemented as sparse matrices in GPU memory. For instance, the operatorhas been performed through a specialized CUDA kernel that constructs the sparse matrix structure.
- TAF Evaluation. The tumor angiogenic factor profile defined in Equation (3) requires evaluation at each grid point. This computation is naturally parallel and is implemented by means of a suitable CUDA kernel:The implementation exploits the embarrassingly parallel nature of this computation, with each thread computing a single point of the profile. Memory access is optimized through coalesced read/write operations:This kernel is designed to handle the exponential computation efficiently while maintaining numerical stability through appropriate scaling of the exponent.
- Nonlinear term assembly and evaluation. The parallel implementation of the nonlinear terms represents one of the most complex aspects of the proposed parallel algorithm. Its structure, as defined in Equation (7), requires careful decomposition for parallel evaluation. We implement this through a series of specialized kernels. Each component requires different computational patterns. The component has been implemented as follows:through a combination of cuBLAS matrix-vector operations [27] and custom CUDA kernels for the nonlinear terms. The remaining components:are implemented using vectorized operations in shared memory to minimize global memory access.
- Time integration and solution update. The time integration follows the explicit forward Euler scheme, which requires an implementation to maintain numerical stability in the parallel setting. The update step, in Equation (8), is implemented through a hybrid approach combining cuBLAS operations for the matrix-vector product with custom CUDA kernels for the nonlinear term evaluation. The implementation follows these key steps:
- (a)
- Evaluation of linear terms:
- (b)
- Nonlinear terms computation:
- (c)
- Solution update:
- Kernel launch overhead: In each time step , the original implementation launches four distinct CUDA kernels:Each kernel launch produces a fixed overhead , resulting in a total launch overhead of:
- Matrix operations: Each time step involves the following matrix operations:
- Sparse matrix-vector multiplication: The discrete Laplacian operator is a sparse matrix of dimension with non-zero entries. Each matrix-vector multiplication requires operations.
- Block matrix assembly: The construction of the block matrix in Equation (11) requires operations for each of the four diagonal blocks, resulting in operations total.
- Nonlinear term evaluation: The evaluation of the nonlinear terms in Equation (12) involves the element-wise operations on vectors of length M: operations, and finite difference approximations (applying and ): operations per component.
- Time integration: The explicit Euler step in Equation (8) requires operations for vector addition and scalar multiplication.The computational work per time step is dominated by the matrix-vector operations, which require operations in total.
- Total computational work: Combining the launch overhead and the computational work over N time steps:Therefore, we have the following:
4.1. Performance Optimization
4.2. Implementation Details
nThrx = 25 |
nThry = 25 |
nBlockx = Int32(ceil(4M / nThrx)) |
nBlocky = Int32(ceil(4M / nThry)) |
@cuda threads=(nThrx, nThry) blocks=(nBlockx, nBlocky) A_kernel!(dC, dP, dI, alpha3, k4, k6, T, L, phi, A) |
@cuda threads = (nThr, nThr) blocks = (nBlk, nBlk) PTGL_kernel!(x, epsi0, Lf, h, alpha4, T, L, G, phi) |
function PTGL_kernel!(x, epsi0::Float64, Lf::Float64, h::Float64, |
alpha4::Float64, T, L, G, phi) |
j = threadIdx().x + (blockIdx().x − 1) * blockDim().x |
i = threadIdx().y + (blockIdx().y − 1) * blockDim().y |
M = size(T, 1) |
if i <= M && j <= M |
@inbounds begin |
# Local calculation to avoid synchronization |
Ti = exp(−epsi0^(−1) * (Lf − x[i])^2) |
# A11, L, G, phi, T |
if j == 1 |
T[i] = Ti |
end |
# Remaining calculations for L, G, and phi… |
end |
end |
return nothing |
end |
# Pre-allocate all intermediate arrays |
xhat, term1, term2, term3, term4 = CuArray{Float64}(undef, M), |
CuArray{Float64}(undef, M), |
CuArray{Float64}(undef, M), |
CuArray{Float64}(undef, M), |
CuArray{Float64}(undef, 4M) |
# Reuse the pre-allocated arrays in the time integration loop |
for i in 1:(N-1) |
CUDA.@sync @cuda threads=nThr blocks=nBlk xhat_kernel!(@view(U[:, i]), |
alpha1, alpha2, xhat) |
CUDA.CUBLAS.gemv!(’N’, 1.0, G, xhat, 1.0, term1) |
# … other operations using pre-allocated arrays |
end |
CUDA.CUBLAS.gemv!(’N’, 1.0, G, xhat, 1.0, term1) |
CUDA.CUBLAS.gemv!(’N’, 1.0, G, @view(U[1:M, i]), 1.0, term2) |
CUDA.CUBLAS.gemv!(’N’, 1.0, L, xhat, 1.0, term3) |
CUDA.@sync CUDA.CUBLAS.gemv!(’N’, 1.0, A, @view(U[:, i]), 1.0, term4) |
CUDA.@sync @cuda threads=nThr blocks=nBlk xhat_kernel!(@view(U[:, i]), alpha1, alpha2, xhat) |
5. Results and Discussion
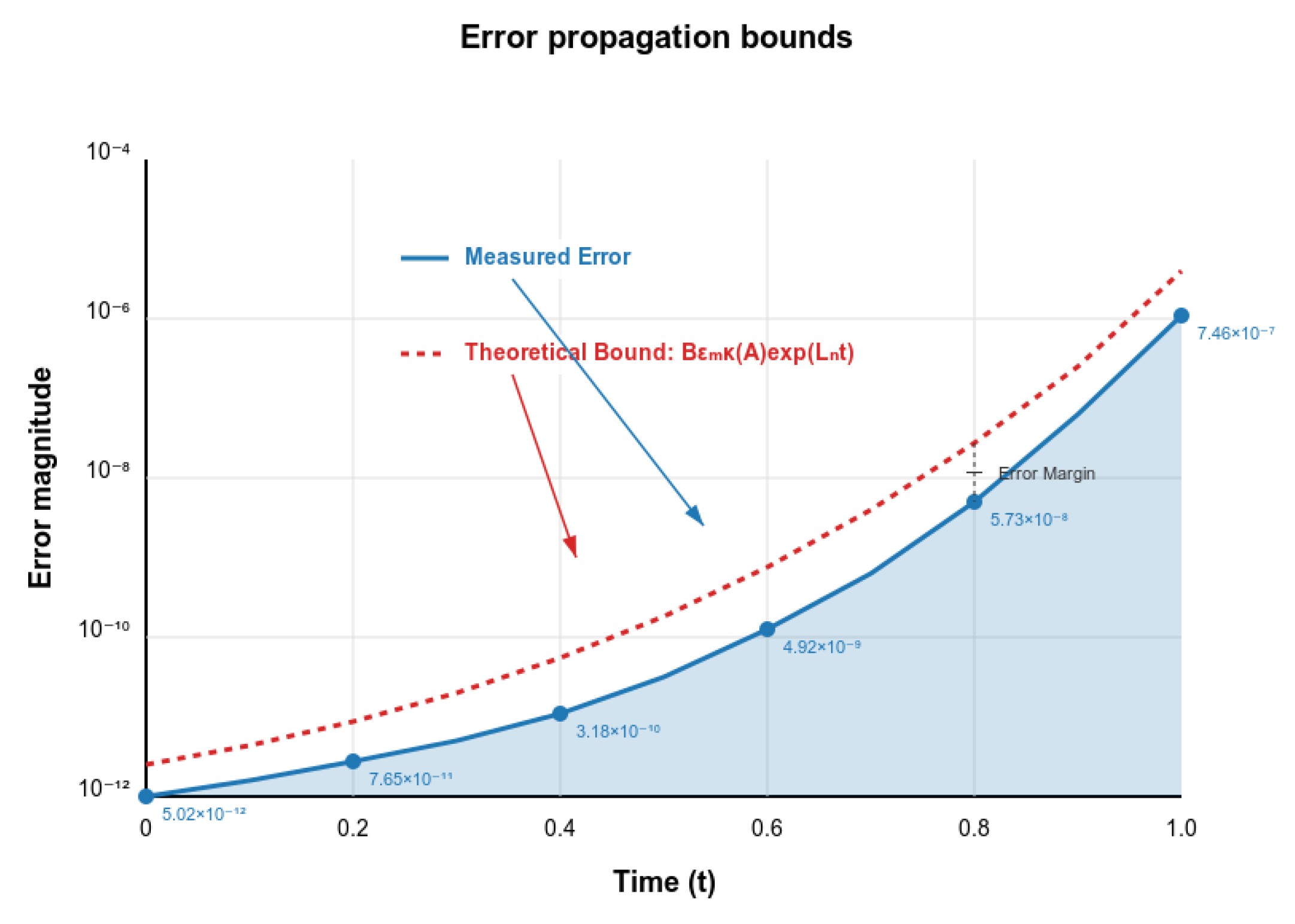
Validation of Theoretical Bounds
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HPC | high-performance computing |
| GPU | graphics processing unit |
| CPU | central processing unit |
| PDE | partial differential equation |
| CUDA | Compute Unified Device Architecture |
| EC | endothelial cell |
| ECM | extracellular matrix |
| TAF | tumor angiogenic factor |
References
- Dongarra, J.; Hittinger, J.; Bell, J.; Chacon, L.; Falgout, R.; Heroux, M.; Hovland, P.; Ng, E.; Webster, C.; Wild, S. Applied Mathematics Research for Exascale Computing; LLNL-TR-651000; Technical Report of the Lawrence Livermore National Lab. LLNL; Lawrence Livermore National Lab. LLNL: Livermore, CA, USA, 2014. [Google Scholar] [CrossRef]
- Chaplain, M.A.J.; Stuart, A.M. A Mathematical Model for the Diffusion of Tumour Angiogenesis Factor into the Surrounding Host Tissue. IMA J. Math. Appl. Med. Biol. 1995, 8, 191–220. [Google Scholar] [CrossRef] [PubMed]
- Anderson, A.R.A.; Chaplain, M.A.J. Continuous and Discrete Mathematical Models of Tumor-induced Angiogenesis. Bull. Math. Biol. 1998, 60, 857–899. [Google Scholar] [CrossRef] [PubMed]
- Bezanson, J.; Edelman, A.; Karpinski, S.; Shah, V.B. Julia: A Fresh Approach to Numerical Computing. SIAM Rev. 2017, 59, 65–98. [Google Scholar] [CrossRef]
- Nickolls, J.; Buck, I.; Garland, M.; Skadron, K. Scalable Parallel Programming with CUDA. Queue 2008, 6, 40–53. [Google Scholar] [CrossRef]
- Conte, D.; De Luca, P.; Galletti, A.; Giunta, G.; Marcellino, L.; Pagano, G.; Paternoster, B. First Experiences on Parallelizing Peer Methods for Numerical Solution of a Vegetation Model. In Proceedings of the International Conference on Computational Science and Its Applications, Malaga, Spain, 4–7 July 2022; Springer International Publishing: Cham, Switzerland, 2022; pp. 384–394. [Google Scholar]
- Fiscale, S.; De Luca, P.; Inno, L.; Marcellino, L.; Galletti, A.; Rotundi, A.; Ciaramella, A.; Covone, G.; Quintana, E. A GPU algorithm for outliers detection in TESS light curves. In Proceedings of the International Conference on Computational Science, Kraków, Poland, 16–18 June 2021; Springer International Publishing: Cham, Switzerland, 2021; pp. 420–432. [Google Scholar]
- De Luca, P.; Galletti, A.; Marcellino, L.; Pianese, M. Exploiting Julia for Parallel RBF-Based 3D Surface Reconstruction: A First Experience. In Proceedings of the 2024 32nd Euromicro International Conference on Parallel, Distributed and Network-Based Processing (PDP), Dublin, Ireland, 20–22 March 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 266–271. [Google Scholar]
- Travasso, R.D.; Poiré, E.C.; Castro, M.; Rodríguez-Manzaneque, J.C.; Hernández-Machado, A. Tumor Angiogenesis and Vascular Patterning: A Mathematical Model. PLoS ONE 2011, 6, e19989. [Google Scholar] [CrossRef]
- Vilanova, G.; Colominas, I.; Gomez, H. A Mathematical Model of Tumour Angiogenesis: Growth, Regression and Regrowth. J. R. Soc. Interface 2017, 14, 20160918. [Google Scholar] [CrossRef] [PubMed]
- Stepanova, D.; Byrne, H.M.; Maini, P.K.; Alarcón, T. A Multiscale Model of Complex Endothelial Cell Dynamics in Early Angiogenesis. PLoS Comput. Biol. 2021, 17, e1008055. [Google Scholar] [CrossRef] [PubMed]
- Mantzaris, N.V.; Webb, S.; Othmer, H.G. Mathematical Modeling of Tumor-induced Angiogenesis. J. Math. Biol. 2004, 49, 111–187. [Google Scholar] [CrossRef] [PubMed]
- Peirce, S.M. Computational and Mathematical Modeling of Angiogenesis. Microcirculation 2008, 15, 739–751. [Google Scholar] [CrossRef] [PubMed]
- Vilanova, G.; Colominas, I.; Gomez, H. Coupling of Discrete Random Walks and Continuous Modeling for Three-Dimensional Tumor-Induced Angiogenesis. Comput. Mech. 2018, 53, 449–464. [Google Scholar] [CrossRef]
- Powathil, G.G.; Gordon, K.E.; Hill, L.A.; Chaplain, M.A.J. Modelling the Effects of Cell-Cycle Heterogeneity on the Response of a Solid Tumour to Chemotherapy: Biological Insights from a Hybrid Multiscale Cellular Automaton Model. J. Theor. Biol. 2012, 308, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Ghaffarizadeh, A.; Heil, R.; Friedman, S.H.; Mumenthaler, S.M.; Macklin, P. PhysiCell: An Open Source Physics-Based Cell Simulator for 3-D Multicellular Systems. PLoS Comput. Biol. 2018, 14, e1005991. [Google Scholar] [CrossRef] [PubMed]
- Rossinelli, D.; Hejazialhosseini, B.; Spampinato, D.G.; Koumoutsakos, P. Multicore/GPU Accelerated Simulations of Multiphase Compressible Flows Using Wavelet Adapted Grids. SIAM J. Sci. Comput. 2011, 33, 512–540. [Google Scholar] [CrossRef]
- Kuckuk, S.; Köstler, H. Automatic Generation of Massively Parallel Codes from ExaSlang. Computation 2018, 6, 41. [Google Scholar] [CrossRef]
- Nugteren, C.; Custers, G.F.F. Algorithmic Species: A Classification of GPU Kernels. ACM Trans. Archit. Code Optim. 2021, 18, 1–25. [Google Scholar]
- Rackauckas, C.; Nie, Q. DifferentialEquations.jl–A Performant and Feature-Rich Ecosystem for Solving Differential Equations in Julia. J. Open Res. Softw. 2017, 5, 15. [Google Scholar] [CrossRef]
- Martinsson, P.G. Fast Direct Solvers for Elliptic PDEs; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2021. [Google Scholar]
- Besard, T.; Foket, C.; De Sutter, B. Effective Extensible Programming: Unleashing Julia on GPUs. IEEE Trans. Parallel Distrib. Syst. 2018, 30, 827–841. [Google Scholar] [CrossRef]
- De Luca, P.; Marcellino, L. Conservation Law Analysis in Numerical Schema for a Tumor Angiogenesis PDE System. Mathematics 2025, 13, 28. [Google Scholar] [CrossRef]
- Kevrekidis, P.G.; Whitaker, N.; Good, D.J. Towards a reduced model for angiogenesis: A hybrid approach. Math. Comput. Model. 2005, 41, 987–996. [Google Scholar] [CrossRef]
- Bellomo, N.; Li, N.K.; Maini, P.K. On the Foundations of Cancer Modelling: Selected Topics, Speculations, and Perspectives. Math. Model. Methods Appl. Sci. 2008, 18, 593–646. [Google Scholar] [CrossRef]
- NVIDIA Corporation. CUDA Toolkit Documentation. NVIDIA. 2024. Available online: https://docs.nvidia.com/cuda/ (accessed on 6 April 2025).
- NVIDIA Corporation. NVIDIA cuBLAS Library. NVIDIA. 2024. Available online: https://docs.nvidia.com/cuda/cublas/index.html (accessed on 6 April 2025).
- Harris, M. Optimizing Parallel Reduction in CUDA. NVIDIA Developer Technology. 2012. Available online: https://developer.download.nvidia.com/assets/cuda/files/reduction.pdf (accessed on 6 April 2025).
- Lorenzo, G.; Scott, M.A.; De Luca, P.; Galletti, A.; Ghehsareh, H.R.; Marcellino, L.; Raei, M. A GPU-CUDA framework for solving a two-dimensional inverse anomalous diffusion problem. In Parallel Computing: Technology Trends; IOS Press: Amsterdam, The Netherlands, 2020; pp. 311–320. [Google Scholar]

| Reference | Mathematical Model | Numerical Method | Implementation | Performance |
|---|---|---|---|---|
| Anderson & Chaplain [3] | Continuous and discrete models | Finite difference, Cellular automaton | Sequential implementation | Baseline |
| Travasso et al. [9] | Phase-field model | Finite difference | C++/OpenMP | 4–8× speedup on multicore |
| Vilanova et al. [10] | Hybrid continuum-discrete | Finite element, Agent-based | C++ | Limited to small domains |
| Ghaffarizadeh et al. [16] | Agent-based model | Cellular automaton | C++/OpenMP | 10–15× speedup on multicore |
| Nugteren & Custers [19] | Optimization taxonomy | Kernel classification | CUDA/C++ | Up to 15× GPU speedup |
| This work | Reaction-diffusion-advection model | Finite difference | Julia/CUDA.jl | Up to 21× GPU speedup with optimized memory management |
| M | N | Sequential | CUDA-V1 | CUDA-V2 |
|---|---|---|---|---|
| 50 | 1510 | 0.234994 | 10.373459 | 6.650091 |
| 100 | 1510 | 0.304203 | 9.785947 | 6.972549 |
| 150 | 1510 | 0.419081 | 10.282258 | 8.561502 |
| M | N | Sequential | CUDA-V1 | CUDA-V2 |
|---|---|---|---|---|
| 50 | 15,100 | 0.362858 | 12.406322 | 8.050883 |
| 100 | 15,100 | 1.374836 | 11.944030 | 8.447822 |
| 150 | 15,100 | 3.118225 | 11.311357 | 8.967368 |
| M | N | Sequential | CUDA-V1 | CUDA-V2 |
|---|---|---|---|---|
| 50 | 151,000 | 38.838768 | 169.094265 | 99.835253 |
| 100 | 151,000 | 96.548160 | 171.512029 | 109.794450 |
| 150 | 151,000 | 256.530769 | 177.381166 | 113.357684 |
| M | Sequential | CUDA-V1 | CUDA-V2 |
|---|---|---|---|
| 150 | 256.530769 | 177.381166 | 113.357684 |
| 200 | 489.873254 | 182.465731 | 117.892456 |
| 250 | 892.156438 | 188.743892 | 122.456789 |
| 300 | 1435.892367 | 195.234567 | 128.345678 |
| 400 | 2876.234589 | 208.567891 | 135.678912 |
| Metric | Sequential | CUDA-V1 | CUDA-V2 |
|---|---|---|---|
| CPU Allocations | 40.77 M | 421.43 M | 228.27 M |
| Memory Usage | 98.536 GiB | 10.834 GiB | 4.918 GiB |
| GC Time | 1.18% | 4.37% | 1.42% |
| GPU Allocations | - | 15.10 M | 12 |
| GPU Memory | - | 33.754 GiB | 6.753 GiB |
| Memory Management Time | - | 20.52% | 0.03% |
| M | N | Sequential | CUDA-V1 | CUDA-V2 | Acceleration | Standard Deviation (%) |
|---|---|---|---|---|---|---|
| 50 | 1510 | 0.234 ± 0.011 | 10.373 ± 0.452 | 6.650 ± 0.128 | 0.035 | 1.92 |
| 100 | 1510 | 0.304 ± 0.015 | 9.786 ± 0.391 | 6.973 ± 0.142 | 0.044 | 2.04 |
| 150 | 1510 | 0.419 ± 0.023 | 10.282 ± 0.419 | 8.562 ± 0.196 | 0.049 | 2.29 |
| 50 | 15,100 | 0.363 ± 0.018 | 12.406 ± 0.587 | 8.051 ± 0.237 | 0.045 | 2.94 |
| 100 | 15,100 | 1.375 ± 0.056 | 11.944 ± 0.521 | 8.448 ± 0.219 | 0.163 | 2.59 |
| 150 | 15,100 | 3.118 ± 0.108 | 11.311 ± 0.483 | 8.967 ± 0.268 | 0.348 | 2.99 |
| 50 | 151,000 | 38.839 ± 0.596 | 169.094 ± 2.963 | 99.835 ± 1.742 | 0.389 | 1.74 |
| 100 | 151,000 | 96.548 ± 1.217 | 171.512 ± 3.124 | 109.794 ± 1.895 | 0.879 | 1.73 |
| 150 | 151,000 | 256.531 ± 2.871 | 177.381 ± 3.305 | 113.358 ± 2.063 | 2.263 | 1.82 |
| 150 | 151,000 | 256.531 ± 2.871 | 177.381 ± 3.305 | 113.358 ± 2.063 | 2.263 | 1.82 |
| 200 | 151,000 | 489.873 ± 4.532 | 182.466 ± 3.418 | 117.892 ± 2.179 | 4.155 | 1.85 |
| 250 | 151,000 | 892.156 ± 7.458 | 188.744 ± 3.519 | 122.457 ± 2.352 | 7.285 | 1.92 |
| 300 | 151,000 | 1435.892 ± 11.621 | 195.235 ± 3.758 | 128.346 ± 2.487 | 11.189 | 1.94 |
| 400 | 151,000 | 2876.235 ± 21.935 | 208.568 ± 4.125 | 135.679 ± 2.653 | 21.198 | 1.96 |
| M | Sequential (Seconds) | CUDA-V2 (Seconds) | Acceleration Factor |
|---|---|---|---|
| 50 | 38.84 ± 0.59 | 99.84 ± 1.74 | 0.39 |
| 100 | 96.55 ± 1.22 | 109.79 ± 1.90 | 0.88 |
| 150 | 256.53 ± 2.87 | 113.36 ± 2.06 | 2.26 |
| 200 | 489.87 ± 4.53 | 117.89 ± 2.18 | 4.16 |
| 250 | 892.16 ± 7.46 | 122.46 ± 2.35 | 7.29 |
| 300 | 1435.89 ± 11.62 | 128.35 ± 2.49 | 11.19 |
| 400 | 2876.23 ± 21.94 | 135.68 ± 2.65 | 21.20 |
| M | Measured | Theoretical |
|---|---|---|
| 50 | 2.48 × 103 | 2.50 × 103 |
| 100 | 9.93 × 103 | 1.00 × 104 |
| 150 | 2.24 × 104 | 2.25 × 104 |
| 200 | 3.96 × 104 | 4.00 × 104 |
| M | Measured | Theoretical Bound |
|---|---|---|
| 50 | 4.27 × 102 | 4.37 × 102 |
| 100 | 1.67 × 103 | 1.71 × 103 |
| 150 | 3.74 × 103 | 3.84 × 103 |
| 200 | 6.63 × 103 | 6.82 × 103 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciaramella, A.; De Angelis, D.; De Luca, P.; Marcellino, L. Accelerated Numerical Simulations of a Reaction-Diffusion- Advection Model Using Julia-CUDA. Mathematics 2025, 13, 1488. https://doi.org/10.3390/math13091488
Ciaramella A, De Angelis D, De Luca P, Marcellino L. Accelerated Numerical Simulations of a Reaction-Diffusion- Advection Model Using Julia-CUDA. Mathematics. 2025; 13(9):1488. https://doi.org/10.3390/math13091488
Chicago/Turabian StyleCiaramella, Angelo, Davide De Angelis, Pasquale De Luca, and Livia Marcellino. 2025. "Accelerated Numerical Simulations of a Reaction-Diffusion- Advection Model Using Julia-CUDA" Mathematics 13, no. 9: 1488. https://doi.org/10.3390/math13091488
APA StyleCiaramella, A., De Angelis, D., De Luca, P., & Marcellino, L. (2025). Accelerated Numerical Simulations of a Reaction-Diffusion- Advection Model Using Julia-CUDA. Mathematics, 13(9), 1488. https://doi.org/10.3390/math13091488








